Как найти любое число геометрической прогрессии

Числовая последовательность

Если ты уже читал тему «Арифметическая прогрессия» ты можешь смело пропускать этот блок и переходить к самой сути.

Если нет, то советую ознакомиться, чтобы иметь общее представление о том, что такое прогрессия в целом и с чем ее едят.

Итак, сядем и начнем писать какие-нибудь числа. Например: ( displaystyle 4,text{ }7,text{ }-8,text{ }13,text{ }-5,text{ }-6,text{ }0,text{ }ldots )

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их ( displaystyle 7)).

Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать. Это и есть пример числовой последовательности:

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и ( displaystyle n)-ное число) всегда одно.

Число с номером ( displaystyle n) называетмя ( displaystyle n)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, ( displaystyle a)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: ( displaystyle {{a}_{1}},text{ }{{a}_{2}},text{ }…,text{ }{{a}_{10}},text{ }…,text{ }{{a}_{n}}).

В нашем случае:

Самые распространенные виды прогрессии это арифметическая и геометрическая. В этой теме мы поговорим о втором виде – геометрической прогрессии.

Ограничения геометрической прогрессии

Первый член {( displaystyle {{b}_{1}})} не равен ( displaystyle 0) и ( displaystyle mathbf{q}text{ }ne text{ }0).

Эти ограничения не случайны!

Допустим, что их нет, и первый член прогрессии все же равен ( displaystyle 0), а q равно, хм.. пусть ( displaystyle 2), тогда получается:

( displaystyle {{b}_{1}}=0)

( displaystyle {{b}_{1}}=0cdot 2=0…) и так далее.

Согласись, что это уже никакая не прогрессия.

Как ты понимаешь, те же самые результаты мы получим, если ( displaystyle {{b}_{1}}) будет каким-либо числом, отличным от нуля, а ( displaystyle q=0).

В этих случаях прогрессии просто не будет, так как весь числовой ряд будут либо все нули, либо одно число, а все остальные нули.

Теперь поговорим поподробнее о знаменателе геометрической прогрессии, то есть о ( displaystyle q).

Знаменатель геометрической прогрессии

Повторим: ( displaystyle q) – это число, во сколько раз изменяется каждый последующий член геометрической прогрессии.

Как ты думаешь, каким может быть ( displaystyle q)? Правильно, положительным и отрицательным, но не нулем (мы говорили об этом чуть выше).

Допустим, что ( displaystyle q) у нас положительное. Пусть в нашем случае ( displaystyle q=3), а ( displaystyle {{b}_{1}}=4).

Чему равен второй член ( displaystyle {{b}_{2}}) и ( displaystyle {{b}_{3}})? Ты без труда ответишь, что:

( displaystyle {{b}_{2}}=4cdot 3=12)

( displaystyle {{b}_{3}}=12cdot 3=36)

Все верно. Соответственно, если ( displaystyle q>0), то все последующие члены прогрессии имеют одинаковый знак – они положительны.

А что если ( displaystyle q) отрицательное? Например, ( displaystyle q=-3), а ( displaystyle {{b}_{1}}=4). Чему равен второй член ( displaystyle {{b}_{2}}) и ( displaystyle {{b}_{3}})?

Это уже совсем другая история

( displaystyle {{b}_{2}}=4cdot -3=-12)

( displaystyle {{b}_{3}}=-12cdot left( -3 right)=36)

Попробуй посчитать ( displaystyle 4) член данной прогрессии. Сколько у тебя получилось? У меня ( displaystyle -108).

Таким образом, если ( displaystyle q<0), то знаки членов геометрической прогрессии чередуются.

То есть, если ты увидишь прогрессию, с чередующимися знаками у ее членов, значит ее знаменатель на ( displaystyle 100%) отрицательный.

Это знание может помочь тебе проверять себя при решении задач на эту тему.

Теперь немного потренируемся:

Пример 1. Попробуй определить, какие числовые последовательности являются геометрической прогрессией, а какие арифметической:

• ( displaystyle 3;text{ }6;text{ }12;text{ }24;text{ }48;text{ }56ldots )
• ( displaystyle 1;text{ }12;text{ }23;text{ }34;text{ }45text{ }ldots )
• ( displaystyle -99;text{ }33;text{ }-11ldots )
• ( displaystyle 5;text{ }7;text{ }9;text{ }11;text{ }13ldots ) 
• ( displaystyle -6;text{ }5;text{ }17;text{ }28;text{ }39ldots ) 
• ( displaystyle 64;text{ }16;text{ }4;text{ }1ldots ) 
• ( displaystyle 2;text{ }4;text{ }8;text{ }18ldots )

Разобрался? Сравним наши ответы:

• Геометрическая прогрессия – 3, 6.
• Арифметическая прогрессия – 2, 4.
• Не является ни арифметической, ни геометрической прогрессиями — 1, 5, 7.

Пример 2. Найти 6-й член прогрессии

Вернемся к нашей последней прогрессии ( displaystyle q=-3), а ( displaystyle {{b}_{1}}=4) и попробуем так же как и в арифметической найти ее ( displaystyle 6) член.

Как ты уже догадываешься, есть два способа его нахождения:

1-й способ. Последовательно умножаем каждый член на ( displaystyle q).

• ( displaystyle {{b}_{1}}=4)
• ( displaystyle {{b}_{2}}=4cdot left( -3 right)=-12)
• ( displaystyle {{b}_{3}}=-12cdot left( -3 right)=36)
• ( displaystyle {{b}_{4}}=36cdot left( -3 right)=-108)
• ( displaystyle {{b}_{5}}=-108cdot left( -3 right)=324)
• ( displaystyle {{b}_{6}}=324cdot left( -3 right)=-972)

Итак, ( displaystyle 6)-ой член описанной геометрической прогрессии равен ( displaystyle -972).

2-й способ. По формуле, которая поможет найти тебе любой член геометрической прогрессии.

( displaystyle {{b}_{6}}={{b}_{1}}cdot q{{ }^{6-1}})

Если нам нужно найти значение числа прогрессии с порядковым номером, то мы умножаем первый член геометрической прогрессии ( displaystyle {{b}_{1}}) на знаменатель ( displaystyle q) в степени, которая на ( displaystyle 1) единицу меньше, чем порядковый номер искомого числа.

( displaystyle {{b}_{6}}=4cdot {{left( -3 right)}^{6-1}}=4cdot {{left( -3 right)}^{5}}=-972)

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}}) — уравнение членов геометрической прогрессии, где

• n — порядковый номер члена прогрессии;
• b1 — первый член прогрессии;
• q — знаменатель.

Данная формула верна для всех значений — как положительных, так и отрицательных.

Как найти член геометрической прогрессии, зная два соседних. Формула в общем виде:

( displaystyle {{b}_{n}}=sqrt{{{b}_{n+1}}cdot {{b}_{n-1}}} ), при ( displaystyle n>2)

Не забывай про условие при ( displaystyle n>2)?

Подумай, почему оно важно, например, попробуй самостоятельно просчитать ( displaystyle {{b}_{n}} ), при ( displaystyle n=1). Что получится в этом случае?

Правильно, полная глупость так как формула выглядит так:

( displaystyle {{b}_{1}}=sqrt{{{b}_{1+1}}cdot {{b}_{1-1}}} )

Соответственно, не забывай это ограничение.

Возьмем, к примеру, простую геометрическую прогрессию, в которой нам известны ( displaystyle {{b}_{2}}=6) и ( displaystyle {{b}_{4}}=54).

И посчитаем, чему же равно ( displaystyle {{b}_{3}})

( displaystyle {{b}_{3}}=sqrt{6cdot 54}=sqrt{324}=…)

Правильный ответ – ( displaystyle {{b}_{3}}=pm 18)!

Теперь, когда ты усвоил основные моменты и вывел формулу на свойство геометрической прогрессии, найди ( displaystyle {{b}_{n}} ), зная ( displaystyle {{b}_{n+1}}) и ( displaystyle {{b}_{n-1}})

• ( displaystyle {{b}_{n+1}}=4), ( displaystyle {{b}_{n-1}}=36)
• ( displaystyle {{b}_{n+1}}=-3), ( displaystyle {{b}_{n-1}}=-12)
• ( displaystyle {{b}_{n+1}}=-2), ( displaystyle {{b}_{n-1}}=-32)

Сравни полученные ответы с правильными:

• ( displaystyle {{b}_{n}}=pm 12 )
• ( displaystyle {{b}_{n}}=pm 6 )
• ( displaystyle {{b}_{n}}=pm 8 )

Как найти равноудаленные члены геометрической прогрессии

Как ты думаешь, а если нам были бы даны не соседние с искомым числом значения членов геометрической прогрессии, а равноудаленные от него.

Например, нам необходимо найти ( displaystyle {{b}_{3}} ), а даны ( displaystyle {{b}_{1}} ) и ( displaystyle {{b}_{5}} ). Можем ли мы в этом случае использовать выведенную нами формулу?

Да! Формула работает не только при соседствующих с искомым членах геометрической прогрессии, но и с равноудаленными от искомого членами.

И она приобретает вид:

( displaystyle {{b}_{n}}=sqrt{{{b}_{n+k}}cdot {{b}_{n-k}}} ), при ( displaystyle k<n, kin N)

То есть, если в первом случае мы говорили, что ( displaystyle k=1), то сейчас мы говорим, что ( displaystyle k) может быть равен любому натуральному числу, которое меньше ( displaystyle n).

Главное, чтобы ( displaystyle k) был одинаков для обоих заданных чисел.

Потренируйся на конкретных примерах, только будь предельно внимателен!

Как найти неравноудаленные члены геометрической прогрессии

На самом деле это не так сложно, как кажется! Давай с тобой распишем, из чего состоит каждое данное нам и искомое числа.

( displaystyle {{b}_{3}}={{b}_{1}}cdot {{q}^{2}} )

( displaystyle {{b}_{6}}={{b}_{5}}cdot q={{b}_{1}}cdot {{q}^{5}} )

( displaystyle {{b}_{4}}={{b}_{3}}cdot q={{b}_{1}}cdot {{q}^{3}})

Итак, у нас есть ( displaystyle {{b}_{3}}) и ( displaystyle {{b}_{6}}). Посмотрим, что с ними можно сделать?

Предлагаю разделить ( displaystyle {{b}_{6}}) на ( displaystyle {{b}_{3}}). Получаем:

( displaystyle frac{{{b}_{6}}}{{{b}_{3}}}=frac{{{b}_{1}}cdot {{q}^{5}}}{{{b}_{1}}cdot {{q}^{2}}}={{q}^{3}})

Подставляем в формулу наши данные:

( displaystyle frac{{{b}_{6}}}{{{b}_{3}}}=frac{486}{18}=27)

Следующим шагом мы можем найти ( displaystyle q) – для этого нам необходимо взять кубический корень из полученного числа.

( displaystyle {{q}^{3}}=27 Rightarrow q=sqrt[3]{27}=3)

А теперь смотрим еще раз что у нас есть. У нас есть ( displaystyle {{b}_{3}}), а найти нам необходимо ( displaystyle {{b}_{4}}), а он, в свою очередь равен:

( displaystyle {{b}_{4}}={{b}_{3}}cdot q)

Все необходимые данные для подсчета мы нашли. Подставляем в формулу:

( displaystyle {{b}_{4}}=18cdot 3=54)

Наш ответ: ( displaystyle 54).

Попробуй решить еще одну такую же задачу самостоятельно:

Дано: ( displaystyle {{b}_{3}}=18), ( displaystyle {{b}_{5}}=648)
Найти: ( displaystyle {{b}_{2}})

Сколько у тебя получилось? У меня:

Получим:

( displaystyle {{S}_{n}}q={{b}_{1}}q+{{b}_{2}}q+{{b}_{3}}q+…+{{b}_{n-2}}q+{{b}_{n-1}}q+{{b}_{n}}q)

Посмотри внимательно: что общего в последних двух формулах? Правильно, общие члены, например ( displaystyle {{b}_{2}}={{b}_{1}}q) и так далее, кроме первого и последнего члена. Давай попробуем вычесть из 2-го уравнения 1-ое.

Что у тебя получилось?

( displaystyle {{S}_{n}}q-{{S}_{n}}={{b}_{n}}q-{{b}_{1}})

Теперь вырази ( displaystyle {{b}_{n}}) через формулу члена геометрической прогрессии и подставь полученное выражение в нашу последнюю формулу:

( displaystyle {{S}_{n}}q-{{S}_{n}}={{b}_{1}}{{q}^{n-1}}q-{{b}_{1}}={{b}_{1}}{{q}^{n}}-{{b}_{1}})

Сгруппируй выражение. У тебя должно получиться:

( displaystyle {{S}_{n}}(q-1)={{b}_{1}}({{q}^{n}}-1))

Все, что осталось сделать – выразить ( displaystyle {{S}_{n}}):

( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1}) или ( displaystyle {{S}_{n}}=frac{{{b}_{1}}(1-{{q}^{n}})}{1-q})

Соответственно, в этом случае ( displaystyle qne 1).

А что если ( displaystyle q=1)? Какая формула работает тогда? Представь себе геометрическую прогрессию при ( displaystyle q=1). Что она из себя представляет?

Правильно ряд одинаковых чисел, соответственно формула будет выглядеть следующим образом:

( displaystyle {{S}_{n}}=n{{b}_{1}})

Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из ( displaystyle 5) членов.

Допустим, ( displaystyle {{b}_{1}}=1), а ( displaystyle q=frac{1}{2}), тогда:

• ( displaystyle {{b}_{2}}=1cdot frac{1}{2}=frac{1}{2})
• ( displaystyle {{b}_{3}}=frac{1}{2}cdot frac{1}{2}=frac{1}{4})
• ( displaystyle {{b}_{4}}=frac{1}{4}cdot frac{1}{2}=frac{1}{8})
• ( displaystyle {{b}_{5}}=frac{1}{8}cdot frac{1}{2}=frac{1}{16})

Мы видим, что каждый последующий член меньше предыдущего в ( displaystyle frac{1}{2}) раза, но будет ли какое-либо число ( displaystyle {{b}_{n}}=0)?

Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.

Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула ( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}}) приобретает следующий вид:

( displaystyle {{b}_{n}}=1cdot {{left( frac{1}{2} right)}^{n-1}}={{left( frac{1}{2} right)}^{n-1}})

На графиках нам привычно строить зависимость ( displaystyle x) от ( displaystyle y), поэтому:

( displaystyle {{b}_{n}}=y(x)),
( displaystyle {{left( frac{1}{2} right)}^{n-1}}={{left( frac{1}{2} right)}^{x-1}})

Суть выражения не изменилась.

В первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера.

А во второй записи – мы просто приняли значение члена геометрической прогрессии за ( displaystyle y), а порядковый номер обозначили не как ( displaystyle n), а как ( displaystyle x).

Все, что осталось сделать – построить график. Посмотрим, что у тебя получилось. Вот какой график получился у меня:

Видишь?

Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая.

Отметим на графике наши точки, а заодно и то, что обозначает координата ( displaystyle x) и ( displaystyle y):

Попробуй схематично изобразить график геометрической прогрессии при ( displaystyle q=2), если первый ее член также равен ( displaystyle 1).

Проанализируй, в чем разница с нашим предыдущим графиком?

Справился? Вот какой график получился у меня:

Сумма членов бесконечно убывающей геометрической прогрессии

Итак, для начала посмотрим еще раз на вот этот рисунок бесконечно убывающей геометрической прогрессии из нашего примера:

А теперь посмотрим на формулу суммы геометрической прогрессии, выведенную чуть ранее:

( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1}) или ( displaystyle {{S}_{n}}=frac{{{b}_{1}}(1-{{q}^{n}})}{1-q})

К чему у нас стремится ( displaystyle {{q}^{n}})? Правильно, на графике видно, что оно стремится к нулю.

То есть при ( displaystyle nto infty ), ( displaystyle {{q}^{n}}) будет почти равно ( displaystyle 0), соответственно, при вычислении выражения ( displaystyle 1-{{q}^{n}}) мы получим почти ( displaystyle 1).

В связи с этим, мы считаем, что при подсчете суммы бесконечно убывающей геометрической прогрессии, данной скобкой можно пренебречь, так как она будет равна ( displaystyle 1).

История возникновения геометрической прогрессии

Еще в древности итальянский математик Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли.

Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар?

В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: ( displaystyle 1,text{ }2,text{ }4,text{ }8,text{ }16…)

Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие.

Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?

В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк под сложные проценты, или при оценке скорости распространения гриппа (или коронавируса), или при… создании финансовых пирамид!

Интересно? Давай разбираться.

Как быстро Вася заразит весь класс гриппом

Ученик 5 А класса Вася, заболел гриппом, но продолжает ходить в школу. Каждый день Вася заражает двух человек, которые, в свою очередь, заражают еще двух человек и так далее. Всего в классе ( displaystyle 31) человек.

Через сколько дней гриппом будет болеть весь класс?

Решение:

Итак, первый член геометрической прогрессии это Вася, то есть ( displaystyle 1) человек. ( displaystyle 2)-ой член геометрической прогрессии, это те два человека, которых он заразил в первый день своего прихода.

Общая сумма членов прогрессии равна количеству учащихся 5А.

Соответственно, мы говорим о прогрессии, в которой:

( displaystyle begin{array}{l}{{b}_{1}}=1\q=2\{{S}_{n}}=31end{array})

Подставим наши данные в формулу суммы членов геометрической прогрессии:

( displaystyle {{S}_{n}}=frac{{{b}_{1}}({{q}^{n}}-1)}{q-1})

( displaystyle 31=frac{1({{2}^{n}}-1)}{2-1}={{2}^{n}}-1)

( displaystyle begin{array}{l}{{2}^{n}}=31+1\{{2}^{n}}=32\{{2}^{n}}={{2}^{5}}\n=5end{array})

Весь класс заболеет за ( displaystyle 5) дней. Не веришь формулам и числам? Попробуй изобразить «заражение» учеников самостоятельно. Получилось?

Посчитай самостоятельно, за сколько дней ученики заболели бы гриппом, если каждый заражал бы по ( displaystyle 3) человека, а в классе училось ( displaystyle 26) человек.

Какое значение у тебя получилось? У меня получилось, что все начали болеть спустя ( displaystyle 3) дня.

Как ты видишь, подобная задача и рисунок к ней напоминает пирамиду, в которой каждый последующий «приводит» новых людей. Однако, рано или поздно настает такой момент, когда последние не могут никого привлечь.

В нашем случае, если представить, что класс изолирован, ( displaystyle 16) человек из ( displaystyle 31) замыкают цепочку (( displaystyle 51,6%)).

Таким образом, если бы ( displaystyle 31) человек были вовлечены в финансовую пирамиду, в которой деньги давались в случае, если ты приведешь двух других участников, то ( displaystyle 16) человек (( displaystyle {{b}_{5}}={{b}_{1}}{{q}^{4}}) или в общем случае ( displaystyle {{b}_{n}}={{b}_{1}}{{q}^{n}})) не привели бы никого, соответственно, потеряли бы все, что вложили в эту финансовую аферу.

Все, что было сказано выше, относится к убывающей или возрастающей геометрической прогрессии, но, как ты помнишь, у нас есть особый вид – бесконечно убывающая геометрическая прогрессия.

Как же считать сумму ее членов? И почему у данного вида прогрессии есть определенные особенности? Давай разбираться вместе.

Легенда о Сете, создателе шахмат

Узнав, что она изобретена одним из его подданных, царь решил лично наградить его. Он вызвал изобретателя к себе и приказал просить у него все, что он пожелает, пообещав исполнить даже самое искусное желание.

Сета попросил время на размышления, а когда на другой день Сета явился к царю, он удивил царя беспримерной скромностью своей просьбы. Он попросил выдать за первую клетку шахматной доски ( displaystyle 1) пшеничное зерно, за вторую ( displaystyle 2) пшеничных зерна, за третью ( displaystyle -4), за четвертую ( displaystyle -8) и т.д.

Царь разгневался, и прогнал Сета, сказав, что просьба слуги недостойна царской щедрости, но пообещал, что слуга получит свои зерна за все ( displaystyle 64) клетки доски.

А теперь вопрос: используя формулу суммы членов геометрической прогрессии, посчитай, сколько зерен должен получить Сета?

Начнем рассуждать.

Так как по условию за первую клетку шахматной доски Сета попросил ( displaystyle 1) пшеничное зерно, за вторую ( displaystyle 2), за третью ( displaystyle -4), за четвертую ( displaystyle -8) и т.д., то мы видим, что в задаче речь идет о геометрической прогрессии.

Чему равно ( displaystyle q) в этом случае? Правильно.

( displaystyle q=frac{2}{1}=frac{4}{2}=frac{8}{4}=2)

Всего клеток шахматной доски ( displaystyle 64). Соответственно, ( displaystyle n=64).

Все данные у нас есть, осталось только подставить в формулу и посчитать.

( displaystyle {{S}_{n}}=frac{1({{2}^{64}}-1)}{2-1}={{2}^{64}}-1)

Чтобы представить хотя бы приблизительно «масштабы» данного числа, преобразуем ( displaystyle {{2}^{64}}), используя свойства степени:

( displaystyle {{2}^{64}}={{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{10}}cdot {{2}^{4}})

Раскроем далее значения ( displaystyle {{2}^{10}}) и ( displaystyle {{2}^{4}}). Как ты знаешь, ( displaystyle {{2}^{10}}=1024), а ( displaystyle {{2}^{4}}=64).

Подставим данное значение в предыдущее выражение:

( displaystyle {{2}^{64}}=1024cdot 1024cdot 1024cdot 1024cdot 1024cdot 1024cdot 64)

Конечно, если ты хочешь, то можешь взять калькулятор и посчитать, что за число в итоге у тебя получится, а если нет, придется поверить мне на слово: итоговым значением выражения будет ( displaystyle 18~ 446~ 744~ 073~ 709~ 551~ 615).

То есть:

( displaystyle 18) квинтильонов ( displaystyle 446) квадрильонов ( displaystyle 744) триллиона ( displaystyle 73) миллиарда ( displaystyle 709) миллионов ( displaystyle 551) тысяч ( displaystyle 615).

Фух) Если желаете представить себе огромность этого числа, то прикиньте, какой величины амбар потребовался бы для вмещения всего количества зерна.

При высоте амбара ( displaystyle 4) м и ширине ( displaystyle 10) м длина его должна была бы простираться на ( displaystyle 300text{ }000text{ }000) км, — т.е. вдвое дальше, чем от Земли до Солнца.

Если бы царь был бы силен в математике, то он мог бы предложить самому ученому отсчитывать зерна, ведь чтобы отсчитать миллион зерен, ему бы понадобилось не менее ( displaystyle 10) суток неустанного счета, а учитывая, что необходимо отсчитать ( displaystyle 18) квинтильонов, зерна пришлось бы отсчитывать всю жизнь.

Задачи на вычисление сложных процентов

Ты наверняка слышал о так называемой формуле сложных процентов. Понимаешь ли ты, что она значит? Если нет, давай разбираться, так как осознав сам процесс, ты сразу поймешь, причем здесь геометрическая прогрессия.

Все мы ходим в банк и знаем, что существуют разные условия по вкладам: это и срок, и дополнительное обслуживание, и процент с двумя различными способами его начисления – простым и сложным.

С простыми процентами все более или менее понятно: проценты начисляются один раз в конце срока вклада.

То есть, если мы говорим о том, что мы кладем 100 рублей на год под ( displaystyle 10%), то ( displaystyle 10%) зачислятся только в конце года.

Соответственно, к окончанию вклада мы получим ( displaystyle 110) рублей.

Сложные проценты — это такой вариант, при котором происходит капитализация процентов, т.е. их причисление к сумме вклада и последующий расчет дохода не от первоначальной, а от накопленной суммы вклада.

Капитализация происходит не постоянно, а с некоторой периодичностью. Как правило, такие периоды равны и чаще всего банки используют месяц, квартал или год.

Допустим, что мы кладем все те же ( displaystyle 100) рублей по ( displaystyle 10%) годовых, но с ежемесячной капитализацией вклада. Что у нас получается?

( displaystyle 1) месяц — ( displaystyle 100cdot left( 1+frac{10}{100cdot 12} right))

Все ли тебе здесь понятно? Если нет, давай разбираться поэтапно.

Мы принесли в банк ( displaystyle 100) рублей. К концу месяца у нас на счете должна появиться сумма, состоящая из наших ( displaystyle 100) рублей плюс процентов по ним, то есть:

Мы можем вынести ( displaystyle 100) за скобку и тогда мы получим:

( displaystyle 100+100cdot x%=100cdot left( 1+x% right))

Согласись, эта формула уже больше похожа на написанную нами в начале. Осталось разобраться с процентами

В условии задачи нам сказано про ( displaystyle 10%) годовых. Как ты знаешь, мы не умножаем ( displaystyle 100) на ( displaystyle 10) – мы переводим проценты в десятичные дроби, то есть:

( displaystyle 10%=frac{10}{100})

Верно? Сейчас ты спросишь, а откуда взялось число ( displaystyle 12)? Очень просто!

Повторюсь: в условии задачи сказано про ГОДОВЫЕ проценты, начисление которых происходит ЕЖЕМЕСЯЧНО.

Как ты знаешь, в году ( displaystyle 12) месяцев, соответственно, банк будет начислять нам в месяц ( displaystyle 12) часть от годовых процентов:

( displaystyle 10% ежегодно =frac{10}{100cdot 12} ежемесячно)

Осознал? А теперь попробуй написать, как будет выглядеть эта часть формулы, если я скажу, что проценты начисляются ежедневно.

Справился? Давай сравним результаты:

( displaystyle 10% ежегодно =frac{10}{100cdot 365} ежедневно)

Молодец!

Вернемся к нашей задаче: напиши, сколько будет начислено на наш счет на второй месяц, с учетом, что проценты начисляются на накопленную сумму вклада.

Вот, что получилось у меня:

( displaystyle 100cdot left( 1+frac{10}{100cdot 12} right)cdot left( 1+frac{10}{100cdot 12} right))

Я думаю, что ты уже заметил закономерность и увидел во всем этом геометрическую прогрессию.

Напиши, чему будет равен ее ( displaystyle 12) член, или, иными словами, какую сумму денежных средств мы получим в конце ( displaystyle 12) месяца.

Сделал? Проверяем!

Еще один тип задач на сложные проценты (о прибыли)

Компания «Звезда» начала инвестировать в отрасль в 2000 году, имея капитал ( displaystyle 5000) долларов. Каждый год, начиная с 2001 года, она получает прибыль, которая составляет ( displaystyle 100%) от капитала предыдущего года.

Сколько прибыли получит компания «Звезда» по окончанию 2003 года, если прибыль из оборота не изымалась?

Думаю, ты уже знаешь, как и что считать, но на всякий случай распишу подробно:

( displaystyle {{b}_{1}}=5000) — капитал компании «Звезда» в 2000 году.
( displaystyle {{b}_{2}}=5000cdot left( 1+frac{100%}{100} right)=5000cdot left( 1+1 right)=5000cdot 2=10000) — капитал компании «Звезда» в 2001 году.
( displaystyle {{b}_{3}}=5000cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)=5000cdot 4=20000) — капитал компании «Звезда» в 2002 году.
( displaystyle {{b}_{4}}=5000cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)cdot left( 1+frac{100%}{100} right)=5000cdot 8=40000) — капитал компании «Звезда» в 2003 году.

Либо мы можем написать кратко:

( displaystyle {{b}_{n}}={{b}_{1}}cdot q{{ }^{n-1}})

Для нашего случая:

( displaystyle {{b}_{1}}=5000)

( displaystyle n=4) — 2000 год, 2001 год, 2002 год и 2003 год.
( displaystyle q =2) — увеличивается на 100%, то есть в 2 раза.

Соответственно:

( displaystyle {{b}_{2003 года}}=5000cdot 2{{ }^{4-1}}=5000cdot {{2}^{3}}=5000cdot 8=40000) рублей

Заметь, в данной задаче у нас нет деления ни на ( displaystyle 12), ни на ( displaystyle 365), так как процент дан ЕЖЕГОДНЫЙ и начисляется он ЕЖЕГОДНО.

То есть, читая задачу на сложные проценты, обрати внимание, какой процент дан, и в какой период он начисляется, и только потом приступай к вычислениям.

Теперь ты знаешь о геометрической прогрессии все.

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

Экономические задачи на вклады очень часто требуют знания геометрической прогрессии.

Эти задачи требуют также очень подробного и чёткого описания решения.

По сути, мы составляем математическую модель какой-то жизненной ситуации (например, связанной с банковскими вкладами или кредитами), и важно научиться ничего не пропускать при описании этой модели: описывать словами все введённые обозначения, обосновывать уравнения, которые мы записываем, и всё в таком духе.

Если не написать эти объяснения, вы гарантированно получите 0 баллов даже за правильно найденный ответ!

В этом видео мы узнаем, как работают вклады, научимся решать и, главное, правильно оформлять решение таких задач.

ЕГЭ №17. Экономическая задача. Вклады

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…)  Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по  формуле:

Осталось выполнить нужные действия с десятичными дробями:

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 декабря 2022 года; проверки требуют 37 правок.

У этого термина существуют и другие значения, см. Прогрессия.

Геометри́ческая прогре́ссия — последовательность чисел , , , (члены прогрессии), в которой каждое последующее число, начиная со второго, получается из предыдущего члена умножением его на фиксированное число (знаменатель прогрессии). При этом ^[1].

Геометрическая прогрессия называется бесконечно убывающей^[2], если знаменатель прогрессии по абсолютной величине меньше единицы.

Произведением первых членов геометрической прогрессии называется произведение от до , то есть выражение вида
Обозначение: .

Описание[править | править код]

Любой член геометрической прогрессии может быть вычислен по формуле

Если и , прогрессия является возрастающей последовательностью, если , — убывающей последовательностью, а при  — знакочередующейся^[3], при  — стационарной (постоянной).

Своё название прогрессия получила по своему характеристическому свойству:

то есть модуль любого члена геометрической прогрессии, кроме первого, равен среднему геометрическому (среднему пропорциональному) двух рядом с ним стоящих членов^[4].

Примеры[править | править код]

• Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата^[5]:8—9.
• Геометрической является последовательность количества зёрен на клетках в задаче о зёрнах на шахматной доске.
• 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — геометрическая прогрессия со знаменателем 2 из тринадцати членов.
• 50; 25; 12,5; 6,25; 3,125; … — бесконечно убывающая геометрическая прогрессия со знаменателем 1/2.
• 4; 6; 9 — геометрическая прогрессия из трёх элементов со знаменателем 3/2.
• , , ,  — стационарная геометрическая прогрессия со знаменателем 1 (и стационарная арифметическая прогрессия с разностью 0).
• 3; −6; 12; −24; 48; … — знакочередующаяся геометрическая прогрессия со знаменателем −2.
• 1; −1; 1; −1; 1; … — знакочередующаяся геометрическая прогрессия со знаменателем −1.

Свойства[править | править код]

Свойства знаменателя геометрической прогрессии[править | править код]

Знаменатель геометрической прогрессии можно найти по формулам:

• 

• 

Свойства членов геометрической прогрессии[править | править код]

• Рекуррентное соотношение для геометрической прогрессии:

• Формула общего (-го) члена:

• Обобщённая формула общего члена:

• Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.

Пусть — соответственно -й, -й, -й члены геометрической прогрессии, где . Тогда для всякой такой тройки выполняется комплементарное свойство геометрической прогрессии, называемое тождеством геометрической прогрессии:

• Произведение членов геометрической прогрессии начиная с k-го члена, и заканчивая n-м членом, можно рассчитать по формуле

  

• Сумма всех членов убывающей прогрессии:

, то при , и

при .

Свойства суммы геометрической прогрессии[править | править код]

• 
• 

где — сумма обратных величин, т. е. .

Свойства произведения геометрической прогрессии[править | править код]

См. также[править | править код]

• Арифметическая прогрессия
• Арифметико-геометрическая прогрессия
• Числа Фибоначчи
• Показательная функция
• Сумма ряда

Примечания[править | править код]

        Формула n-го члена геометрической прогрессии — штука очень простая. Как по смыслу, так и по общему виду. Но задачки на формулу n-го члена встречаются всякие — от совсем примитивных до вполне себе серьёзных. И в процессе нашего знакомства мы обязательно рассмотрим и те и другие. Ну что, знакомимся?)

        Итак, для начала собственно сама формула n-го члена геометрической прогрессии.

        Вот она:

b_n = b₁·q^n-1

       Формула как формула, ничего сверхъестественного. Выглядит даже проще и компактнее, чем аналогичная формула для арифметической прогрессии. Смысл формулы тоже прост, как валенок.

        Эта формула позволяет находить ЛЮБОЙ член геометрической прогрессии ПО ЕГО НОМЕРУ “n“.

        Как вы видите, по смыслу полная аналогия с арифметической прогрессией. Знаем номер n — можем посчитать и член, стоящий под этим номером. Какой хотим. Не умножая последовательно на “q” много-много раз. Вот и весь смысл.)

        Я понимаю, что на данном уровне работы с прогрессиями все входящие в формулу величины вам уже должны быть понятны, но считаю своим долгом всё-таки расшифровать каждую. На всякий случай.

        Итак, поехали:

        b₁ — первый член геометрической прогрессии;

        q — знаменатель геометрической прогрессии;

        n — номер члена;

        b_n — энный (n-й) член геометрической прогрессии.

        Эта формулка связывает четыре главных параметра любой геометрической прогрессии — b_n, b₁, q и n. И вокруг этих четырёх ключевых фигур и вертятся все-все задачки по прогрессии.

        “А как она выводится?” — слышу любопытный вопрос… Элементарно! Смотрите!

        Чему равен второй член прогрессии? Не вопрос! Прямо по смыслу геометрической прогрессии пишем:

       b₂ = b₁·q

        А третий член? Тоже не проблема! Второй член помножаем ещё раз на q.

        Вот так:

        b₃ = b₂·q

        Вспомним теперь, что второй член, в свою очередь, у нас равен b₁·q и подставим это выражение в наше равенство:

        b₃ = b₂·q = (b₁·q)·q = b₁·q·q = b₁·q²

        Получаем:

        b₃ = b₁·q²

       А теперь прочитаем нашу запись по-русски: третий член равен первому члену, умноженному на q во второй степени. Улавливаете? Пока нет? Хорошо, ещё один шаг.

        Чему равен четвёртый член? Всё то же самое! Умножаем предыдущий (т.е. третий член) на q:

        b₄ = b₃·q = (b₁·q²)·q = b₁·q²·q = b₁·q³

        Итого:

        b₄ = b₁·q³

        И снова переводим на русский язык: четвёртый член равен первому члену, умноженному на q в третьей степени.

        И так далее. Ну и как? Уловили закономерность? Да! Для любого члена с любым номером количество одинаковых множителей q (т.е. степень знаменателя) всегда будет на единичку меньше, чем номер искомого члена n.

        Стало быть, наша формула будет, без вариантов:

        b_n = b₁·q^n-1

        Вот и все дела.)

        Ну что, порешаем задачки, наверное?)

Решение задач на формулу n-го члена геометрической прогрессии.

        Начнём, как обычно, с прямого применения формулы. Вот типичная задачка:

        В геометрической прогрессии известно, что b₁ = 512 и q = -1/2. Найдите десятый член прогрессии.

        Конечно, эту задачку можно вообще безо всяких формул решить. Прямо по смыслу геометрической прогрессии. Но нам ведь с формулой n-го члена размяться нужно, правда? Вот и разминаемся.

        Наши данные для применения формулы следующие.

        Известен первый член. Это 512.

        b₁ = 512.

        Известен также знаменатель прогрессии: q = -1/2.

        Остаётся только сообразить, чему равен номер члена n. Не вопрос! Нас интересует десятый член? Вот и подставляем в общую формулу десятку вместо n.

        И аккуратно считаем арифметику:

        

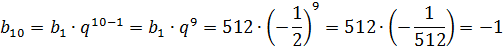
       Ответ: -1

        Как видим, десятый член прогрессии оказался с минусом. Ничего удивительного: знаменатель прогрессии у нас -1/2, т.е. отрицательное число. А это говорит нам о том, что знаки у нашей прогрессии чередуются, да.)

        Здесь всё просто. А вот похожая задачка, но немного посложнее в плане вычислений.

        В геометрической прогрессии известно, что:

        b₁ = 3

        

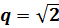
        Найдите тринадцатый член прогрессии.

        Всё то же самое, только в этот раз знаменатель прогрессии — иррациональный. Корень из двух. Ну и ничего страшного. Формула — штука универсальная, с любыми числами справляется.

        Работаем прямо по формуле:

        

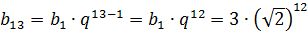
        Формула, конечно, сработала как надо, но… вот тут некоторые и зависнут. Что дальше делать с корнем? Как возвести корень в двенадцатую степень?

        Как-как… Надо понимать, что любая формула, конечно, дело хорошее, но знание всей предыдущей математики при этом не отменяется! Как возвести? Да свойства степеней вспомнить! Превратим корень в степень с дробным показателем и — по формуле возведения степени в степень.

        Вот так:

        

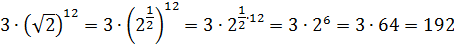
        Ответ: 192

        И все дела.)

        В чём состоит основная трудность при прямом применении формулы n-го члена? Да! Основная трудность — это работа со степенями! А именно — возведение в степень отрицательных чисел, дробей, корней и тому подобных конструкций. Так что те, у кого с этим проблемы, настоятельная просьба повторить степени и их свойства! Иначе и в этой теме будете тормозить, да…)

        А теперь порешаем типовые задачки на поиск одного из элементов формулы, если даны все остальные. Для успешного решения таких задач рецепт един и прост до ужаса — пишем формулу n-го члена в общем виде! Прямо в тетрадке рядышком с условием. А затем из условия соображаем, что нам дано, а чего не хватает. И выражаем из формулы искомую величину. Всё!

        Например, такая безобидная задачка.

        Пятый член геометрической прогрессии со знаменателем 3 равен 567. Найдите первый член этой прогрессии.

        Ничего сложного. Работаем прямо по заклинанию.

        Пишем формулу n-го члена!

        b_n = b₁·q^n-1

        Что нам дано? Во-первых, дан знаменатель прогрессии: q = 3.

        Кроме того, нам дан пятый член: b₅ = 567.

        Всё? Нет! Ещё нам дан номер n! Это — пятёрка: n = 5.

        Надеюсь, вы уже понимаете, что в записи b₅ = 567 скрыты сразу два параметра — это сам пятый член (567) и его номер (5). В аналогичном уроке по арифметической прогрессии я об этом уже говорил, но и здесь считаю не лишним напомнить.)

        Вот теперь подставляем наши данные в формулу:

        567 = b₁·3^5-1

        Считаем арифметику, упрощаем и получаем простенькое линейное уравнение:

        81b₁ = 567

        Решаем и получаем:

        b₁ = 7

        Как вы видите, с поиском первого члена проблем никаких. А вот при поиске знаменателя q и номера n могут встречаться и сюрпризы. И к ним (к сюрпризам) тоже надо быть готовым, да.)

        Например, такая задачка:

        Пятый член геометрической прогрессии с положительным знаменателем равен 162, а первый член этой прогрессии равен 2. Найдите знаменатель прогрессии.

        В этот раз нам даны первый и пятый члены, а найти просят знаменатель прогрессии. Вот и приступаем.

        Пишем формулу n-го члена!

        b_n = b₁·q^n-1

        Наши исходные данные будут следующими:

        b₅ = 162

        b₁ = 2

        n = 5

        Не хватает значения q. Не вопрос! Сейчас найдём.) Подставляем в формулу всё что нам известно.

        Получаем:

        162 = 2·q^5-1

        2q⁴ = 162

        q⁴ = 81

        Простенькое уравнение четвёртой степени. А вот сейчас — аккуратно! На данном этапе решения многие ученики сразу же радостно извлекают корень (четвёртой степени) и получают ответ q=3.

        Вот так:

        q⁴ = 81

        

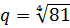
        q = 3

        Но вообще-то, это недоделанный ответ. Точнее, неполный. Почему? Дело в том, что ответ q = -3 тоже подходит: (-3)⁴ тоже будет 81!

        Всё из-за того, что степенное уравнение xⁿ = a всегда имеет два противоположных корня при чётном n. С плюсом и с минусом:

        

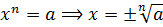
        Оба подходят.

        Например, решая неполное квадратное уравнение (т.е. второй степени)

        x² = 9

        вы же почему-то не удивляетесь появлению двух корней x=±3? Вот и тут то же самое. И с любой другой чётной степенью (четвёртой, шестой, десятой и т.д.) будет так же. Подробности — в теме про арифметический корень n-й степени.

        Поэтому правильное решение будет таким:

        q⁴ = 81

         

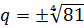
        q = ±3

        Хорошо, со знаками разобрались. Какой же из них правильный — плюс или минус? Что ж, читаем ещё раз условие задачи в поисках дополнительной информации. Её, конечно, может и не быть, но в данной задаче такая информация имеется. У нас в условии прямым текстом сказано, что дана прогрессия с положительным знаменателем.

        Поэтому ответ очевиден:

        q = 3

        Здесь-то всё просто. А как вы думаете, что было бы, если бы формулировка задачи была бы вот такой:

        Пятый член геометрической прогрессии равен 162, а первый член этой прогрессии равен 2. Найдите знаменатель прогрессии.

        В чём отличие? Да! В условии ничего не сказано про знак знаменателя. Ни прямо, ни косвенно. И вот тут задачка уже имела бы два решения!

        q = 3 и q = -3

        Да-да! И с плюсом и с минусом.) Математически сей факт означал бы, что существуют две прогрессии, которые подходят под условие задачи. И для каждой — свой знаменатель. Ради интереса, потренируйтесь и выпишите первые пять членов каждой из них.)

        А теперь потренируемся номер члена находить. Эта задачка самая сложная, да. Но зато и более творческая.)

        Дана геометрическая прогрессия:

        3; 6; 12; 24; …

        Под каким номером в этой прогрессии стоит число 768?

        Первый шаг всё тот же: пишем формулу n-го члена!

        b_n = b₁·q^n-1

        А теперь, как обычно, подставляем в неё известные нам данные. Гм… не подставляется! Где первый член, где знаменатель, где всё остальное?!

        Где-где… А глазки нам зачем? Ресницами хлопать? В этот раз прогрессия задана нам напрямую в виде последовательности. Первый член видим? Видим! Это — тройка (b₁ = 3). А знаменатель? Пока не видим, но он очень легко считается. Если, конечно, понимать, что такое знаменатель геометрической прогрессии.

        Вот и считаем. Прямо по смыслу геометрической прогрессии: берём любой её член (кроме первого) и делим на предыдущий.

        Хотя бы вот так:

        q = 24/12 = 2

        Что ещё нам известно? Нам ещё известен некоторый член этой прогрессии, равный 768. Под каким-то номером n:

        b_n = 768

        Номер его нам неизвестен, но наша задача как раз и состоит в том, чтобы его отыскать.) Вот и ищем. Все необходимые данные для подстановки в формулу мы уже скачали. Незаметно для себя.)

        Вот и подставляем:

        768 = 3·2^n-1

        Делаем элементарные тождественные преобразования — делим обе части на тройку и переписываем уравнение в привычном виде: неизвестное слева, известное – справа.

        Получаем:

        2^n-1 = 256

        Вот такое интересное уравнение. Надо найти “n”. Что, непривычно? Да, я не спорю. Вообще-то, это простейшее показательное уравнение. Оно так называется из-за того, что неизвестное (в данном случае это — номер n) стоит в показателе степени.

        На этапе знакомства с геометрической прогрессией (это девятый класс) показательные уравнения решать не учат, да… Это тема старших классов. Но страшного ничего нет. Даже если вы не в курсе, как решаются такие уравнения, попробуем найти наше n, руководствуясь простой логикой и здравым смыслом.

        Начинаем рассуждать. Слева у нас стоит двойка в какой-то степени. Мы пока не знаем, что это конкретно за степень, но это и не страшно. Но зато мы твёрдо знаем, что эта степень равна 256! Вот и вспоминаем, в какой же степени двойка даёт нам 256. Вспомнили? Да! В восьмой степени!

        256 = 2⁸

        Если не вспомнили или с распознаванием степеней проблемы, то тоже ничего страшного: просто последовательно возводим двойку в квадрат, в куб, в четвёртую степень, пятую и так далее. Подбор, фактически, но на данном уровне — вполне прокатит.

        Так или иначе, мы получим:

        2^n-1 = 2⁸

        А дальше что напрашивается? Правильно, просто убрать одинаковые основания (двойки) и приравнять показатели! Это можно, математика позволяет. Убираем двойки и получаем:

        n-1 = 8

        n = 9

        Итак, 768 — это девятый член нашей прогрессии. Всё, задача решена.)

        Ответ: 9

        Что? Скучно? Надоела элементарщина? Согласен. И мне тоже. Шагаем на следующий уровень.)

Более сложные задачи.

        А теперь решаем задачки покруче. Не то чтобы совсем уж сверхкрутые, но над которыми предстоит немного поработать, чтобы добраться до ответа.

        Например, такая.

        Найдите второй член геометрической прогрессии, если четвёртый её член равен -24, а седьмой член равен 192.

        Это классика жанра. Известны какие-то два разных члена прогрессии, а найти надо ещё какой-то член. Причём все члены НЕ соседние. Что и смущает поначалу, да…

        Как и в уроке по арифметической прогрессии, для решения таких задач рассмотрим два способа. Первый способ — универсальный. Алгебраический. Работает безотказно и с любыми исходными данными. Поэтому именно с него и начнём.)

        Расписываем каждый член по формуле n-го члена!

        Всё точь-в-точь как с арифметической прогрессией. Только в этот раз работаем с другой общей формулой. Вот и всё.) Но суть та же самая: берём и поочерёдно подставляем в формулу n-го члена наши исходные данные. Для каждого члена — свои.

        Для четвёртого члена записываем:

        b₄ = b₁·q³

        -24 = b₁·q³

        Есть. Одно уравнение готово.

        Для седьмого члена пишем:

        b₇ = b₁·q⁶

        192 = b₁·q⁶

        Итого получили два уравнения для одной и той же прогрессии.

        Собираем из них систему:

        

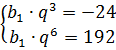
        Несмотря на её грозный вид, системка совсем простая. Самый очевидный способ решения — обычная подстановка. Выражаем b₁ из верхнего уравнения и подставляем в нижнее:

        

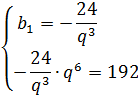
        Немного повозившись с нижним уравнением (сократив степени и поделив на -24), получим:

        q³ = -8

        К этому же уравнению, между прочим, можно прийти и более простым путём! Каким? Сейчас я вам продемонстрирую ещё один секретный, но оч-чень красивый, мощный и полезный способ решения подобных систем. Таких систем, в уравнениях которых сидят только произведения. Хотя бы в одном. Называется метод почленного деления одного уравнения на другое.

        Итак, перед нами система:

        

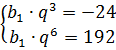
        В обоих уравнениях слева — произведение, а справа — просто число. Это очень хороший знак.) Давайте возьмём и… поделим, скажем, нижнее уравнение на верхнее! Что значит, поделим одно уравнение на другое? Очень просто. Берём левую часть одного уравнения (нижнего) и делим её на левую часть другого уравнения (верхнего). С правой частью аналогично: правую часть одного уравнения делим на правую часть другого.

        Весь процесс деления выглядит так:

        

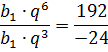
        Теперь, сократив всё, что сокращается, получим:

        q³ = -8

        Чем хорош этот способ? Да тем, что в процессе такого деления всё нехорошее и неудобное может благополучно сократиться и остаться вполне безобидное уравнение! Именно поэтому так важно наличие только умножения хотя бы в одном из уравнений системы. Нету умножения — нечего и сокращать, да…

        А вообще, этот способ (как и многие другие нетривиальные способы решения систем) даже заслуживает отдельного урока. Обязательно его разберу поподробнее. Когда-нибудь…

        Впрочем, неважно, как именно вы решаете систему, в любом случае теперь нам надо решить получившееся уравнение:

        q³ = -8

        Никаких проблем: извлекаем корень (кубический) и — готово!

        

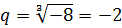
        Прошу заметить, что здесь при извлечении ставить плюс/минус не нужно. Нечётной (третьей) степени у нас корень. И ответ — тоже один, да.)

        Итак, знаменатель прогрессии найден. Минус два. Отлично! Процесс идёт.)

        Для первого члена (скажем, из верхнего уравнения) мы получим:

        

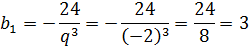
        Отлично! Знаем первый член, знаем знаменатель. И теперь у нас появилась возможность найти любой член прогрессии. В том числе и второй.)

        Для второго члена всё совсем просто:

        b₂ = b₁·q = 3·(-2) = -6

        Ответ: -6

        Итак, алгебраический способ решения задачи мы с вами разложили по полочкам. Сложно? Не очень, согласен. Долго и нудно? Да, безусловно. Но иногда можно существенно сократить объём работы. Для этого есть графический способ. Старый добрый и знакомый нам по задачкам на арифметическую прогрессию.)

        Рисуем задачу!

        Да! Именно так. Снова изображаем нашу прогрессию на числовой оси. Не обязательно по линеечке, не обязательно выдерживать равные интервалы между членами (которые, кстати, и не будут одинаковыми, т.к. прогрессия – геометрическая!), а просто схематично рисуем нашу последовательность.

        У меня получилось вот так:

        

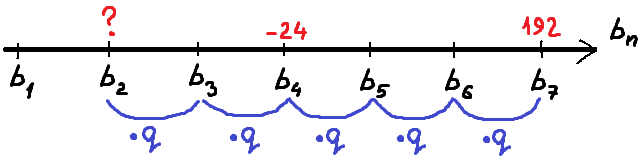
        А теперь смотрим на картинку и соображаем. Сколько одинаковых множителей “q” разделяют четвёртый и седьмой члены? Верно, три!   

        Стало быть, имеем полное право записать:

        -24·q³ = 192

        Отсюда теперь легко ищется q:

        q³ = -8

        q = -2

        Вот и отлично, знаменатель у нас уже в кармане. А теперь снова смотрим на картинку: сколько таких знаменателей сидит между вторым и четвёртым членами? Два! Стало быть, для записи связи между этими членами знаменатель будем возводить в квадрат.

        Вот и пишем:

        b₂·q² = -24, откуда b₂ = -24/q²

        Подставляем наш найденный знаменатель в выражение для b₂, считаем и получаем:

        

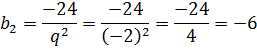
        Ответ: -6

        Как видим, всё гораздо проще и быстрее, чем через систему. Более того, здесь нам вообще даже не понадобилось считать первый член! Совсем.)

        Вот такой простой и наглядный способ-лайт. Но есть у него и серьёзный недостаток. Догадались? Да! Он годится только для очень коротких кусочков прогрессии. Таких, где расстояния между интересующими нас членами не очень большие. А вот во всех остальных случаях картинку рисовать уже затруднительно, да… Тогда решаем задачу аналитически, через систему.) А системы — штука универсальная. С любыми числами справляются.

        Ещё одна эпичная задачка:

        Второй член геометрической прогрессии на 10 больше первого, а третий член на 30 больше второго. Найдите знаменатель прогрессии.

        Что, круто? Вовсе нет! Всё то же самое. Снова переводим условие задачи в чистую алгебру.

        1) Расписываем каждый член по формуле n-го члена!

        Второй член: b₂ = b₁·q

        Третий член: b₃ = b₁·q²

        2) Записываем связь между членами из условия задачи.

        Читаем условие: “Второй член геометрической прогрессии на 10 больше первого”. Стоп, это ценно!

        Так и пишем:

        b₂ = b₁+10

        Читаем дальше: “…третий член на 30 больше второго”.

        И эту фразу переводим в чистую математику:

        b₃ = b₂+30

        Получили два уравнения. Объединяем их в систему:

        

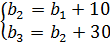
        Система на вид простенькая. Но что-то уж много различных индексов у буковок. Подставим-ка вместо второго и третьего членов их выражения через первый член и знаменатель! Зря, что ли, мы их расписывали?

        Получим:

        

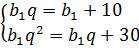
        А вот такая система — уже не подарок, да… Как такое решать? К сожалению, универсального секретного заклинания на решение сложных нелинейных систем в математике нет и быть не может. Это фантастика! Но первое что должно приходить вам в голову при попытке разгрызть подобный крепкий орешек — это прикинуть, а не сводится ли одно из уравнений системы к красивому виду, позволяющему, например, легко выразить одну из переменных через другую?

        Вот и прикинем. Первое уравнение системы явно проще второго. Его и подвергнем пыткам.) А не попробовать ли из первого уравнения что-то выразить через что-то? Раз уж мы хотим найти знаменатель q, то выгоднее всего нам было бы выразить b₁ через q.

        Вот и попробуем проделать эту процедуру с первым уравнением, применяя старые добрые тождественные преобразования:

        b₁q = b₁+10

        b₁q — b₁ = 10

        b₁(q-1) = 10

        

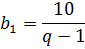
        Всё! Вот мы и выразили ненужную нам переменную (b₁) через нужную (q). Да, не самое простое выражение получили. Дробь какую-то… Но и система у нас приличного уровня, да.)

        А дальше дело техники. Обычный метод подстановки. Подставляем наше полученное выражение для b₁ в нижнее уравнение:

        

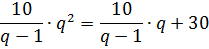
        Типичное дробно-рациональное уравнение. Что делать — знаем.

        Пишем ОДЗ (обязательно!):

        q ≠ 1

        Умножаем всё на знаменатель (q-1) и сокращаем все дроби:

        10q² = 10q + 30(q-1)

        Делим всё на десятку, раскрываем скобки, собираем всё слева:

        q² — 4q + 3 = 0

        Решаем получившееся квадратное уравнение и получаем два корня:

        q₁ = 1

        q₂ = 3

        И что дальше? И какой из корней нам выбрать? Так, стоп! Чего же я туплю-то? А ОДЗ зачем мы выписывали? Для красоты?) Единица никак не катит! В отвал единицу!

        Окончательный ответ один: q = 3.

        Ответ: 3

        Как вы видите, путь решения большинства задач на формулу n-го члена геометрической прогрессии всегда един: читаем внимательно условие задачи и с помощью формулы n-го члена переводим всю полезную информацию в чистую алгебру.

        А именно:

        1) Расписываем отдельно каждый данный в задаче член по формуле n-го члена.

         2)  Из условия задачи переводим связь между членами в математическую форму. Составляем уравнение или систему уравнений.

         3) Решаем полученное уравнение или систему уравнений, находим неизвестные параметры прогрессии.

         4) В случае неоднозначного ответа читаем внимательно условие задачи в поисках дополнительной информации (если таковая присутствует). Также сверяем полученный ответ с условиями ОДЗ (если таковые имеются).

        А теперь перечислим основные проблемы, наиболее часто приводящие к ошибкам в процессе решения задач на геометрическую прогрессию.

        1. Элементарная арифметика. Действия с дробями и отрицательными числами.

        2. Действия со степенями и действия с корнями. Возведение в степень дробей, корней, отрицательных чисел. Извлечение корней n-й степени при решении уравнений.

        3. Решение уравнений и (особенно!) систем уравнений. Тождественные преобразования уравнений.

        Если хотя бы с одним из этих трёх пунктов проблемы, то неизбежно будете ошибаться и в этой теме. К сожалению… Так что не ленитесь и повторите то о чём упомянуто выше. И по ссылочкам — сходите. Иногда помогает.)

        Видоизменённые и рекуррентные формулы.

        А теперь рассмотрим парочку типичных экзаменационных задачек с менее привычной подачей условия. Да-да, вы угадали! Это видоизменённые и рекуррентные формулы n-го члена. С такими формулами мы уже с вами сталкивались и работали в соответствующем уроке по арифметической прогрессии. Здесь всё аналогично. Суть та же.

        Например, такая задачка из ОГЭ:

        Геометрическая прогрессия задана формулой b_n = 3·2ⁿ. Найдите сумму первого и четвёртого её членов.

        В этот раз прогрессия нам задана не совсем привычно. В виде какой-то формулы. Ну и что? Эта формула — тоже формула n-го члена! Мы же с вами знаем, что формулу n-го члена можно записать как в общем виде, через буквы, так и для конкретной прогрессии. С конкретными первым членом и знаменателем.

        В нашем случае нам, на самом деле, задана формула общего члена для геометрической прогрессии вот с такими параметрами:

        b₁ = 6

        q = 2

        Проверим?) Запишем формулу n-го члена в общем виде и подставим в неё b₁ и q. Получим:

        b_n = b₁·q^n-1

        b_n = 6·2^n-1

        Упрощаем, используя разложение на множители и свойства степеней, и получаем:

        b_n = 6·2^n-1 = 3·2·2^n-1 = 3·2^n-1+1 = 3·2ⁿ

        Как видите, всё честно. Но наша с вами цель — не продемонстрировать вывод конкретной формулы. Это так, лирическое отступление. Чисто для понимания.) Наша цель – решить задачу по той формуле, что дана нам в условии. Улавливаете?) Вот и работаем с видоизменённой формулой напрямую.

        Считаем первый член. Подставляем n=1 в общую формулу:

        b₁ = 3·2¹ = 3·2 = 6

        Вот так. Кстати, не поленюсь и ещё раз обращу ваше внимание на типовой ляп с подсчётом первого члена. НЕ НАДО, глядя на формулу b_n = 3·2ⁿ, сразу бросаться писать, что первый член — тройка! Это — грубейшая ошибка, да…)

        Продолжаем. Подставляем n=4 и считаем четвёртый член: 

        b₄ = 3·2⁴ = 3·16 = 48

        Ну и наконец, считаем требуемую сумму:

        b₁ + b₄ = 6+48 = 54

        Ответ: 54

        Ещё задачка.

        Геометрическая прогрессия задана условиями:

        b₁ = -7;

        b_n+1 = 3b_n

        Найдите четвёртый член прогрессии.

        Здесь прогрессия задана рекуррентной формулой. Ну и ладно.) Как работать с такой формулой — тоже знаем.

        Вот и действуем. По шагам.

        1) Считаем два последовательных члена прогрессии.

        Первый член нам уже задан. Минус семь. А вот следующий, второй член, легко можно посчитать по рекуррентной формуле. Если понимать принцип её работы, конечно.)

        Вот и считаем второй член по известному первому:

        b₂ = 3b₁ = 3·(-7) = -21

        2) Считаем знаменатель прогрессии

        Тоже никаких проблем. Прямо по смыслу геометрической прогрессии, делим второй член на первый.

        Получаем:

        q = -21/(-7) = 3

        3) Пишем формулу n-го члена в привычном виде и считаем нужный член.

        Итак, первый член знаем, знаменатель — тоже. Вот и пишем:

        b_n = -7·3^n-1

        Осталось лишь посчитать четвёртый член:

        b₄ = -7·3³ = -7·27 = -189

        Ответ: -189

        Как вы видите, работа с такими формулами для геометрической прогрессии ничем по своей сути не отличается от таковой для прогрессии арифметической. Важно лишь понимать общую суть и смысл этих формул. Ну и смысл геометрической прогрессии тоже надо понимать, да.) И тогда глупых ошибок не будет.

        Ну что, порешаем самостоятельно?)

        Совсем элементарные задачки, для разминки:

        1. Дана геометрическая прогрессия, в которой b₁ = 243, а q = -2/3. Найдите шестой член прогрессии.

        2. Общий член геометрической прогрессии задан формулой b_n = 5∙2ⁿ⁺¹. Найдите номер последнего трёхзначного члена этой прогрессии.

        3. Геометрическая прогрессия задана условиями:

        b₁ = -3;

        b_n+1 = 6b_n

        Найдите пятый член прогрессии.

        Чуть посложнее:

        4. Дана геометрическая прогрессия:

        b₁=2048; q=-0,5

        Чему равен шестой отрицательный её член?

        Что, кажется суперсложно? Вовсе нет. Спасёт логика и понимание смысла геометрической прогрессии. Ну и формула n-го члена, само собой.

        5. Третий член геометрической прогрессии равен -14, а восьмой член равен 112. Найдите знаменатель прогрессии.

        6. Сумма первого и второго членов геометрической прогрессии равна 75, а сумма второго и третьего членов равна 150. Найдите шестой член прогрессии.

        Ответы (в беспорядке): 6; -3888; -1; 800; -32; 448.

        Вот почти и всё. Осталось лишь научиться нам считать сумму n первых членов геометрической прогрессии да открыть для себя бесконечно убывающую геометрическую прогрессию и её сумму. Очень интересную и необычную штуку, между прочим! Об этом — в следующих уроках.)

Геометрическая прогрессия

Кусочек теории.

Геометрическая прогрессия – это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.

Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.

Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.

Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:

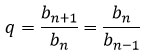
Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:

Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:

И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!

Помимо этих трех формул пригодится еще формула суммы:

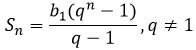
Практика.

Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)

Откинем пока минусы…

Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.

Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.

И 5-ое: 64 : 1,25 = 51,2.

Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое – положительным.

Ответ: 51,2.

Задание 2.

Опять знаки у чисел чередуются, значит число, спрятанное под иксом, будет отрицательным.

Не будем морочить голову формулами, пойдем задом наперед: разделим 4-ое число на 3-ое (найдем знаменатель прогрессии):

96 : 24 = 4 (знаки у чисел мы откинули временно).

Значит, чтобы найти икс надо 24 разделить на знаменатель 4 и взять результат с минусом.

Ответ: -6.

Задание 3.

По данной нам в условии задаче формуле можно сразу понять, что 2 – знаменатель прогрессии. Если это не понятно – вот доказательство:

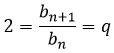
Здесь схитрить не получится, поэтому используем формулу и находим b₆.

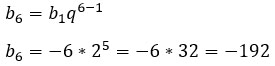
Ответ: -192.

Задание 4.

Каждое следующее число в 4 раза больше предыдущего, значит знаменатель q равен 4.

Зная первый член прогрессии и знаменатель можно найти сумму первых шести членов (n = 6).

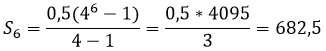
Ответ: 682,5.

Задание 5.

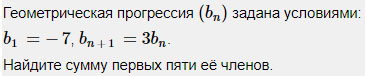
Похожее условие уже встречалось в задании 3. Из данной формулы делаем вывод, что знаменатель q = 3.

Находим сумму:

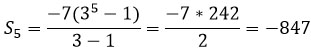
Ответ: -847.

Вот и всё!

С наилучшими пожеланиями, твой персональный препод)