Что такое кратное число
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. В этой статье мы расскажем, что такое КРАТНЫЕ ЧИСЛА.
Эту тему каждый школьник в России проходит в 6 классе, когда подробно изучают деление.
Хотя с самой этой математической функцией дети знакомятся гораздо раньше – уже во 2 классе.
Кратное число — это …
Деление – это математическая операция, благодаря которой можно узнать, сколько частей чего-то одного содержится в другом. Или, другими словами, заменяет многократное вычитание из одного числа другое.
Операция деления в математике может обозначаться разными значками. Это двоеточие (:), косая черта (/), горизонтальная черта (-) или специальным значком под названием «обелюс» (÷).
А у чисел, которые участвуют в делении, есть определенные названия:
- Делимое – то число, которое собираются делить;
- Делитель – число, на которое будут делить делимое. Соответственно, делитель чаще всего меньше делимого. Хотя не исключен и другой вариант. Единственное число, которое не может быть делителем, это ноль.
- Частное – результат деления, то есть число, которое получается в результате выполнения математического действия.
Частное, которое получается полным или не полным. Первый вариант, это когда число-делимое, было полностью поделено на делитель. Например, 12 / 3 = 4. Но бывают варианты и с неполным частным, когда появляется некий остаток. Например, 14 / 3 = 4 (2), где 4 – это неполное частное, а 2 – остаток.
Почему мы так подробно рассказали о делении? Это имеет непосредственное отношение к теме статьи.
Одно число называется кратным другому, если его можно на него поделить без остатка.
Но речь идет только о натуральных числах. То есть тех, которые мы используем для счета в обычной жизни. Например, 1, 2, 5, 10, 35, 100 и так далее. При этом дробные числа (например, 2/5 или 0,5) к натуральным не относятся, а значит, в отношении них понятие «кратности» не применяется.
Например, возьмем число 12. Оно может быть кратно сразу нескольким числам.
12 / 3 = 4
12 / 4 = 3
12 / 6 = 2
12 / 2 = 6
Таким образом, можно сказать, что 12 – кратное число 2, 3, 4 и 6. И точно так же можно разложить по кратности любое число.
Внимательный читатель мог бы возразить, что есть еще два числа, на которые можно поделить 12 без остатка. Во-первых, это само 12. А во-вторых, это единица. Что ж, это абсолютная правда, и ее можно даже записать в одном математическом правиле:
Любое натуральное число всегда кратно само себе и единице. В первом случае получается единица, а во втором само число.
Таблицы чисел кратных 2,3,4,5,6,7,9
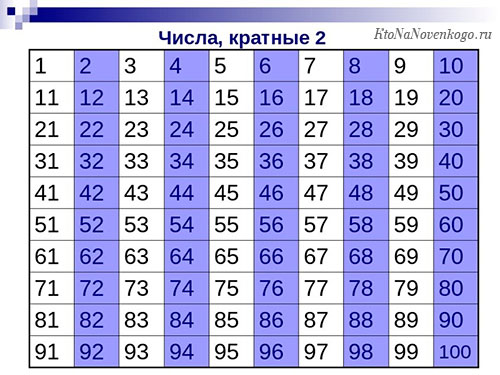
В первую очередь рассмотрим самый простой вариант. Это числа, которые являются кратными двум. Определить их совсем просто, так как к ним относятся все четные числа. Вот, например, как выглядит таблица от 1 до 100.
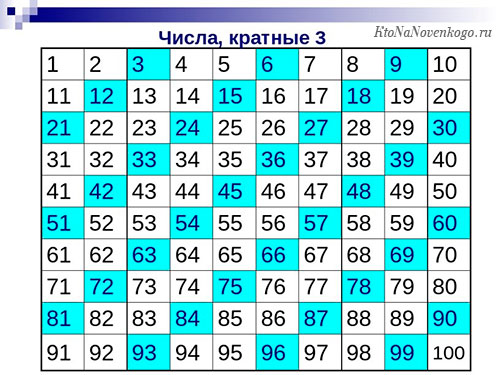
А вот так будет выглядеть таблица чисел кратных трем. Обратите внимание, что все они в результате располагаются по диагонали. Получается весьма красиво.
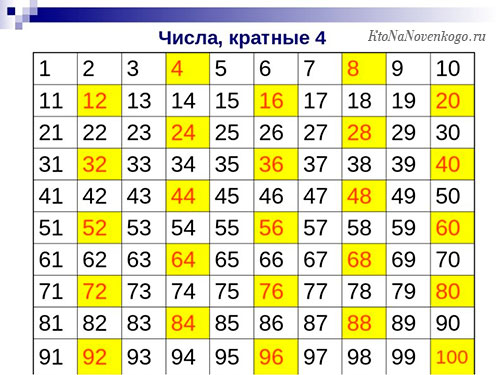
Теперь покажем таблицу чисел, которые можно поделить без остатка на 4. Как можно заметить, это только четные цифры.
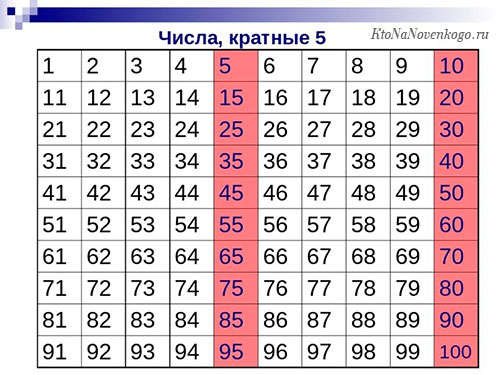
А вот так выглядит таблица чисел, которые кратны пяти. Запомнить их очень просто. Числа, кратные пяти, должны оканчиваться или на 5, или на 0. Других вариантов быть просто не может.
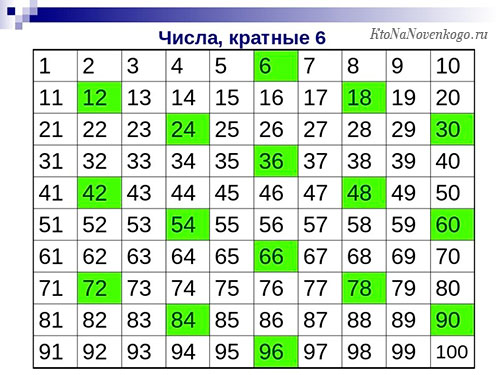
А если взглянуть на таблицу чисел, которые кратны числу 6, то можно сделать интересный вывод. Есть числа, которые никогда не попадут в эту категорию. Они оканчиваются на 1, 3, 5, 7 и 9. Другими словами, только четные числа могут быть кратными 6. Но при этом не все четные числа таковыми являются.
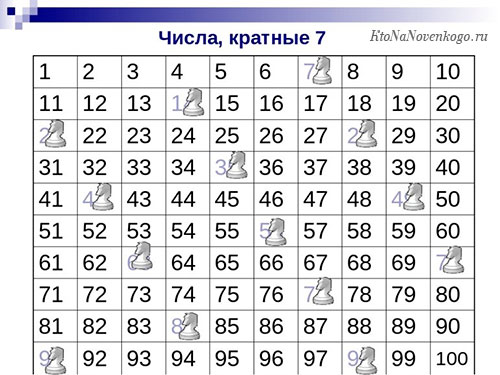
Интересно будет посмотреть и таблицу чисел, которые являются кратными 7. Чтобы определить их, нужно ходить по таблице вниз, как ходить шахматная фигура «конь». В народе это называется «буквой Г», в нашем случае это «шаг влево и два шага вниз».
И наконец, интересно рассмотреть числа, которые кратны 9. Их очень легко определить, это своеобразный математический лайфхак.
Надо просто сложить все цифры в числе, и если в сумме получится 9, то тогда число кратно девятке.
| Числа, кратные 9 | 27 | 198 | 5 877 | 3 816 | 117 | 72 |
|---|---|---|---|---|---|---|
| Сумма | 9 | 18 | 27 | 18 | 9 | 9 |
Да, тут указаны еще и числа 18 и 27. Но они при повторном сложении также дадут девятку.
Вместо заключения
А знаете, что есть число, которое можно назвать кратным всем другим натуральным числам? Это ноль. Ведь если ноль поделить на любое число, то получится опять же ноль. И никакого остатка. А значит, это утверждение верно.
Вот и все, что мы хотели рассказать о КРАТНЫХ ЧИСЛАХ.
Наименьшее о́бщее кратное (HOK) двух целых чисел — это наименьшее натуральное число, которое делится на оба без остатка, то есть кратно им обоим. К примеру, для чисел 6 и 4, наименьшим общим кратным будет 12.
Как найти НОК?
Способов найти НОК несколько. Мы рассмотрим один из часто используемых в математике — это нахождение НОК при помощи разложения чисел на простые множители. В общем случае алгоритм будет выглядеть следующим образом:
- разложить оба числа на простые множители;
- выбрать одну группу множителей;
- добавить к ним множители из второй группы, которые отсутствуют в выбранной;
- найти их произведение.
Примеры нахождения наименьшего общего кратного
Рассмотрим приведенный алгоритм на конкретных примерах:
Пример 1: найти НОК 4 и 6
1. Раскладываем 6 и 4 на простые множители:
2. Возьмем первую группу множителей: 2 · 3.
3. Смотрим вторую группу (2 · 2) и видим, что из двух двоек, одна присутствует в первом разложении. Таким образом, берем только одну двойку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 3 · 2 = 12.
Ответ: НОК (6; 4) = 12
Пример 2: найти НОК 32 и 20
1. Раскладываем 32 и 20 на простые множители:
2. Возьмем первую группу множителей: 2 · 2 · 2 · 2 · 2.
3. Смотрим вторую группу (2 · 2 · 5) и видим, что из двух двоек и пятерки, обе двойки присутствуют в первом разложении. Таким образом, берем только пятерку. Добавляем к первому разложению и получаем: 2 · 3 · 2
4. Вычисляем произведение: 2 · 2 · 2 · 2 · 2 · 5 = 160.
Ответ: НОК (32; 20) = 160
Наименьшее общее кратное
- Общее кратное
- Наименьшее общее кратное
- Как найти НОК
- С помощью разложения на простые множители
- Нахождение НОК через НОД
- Калькулятор НОК
Общее кратное
Число может быть кратно не одному, а сразу нескольким числам, такое число называется общим кратным данных чисел.
Пример.
Числу 3 кратны числа: 6, 9, 12, 15 и т. д.
Числу 4 кратны числа: 8, 12, 16, 20 и т. д.
Можно заметить, что одно и тоже число (12) делится нацело сразу на оба числа 3 и 4. Следовательно, число 12 есть общее кратное чисел 3 и 4.
Общее кратное чисел — это любое число, которое делится без остатка на каждое из данных чисел.
Найти общее кратное нескольких натуральных чисел достаточно легко, можно просто перемножить данные числа, полученное произведение и будет их общим кратным.
Пример. Найти общее кратное для чисел 2, 3, 4, 6.
Решение:
2 · 3 · 4 · 6 = 144.
Число 144 — общее кратное чисел 2, 3, 4 и 6.
Для любого количества натуральных чисел существует бесконечно много кратных.
Пример. Для чисел 12 и 20 кратными будут числа: 60, 120, 180, 240 и т. д. Все они являются общими кратными для чисел 12 и 20.
Наименьшее общее кратное
Наименьшее общее кратное (НОК) нескольких чисел — это самое маленькое натуральное число, которое делится без остатка на каждое из этих чисел.
Пример. Наименьшим общим кратным чисел 3, 4 и 9 является число 36, никакое другое число меньше 36 не делится одновременно на 3, 4 и 9 без остатка.
Наименьшее общее кратное записывается так:
НОК (a, b, …) = x.
Числа в круглых скобках могут быть указаны в любом порядке.
Пример. Запишем наименьшее общее кратное чисел 3, 4 и 9:
НОК (3, 4, 9) = 36.
Как найти НОК
Рассмотрим два способа нахождения наименьшего общего кратного: с помощью разложения чисел на простые множители и нахождение НОК через НОД.
С помощью разложения на простые множители
Чтобы найти НОК нескольких натуральных чисел, надо разложить эти числа на простые множители, затем взять из этих разложений каждый простой множитель с наибольшим показателем степени и перемножить эти множители между собой.
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: разложим каждое из этих чисел на простые множители:
99 = 3 · 3 · 11 = 32 · 11,
54 = 2 · 3 · 3 · 3 = 2 · 33.
Наименьшее общее кратное должно делиться на 99, значит, в его состав должны входить все множители числа 99. Далее НОК должно делиться и на 54, т. е. в его состав должны входить множители и этого числа.
Выпишем из этих разложений каждый простой множитель с наибольшим показателем степени и перемножим эти множители между собой. Получим следующее произведение:
2 · 33 · 11 = 594.
Это и есть наименьшее общее кратное данных чисел. Никакое другое число меньше 594 не делится нацело на 99 и 54.
Ответ: НОК (99, 54) = 594.
Так как взаимно простые числа не имеют одинаковых простых множителей, то их наименьшее общее кратное равно произведению этих чисел.
Пример. Найдите наименьшее общее кратное двух чисел 12 и 49.
Решение: разложим каждое из этих чисел на простые множители:
12 = 2 · 2 · 3 = 22 · 3,
49 = 7 · 7 = 72.
Применяя к этому случаю правило, мы придём к заключению, что взаимно простые числа надо просто перемножить:
22 · 3 · 72 = 12 · 49 = 588.
Ответ: НОК (12, 49) = 588.
Таким же образом надо поступать, когда нужно найти наименьшее общее кратное простых чисел.
Пример. Найдите наименьшее общее кратное чисел 5, 7 и 13.
Решение: так как данные числа являются простыми, то просто перемножим их:
5 · 7 · 13 = 45.
Ответ: НОК (5, 7, 13) = 455.
Если большее из данных чисел делится на все остальные числа, то это число и будет наименьшим общим кратным данных чисел.
Пример. Найдите наименьшее общее кратное чисел 24, 12 и 4.
Решение: разложим каждое из этих чисел на простые множители:
24 = 2 · 2 · 2 · 3 = 23 · 3,
12 = 2 · 2 · 3 = 22 · 3,
4 = 2 · 2 = 22.
Можно заметить, что разложение большего числа содержит все множители остальных чисел, значит большее из этих чисел делится на все остальные числа (в том числе и само на себя) и является наименьшим общим кратным:
23 · 3 = 24.
Ответ: НОК (24, 12, 4) = 24.
Нахождение НОК через НОД
НОК двух натуральных чисел равно произведению этих чисел, поделённого на их НОД.
Правило в общем виде:
НОК (m, n) = m · n : НОД (m, n)
Пример. Найдите наименьшее общее кратное двух чисел 99 и 54.
Решение: сначала находим наибольший общий делитель:
НОД (99, 54) = 9.
Теперь мы можем вычислить НОК этих чисел по формуле:
НОК (99, 54) = 99 · 54 : НОД (99, 54) = 5346 : 9 = 594.
Ответ: НОК (99, 54) = 594.
Чтобы найти НОК трёх или более чисел используется следующий порядок действий:
- Находят НОК любых двух из данных чисел.
- Затем находят наименьшее общее кратное найденного НОК и третьего числа и т. д.
- Таким образом поиск НОК продолжается до тех пор, пока есть числа.
Пример. Найдите наименьшее общее кратное чисел 8, 12 и 9.
Решение: сначала находим наибольший общий делитель любых двух из этих чисел, например, 12 и 8:
НОД (12, 8) = 4.
Вычисляем их НОК по формуле:
НОК (12, 8) = 12 · 8 : НОД (12, 8) = 96 : 4 = 24.
Теперь найдём НОК числа 24 и оставшегося числа 9. Их НОД:
НОД (24, 9) = 3.
Вычисляем НОК по формуле:
НОК (24, 9) = 24 · 9 : НОД (24, 9) = 216 : 3 = 72.
Ответ: НОК (8, 12, 9) = 72.
Калькулятор НОК
Данный калькулятор поможет вам найти наименьшее общее кратное чисел. Просто введите числа через пробел или запятую и нажмите кнопку Вычислить НОК
.
|
В заданиях по математике можно встретить фразы: “найдите число, кратное…” Иногда эта формулировка может вызвать непонимание. Что значит кратно? Это значит, что одно число делится на другое целиком, без остатка. Приведем пример: Найти число, кратное 2. Это значит, что число должно без остатка делиться на 2. Ответом может быть любое четное число. Приведем еще пример: Число, кратное 5. Что это за число? Например, 10, 35, 55, 60 и все другие, которые делятся на 5 без остатка. Про кратность можно сказать и так: Число 16 кратно 4 (шестнадцать кратно четырем) – это значит, что 16 делится без остатка на 4. система выбрала этот ответ лучшим Zummy out off 3 года назад Кратность в математике означает делимость. Кратно, кратный, сократить – это родственные слова, образованные от старинного слова «крат», то есть «раз». Сейчас это слово употребляется только в выражении «во сто крат», то есть «в сто раз». Число Х кратно числу Y – значит, число Х можно разделить (сократить) на Y, то есть Х делится на Y без остатка. Кратное – это число, которое делится на данное число. «Кратно» – краткое прилагательное от «кратный». 12 кратно числу 3, то есть 12 можно сократить на 3, разделить на 3 без остатка. 20 кратно числу 5, то есть 20 можно сократить на 5, разделить на 5 без остатка. З В Ё Н К А 3 года назад Кратно какому-либо числу может быть только другое определённое (меньшее первому) число, обладающее соответствующими свойствами: кратное число должно быть ровно во сколько-то крат (раз) больше другого. Это арифметическое понятие. Примеры:
_ Говорить, например, о том, что число 5 кратно сотне, не совсем верно. Кратное число – это большее, но не меньшее. Кратное число – не делитель, а делимое. Так считать удобнее и грамотнее. 1 не кратно 1000, а вот 1000 кратно 1. Marmeladoff 4 года назад Слово “кратно” напоминает слово “сократить”. Вспомните привычную фразу: “количество сократилось вдвое” – это значит, что изначальное число разделили на два. В математике слово “кратно” можно заменить на слово “делится” (причем подразумевается деление без остатка), например: десять кратно двум = десять делится на два восемь кратно четырем = восемь делится на четыре То есть кратное – это не делитель, а делимое, “кратное” = “делящиеся”. Часто задача звучит так: “Найти наименьшее число, кратное двум и семи”. Это значит, что мы должны узнать, какое число без остатка делится и на два и на семь. Очевидно, что это – 14. Иногда слово “кратное” применяют не только в учебниках математики, но в разговорах, касающихся экономических или других показателей. В математике существует простая формулировка, что такое кратное. Оказывается это просто число, которое можно разделить на другое число без остатка. Скажем дали нам число 5, и спросили, является ли число 73 кратным этому числу. Чтобы ответить на этот вопрос мы должны попытаться 73 поделить на 5. У нас получится 14 и в остатке будет 3. Значит число 73 не является кратным числу 5. Но вот число 70 уже будет являться кратным числу 5, ведь при делении оно даст 14. Заметим, что и для числа 14 число 70 оказывается кратным. Поэтому в математике часто оперируют таким понятием как Наименьшее общее кратное, вот таким наименьшим общим кратным для чисел 5 и 14 и оказывается число 70. Невозмутимый Дождь 3 года назад Понятие кратности предполагает утверждение, часто встречающееся в математике: “данное число кратно другому”. Его можно понять так: “данное число в несколько крат больше другого”. Допустим, в каком-то математическом выражении, в котором участвуют делимое и делитель, есть большее число (это делимое) и меньшее число (делитель). Если делимое делится на делитель без остатка, то это означает, что делимое кратно делителю. Например, 28 кратно 14; 150 кратно и 50, и 3, и 75 одновременно; 1000 кратно 20, 50, 500, 100 и ещё некоторым числам; 66 кратно 33, 11, 2 и так далее. Как видим, то или иное число может быть кратным сразу нескольким числам, но это не обязательно. Master-Margarita 5 лет назад По определению кратное натурального числа а будет натуральное число, делящееся на а без остатка. То есть, при делении одного числа на другого мы всегда получим в результате целое число, а не дробный остаток. 9 на 3 делится без остатка, ибо 9:3=3, значит 3 кратно 9. 9 на 4 без остатка не поделить. 9:4=8 1/4 – то есть 4 уже не кратно 9. Это математическое понятие. Говорить, что число кратно другому число, это значит, что первое можно разделить на второе и получится некое целое число, без остатка, без знаков после запятой. Например, мы можем говорить, что для того, чтобы число было кратно 10, оно должно заканчиваться на 0. Если число кратно 5, то оно должно заканчиваться или на 5, или на 0. Malisch52 5 лет назад Это значит что названное число должно делиться без остатка на то число которому оно кратно. Например числа два, четыре, шесть, восемь, десять кратны двум. При этом число десять например кратно пяти, число шесть еще кратно трем и так далее. Рождённый в С С С Р 5 лет назад Если совсем по простому говорить, кратно числу – значит, равняется этому числу, помноженному на другое целое число. Например, кратные пяти: 10 (5*2), 15 (5*3), 20 и т.д. Кратные трём: 6,9,12… Кратные семнадцати: 34,51,68… Знаете ответ? |
Как определить что число кратно 7?
Следующим кратным числом по возрастанию является это число, умноженное на 2, затем на 3, на 4 и до бесконечности. Например, числами, которые кратны 7, будет 7, затем 14, 21, 28 и далее. Познакомиться с этими числами и проследить их закономерность поможет материал «Карточки Числа кратные 7 в пределах 100».
Что такое кратность?
Кра́тность — научный термин, который может показывать: во сколько раз одна величина больше другой (например, кратность светофильтра); количество вхождений заданного объекта в некоторое множество (например, кратность звёздной системы).
Как найти все кратные числа?
Кратные числа – это такие числа, которые делятся на любое заданное целое число без какого-либо остатка. То есть, в итоге должно получится целое число. Например: число 12 делится без остатка на 3, 4 и 6. Это означает, что 12 является кратным числам 3, 4, 6, так как существуют натуральные числа 4, 3 и 2.
Как определить кратность 3?
Начнем с формулировки признака делимости на 3: целое число делится на 3, если сумма его цифр делится на 3, если же сумма цифр данного числа не делится на 3, то и само число не делится на 3.
Как определить делится ли число на 7?
число делится на 7 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по три цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «−» делится на 7. Например, 138 689 257 делится на 7, так как на 7 делится
Что значит числа кратные 7?
Когда говорят о кратности какому-то числу, это значит, что искомое число должно без остатка делиться на кратное число: результатом должно быть целое число (без дробной части/цифр после запятой). … Аналогично можно проверять любое число на кратность другому числу.
Что такое кратен 4?
Нахождение кратных чисел. Получаем числовой ряд 4, 8 12, 16, 20, 24, 28. Все полученные числа делятся на 4. Поэтому можно сказать, что эти числа кратны 4. Например: в числе 16 чисело 4 взято 4 раза, в числе 24 число 4 взято 6 раз.
Что значит кратность в математике?
Кратность и делимость То есть кратными называют числа, которые можно поделить на заданное число нацело. Делимостью же называют способность самого числа поделиться нацело. То есть для 9 делителями будут числа 9,3,1.
Как быстро найти кратные числа?
Если одно натуральное число нацело делится на другое натуральное число, то первое число называют кратным второму числу, а второе число называют делителем первого числа. Значит, число 45 является кратным числу 9, а число 9 является делителем числа 45.
Какое число кратное девяти?
Число делится на 9 без остатка, если сумма его цифр также делится на 9 без остатка. Например, 7866 делится на 9, т.
Как доказать что число кратно 3?
Некоторые признаки делимости натуральных чисел Число делится на 2, если его последняя цифра есть число четное (то есть 2, 4, 6, 
Когда сумма кратна 3?
Сумма двух чисел может быть кратна 3 в двух случаях: либо оба слагаемых кратны 3, либо остаток от деления на 3 одного из них равен 1, а другого – 2.
Какие числа деляться на 14?
Для того чтобы точно знать делится ли число на 14 если выполняется оба условия:
- последняя цифра в числе это 0,2,4,6 или 8, то есть является четной
- число кроме последней цифры справа (кроме разряда единиц) минус последняя цифра умноженную на два делится на 14.
Какое число делится на 7 без остатка?
На число 7 без остатка (нацело) делятся следующие числа: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84 и многие другие. Какие четные числа делятся на 7? На число 7 делятся следующие четные числа: 14, 28, 42, 56, 70, 84, 98, 112, 126, 140, 154, 168 и многие други.
Что такое кратное число пример?
Кратное число — число, делящееся на данное целое число без остатка, например 12 кратно 4. Общее кратное нескольких целых чисел — число, делящееся на каждое из них в отдельности. Если для двух заданных натуральных чисел и найдется такое натуральное число , что , то говорят, что число делится без остатка на число .
Что значит число кратное числу?
Кратным числу a называют число, которое делится на a без остатка. Кратных чисел у каждого натурального числа бесконечное количество. Натуральное число является кратным самому себе, причём наименьшим кратным.
Что такое кратных 5?
Число делится на 5, если две его последние цифры — нули или образуют число, делящееся на 25.