Решение заданий всех предметов
Сортировать:
По дате добавления
![]()
Дано: объем хлора – 2,24 л (н.у.) Уравнение реакции: 2Al + 3Cl2 → 2AlCl3 Молярная масса AlCl3 = 133,34 г/моль Для расчета массы AlCl3 необходимо определить количество вещества Cl2, используя уравнение и закон простой пропорциональности: 2 моль Al : 3 моль Cl2 x моль Al : 2,24 л Cl2 (н.у.) = x моль Al : 0,0792 моль Cl2 x = (2 моль Al * 0,0792 моль Cl2) / 3 моль Cl2 = 0,0528 моль Al Масса AlCl3 = количество вещества AlCl3 * молярная масса AlCl3 Масса AlCl3 = 0,0528 моль * 133,34 г/моль = 7,04 г Ответ: масса хлорида алюминия, образующегося при взаимодействии избытка алюминия с 2,24 л (н. у.) хлора, равна 7 граммам.
![]()
Дано: масса лития – 3,5 г. Уравнение реакции: 4Li + O2 → 2Li2O Молярная масса Li2O = 29,88 г/моль Рассчитаем количество молей лития: n(Li) = m(Li) / M(Li) = 3,5 г / 6,94 г/моль = 0,504 моль Так как по уравнению 4 моля лития соответствуют 2 молям Li2O, то количество молей Li2O равно: n(Li2O) = 0,504 моль / 2 = 0,252 моль Масса Li2O равна: m(Li2O) = n(Li2O) * M(Li2O) = 0,252 моль * 29,88 г/моль = 7,54 г Ответ: масса оксида лития, образовавшегося при сжигании 3,5 г лития в кислороде, равна 7,5 г.
![]()
Уравнение реакции горения лития в кислороде: 4Li + O2 → 2Li2O Молярная масса Li2O = 29,88 г/моль Масса Li2O, образовавшегося при сгорании 3,5 г Li: 3,5 г Li × (1 моль Li / 6,94 г Li) × (2 моль Li2O / 4 моль Li) × (29,88 г Li2O / 1 моль Li2O) = 14,94 г Li2O Ответ: 14,9 г.
![]()
Правильные ответы: 1, 3, 4, 6. Генные мутации – это изменения в генетической информации, которые могут возникать в результате ошибок в процессе репликации ДНК, воздействия мутагенов (вредных факторов окружающей среды) или случайных мутаций. Мутации могут возникать в пределах одного гена или в пределах хромосомы, а также при замене нуклеотидов, что приводит к изменению последовательности аминокислот в структуре белков.

На этой странице очень подробно решены задачи по всем темам химии.
Страница подготовлена для школьников и студентов любых специальностей и охватывает полный курс предмета «химия».
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!

Химия
Химия — это одна из важнейших и обширных областей естествознания, наука, изучающая вещества, также их состав и строение, их свойствах, зависящих от состава и строения, их превращениях, ведущих к изменению состава — химических реакциях, а также о законах и закономерностях, которым эти превращения подчиняются. Поскольку все вещества состоят из атомов, которые благодаря химическим связям способны формировать молекулы, то химия занимается, прежде всего, рассмотрением перечисленных выше задач на атомно-молекулярном уровне, то есть на уровне химических элементов и их соединений.
Эквиваленты и количество эквивалентов простых и сложных веществ. Закон эквивалентов. Способы выражения концентрации растворов
- Эквиваленты и количество эквивалентов простых и сложных веществ. Закон эквивалентов
- Способы выражения концентрации растворов. Молярная концентрация эквивалента (или нормальность) как один из наиболее рациональных способов выражения концентрации
Задача №1
Определить, сколько эквивалентов (эквивалентных масс) заключается в одном моле (молярной массе) веществ:  .
.
Решение:
Формула расчета эквивалентной массы: Э = М/( );
);
 = М/Э — число эквивалентных масс (эквивалентов) в молярной массе (моле).
= М/Э — число эквивалентных масс (эквивалентов) в молярной массе (моле).
Эквивалентов в моле вещества содержится столько, сколько эквивалентных масс содержится в молярной массе, т.е. ( ).
).

Пояснение. ( ) рассчитывается по любой части молекулы. Например:
) рассчитывается по любой части молекулы. Например:

( ) — суммарная валентность двух атомов азота или пяти кислорода;
) — суммарная валентность двух атомов азота или пяти кислорода;
( ) — суммарный заряд трех ионов
) — суммарный заряд трех ионов  или двух ионов
или двух ионов 
Задача №2
Определить, какова молярная концентрация эквивалента (или нормальность) ЗМ раствора  .
.
Решение:
Формула для расчета:  .
.
Для  (
( ) = 1*3 = 3. Следовательно, Сн = 3*3 = 9.
) = 1*3 = 3. Следовательно, Сн = 3*3 = 9.
Пояснение. Состав данного раствора условно можно изобразить так:


В одном и том же растворе молярных эквивалентных масс в ( ) раз больше, чем молярных, т.е. молярная концентрация эквивалента раствора в (
) раз больше, чем молярных, т.е. молярная концентрация эквивалента раствора в ( ) раз больше, чем его молярная концентрация (кроме растворов типа
) раз больше, чем его молярная концентрация (кроме растворов типа  .
.  и т.п.).
и т.п.).
Задача №3
Определить, какая среда — кислая, щелочная или нейтральная — получится при смешивании 8 г  с 10 г
с 10 г  .
.
Решение:
Формула для расчета:  применительно к задаче записывается так:
применительно к задаче записывается так: 
Подставим числовые значения  , получим: 8/40 < 10/49.
, получим: 8/40 < 10/49.
Учитывая, что

делаем вывод: среда кислая, так как для реакции взято избыточное количество эквивалентов кислоты:

Задача №4
Определить, сколько эквивалентов (эквивалентных масс) и граммов содержалось в растворе, если в результате его взаимодействия с раствором  образовалось 3 моля
образовалось 3 моля  .
.
Решение:
Формула для расчета (выбираем наиболее рациональное выражение закона эквивалентов)  применительно к данной задаче записывается так:
применительно к данной задаче записывается так: 
Определим  учитывая, что по условию задачи
учитывая, что по условию задачи  = 3, а молярная и эквивалентная массы связаны соотношением
= 3, а молярная и эквивалентная массы связаны соотношением 
Значит, 1 молярная масса  содержит 2 эквивалента. Определяем, сколько эквивалентов содержат 3 моля:
содержит 2 эквивалента. Определяем, сколько эквивалентов содержат 3 моля:
1 моль — 2 эквивалента
3 моля — X эквивалентов. X = 6.
В результате реакции образовалось 6 эквивалентов  . Согласно закону эквивалентов столько же должно быть эквивалентов
. Согласно закону эквивалентов столько же должно быть эквивалентов  .
.
Определяем массу прореагировавшей щелочи:

Задача №5
Определить, какой объем эквивалента раствора соляной кислоты концентрации 3 моль/л потребуется для получения 1 л углекислого газа из мрамора.
Решение:
Формула для расчета (при выборе наиболее рационального выражения закона эквивалентов учитываем, что продуктом реакции является газ, а исходное вещество — раствор определенной молярной (нормальной) концентрации):

где  — объем газа
— объем газа  — объем раствора
— объем раствора 
Определим объем эквивалентной массы  , учитывая, что
, учитывая, что  (молярная масса содержит 4 эквивалентные массы). Значит, объем эквивалентной массы: 22,4/4 = 5,6 л.
(молярная масса содержит 4 эквивалентные массы). Значит, объем эквивалентной массы: 22,4/4 = 5,6 л.
Определим объем прореагировавшего раствора соляной кислоты:

Задача №6
Определить, сколько 96%-го раствора  (
( = 1,84 г/мл) потребуется для приготовления 1 л раствора с концентрацией 2 моль/л (
= 1,84 г/мл) потребуется для приготовления 1 л раствора с концентрацией 2 моль/л ( = 2).
= 2).
Решение:
Формула для расчета по приготовлению растворов:

Для использования этой формулы надо определить молярную концентрацию эквивалента (Сн) исходного раствора, т.е. осуществить переход:  . Расчет ведется по алгоритму, приведенному на с.25.
. Расчет ведется по алгоритму, приведенному на с.25.

где 49 — эквивалентная масса  , рассчитанная по формуле
, рассчитанная по формуле

Объем концентрированного раствора серной кислоты

Возможно эта страница вам будет полезна:
Строение атома
Квантовое число. Значения, которые оно принимает. Его физический смысл.
Квантовые числа, как и энергия электрона, могут принимать не любые, а только определенные значения, которые различаются на единицу (табл. 5).
Таблица 5

Окончание табл. 5

Значение главного квантового числа, равного 1 (n = 1), отвечает состоянию электрона с самой низкой энергией (т.е. наибольшей устойчивости электрона в атоме). Если состояние электрона характеризуется значением n = 1, то говорят, что электрон находится на первом энергетическом уровне (электронном слое, оболочке). На этом уровне электроны связаны с ядром наиболее прочно и находятся на наименьшем среднем расстоянии от ядра. Размер орбитали минимален.
Таким образом, главное квантовое число указывает на принадлежность электрона к тому или иному энергетическому уровню. Число энергетических уровней в атоме соответствует номеру периода по таблице Д.И. Менделеева, в котором находится данный элемент. Например, атом серы содержит 16 электронов (Z = 16). Эти электроны распределены по трем энергетическим уровням (атом серы находится в III периоде).
Электроны с одинаковым значением главного квантового числа могут иметь разные по форме атомные орбитали, которые определяются значением орбитальною квантового числа I.
Допустимые значения / ограничены значением квантового числа п (см. табл. 5). Например, если п — 4, то орбитальное квантовое число принимает четыре значения: 0, 1, 2, 3. Атомные орбитали (А) могут иметь четыре различные формы. Условно говоря, четвертый энергетический уровень состоит из четырех энергетических подуровней. Подуровни (и электроны, им соответствующие) обозначаются буквами 

Из значений орбитального квантового числа следует, что число подуровней в энергетическом уровне равно номеру уровня. Для характеристики энергетического состояния электронов в атоме используется краткая запись: энергетические уровни, характеризующиеся главным квантовым числом, обозначаются арабской цифрой, а подуровни энергии, характеризующиеся орбитальным квантовым числом — соответствующей латинской буквой (табл. 6).
Таблица 6

В принципе для обозначения всех возможных энергетических состояний было бы достаточно главного и орбитального чисел, если бы не магнитные свойства атома и электрона.
Во внешнем магнитном поле энергия электрона зависит от расположения орбитали. Ориентация орбитали определяется значением магнитного квантового числа  , которое зависит от l. Например, при l = 1
, которое зависит от l. Например, при l = 1  может принимать значения -1,0, или 1. Это значит, что р-орбитали, имеющие форму гантелей, имеют три разные ориентации. Условно говорят, что p-подуровень имеет три энергетические ячейки. Схематично каждый энергетический подуровень можно изобразить прямоугольником, разделенным на ячейки. Общее количество энергетических ячеек равно числу возможных значений магнитного квантового числа и отвечает формуле 2 l + 1.
может принимать значения -1,0, или 1. Это значит, что р-орбитали, имеющие форму гантелей, имеют три разные ориентации. Условно говорят, что p-подуровень имеет три энергетические ячейки. Схематично каждый энергетический подуровень можно изобразить прямоугольником, разделенным на ячейки. Общее количество энергетических ячеек равно числу возможных значений магнитного квантового числа и отвечает формуле 2 l + 1.
Четвертое квантовое число — спиновое, тл. Оно связано с вращательным движением электрона вокруг собственной оси. Вращение возможно как по часовой, так и против часовой стрелки. Поэтому спиновое квантовое число имеет только два значения. Графически это представляют в виде стрелок, направленных во взаимно противоположные стороны:  . Электроны с одинаковым направлением спина называются параллельными, с противоположным направлением — антипараллельными.
. Электроны с одинаковым направлением спина называются параллельными, с противоположным направлением — антипараллельными.
Принцип Паули
Принцип Паули: в атоме не может быть даже двух электронов с одинаковым набором всех четырех квантовых чисел. Этот принцип позволяет определить емкость атомной ячейки, энергетического подуровня и уровня в целом. Согласно принципу Паули, на одной атомной орбитали может быть не более двух электронов, и то при условии, что они антипараллельны. Нахождение на атомной орбитали третьего электрона означало бы, что у двух из них все четыре квантовых числа одинаковы. Емкость энергетических подуровней и уровней определим с помощью табл. 5. Первый энергетический уровень имеет один подуровень 1s и состоит из одной атомной орбитали, на которой с учетом принципа Паули могут разместиться два электрона, записывается:  . Второй имеет два подуровня 2 sp из одной s-орбитали и трех р-орбиталей, на которых могут разместится два и шесть электронов. Общую емкость второго энергетического уровня — восемь электронов -можно изобразить так:
. Второй имеет два подуровня 2 sp из одной s-орбитали и трех р-орбиталей, на которых могут разместится два и шесть электронов. Общую емкость второго энергетического уровня — восемь электронов -можно изобразить так:  . Графически его можно представить так:
. Графически его можно представить так:

Третий энергетический уровень имеет три подуровня: 3 spd. Общая емкость третьего уровня — 18 электронов. Его изображение:  .
.

Четвертый энергетический уровень имеет четыре подуровня: 4 spdf Общая емкость четвертого уровня — 32 электрона. Изображение:  .
.

Возможно эта страница вам будет полезна:
Принцип наименьшей энергии
Принцип наименьшей энергии: электрон при формировании электронной оболочки атома стремится занять орбиталь с наименьшей энергией, т.е. ту орбиталь, которая расположена «ближе» к ядру. Находясь на такой орбитали, электрон будет прочнее связан с ядром. Реальный порядок заполнения орбиталей в атомах имеет следующий вид: 


Этот порядок может быть выведен на основе двух правил Клечковского:
- При увеличении заряда ядра атома последовательное заполнение орбиталей происходит от орбиталей с меньшим значением суммы (n+1) к орбиталям с большим значением этой суммы.
- При одинаковых значениях этой суммы в первую очередь происходит заполнение орбиталей с меньшим значением п. Исключения из правил: заполнение 5d-орбиталей начинается раньше, чем 4f (атом лантана), и 6d-орбиталей раньше, чем 5 f (атом актиния).
Правило Гунда
Правило Гунда: электроны в пределах подуровня стремятся занять свободные орбитали. Когда все орбитали данного подуровня окажутся занятыми, происходит спаривание электронов в каждой орбитали. Последовательность заполнения электронами трех орбиталей p-подуровня.

Составление электронных формул атомов
При составлении электронных формул атомов и заполнении энергетических уровней и подуровней атомов следует обратить внимание на следующие особенности:
- Начало каждого периода совпадает с началом нового энергетического уровня.
- У атомов I и II главных подгрупп формируется внешний энергетический подуровень
 . Это первые 2 элемента в периоде (s-элементы).
. Это первые 2 элемента в периоде (s-элементы). - У атомов III и VIII главных подгрупп заполняется внешний энергетический подуровень
 . Это последние шесть элементов в каждом периоде (р-элементы).
. Это последние шесть элементов в каждом периоде (р-элементы). - Формирование s— и р-подуровней происходит в соответствии с номером периода: например, в III периоде заполняются 3s— и Зр-подуровни.
- У атомов побочных подгрупп происходит заполнение предвнешних
 -подуровней. Они имеются только в больших периодах и располагаются по 10 элементов между s— и p-элементами. Следовательно, 3d-подуровень впервые формируется у атомов IV периода, а 6d в VII периоде.
-подуровней. Они имеются только в больших периодах и располагаются по 10 элементов между s— и p-элементами. Следовательно, 3d-подуровень впервые формируется у атомов IV периода, а 6d в VII периоде. - Для атомов лантаноидов и актиноидов характерно заполнение глубинных
 -подуровней. Следовательно, 4f-подуровень впервые формируется у атомов VI периода, а 5 f — у атомов VII.
-подуровней. Следовательно, 4f-подуровень впервые формируется у атомов VI периода, а 5 f — у атомов VII.
Задача №7
Используя рациональный способ построения электронных формул, напишите электронную формулу для атома технеция (Z = 43).
Решение:
Электронную формулу можно составить, перемещаясь по периодической системе сразу на целые периоды и записывая заполнение энергетических подуровней, происходящее в каждом периоде:

Итого: 
Полная сумма чисел, указываемых над обозначениями орбиталей, должна совпадать с атомным номером элемента, который для технеция равен 43.
Наиболее рационален способ построения электронных формул по «координатам» периодической системы [20]. Положение элемента в периодической системе определяется «координатами», которые имеют определенный физический смысл, связанный со строением атома:

«Координаты» (2-4) определяют особенности электронной структура атома, то есть «концовку» его электронной формулы:

Задача №8
Написать порядок определения валентности элементов главных подгрупп.
Решение:
1. Записывается электронная конфигурация внешнего энергетического уровня атома:

2. Распределяются электроны внешнего энергетического уровня по орбиталям в соответствии с правилом Гунда:

3. Определяются валентность элемента в стационарном состоянии по количеству неспаренных электронов в орбиталях:

4. Определяется наличие вакантных орбиталей на внешнем энергетическом уровне:  На втором энергетическом уровне имеется два подуровня. Свободных орбиталей нет. На третьем энергетическом уровне — три подуровня, есть свободные d-орбитали.
На втором энергетическом уровне имеется два подуровня. Свободных орбиталей нет. На третьем энергетическом уровне — три подуровня, есть свободные d-орбитали. 
5. Изображается переход электронов на вакантные орбитали: 

6. Определяется валентность элемента в возбужденном состоянии: 
Повышение валентности атома кислорода за счет . возбуждения невозможно. По этой причине кислород имеет постоянную валентность, равную 2. Атом серы при возбуждении проявляет валентность 4, 6.
Примечания.
- Переменные валентности элементов главных подгрупп — отличаются на две единицы.
- Валентности элементов четных подгрупп выражаются четными числами.
- Валентности элементов нечетных подгрупп выражаются нечетными числами.
- Элементы второго периода не проявляют высоких значений валентности, которые известны для их аналогов в периодической системе.
- Высшая валентность элементов третьего и последующих периодов в главных подгруппах равна номеру группы.
Задача №9
Написать порядок определения валентности элементов побочных подгрупп.
Решение:
1. Записывается «концовка» электронной формулы

2. Распределяются электроны по орбиталям:

3. Определяется валентность элемента в стационарном состоянии. При этом следует учитывать, что большинство d-элементов в этом состоянии не склонно проявлять валентность, так как на внешнем уровне нет неспаренных электронов:

Сравните для атома серебра:

4. Определяется минимальная валентность атома при возбуждении. Она, как правило, равняется двум за счет разъединения s-электронов и перехода их на свободный р-подуровень:

5. Определяется наличие вакантных орбиталей на предвнешнем уровне:  . На третьем энергетическом уровне — три подуровня. Свободных орбиталей нет.
. На третьем энергетическом уровне — три подуровня. Свободных орбиталей нет.
 На пятом энергетическом уровне — пять подуровней. Есть свободные f-орбитали.
На пятом энергетическом уровне — пять подуровней. Есть свободные f-орбитали.
6. Изображается переход электронов на вакантные орбитали:

7. Определяется максимальная валентность атома в возбужденном состоянии:

8. Выписываются все возможные валентности от минимальной до максимальной. Следует иметь в виду, что у d-орбиталей валентности отличаются на единицу:

Следует отметить, что спиновая теория валентности носит лишь приближенный характер (особенно по отношению к d-элементам).
Задача №10
Написать электронные формулы атома азота и ионов  ; дать их окислительно-восстановительную характеристику.
; дать их окислительно-восстановительную характеристику.
Решение:
Электронная формула азота:  . Атом азота может принять три электрона на р-подуровень и отдать пять электронов с внешнего энергетического уровня. Следовательно, для него характерны как окислительные, так и восстановительные свойства. Ионизация атома азота идет следующим образом:
. Атом азота может принять три электрона на р-подуровень и отдать пять электронов с внешнего энергетического уровня. Следовательно, для него характерны как окислительные, так и восстановительные свойства. Ионизация атома азота идет следующим образом:

Электронные формулы ионов:

Ион  — абсолютный восстановитель, так как способен только к отдаче электронов со второго энергетического уровня. Ион
— абсолютный восстановитель, так как способен только к отдаче электронов со второго энергетического уровня. Ион  — абсолютный окислитель, так как способен только принимать электроны в свободные орбитали второго энергетического уровня. Ион
— абсолютный окислитель, так как способен только принимать электроны в свободные орбитали второго энергетического уровня. Ион  может быть как восстановителем, так и окислителем.
может быть как восстановителем, так и окислителем.
Вывод.
Атом элемента в высшей степени окисления ( ) — окислитель, а в низшей степени окисления (
) — окислитель, а в низшей степени окисления ( ) — восстановитель. Атом элемента, имеющий промежуточную степень окисления, может проявлять как окислительные, так и восстановительные свойства.
) — восстановитель. Атом элемента, имеющий промежуточную степень окисления, может проявлять как окислительные, так и восстановительные свойства.
Задача №11
Определить свойства элемента с порядковым номером 105.
Решение:
Для определения свойства элемента достаточно знать «концовку» его электронной формулы:
 формируется d-подуровень
формируется d-подуровень
 количество электронов внеш, уровня
количество электронов внеш, уровня
 количество валентных электронов
количество валентных электронов
Нильсборий — элемент d-семейства. Это металл, так как имеет малое число электронов на внешнем энергетическом уровне. В стационарном состоянии не склонен к проявлению валентности, так как на внешнем энергетическом уровне имеет только спаренные электроны:

При возбуждении может быть двухвалентным:

Максимальная валентность равна пяти:

Набор возможных валентностей: 2, 3, 4, 5. Ns — восстановитель. Его возможные окислительные числа (О.Ч.): +2, +3, +4, +5.
Формы и свойства соединений, образуемых данным элементом, определяет окислительное число его атомов. Например, возможные формулы оксидов данного элемента: 

Известно, что, проявляя высшее значение О.Ч., равное номеру группы, элементы главной и побочной подгрупп образуют соединения, близкие по своим свойствам. Для Ns высшее значение О.Ч. равно +5. Этому значению О.Ч. соответствуют оксид  и гидроксид
и гидроксид  , аналогичные по форме и свойствам оксиду и гидроксиду элемента фосфора
, аналогичные по форме и свойствам оксиду и гидроксиду элемента фосфора  . Причина такого сходства — аналогичное строение электронных оболочек ионов:
. Причина такого сходства — аналогичное строение электронных оболочек ионов:

Примечание. Количество (число) электронов на внешнем энергетическом уровне иона называют типом иона. У ионов  тип иона восьмиэлектронный (
тип иона восьмиэлектронный ( ). Тип иона влияет на свойства соединений и учитывается в теории поляризации ионов.
). Тип иона влияет на свойства соединений и учитывается в теории поляризации ионов.
Возможно эта страница вам будет полезна:
Периодическая система элементов
Периодический закон, открытый в 1869 году Д.И. Менделеевым, положил начало новой эпохе в химии. Этот этап развития химии является важнейшим после открытия атомно-молекулярной теории.
Периодическая система состоит из 12 горизонтальных и 8 вертикальных рядов. Горизонтальные ряды называются периодами, а вертикальные — группами.
1-й ряд состоит из двух элементов. 2-й и 3-й ряды — из восьми; они начинаются щелочным металлом и заканчиваются инертным газом. Первые три периода называются малыми, остальные — большими.
Элементы по сходству и различию разделены на главные и побочные подгруппы. Это происходит оттого, что элемент имеет большое сходство с другим элементом, стоящим не рядом, а через клетку. Например: хлор имеет большое сходство с бромом, но отделен марганцем; селен похож на теллур, но он отделен молибденом; калий имеет сходные свойства с рубидием, но через медь. Чтобы отметить такое различие между рядами, элементы четных рядов в больших периодах сдвинуты влево, а элементы нечетных рядов — вправо. Таким образом, начиная с IV периода каждую группу можно разделить на две подгруппы: главную и побочную.
Главная подгруппа составлена из элементов, состоящих из четных и нечетных рядов  . Побочная подгруппа —
. Побочная подгруппа — 
Принцип расположения элементов по возрастанию заряда ядер атомов служил руководством для Д.И. Менделеева при построении периодической системы. Однако в периодической системе имеются отклонения от этого принципа. Так, аргон стоит впереди калия, хотя его масса больше, чем масса ядра калия. Кобальт находится впереди никеля, теллур — впереди йода. Д.И. Менделеев здесь отступил от основного принципа закона и руководствовался всей совокупностью индивидуальных свойств. Впоследствии это подтвердилось и соответствует строению атома. Безупречность периодической системы доказана экспериментально на основе закона Мозли.
В 1920 г. английский ученый Д. Чедвик экспериментально установил, что порядковый номер элемента численно равен положительному заряду ядра атома этого элемента, т.е. числу протонов в ядре.
Химическим элементом называют определенный вид атомов, имеющих одинаковый заряд ядра — одинаковое число протонов в ядре.
Современная формулировка периодического закона гласит: свойства элементов и их соединений находятся в периодической зависимости от заряда ядер их атомов.
Номер группы указывает на высшую валентность элемента и выявляет тем самым максимальное число электронов атома того или иного элемента, которое может участвовать в образовании химической связи.
Номер периода оказался связанным с числом энергетических уровней, имеющихся в электронной оболочке атома элемента данного периода.
Итак, горизонтальные ряды таблицы названы периодами, а вертикальные ряды — группами. В периодах свойства элементов изменяются последовательно. При этом элементы, имеющие одинаковую высшую валентность, попадают в один вертикальный ряд, который составляет одну группу.
Задача №12
Определить, у какого из элементов IV периода -марганца или брома — сильнее выражены металлические свойства.
Решение:
Электронные формулы 

Марганец — d-элемент VII В-группы, а бром — p-элемент VII A-группы. На внешнем энергетическом уровне у атома марганца 2 электрона, у атома брома — 7.
Атомы типичных металлов характеризуются наличием небольшого числа электронов на внешнем энергетическом уровне, а следовательно, тенденцией терять эти электроны. Они обладают только восстановительными свойствами и не обладают отрицательными ионами. Элементы, атомы которых на внешнем энергетическом уровне содержат более трех электронов, обладают определенным сродством к электрону, а следовательно, приобретают отрицательно заряженные ионы. Поэтому марганец, как и другие металлы, обладает только восстановительными свойствами, тогда как для брома характерны окислительные свойства. Общей закономерностью для всех групп, содержащих р— и d-элементы, является преобладание металлических свойств у d-элементов. Таким образом, металлические свойства у марганца выражены сильнее, чем у брома.
Химическая связь и строение (геометрия) молекул
Задача №13
Определить тип иона у катионов ( ,
,  ).
).
Решение:
- Необходимо записать электронные формулы элементов.
- С внешней электронной оболочки атома необходимо убрать такое число электронов, которое бы соответствовало заряду катиона.
- Подсчитать число электронов, оставшееся на внешней оболочке катиона, и определить тип иона (табл.7).
Таблица 7

Определите тип иона у аниона  (табл.8).
(табл.8).
Таблица 8

Окончание табл. 8

Из табл. 8 видно, что повторяется вся последовательность решения предыдущего примера. Однако в данном случае необходимо прибавить такое число электронов, которое бы соответствовало заряду аниона.
Выводы.
- Тип иона у всех простых анионов
 .
. - В общем случае тип иона соответствует числу электронов на внешней оболочке анионов и катионов. Исключение составляют ионы типа (18 + n).
Задача №14
Объяснить изменение окраски в ряду следующих соединений: a)  (белый),
(белый),  (желтый); б)
(желтый); б)  (белый),
(белый),  (черный).
(черный).
Решение:
Первоначально рассмотрим изменение окраски в ряду галогенидов серебра. Соединения содержат в своем составе один и тот же катион —  , а потому изменение окраски связано только с деформируемостью анионов хлора и йода. Для доказательства детально обсудим свойства анионов (заряд, радиус, тип иона) — см. табл. 9.
, а потому изменение окраски связано только с деформируемостью анионов хлора и йода. Для доказательства детально обсудим свойства анионов (заряд, радиус, тип иона) — см. табл. 9.
Вывод. Два свойства анионов хлора и йода (заряд и тип иона) одинаковы, наблюдается лишь увеличение радиуса при переходе от хлора к йоду. Увеличение же радиуса аниона приводит к увеличению его деформируемости и соответственно — поляризации ионов, что приводит к уменьшению степени ионности связи в молекуле  , отчего соединение приобретает окраску.
, отчего соединение приобретает окраску.
Таблица 9

Итак, йодиды в соединениях q одинаковыми катионами должны быть чаще окрашены, чем соответствующие хлориды, сходная закономерность характерна для перехода по ряду оксиды — сульфиды: сульфиды окрашены, как правило, интенсивнее, чем соответствующие оксиды (табл. 10).
Таблица 10

Вывод. Увеличение прежде всего отрицательного заряда аниона в ряду  — способствует увеличению деформируемости
— способствует увеличению деформируемости  , уменьшению степени ионности связи в ряду
, уменьшению степени ионности связи в ряду  и появлению черной окраски у
и появлению черной окраски у  . Аналогичным образом можно объяснить, почему гидроксиды металлов (производные
. Аналогичным образом можно объяснить, почему гидроксиды металлов (производные  имеют менее глубокое окрашивание, чем соответствующие оксиды (это связано с меньшей деформируемостью
имеют менее глубокое окрашивание, чем соответствующие оксиды (это связано с меньшей деформируемостью  по сравнению с
по сравнению с  ).
).
Задача №15
Объяснить изменение окраски в ряду следующих оксидов:  (белый),
(белый),  (оранжевый),
(оранжевый),  (красный),
(красный),  (темно-зеленый).
(темно-зеленый).
Решение:
Указанные оксиды отличаются лишь природой условного катиона, следовательно, изменение окраски связано с изменением их поляризующего действия на  . Сопоставим свойства и поляризующее действие соответствующих катионов (табл. 11).
. Сопоставим свойства и поляризующее действие соответствующих катионов (табл. 11).
Таблица 11

Вывод. В ряду оксидов  наблюдается изменение двух свойств соответствующих катионов (заряда, радиуса), а увеличение заряда и уменьшение радиуса способствует увеличению поляризующего действия катиона и аниона, увеличению деформации последнего, что приводит к уменьшению степени ионности связи в оксидах и соответственно — к усилению интенсивности их окраски.
наблюдается изменение двух свойств соответствующих катионов (заряда, радиуса), а увеличение заряда и уменьшение радиуса способствует увеличению поляризующего действия катиона и аниона, увеличению деформации последнего, что приводит к уменьшению степени ионности связи в оксидах и соответственно — к усилению интенсивности их окраски.
Задача №16
Объяснить изменение окраски соединений в ряду следующих сульфидов:  (белый),
(белый),  (желтый),
(желтый),  (черный).
(черный).
Решение:
Формулы соединений показывают, что изменение окраски связано с изменением поляризующего действия катионов. Свойства и поляризующее действие катионов данных сульфидов представлены в табл. 12.
Вывод. В ряду сульфидов наблюдается увеличение радиуса у 18 электронных катионов, имеющих одинаковый заряд, что способствует увеличению их деформируемости и соответственно — увеличению их суммарного поляризующего действия. Следовательно, поляризующее действие наиболее велико у  , имеющего наибольший радиус (при прочих равных условиях), степень ионности химической связи в
, имеющего наибольший радиус (при прочих равных условиях), степень ионности химической связи в  соответственно меньше, чем у других сульфидов, а потому
соответственно меньше, чем у других сульфидов, а потому  имеет наиболее интенсивную черную окраску.
имеет наиболее интенсивную черную окраску.
Таблица 12

Задача №17
Определить закономерности изменения силы кислот и оснований по периоду и по группе.
Решение:
Изменение кислотно-основных свойств гидроксидов по периоду рассмотрим на примере элементов III периода системы Д.И. Менделеева: с этой целью разделим элементы периода на металлы и неметаллы; отметим основные свойства ионов элементов (заряд, равный номеру группы, сравнительный радиус, тип иона); уменьшение или увеличение поляризующего действия  соответственно увеличение или уменьшение степени ионности связи, согласуя все это с характеристикой силы оснований и кислот по периоду:
соответственно увеличение или уменьшение степени ионности связи, согласуя все это с характеристикой силы оснований и кислот по периоду:




Вывод. Степень ионности химической связи  и кислотно-основные свойства гидроксидов элементов одного и того же периода зависят от двух свойств ионов: заряда и радиуса. Изменение кислотно-основных свойств гидроксидов по подгруппе на примере элементов II A-группы (основные свойства) и некоторых элементов VI A-группы (кислотные свойства) показано в табл.13, 14.
и кислотно-основные свойства гидроксидов элементов одного и того же периода зависят от двух свойств ионов: заряда и радиуса. Изменение кислотно-основных свойств гидроксидов по подгруппе на примере элементов II A-группы (основные свойства) и некоторых элементов VI A-группы (кислотные свойства) показано в табл.13, 14.
Таблица 13

Таблица 14

Вывод. Степень ионности химической связи  и кислотно-основные свойства гидроксидов элементов в подгруппе периодической системы зависят от радиусов ионов.
и кислотно-основные свойства гидроксидов элементов в подгруппе периодической системы зависят от радиусов ионов.
Задача №18
Что такое гибридизация валентных орбиталей и каково строение молекулы типа  ?
?
Решение:
Теория валентных связей (ВС) предполагает участие в образовании ковалентных связей не только «чистых» атомных орбиталей (АО), но и «смешанных», так называемых гибридных АО. При гибридизации первоначальная форма и энергия орбиталей (электронных облаков) взаимно изменяются, и образуются орбитали (облака) новой одинаковой формы и одинаковой энергии. Число гибридных орбиталей  равно числу исходных. Ответ на поставленный вопрос отражен в табл. 15.
равно числу исходных. Ответ на поставленный вопрос отражен в табл. 15.
Таблица 15

Задача №19
Определить тип связей в  ,
,  .
.
Решение:
Для определения типа связи необходимо:
- Выписать (из таблицы в приложении) и сопоставить значения относительной электроотрицательности (ОЭО) для атомов, входящих в состав соединений, на основе сопоставления вычислить
 для них.
для них. - Сделать на основании вычисленного
 и состава соединения вывод о типе связи в данном соединении:
и состава соединения вывод о типе связи в данном соединении:
а) для совокупности атомов  , следовательно, связь между данными атомами ковалентно-неполярная;
, следовательно, связь между данными атомами ковалентно-неполярная;
б) для совокупности атомов  , но к ионному соединению следует отнести лишь
, но к ионному соединению следует отнести лишь  , так как известно, что лишь галогениды щелочных и щелочно-земельных металлов образуют ионные соединения. Образование же таких многозарядных катионов, как
, так как известно, что лишь галогениды щелочных и щелочно-земельных металлов образуют ионные соединения. Образование же таких многозарядных катионов, как  , и анионов, как
, и анионов, как  , энергетически невыгодно, а потому
, энергетически невыгодно, а потому  — ковалентно-полярные соединения.
— ковалентно-полярные соединения.
Вследствие волновых свойств электронов чистых типов связей нет. Поэтому по разности в электроотрицательности атомов (соединяющих молекулу) чаще всего судят о степени ионности химической связи. Согласно Полингу, чем больше разница в электроотрицательности атомов (входящих в состав молекулы), тем больше степень ионности химической связи.
Задача №20
Найти геометрию молекул  .
.
Решение:
Для определения геометрии ковалентных молекул необходимо:
- Выписать концовки электронных формул атомов, входящих в состав молекул.
- Распределить электроны многовалентного атома по атомным орбиталям согласно правилу Гунда и проявляемой им валентности в данном соединении и определить форму взаимодействующих электронных облаков атома.
- Найти ориентацию взаимодействующих электронных облаков многовалентного атома и распределение химических связей в пространстве, т.е. геометрию молекулы.
В состав молекулы  входят атомы водорода и селена, концовки их электронных формул будут:
входят атомы водорода и селена, концовки их электронных формул будут:  .
.
Распределим электроны Se по атомным орбиталям:

Так как Se в  двухвалентен, то, следовательно, валентными будут лишь два р-электрона на 4 р-подуровне.
двухвалентен, то, следовательно, валентными будут лишь два р-электрона на 4 р-подуровне.
Согласно квантовой механике два р-облака одного и того же атома (в данном случае селена) будут ориентированы в пространстве под углом 90°. Следовательно, s-облака двух атомов водорода будут перекрываться двумя р-облаками по схеме:

Угол между двумя химическими связями будет равен 90°, и поэтому молекула имеет угловую геометрическую конфигурацию.
Нетрудно сделать вывод, что если многовалентный атом молекулы трехвалентен и в образовании связи участвуют 3 р-облака, то они также будут ориентированы под углом 90° относительно друг друга, и молекула будет иметь в этом случае пирамидальную конфигурацию, как у  :
:

Примечание. Возможно отклонение ориентации нескольких р-облаков от угла 90°. Так, угол между двумя связями О-Н в молекуле воды равен 104°28’. Отклонение от угла 90° объясняется полярностью связи О-Н, в результате чего у атома водорода появляется положительный заряд; отталкивание этих зарядов увеличивает угол между связями.
Вывод. Если в образовании химической связи участвуют несколько одинаковых электронных облаков одного и того же атома, то геометрическая конфигурация молекул асимметрична (угловые, пирамидальные молекулы).
Молекула  в состав этой молекулы входят атомы хлора и бериллия, и концовки их электронных формул выглядят:
в состав этой молекулы входят атомы хлора и бериллия, и концовки их электронных формул выглядят: 
Распределим электроны бериллия по АО 2-го энергетического уровня с учетом его валентности в  :
:

Валентными электронами у бериллия будут s— и р-электроны. Но известно? что во всех случаях, когда в образовании химических -связей у данного атома участвуют электроны разных’-подуровней, наблюдается гибридизация, или смешение электронных облаков. Гибридизация одного s— и одного р-электронных облаков приводит к образованию двух гибридных облаков —  . Это sp-гибридизация.
. Это sp-гибридизация.
Схема гибридизации электронных облаков Be:

Относительно друг друга гибридные облака всегда ориентируются симметрично. В данном случае симметричность достигается, если между двумя g-облаками будет угол 180°. Две химические связи, образованные путем перекрытия двух р-облаков двух атомов хлора, двух g-облаков атома бериллия, расположены по прямой и противоположно направлены. Поэтому молекулы с этим видом гибридизации линейны:

Нетрудно представить, что если у атома в результате  — или
— или  -гибридизации участвуют соответственно
-гибридизации участвуют соответственно  — облака, то их симметричное распределение в пространстве достигается, если в первом случае угол между ними будет 120°, а во втором — 109°28’ (треугольная и тетраэдрическая молекулы).
— облака, то их симметричное распределение в пространстве достигается, если в первом случае угол между ними будет 120°, а во втором — 109°28’ (треугольная и тетраэдрическая молекулы).
Вывод. Участие гибридных облаков в химической связи приводит к возникновению молекул с симметричной геометрической конфигурацией (линейная, треугольная, тетраэдрическая и т.д.).
Задача №21
Определить тип ковалентных молекул.
Решение:
Различают два типа ковалентных молекул: неполярные (дипольный момент молекулы  равен 0), полярные молекулы (дипольный момент
равен 0), полярные молекулы (дипольный момент  > 0). Но дипольный момент молекулы
> 0). Но дипольный момент молекулы  только для двухатомной молекулы совпадает по значению и направлению с
только для двухатомной молекулы совпадает по значению и направлению с  . В общем случае дипольный момент молекулы (
. В общем случае дипольный момент молекулы ( ) есть геометрическая сумма дипольных моментов
) есть геометрическая сумма дипольных моментов  всех связей. Следовательно, для того чтобы определить дипольный момент молекулы, необходимо знать: а) полярность химических связей (т.е.
всех связей. Следовательно, для того чтобы определить дипольный момент молекулы, необходимо знать: а) полярность химических связей (т.е.  связей равен нулю или больше нуля); б) геометрическую конфигурацию молекул. Здесь можно встретиться со следующим: если дипольный момент
связей равен нулю или больше нуля); б) геометрическую конфигурацию молекул. Здесь можно встретиться со следующим: если дипольный момент  связей равен нулю, то молекула в целом неполярная (
связей равен нулю, то молекула в целом неполярная ( равен нулю); если
равен нулю); если  больше нуля, то тип молекулы будет определяться всецело геометрической конфигурацией молекулы. Если геометрия молекулы асимметрична, то дипольные моменты
больше нуля, то тип молекулы будет определяться всецело геометрической конфигурацией молекулы. Если геометрия молекулы асимметрична, то дипольные моменты  связей складываются по правилу параллелограмма и дипольный момент молекулы
связей складываются по правилу параллелограмма и дипольный момент молекулы  больше нуля, т.е. молекула полярна.
больше нуля, т.е. молекула полярна.
Если геометрическая конфигурация симметрична, То дипольный момент  молекулы равен 0, т.е. молекула неполярная.
молекулы равен 0, т.е. молекула неполярная.
Определим тип молекулы  . Для этого:
. Для этого:
1. Определяем полярность связи H-Se-H на основе электроотрицательности Н и Se. Так как  , то связь полярна.
, то связь полярна.
2. Определяем геометрическую конфигурацию молекулы  . Делаем вывод:
. Делаем вывод:  — молекула угловая, т.е. асимметрична.
— молекула угловая, т.е. асимметрична.
3. Складываем дипольные моменты связей  по правилу параллелограмма и находим дипольный момент молекулы
по правилу параллелограмма и находим дипольный момент молекулы  :
:

Дипольный момент молекулы  в данном случае больше О, следовательно, молекула полярна.
в данном случае больше О, следовательно, молекула полярна.
Определим тип молекулы  . Для этого:
. Для этого:
- Определяем полярность связи
 на основе электроотрицательности. Так как
на основе электроотрицательности. Так как  , то связь полярна.
, то связь полярна. - Определяем геометрическую конфигурацию
 . Делаем вывод: молекула линейна (симметрична).
. Делаем вывод: молекула линейна (симметрична). - Складываем дипольные моменты связей
 :
:

но геометрическая сумма двух равных векторов, имеющих различное направление, равна 0, т.е. дипольный момент молекулы равен 0, а молекула неполярна.
Задача №22
Описать строение двухатомных гомоядерных молекул элементов И периода на основе молекулярных орбиталей (МО).
Решение:
В методе молекулярных орбиталей состояние молекулы описывается как совокупность электронных МО. При этом число МО равно сумме АО; МО, возникающей от сложения АО, соответствует более низкая энергия, чем исходным орбиталям. Такая МО имеет повышенную электронную плотность в пространстве между ядрами, способствует образованию химической связи и называется связывающей. МО, образовавшейся от вычитания атомных орбиталей, соответствует более высокая энергия, чем АО. Электронная плотность в этом случае сконцентрирована за ядрами атомов, а между ними равна 0. Подобные МО энергетически менее выгодны, чем исходные АО, они приводят к ослаблению химической связи и называются разрыхляющими. Электроны, занимающие связывающие и разрыхляющие орбитали, называют соответственно связывающими и разрыхляющими электронами. Заполнение молекулярных орбиталей происходит при соблюдении принципа Паули и правила Гунда по мере увеличения их энергии в такой последовательности:

При образовании молекулярных орбиталей из атомных для двухатомных гомоядерных (одного и того же элемента) молекул элемента II периода число связывающих и разрыхляющих электронов зависит от их числа в атомах исходных элементов (рис.1):

Рис. 1. Энергетическая схема образования молекулярных орбиталей из атомных для гомоядерных молекул 11 периода
Следует отметить, что при образовании молекул  энергия связывающей сигма
энергия связывающей сигма  -орбитали больше энергии связывающих
-орбитали больше энергии связывающих  -орбиталей, тогда как в молекулах кислорода и фтора, наоборот, энергия связывающих
-орбиталей, тогда как в молекулах кислорода и фтора, наоборот, энергия связывающих  — и
— и  .-орбиталей больше энергии связывающей ст2рг-орбитали. Это нужно учитывать при изображении энергетических схем соответствующих молекул.
.-орбиталей больше энергии связывающей ст2рг-орбитали. Это нужно учитывать при изображении энергетических схем соответствующих молекул.
Порядок связи в молекуле определяется разностью чисел связывающих и разрыхляющих орбиталей, деленной на два. Порядок связи может быть равен 0 (молекула не существует), целому или дробному положительному числу.
Подобно электронным формулам, показывающим распределение электронов в атоме по атомным орбиталям, в методе МО составляются формулы молекул, отражающие их электронную конфигурацию. По аналогии с атомными s-, p-,d-, f-орбиталями МО обозначаются греческими буквами  . Так, электронная конфигурация молекул кислорода описывается следующим образом:
. Так, электронная конфигурация молекул кислорода описывается следующим образом:

Буквами КК показано, что четыре 15-электрона (два связывающих и два разрыхляющих) практически не оказывают влияния на химическую связь.
Основы химической термодинамики
Химическая термодинамика — наука, изучающая переходы энергии из одной формы в другую при химических реакциях и устанавливающая направление и пределы их самопроизвольного протекания в заданных условиях.
Итак, наука о взаимных превращениях различных видов энергии называется термодинамикой. Термодинамика устанавливает законы этих превращений, а также направление самопроизвольного течения различных процессов в данных условиях.
Тенденция к беспорядку характеризует величину, которую называют энтропией (S). Энтропия S и энтальпия Н являются свойством вещества: энтропия 5 отражает движение частиц вещества и является мерой неупорядоченности системы.
Движущаяся сила процесса складывается из двух сил: стремления к упорядочению Н и стремления к беспорядку TS. При постоянном значении давления Р и абсолютной температуре Т общую движущую силу обозначают 
Величина G называется изобарно-изотермическим потенциалом, или энергией Гиббса. Общую движущую силу процесса G можно найти из соотношения: 
Мерой химического сродства является убыль энергии Гиббса  , зависящая от природы вещества, его количества и температуры. Энергия Гиббса является функцией состояния
, зависящая от природы вещества, его количества и температуры. Энергия Гиббса является функцией состояния  поэтому
поэтому  может принимать три значения:
может принимать три значения: 
 . Если
. Если  процесс самопроизвольно проходить не может. Если же
процесс самопроизвольно проходить не может. Если же  то процесс проходит самопроизвольно слева направо. При значении
то процесс проходит самопроизвольно слева направо. При значении  система находится в равновесии.
система находится в равновесии.
Использование изобарных потенциалов в общей химии
Используя значения изобарных потенциалов, можно:
- Определить возможность или направление реакций в любых условиях (в частном случае коррозионную устойчивость металлов в различных агрессивных средах).
- Установить влияние температуры на направление химического процесса.
- Сопоставить химические свойства элементов, простых и сложных веществ.
- Вычислить константу равновесия при различных температурах и определить оптимальные физико-химические условия образования химических веществ.
- Находить стандартную ЭДС — Е° и теоретический (термодинамический) КПД любого химического источника тока (гальванического элемента, топливного элемента, аккумулятора), в котором в качестве электролита могут быть использованы водные и неводные растворы электролитов и так называемые твердые электролиты.
- Рассчитать теоретический потенциал разложения и КПД для низко- и высокотемпературных реакций, протекающих в электролизере.
Задача №23
Доказать, возможна ли химическая коррозия алюминия в атмосфере сухого воздуха при температуре 25°C по реакции:

Решение:
Так как  для алюминия и кислорода равны 0, то
для алюминия и кислорода равны 0, то  Полученная величина
Полученная величина  меньше 0, поэтому окисление алюминия возможно не только в стандартных условиях (в чистом кислороде, парциальное давление которого равно 1 атм.), но и в нестандартных условиях (в воздухе, в газовой смеси, с незначительным содержанием кислорода).
меньше 0, поэтому окисление алюминия возможно не только в стандартных условиях (в чистом кислороде, парциальное давление которого равно 1 атм.), но и в нестандартных условиях (в воздухе, в газовой смеси, с незначительным содержанием кислорода).
Повышенную коррозионную устойчивость алюминия придает прочный защитный слой из  (оксидная изоляция). Этой особенностью алюминия объясняется большая популярность алюминия в энергетике (в настоящее время длина алюминиевых проводов на линии высоковольтных передач во всем мире превышает
(оксидная изоляция). Этой особенностью алюминия объясняется большая популярность алюминия в энергетике (в настоящее время длина алюминиевых проводов на линии высоковольтных передач во всем мире превышает  км); в электротехнике (половина всех кабелей с резиновой, полиэтиленовой, поливинилхлоридной изоляцией выпускается с алюминиевыми токопроводящими жилами).
км); в электротехнике (половина всех кабелей с резиновой, полиэтиленовой, поливинилхлоридной изоляцией выпускается с алюминиевыми токопроводящими жилами).
Задача №24
Возможна ли реакция фиксации азота водой: 
если  ?
?
Решение:
 имеет положительное значение, поэтому реакция невозможна при любых условиях. (Для смещения равновесия в этом случае потребовалось бы давление порядка
имеет положительное значение, поэтому реакция невозможна при любых условиях. (Для смещения равновесия в этом случае потребовалось бы давление порядка  атм., что практически недостижимо.)
атм., что практически недостижимо.)
Влияние температуры на направление химического процесса
Задача №25
Восстановление  водородом идет по уравнению:
водородом идет по уравнению:

Определить, возможна ли эта реакция в стандартных условиях, если изменение энтропии  = 0,1387 кДж/(моль-К)? При какой температуре начинается восстановление
= 0,1387 кДж/(моль-К)? При какой температуре начинается восстановление  ?
?
Решение:

Так как  то реакция в стандартных условиях невозможна. Более того, в этих условиях идет обратный процесс окисления железа (коррозия). Найдем температуру, при которой
то реакция в стандартных условиях невозможна. Более того, в этих условиях идет обратный процесс окисления железа (коррозия). Найдем температуру, при которой 

Вывод. Следовательно, восстановление  начнется при
начнется при 
Возможно эта страница вам будет полезна:
Использование изобарного потенциала для характеристики химических свойств элементов, простых и сложных веществ
Задача №26
Вычислить изменение  по значениям стандартных потенциалов образования
по значениям стандартных потенциалов образования  реагирующих веществ для процессов:
реагирующих веществ для процессов:

1) решить вопрос о термодинамической устойчивости смесей веществ: 
2) сделать заключение о возможности контакта указанных веществ при создании резистивных пленок.
Решение:

Учитывая, что  всех простых веществ равно О, находим:
всех простых веществ равно О, находим:
 прод.реакиии —
прод.реакиии —  исх.веществ и по знаку и числовому значению
исх.веществ и по знаку и числовому значению  делаем вывод о возможном направлении реакций при стандартной температуре в стандартных условиях:
делаем вывод о возможном направлении реакций при стандартной температуре в стандартных условиях:

Выводы.
- Первая реакция возможна. Следовательно, комбинация указанных веществ
 термодинамически неустойчива, поэтому при напылении алюминия на оксид олова (для осуществления электрического контакта в резистентной пленке) образуется изолирующий слой оксида алюминия, который прерывает пленку.
термодинамически неустойчива, поэтому при напылении алюминия на оксид олова (для осуществления электрического контакта в резистентной пленке) образуется изолирующий слой оксида алюминия, который прерывает пленку. - Вторая реакция невозможна, т.е. комбинации
 термодинамически устойчивы. Так как никель не реагирует с оксидом олова, а также с алюминием, то можно создать резистор на основе оксида олова и алюминия путем ввода Ni в качестве промежуточного слоя, что обеспечивает надежный контакт.
термодинамически устойчивы. Так как никель не реагирует с оксидом олова, а также с алюминием, то можно создать резистор на основе оксида олова и алюминия путем ввода Ni в качестве промежуточного слоя, что обеспечивает надежный контакт.
Таким образом, вопрос совместимости металлических резистивных и диэлектрических материалов, используемых в создании микроэлектронных и особенно пленочных схем, требует тщательного изучения.
Задача №27
 (карбид кремния) — карборунд интересен как полупроводник и как термически устойчивое твердое вещество (абразив). Находит широкое применение в технике:
(карбид кремния) — карборунд интересен как полупроводник и как термически устойчивое твердое вещество (абразив). Находит широкое применение в технике:
- Из
 изготовляют нелинейные сопротивления (варисторы), т.е. приборы, значение омического сопротивления которых зависит от приложения к ним напряженности электрического поля.
изготовляют нелинейные сопротивления (варисторы), т.е. приборы, значение омического сопротивления которых зависит от приложения к ним напряженности электрического поля. - Диоды и транзисторы, работающие при высокой температуре.
- Входит в состав силита (смесь кремния и глицерина), используется как нагревательный элемент в электропечах, работающих при температуре выше 1000 °C, из
 вместе с В4С конструируют высокотемпературную термопару.
вместе с В4С конструируют высокотемпературную термопару.  получают нагреванием до 2000 °C в электропечах. Студентам электроэнергетического профиля надо знать, как определяют оптимальные физико-химические условия получения
получают нагреванием до 2000 °C в электропечах. Студентам электроэнергетического профиля надо знать, как определяют оптимальные физико-химические условия получения  в электропечах по реакции:
в электропечах по реакции:

Решение:
1. Выпишем  для всех участников реакции:
для всех участников реакции:

2. Подсчитаем 

3. Подсчитаем 

Выводы. Так как  то данный процесс обратим, невозможен при низкой температуре. Указанный вывод можно подтвердить путем расчета
то данный процесс обратим, невозможен при низкой температуре. Указанный вывод можно подтвердить путем расчета  и
и 

реакция при низких температурах невозможна.
4. Прежде чем вычислить  , определим температуру начала реакции, когда
, определим температуру начала реакции, когда  . = 0 по уравнению:
. = 0 по уравнению:


реакция протекает слева направо лишь при температуре выше 1783 К.
5. Подсчитаем  . при любой температуре выше 1783 К, например, при Т — 273 К:
. при любой температуре выше 1783 К, например, при Т — 273 К:

реакция невозможна.
6. Определим глубину протекания прямого процесса при Т = 2273 К, т.е. определим  по формуле:
по формуле:


Вывод. Кр = 4. Это свидетельствует о резком смещении равновесия в сторону прямого процесса при данных температурных условиях.
7. Следует отметить, что для определения оптимальных температур процесса необходимо проводить расчет  для ряда температур выше 1783 К. Причем, если расчет покажет, что дальнейшее повышение температуры мало меняет
для ряда температур выше 1783 К. Причем, если расчет покажет, что дальнейшее повышение температуры мало меняет  , то целесообразно остановить свой выбор на меньшем значении абсолютной температуры: Т > 1783 К.
, то целесообразно остановить свой выбор на меньшем значении абсолютной температуры: Т > 1783 К.
Задача №28
Найти стандартную ЭДС (Е°) и КПД для кислородно-водородного топливного элемента.
Решение:
1. Запишем анодные и катодные процессы и суммарную окислительно-восстановительную реакцию, т.е. токообразующую реакцию топливного элемента:

2. Выпишем из табл. 16, 17 значения 
 соответственно: -273 кДж/моль; -286 кДж/моль.
соответственно: -273 кДж/моль; -286 кДж/моль.
Определим Е (стандартную ЭДС) на основании соотношения  где число электронов, отдаваемых восстановителем или получаемых окислителем при образовании 1 моль воды (ж).
где число электронов, отдаваемых восстановителем или получаемых окислителем при образовании 1 моль воды (ж).

Обратим внимание на число Фарадея, вспомнив, что 1Дж равен 1 Кл-1 В, а следовательно, 1 Кл = Дж/В,
4. На основании второго закона термодинамики, который математически можно записать в виде формулы:
 , где
, где  — связанная энергия и не может быть превращена в работу’ (в данном случае электрическую), определим, какая часть теплоты реакции превращается в максимально полезную работу-, или найдем теоретический (термодинамический) КПД топливного элемента, %:
— связанная энергия и не может быть превращена в работу’ (в данном случае электрическую), определим, какая часть теплоты реакции превращается в максимально полезную работу-, или найдем теоретический (термодинамический) КПД топливного элемента, %:

Задача №29
Опытным путем было определено напряжение на клеммах при электролизе воды в электролизере с ртутным катодом  . Найти теоретический потенциал разложения воды
. Найти теоретический потенциал разложения воды  и КПД электролизера с ртутным катодом.
и КПД электролизера с ртутным катодом.
Решение:
1. На основании катодных и анодных процессов запишем суммарную реакцию электролиза воды:

Итог: 
2. Обратим внимание на то, что суммарная реакция электролиза представляет собой реакцию разложения воды (ж) на соответствующие простые вещества, т.е.

3. Вычислим теоретический потенциал разложения воды на основании соотношения:

4. Определим КПД электролизера  :
:

Задача №30
Определите устойчивость соединений:

Вывод. Известно положение, что чем меньше алгебраическая величина  образования, тем устойчивее соединение. В этом примере среди гидридов самое устойчивое соединение — вода, а неустойчивое —
образования, тем устойчивее соединение. В этом примере среди гидридов самое устойчивое соединение — вода, а неустойчивое —  Следовательно, устойчивость гидридов по подгруппе сверху вниз падает.
Следовательно, устойчивость гидридов по подгруппе сверху вниз падает.
Таблица 16
Стандартные теплоты (энтальпии) образования  некоторых веществ
некоторых веществ

Таблица 17
Стандартная энергия Гиббса образования  некоторых веществ
некоторых веществ

Таблица 18
Стандартные абсолютные энтропии  некоторых веществ
некоторых веществ

- Скорость химических реакций и химическое равновесие. Катализ
Раздел химии, изучающий скорости химических процессов, называется химической кинетикой. Основной величиной химической кинетики является скорость химической реакции. Химические реакции протекают с различной скоростью: со взрывом и медленно. Скоростью химической реакции называется число элементарных актов реакции, происходящих в единицу времени в единице объема. Скорость химической реакции выражается изменением концентрации реагирующих веществ в единицу времени.
Количественная зависимость между скоростью реакции и концентрациями реагирующих веществ выражается законом действия масс. Это важное положение установлено в 1867 году норвежскими учеными Гулдбергом и Вааге.
Концентрацию в данных условиях выражают количеством в молях вещества в 1 л.
Скорость химической реакции зависит от ряда факторов. Важнейшими факторами, влияющими на скорость реакции, являются температура, давление, концентрация, катализатор и природа реагирующих веществ.
Критерием осуществления реакций является выполнение условия 
Задача №31
Во сколько раз увеличится скорость реакции при повышении температуры от 20 до 80 °C, если температурный коэффициент равен 2?
Решение:
По формуле  находим, что
находим, что

Следовательно, скорость реакции увеличивается в 64 раза.
Задача №32
Как изменится скорость реакции

если уменьшить объем газовой смеси в 5 раз?
Решение:
Пусть концентрации  до изменения объема равнялись:
до изменения объема равнялись:  . Тогда скорость реакции
. Тогда скорость реакции 
При уменьшении объема в 5 раз концентрации веществ увеличились в 5 раз и поэтому составили:  . В этом случае
. В этом случае  Сопоставляя
Сопоставляя  видим, что скорость реакции увеличилась в 125 раз.
видим, что скорость реакции увеличилась в 125 раз.
Задача №33
При состоянии равновесия системы

концентрация оксида азота оказалась равной 0,056; кислорода -0,028; диоксида азота — 0,044 моль/л. Вычислить исходные концентрации  .
.
Решение:
В первоначальный момент концентрация двуокиси азота равна 0. Каждый моль образуется из одного моля  и 0,5 моля кислорода. Тогда для образования 0,044 моль/л
и 0,5 моля кислорода. Тогда для образования 0,044 моль/л  в соответствии с уравнением реакции израсходовано
в соответствии с уравнением реакции израсходовано  0,044; кислорода — 0,044/2 = 0,022 моль/л. Исходные концентрации оксида азота и кислорода:
0,044; кислорода — 0,044/2 = 0,022 моль/л. Исходные концентрации оксида азота и кислорода:

Задача №34
Исходная молярная концентрация йода  равна 1 моль/л, водорода
равна 1 моль/л, водорода  — 2 моль/л. Вычислить равновесные концентрации веществ при температуре 500 °C, если константа химического равновесия реакции
— 2 моль/л. Вычислить равновесные концентрации веществ при температуре 500 °C, если константа химического равновесия реакции  при этой температуре равна 50.
при этой температуре равна 50.
Решение:
Обозначим количество водорода, прореагировавшего к моменту наступления равновесия на каждый литр смеси, через х. Из уравнения реакции видно, что должно было одновременно прореагировать х йода, тогда количество образовавшегося  будет равно 2х.
будет равно 2х.


Решая уравнение, получим: x = 0,93.
Равновесные концентрации:

Задача №35
Как отразится повышение давления на следующем равновесии:  ?
?
Решение:
Повышение давления вызовет смещение равновесия влево, т.е. в сторону процесса, идущего с уменьшением количества реагирующего вещества. Уменьшение давления влечет смещение равновесия в обратном направлении.
Физико-химические свойства растворов
Свойства растворов подчиняются законам Вант-Гоффа и Рауля, которые:
- Позволяют определять молекулярные массы растворенных веществ.
Задача №36
При растворении 15 г хлороформа в 400 г эфира, эбулиоскопическая константа которого 2,12 °C, температура кипения повысилась на 0,665 °C. Определите молекулярную массу хлороформа.
Решение:

где К — криоскопическая или эбулиоскопическая константа, К -2,12; М — молекулярная масса,  — масса растворенного вещества,
— масса растворенного вещества,  = 15 г; м2 — масса растворителя,
= 15 г; м2 — масса растворителя,  = 400 г;
= 400 г;  -понижение температуры замерзания или повышение температуры кипения,
-понижение температуры замерзания или повышение температуры кипения,  — 0,665 °C.
— 0,665 °C.

2. Позволяют определять природу растворенного вещества.
Задача №37
При растворении 3,24 г серы в 40 г бензола температура кипения последнего повысилась на 0,81 °C. Из скольких атомов состоят молекулы серы в растворе? (К = 2,57.)
Решение:

(Ответ: молекула серы состоит из 8 атомов — Se.)
3. Позволяют рассчитать холодильные смеси (расчет состава антифризов, радиаторных жидкостей).
Задача №38
В радиатор автомобиля налили 9 л воды и прибавили 2 л метилового спирта (р = 0,8). При какой наинизшей температуре можно после этого оставлять автомобиль на открытом воздухе, не боясь, что вода в радиаторе замерзнет?
Решение:

4. Позволяют вычислить степень диссоциации электролита (а), если известен коэффициент Вант-Гоффа i, который можно найти по понижению температуры замерзания или повышению температуры кипения раствора.
Задача №39
Раствор, содержащий 0,1 моль бинарного электролита в 1000 г воды, замерзает при t = -0,196 °C. Определить степень диссоциации электролита. >
Решение:

Находим числовое значение понижения температуры замерзания раствора по формуле  . Так как для воды
. Так как для воды

Определяем коэффициент Вант-Гоффа i:

Вычисляем степень диссоциации электролита, учитывая, что молекула его диссоциирует на два иона:

нового эфира (С2Н5)2О температура кипения повысилась на 0,453 °C, определите относительную молекулярную массу растворенного вещества. (Ответ: 145.)
Ионные реакции и ионные уравнения
Для выражения сущности реакций, протекающих при взаимодействий между электролитами в растворах, пользуются так называемыми ионными уравнениями.
В ионных реакциях, протекающих в растворах электролитов, не происходит изменения заряда ионов. Такие реакции называются ионообменными. Ионные реакции могут протекать между ионами практически до конца с образованием газов, осадков, слабых электролитов и комплексных ионов (правило Бертолле). При образовании указанных веществ происходит стяжение ионов, что энергетически выгодно. При стяжении ионов концентрация их понижается, и согласно принципу Ле Шателье равновесие смещается в сторону наибольшего стяжения ионов. Например:

Для выражения сущности ионообменных реакций используют особую форму записи уравнений — ионные уравнения. При составлении ионных уравнений учитываются основные свойства веществ: сила электролита, его растворимость. В ионных уравнениях сильные растворимые электролиты записываются в виде ионов, ибо они в растворе находятся именно в таком состоянии. Слабые электролиты, газы и малорастворимые соединения (даже если они являются сильными электролитами) — в виде молекул, независимо от того, являются ли они исходными веществами или продуктами реакции.
Запишем приведенные реакции в виде ионов:

Исключив из уравнений ионы, которые не принимают участия в реакции, получим сокращенные ионные уравнения, отображающие сущность реакций:

Методика составления ионных уравнений
- Записывается молекулярное уравнение реакции.
- Составляется полное ионное уравнение процесса. Для этого осадки, газы, слабые электролиты записываются в виде молекул, а остальные вещества (сильные и хорошо растворимые электролиты) — в виде ионов (прил.2).
- Вычеркиваются ионы, не принимавшие участия в процессе (эти ионы находятся в обеих частях равенства в одинаковом количественном и качественном состоянии).
- Записывается сокращенное ионное уравнение, т.е. химические формулы только тех молекул и ионов, которые участвуют в обменном процессе, а также продукты их взаимодействия.
- Если коэффициенты в сокращенном ионном уравнении содержат общие множители, то их сокращают на эти множители.
Задача №40

В ионных реакциях знак равновесия  ставится в реакциях, идущих в слабых электролитах. В реакциях с сильными электролитами ставится знак
ставится в реакциях, идущих в слабых электролитах. В реакциях с сильными электролитами ставится знак  который показывает преимущественное направление процесса в сторону образования менее растворенного вещества.
который показывает преимущественное направление процесса в сторону образования менее растворенного вещества.
Задача №41

Вода в этой реакции является более слабым электролитом, чем уксусная кислота, поэтому равновесие этой реакции смещено вправо.
Задача №42

Здесь при добавлении ионов  (щелочи) в растворе появляются анионы
(щелочи) в растворе появляются анионы  .
.
Гидролиз солей
Химическое обменное взаимодействие ионов растворенной соли с ионами водорода или ионами гидроксида воды, сопровождающееся изменением pH-среды, называется гидролизом.
Гидролиз по аниону сводится к взаимодействию аниона слабой кислоты  , входящего в состав соли, с ионами воды Н+. В результате концентрация ионов понижается, равновесие диссоциации воды смещается вправо
, входящего в состав соли, с ионами воды Н+. В результате концентрация ионов понижается, равновесие диссоциации воды смещается вправо
(в сторону продуктов реакции), повышается pH раствора:

где МА — формула соли,  — катион сильного основания,
— катион сильного основания,  — анион слабой кислоты.
— анион слабой кислоты.
Гидролиз по катиону сводится к взаимодействию катиона слабого основания  , входящего в состав соли, с ионами воды
, входящего в состав соли, с ионами воды  . Концентрация ионов
. Концентрация ионов  и pH раствора ‘понижается, равновесие диссоциации воды смещается вправо:
и pH раствора ‘понижается, равновесие диссоциации воды смещается вправо:

где  — катион слабого основания,
— катион слабого основания,  — анион сильной кислоты. Ионы солей, образованных сильным основанием и сильной кислотой, не взаимодействуют с ионами воды:
— анион сильной кислоты. Ионы солей, образованных сильным основанием и сильной кислотой, не взаимодействуют с ионами воды:

Между ионами  и
и  ,
,  и
и  нет стяжения, так как
нет стяжения, так как  — сильные электролиты. Равновесие диссоциации воды не смещается. Поэтому водные растворы солей типа
— сильные электролиты. Равновесие диссоциации воды не смещается. Поэтому водные растворы солей типа  гидролизу не подвергаются и их водные растворы имеют pH = 7. Соли, образуемые от взаимодействующих сил кислот и оснований, подразделяются на 4 типа:
гидролизу не подвергаются и их водные растворы имеют pH = 7. Соли, образуемые от взаимодействующих сил кислот и оснований, подразделяются на 4 типа:
- Соли, образованные сильной кислотой и сильным основанием:

- Соли, образованные слабой кислотой и сильным основанием:

- Соли, образованные сильной кислотой и слабым основанием:

- Соли, образованные слабой кислотой и слабым основанием:


Соли 1 типа гидролизу не подвергаются. Гидролиз солей 2-4 типов может быть по форме простым и ступенчатым. Некоторые соли 4 типа подвергаются полному гидролизу.
Методика составления уравнений гидролиза
1. По составу соли определяют тип гидролиза по:
а) катиону; б) аниону; в) катиону и аниону.
2. Записывают сокращенное ионное уравнение, которое отражает взаимодействие иона соли (аниона, катиона, катиона и аниона) с одной молекулой воды (в форме НОН). В уравнении стрелкой указывают стяжение ионов.
3. По сокращенному ионному уравнению находят молекулярное уравнение. При этом нужно помнить, что двух- и более зарядные ионы гидролизуются ступенчато, образуя по 1-й ступени кислую или основную соль (но не свободную кислоту и основание), а по другим — образуют свободную кислоту или основание. Число ступеней гидролиза равно заряду иона.
Задача №43
Напишите уравнение взаимодействия цианистого калия с водой.

где К — ион сильного электролита КОН, гидролизу не подвергается;  — однозарядный ион слабой кислоты, подвергается простому гидролизу. Сокращенное ионное уравнение:
— однозарядный ион слабой кислоты, подвергается простому гидролизу. Сокращенное ионное уравнение:

Молекулярное уравнение:

Задача №44
Составить ионно-молекулярные и молекулярные уравнения гидролиза сульфида натрия.
 — ион сильного электролита
— ион сильного электролита  , не гидролизуется;
, не гидролизуется;
 — двухзарядный ион слабой кислоты
— двухзарядный ион слабой кислоты  гидролизуется ступенчато. Сокращенные ионные уравнения:
гидролизуется ступенчато. Сокращенные ионные уравнения:

Молекулярные уравнения:

Гидролиз идет, в основном, по 1-й ступени по следующим причинам:
- Процесс между электролитами направлен в сторону наиболее полного связывания ионов (в сторону образования более слабого электролита). Сравнение диссоциации
 и
и  показывает, что ионы полнее связаны в
показывает, что ионы полнее связаны в  Именно ион
Именно ион  — получается в результате гидролиза (что соответствует кислой соли
— получается в результате гидролиза (что соответствует кислой соли  ).
). - Вследствие накопления в растворе значительного количества ионов
 , способствующих протеканию процесса справа налево (согласно принципу Ле Шателье, 2-я ступень гидролиза практически не идет).
, способствующих протеканию процесса справа налево (согласно принципу Ле Шателье, 2-я ступень гидролиза практически не идет).
Задача №45
Составить ионно-молекулярные и молекулярные уравнения гидролиза хлорида аммония  .
.

где  — ион сильного электролита НС1, в гидролизе не участвует;
— ион сильного электролита НС1, в гидролизе не участвует;  — однозарядный ион слабого электролита
— однозарядный ион слабого электролита  , подвергается простому гидролизу.
, подвергается простому гидролизу.
Сокращенное ионное уравнение.

Молекулярное уравнение гидролиза:

Задача №46
Составить ионно-молекулярные и молекулярные уравнения гидролиза сульфата алюминия  .
.

где  — ион сильного электролита
— ион сильного электролита  , гидролизу не подвергается;
, гидролизу не подвергается;  — трехзарядный ион слабого электролита
— трехзарядный ион слабого электролита  , подвергается гидролизу ступенчато.
, подвергается гидролизу ступенчато.
Сокращенные ионные уравнения:

Молекулярные уравнения:

Накопление значительных количеств ионов Н+ способствует протеканию процесса справа налево, и поэтому реакция гидролиза ограничивается 1-й и частично 2-й ступенями.
Задача №47
Составьте ионно-молекулярные и молекулярные уравнения гидролиза уксуснокислого аммония 

где  — анион слабой кислоты
— анион слабой кислоты  — катион слабого основания
— катион слабого основания  .
.
Ионное уравнение гидролиза:

Молекулярное уравнение:

Силы образовавшихся электролитов примерно одинаковы:

Соль гидролизуется значительно, ибо оба продукта гидролиза  — слабые электролиты.
— слабые электролиты.
Окислительно-восстановительные реакции
Реакции, протекающие с изменением окислительных чисел атомов реагирующих веществ, называются окислительно-восстановительными.
Изменение окислительных чисел (о.ч.) происходит в результате перехода электронов от одних атомов или ионов к другим. Окислительные числа атомов могут иметь положительное, нулевое и отрицательное значения (o.4.Na = +1; Ва = +2; Fe = +3). Процесс отдачи атомом (ионом или молекулой) электронов называется окислением, процесс присоединения электронов атомами или ионами — восстановлением.
Вещество, атомы или ионы которого отдают электроны, называется восстановителем. Например,  . Здесь нейтральный атом алюминия, теряет 3 электрона, окисляется в трехзарядный положительный ион алюминия. Происходит повышение окислительного числа (признак окисления). Восстановитель отдает электроны, и алгебраическая его степень окисления (о.ч.) повышается. В нашем примере атом алюминия, теряя электроны, является восстановителем, о.ч. его повышается от 0 до +3.
. Здесь нейтральный атом алюминия, теряет 3 электрона, окисляется в трехзарядный положительный ион алюминия. Происходит повышение окислительного числа (признак окисления). Восстановитель отдает электроны, и алгебраическая его степень окисления (о.ч.) повышается. В нашем примере атом алюминия, теряя электроны, является восстановителем, о.ч. его повышается от 0 до +3.
Вещество, атомы или ионы которого присоединяют электроны, называется окислителем. При этом о.ч. понижается:  , присоединяя
, присоединяя  , восстанавливается в нейтральный атом меди. Ион
, восстанавливается в нейтральный атом меди. Ион  , присоединяя электроны, является окислителем, причем о.ч. меди понижается от 2+ до 0.
, присоединяя электроны, является окислителем, причем о.ч. меди понижается от 2+ до 0.
В окислительно-восстановительных реакциях (ОВР) окисление и восстановление протекают одновременно: одни элементы окисляются, другие — восстанавливаются. Окислительно-восстановительные реакции, следовательно, представляют собой единство двух противоположных тенденций. В этом заключается проявление основных законов материалистической философии: закона единства и борьбы противоположностей, перехода количественных изменений в качественные.
В окислительно-восстановительных реакциях неважен тип химической связи, важен только переход электронов.
У иона N с о.ч. +5  проявляются только окислительные свойства.
проявляются только окислительные свойства.
У иона N с о.ч. +4  — окислительно-восстановительные.
— окислительно-восстановительные.

У иона N с о.ч. -3  — только восстановительные свойства (см. табл. 19).
— только восстановительные свойства (см. табл. 19).
Таблица 19
Окислительно-восстановительные свойства атомов и сложных веществ


Задача №48
Составить уравнения окислительно-восстановительной реакции, идущей по схеме:

Если в условиях задачи даны исходные и конечные продукты, то написание уравнения сводится к нахождению и расстановке коэффициентов. Коэффициенты определяют методом электронного или электронно-ионного баланса с помощью полуреакций.
Решение:

Задача №49
Составить уравнение реакции взаимодействия марганцово-кислого калия с сернисто-кислым натрием в кислой среде  .
.
Решение:

Как показывают примеры, целесообразно придерживаться определенного порядка (алгоритма) составления окислительно-восстановительных уравнений.
- Составить молекулярную или ионную схему реакции.
- Определить, какие элементы изменяют окислительное число, значение окислительного числа написать над формулами в левой и правой частях схемы.
- Составить электронно-ионные уравнения для процессов окисления и восстановления.
- Определить ион-окислитель и ион-восстановитель, а также продукт восстановления иона-окислителя (его восстановленную форму) и продукт окисления иона-восстановителя (его окисленную форму).
- Найти коэффициент для восстановителя и окислителя и для продуктов их превращения. Для этого нужно суммировать электронно-ионные уравнения, предварительно умножив найденные коэффициенты. (Нужно помнить, что число электронов, теряемых восстановителем, должно равняться числу электронов, присоединяемых окислителем).
- Проверить число атомов каждого элемента в обеих частях и подобрать коэффициенты для всех остальных веществ.
Различная степень стремления элементов к приобретению или отдаче электронов более полно выражена в окислительно-восстановительных потенциалах или редоксипотенциалах. Чем
больше числовое значение потенциала со знаком плюс (+) данного атома, тем больше его окислительные свойства. При отрицательном значении потенциала у атома или иона выражены восстановительные свойства (стремление к отдаче электронов).
О полноте протекания окислительно-восстановительной реакции можно судить по разности окислительно-восстановительных потенциалов (двух систем или ЭДС). Если ЭДС ОВР имеет положительное значение, то реакция идет слева направо.
Значения окислительно-восстановительных потенциалов систем приводятся в прил. 13. Они получены измерением с помощью нормального водородного электрода, потенциал которого принят равным нулю. Таблица нормальных окислительно-восстановительных потенциалов позволяет:
Для правильного составления окислительно-восстановительной реакции важно знать закономерности взаимодействия металлов с водой, кислотами и водными растворами щелочей. При взаимодействии металлов с водой, простыми кислотами и щелочами в роли окислителя будет ион водорода воды.
Условия растворения металла в воде:
1. 
2) растворимость естественной оксидной пленки металла в воде;
3) растворимость продукта взаимодействия металла с водой (гидроксид) в воде.
Указанным условиям при обыкновенной температуре удовлетворяют лишь щелочные и щелочно-земельные металлы.
Условия растворения металла в щелочи:
1) 
2) естественная оксидная пленка металла растворяется в щелочи;
3) гидроксид металла растворяется в щелочи.
Указанным условиям удовлетворяют амфотерные металлы  .
.
Условия, необходимые для растворения металла в простых кислотах:
1) металл в ряду напряжений должен располагаться левее водорода, или 
2) образуется продукт взаимодействия металла с кислотой (соль);
3) этот продукт (соль) растворяется в воде.
В азотной кислоте окислителем является азот, в концентрированной серной кислоте — сера.
Концентрированная азотная кислота с металлом реагирует по схеме:

в разбавленной азотной кислоте:

Некоторые металлы  при взаимодействии с холодной концентрированной азотной и серной кислотами образуют пассивную пленку (пассивируются):
при взаимодействии с холодной концентрированной азотной и серной кислотами образуют пассивную пленку (пассивируются):

При нагревании пленка разрушается (депассивируется), металл растворяется:

В зависимости от активности металла серная кислота восстанавливается до 

Некоторые металлы  растворяются только в «царской водке». «Царская водка» представляет собой смесь, состоящую из одного объема концентрированной азотной кислоты и трех объемов концентрированной соляной кислоты. Эта смесь обладает повышенными окислительными свойствами за счет появления атомарного хлора:
растворяются только в «царской водке». «Царская водка» представляет собой смесь, состоящую из одного объема концентрированной азотной кислоты и трех объемов концентрированной соляной кислоты. Эта смесь обладает повышенными окислительными свойствами за счет появления атомарного хлора:

В подобных реакциях  выполняет роль окислителя, а
выполняет роль окислителя, а  — поставщика лигандов для образования комплексного соединения.
— поставщика лигандов для образования комплексного соединения.
Возможно эта страница вам будет полезна:
Электродные потенциалы. Электродвижущие силы. Гальванические элементы
При помещении металлической пластинки в воду можно заметить протекание следующего процесса: расположенные на ее поверхности катионы металла будут гидратироваться полярными молекулами воды и переходить в раствор. А электроны, остающиеся в металле, заряжают его поверхностный слой отрицательно. Возникает электростатическое притяжение между перешедшими в раствор гидратированными катионами и поверхностью металла. В результате устанавливается подвижное (динамическое) равновесие:

Здесь n — число электронов, принимающих участие в процессе. На границе металл — раствор возникает двойной электрический слой. Заряженная поверхность электрода вместе с прилегающим противоположно заряженным слоем раствора называется двойным электрическим слоем. Двойной электрический слой состоит из плотной части и диффузной части двойного электрического слоя. На границе металл-раствор возникает скачок потенциала — электродный потенциал.
Стандартным электродным потенциалом металла называют его электродный потенциал, возникающий при погружении металла в раствор его иона с концентрацией, равной 1 моль/л, измеренный по сравнению со стандартным водородным электродом, потенциал которого при 25 °C условно принимается равным нулю. Электронный потенциал измеряют приборами, называемыми гальваническими элементами. ЭДС должна иметь положительные значения.

Электродный потенциал зависит от концентрации его ионов в растворе, которая выражается уравнением Нернста — Тюрина:

где  — электродный потенциал металла;
— электродный потенциал металла;  — стандартный электродный потенциал; n — число электронов, принимающих участие в процессе; Са — активная концентрация гидратированных ионов металла в растворе, моль/л.
— стандартный электродный потенциал; n — число электронов, принимающих участие в процессе; Са — активная концентрация гидратированных ионов металла в растворе, моль/л.
Химическая реакция, на основе которой работает элемент, называется токообразующей. Вследствие работы гальванического элемента (протекания токообразукзщей реакции во внешней цепи) появляется электрический ток, который используется для работы, что является целью применения элемента в качестве химического источника тока.
Условная схема записи гальванических элементов составляется по следующим правилам:
1. Все фазы, составляющие элемент, записываются в одну строчку в том порядке, потенциал которого имеет меньшее значение. К примеру, для медно-цинкового элемента:  ,
, 
Вместо солей, находящихся в растворе, можно записывать только потенциалопределяющие ионы:  .
.
Поверхность раздела между материалом электрода и раствором обозначается одной вертикальной чертой, а между растворами — двумя сплошными вертикальными чертами:  Поэтому слева и справа от двойной черты записывают частицы, находящиеся в растворе, — ионы.
Поэтому слева и справа от двойной черты записывают частицы, находящиеся в растворе, — ионы.
Если имеются несколько электродов, то их перечисляют, разделяя запятыми. Например, водородно-цинковый электрод будег записан гак:  находят по формуле:
находят по формуле:

Встречается менее строгая запись:  в которой материал “подкладки” (платина) заключен в круглые скобки. “Подкладка” — основа, на которой адсорбируется газ, поэтому ее указывают рядом с молекулами газа.
в которой материал “подкладки” (платина) заключен в круглые скобки. “Подкладка” — основа, на которой адсорбируется газ, поэтому ее указывают рядом с молекулами газа.
4. В более деятельной схеме стрелками показывают направление перехода электронов во внешней цепи и ионов во внутренней цепи. К схеме добавляют уравнения электродных реакций и токообразующую реакцию:

Гальванические элементы делятся на химические и концентрационные.
В химических элементах электрический ток возникает за счет протекания в элементе химической реакции. Они могут быть построены:
1) из металлических электродов:

2) из газового и металлического электродов:

3) из газовых электродов (водородно-хлорный электрод):

4) из окислительно-восстановительных электродов:

Концентрационные элементы — элементы, составленные из электродов одной природы, опущенных в раствор своих ионов, но различной концентрации.
ЭДС гальваническогр элемента рассчитывают как разность равновесных электродных потенциалов по формуле:

где  — равновесные потенциалы катода и анода.
— равновесные потенциалы катода и анода.
ЭДС элемента должна иметь положительное значение. ЭДС рассчитывают также по энергии Гиббса по формуле:

При работе гальванического элемента ЭДС постепенно уменьшается из-за возникающей поляризации. Поляризация бывает химической, концентрационной и собственно электрохимической.
Концентрационная поляризация возникает из-за изменения молярной концентрации тех или иных ионов в анодной и катодной зонах. Активные вещества не успевают доставляться в глубину раствора или из глубины раствора вследствие медленной диффузии ионов к электродам.
Химическая поляризация возникает вследствие изменения химического состава электродов. Образующийся на электроде водород адсорбируется на его поверхности и как бы изолирует его от раствора или электролита (газовая поляризация). Ионы водорода не могут подойти к поверхности электрода и соединиться с электронами. Электродный потенциал катода становится более отрицательным. Это сильно влияет на ЭДС элемента, снижая потенциал.
Электрохимическая поляризация вызвана изменением потенциала, обусловленным замедленностью собственно электрохимической стадии реакции. Поляризация электрохимической стадии объясняется существенной перестройкой реагирующих частиц в ходе реакции.
Процесс уменьшения и устранения поляризации электродов называется деполяризацией. Вещества, снижающие поляризацию, называются деполяризаторами  ,
,  .
.
Задача №50
Стандартный электродный потенциал никеля больше, чем кобальта. Изменится ли соотношение, если
измерить потенциал никеля в растворе его ионов концентрации 0,001 моль/л, а потенциал кобальта — в растворе концентрации 0,1 моль/л?
Решение:
Электродный потенциал металла (ф) зависит от концентрации его ионов в растворе. Эта зависимость выражется уравнением Нернста: 

Таким образом, при изменившейся концентрации потенциал кобальта стал больше потенциала никеля.
Задача №51
Магниевую пластинку опустили в раствор его соли. При этом электродный потенциал магния оказался равным -2,41 В. Вычислить молярную концентрацию ионов магния.
Решение:
На основе уравнения Нернста имеем:

Задача №52
Составить схему гальванического элемента, в котором электродами являются магниевая и цинковая пластинка, опущенные в растворы их ионов активной концентрации 1 моль/л. Какой металл является анодом, какой -катодом? Написать уравнение окислительно-восстановительной реакции, протекающей в этом гальваническом элементе, и вычислить его ЭДС. Потенциал магния -2,37 В, цинка -0,67 В.
Решение:
Магний имеет меньший потенциал и является анодом, цинк — катодом.

На магниевом электроде идет окисление, на цинковом -восстановление:

 — реакция, характеризующая работу гальванического элемента.
— реакция, характеризующая работу гальванического элемента.
Для определения ЭДС гальванического элемента из потенциала катода следует вычесть потенциал анода:

Задача №53
Вычислить электродный потенциал полуэлемента 
Решение:
Молярная концентрация ионов железа в растворе  концентрации 0,01 моль/л:
концентрации 0,01 моль/л:

Электродный потенциал рассчитывают по уравнению Нернста:

Задача №54
Рассчитать потенциал водородного электрода при стандартном давлении водорода и pH = 2.
Решение:
В уравнении Нернста для водородного электрода имеем:

При стандартном давлении водорода и  имеем:
имеем:

Задача №55
Вычислить потенциал кислородного электрода в кислой среде на воздухе при  (на воздухе).
(на воздухе).
Решение:
Уравнение электродной реакции с учетом среды:

На воздухе  Потенциал кислородного электрода:
Потенциал кислородного электрода:

Задача №56
Дать схему работы концентрационного элемента, состоящего из серебряных электродов, опущенных в раствор азотнокислого.серебра концентрацией 0,001 моль/л (1-й) и 1 моль/л (2-й).
Решение:
Рассчитываем значения потенциалов, определяем знаки электродов и направление движения электронов во внешней цепи:
концентрации 

В таком элементе электрод в растворе меньшей концентрации ионов — восстановитель. Он отдает во внешнюю цепь электроны, на нем идет процесс окисления, и следовательно, он будет анодом. Электрод в растворе большей концентрации — окислитель, на нем идет процесс восстановления, и он будет катодом.
Условная схема элемента:

Такой элемент работает до тех пор, пока не выравняются концентрации в анодной и катодной зонах.
Задача №57
Определить ЭДС элемента, построенного из электродов: а) меди, погруженной в растворах сернокислой меди — концентрации 0,1 моль/л с  = 80 %; б) водородного электрода при стандартном давлении водорода и pH = 5 («подкладка» — черненая пластина).
= 80 %; б) водородного электрода при стандартном давлении водорода и pH = 5 («подкладка» — черненая пластина).
Решение:
Определим потенциал медного электрода, предварительно вычислив концентрацию ионов 

Электродный потенциал водороднго электрода при стандартном давлении удобно выислять по формуле:

Задача №58
Вычислить концентрационную поляризацию медно-цинкового электрода, если в процессе его работы концентрации потенциалопределяющих ионов изменились на порядок при данной плотности тока. Начальная концентрация потенциалопределяющих веществ — стандартная.
Решение:

При работе элемента концентрация ионов  в приэлектродном слое уменьшается до 0,1 моль/л, а концентрация ионов
в приэлектродном слое уменьшается до 0,1 моль/л, а концентрация ионов  растет до 10 моль/л (за счет замедленной диффузии ионов меди из глубины раствора к медной пластинке, а ионов цинка — в глубь раствора от цинковой пластинки).Тогда
растет до 10 моль/л (за счет замедленной диффузии ионов меди из глубины раствора к медной пластинке, а ионов цинка — в глубь раствора от цинковой пластинки).Тогда

Рассчитываем значение ЭДС при новых концентрациях потенциалопределяющих ионов:

Концентрированная поляризация составит:
1.1 — 1,045 = 0,055 В.
Небольшое значение свидетельствует о том, что медно-цинковый элемент практически не поляризуется при работе.
Задача №59
Пояснить сущность химической поляризации при работе элемента, схема которого: 
Решение:
Химическая поляризация сводится к изменению химической природы электродов при работе элемента.
Анодный процесс:  . На поверхности анода возможно образование пленки труднорастворимой соли
. На поверхности анода возможно образование пленки труднорастворимой соли  которая будет препятствовать дальнейшему растворению свинца (переход ионов свинца с поверхности свинцовой пластинки в раствор будет затруднен). Накопление ионов свинца изменит потенциал в сторону положительных значений (пленочной поляризации).
которая будет препятствовать дальнейшему растворению свинца (переход ионов свинца с поверхности свинцовой пластинки в раствор будет затруднен). Накопление ионов свинца изменит потенциал в сторону положительных значений (пленочной поляризации).
Катодный процесс:  На поверхности пластины возможно образование газовой «шубы» — слоя адсорбированного водорода. Доступ ионов водорода к поверхности электрода затрудняется. На электроде скапливаются избыточные электроны, и потенциал катода смещается в отрицательную сторону. Возникает газовая поляризация электрода. Разность потенциалов при отборе тока уменьшается. Газовую поляризацию можно уменьшить введением «деполяризаторов» -веществ, взаимодействующих с газами. Для снятия водородной «шубы» используются окислители
На поверхности пластины возможно образование газовой «шубы» — слоя адсорбированного водорода. Доступ ионов водорода к поверхности электрода затрудняется. На электроде скапливаются избыточные электроны, и потенциал катода смещается в отрицательную сторону. Возникает газовая поляризация электрода. Разность потенциалов при отборе тока уменьшается. Газовую поляризацию можно уменьшить введением «деполяризаторов» -веществ, взаимодействующих с газами. Для снятия водородной «шубы» используются окислители  При этом может измениться и сам катодный процесс.
При этом может измениться и сам катодный процесс.
Задача №60
Вычислить ЭДС элемента с учетом собственно электрохимической поляризации или активационной поляризации. Концентрации потенциалопределяющих веществ равны единице, перенапряжение выделения водорода на меди равно 0,48 В. Схема элемента:

Решение:
Потенциалы электродов при концентрации потенциал- определяющих веществ, равных единице, являются стандартными:

Потенциал водородного электрода с учетом
перенапряжения на меди:

Возможно эта страница вам будет полезна:
Электролиз
Электролизом называется окислительно-восстановительный процесс, протекающий при прохождении постоянного электрического тока через раствор электролита или через электролит, находящийся в расплавленном состоянии. Этот процесс сопровождается превращением электрической энергии в химическую.
Процессы, протекающие при электролизе, противоположны процессам, протекающим в гальванических элементах.
- Электролиз расплавов в химии
- Электролиз водных растворов в химии
Кинетика электродных реакций. поляризация при электролизе. Потенциал разложения. Перенапряжение. закон электролиза. Выход по току
- Кинетика электродных реакций в химии
- Поляризация в химии
- Законы электролиза (фарадея) в химии
- Выход по току в химии
Электролиз водных растворов солей
Задача №61
Электролиз водного раствора  с графитовыми электродами. Соль
с графитовыми электродами. Соль  гидролизу не подвергается. Среда нейтральная.
гидролизу не подвергается. Среда нейтральная.


Продуктами электролиза являются:  (катодная, анодная зоны разделены). В условиях свободного перемещения продуктов возможно их взаимодействие по схеме:
(катодная, анодная зоны разделены). В условиях свободного перемещения продуктов возможно их взаимодействие по схеме:  (при избытке продуктов)
(при избытке продуктов)  (при недостатке)
(при недостатке)
Составляем микрогальванический элемент:

Задача №62
Электролиз раствора сульфата меди  с медным анодом. Схема электролиза:
с медным анодом. Схема электролиза:

В процессе электролиза с растворимым анодом происходит перенос меди с анода на катод. Этот процесс применяется при рафинировании (электролитической очистке) меди.
Задача №63
Электролиз раствора  с графитовыми электродами. Соль
с графитовыми электродами. Соль  гидролизуется по катиону. Среда кислая.
гидролизуется по катиону. Среда кислая.

Задача №64
С помощью поляризованных кривых (рис. 3) определите условия выделения  при электролизе кислого раствора
при электролизе кислого раствора 

Рис. 3. Поляризационные кривые катодного выделения 
Решение.
По характеру восстановления поляризационных кривых можно определить характер выделения  :
:

На катоде должен восстанавливаться более сильный окислитель  Выделение цинка на катоде невозможно при подобном соотношении потенциалов. Реальные электродные потенциалы существенно отличаются от равновесных под током. При потенциале катода, равном -0,76 В, цинк не выделяется. Идет восстановление ионов водорода. При небольшом смещении потенциала катода в сторону отрицательных значений
Выделение цинка на катоде невозможно при подобном соотношении потенциалов. Реальные электродные потенциалы существенно отличаются от равновесных под током. При потенциале катода, равном -0,76 В, цинк не выделяется. Идет восстановление ионов водорода. При небольшом смещении потенциала катода в сторону отрицательных значений  обе реакции идут параллельно, но с преимущественным выделением водорода
обе реакции идут параллельно, но с преимущественным выделением водорода  .
.
В точке пересечения поляризационных кривых скорости выделения водорода и цинка одинаковы  . При дальнейшем смещении потенциала катода в сторону отрицательных значений на электроде выделяется в основном цинк
. При дальнейшем смещении потенциала катода в сторону отрицательных значений на электроде выделяется в основном цинк  .
.
Выделение  и других металлов средней активности из водных растворов возможно благодаря высокому перенапряжению выделения водорода на катоде. При высоких потенциалах тока электродный потенциал выделения водорода становится более отрицательным, чем потенциал выделения цинка. Высокое перенапряжение водорода — явление положительное для данного процесса.
и других металлов средней активности из водных растворов возможно благодаря высокому перенапряжению выделения водорода на катоде. При высоких потенциалах тока электродный потенциал выделения водорода становится более отрицательным, чем потенциал выделения цинка. Высокое перенапряжение водорода — явление положительное для данного процесса.
Для выделения цинка необходимо: 1) подобрать материал катода, на котором водород выделяется с высоким перенапряжением; 2) электролиз вести при высокой плотности тока.
Для выделения хлора нужно: 1) подобрать материал анода; 2) вести электролиз при высоких плотностях тока.
Выделение кислорода протекает с более значительной поляризацией, чем выделение хлора (рис. 4.). Поэтому при малых плотностях тока выделяется лишь кислород. В точке  токи на выделение хлора и кислорода сравниваются, а при потенциале
токи на выделение хлора и кислорода сравниваются, а при потенциале  (высокая плотность тока) выделяется в основном хлор.
(высокая плотность тока) выделяется в основном хлор.

Рис. 4. Поляризационные кривые анодного выделения кислорода и хлора
Задача №65
Напишите уравнения реакций, протекающих на графитовых электродах при электролизе раствора  . Какой внутренний гальванический элемент при этом образуется и какова его роль? Рассчитайте напряжение разложения.
. Какой внутренний гальванический элемент при этом образуется и какова его роль? Рассчитайте напряжение разложения.
Решение:
 — гидролизуется по катиону и раствор имеет слабокислую реакцию. Пренебрегая гидролизом, можно считать pH = 7.
— гидролизуется по катиону и раствор имеет слабокислую реакцию. Пренебрегая гидролизом, можно считать pH = 7.

Суммарное уравнение реакции:

Электролиз соли типа  ведут с целью выделения металла. Поэтому основными продуктами электролиза в этом случае следует считать цинк и кислород. Однако выделяющийся водород вызывает повышение напряжения.
ведут с целью выделения металла. Поэтому основными продуктами электролиза в этом случае следует считать цинк и кислород. Однако выделяющийся водород вызывает повышение напряжения.
В процессе электролиза изменяется химическая природа электродов: вместо одинаковых вначале графитовых электродов образовались разные — цинковый, кислородный, водородный, подкладкой которых является графит. Возникают кислородно-цинковый и водородно-кислородный гальванические элементы:

Внутренний гальванический элемент тормозит процесс электролиза, так как вызывает процессы, противоположные тем, которые идут на электродах и требуют добавочного напряжения.
Напряжение разложение  рассчитывается как ЭДС внутреннего гальванического элемента:
рассчитывается как ЭДС внутреннего гальванического элемента:

 двух гальванических элементов соответственно можно рассчитать, складывая их значения.
двух гальванических элементов соответственно можно рассчитать, складывая их значения.
Задача №66
При электролитическом рафинировании кобальта аноды, содержащие в своем составе кроме кобальта никель, железо, медь, в условиях процесса полностью окисляются. Требуется ли очистка электролита от указанных примесей для получения чистого катодного кобальта? Ответ обоснуйте. Напишите уравнения реакций.
Решение:
На аноде идут реакции:

Выделение металлов на катоде происходит в последовательности:

способность к присоединению электронов уменьшается
При получении чистого кобальта на катоде (-) должна быть единственная реакция:

Это возможно при отсутствии в электролите более сильных окислителей. Следовательно, очистка электролита от ионов меди, никеля необходима. Ионы железа не препятствуют получению чистого кобальта при условии: 
Задача №67
Сколько цинка и водорода выделится на катоде , при электролизе кислого раствора хлорида никеля, если •процесс ведут в течение 1 ч с силой тока 5 А и выходом по току никеля 60 %?
Решение:
Цинк — металл средней активности. На катоде идут процессы восстановления ионов цинка и водорода (в кислой среде). На аноде идет окисление ионов хлора.
Схема электролиза:

Теперь рассчитаем массу цинка по закону Фарадея с учетом выхода по току цинка (60 %):

Рассчитаем объем водорода по закону Фарадея с учетом выхода по току водорода (1 — 0,6 = 0,4):

Задача №68
Серебрение используется для уменьшения сопротивления электрических контактов. Определите время, необходимое для нанесения слоя серебра толщиной 5 мкм, если известны плотность серебра  выход по току серебра 98 % и рекомендуемая плотность тока
выход по току серебра 98 % и рекомендуемая плотность тока  Электролит
Электролит  . Напишите уравнения электродных реакций.
. Напишите уравнения электродных реакций.
Решение:
При серебрении комплексный электролит  диссоциирует на ионы
диссоциирует на ионы  , частично на
, частично на  . Серебрение ведут с серебряным анодом, который в растворе
. Серебрение ведут с серебряным анодом, который в растворе  легко окисляется. При электролизе с растворимым анодом происходит перенос серебра с анода на катод.
легко окисляется. При электролизе с растворимым анодом происходит перенос серебра с анода на катод.

Толщину покрытия определяют по формуле:

которую можно вывести, используя соотношения:

m — масса; Э — эквивалентная масса;  — плотность металла; V — объем; (5 — толщина покрытия; S — площадь покрытия;
— плотность металла; V — объем; (5 — толщина покрытия; S — площадь покрытия;  — выход по току; i — плотность тока; t — время электролиза; J — сила тока.
— выход по току; i — плотность тока; t — время электролиза; J — сила тока.
Теперь определяем время, необходимое для нанесения слоя заданной толщины:

Задача №69
Какая масса гидроксида калия образовалась на катоде при электролизе раствора K2SO4, если на аноде выделилось 11,2 л кислорода при нормальных условиях (н.у.)?
Решение:
Молярный объем кислорода (н.у.) равен 22,4 / 4 = 5,6 л. Следовательно, 11,2 л содержат две молярные массы кислорода. Столько же молярных масс КОН образовалось у катода или
56,11 -2 = 112,22 г
(56,11 г/моль — молярная эквивалентная масса КОН).
Коррозия металлов
Коррозия металлов — процесс самопроизвольного разрушения (окисления) металлов при их химическом, электрохимическом или биохимическом взаимодействии с окружающей средой.
- Коррозия металлов в химии
- Защита металлов от коррозии в химии
Возможно эта страница вам будет полезна:
Задача №70
Дать обоснованную расчетом схему коррозии луженого железа (целостность покрытия нарушена) в кислой среде.
Решение:
1. Электродные потенциалы олова и железа в кислой среде (см. табл. 20):

Так как  , то в качестве анодного участка выступает железо, а олово играет роль катодного участка. В первую очередь будет разрушаться как более активный металл железо, а олово — служить прокладкой для газового электрода.
, то в качестве анодного участка выступает железо, а олово играет роль катодного участка. В первую очередь будет разрушаться как более активный металл железо, а олово — служить прокладкой для газового электрода.
2. Электродные потенциалы возможных окислителей ( и
и  ) в кислой среде на воздухе с учетом перенапряжения на олове (см. табл. 21 и 22).
) в кислой среде на воздухе с учетом перенапряжения на олове (см. табл. 21 и 22).

где 0,63 и 1,21 — перенапряжение водорода и кислорода на олове.
3. Сравнивая потенциалы предполагаемых окислителей  с потенциалом возможного анода
с потенциалом возможного анода  , делаем выводы:
, делаем выводы:
1) так как  , ионы водорода не могут в данных условиях вызывать коррозию железа;
, ионы водорода не могут в данных условиях вызывать коррозию железа;
2)  удовлетворяет условию самопроизвольного протекания коррозии. Следовательно, железо разрушается в кислой среде за счет растворенного кислорода.
удовлетворяет условию самопроизвольного протекания коррозии. Следовательно, железо разрушается в кислой среде за счет растворенного кислорода.
Схема работы гальванического элемента:

Коррозия олова идет с кислородной деполяризацией. Поскольку электрохимическая коррозия обусловлена деятельностью микрогальванических элементов, можно сделать вывод, что все факторы, способствующие деятельности гальванического элемента, усиливают коррозию: значительная ЭДС, малое внутреннее сопротивление коррозионных элементов, небольшая поляризация.
Комплексные соединения
- Комплексные соединения в химии
Химия элементов. Краткая характеристика свойств элементов и их соединений. Последовательность их описания
- Химия элементов
Задача №71
На титрование 100 мл воды, содержащей гидрокарбонат кальция, израсходовано 2,5 мл 0,12 молярной концентрации эквивалента раствора соляной кислоты. Рассчитать жесткость воды.
Решение:
Исходя из данных задачи, определяем молярную концентрацию эквивалента раствора гидрокарбоната. Обозначив число эквивалентов гидрокарбоната в литре воды через х, получим:

Следовательно, 1л воды содержит 3 ммоль/л  или кальция. Жесткость воды — 3 ммоль/л.
или кальция. Жесткость воды — 3 ммоль/л.
Задача №72
Сколько граммов  надо прибавить к. 10 л воды, чтобы устранить ее общую жесткость, равную 4,64 ммоль/л?
надо прибавить к. 10 л воды, чтобы устранить ее общую жесткость, равную 4,64 ммоль/л?
Решение:
Из уравнений

следует, что 1 моль соды взаимодействует с 1 молем  или с 1 молем
или с 1 молем  . Переходя к ммоль/л находим, что 1 ммоль соды взаимодействует с 1 ммоль/л
. Переходя к ммоль/л находим, что 1 ммоль соды взаимодействует с 1 ммоль/л  или
или  , т.е с 1 ммоль/л ионов
, т.е с 1 ммоль/л ионов  . Так как молярная масса соды 106, а эквивалент ее равен 0,5 молярной массы, то 1 ммоль/л соды равняется 53 мг. В 10 л воды содержится 4,64 • 10 = 46,4 ммоль/л ионов кальция. Количество соды (х), которое потребуется для устранения жесткости:
. Так как молярная масса соды 106, а эквивалент ее равен 0,5 молярной массы, то 1 ммоль/л соды равняется 53 мг. В 10 л воды содержится 4,64 • 10 = 46,4 ммоль/л ионов кальция. Количество соды (х), которое потребуется для устранения жесткости:  мг, или 2,46 г.
мг, или 2,46 г.
Задача №73
Вычислить постоянную жесткость воды, зная, что для устранения ионов кальция, содержащихся в 50 л воды, потребовалось прибавить к воде 10,8 г безводной буры  .
.
Решение:
При действии буры на воду, содержащую сернокислый кальций, ионы кальция переходят в осадок вследствие реакции:

Из уравнения реакции следует, что для осаждения ионов кальция, надо взять 1экв. буры или на 1 ммоль/л ионов кальция -1 ммоль/л буры. Молярная масса буры 2002,, следовательно, 1 ммоль/л ее равен 101 мг. На осаждение ионов кальция, содержащихся в 50 л воды, израсходовано 108 г или 10800 мг буры. Количество ионов кальция в 50 л воды находим из пропорции: 
Найденное количество вещества ионов содержится в 50 л воды. Жесткость воды Ж = 107/ 50 = 2,14 ммоль/л.
Органические соединения. Полимеры
- Полимеры: органические соединения
Приложения
Периодическая система элементов Д.И. Менделеева


Периодическая система элементов Д.И. Менделеева (длиннопериодический вариант)


Константы и степени диссоциации некоторых слабых электролитов, %

Растворимость солей и оснований в воде
Условные обозначения:
Р — растворимое, М — малорастворимое, Н — практически нерастворимое вещество, — разлагается водой, ? — нет достоверных сведений о существовании соединений.

Основные классы неорганических веществ

Взаимосвязь простых веществ, оксидов, оснований и кислот (реакции солеобразования)
1. Металл + кислота —> соль + водород

2. Металл + неметалл —> соль бескислородной кислоты

3. Металл (1) + соль (1) —> соль (2) + металл (2)

4. Основной оксид + кислотный оксид —> соль

5. Основной оксид + кислота —> соль + вода

6. Основание + кислота —> соль + вода (реакция нейтрализации)

7. Основание + кислотный оксид —> соль + вода

8. Основание (1) + соль (1) —> соль (2) + кислота (2)

9. Соль (1) + кислота (1) —> соль (2) + кислота (2)

10. Соль (1) + соль (2) —> соль (3) + соль (4)

Округлённые значения относительных атомных масс некоторых химических элементов

Относительные молекулярные массы неорганических соединений

Относительная электроотрицательность элементов

Взаимная связь между физическими величинами

Значения фундаментальных физических постоянных

Криоскопические и эбулиоскопические константы растворителей

Электрохимический ряд напряжений металлов

Давление насыщенного водяного пара при разных температурах

Стандартные окислительно-восстановительные потенциалы




Кстати готовые на продажу задачи тут, и там же теория из учебников может быть вам поможет она.
Словарь химических терминов
АКТИНОИДЫ — название элементов с порядковыми номерами 89 — 103 (Ас — Lr).
АЛЛОТРОПИЯ — способность химического элемента образовывать несколько простых веществ, отличающихся по строению и свойствам.
АЛЮМИНОТЕРМИЯ — восстановление металла из его оксида с помощью металлического алюминия.
АМФОТЕРНОСТЬ ГИДРОКСИДОВ — способность соединения проявлять кислотные или основные свойства в зависимости от природы партнера по реакции в кислотно-основном взаимодействии.
АТОМ — наименьшая частица химического элемента, являющаяся носителем его свойств.
АТОМНАЯ ЕДИНИЦА МАССЫ (а.е.м.) — условная единица, представляющая собой 1/12 часть массы атома углерода.
АТОМНАЯ МАССА (относительная) — отношение средней массы атома естественного изотонического состава элемента к 1/12 массы атома углерода  .
.
АТОМНО-МОЛЕКУЛЯРНАЯ ТЕОРИЯ — одно из важнейших учений в химии, базирующееся на представлениях о строении веществ из атомов и молекул.
АТОМНАЯ ОРБИТАЛЬ — полный набор волновых функций электрона в атоме. Для каждой заданной волновой функции существует граничная область, в которой сосредоточена определенная доля электронного заряда.
БЛАГОРОДНЫЕ ГАЗЫ — гелий, неон, аргон, криптон, ксенон, радон — элементы главной подгруппы VIII группы.
ВАЛЕНТНОСТЬ — свойство атомов данного элемента образовывать определенное число связей с атомами других элементов.
ВАЛЕНТНЫЕ ЭЛЕКТРОНЫ — электроны, принимающие участие в образовании химической связи.
ВАН-ДЕР-ВААЛЬСОВЫ СИЛЫ — силы, определяющие взаимодействие частиц вещества, находящегося в одном из трех агрегатных состояний.
ВОДОРОДНАЯ СВЯЗЬ — межмолекулярное взаимодействие молекул, содержащих атом водорода, связанный с сильно электроотрицательным атомом.
ВОДОРОДНЫЙ ПОКАЗАТЕЛЬ (pH) — отрицательный десятичный логарифм концентрации водородных ионов.
ВОССТАНОВИТЕЛЬ — процесс присоединения электронов.
ВОЛНОВАЯ ФУНКЦИЯ — математическое описание состояния электрона в атоме. Квадрат этой функции определяет относительную вероятность пребывания электрона в любой данной точке пространства.
ГАЛОГЕНЫ — общее название элементов главной подгруппы VII группы, в которую входят фтор, хлор, бром, йод, астат.
ГЕОМЕТРИЧЕСКАЯ ИЗОМЕРИЯ — вид изомерии, обусловленный различным расположением одинаковых атомов или атомных групп относительно плоскости  связи.
связи.
ГЕТЕРОГЕННЫЙ КАТАЛИЗ — процесс, в котором реагенты и катализатор находятся в разном фазовом состоянии.
ГИБРИДИЗАЦИЯ — комбинация («смешивание») атомных орбиталей разного типа, вследствие чего образуется набор эквивалентных (равноценных) гибридных орбиталей.
ГИДРОЛИЗ — взаимодействие ионов соли с водой, приводящее к изменению реакции среды, т.е. pH.
ГЛАВНОЕ КВАНТОВОЕ ЧИСЛО (n) — параметр, характеризующий размер электронного облака и энергию электрона на данной оболочке.
ГОМОГЕННЫЙ КАТАЛИЗ — процесс, в котором катализатор и реагенты находятся в одинаковом фазовом состоянии.
ГРУППА ЭЛЕМЕНТОВ — вертикальный ряд элементов, объединенных по признаку одинаковой степени окисления в высших оксидах.
ДЛИНА СВЯЗИ — расстояние между ядрами связанных между собой атомов.
ДОНОРНО-АКЦЕПТОРНАЯ КОВАЛЕНТНАЯ СВЯЗЬ — связь, формирующаяся за счет неподеленной электронной пары одного атома и свободной орбитали другого атома.
ЗАКОН АВОГАДРО — закон, по которому в равных объемах различных газов при одинаковых условиях содержится одинаковое число молекул.
ЗАКОН ПОСТОЯНСТВА СОСТАВА — закон, по которому любое вещество независимо от способа получения имеет свой постоянный качественный и количественный состав.
ЗАКОН ДЕЙСТВУЮЩИХ МАСС — закон, учитывающий соотношение между скоростью химической реакции и концентрацией реагентов: при постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ.
ЗАКОН ГЕНРИ — масса газа, растворяющегося в данном объеме жидкости при постоянной температуре, прямо пропорциональна парциальному давлению газа.
ЗАКОН ПЕРИОДИЧНОСТИ — закон, на котором основана периодическая система элементов: периодическое изменение строения электронной оболочки определяет периодичность изменения свойств элементов.
ЗАМЕЩЕНИЕ — реакция, при которой частица замещает атом или группу атомов в другой молекуле.
ИЗОТОПЫ — атомы, имеющие одинаковый заряд ядер, но различные массовые числа.
ИОНИЗАЦИОННЫЙ ПОТЕНЦИАЛ — количество энергии (кДж/моль), затрачиваемое на полное удаление электрона от атома.
ИОННАЯ СВЯЗЬ — разновидность химической связи, в основе которой лежит электростатическое взаимодействие ионов.
ИОННОЕ ПРОИЗВЕДЕНИЕ ВОДЫ  — произведение концентрации водородных и гидроксильных ионов.
— произведение концентрации водородных и гидроксильных ионов.
КАТАЛИЗАТОР — вещество, увеличивающее скорость химической реакции, но в конечном итоге остающееся неизменным качественно и количественно.
КИСЛОТА ПО АРРЕНИУСУ — это электролит, при диссоциации высвобождающий ион  ; по Бренстеду-Лоури — любое вещество, являющееся источником ионов
; по Бренстеду-Лоури — любое вещество, являющееся источником ионов  ; по Льюису -вещество, способное быть акцептором электронной пары.
; по Льюису -вещество, способное быть акцептором электронной пары.
КОВАЛЕНТНАЯ СВЯЗЬ — связь атомов посредством электронных пар.
КОНСТАНТА СКОРОСТИ — скорость реакции при конценг трации реагентов, равной 1.
КОНЦЕНТРАЦИЯ — доля вещества (выраженная его массой, объемом или числом) в массе, объеме или молярном количестве смеси.
КОРРОЗИЯ — разрушение металла вследствие физико-химического воздействия окружающей среды.
ЛАНТАНОИДЫ — название элементов с порядковыми номерами 57-71 ( ).
).
МАГНИТНОЕ (ориентационное) КВАНТОВОЕ ЧИСЛО  — параметр, характеризующий ориентацию орбитали в пространстве.
— параметр, характеризующий ориентацию орбитали в пространстве.
МЕТАЛЛИЧЕСКАЯ СВЯЗЬ — химическая связь, основанная на обобществлении валентных электронов, принадлежащих не двум, а практически всем атомам в кристалле.
МОЛЬ — количество вещества, содержащее такое же число структурных единиц (атомов, молекул, ионов, электронов и т.д.), какое содержится в 0,012 кг атома  , т.е. 6,02 •
, т.е. 6,02 •  .
.
МОЛЯРНАЯ МАССА — величина, равная отношению массы вещества в граммах на количество вещества в молях. Численно совпадает с относительной молекулярной массой.
МОЛЕКУЛЯРНАЯ МАССА (относительная) — отношение средней массы молекулы естественного изотонического состава вещества к 1/12 массы атома углерода  .
.
НАПРАВЛЕННОСТЬ СВЯЗИ — свойство ковалентной связи, обусловливающее пространственную структуру (геометрию) молекул.
ОКИСЛЕНИЕ — процесс отдачи электронов.
ОКИСЛИТЕЛЬ — вещество, которое восстанавливается в химической реакции, будучи причиной окисления другого вещества.
ОКСИДЫ — соединения, состоящие из атомов двух элементов, один из которых — кислород.
ОКСИДЫ АМФОТЕРНЫЕ — оксиды, проявляющие свойства как основных, так и кислотных оксидов.
ОРБИТАЛЬНОЕ КВАНТОВОЕ ЧИСЛО 1 — параметр, определяющий форму атомной орбитали. Может принимать целочисленные значения от 0 до n-1.
ОСНОВАНИЕ ПО АРРЕНИУСУ — это электролит, при диссоциации высвобождающий  -ионы, по Бренстеду-Лори -любое вещество, способное быть акцептором ионов
-ионы, по Бренстеду-Лори -любое вещество, способное быть акцептором ионов  ; по Льюису — вещество, являющееся донором электронной пары.
; по Льюису — вещество, являющееся донором электронной пары.
ПЕРИОД — горизонтальный ряд элементов, в котором имеет место закономерное изменение свойств элементов от типично металлических к типично неметаллическим.
ПОЛЯРНОСТЬ СВЯЗИ — несимметричное распределение электронной плотности между атомами.
ПЕРИОДИЧЕСКИЙ ЗАКОН (в формулировке Д.И.Менделеева) — свойства простых тел, а также формы и свойства соединений химических элементов находятся в периодической зависимости от величин атомных весов (масс) элементов.
ПОЛЯРИЗУЕМОСТЬ СВЯЗИ — перераспределение электронной плотности в молекуле под влиянием внешнего воздействия.
ПИ-СВЯЗЬ ( -связь) — ковалентная связь, формирующаяся при боковом перекрывании негибридных p-орбиталей по обе стороны от линии, связывающей центры соединяющихся атомов.
-связь) — ковалентная связь, формирующаяся при боковом перекрывании негибридных p-орбиталей по обе стороны от линии, связывающей центры соединяющихся атомов.
ПОДГРУППА — подразделение элементов внутри группы. Каждая подгруппа объединяет элементы, являющиеся химическими аналогами.
ПРИНЦИП ЛЕ ШАТЕЛЬЕ — если на систему в состоянии равновесия оказывается воздействие, то положение равновесия смещается в том направлении, которое сводит к минимуму влияния внешнего воздействия.
РАСТВОР — гомогенная (однородная) система переменного состава, состоящая из двух и более компонентов.
РАСТВОРИМОСТЬ — способность вещества растворяться в данном растворителе с образованием насыщенного при данной температуре раствора.
СЕМЕЙСТВО ЭЛЕМЕНТОВ — совокупность элементов, в атомах которых заселение орбиталей наружных электронных оболочек осуществляется по одинаковому принципу. В соответствии с этим различают s-, р-, d- и f-семейства элементов.
СОЛИ — продукты замещения атомов водорода в кислоте на металл (или ОН-групп в основании на кислотный остаток).
СИГМА-СВЯЗЬ ( -связь) — ковалентная связь, образующаяся при перекрывании орбиталей вдоль линии, связывающей центры соединяющих атомов.
-связь) — ковалентная связь, образующаяся при перекрывании орбиталей вдоль линии, связывающей центры соединяющих атомов.
ЭНЕРГИЯ СВЯЗИ — энергия, необходимая для разрыва химической связи.
СПИНОВОЕ КВАНТОВОЕ ЧИСЛО — S-параметр, характеризующий угловой момент импульса электрона.
СПЛАВ — система, образующаяся при кристаллизации расплавленной смеси металлов.
СТЕХИОМЕТРИЯ РЕАКЦИИ — соотношение между количествами вступивших в реакцию реагентов и образующихся продуктов.
ПРИНЦИП ПАУЛИ утверждает, что в атоме не может быть двух электронов, состояние которых определяется одинаковой комбинацией всех четырех квантовых чисел. Из этого следует, что на любой орбитали не может быть более двух электронов: при одинаковых значениях  спиновые квантовые числа их всегда будут разные
спиновые квантовые числа их всегда будут разные  .
.
ХАЛЬКОГЕНЫ — общее название элементов главной подгруппы VI группы, в которую входят кислород, сера, селен, теллур и полоний.
ХИМИЧЕСКАЯ КОРРОЗИЯ — взаимодействие металла с химически активными веществами, содержащимися в природных и технологических средах.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ — состояние системы, в которой скорость прямой реакции равна скорости обратной реакции.
ЩЕЛОЧИ — гидроксиды щелочных и щелочно-земельных металлов.
ЩЕЛОЧНЫЕ МЕТАЛЛЫ — общее название элементов главной подгруппы I группы, в которую входят литий, натрий, калий, рубидий, цезий, франций.
ЭКЗОТЕРМИЧЕСКИЕ РЕАКЦИИ — реакции, протекающие с выделением теплоты.
ЭНДОТЕРМИЧЕСКИЕ РЕАКЦИИ — реакции, протекающие с поглощением теплоты.
ЭЛЕКТРОЛИЗ — совокупность реакций, происходящих в растворах или расплавах электролитов при прохождении через них электрического тока.
ЭЛЕКТРООТРИЦАТЕЛЬНОСТЬ — относительная способность атомов элемента притягивать электроны, участвующие в образовании химической связи.
ЭЛЕКТРОННАЯ КОНФИГУРАЦИЯ — распределение электронов по орбиталям.
ЭЛЕКТРОЛИТ — вещество, проводящее в водных растворах электрический ток.
ЭЛЕКТРОХИМИЧЕСКАЯ КОРРОЗИЯ — разрушение металла под действием водных растворов химически активных соединений.
ЯДРО — положительно заряженная частица, в которой практически сосредоточена вся масса атома. Заряд ядра атома элемента равен его порядковому номеру.
Дополнительные темы и примеры по химии
Химия — это одна из важнейших и обширных областей естествознания, наука, изучающая вещества, также их состав и строение, их свойствах, зависящих от состава и строения, их превращениях, ведущих к изменению состава — химических реакциях, а также о законах и закономерностях, которым эти превращения подчиняются. Поскольку все вещества состоят из атомов, которые благодаря химическим связям способны формировать молекулы, то химия занимается, прежде всего, рассмотрением перечисленных выше задач на атомно-молекулярном уровне, то есть на уровне химических элементов и их соединений.
Установление формулы химического вещества. Алгоритмы решения задач на определение формулы химического вещества по данным о его количественном составе
Алгоритм решения задач, рассматривающих вывод формулы химического вещества по их количественному составу, является, по-видимому, простейшим.
К задачам этого типа относятся задачи, в которых наличие полной информации о качественном составе вещества является обязательным условием. При этом количественные соотношения компонентов задаются, как правило, их массовыми долями (в масс. %), по которым рассчитывают молярные соотношения компонентов, что и приводит к установлению простейшей формулы химического вещества.
Необходимо отметить, что установление простейшей формулы химического вещества, когда анализируемый объект — неорганическое соединение, обычно является окончательным решением задачи (из-за существования однозначности и единственности решения). В то же время, при анализе органических объектов решение задачи об установлении формулы химического вещества только по данным о его количественном составе становится неоднозначным (изомерия, гомология и т. д.) и требует использования дополнительных данных. Поэтому в настоящем разделе приведены лишь те задачи, в которых в качестве объектов выступают неорганические соединения. Задачи, посвященные установлению формулы органических веществ, будут рассмотрены в разделе 1.4 этой главы.
Приведем решение типичной задачи о выводе формулы неорганического вещества по его количественному составу.
Пример №1-1.
Установить формулу химического соединения на основании данных о его количественном составе: железо — 46,67 % и сера — 53,33 %.
Решение:
Возьмем 100 г неизвестного вещества. Тогда в выбранной навеске последнего будет содержаться 46,67 г железа и 53,33 г серы. Определим количество вещества (железа и серы) в соответствующих им массах:

Проведенные расчеты показывают, что молярное соотношение компонентов:

позволяет приписать неизвестному веществу формулу  .
.
Действительно, такое вещество существует. Это известный минерал — пирит.
Рассмотрим алгоритм решения «обратных» задач.
Пример №1-2.
Ионы аммония образуют с некоторыми элементами X и Y соединения  (массовая доля ионов аммония равна 22,5 %) и
(массовая доля ионов аммония равна 22,5 %) и  (массовая доля ионов аммония равна 28,125 %). Определите элементы X и Y.
(массовая доля ионов аммония равна 28,125 %). Определите элементы X и Y.
Решение:
Обозначим молярную массу элемента X символом  . Тогда на основании определения массовой доли компонента в соединении можем записать два уравнения для соединений
. Тогда на основании определения массовой доли компонента в соединении можем записать два уравнения для соединений  соответственно:
соответственно:

Решение полученной системы уравнений позволяет установить, что

Задачи на установление формулы химического вещества с использованием молярных масс эквивалентов простых и сложных веществ. Алгоритмы их решений
Алгоритм решения задач этого типа основан на использовании закона эквивалентов, сформулированного В. Рихтером в 1792-1794 гг.: химические элементы соединяются друг с другом в строго определенных количествах, соответствующих молярным массам их эквивалентов. Понятие молярной массы эквивалента элементов было введено для сопоставления их «соединительной» способности и до сих пор является в химии (особенно в аналитической химии) одним из важнейших.
Молярной массой эквивалента химического элемента называют такую его массу, которая соединяется с 1,008 ч. м. (части массы) водорода или 8,0 ч. м. кислорода или замещает эти массы в соединениях.
Отметим, что один и тот же элемент может иметь не одну, а несколько молярных масс эквивалентов. Так, молярная масса эквивалента углерода в оксиде углерода (IV) равна трем, а в оксиде углерода (II) — шести.
Понятие молярной массы эквивалента широко используют и для сложных соединений.
Молярной массой эквивалента сложного соединения называют массу этого соединения, являющуюся суммой молярных масс эквивалентов образующих его компонентов.
Рассмотрим способы оценки молярных масс эквивалентов основных классов химических соединений (оксидов, кислот, оснований и солей).
1. Молярная масса эквивалента оксида Э(окс) равна сумме молярных масс эквивалентов кислорода  и образующего оксид элемента R:
и образующего оксид элемента R:  , где n — степень окисления элемента R. При этом используется основное соотношение между величинами молярной массы M(R), молярной массы эквивалента элемента 3(R) и степенью его окисления — n:
, где n — степень окисления элемента R. При этом используется основное соотношение между величинами молярной массы M(R), молярной массы эквивалента элемента 3(R) и степенью его окисления — n:

Таким образом, формула любого оксида может быть представлена в следующем общем виде:  , из которого видно, что для всех оксидов величина
, из которого видно, что для всех оксидов величина  .
.
Отметим, что величина Э(окс) может быть также рассчитана на основе соотношения:

где М(окс) — молярная масса оксида, х — число атомов кислорода в молекуле оксида, у — число атомов элемента R в молекуле оксида.
2. Молярная масса эквивалента кислоты Э(кисл) равна сумме молярных масс эквивалента водорода 3(H) = М(Н) = 1 и кислотного остатка  :
:  , где m — заряд иона кислотного остатка, а
, где m — заряд иона кислотного остатка, а  — его молярная масса.
— его молярная масса.
Таким образом, формула любой кислоты может быть представлена в следующем общем виде:  из которого видно, что для всех кислот величина
из которого видно, что для всех кислот величина 
Отметим, что величина Э(кисл) может быть также рассчитана по уравнению:

где  — молярная масса кислоты, m — основность кислоты или заряд иона кислотного остатка.
— молярная масса кислоты, m — основность кислоты или заряд иона кислотного остатка.
1. Молярная масса эквивалента основания Э(осн) равна сумме молярных масс эквивалентов образующего основание элемента R:  , где n — заряд иона элемента R, и гидроксид-иона
, где n — заряд иона элемента R, и гидроксид-иона 
Таким образом, формула любого основания может быть представлена в следующем общем виде:  , из которого видно, что для всех оснований величина
, из которого видно, что для всех оснований величина  .
.
Отметим, что величина Э(осн) может быть также рассчитана по уравнению:

где М(осн) — молярная масса основания, n — кислотность основания или заряд катиона образующего его элемента.
- Молярная масса эквивалента соли Э(сол) равна сумме молярных масс эквивалентов образующих соль компонентов — металла R:

 , где n — заряд иона металла
, где n — заряд иона металла  , и иона кислотного остатка
, и иона кислотного остатка  , где m — заряд этого иона.
, где m — заряд этого иона.
Таким образом, формула любой соли может быть представлена в следующем общем виде:  , из которого видно, что для всех солей величина
, из которого видно, что для всех солей величина  .
.
Отметим, что величина Э(сол) может быть также рассчитана по уравнению:

где М(сол) — молярная масса соли.
Таким образом, в общем виде закон эквивалентов можно сформулировать следующим образом:
Во всех химических реакциях взаимодействие различных веществ друг с другом происходит в соответствии с молярными массами их эквивалентов, независимо от того, являются ли эти вещества простыми или сложными.
Пример №1-3.
Определите формулу соединения, если известно, что оно содержит 15,79 % металла, 28,07 % серы и 56,14 % кислорода по массе.
Решение:
На первый взгляд, эта задача напоминает уже разбиравшиеся нами в разделе 2.1. Однако ее решение заметно осложнено тем, что металл неизвестен. Именно поэтому единственный путь решения — использование на одном из его этапов понятия молярной массы эквивалента.
Возьмем 100 г неизвестного вещества. Тогда в этой навеске будет содержаться: 15,79 г определяемого металла, 28,07 г серы и 56,14 г кислорода. Рассчитаем количество вещества (серы и кислорода) в соответствующих им массах:

Проведенные оценки показывают, что атомное соотношение этих компонентов составляет  Это позволяет утверждать, что в неизвестном веществе присутствуют сульфат-ионы. Далее, целесообразно предположить, что неизвестное вещество — сульфат неизвестного металла. После записи формулы сульфата в общем виде с использованием закона эквивалентов:
Это позволяет утверждать, что в неизвестном веществе присутствуют сульфат-ионы. Далее, целесообразно предположить, что неизвестное вещество — сульфат неизвестного металла. После записи формулы сульфата в общем виде с использованием закона эквивалентов:  , получаем, что Э(Ме) соединен в нем с
, получаем, что Э(Ме) соединен в нем с  = 48,0 г/моль, а по условию задачи 15,79 г Me приходится на 84,21 г сульфат-иона. Решение полученной пропорции
= 48,0 г/моль, а по условию задачи 15,79 г Me приходится на 84,21 г сульфат-иона. Решение полученной пропорции

дает 
Теперь приступим к заключительной (и очень важной!) стадии решения задачи — определению неизвестного металла по молярной массе его эквивалента. Для этого воспользуемся соотношением  . При этом определение необходимо проводить по двум критериям.
. При этом определение необходимо проводить по двум критериям.
Первый из них использует равенство величины степени окисления (заряда ионов) и номера группы периодической системы Д. И. Менделеева. Этот критерий наиболее прост, но носит частный характер, поскольку строго выполняется и.может быть применен только для ионов s- и р-металлов.
Второй критерий рассматривает возможность проявления элементом, характеризующимся рассчитанной величиной молярной массы М, данной степени окисления п. Этот критерий является, по-видимому, наиболее общим и может быть применен к любым элементам периодической системы.
Итак, приступим к определению качественного состава неизвестного соединения. При этом для первой задачи приведем полный анализ решения.
При  . Металл с такой молярной массой в I группе периодической системы отсутствует (1 критерий). В то же время величине M(R) = 9 г/моль соответствует элемент II группы — бериллий. Однако этот металл не проявляет степень окисления n = 1, и это решение не подходит (II критерий).
. Металл с такой молярной массой в I группе периодической системы отсутствует (1 критерий). В то же время величине M(R) = 9 г/моль соответствует элемент II группы — бериллий. Однако этот металл не проявляет степень окисления n = 1, и это решение не подходит (II критерий).
При  . Металл с такой молярной массой как во II группе, так и в других группах периодической системы отсутствует.
. Металл с такой молярной массой как во II группе, так и в других группах периодической системы отсутствует.
При  . Этой величине молярной массы соответствует металл III группы периодической системы — алюминий (I критерий).
. Этой величине молярной массы соответствует металл III группы периодической системы — алюминий (I критерий).
В принципе, анализ необходимо проводить до n = 8, не останавливаясь на первом же найденном решении, удовлетворяющем условию задачи. Действительно, далее будет показано, что в некоторых задачах одним и тем же условиям удовлетворяют несколько решений.
Однако в данной задаче решение  является единственным и дальнейший анализ можно не проводить, т. к. сульфаты, в состав которых входят ионы металла с зарядом больше, чем 3+, в природе не существуют (для ионов металла с большим зарядом характерно образование оксисульфатов).
является единственным и дальнейший анализ можно не проводить, т. к. сульфаты, в состав которых входят ионы металла с зарядом больше, чем 3+, в природе не существуют (для ионов металла с большим зарядом характерно образование оксисульфатов).
Если же формально провести анализ до n = 8, то мы получим тот же ответ:  .
.
Действительно, при n = 4 в таблице Менделеева отсутствует металл с молярной массой  = 36 г/моль. При n = 5 металл с
= 36 г/моль. При n = 5 металл с  = 45 г/моль существует. Это — скандий. Однако он в принципе не может давать ионы
= 45 г/моль существует. Это — скандий. Однако он в принципе не может давать ионы  . По этой же причине отпадают марганец [
. По этой же причине отпадают марганец [ = 54 г/моль при n = 6], медь [
= 54 г/моль при n = 6], медь [ = 63 г/моль при n = 7] и германий [
= 63 г/моль при n = 7] и германий [ = 72 г/моль при n = 8]. Одновременно необходимо отметить, что во всех трех последних случаях рассчитанные величины A(R) несколько ниже значений средних молярных масс, приведенных в таблице Менделеева.
= 72 г/моль при n = 8]. Одновременно необходимо отметить, что во всех трех последних случаях рассчитанные величины A(R) несколько ниже значений средних молярных масс, приведенных в таблице Менделеева.
Ответ: неизвестное вещество имеет формулу  .
.
Пример №1-4.
Неизвестное соединение содержит 24,68 % калия, 34,81 % неизвестного металла и 40,51 % кислорода по массе. Определите формулу этого соединения.
Решение:
Возьмем 100 г неизвестного вещества. Тогда в этой навеске будет содержаться: 24,68 г калия, 34,81 г определяемого металла и 40,51 г кислорода. Рассчитаем количество вещества (калия и кислорода) в соответствующих им массах:

Проведенные оценки показывают: что молярное соотношение этих компонентов составляет  . Это позволяет утверждать, что неизвестное вещество — соль калия, а кислород входит в состав аниона, формируемого переходным металлом Me. После записи формулы соединения в общем виде с использованием закона эквивалентов:
. Это позволяет утверждать, что неизвестное вещество — соль калия, а кислород входит в состав аниона, формируемого переходным металлом Me. После записи формулы соединения в общем виде с использованием закона эквивалентов:  , получаем, что Э(К) = 39 соединен в нем с
, получаем, что Э(К) = 39 соединен в нем с  , а по условию задачи 24,68 г К приходится на 75,32 г иона
, а по условию задачи 24,68 г К приходится на 75,32 г иона  . Решение полученной пропорции
. Решение полученной пропорции

дает  = 119,0 г/моль, М(Ме) = 55,0 г/моль и неизвестный металл — марганец.
= 119,0 г/моль, М(Ме) = 55,0 г/моль и неизвестный металл — марганец.
Ответ: формула неизвестного вещества —  .
.
Дополнительные примеры с решением:
- Пример №1-5. Часто примером задач, для решения которых применяется понятие молярной массы эквивалента, является задача о растворении металла в кислоте.
- Пример №1-6. 54,92 г йодида неизвестного металла было подвергнуто разложению. При этом получено 40,64 г чистого йода. Определите неизвестный металл.
- Пример №1-7. Для восстановления 23,2 г одного из оксидов железа до металла потребовалось 8,96 л водорода (н. у.). Какой именно оксид железа был взят дли восстановления?
- Пример №1-8. Какие химические соединения с общей формулой содержат 12,5 % водорода по массе?
Методы решения задач на определение формулы химического вещества на основании данных о химических реакциях, протекающих с его участием
Рассмотрим еще один тип задач, в которых определение состава химического вещества основано на данных о химических реакциях, протекающих с его участием.
Простейшими реакциями, рассматриваемыми в задачах этого типа, являются реакции полного окисления (горения) исходных веществ до более простых продуктов. Идея задач, анализирующих реакции горения, заключается в следующем: после сжигания образца неизвестного вещества определенной массы фиксируются массы всех образующихся продуктов. Алгоритм решения таких задач сводится к определению количества вещества каждого из компонентов, входящих в состав неизвестного вещества, и последующего его «конструирования» по рассчитанным величинам.
Отметим, что аналогичный алгоритм используется и для решения задач, рассматривающих другие химические реакции.
Разберем некоторые конкретные примеры.
Пример №1-9.
6,8 г неизвестного вещества сожгли в избытке кислорода. При этом было получено 14,2 г  и 5,4 г воды. Определите состав и формулу неизвестного вещества.
и 5,4 г воды. Определите состав и формулу неизвестного вещества.
Решение:
Состав продуктов реакции  позволяет утверждать, что в состав неизвестного вещества входят фосфор и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала количества фосфора и водорода, входящие в его состав.
позволяет утверждать, что в состав неизвестного вещества входят фосфор и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала количества фосфора и водорода, входящие в его состав.

Суммируя массы фосфора и водорода, получаем:

что равно массе исходного образца. Следовательно, в состав неизвестного вещества входят только фосфор и водород, а кислород в нем не содержится.
Теперь непосредственно перейдем к установлению формулы неизвестного вещества. Из проведенных расчетов видно, что молярное соотношение компонентов в искомом соединении равно:

Очевидно, что неизвестное вещество — фосфин.
Ответ:  .
.
Пример №1-10.
В результате сжигания 15,6 г неизвестного вещества в избытке кислорода было получено 8,8 г  и 10,8 г воды. Определите состав и формулу неизвестного вещества.
и 10,8 г воды. Определите состав и формулу неизвестного вещества.
Решение:
Состав продуктов реакции  позволяет утверждать, что в состав неизвестного вещества входят углерод, азот и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала количества углерода, азота и водорода, входящие его состав.
позволяет утверждать, что в состав неизвестного вещества входят углерод, азот и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала количества углерода, азота и водорода, входящие его состав.

Суммируя массы углерода, азота и водорода, получаем:

что не равно массе исходного образца. Следовательно, в состав неизвестного вещества входят не только углерод, азот и водород, но и кислород, масса которого составляет

Теперь непосредственно перейдем к установлению формулы неизвестного вещества. Из проведенных расчетов видно, что молярное соотношение компонентов в искомом соединении равно:

Очевидно, что полученному соотношению компонентов наилучшим образом отвечает карбамат аммония  — продукт взаимодействия диоксида углерода с аммиаком.
— продукт взаимодействия диоксида углерода с аммиаком.
Ответ: 
Дополнительные примеры с решением:
- Пример №1-11. При разложении 49 г неизвестного вещества выделилось 13,44 л кислорода и осталось твердое вещество, содержащее 52,35 % калия и 47,65 % хлора. Определите формулу неизвестного вещества.
- Пример №1-12. Два элемента принадлежат одной группе четного периода периодической системы и образуют водородные соединения, высшие оксиды и гидраты высших оксидов одного и того же состава. Отношение молярных масс их водородных соединений равно 2,3824, высших оксидов — 1,5875 и гидратов высших оксидов — 1,4796. Определите эти элементы.
Задачи на установление формулы органического вещества.и основные алгоритмы их решений
В этом разделе будут рассмотрены подходы к решению задач на установление формулы органического вещества. С некоторыми из них мы уже познакомились в предыдущих разделах. Так, в примере 1-12 применяется алгоритм решения, который уже использовался в разделе 1.1 (пример 1-1), а в примерах 1-13, 1-16 и 1-17 — алгоритм решения раздела 1.3 (примеры 1-9 и 1-10). Это и понятно, поскольку формулировки задач, разбираемых в соответствующих примерах, не отражают «специфики» органической химии, т. е. они «безразмерны» по отношению к рассматриваемому объекту. Алгоритмы решения задач на установление формулы вещества (см. разделы 1.1 и 1 .3), разработанные для общего случая анализа систем 
 , и т. п. (где R — любой химический элемент), можно, естественно, с успехом использовать и для определения формулы органического вещества, когда R = С.
, и т. п. (где R — любой химический элемент), можно, естественно, с успехом использовать и для определения формулы органического вещества, когда R = С.
Однако если в формулировке задачи неизвестное анализируемое вещество отнесено к тому или иному классу органических соединений, то при анализе задачи сразу же возникает особая «органическая» специфика, что требует разработки и применения соответствующих алгоритмов. В этом случае специфика задач на установление формулы неизвестного вещества проявляется в возможности использования общих формул, соответствующих тому или иному классу органических соединений. Благодаря этому число неизвестных параметров, вводимых при решении задачи, заметно сокращается. Так, если неорганическое вещество состоит из  , то его формула может быть записана в виде
, то его формула может быть записана в виде  . Если решается задача об органическом веществе, состоящем из
. Если решается задача об органическом веществе, состоящем из  (при этом класс органического вещества не указан), то ситуация остается неизменной и его формула записывается аналогичным образом:
(при этом класс органического вещества не указан), то ситуация остается неизменной и его формула записывается аналогичным образом:  . Однако если класс того же вещества, состоящего из
. Однако если класс того же вещества, состоящего из  , указан (например, в задаче рассматривается насыщенная монокарбоновая кислота), то при решении можно использовать общую формулу для этого класса соединений:
, указан (например, в задаче рассматривается насыщенная монокарбоновая кислота), то при решении можно использовать общую формулу для этого класса соединений:  , для которых молярная масса также может быть представлена общей формулой:
, для которых молярная масса также может быть представлена общей формулой:  Указанный подход создает дополнительные возможности и широко используется при решении задач, объектами которых являются органические вещества определенного класса.
Указанный подход создает дополнительные возможности и широко используется при решении задач, объектами которых являются органические вещества определенного класса.
Ниже приведены наиболее часто встречающиеся классы органических веществ, их общие формулы и соответствующие им общие формулы для молярных масс.
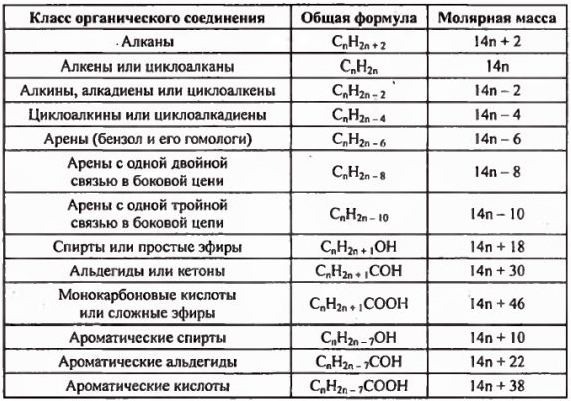
Очевидно, что общие формулы и молярные массы по мере необходимости можно вывести для любого класса органических соединений, что и предлагается делать читателям при решении той или иной конкретной задачи.
Пример №1-13.
Газообразный углеводород имеет такую же плотность, как углекислый газ, а массовая доля углерода и водорода нем составляет соответственно 81,8 % и 18,2 % по массе. Какое это соединение?
Решение:
Возьмем 100 г неизвестного углеводорода. Тогда в выбранной навеске последнего будет содержаться: 81,8 г углерода и 18,2 г водорода. Определим количество вещества (углерода и водорода) в соответствующих им массах.

Проведенные расчеты показывают, что молярное соотношение компонентов:

позволяет приписать неизвестному углеводороду формулу  . Действительно, молярная масса этого вещества равна 44,0 г/моль =
. Действительно, молярная масса этого вещества равна 44,0 г/моль =  , что отвечает условию задачи.
, что отвечает условию задачи.
Ответ:  .
.
Пример №1-14.
Образец органического вещества массой 2,15 г сожгли в избытке кислорода. Продуктами реакции являются оксид углерода (IV) объемом 3,36 л (н. у.) и вода массой 3,15 г. Плотность паров исходного вещества по водороду равна 43. Определите формулу вещества.
Решение:
Состав продуктов реакции  позволяет утверждать, что в состав неизвестного органического вещества входят углерод и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала массы углерода и водорода, входящие в его состав.
позволяет утверждать, что в состав неизвестного органического вещества входят углерод и водород, а также, вероятно, кислород. Для окончательного решения вопроса о качественном составе неизвестного вещества определим сначала массы углерода и водорода, входящие в его состав.

Суммируя массы углерода и водорода, получаем:

что равно массе исходного образца. Следовательно, в состав неизвестного вещества входят только углерод и водород, а кислород в нем не содержится.
Теперь непосредственно перейдем к установлению формулы неизвестного вещества. Из проведенных расчетов видно, что молярное соотношение компонентов в искомом соединении равно:

Очевидно, что неизвестное вещество — углеводород состава  . Действительно, молярная масса этого соединения равна 86,0 г/моль (12 • 6 + 14), что отвечает условию задачи (43 • 2 г/моль).
. Действительно, молярная масса этого соединения равна 86,0 г/моль (12 • 6 + 14), что отвечает условию задачи (43 • 2 г/моль).
Ответ:  .
.
Дополнительные примеры с решением:
- Пример №1-15. Установите формулу гомолога этилена, 1,68 г которого полностью обесцвечивают 128,0 г раствора брома в хлороформе (массовая доля брома в растворе составляет 5,0 %).
- Пример №1-16. Углеводород с содержанием водорода 7,692 % по массе имеет плотность по воздуху 3,586. Определите формулу углеводорода, если известно, что он вступает в реакцию с бромом в молярном соотношении 1:1.
- Пример №1-17. Отношение молярных масс двух алканов составляет величину 1,9333. Отношение же молярных масс их монобромпроизводных равно 1,2569. Установите формулы исходных алканов.
- Пример №1-18. Образец органического вещества массой 8,7 г сожгли в избытке кислорода. Продуктами реакции являются оксид углерода (IV) объемом 10,08 л (н. у.) и вода массой 8,1 г. Плотность паров исходного вещества по гелию равна 14,5. Определите формулу вещества, если известно, что анализируемое вещество не обесцвечивает раствор брома в четырех хлористом углероде и не взаимодействует с аммиачным раствором оксида серебра.
- Пример №1-19. Образец органического вещества массой 1,5 г сожгли в избытке кислорода. Продуктами реакции являются оксид углерода (IV) объемом 896 мл (н. у.), азот — 224 мл (и. у.) и вода массой 0,9 г. Плотность паров исходного вещества по воздуху равна 2,5862. Определите формулу вещества, если известно, что анализируемое вещество взаимодействует с равным числом молей , а полученный продукт — с удвоенным числом молей .
Газовые законы.
Основные соотношения
Параметры состояния газов (давление Р, объем V и температура Т) связаны между собой следующими фундаментальными соотношениями.
Закон Бойля—Мариотта (описывает поведение идеального газа при изотермических условиях Т = const):

Закон Гей-Люссака (описывает поведение идеального газа при изобарических условиях Р = const):

Закон Шарля (описывает поведение идеального газа при изохорических условиях V = const):

Объединенный газовый закон описывает поведение идеального газа при одновременном изменении трех его параметров состояния:

Отметим, что все перечисленные законы справедливы только для постоянного числа молей рассматриваемого газа.
Для одного моля газа уравнение (2.4) можно записать в виде соотношения

где R — универсальная газовая постоянная.
Величина R может быть рассчитана, учитывая, что 1 моль любого газа при нормальных условиях  занимает объем 22,4 л:
занимает объем 22,4 л:

Величину R оценить не только в системе СИ, но и для тех случаев, когда основные параметры состояния газовой системы (Р, V) приведены с использованием внесистемных единиц.
Так, если значение давления приводится в атмосферах, то величина R равна

Если величина давления дается в миллиметрах ртутного столба (мм рт. ст.), то

Уравнение Клапейрона—Менделеева:

где v — число молей газа; m — масса газа; М — молекулярная масса газа.
Из уравнения Клапейрона-Менделеева можно вывести ряд важных следствий
1. При постоянных Р и Т из уравнения (2.6) следует закон Авогадро — в равных объемах газов при постоянных Р и Т содержится одинаковое число молекул:

2. При постоянных Р и Т уравнение (2.6) можно представить в следующем виде

Уравнение (2.8) означает, что при указанных условиях величина плотности газа р определяется только его молекулярной массой. Это позволяет ввести понятие относительной плотности одного газа по другому:

3. При постоянных V и T из уравнения (2.6) следует:

Это означает, что глубина протекания химической газовой реакции в замкнутом сосуде  полностью определяется давлением, поскольку оно зависит только от общего числа молей газа, присутствующих в системе.
полностью определяется давлением, поскольку оно зависит только от общего числа молей газа, присутствующих в системе.
Все рассуждения и выкладки, приведенные для одного газа, полностью сохраняются для смеси газов. В этом случае вводится понятие средней молярной массы:

Отметим, что переход от числа молей к парциальным объемам V, (парциальный объем — объем, который занимал бы данный компонент газовой смеси при соответствующих Р и Т) возможен, поскольку газы в смеси находятся при одинаковых условиях и к ним применим закон Авогадро.
Часто для оценки относительной плотности одного газа по другому в качестве газа-сравнителя используется воздух (см. уравнение (2.9)). Для этого используется величина средней молекулярной массы воздуха, которая может быть оценена:

(в приведенном расчете 0,79 и 0,21 — объемные доли азота и кислорода соответственно).
Алгоритмы решения задач с использованием газовых законов
Задачи, приведенные в этом разделе, можно разделить на две группы.
К первой из них нужно отнести задачи, решение которых следует искать на основе трех рассмотренных выше физических законов (Бойля—Мариотта, Гей-Люссака, Шарля). Естественно, что в «чистом» виде физические законы, устанавливающие те или иные корреляции между физическими параметрами состояния системы, в явном виде не связаны с химическими параметрами этой системы (например, с числом молей ее компонентов).
Взаимосвязь между физическими и химическими параметрами системы успешно достигается благодаря использованию следствия из закона Авогадро (один моль газа при нормальных условиях занимает объем 22,4 л).
Ко второй группе относятся задачи, решение которых полностью основано на использовании уравнения Клапейрона—Менделеева.
Рассмотрим в качестве примера решение типичной задачи первой группы.
Пример №2-1.
Смесь  при 0°С и Р = 84,04 кПа находится в замкнутом реакторе объемом 13,5 л. После введения в систему свежеприготовленного
при 0°С и Р = 84,04 кПа находится в замкнутом реакторе объемом 13,5 л. После введения в систему свежеприготовленного  и длительной выдержки системы при 0°С давление в системе понизилось до 50,42 кПа. Определить состав исходной газовой смеси.
и длительной выдержки системы при 0°С давление в системе понизилось до 50,42 кПа. Определить состав исходной газовой смеси.
Решение:
Используя выражение для закона Бойля—Мариотта  , где
, где  — параметры, отвечающие нормальным условиям, получаем следующее численное соотношение:
— параметры, отвечающие нормальным условиям, получаем следующее численное соотношение:

Следовательно, общее число молей в исходной газовой смеси составляет величину  .
.
После поглощения  рассмотренное выше соотношение принимает вид:
рассмотренное выше соотношение принимает вид:

Следовательно, число молей кислорода в исходной газовой смеси составляет величину  , а число молей углекислого газа в исходной газовой смеси —
, а число молей углекислого газа в исходной газовой смеси — 
Уравнение Клапейрона—Менделеева
Уравнение Клапейрона—Менделеева непосредственно связывает физические и химические параметры системы, а его использование столь очевидно, что не требует специального разбора. Тем не менее убедимся в правильности его применения на ранее разобранном примере.
Пример №2-2.
Смесь  находится в замкнутом реакторе объемом 13,5 л. После введения в систему свежеприготовленного СаО и длительной выдержки системы при 0°С давление в системе понизилось до 50,42 кПа. Определить состав исходной смеси.
находится в замкнутом реакторе объемом 13,5 л. После введения в систему свежеприготовленного СаО и длительной выдержки системы при 0°С давление в системе понизилось до 50,42 кПа. Определить состав исходной смеси.
Решение:
Пользуясь следствием из уравнения Клапейрона—Менделеева для постоянных V и Т:

получаем соотношение, связывающее давления и количества газов в исходном  и конечном
и конечном  состояниях:
состояниях:

Из уравнения Клапейрона—Менделеева находим общее число молей в исходной смеси

откуда 
Используя выражение (I), рассчитываем количество кислорода  моль, содержащегося в реакторе после поглощения
моль, содержащегося в реакторе после поглощения  . Следовательно, количества
. Следовательно, количества  и
и  в исходной смеси соответственно равны 0,2 моль и 0,3 моль.
в исходной смеси соответственно равны 0,2 моль и 0,3 моль.
Ответ:  .
.
Вычисление относительной плотности газа по его молярной массе
Рассмотрим в качестве примера следующую задачу.
Пример №2-3.
Вычислите относительную плотность диоксида серы по воздуху.
Решение:
Из закона Авогадро следует, что относительная плотность одного газа по другому равна отношению молярных масс этих газов, т. е.  . Принимая
. Принимая  , получаем:
, получаем:

Ответ.  .
.
Определение средней молярной массы и относительной плотности смеси газов
Рассмотрим в качестве примера следующие задачи.
Пример №2-4.
Вычислите молярную массу газовой смеси, состоящей из 70 % азота и 30 % кислорода по объему.
Решение:
Из следствия закона Авогадро вытекает, что 1 моль данной смеси содержит 0,7 моль азота и 0,3 моль кислорода (объемная доля газа в смеси газов равна его мольной доле)
Среднюю молярную массу газовой смеси рассчитываем по уравнению:

Ответ: 29,2 г/моль.
Пример №2-5.
Газовую смесь, состоящую из 5 л азота и 6 л водорода, пропустили через катализатор. После реакции-объем смеси составил 10 л. Определите относительную плотность по гелию полученной смеси.
Решение:
Запишем исходные «0» и конечные (равновесные) «р» объемы реагентов и продуктов реакции, принимая, что в реакцию вступило х л азота:

Общий объем полученной смеси равен  , откуда х = 0,5 л. Таким образом, конечная смесь состоит из 4,5 л
, откуда х = 0,5 л. Таким образом, конечная смесь состоит из 4,5 л  . Средняя молярная масса конечной смеси составляет:
. Средняя молярная масса конечной смеси составляет:

Относительная плотность по гелию равна:

Ответ: 
Определение состава газовой смеси по ее молярной массе и плотности
Рассмотрим в качестве примеров следующие задачи
Пример №2-6.
Вычислите массовые и объемные доли кислорода и озона в газовой смеси, если ее средняя молярная масса равна 36 г/моль.
Решение:
Возьмем 1 моль газовой смеси и обозначим число молей кислорода через х, а число молей озона через 1 — х. Тогда масса 1 моля равна:

Решая уравнение, получаем 
Следовательно, объемные доли кислорода и озона соответственно равны 0,75 (или 75 %) и 0,25 (или 25 %).
Находим массовые доли газов:

Ответ: 
Пример №2-7.
Рассчитайте массовые доли газов в смеси, состоящей из азота и фтороводорода, если плотность ее при нормальном давлении и температуре 70° С равна 0,886 г/л.
Решение:
Используя уравнение Клапейрона—Менделеева, рассчитаем среднюю молярную массу смеси:

Возьмем 1 моль газовой смеси и обозначим число молей азота через х, а число молей HF через I — х, тогда масса 1 моля смеси равна:

Решая уравнение, получаем:

Находим массовые доли азота и фтороводорода:

Ответ: 
Приведем еще один пример.
Пример №2-8.
При каталитическом гидрировании смеси пропена и водорода с плотностью по гелию 3 образовалось газовая смесь с плотностью по гелию 3,125. Определите объемную долю пропана в конечной смеси.
Решение:
Возьмем 1 моль газовой смеси и обозначим число молей пропена через х, а число молей водорода через 1 — х, тогда масса 1 моля смеси равна:

откуда х = 0,25 моль, а 1 — х — 0,75 моль.
Запишем исходные «0» и конечные (равновесные) «р» концентрации реагентов и продуктов реакции, принимая, что в реакцию вступило у моль пропена:

Общее число молей в конечной газовой смеси составляет (I — у), а средняя молярная масса ее равна 3,125 * 4 = 12,5 г/моль. Поскольку массы конечной и исходной смесей равны (12 г), выражение для молярной массы конечной смеси примет вид:

Следовательно, мольная и объемная доли пропана равны  .
.
Ответ:  .
.
Строение атома и периодический закон. Основные представления о строении атома
К середине XIX в. — периода завершения второго химико-аналитического этапа развития химии — было неоспоримо доказано существование атомов и молекул и создано атомно-молекулярное учение, которое имело огромное значение для становления химии как науки. Однако основные положения научной концепции, сложившейся к тому времени, базировались на представлении о том, что атом — не только наименьшая, но и элементарная (т. е. неделимая) частица.
Прямым доказательством сложности строения атома стало открытие самопроизвольного распада атомов некоторых элементов, названное радиоактивностью. В 1896 г. французский физик Л. Беккерель обнаружил, что материалы, содержащие уран, засвечивают в темноте фотопластинку, ионизируют газы, вызывают свечение флюоресцирующих веществ. В дальнейшем выяснилось, что этой способностью обладает не только уран. Титанические усилия, связанные с переработкой огромных масс урановой смоляной руды, позволили П. Кюри и М. Склодовской открыть два новых радиоактивных элемента: полоний и радий. Последовавшее за этим установление природы  -лучей, образующихся при радиоактивном распаде (Э. Резерфорд, 1899-1903), открытие ядер атомов диаметром 10 нм, занимающих незначительную долю объема атома (диаметр
-лучей, образующихся при радиоактивном распаде (Э. Резерфорд, 1899-1903), открытие ядер атомов диаметром 10 нм, занимающих незначительную долю объема атома (диаметр  нм) (Э. Резерфорд, 1909-1911), определение заряда электрона (Р. Милликен, 1909-1914) и доказательство дискретности его энергии в атоме (Дж. Франк, Г. Герц, 1912), установление заряда ядра, равного номеру элемента (Г. Мозли, 1913), и, наконец, открытие протона (Э. Резерфорд, 1920) и нейтрона (Дж. Чедвик, 1932) позволили предложить следующую модель строения атома:
нм) (Э. Резерфорд, 1909-1911), определение заряда электрона (Р. Милликен, 1909-1914) и доказательство дискретности его энергии в атоме (Дж. Франк, Г. Герц, 1912), установление заряда ядра, равного номеру элемента (Г. Мозли, 1913), и, наконец, открытие протона (Э. Резерфорд, 1920) и нейтрона (Дж. Чедвик, 1932) позволили предложить следующую модель строения атома:
- В центре атома находится положительно заряженное ядро, занимающее ничтожную часть пространства внутри атома (радиус атома водорода 0,046 нм, радиус протона — ядра атома водорода — 6,5 •
 нм).
нм). - Весь положительный заряд и почти вся масса атома сосредоточены в его ядре (масса электрона равна 1/836 а. с. м.).
- Ядра атомов состоят из протонов и нейтронов (общее название — нуклоны). Число протонов в ядре равно порядковому номеру элемента, а сумма чисел протонов и нейтронов соответствует его массовому числу.
- Вокруг ядра по замкнутым орбитам вращаются электроны. Как видно из таблицы 3.1, их число равно положительному заряду ядра.
Различные виды атомов имеют общее название — нуклиды. Нуклиды достаточно характеризовать двумя числами из трех фундаментальных параметров: А — массовое число, Z — заряд ядра, равный числу протонов, и N — число нейтронов в ядре, тогда как третье определяется соотношениями:

Таблица 3.1.

Перейдем к рассмотрению закономерностей поведения электронов в атоме.
Согласно квантовомеханическим представлениям о строении атома, электрон имеет двойственную природу. Он способен проявлять одновременно как свойства частиц, так и свойства волн: подобно частице электрон обладает определенной массой и зарядом; движущийся поток электронов проявляет волновые свойства, например, характеризуется способностью к дифракции. В отличие от обычных тел для электрона нельзя одновременно определить его координаты в атоме и скорость. Электрон может находиться в любой части околоядерного пространства, однако вероятность его нахождения в разных частях этого пространства неодинакова. Пространство вокруг ядра, в котором вероятность нахождения электрона достаточно велика, называют орбиталью.
В современной модели атома состояние в нем электрона определяется четырьмя энергетическими параметрами — квантовыми числами.
Главное квантовое число п определяет энергию электрона и степень его удаления от ядра; оно принимает любые целочисленные значения, начиная с 
Побочное (орбитальное) квантовое число l определяет форму атомной орбитали. Оно может принимать целочисленные значения от 0 до n — 1  . Каждому значению l соответствует орбиталь особой формы. При l = 0 атомная орбиталь, независимо от значения главного квантового числа, имеет сферическую форму (s-орбиталь). Значению l = 1 соответствует атомная орбиталь, имеющая форму гантели (р-орбиталь). Еще более сложную форму имеют орбитали, отвечающие высоким значениям l , равным 2, 3 и 4 (d-, f-, g-орбитали).
. Каждому значению l соответствует орбиталь особой формы. При l = 0 атомная орбиталь, независимо от значения главного квантового числа, имеет сферическую форму (s-орбиталь). Значению l = 1 соответствует атомная орбиталь, имеющая форму гантели (р-орбиталь). Еще более сложную форму имеют орбитали, отвечающие высоким значениям l , равным 2, 3 и 4 (d-, f-, g-орбитали).
Магнитное квантовое число m определяет положение атомной орбитали в пространстве относительно внешнего магнитного или электрического поля. Магнитное квантовое число связано с орбитальным квантовым числом, изменяясь от — l до + l , включая 0. Следовательно, каждому значению / соответствует 2 l + 1 значений магнитного квантового числа.
Таблица 3.2
Распределение электронов по квантовым уровням

Спиновое квантовое число s может принимать лишь два возможных значения:  . Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона.
. Они соответствуют двум возможным и противоположным друг другу направлениям собственного магнитного момента электрона.
Схема распределения электронов по квантовым уровням представлена в табл. 3.2.
Подобно любой системе, атомы стремятся к минимуму энергии. Это достигается при определенном состоянии электронов, т. е. при определенном распределении электронов по орбиталям. которое можно оценить на основе следующих закономерностей:
Принцип Паули: в атоме не может быть электронов с одинаковым значением всех четырех квантовых чисел.
Правило Хунда: электроны располагаются на одинаковых орбиталях таким образом, чтобы суммарный спин был максимален.
Правило Клечковского: порядок заполнения энергетических состояний определяется стремлением атома к минимальному значению суммы главного и побочного квантовых чисел, причем в пределах фиксированного значения л + I в первую очередь заполняются состояния, отвечающие минимальным значениям и.
Пример:
Рассмотрим применение правила Клечковского для определения распределения электронов по орбиталям для атомов калия (Z = 19) и скандия (Z = 21).
1. Предшествующий калию элемент аргон (Z = 18) имеет следующее распределение электронов по орбиталям: 
При распределении электронов по орбиталям в атоме К в соответствии с правилом Клечковского предпочтение отдается орбитали 4s (сумма квантовых чисел  равна 4 + 0 = 4) по сравнению с орбиталью 3d (сумма квантовых чисел
равна 4 + 0 = 4) по сравнению с орбиталью 3d (сумма квантовых чисел  равна 3 + 2 = 5), как орбитали, имеющей минимальное значение
равна 3 + 2 = 5), как орбитали, имеющей минимальное значение  .
.
Следовательно, для атома К:  .
.
2. Предшествующий скандию элемент кальций (Z = 20) имеет следующее распределение электронов по орбиталям: 
Из орбиталей  при распределении электронов в атоме Sc по орбиталям предпочтение следует отдать орбитали 3d как орбитали, имеющей минимальное значение n = 3 при одинаковых суммах квантовых чисел
при распределении электронов в атоме Sc по орбиталям предпочтение следует отдать орбитали 3d как орбитали, имеющей минимальное значение n = 3 при одинаковых суммах квантовых чисел  , равных 5.
, равных 5.
Атом скандия характеризуется следующим распределением электронов по орбиталям:  .
.
В табл. 3.3 представлены электронные конфигурации атомов первых тридцати элементов периодической системы химических элементов Д. И. Менделеева.
Таблица 3.3
Электронные конфигурации атомов первых тридцати элементов периодической системы химических элементов Д. И. Менделеева

Периодический закон и строение атома
Данные о строении ядра и о распределении электронов в атомах (см. табл. 3.3) позволяют рассмотреть периодическую систему химических элементов Д. И. Менделеева с фундаментальных физических позиций.
Из данных о строении ядра следует, что однозначным признаком химического элемента является заряд ядра Z, определяемый числом протонов в ядре и равный атомному номеру элемента в периодической таблице химических элементов Д. И. Менделеева. Относительные атомные массы элементов, приводимые в периодической таблице, представляют собой усредненные значения из относительных атомных масс изотопов, составляющих естественную, природную смесь.
Общее число электронов в электронейтральных атомах равно числу протонов в ядре, т. е. атомному номеру элемента 7. Число энергетических уровней, на которых располагаются электроны в атоме, определяется номером периода. Чем больше номер периода, тем больше энергетических уровней, на которых располагаются электроны, и тем больше внешние энергетические уровни удалены от ядра.
Число элементов в периоде определяется формулами:
• для нечетных периодов

• для четных периодов

где  — число элементов в периоде, n — номер периода.
— число элементов в периоде, n — номер периода.
Приведенные формулы позволяют легко определить, что в 1 -м периоде должно содержаться 2 элемента, во 2-м и 3-м — по 8, в 4-м и 5-м — по 18, в 6-м — 32, в незавершенном 7-м периоде также должно быть 32 элемента. Итак, число элементов в периодах совпадает с максимальным числом электронов на энергетических уровнях 2-8-18-32 (см. табл. 3.2).
Число главных подгрупп также определяется максимальным числом электронов на энергетическом уровне 8. Число переходных элементов в 4-м  периодах равно 10 и определяется разностью между максимальными числами электронов на третьем и втором энергетических уровнях: 18 — 8 = 10, т. е. равно максимальному числу электронов на d-подуровне (см. табл. 3.2).
периодах равно 10 и определяется разностью между максимальными числами электронов на третьем и втором энергетических уровнях: 18 — 8 = 10, т. е. равно максимальному числу электронов на d-подуровне (см. табл. 3.2).
Так как в периодической системе химических элементов Д. И. Менделеева одна из побочных подгрупп содержит сразу три переходных элемента (для каждого из больших периодов), близких по химическим свойствам:

то число побочных подгрупп, так же как и главных, равно 8.
По аналогии с переходными элементами число лантаноидов и актиноидов, вынесенных внизу периодической системы в виде самостоятельных рядов, должно быть равно разности между максимальными числами электронов на четвертом и третьем энергетических уровнях: 32 — 18 = 14, т. е. равно максимальному числу электронов на f-подуровне (см. табл. 3.1). Таким образом, строгая периодичность расположения элементов в периодической системе химических элементов Д. И. Менделеева полностью объясняется последовательным характером заполнения энергетических уровней.
Следующим важнейшим выводом, который следует из анализа данных, приведенных в табл. 3.3, является вывод о периодическом изменении характера заполнения электронами внешних энергетических уровней, что и вызывает периодические изменения химических свойств элементов и их соединений.
Так, 2-й период состоит из следующих 8 элементов:

При переходе от лития к неону заряд ядра постепенно увеличивается (от Z = 3 до Z = 10), что вызывает увеличение сил притяжения электронов к ядру. В результате радиусы атомов R уменьшаются:

Поэтому способность атомов отдавать электроны (типично металлические свойства), ярко выраженная у атомов лития, постепенно ослабевает при переходе от лития к фтору. Последний является уже типичным неметаллом, т. е элементом, атомы которого способны присоединять электроны.
Начиная со следующего за неоном элемента — натрия (Z = 11), электронные структуры элементов повторяются. Поэтому внешние электронные конфигурации для элементов-аналогов могут быть представлены в общем виде:
• для лития и натрия —  (n — номер периода),
(n — номер периода),
• для бериллии и магния —  ,
,
• для бора и алюминия —  ,
,
• для углерода и кремния —  и т. д.
и т. д.
В 4-м периоде появляются переходные элементы, которые принадлежат побочным подгруппам.
Элементы, принадлежащие одной и той же подгруппе, имеют идентичный характер расположения электронов на внешних электронных уровнях, а принадлежащие разным подгруппам одной и той же группы — сходный. Например, галогены (главная подгруппа VII группы) имеют идентичную электронную конфигурацию  , а элементы побочной подгруппы —
, а элементы побочной подгруппы — 
Сходство указанных элементов заключается в наличии у атомов как главной, так и побочной подгруппы 7 валентных электронов:  и
и  но их расположение по подуровням существенно различается: все валентные электроны элементов главной подгруппы расположены на двух подуровнях одного уровня п, а элементов побочной — на двух подуровнях двух различных уровней
но их расположение по подуровням существенно различается: все валентные электроны элементов главной подгруппы расположены на двух подуровнях одного уровня п, а элементов побочной — на двух подуровнях двух различных уровней  .
.
Таким образом, наиболее важным выводом, следующим из сопоставления данных, приведенных в табл. 3.3, с периодической системой химических элементов Д. И. Менделеева, является вывод о строгой периодичности изменения электронных конфигураций атомов элементов в их естественном ряду, что отвечает периодичности изменения их свойств.
Растворы
Наиболее распространенными физико-химическими системами являются растворы, среди которых заметно выделяются истинные растворы. Самая характерная особенность истинного раствора состоит в том, что растворенное вещество находится в нем в виде атомов, молекул или ионов, равномерно окруженных атомами, молекулами или ионами растворителя. Иначе говоря, истинные растворы однофазны, т. е. в них отсутствует граница раздела между растворителем и растворенным веществом.
Растворы могут существовать в любом из агрегатных состояний: газообразном, жидком и твердом. Например, воздух можно рассматривать как раствор кислорода и других газов (углекислый газ, благородные газы) в азоте. Морская вода — это водный раствор различных солей в воде. Металлические сплавы — твердые растворы одних металлов в других.
Итак, любой раствор состоит, как минимум, из двух индивидуальных веществ, одно из которых считают растворителем, а другое — растворенным веществом. Однако такое деление очень условно, а для веществ, смешивающихся в любых соотношениях (например, вода — серная кислота, серебро — золото), лишено смысла.
Способность к образованию растворов выражена в различной степени у различных индивидуальных веществ. Одни вещества способны растворяться друг в друге неограниченно (вода — спирт), другие — лишь в ограниченных количествах (подавляющее большинство солей, кислот и оснований в воде).
Растворимость веществ существенно зависит от природы растворяемого вещества и растворителя, температуры и давления. Различная растворимость веществ тесно связана с характером взаимодействия молекул растворителя и растворенного вещества.
Раствор, в котором данное вещество при данной температуре уже больше не растворяется, т. е. раствор, находящийся в равновесии с растворенным веществом, называется насыщенным, а раствор, в котором еще можно растворить некоторое количество данного вещества, — ненасыщенным. Для подавляющего большинства растворов растворимость растворенных веществ в воде увеличивается с повышением температуры. Если раствор, насыщенный при нагревании, осторожно охладить до комнатной температуры так, чтобы растворенное вещество не выделилось в виде отдельной фазы, то образуется пересыщенный раствор. Таким образом, пересыщенным называется раствор, в котором при данной температуре содержится большее количество растворенного вещества, чем в насыщенном растворе. Пересыщенный раствор нестабилен (часто также встречается термин «метастаби-лен»), и при изменении условий (например, энергичное встряхивание раствора «соль — вода» или внесение в него кристаллика той же соли — затравки для кристаллизации) образуется насыщенный раствор и выпадают кристаллы соли, находящейся в пересыщенном растворе в избытке.
Для различных практических расчетов в химии широко используются внесистемные единицы, характеризующие концентрацию раствора, — массовая и молярная доли.
Массовой долей со растворенного вещества называется отношение массы растворенного вещества к общей массе раствора:

Массовая доля в этом случае выражается в долях единицы. Однако в подавляющем большинстве случаев при решении задач массовая доля выражается в процентах (% по массе или в мае. %). Тогда для расчетов используют соотношение:

Например, для сплава Вуда, содержащего 4 мас. ч.  .
.  , массовая доля компонентов твердого раствора соответственно равна 0,50 : 0,25 : 0,125 : 0,125 (4 : 8; 2 : 8; 1 : 8; 1 : 8).
, массовая доля компонентов твердого раствора соответственно равна 0,50 : 0,25 : 0,125 : 0,125 (4 : 8; 2 : 8; 1 : 8; 1 : 8).
Молярная доля  — отношение числа молей данного вещества в растворе к общему числу молей веществ, образующих раствор (в общем случае число компонентов раствора
— отношение числа молей данного вещества в растворе к общему числу молей веществ, образующих раствор (в общем случае число компонентов раствора  ):
):

где  — число молей i-компонента,
— число молей i-компонента,  — общее число молей.
— общее число молей.
Например, для сплава Вуда, массовое содержание компонентов в котором приведено выше, можно показать, что на 1,00 моль Bi приходится 0,505 моль РЬ, 0.440 моль Sn и 0,467 моль Cd, при этом молярные доли компонентов будут соответственно равны: 0,4146; 0,2094; 0,1824 и 0,1936 ( = 2,412 моль).
= 2,412 моль).
Необходимо также напомнить еще об одной внесистемной величине, широко применяемой при практических расчетах, — растворимости.
Растворимость вещества показывает сколько безводного вещества в граммах может раствориться в 100 г растворителя (или, реже, сколько безводного вещества в граммах может раствориться в 1,0 л растворителя). Единицами растворимости являются грамм вещества на 100 г растворителя или грамм вещества на литр растворителя (г/л).
Важной системной величиной (в системе СИ), количественно характеризующей концентрацию раствора, является молярная концентрация — число молей растворенного вещества в 1,0 л раствора.

Например, раствор, содержащий 49,0 г серной кислоты в 1,0 л, имеет концентрацию 0,5 моль/л, т. к. молярная масса кислоты равна 98,0 г/моль, а раствор, содержащий 40,0 г гидроксида натрия в 0,5 л, имеет концентрацию 2,0 моль/л, т. к. молярная масса щелочи равна 40,0 г/моль.
Алгоритмы расчетов количественных характеристик растворов солей, кислот и оснований
Задачи этого типа являются, по-видимому, простейшими среди задач четвертого раздела. Действительно, все расчеты, проводимые при их решении, основаны на формуле (4.2):

и формуле (4.4):

Из формул видно, что для определения любого из параметров раствора [ (вещества) или m(раствора) — формула (4.2);
(вещества) или m(раствора) — формула (4.2);  (вещества) или V(раствора) — формула (4.4)] необходимо задать два других его параметра. Таким образом, может существовать три подтипа задач, решаемых с использованием уравнения (4.2), и три подтипа задач, решаемых с использованием уравнения (4.4). Однако реально на каждую из формул подтипов задач оказывается несколько больше— вместо массы раствора в тексте задачи могут быть даны:
(вещества) или V(раствора) — формула (4.4)] необходимо задать два других его параметра. Таким образом, может существовать три подтипа задач, решаемых с использованием уравнения (4.2), и три подтипа задач, решаемых с использованием уравнения (4.4). Однако реально на каждую из формул подтипов задач оказывается несколько больше— вместо массы раствора в тексте задачи могут быть даны:
• либо масса растворителя, необходимая для получения раствора [напомним, что m(раствора) = m(вещества) + m(растворителя)];
• либо объем и плотность полученного раствора.
Таблица 4.1

Все возможные варианты задач, решаемые с использованием уравнения (4.2), в виде заданных и неизвестных величин приведены в табл. 4.1.
Рассмотрим в качестве примера следующую задачу:
Пример №4-1.
В какой массе воды следует растворить 11,7 г хлористого натрия, чтобы получить раствор  с массовой долей 7,5 %?
с массовой долей 7,5 %?
Решение:
Исходя из условий задачи и обозначив искомую величину (массу воды) через х, можно записать:

Решение полученного соотношения дает х = 144,3 г.
Ответ: 144,3 г воды.
Таблица 4.2

Среди задач, предложенных для самостоятельного решения (№ 4.1-4.6), естественно, приведены далеко не все варианты (см. крайнюю правую колонку в табл. 4.1), представляющие те или иные комбинации заданных и неизвестных параметров растворов. Авторы рекомендуют читателям определить варианты приведенных задач, составить задачи на все не приведенные варианты и решить их.
Теперь перейдем к задачам, в которых концентрация раствора задается величиной см — молярной концентрацией.
Рассуждения, аналогичные тем, которые привели нас к табл. 4.1, приводят и к табл. 4.2. В этой таблице приведены все возможные варианты задач, решаемых с использованием уравнения (4.4), в виде определенной комбинации заданных и неизвестных величин.
Рассмотрим в качестве примера следующую задачу:
Пример №4-2.
50,0 г серной кислоты (49,0 %) растворили в воде, и объем раствора довели до 500,0 мл. Определите молярную концентрацию полученного раствора.
Решение:
Определим количество вешества в исходном растворе:

Теперь для раствора, полученного после разбавления, можно записать следующую пропорцию:

решение которой позволяет определить искомую величину —  .
.
Ответ: 0.5 М.
Алгоритмы расчетов количественных характеристик растворов веществ, образующих кристаллогидраты
Задачи, посвященные расчетам количественных характеристик растворов веществ, образующих кристаллогидраты, также решаются с использованием уравнения (4.2). Необходимо только подчеркнуть, что масса растворенного в растворе вещества и масса кристаллогидрата связаны между собой простым соотношением:

где  — массовая доля соли в кристаллогидрате, которую легко можно оценить по формуле:
— массовая доля соли в кристаллогидрате, которую легко можно оценить по формуле:

Все возможные варианты задач приведены в виде заданных и неизвестных величин в табл. 4.3 и табл. 4.4.
Таблица 4.3

Таблица 4.4

Рассмотрим в качестве примера следующую задачу:
Пример №4-3.
Определите массовую долю и молярную концентрацию сульфата меди в растворе, полученном при растворении 50 г медного купороса в 750 г воды. Плотность полученного раствора р равна 1,04 г / мл.
Решение:
Определим вначале массовую долю сульфата меди в кристаллогидрате: 
Теперь запишем выражение для массовой доли сульфата меди в растворе:

Определим объем раствора:  , и число молей сульфата меди, находящееся в растворе:
, и число молей сульфата меди, находящееся в растворе:  . Это позволяет составить следующую пропорцию:
. Это позволяет составить следующую пропорцию:

Решая эту пропорцию, получаем  .
.
Ответ: 
Основные алгоритмы расчетов, проводимых на основании уравнений химических реакций, протекающих с избытком (недостатком) одного из компонентов
Рассмотрим один из важнейших алгоритмов расчетов, проводимых на основании уравнений химических реакций и учитывающих, что один из компонентов химического взаимодействия взят с избытком (недостатком) по сравнению со стехиометрическим соотношением.
Рассмотрим в качестве примера следующую задачу:
Пример №4-4.
К 159 мл 10,0% раствора  добавлено 47 мл 25,0 %
добавлено 47 мл 25,0 %  . Определить массовую долю и молярную концентрацию соединений, содержащихся в растворе после завершения реакции, если плотность конечного раствора
. Определить массовую долю и молярную концентрацию соединений, содержащихся в растворе после завершения реакции, если плотность конечного раствора  = 1,029 г/мл.
= 1,029 г/мл.
Решение:
Определим массу растворов 

а также массу солей, содержащихся в этих растворах:

Вычислим количества веществ, содержащихся в соответствующих массах солей, учитывая, что их молярные массы равны  106 г/моль:
106 г/моль:

Теперь запишем уравнение реакции взаимодействия между  , отметив при этом непосредственно под каждым из веществ их начальное и конечное содержание в системе (в молях):
, отметив при этом непосредственно под каждым из веществ их начальное и конечное содержание в системе (в молях):

Анализ начального состояния системы (первая строка под уравнением реакции, индекс «0») показывает, что в избытке взят  (0,15 моля > 0,12 моля) и, следовательно, он остается в растворе после завершения реакции (в количестве 0,03 моля; вторая строка под уравнением реакции, индекс «к»). В растворе после завершения реакции также останется
(0,15 моля > 0,12 моля) и, следовательно, он остается в растворе после завершения реакции (в количестве 0,03 моля; вторая строка под уравнением реакции, индекс «к»). В растворе после завершения реакции также останется  (0,24 моля). В то же время
(0,24 моля). В то же время  , выпадающий в осадок, выделяется из раствора (0,12 моля). Поэтому масса раствора
, выпадающий в осадок, выделяется из раствора (0,12 моля). Поэтому масса раствора  , образуюшегося после завершения реакции, равна сумме масс двух исходных растворов без массы образовавшегося
, образуюшегося после завершения реакции, равна сумме масс двух исходных растворов без массы образовавшегося  :
:

Этот раствор занимает объем:

Тогда массовые доли  могут быть найдены по известным формулам:
могут быть найдены по известным формулам:

Молярные же концентрации  будут соответственно равны:
будут соответственно равны:

Ответ: Массовые доли  , оставшихся в растворе после реакции, равны 1,62 % и 6,82 % соответственно; их молярные концентрации равны
, оставшихся в растворе после реакции, равны 1,62 % и 6,82 % соответственно; их молярные концентрации равны 

Рассмотрим еще один вариант задач на «избыток—недостаток».
Пример №4-5.
Сколько  необходимо добавить к 159,0 мл 10,0 % раствора
необходимо добавить к 159,0 мл 10,0 % раствора  (плотность
(плотность  = 1,05 г/мл), чтобы получить: 1) раствор с массовым содержанием хлорида кальция
= 1,05 г/мл), чтобы получить: 1) раствор с массовым содержанием хлорида кальция  = 5,0 %; 2) раствор с массовым содержанием хлорида натрия
= 5,0 %; 2) раствор с массовым содержанием хлорида натрия  = 5,0 %; 3) раствор с массовым содержанием карбоната натрия
= 5,0 %; 3) раствор с массовым содержанием карбоната натрия  = 5,0 %?
= 5,0 %?
Решение:
Эта задача также относится к так называемым задачам на «избыток—недостаток». Однако отличие таких задач от задач «классического» типа заключается в неопределенности используемого количества одного из исходных компонентов реакции. Поэтому такие задачи требуют специфического подхода, который и рассмотрен ниже.
Сначала рассмотрим первое из условий задачи.
Для этого определим исходные величины, характеризующие раствор хлорида кальция:

Теперь запишем уравнение реакции взаимодействия между  , отмечая, как обычно, при решении задач на «избыток—недостаток» непосредственно под каждым из веществ их начальное и конечное содержание в системе (в молях). При этом искомую по условию задачи величину — количество введенного в систему кристаллогидрата — десятиводного карбоната натрия
, отмечая, как обычно, при решении задач на «избыток—недостаток» непосредственно под каждым из веществ их начальное и конечное содержание в системе (в молях). При этом искомую по условию задачи величину — количество введенного в систему кристаллогидрата — десятиводного карбоната натрия  , а, следовательно, и количество карбоната натрия в растворе
, а, следовательно, и количество карбоната натрия в растворе  обозначим через х. Тогда:
обозначим через х. Тогда:

Очевидно, что условие (1):  = 5,0 %, сформулированное для конечного раствора, свидетельствует о существовании в исходном растворе избытка СаС12 (0,15 моль > х моль). Это позволяет следующим образом оценить количества веществ в конечном раст воре (вторая строка под реакцией, индекс «к»). Исходя из этого, можно записать:
= 5,0 %, сформулированное для конечного раствора, свидетельствует о существовании в исходном растворе избытка СаС12 (0,15 моль > х моль). Это позволяет следующим образом оценить количества веществ в конечном раст воре (вторая строка под реакцией, индекс «к»). Исходя из этого, можно записать:

В последнем выражении масса всего раствора может быть представлена соотношением:

И окончательно получаем:

Аналогично решается задача и при условиях (2) и (3).
Для условия (2) можно записать:

или 
Очевидно, что условие (3) будет выполняться только в том случае, когда х моль > 0,15 моль. Тогда, записав уравнение реакции взаимодействия между  , можно оценить конечное количество веществ в системе (в молях) следующим образом:
, можно оценить конечное количество веществ в системе (в молях) следующим образом:

Для данного случая масса конечного раствора равна:

Проведенные оценки позволяют получить:

или 
Интересно отметить, что для случая х моль >0,15 моль существует также второе решение для условия (2). Действительно:

Ответ: Для получения растворов с заданным массовым содержанием соответствующих солей необходимо добавить следующие количества  1) 0,069 моль или 19,7 г; 2) 0,0815 моль или 23,3 г; 3) 0,256 моль или 73,3 г; 4) второе решение для условия (2): 0,64 моль или 183,0 г.
1) 0,069 моль или 19,7 г; 2) 0,0815 моль или 23,3 г; 3) 0,256 моль или 73,3 г; 4) второе решение для условия (2): 0,64 моль или 183,0 г.
Алгоритмы решения задач о процессах, связанных с изменением концентрации растворов солей, кислот и оснований
Выпаривание растворителя из растворов
Рассмотрим в качестве примера следующую задачу:
Пример №4-6.
Определите массу воды, выделившуюся при упаривании 50,0 г 5,6 % раствора гидроксида калия, если в результате был получен 12,0% раствор.
Решение:
Определим массу гидроксида калия, находящуюся в исходном растворе:  = 50,0 г * 0,056 = 2,8 г. Тогда для раствора, полученного после упаривания, можно записать следующее уравнение:
= 50,0 г * 0,056 = 2,8 г. Тогда для раствора, полученного после упаривания, можно записать следующее уравнение:

решение которого позволяет найти х = 26,67 г.
Ответ: 26,67 г воды.
Разбавление растворов
Рассмотрим в качестве примера следующую задачу:
Пример №4-7.
В какой массе воды следует растворить 300 г 30,0 % раствора гидроксида калия, чтобы получить 10,0 % раствор?
Решение:
Определим массу гидроксида калия, находящуюся в исходном растворе:  = 300,0 г • 0,3 = 90,0 г. Тогда для раствора, полученного после разбавления, можно записать следующее уравнение:
= 300,0 г • 0,3 = 90,0 г. Тогда для раствора, полученного после разбавления, можно записать следующее уравнение:

решение которого позволяет найти х = 600,0 г.
Ответ: 600,0 г воды.
Смешение двух и более числа растворов. Квадрат Пирсона (правило креста)
Рассмотрим в качестве примера следующую задачу:
Пример №4-8.
В каких соотношениях надо смешать растворы серной кислоты с массовыми долями 90,0 % и 8 % соответственно, чтобы приготовить 48,0 % раствор  ?
?
Решение:
Предположим, что для приготовления 48,0% раствора  было взято 100г раствора с массовой долей 90,0% и хг раствора с массовой долей 8,0 %. Тогда можно записать:
было взято 100г раствора с массовой долей 90,0% и хг раствора с массовой долей 8,0 %. Тогда можно записать:

Решение этого уравнения дает х = 105,0 г и, следовательно, соотношение, в котором необходимо смешать растворы с массовыми долями 90,0 % и 8 %, составляет 100: 105 = 20:21.
Ответ: 20:21.
Этот же результат можно получить, используя так называемый квадрат Пирсона— закономерность, более известную как «правило креста». Использование этого приема заключается в следующем: в углах предполагаемого квадрата, прилежащих его левой стороне, записываются массовые доли смешиваемых растворов одного и того же вещества  . В центре квадрата — массовая доля раствора, получаемого в результате смешения,
. В центре квадрата — массовая доля раствора, получаемого в результате смешения,  . В углах квадрата, прилежащих его правой стороне, записываются соответствующие разности массовых долей
. В углах квадрата, прилежащих его правой стороне, записываются соответствующие разности массовых долей  . Полученные разности массовых долей и указывают, что для получения раствора с массовой долей
. Полученные разности массовых долей и указывают, что для получения раствора с массовой долей  необходимо смешать
необходимо смешать  массовых частей более концентрированного раствора
массовых частей более концентрированного раствора  массовых частей раствора менее концентрированного
массовых частей раствора менее концентрированного  . Применение правила креста для рассматриваемого случая дает:
. Применение правила креста для рассматриваемого случая дает:

Таким образом, для получения раствора  с массовой долей 48,0 % необходимо смешать 40 массовых частей раствора
с массовой долей 48,0 % необходимо смешать 40 массовых частей раствора  с массовой долей 90,0 % и 42 массовые части раствора
с массовой долей 90,0 % и 42 массовые части раствора  с массовой долей 8,0%. Сокращение дает окончательное соотношение масс смешиваемых растворов 20 : 21.
с массовой долей 8,0%. Сокращение дает окончательное соотношение масс смешиваемых растворов 20 : 21.
Ответ: 20 : 21.
Изменение концентрации серной кислоты растворением оксида серы (VI). Образование олеума
Рассмотрим в качестве примера следующие задачи:
Пример №4-9.
В какой массе 32,0 % раствора серной кислоты следует растворить 40,0 г серного ангидрида, чтобы получить раствор с массовой долей кислоты 50,0 %?
Решение:
Рассмотрим реакцию взаимодействия оксида серы (VI) с водой, которая протекает при растворении  в разбавленном растворе серной кислоты (32,0 %):
в разбавленном растворе серной кислоты (32,0 %):

Из реакции видно, что растворение 40 г (0,5 моль) оксида серы (VI) в разбавленном растворе серной кислоты (32,0 %) приводит к дополнительному образованию 0,5 моль  (49,0 г). Следовательно, обозначив массу исходного раствора за х, можно записать:
(49,0 г). Следовательно, обозначив массу исходного раствора за х, можно записать:

Решая полученное уравнение, находим, что масса исходного раствора должна быть равна 161,1 г.
Ответ: 161,1 г.
Пример №4-10.
Какую массу  необходимо добавить к 200 мл 80 %
необходимо добавить к 200 мл 80 %  (плотность р = 1,732 г/мл), чтобы получить олеум с массовой долей
(плотность р = 1,732 г/мл), чтобы получить олеум с массовой долей  = 20 %? Полученный результат подтвердить, используя квадрат Пирсона (правило креста).
= 20 %? Полученный результат подтвердить, используя квадрат Пирсона (правило креста).
Решение:
Образование олеума из концентрированной серной кислоты можно представить двумя процессами. Первый из них — химическая реакция взаимодействия оксида серы (VI) с водой  и получение 100.0 % серной кислоты. Второй процесс — растворение оксида серы (VI) в 100,0 % серной кислоте
и получение 100.0 % серной кислоты. Второй процесс — растворение оксида серы (VI) в 100,0 % серной кислоте  :
:

Сначала оценим величину  . Для этого проведем несложные расчеты:
. Для этого проведем несложные расчеты:

необходимая для получения 100,0 % серной кислоты.
Теперь запишем условие получения олеума с массовой долей  = 20 %:
= 20 %:

Попробуем подтвердить полученный результат, используя квадрат Пирсона (правило креста). Очевидно, что в общем виде квадрат Пирсона для системы  будет выглядеть следующим образом:
будет выглядеть следующим образом:

Проведем количественные оценки величин, которые фигурируют в квадрате Пирсона:

Расположим полученные величины и проведем соответствующие вычисления:

Решение пропорции, которую составляют три цифры, записанные справа, и неизвестная величина х, дает

Ответ: таким образом, оба использованных подхода дают одинаковые результаты  = 471,5 г.
= 471,5 г.
Кристаллизация из раствора солей
а) Определение растворимости вещества.
Рассмотрим в качестве примера следующую задачу:
Пример №4-11.
Вычислите растворимость хлорида натрия в воде при 40° С, если в 500 г раствора при этой температуре растворяется 133,43 г соли.
Решение:
Согласно определению, растворимость вещества — масса безводного вещества, которая может растворится в 100 г растворителя. Из условия задачи следует, что 133,43 г хлорида натрия растворено в массе воды равной  = 500 г — 133,43 г = 366,57 г. Тогда, используя условия задачи и определение растворимости, можно записать следующую пропорцию:
= 500 г — 133,43 г = 366,57 г. Тогда, используя условия задачи и определение растворимости, можно записать следующую пропорцию:

решение которой даег х = 36,4 г.
Ответ: растворимость хлорида натрия при 40° С — 36,4 г.
б) Определение массы выпавших кристаллов при охлаждении раствора, насыщенного при повышенной температуре.
Рассмотрим в качестве примера следующую задачу:
Пример №4-12.
Растворимость хлорида натрия при 0°С и 80° С равна соответственно 35,7 г и 38,1 г. Какая масса хлорида натрия выпадет в осадок, если охладить 500 г насыщенного раствора хлорида натрия от 80° С до 0° С?
Решение:
Определим массовые доли хлорида натрия в насыщенных водных растворах при 0°С и 80° С:

В 500 г насыщенного раствора хлорида натрия при 80° С будет растворено  = 500 г * 0,2759 = 137,95 г. При охлаждении этого раствора до 0°С из него выпадет х г хлорида натрия. Этот процесс можно выразить следующим соотношением:
= 500 г * 0,2759 = 137,95 г. При охлаждении этого раствора до 0°С из него выпадет х г хлорида натрия. Этот процесс можно выразить следующим соотношением:

Решение этого уравнения дает х = 8,75 г.
Ответ: при охлаждении выпадет 8,75 г хлорида натрия.
Кристаллизация из растворов солей, образующих кристаллогидраты
Рассмотрим в качестве примера следующую задачу:
Дополнительные примеры с решением:
- Пример №4-13. Определите количество кристаллогидрата * , который выкристаллизовался при охлаждении 513,2 г насыщенного при 80° С раствора сульфата натрия до 10° С. Растворимость безводного сульфата натрия при 80° С равна 28,3 г, а при 10° С — 9,0 г в 100 г воды.
- Пример №4-14. Хлорид железа (III) образует три кристаллогидрата: и 128,1 г смеси и , содержащей 0,6 моль безводной соли, нагрели до 80° С. При этом кристаллогидраты расплавились и образовали гомогенный раствор. После испарения из раствора 5,4 г воды, систему охладили до комнатной температуры. При этом образовалась равновесная смесь кристаллогидратов. Определите качественный и количественный состав системы после охлаждения.
Жесткость воды и методы ее устранения
Жесткость воды обусловлена наличием в ней солей кальция и магния. Различают временную (или карбонатную) и постоянную жесткость воды. Временная жесткость, вызванная присутствием гидрокарбонатов кальция и магния, устраняется кипячением:

При этом образуется осадок труднорастворимого карбоната кальция (магния), содержание кальция (магния) в воде снижается, и жесткость воды уменьшается.
Наличие в воде нитратов и хлоридов кальция и магния обусловливает постоянную жесткость воды. Эти соли не выделяются в осадок при кипячении, и для их устранения воду подвергают специальной химической очистке.
Различают кальциевую жесткость, обусловливаемую содержанием в воде кальциевых солей, и магниевую, связанную с наличием магниевых солей. Суммарную кальциевую и магниевую жесткость называют общей жесткостью.
Общую жесткость воды обычно определяют по формуле:

где  — содержание кальция и магния (мг) в 1 л воды. Следовательно, общая жесткость воды — параметр, устанавливающий число миллимолей эквивалентов
— содержание кальция и магния (мг) в 1 л воды. Следовательно, общая жесткость воды — параметр, устанавливающий число миллимолей эквивалентов  в одном литре раствора (ммоль экв/л), поскольку 20,04 и 12,16 — величины
в одном литре раствора (ммоль экв/л), поскольку 20,04 и 12,16 — величины  соответственно.
соответственно.
В настоящее время разработаны методы, позволяющие определять общую жесткость воды без раздельного определения содержания ионов кальция и магния. В этом случае находят сумму миллиграмм-эквивалентов кальция и магния в 1 л воды.
Для умягчения воды (для устранения жесткости — выделения ионов кальция и магния) чаще всего применяют два метода: осаждение или ионный обмен. Для осаждения ионов кальция и магния используют преимущественно соду, известь или фосфат натрия. Известь осаждает магний в виде гидроксида:

Сода образует труднорастворимый карбонат кальция:

Для устранения временной жесткости методом осаждения используют известковый, натронный и содовый методы:
Известковый метод:
• 
Натронный метод:
• 
Содовый метод:
• 
Для удаления солей, обусловливающих постоянную жесткость, используют содовый и фосфатный методы:
Содовый метод:
• 
Фосфатный метод:
• 
В настоящее время для очистки воды широко применяют иониты — неплавкие и нерастворимые (или малорастворимые) вещества, которые ограниченно набухают в воде и содержат в своей структуре функциональные группы кислотного и основного характера, способные обмениваться на ионы веществ, растворенных в воде. Чаще всего иониты представляют собой твердые высокомолекулярные поликислоты или полиоснования или их соли. В зависимости от характера функциональных групп иониты могут обмениваться катионами (катиониты) или анионами (аниониты).
а) Определение общей жесткости воды по массе содержащихся в воде солей.
Рассмотрим в качестве примера следующую задачу:
Пример №4-15.
Жесткость некоторого образца воды обусловливается только гидрокарбонатом железа. При кипячении 0,25 л воды в осадок выпадает 4,0 мг  . Чему равна жесткость воды?
. Чему равна жесткость воды?
Решение:
Поскольку при кипячении 0,25 л воды в осадок выпадает 4,0 мг  , то из 1,0 л будет выпадать 16,0 мг/л карбоната железа (II). Указанная масса соответствует v(
, то из 1,0 л будет выпадать 16,0 мг/л карбоната железа (II). Указанная масса соответствует v( ) = (0,016 г/л) /(116 г/моль) = 0,138 ммоль/л или 0,276 ммоль зкв/л.
) = (0,016 г/л) /(116 г/моль) = 0,138 ммоль/л или 0,276 ммоль зкв/л.
Ответ: 0,276 ммоль экв/л.
б) Определение временной и постоянной жесткости воды по количеству реагентов, необходимых для устранения жесткости.
Рассмотрим в качестве примера следующую задачу:
Пример №4-16.
При действии на 5,0 л воды раствором, содержащим 10,6 г соды, образовалось 9,04 г карбонатов кальция и магния. Определите жесткость воды и состав осадка карбонатов.
Решение:
Для осаждения карбонатов кальция и магния было использовано  = 10,6 г/(106,0 г/моль) = 0,1 моль, что равно 0,2 моль эквивалентов или 200 ммоль эквивалентов. Следовательно, жесткость воды составляет 200 ммоль экв / 5 л = 40,0 ммоль экв/л.
= 10,6 г/(106,0 г/моль) = 0,1 моль, что равно 0,2 моль эквивалентов или 200 ммоль эквивалентов. Следовательно, жесткость воды составляет 200 ммоль экв / 5 л = 40,0 ммоль экв/л.
Для определения состава осадка карбонатов обозначим число молей карбоната кальция через х, а число молей карбоната магния через у. Тогда, учитывая, что найденная величина  = 0,1 моль равна суммарному числу молей осажденных карбонатов, можно составить следующую пропорцию:
= 0,1 моль равна суммарному числу молей осажденных карбонатов, можно составить следующую пропорцию:

решая которую получаем х = 0,04 и у = 0,06. Откуда следует, что массы карбонатов в осадке соответственно равны 
Ответ: 40,0 ммоль экв/л; 4,0 г 
Смеси веществ
Существование исходных реагентов или продуктов реакции в виде смеси веществ — ситуация в химии довольно распространенная. Для решения задач «на смеси» необходимо знание ряда алгоритмов, которые будут рассмотрены ниже.
Наиболее простыми задачами «на смеси» являются задачи, в которых на смесь веществ действуют тем или иным реагентом, селективно взаимодействующим с одним из компонентов смеси. Состав смеси в этом случае устанавливают, используя необходимое число селективных реагентов, которое на единицу меньше, чем число компонентов смеси.
Рассмотрим в качестве примера следующую задачу.
Пример №5-1.
23,6 г сплава меди с алюминием обработали раствором щелочи. Остаток растворили в концентрированной азотной кислоте, образовавшуюся при этом соль выделили и прокалили. Масса остатка после прокаливания составляет 16,0 г. Определите молярное соотношение меди и алюминия в исходной смеси и объем израсходованного 40 % раствора гидроксида натрия (плотность р = 1,43 г/мл).
Решение:
Очевидно, что обработка сплава меди с алюминием раствором щелочи приведет к растворению алюминия, обладающего амфотерными свойствами. При этом твердым остатком взаимодействия, естественно, является медь, растворение которой в концентрированной азотной кислоте можно описать реакцией:

Дальнейшее прокаливание продукта реакции — нитрата меди  приводит к получению оксида меди
приводит к получению оксида меди  :
:

количество которого  .
.
Из приведенных выше реакций видно, что:

Итак, молярное соотношение меди и алюминия в исходной смеси равно:

Теперь определим объем израсходованного на растворение алюминия 40 % раствора гидроксида натрия:

Поскольку 
Это отвечает массе раствора

и соответствующему объему раствора:

Ответ: 
Далее проанализируем более сложную ситуацию, когда реагент одновременно взаимодействует с обоими компонентами смеси (естественно, что разбор задачи-примера проводится на простейшей, бинарной смеси). Для решения подобных задач существует изящный алгоритм, применение которого иллюстрируется следующим примером.
Пример №5-2.
15 г сплава серебра с медью растворили в концентрированной азотной кислоте, получив раствор, содержавший 36,7 г нитратов этих металлов. Раствор разбавили водой и смешали с избытком раствора хлорида натрия. Какова масса выпавшего осадка?
Решение:
Растворение сплава серебра с мелью в концентрированной азотной кислоте можно описать следующими уравнениями реакций:

Предположим, что в сплаве содержится х молей серебра и у молей меди. Это позволяет (с учетом стехиометрических коэффициентов записанных реакций) составить систему, состоящую из двух уравнений:

или

Решение этой системы лает: х = 0,05 и у = 0,15.
Полученное промежуточное решение, дающее состав исходной смеси, позволяет ответить на вопрос, поставленный в задаче. Действительно, добавление избытка раствора хлорида натрия к образовавшемуся раствору нитратов приводит к образованию осадка хлорида серебра:

Учитывая стехиометрические коэффициенты приведенного уравнения  , окончательно получаем:
, окончательно получаем:

Ответ: 7,18 г. 
Алгоритм, аналогичный тому, который был рассмотрен в примере 5-2 в отношении смеси исходных веществ, можно с успехом применить и для определения состава смеси продуктов химической реакции.
Рассмотрим соответствующий пример.
Пример №5-3.
Оксид фосфора (V), количественно выделенный из 15,5 г трикальцийфосфата, растворен в: а) 200 г 5,0% раствора гидроксида натрия; б) 120 г 5,0 % раствора гидроксида натрия; в) 40 г 5,0 % раствора гидроксида натрия. Какие вещества и в каком количестве содержатся в образующихся растворах?
Решение:
Рассмотрим реакцию взаимодействия оксида фосфора (V) с гидроксидом натрия. Очевидно, что состав образующегося продукта в значительной мере определяется соотношением количеств реагентов, вступающих в реакцию:

Действительно, для образования средней соли необходимо соотношение  :
:  =1:6, для образования гидрофосфата — I : 4 и, наконец, для образования дигидрофосфата — 1:2. Поэтому для решения подобных задач прежде всего необходимо оценить задаваемое в условии задачи мольное соотношение реагентов.
=1:6, для образования гидрофосфата — I : 4 и, наконец, для образования дигидрофосфата — 1:2. Поэтому для решения подобных задач прежде всего необходимо оценить задаваемое в условии задачи мольное соотношение реагентов.
Рассмотрим вариант а).
Масса трикальцийфосфата, равная 15,5 г, соответствует величине:

Поскольку из одного моля трикальцийфосфата при количественном выделении можно получить один моль оксида фосфора (V), то 
Число молей гидроксида натрия также можно легко оценить:

Следовательно, мольное соотношение реагентов в этом случае равно  :
:  = 0,05 : 0,25 = 1:5. Очевидно, что для решения задачи [случай а)] необходимо рассмотреть две реакции:
= 0,05 : 0,25 = 1:5. Очевидно, что для решения задачи [случай а)] необходимо рассмотреть две реакции:

поскольку реальное соотношение реагентов — 1:5 лежит между двумя соотношениями, необходимыми для получения того или иного продукта и приводимыми после записи каждой из реакций. Для решения задачи обозначим число молей  , идущих на образование
, идущих на образование  , через х, а число молей
, через х, а число молей  , идущих на образование
, идущих на образование  , через у. Тогда число молей
, через у. Тогда число молей  , идущих на образование
, идущих на образование  , составит величину 6х, а число молей
, составит величину 6х, а число молей  , идущих на образование
, идущих на образование  — 4 у и, следовательно, можно получить следующую систему уравнений:
— 4 у и, следовательно, можно получить следующую систему уравнений:

решение которой дает х = у = 0,025 моль, т. е. количества образующихся  и
и  равны (по количеству молей). Массы же продуктов равны m(
равны (по количеству молей). Массы же продуктов равны m( ) = 4,1 г и m(
) = 4,1 г и m( ) = 3,55 г.
) = 3,55 г.
Вариант б) решается, в принципе, по схеме, аналогичной рассмотренной, и читателям предлагается самостоятельно рассмотреть этот случай.
Мы же рассмотрим решение задачи для случая в).
Для этого случая число молей  , как и в случае а), равно 0,05 моль, а
, как и в случае а), равно 0,05 моль, а  = 0,05 моль. Эго означает, что соотношение реагентов v(0,05):
= 0,05 моль. Эго означает, что соотношение реагентов v(0,05):  = 0,05:0,05 = 1 : 1 и, поскольку часть
= 0,05:0,05 = 1 : 1 и, поскольку часть  в реакции нейтрализации остается неиспользованной, для решения задачи необходимо рассмотреть следующие уравнения реакций:
в реакции нейтрализации остается неиспользованной, для решения задачи необходимо рассмотреть следующие уравнения реакций:

Далее обозначим число молей  , идущих на образование
, идущих на образование  , через х, а число молей
, через х, а число молей  , идущих на образование
, идущих на образование  , через у. Тогда число молей
, через у. Тогда число молей  , идущих на образование
, идущих на образование  , составит величину 2 х, и, следовательно, можно получить следующую систему уравнений:
, составит величину 2 х, и, следовательно, можно получить следующую систему уравнений:

решение которой дает х = у = 0,025 моль, т. е. количества образующихся в этом случае  и
и  равны (по количеству молей). Массы же продуктов равны m(
равны (по количеству молей). Массы же продуктов равны m( ) = 3,0 г и m(
) = 3,0 г и m( ) = 2,45 г.
) = 2,45 г.
Химическая кинетика
Химическая кинетика — одни из важнейших разделов химии, задача которого — трактовка качественных и количественных изменений химического процесса, происходящих во времени. Обычно эту общую задачу подразделяют на две более конкретные:
- выявление механизма реакции — установление элементарных стадий процесса и последовательности их протекания (качественные изменения);
- количественное описание химической реакции — установление строгих соотношений, которые могли бы удовлетворительно предсказывать изменения количества исходных реагентов и продуктов по мере протекания реакции.
Основные представления о механизме химических реакций
Установление всех элементарных стадий и последовательности их протекания при выявлении механизма конкретной химической реакции является, безусловно, задачей-максимумом. Такой подход имеет важное теоретическое значение. Действительно, накопление информации о механизме отдельных химических реакций позволит не только классифицировать их по тем или иным признакам, но и будет в дальнейшем способствовать созданию общей теории химических реакций (как это произошло, например, с цепными химическими реакциями). Однако для любого, даже достаточно простого химического процесса решение указанной задачи-максимума представляет собой чрезвычайно сложную (а порой — просто нерешаемую) проблему.
Поэтому выявление механизма конкретной химической реакции, как правило, ограничивается лишь решением задачи-минимума — определением наиболее медленной элементарной стадии, которую принято называть лимитирующей, то есть определяющей скорость всего химического процесса в целом. Поскольку выбранный упрощенный подход, тем не менее, позволяет решить важную практическую задачу ускорения химической реакции (за счет воздействия на ее лимитирующую стадию), то для большинства реакций такой уровень выявления механизма протекающего процесса оказывается вполне достаточным.
Решая задачу о выявлении механизма конкретной химической реакции (на мини- или макси- уровне), следует прежде всего иметь в виду, что характер взаимодействия существенно зависит от агрегатного состояния реагентов и продуктов. Реагенты и продукты, вместе взятые, образуют так называемую физико-химическую систему.
Совокупность однородных частей системы, обладающих одинаковым химическим составом и свойствами и отделенных от остальных частей системы поверхностью раздела, называют фазой. Например, смеси газов при нормальных условиях независимо от их природы образуют одну фазу.
Жидкие системы могут быть однофазны (например, система «вода — спирт») или многофазны (система «вода — бензол» двухфазна, а система «вода — бензол — ртуть» состоит из трех фаз). Более сложным является поведение с участием твердых фаз: если в стакан с водой внести несколько кристаллов поваренной соли, то в первый момент образуется двухфазная система, которая превратится в однофазную после полного растворения соли. Системы, состоящие из одной фазы, называются гомогенными, а системы, содержащие несколько фаз, — гетерогенными.
Соответственно этому в химии введено понятие о гомогенных и гетерогенных реакциях. Реакцию в целом называют гомогенной, если реагенты и продукты составляют одну фазу. Это хорошо иллюстрируется так называемыми обратимыми химическими реакциями. В качестве примера таких реакций рассмотрим синтез йодоводорода из простых веществ:

Действительно, для приведенной реакции и реагенты  , и продукт (HI) находятся в одной фазе, и в системе «
, и продукт (HI) находятся в одной фазе, и в системе « » возможно одновременное протекание как прямой (синтез йодоводорода из водорода и йода), так и обратной (распад HI на простые исходные вещества) реакций. Поэтому реакция в целом (и прямая, и обратная) является гомогенной.
» возможно одновременное протекание как прямой (синтез йодоводорода из водорода и йода), так и обратной (распад HI на простые исходные вещества) реакций. Поэтому реакция в целом (и прямая, и обратная) является гомогенной.
Для необратимых химических реакций (как известно, признаком протекания таких реакций является образование газа, осадка или слабо диссоциирующего соединения) реакция в целом не может являться гомогенной. В этом случае гомогенными являются только прямые реакции, поскольку обратные реакции практически не протекают.
Более того, при выделении газа или выпадении осадка в обратную реакцию должны вступать реагенты, находящиеся в разных фазах соответствующих систем «жидкость — газ» и «жидкость — твердое», что само по себе уже является признаком гетерогенности.
Наконец, к гетерогенным реакциям в целом относятся обычно такие процессы, в которых гетерогенными являются и прямая, и обратная реакции. Так, например, процесс растворения металла в кислоте:

является в целом гетерогенной реакцией, в которой и прямая — растворение  , и обратная — восстановление
, и обратная — восстановление  водородом (в случае возможности ее протекания) реализуются в гетерогенных системах «твердое — жидкость» и «жидкость — газ» соответственно.
водородом (в случае возможности ее протекания) реализуются в гетерогенных системах «твердое — жидкость» и «жидкость — газ» соответственно.
В настоящем пособии мы будем рассматривать только гомогенные химические реакции, протекающие в газах или в разбавленных растворах.
Одним из важнейших понятий механизма гомогенных химических реакций является молекулярность элементарной стадии — число молекул, участвующих в конкретном элементарном акте взаимодействия. По этому признаку различают реакции мономолекулярные, бимолекулярные и три-молекулярные.
Мономолекулярными называют такие элементарные реакции, в которых происходят химические превращения одной молекулы в одну, две или более других. Мономолекулярные реакции в общем виде можно описать одним из следующих уравнений:

Бимолекулярные — это такие элементарные реакции, в которых химическое превращение осуществляется при столкновении двух молекул:

Наконец, в тримолекулярных элементарных реакциях химическое превращение происходит при тройном молекулярном соударении (что само по себе — достаточно редкое явление):

Поскольку вероятность одновременного столкновения четырех и более молекул чрезвычайно низка (точнее, вероятность такого события — бесконечно мала), то реакции большей молекулярности (то есть более чем тримолекулярные) практически не встречаются и теоретически не рассматриваются.
Хотя введенная классификация механизма химических реакций, основанная на понятии молекулярности элементарных стадий, описывает происходящие процессы на микрокинетическом уровне (на уровне молекул), развитые представления, тем не менее, носят наглядный и понятный характер.
Вместе с тем возможность использования этих представлений весьма проблематична. Действительно, в каждом конкретном случае достаточно трудно (более точно — невозможно) перекинуть логический «мост» между уравнением химической реакции и ее молекулярностью.
Это связано с тем, что в подавляющем большинстве случаев уравнение химической реакции свидетельствует только о том, какие вещества и в каких количествах вступают в реакцию, какие — образуются, но ничего не говорит о механизме реакции. Между тем в большинстве случаев даже для гомогенных реакций механизм очень сложен, и реакция протекает в несколько стадий, что, естественно, «маскируется» ее уравнением. Болес того, определение механизма химической реакции является специальной задачей химической кинетики, которую решают, используя современные химические и физические методы исследования, и к настоящему времени окончательно выявлен механизм лишь ограниченного числа реакций.
В связи с этим в химической кинетике введено понятие о простой реакции — такой гипотетической реакции, уравнение которой полностью совпадает с элементарным актом химического взаимодействия. Данный подход позволяет выделять из всего множества химических реакций те гомогенные реакции, для которых суммарный коэффициент при исходных веществах в уравнении реакции является целым числом, не превышающим 3, и условно отождествлять их с «элементарными» реакциями. Это дает право применять количественный аппарат, используемый обычно лишь при анализе элементарных стадий химического процесса, к описанию широкого круга выделенных таким образом реальных химических взаимодействий.
Действительно, примерами реакций, которые, по-видимому, являются элементарными, могут служить лишь реакции переноса электрона между двумя различными ионами в растворе, например:

После введения понятия простой реакции круг химических реакций, которые условно можно считать «элементарными» значительно расширяется. Например, прямые и обратные реакции, описываемые приведенными ниже уравнениями:

целесообразно условно рассматривать как «элементарные», несмотря на их достаточно сложный механизм. Такая двойственная ситуация (реакция — «элементарная», а механизм — сложный) формально ликвидируется переводом этих реакций в «ранг» простых (суммарные коэффициенты при исходных веществах в уравнениях прямых и обратных реакций являются целыми числами, не превышающими 3). Этот подход позволяет формально применять кинетические уравнения для описания подобных реакций, не рассматривая их механизм.
По тем же соображениям кинетическое описание можно применить к прямой реакции:

для которой сумма коэффициентов при исходных реагентах ( и
и  ) равна 2 и, следовательно, она является простой.
) равна 2 и, следовательно, она является простой.
В то же время, несмотря на то, что сумма коэффициентов при реагентах  и S равна 3, обратная реакция является гетерогенной и не может рассматриваться как простая.
и S равна 3, обратная реакция является гетерогенной и не может рассматриваться как простая.
Таким образом, все наши дальнейшие рассуждения, кроме особо оговоренных случаев, будут относиться к простым реакциям.
Скорость химической реакции
Основным понятием в химической кинетике является понятие о скорости реакции: скорость химической реакции w определяется изменением концентрации реагирующих веществ в единицу времени. Если при неизменных объеме и температуре концентрация одного из реагирующих веществ уменьшилась от  за промежуток времени от
за промежуток времени от  , то в соответствии с определением скорость реакции за данный промежуток времени равна:
, то в соответствии с определением скорость реакции за данный промежуток времени равна:

Знак «-» в правой части уравнения (6-1) появляется по следующей причине. По мере протекания реакции  концентрация реагентов убывает, следовательно,
концентрация реагентов убывает, следовательно,  , а так как скорость реакции всегда положительна, то перед дробью следует поставить знак «-».
, а так как скорость реакции всегда положительна, то перед дробью следует поставить знак «-».
Обратите внимание на то, что скорость реакций можно измерять по изменению концентрации любого из реагентов или продуктов, но численное значение скорости зависит от этого выбора, например:

В этой реакции взаимодействие 1 моль  с 3 моль
с 3 моль  сопровождается появлением 2 моль
сопровождается появлением 2 моль  . Поэтому значения скорости реакции, рассчитанные по изменению концентраций
. Поэтому значения скорости реакции, рассчитанные по изменению концентраций  ,
,  или
или  неодинаковы, но связаны между собой соотношением 1:3:2. Отметим, что реакция синтеза аммиака является, по-видимому, одним из немногочисленных исключений. Несмотря на то, что в этой реакции сумма коэффициентов при исходных реагентах (
неодинаковы, но связаны между собой соотношением 1:3:2. Отметим, что реакция синтеза аммиака является, по-видимому, одним из немногочисленных исключений. Несмотря на то, что в этой реакции сумма коэффициентов при исходных реагентах ( и
и  ) равна 4, ее часто используют для иллюстрации в разделах «Химическая кинетика» и «Химическое равновесие», т. е. условно считают простой реакцией.
) равна 4, ее часто используют для иллюстрации в разделах «Химическая кинетика» и «Химическое равновесие», т. е. условно считают простой реакцией.
Отметим, что для реакций, протекающих в растворах, концентрации реагентов выражают в молях на 1 л (моль/л), а скорость реакции — в молях на 1 л за 1 с (моль/лс).
Как же можно проследить за скоростью протекания реакции? В простейшем случае для реакции, протекающей в растворе, это можно сделать непосредственно, измеряя концентрацию реагентов или продуктов через определенные промежутки времени. Иногда о скорости взаимодействия судят по изменению других свойств системы, если эти свойства изменяются пропорционально концентрации; например, изменение;
а) интенсивности окраски: 
б) объема;  ;
;
в) давления: 
г) массы твердого продукта:  и т. д.
и т. д.
Как уже указывалось выше, скорость химической реакции зависит от многих факторов, включая природу реагентов, концентрацию реагирующих веществ и температуру, наличие катализаторов.
Рассмотрим главные из этих факторов.
Влияние концентрации реагентов может быть объяснено на основе уже рассмотренных выше представлений, согласно которым химическое взаимодействие является результатом столкновения частиц реагирующих веществ. Увеличение числа частиц в данном объеме приводит к более частым их столкновениям, то есть к увеличению скорости реакции. Если при химическом взаимодействии сталкиваются частицы нескольких видов, то число таких столкновений пропорционально произведению концентраций этих частиц.
Влияние концентрации реагентов на скорость химического взаимодействия выражается основным законом химической кинетики — законом действующих масс:
Скорость простой гомогенной химической реакции прямо пропорциональна произведению концентраций реагирующих веществ, возведенных в степень их стехиометрических коэффициентов.
Скорость простой реакции А + В = АВ равна:

Скорость простой реакции А + В + С = АВС равна:

В общем случае для скорости простой реакции имеем:

Уравнения (6-2)-(6-4) называются кинетическими уравнениями химической реакции, в которых k — константа скорости.
Физический смысл константы скорости можно установить, если принять, что  = 1 моль/л. Тогда константа скорости k численно равна скорости реакции w, с которой реагируют вещества при их концентрации, равной единице.
= 1 моль/л. Тогда константа скорости k численно равна скорости реакции w, с которой реагируют вещества при их концентрации, равной единице.
Отметим также, что для уравнения (6-4), как и для других уравнений, существует эквивалентная запись:

Алгоритмы использования основного уравнения химической кинетики
Пример №6-1.
Реакцию между веществами А и В можно описать уравнением 2А + В = С; концентрация вещества А равна 8 моль/л, а вещества В — 5 моль/л. Как изменится скорость химической реакции в момент, когда в реакционной смеси останется 40 % вещества В, по отношению к начальной скорости реакции?
Решение:
Определим начальные и конечные концентрации реагентов (моль/л) в рассматриваемой реакции, учитывая, что при достижении конечных условий в реакционной смеси остается 40 % вещества В.

Тогда скорость реакции в начальный и конечный моменты можно представить следующими соотношениями:

Откуда следует, что скорость уменьшается в

Ответ: скорость уменьшится в 40 раз.
Пример №6-2.
Определите, как изменится скорость прямой реакции  , если общее давление в системе увеличить в 4 раза?
, если общее давление в системе увеличить в 4 раза?
Решение:
Поскольку реакция, приведенная в задаче, является простой гомогенной реакцией, то для нее можно записать выражения закона действующих масс: 
После увеличения давления в системе в четыре раза, что отвечает увеличению концентрации обоих реагентов (и  ) в четыре раза, имеем:
) в четыре раза, имеем:

Ответ: скорость реакции возрастет в 64 раза.
Алгоритмы использования уравнений, учитывающих влияние температуры на скорость химической реакции
Многочисленные опыты показывают, что при повышении температуры скорость большинства химических реакций существенно увеличивается, причем для реакций в гомогенных системах при нагревании на каждые десять градусов скорость реакции возрастает в 2-4 раза (правило Вант-Гоффа). Иначе говоря, при повышении температуры в арифметической прогрессии скорость реакции возрастает в геометрической прогрессии. Как объяснить столь высокую температурную чувствительность скорости реакции? На первый взгляд может показаться, что она связана с увеличением числа молекулярных столкновений, однако это не так. Согласно расчетам, общее число столкновений молекул при повышении температуры на десять градусов возрастает только на 1,6 %, а число прореагировавших молекул возрастает на 200-400 %.
Чтобы объяснить наблюдаемые расхождения, С. Аррениус предположил, что влияние температуры сводится, главным образом, к увеличению числа активных молекул, т. е. молекул, столкновение которых приводит к образованию продукта (эффективные столкновения). Согласно С. Аррениусу, доля эффективных столкновений, равная отношению их числа  к общему числу столкновений (n), изменяется с температурой:
к общему числу столкновений (n), изменяется с температурой:

В этом уравнении фигурирует величина Е, имеющая размерность энергии (Дж/моль) и названная энергией активации, R — молярная газовая постоянная, равная 8,31 Дж/(моль К). Энергия активации — это та энергия, которой должны обладать молекулы для эффективного столкновения. Естественно, что она в большинстве случаев больше, чем средняя энергия молекул.
Приведем решения нескольких типичных задач, связанных с изменением кинетических параметров с температурой.
Пример №6-3.
Скорость реакции при 0° С равна 1 моль/л с. Вычислите скорость этой реакции при 30° С, если температурный коэффициент скорости реакции равен 3.
Решение:
Воспользуемся формулой, количественно выражающей правило Вант-Гоффа:

Подставляя данные задачи в приведенное выражение, получаем:

Ответ: 27 моль/л*с.
Пример №6-4.
Реакция при температуре 50° С протекает за 2 мин 15 с. За сколько времени закончится эта реакция при температуре 70° С, если в данном температурном интервале температурный коэффициент скорости реакции равен 3?
Решение:
Учитывая, что скорость химической реакции при данной температуре обратно пропорциональна продолжительности ее протекания, подставим данные, приведенные в задаче, в формулу, количественно выражающую правило Вант-Гоффа:

Ответ: 15 c.
Рассмотрим пример, связанный с вычислением энергии активации химической реакции.
Пример №6-5.
Установите взаимосвязь между температурным коэффициентом скорости реакции и энергией активации некоторой химической реакции.
Решение:
Логарифмируя выражение, количественно выражающее правило Вант-Гоффа:

получаем:

Запишем теперь уравнение Аррениуса:

Прологарифмируем приведенное выражение и запишем полученное соотношение для температур  .
.
Получаем:

Вычитание из верхнего выражения нижнего дает:

При фиксированных концентрациях компонентов, участвующих в химической реакции, можно записать:

Сопоставление уравнений (6-7) и (6-8) дает:

или

Ответ: Взаимосвязь между температурным коэффициентом скорости реакции и энергией активации некоторой химической реакции можно представить соотношением  ,.
,.
Анализ выражения, приведенного в решении примера 6-5:

показывает, что условие у = const при увеличении (уменьшении) температурного интервала  будет выполняться, если величина энергии активации также будет увеличиваться (уменьшаться). Однако теоретические соображения указывают на то, что величина энергии активации является фундаментальной характеристикой реакции и, как правило, сохраняет постоянное значение в достаточно широком интервале температур. Отсюда следует вывод, что величина температурного коэффициента скорости реакции не является строго постоянной величиной. Ее постоянство сохраняется лишь в достаточно узком интервале температур.
будет выполняться, если величина энергии активации также будет увеличиваться (уменьшаться). Однако теоретические соображения указывают на то, что величина энергии активации является фундаментальной характеристикой реакции и, как правило, сохраняет постоянное значение в достаточно широком интервале температур. Отсюда следует вывод, что величина температурного коэффициента скорости реакции не является строго постоянной величиной. Ее постоянство сохраняется лишь в достаточно узком интервале температур.
В связи с этим целесообразно рассмотреть еще один пример.
Пример №6-6.
В интервале температур 200-300° С реакция характеризуется энергией активации 30 кДж/моль. Во сколько риз изменится величина температурного коэффициента реакции у в данном температурном интервале, если точное значение у может быть определено для отрезка  = 5° С?
= 5° С?
Решение:
Рассмотрим приближенную зависимость:

Тогда

где  — температурный коэффициент реакции в интервале температур
— температурный коэффициент реакции в интервале температур  , лежащем вблизи температуры 200° С.
, лежащем вблизи температуры 200° С.
Если описать температурный ход реакции более точной зависимостью — уравнением Аррениуса, то получим:

Сопоставляя уравнения (6-9) и (6-10), имеем:

или после преобразований получаем:

Аналогично, для  — температурного коэффициента реакции, который описывает ее поведение в интервале температур
— температурного коэффициента реакции, который описывает ее поведение в интервале температур  , лежащем вблизи температуры 300° С, имеем:
, лежащем вблизи температуры 300° С, имеем:

Поскольку  , оценим разность (6-11)-(6-12):
, оценим разность (6-11)-(6-12):

Подставляя величины

для нижнего измеряемого интервала температур, а также 
 для верхнего измеряемого интервала температур, получаем:
для верхнего измеряемого интервала температур, получаем:

Ответ:  больше
больше  в 1,05 раза.
в 1,05 раза.
Химическое равновесие
До сих пор мы рассматривали химические реакции, условно полагая, что они идут до конца, т. е. реагенты полностью превращаются в продукты реакции.
В действительности же такое положение справедливо лишь для некоторых реакций, называемых необратимыми.
Примером необратимых реакций могут служить реакции разложения известняка, реакции в растворах, сопровождающиеся образованием газообразного или труднорастворимого продукта, и др.:

Большинство химических процессов являются обратимыми, и по мере их протекания в системе создаются условия для противоположных изменений. Например, если смесь водорода и йода нагревать при 410° С в закрытом сосуде, то лишь 78 % исходных реагентов превращаются в йодоводород. При тех же условиях чистый йодоводород распадается на водород и йод, но не полностью, а лишь на 22 %. Как в первом, так и во втором случае устанавливается состояние, которое при данной температуре характеризуется вполне определенным соотношением участников реакции. Строго говоря, необратимых реакций нет, и любой из процессов, рассмотренных как необратимый, может быть превращен в обратимый.
Например, разложение карбоната кальция — реакция необратимая, если осуществляться в открытой системе, т. е. в системе, в которой возможно удаление оксида углерода (IV) из сферы реакции. Но при осуществлении той же реакции в замкнутой системе процесс диссоциации карбоната кальция идет не полностью, а лишь до тех пор, пока в системе не установится вполне определенное давление газа, препятствующее дальнейшей диссоциации. Абсолютное значение этого давления определяется температурой.
Рассмотрим более подробно процессы, протекающие в обратимых системах. В качестве примера возьмем некоторую простую реакцию:

Если система первоначально состоит из чистых реагентов, то согласно основному закону химической кинетики скорость взаимодействия выражается соотношением:

где  — скорость прямой реакции;
— скорость прямой реакции;  — константа скорости прямой реакции; [А] — концентрация реагента А; [В] — концентрация реагента В.
— константа скорости прямой реакции; [А] — концентрация реагента А; [В] — концентрация реагента В.
По мере химического превращения концентрации веществ А и В уменьшаются и, следовательно, скорость прямой реакции понижается. Вместе с тем появление в системе продуктов означает возможность протекания обратной реакции, скорость которой непрерывно возрастает:

где  — скорость обратной реакции;
— скорость обратной реакции;  — константа скорости обратной реакции; [С] — концентрация продукта реакции С; [D] — концентрация продукта реакции D.
— константа скорости обратной реакции; [С] — концентрация продукта реакции С; [D] — концентрация продукта реакции D.
Рано или поздно будет достигнуто состояние, при котором скорости прямой и обратной реакций сравняются. Состояние системы, при котором скорость прямой реакции равна скорости обратной реакции, называется химическим равновесием. Концентрации реагентов и продуктов, отвечающие состоянию равновесия, называются равновесными и обозначаются символами  .
.
Так как в состоянии равновесия  , то
, то

Следовательно,

Отношение констант скоростей прямой и обратной реакций является постоянной величиной, получившей название константы химического равновесия. Подобно константам скорости прямой и обратной реакций, константа химического равновесия тоже зависит от температуры. Уравнение (7-3) является математическим выражением закона действующих масс при химическом равновесии.
Отношение произведений равновесных концентраций веществ правой и левой частей уравнения, возведенных в степени их стехиометрических коэффициентов, представляет постоянную величину независимо от тех условий, при которых осуществляется реакция, если только температура считается постоянной.
Состояние химического равновесия при неизменных внешних условиях может сохраняться сколь угодно долго. В действительности же реальные системы обычно испытывают различные воздействия (изменение температуры, давления или концентрации реагентов), выводящие систему из состояния равновесия.
Как только в системе нарушается равновесие, скорости прямой и обратной реакций становятся неодинаковыми, и в системе преимущественно протекает процесс, который опять приводит ее к состоянию равновесия, но уже отвечающему новым условиям. Изменения, происходящие в равновесной системе в результате внешних воздействий, определяются принципом подвижного равновесия — принципом Ле Шателье.
Внешнее воздействие на систему, находящуюся в состоянии равновесия, приводит к смещению этого равновесия в направлении, при котором эффект произведенного воздействия ослабляется.
Итак, внешнее воздействие на систему изменяет соотношение между скоростями прямого и обратного процессов, благоприятствуя тому из них, который противодействует внешнему влиянию.
Принцип Ле Шателье универсален, так как применим не только к чисто химическим процессам, но и к физико-химическим явлениям, таким, как растворение и кристаллизация, конденсация и кипение, фазовые превращения в твердых телах и др.
Рассмотрим применение принципа Ле Шателье к различным типам воздействий.
Влияние изменения температуры. При повышении температуры ускоряются как прямая, так и обратная реакции, но в различной степени. Как правило, эндотермический процесс ускоряется в большей степени, чем экзотермический. При понижении температуры в системе из двух реакций быстрее протекает экзотермическая. Следовательно, для выяснения влияния температуры на химическое равновесие необходимо знать знак и значение теплового эффекта реакции. Чем больше тепловой эффект реакции, тем сильнее влияние температуры.
Влияние изменения давления. При повышении давления равновесие реакции смещается в направлении образования веществ, занимающих меньший объем, и наоборот, понижение давления способствует процессу, сопровождающемуся увеличением объема.
В реакции синтеза аммиака из азота и водорода повышение давления способствует накоплению аммиака, так как при реакции из каждых четырех молей исходных газообразных веществ (1 моль азота и 3 моль водорода) образуется два моля газообразного продукта (NH}), при этом объем реакционной смеси уменьшается вдвое.
Влияние изменения концентрации. Если к системе, находящейся в состоянии равновесия, прибавлять дополнительные количества одного из веществ, участвующих в реакции, то скорости прямого и обратного процессов изменятся, но таким образом, что система снова придет в состояние равновесия, В этом новом состоянии концентрации всех веществ будут отличаться от первоначальных, но соотношение между ними (определяемое константой равновесия) останется прежним. Иначе говоря, в равновесной системе нельзя изменить концентрацию только одного из веществ, не вызывая изменения концентрации остальных. В соответствии с принципом Ле Шателье в системе развивается процесс, уменьшающий концентрацию дополнительно вводимого вещества.
Вычисление константы равновесия химической реакции
Рассмотрим в качестве примера следующую задачу:
Пример №7-1.
Объемный состав реакционной смеси в момент равновесия для реакции  был следующий: 87,7 %
был следующий: 87,7 %  , 8,2 % СО, 4,1 %
, 8,2 % СО, 4,1 %  . Найдите
. Найдите  для этой реакции, если общее давление в системе при данной температуре (2000°С) равно 1,0133 * 105Па.
для этой реакции, если общее давление в системе при данной температуре (2000°С) равно 1,0133 * 105Па.
Решение:
Определим парциальные давления всех компонентов реагирующей газовой смеси:

Тогда константа  может быть представлена следующим выражением:
может быть представлена следующим выражением:

На основании уравнения состояния идеального газа Менделеева—Клапейрона  ,
,
где  — разность между числом молей газообразных веществ после и до реакции. Учитывая, что в нашем случае
— разность между числом молей газообразных веществ после и до реакции. Учитывая, что в нашем случае  = 3 — 2 = 1, имеем:
= 3 — 2 = 1, имеем:

Ответ: 
Вычисление равновесных и исходных концентраций реагирующих веществ по известной константе равновесия
Рассмотрим в качестве примера следующую задачу:
Пример №7-2.
Реакция протекает по уравнению А + 2В = С. Определите равновесные концентрации реагирующих веществ и продуктов реакции, если исходные концентрации веществ А и В соответственно равны 0,3 и 0,8 моль/л, а константа равновесия реакции  = 10.
= 10.
Решение:
Запишем исходные «0» и равновесные «р» концентрации реагирующих веществ и продуктов реакции (моль/л), принимая, что концентрация компонента А в момент установления равновесия понизилась на х моль/л:

Тогда выражение для константы равновесия примет вид:

Решая это уравнение, получаем х = 0,191.
Ответ: 
Определение направления сдвига химического равновесия
Принцип Ле Шателье
Рассмотрим в качестве примера следующую задачу:
Пример №7-3.
После установления равновесия в системе 
 концентрации реагирующих веществ оказались равными (моль/л):
концентрации реагирующих веществ оказались равными (моль/л):  Как изменятся скорости прямой и обратной реакций, если в системе увеличить общее давление в 3 раза? В каком направлении сместится равновесие?
Как изменятся скорости прямой и обратной реакций, если в системе увеличить общее давление в 3 раза? В каком направлении сместится равновесие?
Решение:
Используя определение скорости химической реакции, можно записать:

Скорость прямой реакции увеличилась в 27 раз.

Скорость обратной реакции увеличилась в 9 раз.
Равновесие сместится слева направо.
Ответ: скорость прямой реакции увеличилась в 27 раз. Скорость обратной реакции увеличилась в 9 раз. Равновесие сместится слева направо.
Рассмотрим еще один пример.
Пример №7-4.
Химическое равновесие реакции  установилось при следующих концентрациях реагирующих веществ (моль/л):
установилось при следующих концентрациях реагирующих веществ (моль/л):  . Равновесие системы было нарушено из-за уменьшения концентрации СО до 2 моль/л. Вычислите, какими стали новые равновесные концентрации реагирующих веществ после сдвига равновесия.
. Равновесие системы было нарушено из-за уменьшения концентрации СО до 2 моль/л. Вычислите, какими стали новые равновесные концентрации реагирующих веществ после сдвига равновесия.
Решение:
Оценим константу равновесия  на основании приведенных в условии задачи величин равновесных концентраций реагирующих веществ:
на основании приведенных в условии задачи величин равновесных концентраций реагирующих веществ:

После того, как концентрацию СО в равновесной смеси понизили до 2 моль/л, в системе должен наблюдаться сдвиг равновесия согласно принципу Ле Шателье в сторону увеличения концентрации СО и  в газовой фазе. После установления равновесия новые равновесные концентрации реагирующих веществ будут равны:
в газовой фазе. После установления равновесия новые равновесные концентрации реагирующих веществ будут равны:

а выражение для константы  можно представить в виде:
можно представить в виде:

Решение этого уравнения даст значение х = 0,45.
Ответ: 
Пример №7-5.
Для проведения реакции  использована исходная концентрация вещества А, равная 2 моль/л. Равновесие в системе установилось, после того как 2/3 вещества А прореагировало. После установления равновесия продукты реакции В и С были удалены из системы, и в реакторе вновь установилось равновесие. Определить концентрации веществ А, В и С после повторного установления равновесия в системе.
использована исходная концентрация вещества А, равная 2 моль/л. Равновесие в системе установилось, после того как 2/3 вещества А прореагировало. После установления равновесия продукты реакции В и С были удалены из системы, и в реакторе вновь установилось равновесие. Определить концентрации веществ А, В и С после повторного установления равновесия в системе.
Решение:
Определим начальные и равновесные концентрации веществ, участвующих в реакции:

Тогда константа равновесия может быть оценена величиной:

В новых условиях:

и константа равновесия записывается как:

Решение последнего выражения дает: х = 0,5525.
Следовательно, после повторного установления равновесия в системе концентрации веществ станут:

Ответ: 
Рассмотрим в качестве примера усложненный вариант рассмотренных выше задач (7.24)-(7.26).
Пример №7-6.
Для проведения реакции  использована исходная концентрация вещества А, равная 2 моль/л. Равновесие в системе установилось, после того как 2/3 вещества А прореагировало. После установления равновесия продукты реакции В и С были удалены из системы, а давление в реакторе понизили в 2 раза. Определить концентрации веществ А, В и С после повторного установления равновесия в системе.
использована исходная концентрация вещества А, равная 2 моль/л. Равновесие в системе установилось, после того как 2/3 вещества А прореагировало. После установления равновесия продукты реакции В и С были удалены из системы, а давление в реакторе понизили в 2 раза. Определить концентрации веществ А, В и С после повторного установления равновесия в системе.
Решение:

Тогда константа равновесия может быть оценена как:

В новых условиях:

и константа равновесия записывается как:

Решение последнего выражения дает: х = 0.3.
Следовательно, после повторного установления равновесия в системе концентрации веществ станут:

Ответ: 
Ионные равновесия в растворах электролитов
Действие растворителя на растворенное вещество настолько велико, что может вызывать электролитическую диссоциацию веществ, не обладающих ионным типом связи. Например, полярные молекулы хлороводорода, растворяясь в воде, разрываются ее молекулами на ионы. При растворении хлороводорода в бензоле, являющемся менее полярным растворителем, чем вода, диссоциации молекул не происходит. Поэтому раствор хлороводорода (кислота) в воде проводит электрический ток, а в бензоле нет.
Все электролиты условно делят на три группы. К сильным электролитам относят вещества, которые практически полностью (в данном растворителе) диссоциируют на ионы:  ,
,  и почти все соли. К слабым электролитам относят вещества, диссоциирующие на ионы в незначительной степени:
и почти все соли. К слабым электролитам относят вещества, диссоциирующие на ионы в незначительной степени:  ,
,  и некоторые другие. У слабых электролитов большая часть растворенного вещества находится в форме молекул. Наконец, существует относительно небольшая группа электролитов, которые принято называть электролитами средней силы. К ним относят такие вещества, в растворах которых число диссоциирующих молекул примерно равно числу молекул, не подвергающихся диссоциации:
и некоторые другие. У слабых электролитов большая часть растворенного вещества находится в форме молекул. Наконец, существует относительно небольшая группа электролитов, которые принято называть электролитами средней силы. К ним относят такие вещества, в растворах которых число диссоциирующих молекул примерно равно числу молекул, не подвергающихся диссоциации:  и т. д. При решении тех или иных химических задач наиболее часто приходится использовать представления о поведении двух групп электролитов — сильных и слабых.
и т. д. При решении тех или иных химических задач наиболее часто приходится использовать представления о поведении двух групп электролитов — сильных и слабых.
Для более строгой, количественной характеристики состояния растворенного вещества в растворах вводится понятие о степени диссоциации.
Степень электролитической диссоциации а — число, показывающее, какая часть молекул электролита находится в растворе в виде ионов.
Согласно этому определению

Очевидно, во всех растворах неэлектролитов, где диссоциация на ионы полностью отсутствует,  , а в растворах, в которых все растворенное вещество присутствует в форме ионов (полная диссоциация),
, а в растворах, в которых все растворенное вещество присутствует в форме ионов (полная диссоциация),  . Очень часто для растворов средней концентрации
. Очень часто для растворов средней концентрации  считают, что слабые электролиты характеризуются
считают, что слабые электролиты характеризуются  < 0,03, а сильные —
< 0,03, а сильные —  > 0,30. Следовательно, электролиты средней силы характеризуются промежуточными значениями степени диссоциации: 0,03 <
> 0,30. Следовательно, электролиты средней силы характеризуются промежуточными значениями степени диссоциации: 0,03 <  < 0,30. Однако необходимо отметить, что предложенная классификация является в значительной степени условной (особенно в случае слабых электролитов и электролитов средней силы). Это объясняется тем, что степень диссоциации в общем случае зависит от природы электролита и растворителя, от концентрации и температуры раствора.
< 0,30. Однако необходимо отметить, что предложенная классификация является в значительной степени условной (особенно в случае слабых электролитов и электролитов средней силы). Это объясняется тем, что степень диссоциации в общем случае зависит от природы электролита и растворителя, от концентрации и температуры раствора.
Для растворов, образованных одними и теми же компонентами (растворителем и растворенным веществом), наибольший интерес представляет зависимость степени диссоциации от концентрации раствора. Для слабых электролитов типа  (кислота) или
(кислота) или  (основание) степень диссоциации
(основание) степень диссоциации  и молярная концентрация раствора с связаны зависимостью:
и молярная концентрация раствора с связаны зависимостью:

где  — константа, характеризующая способность того или иного слабого электролита к диссоциации.
— константа, характеризующая способность того или иного слабого электролита к диссоциации.
При малых значениях  разность (1 —
разность (1 —  ) приблизительно равна 1. Тогда из уравнения (8-2) можно получить:
) приблизительно равна 1. Тогда из уравнения (8-2) можно получить:

что является математическим выражением закона разведения Оствальда.
Из уравнения (8-3) следует важный вывод: степень диссоциации слабого электролита в растворе тем выше, чем более разбавлен раствор. Так, степень диссоциации уксусной кислоты в ее водных растворах изменяется при разбавлении следующим образом (см. табл. 8.1).
Таблица 8.1
Степень электролитической диссоциации уксусной кислоты в ее водных растворах в зависимости от концентрации

Степень диссоциации рассчитывали по уравнению (8-2), так как значением а в разности (I —  ) пренебрегать нельзя; для
) пренебрегать нельзя; для  М значение а оценивали по уравнению (8-3).
М значение а оценивали по уравнению (8-3).
Из приведенных данных видно, что в бесконечно разбавленных растворах степень диссоциации любого (даже слабого!) электролита равна 1.
Необходимо помнить, что классификационные границы, введенные для деления электролитов на сильные и слабые, а также на электролиты средней силы  , условны и справедливы для растворов определенной концентрации (5,0-10,0 %). По тем же причинам электролит средней силы — сернистая кислота
, условны и справедливы для растворов определенной концентрации (5,0-10,0 %). По тем же причинам электролит средней силы — сернистая кислота  в разбавленных растворах
в разбавленных растворах  «попадает» в соответствии с введенной классификацией в группу сильных электролитов, так как в этих условиях
«попадает» в соответствии с введенной классификацией в группу сильных электролитов, так как в этих условиях  (табл. 8.2).
(табл. 8.2).
Рассмотренный пример с электролитом средней силы очень важен для более глубокого понимания теории электролитической диссоциации. Не менее важен для понимания этой теории и тот факт, что значение степени электролитической диссоциации сильных электролитов, оцененное на основании результатов физико-химических измерений, является, напротив, заниженным (особенно для растворов средней и высокой концентраций). Так, наиболее распространенным методом измерения степени диссоциации сильных электролитов является метод, основанный на сопоставлении электрической проводимости данного раствора и бесконечно разбавленного раствора того же вещества. Значение этой величины всегда оказывается меньше единицы и носит название кажущейся степени диссоциации  .
.
Таблица 8.2
Степень электролитической диссоциации электролитов в 0,1 моль экв/л растворе при 18° С (для сильных электролитов — кажущаяся)


Нужно помнить, что  вовсе не характеризует истинной степени диссоциации; истинная степень диссоциации сильных электролитов всегда близка к единице.
вовсе не характеризует истинной степени диссоциации; истинная степень диссоциации сильных электролитов всегда близка к единице.
Ситуация, при которой  объясняется тем, что появление в растворе значительного числа противоположно заряженных ионов, образующихся при полной диссоциации сильного электролита, не может обеспечить их независимого поведения (особенно в растворах средней и высокой концентраций). Но это утверждение не означает, что ионы соединяются в молекулы. Так как каждый ион всегда окружен как бы атмосферой из противоположно заряженных ионов, это приводит к заметному снижению динамических свойств ионов обоих знаков по сравнению с их поведением в бесконечно разбавленных растворах.
объясняется тем, что появление в растворе значительного числа противоположно заряженных ионов, образующихся при полной диссоциации сильного электролита, не может обеспечить их независимого поведения (особенно в растворах средней и высокой концентраций). Но это утверждение не означает, что ионы соединяются в молекулы. Так как каждый ион всегда окружен как бы атмосферой из противоположно заряженных ионов, это приводит к заметному снижению динамических свойств ионов обоих знаков по сравнению с их поведением в бесконечно разбавленных растворах.
Ионное произведение воды pH и pOH растворов
Различные формы растворенного вещества (ионы, недиссоциировап-ные молекулы) находятся в растворе в равновесии друг с другом: скорость диссоциации молекул на ионы равна скорости образования молекул из ионов. Рассмотрим это на примере раствора уксусной кислоты в воде. Процесс диссоциации и обратный ему процесс ассоциации выражается уравнением:

Отметим, что символ  указывает на обратимость процесса диссоциации слабого электролита; напротив, символ
указывает на обратимость процесса диссоциации слабого электролита; напротив, символ  указывает на то, что рассматривается процесс диссоциации сильного электролита, т. е. полная диссоциация (равновесие полностью смещено вправо).
указывает на то, что рассматривается процесс диссоциации сильного электролита, т. е. полная диссоциация (равновесие полностью смещено вправо).
Опыт показывает, что даже химически чистая вода проводит электрический ток, хотя и очень слабо. Эта проводимость возникает за счет диссоциации молекул воды:

В чистой воде 
Измерения проводимости чистой воды показали, что при 22° С степень ее диссоциации  . Так как в 1 л воды содержится 55,5 моль
. Так как в 1 л воды содержится 55,5 моль  (1000 : 18), то концентрация ионов будет равна:
(1000 : 18), то концентрация ионов будет равна:

Тогда произведение 
Очевидно, что при данной температуре величина  является постоянной и называется ионным произведением воды.
является постоянной и называется ионным произведением воды.
Постоянство величины  (при t = const) позволяет утверждать, что при увеличении в растворе концентрации ионов
(при t = const) позволяет утверждать, что при увеличении в растворе концентрации ионов  (растворение кислоты) происходит уменьшение концентрации ионов
(растворение кислоты) происходит уменьшение концентрации ионов  . Напротив, растворение в воде щелочи ведет к увеличению концентрации гидроксидных ионов и к снижению концентрации ионов
. Напротив, растворение в воде щелочи ведет к увеличению концентрации гидроксидных ионов и к снижению концентрации ионов  . Однако уменьшение концентрации ионов
. Однако уменьшение концентрации ионов  или
или  в соответствующих случаях происходит до значений, отвечающих постоянству ионного произведения воды. Так, если в растворе [
в соответствующих случаях происходит до значений, отвечающих постоянству ионного произведения воды. Так, если в растворе [ ] =
] =  моль/л (при t = 22° С), то концентрация ионов
моль/л (при t = 22° С), то концентрация ионов  уменьшится до значений
уменьшится до значений  моль/л.
моль/л.
Итак, [ ] = [
] = [ ] =
] =  моль/л является условием нейтральности раствора, а выполнение условия [
моль/л является условием нейтральности раствора, а выполнение условия [ ] >
] >  моль/л указывает на кислотность среды (при [
моль/л указывает на кислотность среды (при [ ] >
] >  моль/л — среда щелочная).
моль/л — среда щелочная).
Поскольку значения [ ] (или [
] (или [ ]) в химии растворов используются очень часто, то для удобства введено представление о водородном показателе (символ — pH). Водородный показатель — величина, характеризующая концентрацию водородных ионов и численно равная десятичному логарифму этой концентрации, выраженной в молях на литр с обратным знаком. Например, при
]) в химии растворов используются очень часто, то для удобства введено представление о водородном показателе (символ — pH). Водородный показатель — величина, характеризующая концентрацию водородных ионов и численно равная десятичному логарифму этой концентрации, выраженной в молях на литр с обратным знаком. Например, при  ; при
; при 
Таким образом, при pH = 7 среда нейтральная, при pH < 7 — кислая и при pH > 7 — щелочная.
Рассмотрим в качестве примера следующую количественную задачу:
Пример №8-1.
Определите pH раствора, в 4 л которого содержится  моль ионов
моль ионов  .
.
Решение:
Концентрация  ионов, очевидно, составляет
ионов, очевидно, составляет 
 . Поскольку по определению
. Поскольку по определению 

Ответ: pH = 11,2.
Ионные равновесия в растворах слабых электролитов. Вычисление степени диссоциации слабого электролита по числу растворенных частиц
Рассмотрим в качестве примера следующую задачу:
Пример №8-2.
В 1л  М раствора бинарного электролита содержится 6.041 •
М раствора бинарного электролита содержится 6.041 •  недиссоциированных молекул и ионов. Определите степень диссоциации.
недиссоциированных молекул и ионов. Определите степень диссоциации.
Решение:
Запишем уравнение реакции диссоциации слабого бинарного электролита, например, НВ и оценим начальные «0» и конечные (равновесные) «р» концентрации молекул и ионов, обозначив степень диссоциации через  :
:

Теперь оценим, какое число недиссоциированных молекул присутствовало бы в системе при гипотетических начальных условиях «0».
При концентрации электролита в системе  моль/л и объеме системы — 1 л имеем число молей
моль/л и объеме системы — 1 л имеем число молей  моль. Эта величина соответствует числу молекул
моль. Эта величина соответствует числу молекул  . Поскольку число нсдиссоциированных молекул и образовавшихся ионов будет пропорционально величине с
. Поскольку число нсдиссоциированных молекул и образовавшихся ионов будет пропорционально величине с  , то можно составить пропорцию:
, то можно составить пропорцию:

Решение полученной пропорции дает  = 0,35 %.
= 0,35 %.
Ответ: 0,35 %.
Вычисление степени диссоциации слабого электролита по значению его константы диссоциации
Рассмотрим в качестве примера следующую задачу:
Пример №8-3.
Найдите степень диссоциации в 0,1 М растзорс уксусной кислоты  .
.
Решение:
Подставляя величины молярной концентрации соответствующей кислоты и се константы диссоциации в уравнение, описывающее закон Оствальда: 
получаем искомое решение:  = 1,32 %.
= 1,32 %.
Ответ: 1,32%.
Вычисление концентрации ионов в растворе слабого электролита
Рассмотрим в качестве примера следующую задачу:
Пример №8-4.
Определите концентрацию ионов водорода в 1 М растворе муравьиной кислоты, если 
Решение:
Подставляя величины молярной концентрации муравьиной кислоты и ее константы диссоциации в уравнение, описывающее закон Оствальда:

получаем величину степени диссоциации  = 0,0133. Тогда концентрация ионов водорода [
= 0,0133. Тогда концентрация ионов водорода [ ] =
] =  = 0,0133 • 1 = 0,0133 моль/л.
= 0,0133 • 1 = 0,0133 моль/л.
Ответ: 0,0133 моль/л.
Расчет константы диссоциации
Рассмотрим в качестве примера следующую задачу:
Пример №8-5.
В 1,0 М растворе  концентрация ионов водорода составляет 0,0225 моль/л. Определите константу диссоциации азотистой кислоты.
концентрация ионов водорода составляет 0,0225 моль/л. Определите константу диссоциации азотистой кислоты.
Решение:
Для определения константы диссоциации азотистой кислоты запишем уравнение ее диссоциации, обозначив степень диссоциации —  :
:

Следовательно, зная равновесные концентрации («р») азотистой кислоты, а также ионов водорода и нитрит-ионов константу диссоциации азотистой кислоты можно записать следующим образом:

Считая, что  и пренебрегая величиной а в разности (1 —
и пренебрегая величиной а в разности (1 —  ), получаем
), получаем  Подчеркнем, что мы получили приближенное решение.
Подчеркнем, что мы получили приближенное решение.
Теперь получим точное решение. Для этого подставим в разность (1 — а) величину  . Точное решение дает значение
. Точное решение дает значение 
Ответ:  .
.
Вычисление концентрации раствора по константе диссоциации и величине pH
Рассмотрим в качестве примера следующую задачу:
Пример №8-6.
В растворе сернистой кислоты концентрация ионов водорода равна  моль/л. Вычислить молярную концентрацию сернистой кислоты в этом растворе, если первая константа ее диссоциации
моль/л. Вычислить молярную концентрацию сернистой кислоты в этом растворе, если первая константа ее диссоциации  , а диссоциацией кислоты по второй ступени можно пренебречь.
, а диссоциацией кислоты по второй ступени можно пренебречь.
Решение:
Запишем уравнение диссоциации (для первой ступени) сернистой кислоты, обозначив под каждым из видов взаимодействующих вешеств и ионов их концентрации в исходном («0») и равновесном состояниях («р»):

Тогда

Рассмотрим еще один пример.
Пример №8-7.
Растворы монохлоруксусной и уксусной кислот имеют одинаковую концентрацию  = 0,1 моль/л. и характеризуются степенями диссоциации 0,112 и 0,0132 соответственно. До какой концентрации необходимо довести раствор уксусной кислоты, чтобы степень его диссоциации достигла величины, характеризующий исходный раствор монохлоруксусной кислоты?
= 0,1 моль/л. и характеризуются степенями диссоциации 0,112 и 0,0132 соответственно. До какой концентрации необходимо довести раствор уксусной кислоты, чтобы степень его диссоциации достигла величины, характеризующий исходный раствор монохлоруксусной кислоты?
Решение:
Оценим сначала константу диссоциации уксусной кислоты (эта величина в задаче не приводится):

Теперь находим концентрацию раствора уксусной кислоты, при которой степень ее диссоциации станет равной величине 0,112:

Ответ: концентрация раствора уксусной кислоты, при которой степень ее диссоциации станет равной величине 0,112, равна  моль/л.
моль/л.
Гидролиз
Рассмотрим гидролиз — одно из важнейших явлений, протекающих в ионных растворах и трактуемых с позиций химического равновесия.
Гидролизом называется химическое взаимодействие солей с водой, приводящее к образованию слабого электролита.
Если рассматривать соли как продукты взаимодействия кислот с основаниями, то в зависимости от их силы различают четыре типа солей:
- соли, образованные сильной кислотой и сильным основанием;
- соли, образованные слабой кислотой и сильным основанием;
- соли, образованные сильной кислотой и слабым основанием;
- соли, образованные слабой кислотой и слабым основанием.
Соли первого типа не подвергаются гидролизу, так как не взаимодействуют с водой и не образуют слабых электролитов.
Рассмотрим гидролиз солей, образованных сильным основанием и слабой кислотой на примере цианида калия. В системе, состоящей из молекул  происходят следующие процессы диссоциации:
происходят следующие процессы диссоциации:

В результате диссоциации в растворе наряду с молекулами воды присутствуют ионы  . Последние взаимодействуют между собой, образуя малодиссоциированные молекулы
. Последние взаимодействуют между собой, образуя малодиссоциированные молекулы  . Это означает, что соль подвергается гидролизу. Для процесса гидролиза принято записывать три уравнения: в молекулярной, в полной ионной и в сокращенной ионной формах. В молекулярной форме этот процесс можно представить реакцией:
. Это означает, что соль подвергается гидролизу. Для процесса гидролиза принято записывать три уравнения: в молекулярной, в полной ионной и в сокращенной ионной формах. В молекулярной форме этот процесс можно представить реакцией:

а в полной ионной форме реакция записывается в виде уравнения:

Наконец, в сокращенной ионной форме в уравнении реакции остаются лишь ионные и молекулярные частицы, изменяющие свой состав в ходе процесса:

В результате гидролиза солей этого типа увеличивается концентрация ионов  раствора возрастает.
раствора возрастает.
При растворении в воде соли, образованной сильной кислотой и слабым основанием, например, хлорида аммония, в системе происходят следующие процессы:

В растворе появляются ионы  . Ионы
. Ионы  , взаимодействуя друг с другом, образуют слабодиссоциирующие молекулы
, взаимодействуя друг с другом, образуют слабодиссоциирующие молекулы  . Это означает, что соль подвергается гидролизу. В этом случае три уравнения, которые необходимы для описания процесса гидролиза, можно представить следующим образом:
. Это означает, что соль подвергается гидролизу. В этом случае три уравнения, которые необходимы для описания процесса гидролиза, можно представить следующим образом: (молекулярная форма);
(молекулярная форма);
 (полная ионная форма);
(полная ионная форма);
 (сокращенная ионная форма).
(сокращенная ионная форма).
В результате гидролиза этого типа солей увеличивается концентрация ионов водорода  уменьшается.
уменьшается.
Наиболее полному гидролизу подвергаются соли, образованные слабой кислотой и слабым основанием. Так, в результате растворения цианида аммония в воде в растворе появляются четыре вида ионов:  ,
,  , которые попарно взаимодействуют с образованием слабой кислоты
, которые попарно взаимодействуют с образованием слабой кислоты  и слабого основания
и слабого основания  . Суммарный процесс гидролиза выражается уравнением:
. Суммарный процесс гидролиза выражается уравнением:

В результате гидролиза солей, подобных цианиду аммония, в растворе образуются слабая кислота и слабое основание, а pH раствора остается достаточно близким к 7.
При растворении солей многоосновных кислот или оснований гидролиз протекает ступенчато. Например, при взаимодействии сульфида натрия с водой происходят следующие процессы.
На первой стадии (ступени):
 (молекулярная форма);
(молекулярная форма);
 (полная ионная форма);
(полная ионная форма);
 (сокращенная ионная форма).
(сокращенная ионная форма).
На второй ступени:
 (молекулярная форма);
(молекулярная форма);
 (полная ионная форма);
(полная ионная форма);
 (сокращенная ионная форма).
(сокращенная ионная форма).
Степень гидролиза зависит от химической природы образующегося при гидролизе слабого электролита, и она тем выше, чем слабее этот электролит. Например, при прочих равных условиях ацетат натрия гидролизуется слабее, чем цианид натрия, так как уксусная кислота сильнее синильной (см. табл. 8.3 и табл. 8.4).
Таблица 8.3
Константы диссоциации некоторых кислот

Таблица 8.4
Константы диссоциации некоторых оснований

Так как гидролиз является обратимым процессом, то влияние на него различных факторов может быть выяснено на основании принципа Ле Шателье. Напомним, что в соответствии с этим принципом внешнее воздействие на систему, находящуюся в равновесии, приводит к смещению этого равновесия в направлении, при котором эффект произведенного воздействия ослабляется. Так как гидролиз — процесс эндотермический, то повышение температуры (нагревание) должно увеличивать его интенсивность. Аналогичным образом разбавление водой способствует протеканию процесса, связанного с поглощением воды, т. е. усилению гидролиза. Наконец, в рассмотренном выше примере двухступенчатого гидролиза сульфида натрия реально будет протекать лишь первая стадия процесса. Это происходит потому, что на первой стадии накапливается такое количество гидроксидных ионов, которого достаточно, чтобы полностью подавить реакцию гидролиза по второй стадии, т. е. сместить процесс справа налево.
Пример №8-8.
Вычислить концентрацию ионов серебра в насыщенном растворе  , если
, если  .
.
Решение:
Примем растворимость  , за х моль/л. Тогда записав реакцию диссоциации
, за х моль/л. Тогда записав реакцию диссоциации  , имеем
, имеем

Зная молярные концентрации ионов  , можно записать выражение для произведения растворимости:
, можно записать выражение для произведения растворимости:

Решая полученное уравнение, получаем, что растворимость  моль/л, а концентрация ионов серебра в насыщенном растворе
моль/л, а концентрация ионов серебра в насыщенном растворе  , равная 3 х, составляет
, равная 3 х, составляет  моль/л.
моль/л.
Ответ:  моль/л.
моль/л.
Рассмотрим еще один пример.
Пример №8-9.
В двух растворах, находящимися над осадками  и
и  , количество ионов серебра одинаково. С каким объемом воды находится в равновесии осадок
, количество ионов серебра одинаково. С каким объемом воды находится в равновесии осадок  , если осадок
, если осадок  находится в равновесии с объемом 100 мл. Произведение растворимости
находится в равновесии с объемом 100 мл. Произведение растворимости  и
и  при 15°С составляют величины
при 15°С составляют величины  соответственно.
соответственно.
Решение:
Предположим, что растворимость  составляет х моль/л.
составляет х моль/л.
Тогда имеем:

И произведение растворимости можно записать:

Предположим, что растворимость  составляет у моль/л.
составляет у моль/л.
Тогда имеем:

И произведение растворимости можно записать:

При этом  моль/л. Эта величина в 14,98 раз больше величины у. Следовательно, объем воды, с которым находится в равновесии осадок
моль/л. Эта величина в 14,98 раз больше величины у. Следовательно, объем воды, с которым находится в равновесии осадок  , составляет 1498 мл.
, составляет 1498 мл.
Ответ: объем воды, с которым находится в равновесии осадок  , составляет 1498 мл.
, составляет 1498 мл.
Вычисление произведения растворимости малорастворимого электролита
Рассмотрим следующий пример.
Пример №8-10.
Вычислить произведение растворимости хромата бария, если его растворимость при 25°С равна  г/л.
г/л.
Решение:
Обозначим растворимость  за х моль/л. Тогда записав реакцию диссоциации
за х моль/л. Тогда записав реакцию диссоциации  имеем
имеем

Зная молярные концентрации ионов  ), можно записать выражение для произведения растворимости:
), можно записать выражение для произведения растворимости:

Подставляя в полученное уравнение величину растворимости  моль/л, получаем
моль/л, получаем 
Ответ: 1
Определение условий выпадения осадка
Рассмотрим следующий пример.
Пример №8-11.
Выпадет ли осадок при смешении равных объемов:
а) 0,1 М раствор  и 0,1 М раствор
и 0,1 М раствор  ; б) 0,01 М раствор
; б) 0,01 М раствор  и 0,01 М раствор
и 0,01 М раствор  .
. 
Решение:
а) Поскольку, согласно условию задачи, были слиты равные объемы растворов  и
и  , то их концентрации уменьшились вдвое и
, то их концентрации уменьшились вдвое и 
 . Тогда величина
. Тогда величина  . Поскольку произведение концентраций ионов кальция и сульфат-ионов больше произведения растворимости, то осадок выпадает.
. Поскольку произведение концентраций ионов кальция и сульфат-ионов больше произведения растворимости, то осадок выпадает.
Аналогичным образом решая вторую задачу (условие б), получаем 
 . В этих условиях осадок не выпадает.
. В этих условиях осадок не выпадает.
Ответ: а) осадок выпадает; б) осадок не выпадает.
Определение растворимости малорастворимого электролита в присутствии одноименного иона.
Рассмотрим следующий пример.
Пример №8-12.
Во сколько раз концентрация ионов бария в насыщенном растворе сульфата бария в воде больше, чем в 0,01 М растворе сульфата натрия?  равно
равно 
Решение:
Поскольку  . где х — растворимость
. где х — растворимость  в чистой воде, то
в чистой воде, то  растворе сульфата натрия концентрация сульфат-ионов
растворе сульфата натрия концентрация сульфат-ионов  моль/л, следовательно, концентрация ионов бария в насыщенном растворе сульфата бария в 0,01 М растворе сульфата натрия будет равна:
моль/л, следовательно, концентрация ионов бария в насыщенном растворе сульфата бария в 0,01 М растворе сульфата натрия будет равна:

Таким образом, концентрация ионов бария в насыщенном растворе сульфата бария в воде больше, чем в 0,01 М растворе сульфата натрия в 963 раза.
Ответ: в 963 раза.
Окислительно-восстановительные реакции
Окислительно-восстановительные реакции (ОВР) составляют особый класс химических процессов, характерной особенностью которых является изменение степени окисления (окислительных чисел), по крайней мере, пары атомов: окисление одного (потеря электронов) и восстановление другого (присоединение электронов). Окисление и восстановление, следовательно, такие два «полупроцесса», самостоятельное существование каждого из которых невозможно, однако их одновременное протекание обеспечивает реализацию единого окислительно-восстановительного процесса. Хотя главную роль в последнем играют атомы, изменяющие свои степени окисления, окислителями и восстановителями принято называть не отдельные атомы, а вещества, которые эти атомы содержат. Вещества, содержащие атомы, которые понижают степень окисления, называются окислителями, а вещества, содержащие атомы, которые степень окисления повышают — восстановителями. Отметим, что в частном случае, когда в качестве окислителей и восстановителей выступают простые вещества, названия реагентов, естественно, совпадают с названием атомов, изменяющих свои степени окисления.
Так, в реакции

окислителем является простое вещество — хлор, поскольку оно содержит атомы хлора, присоединяющие электроны, а восстановителем — металлический натрий, содержащий атомы натрия, которые электроны отдают.
Что же касается реакции

то окислителем в этом случае является дихромат калия, содержащий атомы хрома, присоединяющие электроны, восстановителем — металлический натрий, содержащий атомы серы, которые электроны отдают.
Итак, в результате окислительно-восстановительных реакций изменяется степень окисления, по крайней мере, пары атомов.
Напомним, что степенью окисления принято называть заряд атома в молекуле, рассчитываемый в предположении, что все связи в молекуле носят ионный характер. Следовательно, степень окисления атома того или иного элемента — условная величина, формально оцениваемая с использованием следующих правил:
1) степень окисления атома в молекуле может быть равна нулю или выражена отрицательным или положительным числом (целочисленным или дробным);
2) молекула всегда электронейтральна: сумма положительных и отрицательных формальных зарядов, которые характеризуют степень окисления атомов, образующих молекулу, равна нулю;
3) при оценке степени окисления атомов в сложных ионах заряд иона, естественно, учитывается; при этом алгебраическая сумма степеней окисления всех атомов, составляющих сложный ион, равна заряду последнего;
4) атомы кислорода во всех соединениях имеют степень окисления -2. Исключение составляют:
а) пероксиды типа  , в которых степень окисления атомов кислорода равна -1;
, в которых степень окисления атомов кислорода равна -1;
б) надпероксиды типа  , в которых степень окисления -1 имеет сложный надпероксидный ион
, в которых степень окисления -1 имеет сложный надпероксидный ион  и, следовательно, формально степень окисления атома кислорода равна —1/2;
и, следовательно, формально степень окисления атома кислорода равна —1/2;
в) озониды типа  , в которых степень окисления-1 имеет сложный озонид-ион
, в которых степень окисления-1 имеет сложный озонид-ион  и, следовательно, формально степень окисления атома кислорода равна -1/3;
и, следовательно, формально степень окисления атома кислорода равна -1/3;
г) смешанные пероксид-надпероксидные соединения типа 
 где
где  , в которых атомы кислорода формально характеризуются двумя степенями окисления -1 и -1/2;
, в которых атомы кислорода формально характеризуются двумя степенями окисления -1 и -1/2;
д) наконец, оксид и пероксид фтора  , в которых степень окисления атомов кислорода равна +2 и +1 соответственно;
, в которых степень окисления атомов кислорода равна +2 и +1 соответственно;
5) атомы водорода во всех соединениях имеют степень окисления +1; исключение составляют гидриды, в которых степень окисления атома водорода равна-1;
6) степень окисления атомов металлов в соединениях с неметаллами всегда положительна; при этом целый ряд металлических атомов имеет постоянную степень окисления; так, например, атомы щелочных металлов (+1), атомы щелочноземельных металлов (+2) и др.; атомы большинства переходных металлов, напротив, могут изменять свою степень окисления; исключение составляют так называемые интерметаллиды — соединения, образованные при взаимодействии двух или более металлов, степень окисления компонентов в которых, как правило, не оценивается;
7) степень окисления атомов элементов в простом соединении равна нулю;
8) степень окисления кислорода в органических молекулах и ионах равна -2 (встречающиеся исключения в органической химии необходимо рассматривать в каждом конкретном случае).
Итак, пользуясь введенными правилами, в результате несложных арифметических подсчетов можно оценить степень окисления атомов, образующих молекулы или сложные ионы.
В заключение введем еще одно важное практическое правило, связанное с понятием степени окисления. При записи последней поступают следующим образом: сначала записывают над символом атома знак степени окисления (положительный или отрицательный), а затем ее численное значение (в отличие от ионов, когда сначала записывают численное значение заряда, а затем его знак!).
Рассмотрим основные типы окислительно-восстановительных реакций.
1. Межмолекулярные (межатомные) окислительно-восстановительные реакции характеризуются тем, что атомы, изменяющие свои степени окисления, находятся в разных по своей химической природе атомных или молекулярных частицах. Другими словами, одни вещества (простые или сложные), вступающие в химические реакции, являются окислителями, а другие — восстановителями. Указанные реакции составляют наиболее обширную группу окислительно-восстановительных реакций. Примерами реакций межмолекулярного типа могут служить реакции с участием простых и сложных веществ, а также различных атомных и молекулярных частиц (радикалов, ионов и ион-радикалов):

2. Внутримолекулярные окислительно-восстановительные реакции характеризуются тем, что атомы, изменяющие свои степени окисления, находятся в одной и той же молекулярной частице:

В приведенной реакции атомы хрома, изменяющие степень окисления от +6 до +3, принимают электроны, а атомы азота, степень окисления которых меняется от -3 до 0, их отдают.
Среди внутримолекулярных окислительно-восстановительных реакций выделяют реакции диспропорционирования (самоокисление-самовосстановление). Они сопровождаются одновременным увеличением и уменьшением степени окисления атомов одного и того же элемента, первоначально находившихся в одном, определенном состоянии. Например, при термическом разложении бертолетовой соли часть атомов хлора восстанавливается, изменяя степень окисления от +5 до -1, а другая окисляется от +5 до +7:

Среди внутримолекулярных окислительно-восстановительных реакций также выделяют реакции конпропорционирования — процессы, в результате которых происходит выравнивание степени окисления атомов одного и того же элемента, находящегося в исходном веществе в различных состояниях. Например:

В приведенной реакции происходит выравнивание степени окисления атомов азота: в исходном веществе существует два атома со степенями окисления -3 и +3, а в результате реакции образуется молекула, в которой атомы азота имеют нулевую степень окисления.
Итак, окислительно-восстановительные реакции делятся на межмолекулярные (межатомные) и внутримолекулярные. Среди последних особо необходимо выделить реакции диспропорционирования (самоокисление-самовосстановление) и реакции конпропорционирования.
Составление уравнений окислительно-восстановительных реакций
Для составления уравнений окислительно-восстановительных реакций используют два метода: метод электронного баланса и метод полуреакций (электронно-ионный метод). Составление уравнений окислительно-восстановительных реакций методом электронного баланса осуществляется в несколько стадий:
- записывают уравнение реакции со всеми участвующими в ней веществами без коэффициентов;
- выделяют элементы, изменяющие степени окисления в результате реакции и определяют число электронов, приобретенных окислителем и отдаваемых восстановителем;
- уравнивают число электронов, приобретаемых и отдаваемых элементами, устанавливая тем самым коэффициенты для соединений, в которых присутствуют элементы, изменяющие степени окисления;
- подбирают коэффициенты для всех остальных участников реакции.
Рассмотрим в качестве примера реакцию, которая протекает при взаимодействии между бромом и сероводородом:

После записи уравнения реакции и выделения элементов, изменяющих степени окисления, определяют число электронов, приобретаемых бромом и отдаваемых серой:

В данном случае число отдаваемых электронов равно 8, а приобретаемых бромом — 2, следовательно, для брома следует ввести коэффициент, равный 4:

и записать суммарное, сбалансированное по числу отдаваемых и присоединенных электронов уравнение:

После перенесения полученных коэффициентов в исходное уравнение и подбора коэффициентов для остальных участников реакции (в данном случае воды), получаем:

Метод электронного баланса достаточно прост, и составление уравнений окислительно-восстановительных реакций не вызывает затруднений, когда в качестве исходных веществ и продуктов реакции выступают вещества, не диссоциирующие на ионы. Однако составление уравнений окислительно-восстановительных реакций значительно осложняется, если в реакции принимают участие соединения с ионной связью. В этом случае элементы, присутствующие в ионах, как правило, лишь частично участвуют в окислительно-восстановительных процессах, в то время как другая часть этих ионов участвует в реакциях обмена. Поэтому метод электронного баланса, рассматривающий лишь переход электронов от восстановителя к окислителю, не позволяет непосредственно определить коэффициенты в окислительно-восстановительном уравнении без дополнительного использования приема проб и ошибок. Это достигается путем использования электронно-ионного метода или метода полуреакций.
Чтобы составить такое уравнение окислительно-восстановительной реакции, необходимо:
1) записать ионную схему реакции, определив окислитель, восстановитель и продукты их взаимодействия. При этом сильные электролиты следует записывать в виде ионов, а слабые электролиты, осадки и газы — в виде молекул (продукты реакции определяют опытным путем или на основании справочных данных);
2) составить электронно-ионные уравнения отдельно для процесса восстановления и процесса окисления, руководствуясь следующими правилами:
а) если продукт реакции содержит меньше кислорода, чем исходное вещество, то в кислой среде избыточной кислород связывается с ионами водорода с образованием молекул воды. В нейтральной и щелочной средах избыточный кислород взаимодействует с водой, образуя удвоенное число гидроксогрупп;
б) при составлении уравнений следует соблюдать баланс вещества и баланс зарядов.
Для примера рассмотрим реакцию, которая протекает при взаимодействии перманганата калия с нитритом в кислой среде.
1. При сливании растворов исходных веществ окраска быстро изменяется от малиновой до почти бесцветной в результате восстановления иона  :
:
а)  . Избыточный в левой части уравнения атом кислорода следует связать ионами водорода, так как реакция происходит в кислой среде:
. Избыточный в левой части уравнения атом кислорода следует связать ионами водорода, так как реакция происходит в кислой среде:
б)  . Учитывая необходимость сохранения баланса зарядов, предыдущая схема должна быть дополнена:
. Учитывая необходимость сохранения баланса зарядов, предыдущая схема должна быть дополнена:
в) 
2. Ионы  в процессе реакции окисляются, превращаясь в ионы
в процессе реакции окисляются, превращаясь в ионы  :
:
а)  . Избыточный в правой части уравнения кислород следует связать с ионами водорода. При этом для сохранения баланса вещества в левой части реакции следует записать одну молекулу воды:
. Избыточный в правой части уравнения кислород следует связать с ионами водорода. При этом для сохранения баланса вещества в левой части реакции следует записать одну молекулу воды:
б)  . При соблюдении равенства зарядов правой и левой частей уравнения схема принимает следующий вид:
. При соблюдении равенства зарядов правой и левой частей уравнения схема принимает следующий вид:
в)  .
.
3. Для составления полного ионного уравнения этой окислительно-восстановительной реакции следует суммировать полученные уравнения полуреакций окисления и восстановления. Так как общее число электронов, принятых окислителем, должно быть равно общему числу электронов, отданных восстановителем, умножаем уравнения полуреакции восстановления на два, полуреакции окисления на пять, а затем складываем их:

4. Производим возможные упрощения (приведение подобных членов):

5.Для составления уравнения в молекулярном виде следует приписать в правую и левую части уравнения недостающие ионы в одинаковом числе:

Следуя тем же принципам, легко составить уравнение окислительно-восстановительной реакции для указанных выше реагентов, взаимодействующих в щелочной среде (КОН).
1. Для процесса восстановления перманганата калия имеем:

2. Для процесса окисления нитрата калия имеем:

3. Суммируя уравнения полуреакций окисления и восстановления получаем полное ионное уравнение:

4. Приведение подобных членов:

5. Составление уравнения окислительно-восстановительной реакции в молекулярном виде:

Представленная выше схема применима практически ко всем окислительно-восстановительным реакциям. Она более универсальна по сравнению с методом электронного баланса и имеет несомненные преимущества при составлении уравнений окислительно-восстановительный реакций с участием, в частности, органических соединений, пероксида водорода, некоторых соединений серы и т. д.
Рассмотрим, например, процесс окисления ацетилена, происходящий при пропускании последнего через раствор перманганата калия. Опыт показывает, что при этом в растворе образуется бурый осадок оксида марганца (IV).
1. Перманганат марганца восстанавливается до оксида марганца (IV):

2. Ацетилен под действием водного раствора перманганата калия окисляется с образованием оксалат-иона:

3. Умножая уравнения полуреакций окисления и восстановления на соответствующие множители и складывая их, получаем полное ионное уравнение окислительно-восстановительной реакции:

4. Производим необходимые сокращения:

5. Записываем уравнение в молекулярном виде:

Итак, в этой главе мы познакомились с двумя методами составления уравнений окислительно-восстановительных реакций: методом электронного баланса и методом полуреакций (электронно-ионным методом).
Основные окислители и восстановители
Рассмотрим особенности поведения важнейших окислителей.
Перманганат калия как окислитель
В качестве окислителя часто используется перманганат калия  . Необходимо отметить, что окислительная способность перманганата калия существенно изменяется в зависимости от среды (кислая, нейтральная или щелочная), в которой протекает окислительно-восстановительная реакция. Эту особенность можно отразить в виде следующих полуреакций:
. Необходимо отметить, что окислительная способность перманганата калия существенно изменяется в зависимости от среды (кислая, нейтральная или щелочная), в которой протекает окислительно-восстановительная реакция. Эту особенность можно отразить в виде следующих полуреакций:

Из приведенных полуреакций видно, что продукты восстановления окислителя  изменяются в зависимости от среды:
изменяются в зависимости от среды:

Отметим также, что в нейтральной среде (реально же среда является либо слабокислой, либо слабощелочной) существуют две альтернативные полуреакции (уравнение 9-2). Использование той или иной полуреакции целесообразно связывать с конкретными условиями осуществления окислительно-восстановительных реакций.
Особенности поведения марганецсодержащих соединений (II), (IV), (VI) в окислительно-восстановительных реакциях
Опираясь на схему превращений перманганата калия в окислительно-восстановительных процессах, когда состав продукта восстановления окислителя изменяется в зависимости от среды (см. разд. 9.3.1.), можно записать следующие важные полуреакции:

Хромсодержащие соединения как окислители и восстановители
Для хрома известны две наиболее устойчивые степени окисления: +3 и +6.
Хром в степени окисления +3 проявляет ярко выраженные амфотерные свойства:

Что же касается соединений хрома, имеющих степень окисления +6, то они также имеют две формы: дихромат калия устойчив в кислой среде, а в щелочной среде он превращается в хромат калия:

Следовательно, взаимное превращение дихромат-иона в хромат-ион, и наоборот, можно изобразить схемой:

Отсюда следует, что окислительно-восстановительные реакции с участием дихромата калия протекают только в кислой среде, а продуктом его восстановления являются ионы  . Напротив, когда реакция с участием дихромата калия протекает в щелочной среде, то дихромат сначала переходит в хромат и в дальнейшем одним из продуктов окислительно-восстановительной реакции является гексагидроксихромит-ион
. Напротив, когда реакция с участием дихромата калия протекает в щелочной среде, то дихромат сначала переходит в хромат и в дальнейшем одним из продуктов окислительно-восстановительной реакции является гексагидроксихромит-ион  . Все эти превращения можно представить обобщенной схемой (9-6), а также двумя соответствующими полуреакциями (9-7) с участием дихромат- и хромат-ионов в кислой и щелочной средах соответственно:
. Все эти превращения можно представить обобщенной схемой (9-6), а также двумя соответствующими полуреакциями (9-7) с участием дихромат- и хромат-ионов в кислой и щелочной средах соответственно:

Азотная кислота
Реакции растворения металлов в кислотах относятся к типичным окислительно-восстановительным процессам. В этих реакциях атомы металла (восстановителя) отдают электроны, а ионы водорода, образовавшиеся в результате электролитической диссоциации кислоты (окислителя) их принимают.
Азотная кислота при взаимодействии с металлами проявляет уникальные свойства в том смысле, что в указанных реакциях она по-прежнему играет роль окислителя, однако электроны принимают не ионы водорода, а атомы
азота. Эти уникальные свойства проявляет азотная кислота любой концентрации, как концентрированная, так и разбавленная. Как следствие этого:
1) при взаимодействии азотной кислоты с металлами никогда не выделяется газообразный водород;
2) из-за смены механизма обычно протекающего окислительно-восстановительного процесса в азотной кислоте могут легко растворяться не только металлы, стоящие в ряду напряжений левее водорода, но и металлы, расположенные правее его.
Аналогично ведет себя азотная кислота-окислитель и по отношению к неметаллам-восстановителям: электроны принимают не ионы водорода, а атомы азота.
В результате окислительно-восстановительных реакций с участием азотной кислоты всегда появляются продукты ее восстановления —  ,
,  (с избытком азотной кислоты обычно получают
(с избытком азотной кислоты обычно получают  ). Состав продуктов восстановления зависит от концентрации азотной кислоты, температуры и реакционной способности восстановителей.
). Состав продуктов восстановления зависит от концентрации азотной кислоты, температуры и реакционной способности восстановителей.
При использовании неметаллов-восстановителей реакция с азотной кислотой протекает достаточно просто: с концентрированной азотной кислотой, как правило, выделяется  , с разбавленной —
, с разбавленной —  (реакционная способность неметаллов-восстановителей обычно нс учитывается).
(реакционная способность неметаллов-восстановителей обычно нс учитывается).
При использовании металлов-восстановителей реакция с азотной кислотой протекает значительно сложнее.
Во-первых, в этом случае необходимо рассматривать три уровня концентрации азотной кислоты: концентрированная  (конц.), разбавленная
(конц.), разбавленная  (разб.) и очень разбавленная
(разб.) и очень разбавленная  (оч. разб.); во-вторых, необходимо учитывать различия в реакционной способности металлов-восстановителей. Для этого металлы в ряду напряжений обычно условно делят по их реакционной способности на 4 группы (так, чтобы в пределах одной группы были собраны металлы примерно равной или достаточно близкой реакционной способности):
(оч. разб.); во-вторых, необходимо учитывать различия в реакционной способности металлов-восстановителей. Для этого металлы в ряду напряжений обычно условно делят по их реакционной способности на 4 группы (так, чтобы в пределах одной группы были собраны металлы примерно равной или достаточно близкой реакционной способности):
1) высокоактивные (щелочные и щелочноземельные) металлы от  до
до  включительно;
включительно;
2) активные металлы (от  );
);
3) малоактивные металлы (от  );
);
4) тяжелые, инертные металлы (от  ).
).
Все возможные типы окислительно-восстановительных реакций, определяемые различной концентрацией азотной кислоты с одной стороны, и реакционной способностью металлов-восстановителей с другой, можно представить в виде таблицы (см. табл. 9.1). Для этого в каждой клетке таблицы следует поместить продукт восстановления азотной кислоты, образующийся в результате протекания реакции при определенном сочетании свойств окислителя ( ) и восстановителя (Me).
) и восстановителя (Me).
Таблица 9.1

См. ниже приведенные уравнения реакций: * — 9-8. ** — 9-9, *** — 9-10.
В табл. 9.1 приведены продукты восстановления  для трех частных случаев, которые обычно приводят в учебниках и рекомендуют запомнить в качестве иллюстрации специфичности свойств азотной кислоты-окислителя:
для трех частных случаев, которые обычно приводят в учебниках и рекомендуют запомнить в качестве иллюстрации специфичности свойств азотной кислоты-окислителя:

Из табл. 9.1 видно, что три рассмотренные реакции далеко нс исчерпывают все возможные случаи, которые можно встретить на практике. Поэтому попытаемся построить общую модель, которая, опираясь на приведенные выше известные реакции (9-8)-(9-10), позволит предсказать продукты восстановления окислителя —  для всех других возможных реакций.
для всех других возможных реакций.
Влияние концентрации азотной кислоты. При фиксированной реакционной способности металла-восстановителя уменьшение концентрации окислителя в растворе должно привести к тому, что каждая молекула окислителя может быть одновременно «атакована» большим числом электронов. Это приводит к снижению степени окисления азота в продуктах восстановления. Действительно, для двух известных полуреакций (9-8)-(9-9) сделанное предположение хорошо выполняется. При переходе  происходит снижение степени окисления азота от +4 до +2
происходит снижение степени окисления азота от +4 до +2  . Поэтому, рассматривая более полный ряд:
. Поэтому, рассматривая более полный ряд:

в реакциях с тяжелыми, инертными металлами на основе сделанного предположения можно ожидать следующих изменений характера продуктов восстановления:

Это позволяет заполнить нижнюю графу в крайнем правом столбце табл. 9.1.
Влияние реакционной способности металлов-восстановителей. При фиксированной концентрации HNOj увеличение реакционной способности металлов-восстановителей также должно приводить к тому, что молекулы окислителя могут быть одновременно «атакованы» большим числом электронов. Это приводит к снижению степени окисления азота в продуктах восстановления  . Например, для очень разбавленной
. Например, для очень разбавленной  , имея два «опорных» случая, характеризующихся выделением
, имея два «опорных» случая, характеризующихся выделением  при взаимодействии окислителя с тяжелыми металлами, и
при взаимодействии окислителя с тяжелыми металлами, и  (или
(или  ) при взаимодействии с активными металлами, получаем промежуточный случай: для малоактивных металлов продуктом восстановления
) при взаимодействии с активными металлами, получаем промежуточный случай: для малоактивных металлов продуктом восстановления  должен являться
должен являться  (см. табл. 9.1):
(см. табл. 9.1):
Таблица 9.2

Используя две найденные закономерности, регулирующие влияние концентрации  и реакционной способности металлов-восстановителей на характер продуктов восстановления
и реакционной способности металлов-восстановителей на характер продуктов восстановления  , окончательно заполним таблицу (см. табл. 9.2), с помощью которой в дальнейшем можно написать практически любую реакцию взаимодействия азотной кислоты с металлами.
, окончательно заполним таблицу (см. табл. 9.2), с помощью которой в дальнейшем можно написать практически любую реакцию взаимодействия азотной кислоты с металлами.
В заключение отметим, что прочерки в первом столбце таблицы отражают следующее обстоятельство: щелочные металлы обладают столь высокой активностью, что они, в первую очередь, взаимодействуют с водой, содержащейся в растворах  , выделяя при этом водород. Отметим, что концентрированной азотной кислотой считается раствор, содержащий более 65 %
, выделяя при этом водород. Отметим, что концентрированной азотной кислотой считается раствор, содержащий более 65 %  и остальное — воду.
и остальное — воду.
Серная кислота
Серная кислота обладает окислительными свойствами (сходными со свойствами азотной кислоты) если ее концентрация превосходит 70 %. Только тогда принято говорить о специфических свойствах  как окислителя. При содержании
как окислителя. При содержании  в растворе менее 70 % (разбавленная серная кислота) ее поведение описывается в рамках обычных представлений: при взаимодействии такой кислоты с металлами, стоящими в электрохимическом раду напряжений левее водорода, выделяется
в растворе менее 70 % (разбавленная серная кислота) ее поведение описывается в рамках обычных представлений: при взаимодействии такой кислоты с металлами, стоящими в электрохимическом раду напряжений левее водорода, выделяется  .
.
Для описания свойств концентрированной  целесообразно воспользоваться схемой, которая была рассмотрена при анализе свойств азотной кислоты:
целесообразно воспользоваться схемой, которая была рассмотрена при анализе свойств азотной кислоты:
Таблица 9.3

Пероксид водорода
В отличие от рассмотренных выше веществ, пероксид водорода  может выполнять двойственную функцию, в зависимости от природы реагента, с которым он вступает в химическую реакцию. При взаимодействии с восстановителями пероксид водорода выполняет роль окислителя, а в реакциях с окислителями он берет на себя функции восстановителя.
может выполнять двойственную функцию, в зависимости от природы реагента, с которым он вступает в химическую реакцию. При взаимодействии с восстановителями пероксид водорода выполняет роль окислителя, а в реакциях с окислителями он берет на себя функции восстановителя.
Обычно используют одну из следующих четырех полуреакций:
 — окислитель
— окислитель
— кислая среда: 
— щелочная среда: 
 — восстановитель
— восстановитель
— кислая среда: 
— щелочная среда: 
Органические вещества как восстановители
Рассмотрим основные полуреакции, в которых участвуют восстановители — органические вещества.
1) Полное окисление углеводородов:

2) Полное окисление кислородсодержащих органических веществ:

3) Окисление непредельных углеводородов, приводящее к разрыву кратной связи (в кислой или щелочной средах):

или

или

или

4) Окисление непредельных углеводородов с одной двойной связью в щелочной среде:

5) Окисление боковых цепей в ароматических углеводородах:

или

Этот список основных полуреакций, в которых участвуют восстановители — органические вещества, вы можете продолжить самостоятельно.
Электрохимия
Электрохимические процессы
Химические процессы, сопровождающиеся возникновением электрического тока или вызываемые им, называются электрохимическими.
Чтобы понять природу электрохимических процессов, обратимся к более простому случаю. Представим себе металлическую пластинку, погруженную в воду. Под действием полярных молекул воды ионы металла отрываются от поверхности пластинки и гидратированными переходят в жидкую фазу. Последняя при этом заряжается положительно, а на металлической пластинке появляется избыток электронов.
Благодаря электростатическому притяжению катионов раствора и избыточных электронов металла на границе раздела фаз возникает двойной электрический слой.
Естественно, что он тормозит дальнейший переход ионов металла в жидкую фазу. Наконец, наступает момент, когда между раствором и металлической пластинкой устанавливается равновесие, которое можно выразить уравнением:

или с учетом гидратации ионов в растворе:

Состояние этого равновесия зависит от природы металла, концентрации его ионов в растворе, от температуры и давления.
При погружении металла не в воду, а в раствор соли этого металла равновесие в соответствии с принципом Ле Шателье смещается влево, и тем больше, чем выше концентрация ионов металла в растворе. Активные металлы, ионы которых обладают хорошей способностью переходить в раствор, будут и в этом случае заряжаться отрицательно, хотя в меньшей степени, чем в чистой воде.
Равновесие (10-2) можно сместить вправо, если тем или иным способом удалять электроны из металла. Это приведет к растворению металлической пластинки. Наоборот, если к металлической пластинке подводить электроны извне, то на ней будет происходить осаждение ионов из раствора.
Как уже отмечалось, при погружении металла в воду (раствор) на границе раздела фаз образуется двойной электрический слой. Разность потенциалов, возникающая между металлом и окружающей его жидкой средой, называется электродным потенциалом. Этот потенциал является характеристикой окислительно-восстановительной способности металла в виде твердой фазы.
Абсолютное значение электродного потенциала нельзя измерить непосредственно. Вместе с тем не представляет труда измерение разности электродных потенциалов, которая возникает в системе, состоящей из двух пар «металл—раствор». Такие пары называются полуэлементами. Условились определять электродные потенциалы металлов по отношению к так называемому стандартному водородному электроду, потенциал которого произвольно принят за нуль. Стандартный водородный электрод состоит из специально приготовленной платиновой пластинки, погруженной в раствор серной кислоты с концентрацией ионов водорода, равной 1 моль/л, и омываемой струей газообразного водорода под давлением  Па, при температуре 25° С.
Па, при температуре 25° С.
Возникновение потенциала на стандартном водородном электроде можно представить следующим образом. Газообразный водород, адсорбируясь платиной, переходит в атомное состояние:

Между атомным водородом в платине и ионами водорода в растворе возникает динамическое равновесие:

Суммарный процесс выражается уравнением

Платина не принимает участия в окислительно-восстановительном процессе, а является лишь носителем атомного водорода.
Если пластинку металла, погруженную в раствор его соли с концентрацией ионов металла, равной 1 моль/л, соединить со стандартным водородным электродом, то получится гальванический элемент. Электродвижущая сила этого элемента (ЭДС), измеренная при 25° С, и характеризует стандартный электродный потенциал металла.
В табл. 10.1 представлены значения стандартных электродных потенциалов некоторых металлов. Символом Ме+/Ме обозначен металл Me, погруженный в раствор его соли. Стандартные потенциалы электродов, выступающих как восстановители по отношению к водороду, имеют знак «-», а знаком «+» отмечены стандартные потенциалы электродов, являющихся окислителями.
Таблица 10.1
Стандартные электродные потенциалы металлов

Металлы, расположенные в порядке возрастания их стандартных электродных потенциалов, образуют так называемый электрохимический ряд напряжений металлов:

Ряд напряжений характеризует химические свойства металлов:
- Восстановительная способность металла тем выше, чем более отрицательной величиной характеризуется его электродный потенциал.
- Каждый металл способен вытеснять (восстанавливать) из растворов солей те металлы, которые стоят в электрохимическом ряду напряжений металлов после него.
- Все металлы, имеющие отрицательный стандартный электродный потенциал, т. е. находящиеся в электрохимическом ряду напряжений металлов левее водорода, способны вытеснять его из растворов кислот.
Необходимо отметить, что представленный ряд характеризует поведение металлов и их солей только в водных растворах и при комнатной температуре. Кроме того, нужно иметь в виду, что указанные в табл. 10.1
Стандартные электродные потенциалы учитывают особенности взаимодействия того или иного иона с молекулами растворителя. Эго может нарушать некоторые ожидаемые закономерности в расположении металлов в электрохимическом ряду напряжений металлов. Например, электрохимический ряд напряжений металлов начинается литием, тогда как более активные в химическом отношении рубидий и калий находятся правее лития. Это связано с исключительно высокой энергией процесса гидратации ионов лития по сравнению с ионами других щелочных металлов.
Приведем решение типичной задачи, рассматривающей электрохимический процесс.
Пример №10-1.
Цинковая пластинка массой 8,0 г помещена в раствор сульфата меди (II). После окончания реакции промытая и высушенная пластинка имеет массу 7,94 г. Объясните наблюдаемые изменения массы пластинки. Определите массу сульфата меди (II), которая находилась в растворе до начала реакции. Для решения задачи рекомендуется использовать следующие величины:  = 63,54 г/моль,
= 63,54 г/моль,  = 65,38 г/моль.
= 65,38 г/моль.
Решение:
Поскольку цинк расположен в ряду напряжений левее меди, то в системе протекает реакция

Если бы в реакции участвовало по 1 моль обоих веществ  , то масса пластины уменьшилась бы на 65,38 г — 63,54 г = 1,84 г. Однако по условию задачи ее масса понизилась лишь на 0,06 г. Следовательно, в реакции участвовало по v = 0,0326 моль (0,06/1,84) обоих веществ. Тогда масса сульфата меди (II), которая находилась в растворе до начала реакции, равна m = 159,54 и 0,0326 = 5,20 г.
, то масса пластины уменьшилась бы на 65,38 г — 63,54 г = 1,84 г. Однако по условию задачи ее масса понизилась лишь на 0,06 г. Следовательно, в реакции участвовало по v = 0,0326 моль (0,06/1,84) обоих веществ. Тогда масса сульфата меди (II), которая находилась в растворе до начала реакции, равна m = 159,54 и 0,0326 = 5,20 г.
Ответ: 5,20 г.
Электролиз
Совокупность химических реакций, которые протекают на электродах в растворах или расплавах при пропускании через них электрического тока, называется электролизом.
Зависимость количества вещества, образовавшегося под действием электрического тока, от времени, силы тока и природы электролита может быть установлена на основании обобщенного закона Фарадея:

где m — масса образовавшегося при электролизе i-вещества (г); Э — эквивалентная масса i-вещества (г/моль); М — молярная масса i-вещества (г/моль); п — заряд i-иона; I — сила тока (A); t — продолжительность процесса; F — константа Фарадея, характеризующая количество электричества, необходимое для выделения 1 эквивалентной массы вещества (F = 96 500 К /моль = 26,8 А-ч).
При электролизе, как и при работе химического источника тока, на аноде происходят процессы окисления, а на катоде — восстановления. При этом анод заряжен положительно (+), а катод — отрицательно (-). Отметим, что при работе химического источника тока, напротив, анод заряжается отрицательно, а катод — положительно, поскольку в этом случае протекают процессы, обратные электролизу.
При электролизе как на аноде, так и на катоде могут происходить конкурирующие процессы.
При проведении электролиза с использованием инертного (нерасхо-дуемого) анода (например, графита), как правило, конкурирующими являются два окислительных и два восстановительных процесса:
• на аноде — окисление анионов и гидроксид-иоиов;
• на катоде — восстановление катионов и ионов водорода.
При проведении электролиза с использованием активного (расходуемого) анода процесс усложняется и конкурирующими реакциями на электродах являются следующие:
• на аноде — окисление анионов и гидроксид-ионов, а также анодное растворение металла — материала анода;
• на катоде — восстановление катиона соли и ионов водорода, а также восстановление катионов металла, образующихся при растворении анода.
При выборе наиболее вероятного процесса на аноде и катоде следует исходить из положения, что будет протекать та реакция, для которой требуется наименьшая затрата энергии. Кроме того, для выбора наиболее вероятного процесса на аноде и катоде при электролизе растворов солей с нерас-ходуемым (пассивным) электродом используют следующие правила.
1. На аноде могут образовываться следующие продукты:
а) при окислении анионов  выделяется кислород;
выделяется кислород;
б) при окислении анионов  выделяются соответственно хлор, бром,йод;
выделяются соответственно хлор, бром,йод;
в) при окислении анионов органических кислот происходит процесс

2. Если конкурирующими процессами на катоде является восстановление катионов Меп+ и ионов водорода, то для определения качественного состава продуктов электролиза в водных растворах обычно используют следующий ряд разряжаемости на катоде:

Учитывая сформулированные правила, проанализируем возможные варианты протекания электролиза растворов, содержащих конкретные вещества-электролиты: щелочи, кислоты или соли.
Своеобразную группу электролитов составляют щелочи и кислородсодержащие кислоты. Анализ процессов, происходящих в растворах этих электролитов под действием электрического тока, показывает, что электролизу в них подвергается только вода, Сами же электролиты количественно сохраняются на любом этапе процесса, постоянно играя роль веществ, обеспечивающих перенос тока через рабочее вещество — воду, которая в чистом состоянии плохо проводит электрический ток. Поэтому на любом этапе процесса электролиза на электродах выделяются: водород (катод) и кислород (анод). При этом концентрация электролита в растворе постоянно растет. Отметим, что при рассмотрении этой группы электролитов выделение отдельных этапов процесса электролиза является, в значительной степени, условным. Важно также подчеркнуть, что подобным же образом ведет себя и еще одна группа электролитов. Это — соли, состоящие из катиона активного металла и аниона кислородсодержащей кислоты (см. табл. 10.2).
По иному ведут себя при электролизе растворы бескислородных кислот  . Эти электролиты сами подвергаются электролизу и выделяют на электродах водород (катод) и галоген (анод). В зависимости от химической природы галогена характер процесса электролиза может заметно меняться. Так, если в процессе участвует соляная кислота, то электролиз в этой системе после выделения на электродах водорода и хлора, количества которых равны их содержанию в исходном
. Эти электролиты сами подвергаются электролизу и выделяют на электродах водород (катод) и галоген (анод). В зависимости от химической природы галогена характер процесса электролиза может заметно меняться. Так, если в процессе участвует соляная кислота, то электролиз в этой системе после выделения на электродах водорода и хлора, количества которых равны их содержанию в исходном  , прекращается (см. табл. 10.2). Поведение растворов
, прекращается (см. табл. 10.2). Поведение растворов  несколько сложнее, поскольку накопление брома (йода) в анодном пространстве приводит к диспропорционированию галогена, которое не только регенерирует галой-одоводородную кислоту, но и обеспечивает появление и последующее накопление в растворе кислородсодержащей кислоты
несколько сложнее, поскольку накопление брома (йода) в анодном пространстве приводит к диспропорционированию галогена, которое не только регенерирует галой-одоводородную кислоту, но и обеспечивает появление и последующее накопление в растворе кислородсодержащей кислоты  ):
):

Это, в свою очередь, создает предпосылки для смены механизма процесса: с момента полного исчезновения из раствора  на электродах начинают выделяться водород (катод) и кислород (анод), т. е. на последней стадии электролиза происходит электролиз воды. Таким образом, электролиз раствора
на электродах начинают выделяться водород (катод) и кислород (анод), т. е. на последней стадии электролиза происходит электролиз воды. Таким образом, электролиз раствора  на последних этапах не прекращается (так как это имеет место в случае
на последних этапах не прекращается (так как это имеет место в случае  ). Важно также подчеркнуть, что подобным же образом себя ведет еще одна группа электролитов. Это — соли, состоящие из катиона малоактивного металла и аниона бескислородной кислоты (см. табл. 10.2). Действительно, при электролизе раствора
). Важно также подчеркнуть, что подобным же образом себя ведет еще одна группа электролитов. Это — соли, состоящие из катиона малоактивного металла и аниона бескислородной кислоты (см. табл. 10.2). Действительно, при электролизе раствора  образующиеся продукты (
образующиеся продукты ( — на катоде и
— на катоде и  на аноде) в точности отвечают составу исходного электролита (как и в случае с
на аноде) в точности отвечают составу исходного электролита (как и в случае с  ) и в этом случае процесс прекращается в результате его полного электролиза. Напротив, при электролизе раствора
) и в этом случае процесс прекращается в результате его полного электролиза. Напротив, при электролизе раствора  на начальных этапах процесса накапливается
на начальных этапах процесса накапливается  , диспропорционирование которого ведет к последующему формированию в растворе бромноватой кислоты. Это также обеспечивает смену механизма электролиза и на последних этапах процесс не прекращается.
, диспропорционирование которого ведет к последующему формированию в растворе бромноватой кислоты. Это также обеспечивает смену механизма электролиза и на последних этапах процесс не прекращается.
Электролиз растворов солей, образованных малоактивным металлом и кислородсодержащей кислотой, протекает более предсказуемо. В этом случае на электродах выделяются металл (катод) и кислород (анод), а в растворе постепенно накапливается соответствующая кислота. После завершения электролиза исходного электролита в растворе остается только кислородсодержащая кислота. В этот момент механизм электролиза изменяется, и на электродах начинают выделяться водород (катод) и кислород (анод), т. е. в системе, как и следовало ожидать, идет электролиз воды.
При решении задач, рассматривающих электролиз электролитов этого типа, целесообразно ввести и использовать критерий полноты электролиза — любую количественную характеристику  (массу или объем продукта, выделившегося на аноде или катоде, суммарную массу выделившихся продуктов и т. д.), которая эквивалентна количеству исходного электролита. Оценка этой величины на старте решения задачи позволит количественно определить точку, отвечающую смене механизма электролиза, и установить: какая стадия процесса рассматривается в задании (см. пример 10-3).
(массу или объем продукта, выделившегося на аноде или катоде, суммарную массу выделившихся продуктов и т. д.), которая эквивалентна количеству исходного электролита. Оценка этой величины на старте решения задачи позволит количественно определить точку, отвечающую смене механизма электролиза, и установить: какая стадия процесса рассматривается в задании (см. пример 10-3).
Электролиз растворов солей, образованных при взаимодействии активного металла и бескислородной кислоты, также протекает предсказуемо. В этом случае на электродах выделяются водород (катод) и галоген (анод), а в растворе постепенно накапливается соответствующая щелочь. После завершения электролиза исходного электролита в системе идет только электролиз воды. При решении задач, рассматривающих электролиз электролитов этого типа, также целесообразно ввести и использовать критерий полноты электролиза. Особенно это полезно в тех случаях, когда галоген — бром или йод (см. пример 10-3). Результаты проведенного анализа приведены в таблице 10.2.
Таблица 10.2
Возможные продукты электролиза, образующиеся на катоде и аноде, в зависимости от типа электролита и полноты протекания процесса

1) при электролизе бромсодержащих электролитов указанных типов процесс не прекращается (см. пояснения к таблице).
В тех случаях, когда в процессе электролиза используется расходуемый (активный) анод, то последний будет окисляться в ходе электролиза, переходить в раствор в виде катионов и «переосаждаться» на катоде. Следовательно, энергия электрического тока при этом расходуется на перенос металла с анода на катод. Данный процесс широко используется при рафинировании (очистке) металлов. Так, на этом принципе основано, в частности, получение чистой меди из загрязненной. В раствор медного купороса погружают пластины из очищенной и неочищенной меди. Пластины соединяют с источником постоянного тока таким образом, чтобы первая из
них (очищенная медь) была отрицательным электродом (катод), а вторая — положительным (анод). В результате неочищенная медь с содержащимися в ней примесями растворяется, а на катоде из раствора осаждаются только ионы меди. При этом примесь остается в растворе или оседает на дно ванны. Этот же принцип используется для защиты металлов от коррозии путем нанесения на защищаемое изделие тонких слоев хрома или никеля.
Для получения высокоактивных металлов (натрия, кальция, магния, алюминия и др.), легко вступающих во взаимодействие с водой, применяют электролиз расплава солей или оксидов. Например:

Рассмотрим несколько типов задач на электролиз. Сначала рассмотрим задачи, алгоритм решения которых основан на использовании закона Фарадея.
Пример №10-2.
После проведения электролиза водного раствора гидроксида калия током 20 А в течение 67 ч было получено 200 г 10 %-го раствора. Найдите массы образовавшихся продуктов и концентрацию исходного раствора.
Решение:
Поскольку при действии электрического тока на раствор гидроксида калия происходит электролиз воды, то массы образующихся продуктов — водорода (катод) и кислорода (анод) можно оценить по формуле (10-3):

Следовательно, масса исходного раствора составляла m(р-р) = 200 + 50 + 400 = 650 г, а масса гидроксида калия, остающаяся в течении всего процесса неизменной, — 20 г. Тогда массовая доля исходного раствора:

Ответ: 3,08 %.
Электролиз растворов солей, образованных малоактивным металлом и кислородсодержащей кислотой
Рассмотрим в качестве примера следующую задачу.
Пример №10-3.
При электролизе 200 г 16 % раствора сульфата меди (II) последовательно наблюдали уменьшение массы раствора а) на 8 г, б) на 16 г и в) на 25 г. Вычислите массовые доли соединений в растворе и массы веществ, выделившихся на инертных электродах в каждом из трех рассмотренных случаев.
Решение:
Поскольку при действии электрического тока на раствор сульфате меди (II) на электродах происходит выделение меди (катод) и газообразного кислорода (анод), то в качестве критерия полноты электролиза в данном случае целесообразно выбрать такое уменьшение массы раствора  которое соответствует количеству соли в исходном растворе. Приведем оценку этого критерия.
которое соответствует количеству соли в исходном растворе. Приведем оценку этого критерия.
Масса сульфата меди в растворе 
Это отвечает количеству вещества  Следовательно, критерий полноты электролиза
Следовательно, критерий полноты электролиза

Итак, если уменьшение массы раствора  при электролизе отвечает величине меньшей, чем
при электролизе отвечает величине меньшей, чем  = 16 г, то процесс протекает по указанному выше механизму. Если же уменьшение массы превышает величину критерия полноты электролиза, то механизм процесса претерпевает изменение: в результате полного электролиза соли
= 16 г, то процесс протекает по указанному выше механизму. Если же уменьшение массы превышает величину критерия полноты электролиза, то механизм процесса претерпевает изменение: в результате полного электролиза соли  образуется раствор
образуется раствор  . При дальнейшем же воздействии электрического тока на раствор
. При дальнейшем же воздействии электрического тока на раствор  протекает лишь электролиз воды.
протекает лишь электролиз воды.
Таким образом, случаи (а)-(в), рассмотренные в задаче, относятся к трем различным случаям протекания процесса электролиза:
а) Понижение массы раствора (8 г) меньше величины  — электролиз соли прошел лишь частично: на электродах происходит выделение меди (катод) и газообразного кислорода (анод), а в растворе помимо оставшейся соли образовалась серная кислота.
— электролиз соли прошел лишь частично: на электродах происходит выделение меди (катод) и газообразного кислорода (анод), а в растворе помимо оставшейся соли образовалась серная кислота.
Количества веществ, образовавшихся на электродах:  0,05 моль, а массы
0,05 моль, а массы 
Количества веществ в растворе:  , а массы
, а массы  . Масса раствора: m(р-ра) = 200 — 8 = 192 г. Массовые доли веществ в растворе:
. Масса раствора: m(р-ра) = 200 — 8 = 192 г. Массовые доли веществ в растворе: 
б) Понижение массы раствора (16 г) равно величине А — электролиз соли прошел полностью: на электродах происходит выделение меди (катод) и газообразного кислорода (анод), а в растворе остается лишь образующаяся при электролизе серная кислота.
— электролиз соли прошел полностью: на электродах происходит выделение меди (катод) и газообразного кислорода (анод), а в растворе остается лишь образующаяся при электролизе серная кислота.
Количества веществ, образовавшихся на электродах:  0,1 моль, а массы
0,1 моль, а массы  .
.
Количество серной кислоты в растворе:  , а ее масса
, а ее масса  . Масса раствора: m(р-ра) = 200 — 16 = 184 г. Массовая доля серной кислоты в растворе:
. Масса раствора: m(р-ра) = 200 — 16 = 184 г. Массовая доля серной кислоты в растворе: 
в) Понижение массы раствора (25 г) больше величины А — электролиз соли прошел полностью, после чего происходит электролиз воды  0,5 моль): на электродах выделяются медь и водород (катод) и газообразный кислород (анод), а концентрация единственного оставшегося в растворе вещества — серной кислоты — нарастает (хотя ее количество и сохраняется неизменным).
0,5 моль): на электродах выделяются медь и водород (катод) и газообразный кислород (анод), а концентрация единственного оставшегося в растворе вещества — серной кислоты — нарастает (хотя ее количество и сохраняется неизменным).
Количества веществ, образовавшихся на электродах:  моль и
моль и  моль (катод);
моль (катод);  моль (анод), а массы
моль (анод), а массы  = 12,8 г и
= 12,8 г и  г.
г.
Количество серной кислоты в растворе:  = 0,2 моль, а ее масса
= 0,2 моль, а ее масса  = 19,6 г. Масса раствора: m(р-ра) = 200 — 25 = 175 г. Массовая доля серной кислоты в растворе:
= 19,6 г. Масса раствора: m(р-ра) = 200 — 25 = 175 г. Массовая доля серной кислоты в растворе:  =11,2 %.
=11,2 %.
Химические источники тока
Зная стандартные электродные потенциалы  металлов, легко рассчитать ЭДС любого гальванического элемента. Для этого из потенциала электрода, имеющего большее алгебраическое значение, следует вычитать потенциал электрода, алгебраическое значение которого меньше. В качестве примера вычислим ЭДС элемента, составленного из железного и медного электродов, погруженных в растворы их солей (с = 1 моль/л, стандартные условия). Из табл. 10.1 следует, что
металлов, легко рассчитать ЭДС любого гальванического элемента. Для этого из потенциала электрода, имеющего большее алгебраическое значение, следует вычитать потенциал электрода, алгебраическое значение которого меньше. В качестве примера вычислим ЭДС элемента, составленного из железного и медного электродов, погруженных в растворы их солей (с = 1 моль/л, стандартные условия). Из табл. 10.1 следует, что

Следовательно,

Чем больше стандартные электродные потенциалы металлических электродов отличаются друг от друга, тем выше значение ЭДС гальванического элемента, построенного из этих металлов.
Первый гальванический элемент был построен А. Вольта. Элемент состоял из медных и цинковых пластинок, между которыми помещались смоченные в уксусной кислоте прокладки из сукна. Возникновение электрического тока в нем сопровождается химическими превращениями па электродах. Так как электродный потенциал цинка более отрицателен, чем потенциал меди, то цинк, отдавая электроны, окисляется:

При этом избыточные электроны поступают по внешней цепи к медному электроду и восстанавливают на нем ионы  из раствора:
из раствора:

Для получения высоких значений ЭДС отдельные гальванические элементы, соединяя последовательно, объединяют в батареи.
Гальванические элементы, в том числе и упомянутые выше, не могут служить источниками электрического тока в течение длительного срока.
Электрическая энергия в элементе возникает за счет энергии химических процессов, а запас последней, естественно, ограничен массой веществ, подвергающихся в данной системе превращению. Однако способность системы выступать в качестве источника электрического тока можно восстановить, если через разряженную батарею пропускать ток от внешнего источника. Такие гальванические батареи обратимого действия называют аккумуляторами.
Рассмотрим принцип работы аккумуляторов на примере наиболее распространенного — свинцового. В простейшем случае такой аккумулятор состоит из двух свинцовых пластин, похожих на соты благодаря наличию многочисленных мелких пор. Эти поры заполнены пастой из оксида свинца РЬО, а сами пластины погружены в 30%-й раствор серной кислоты. В результате взаимодействия оксида с кислотой на поверхности пластин образуется слой труднорастворимого сульфата свинца:

При соединении пластин с внешним источником напряжения на одной из них — катоде — происходит процесс восстановления ионов  до металлического свинца:
до металлического свинца:

а на другой — аноде — процесс окисления ионов  до оксида свинца (IV):
до оксида свинца (IV):

Суммарный химический процесс выражается уравнением:

Этот процесс, называемый зарядкой аккумулятора, приводит к тому, что одинаковые первоначально электроды становятся химически различными и между ними появляется разность потенциалов.
Если пластины заряженного аккумулятора соединить проводником, то от пластины, покрытой свинцом, к пластине с оксидом свинца (IV).будут перемещаться электроны, т. е. появится электрический ток. Иначе говоря, при разрядке аккумулятор работает как гальванический элемент. Происходящие на электродах процессы можно выразить уравнениями:
• на аноде: 
• на катоде: 
• в суммарном виде:  .
.
Часто используют и другие аккумуляторы, например железо-никелевые и кадмий-никелевые. Особенно перспективен разрабатываемый в последнее’ время натрий-серный аккумулятор, применение которого делает возможным создание достаточно экономичного электромобиля.
В последнее время большое внимание уделяется созданию так называемых топливных элементов. В топливных элементах энергия химических реакций, выделяющаяся в процессе окисления топлива, непосредственно преобразуется в электричество. Коэффициент полезного действия таких топливных элементов вдвое превышает коэффициент полезного действия паровых турбин и двигателей внутреннего сгорания и достигает 80 %.
Наиболее разработан в настоящее время водородно-кислородный топливный элемент. Этот элемент представляет собой герметически закрытую камеру с двумя пористыми (металлическими или графитовыми) электродами, погруженными в раствор щелочи (например, КОН). В камеру непосредственно к поверхностям электродов подаются газообразные водород и кислород. При этом на одном электроде — на аноде — происходит электрохимическое окисление водорода с одновременной отдачей электронов во внешнюю цепь:

На катоде протекает реакция восстановления кислорода:

Суммарные химические изменения в системе характеризуются следующим уравнением:

Помимо водорода, в топливных элементах в качестве топлива можно использовать и другие газообразные вещества — оксид углерода (II), этилен, пропан и т. п., а также и жидкие — спирты, гидразин. Разрабатывается проект получения энергии без загрязнения окружающей среды. Согласно этому проекту тепловая энергия, получаемая в атомных реакторах, расположенных на плавучих платформах в море, используется для разложения воды на водород и кислород. Образовавшиеся газы по трубопроводам поступают на подстанции, где в топливных элементах энергия реакции  с высоким коэффициентом полезного действия превращается в электричество.
с высоким коэффициентом полезного действия превращается в электричество.
Термохимия
Для решения термохимических задач необходимо знание ряда алгоритмов, основанных на фундаментальных термохимических представлениях, которые будут рассмотрены ниже.
Тепловые эффекты химических реакций
Одним из признаков химической реакции является выделение или поглощение теплоты, происходящее при химических превращениях одних веществ в другие. Реакции, протекающие с выделением теплоты, носят название экзотермических реакций, а сопровождающиеся поглощением теплоты — эндотермических. К первым относятся, как правило, все реакции соединения, а типичными реакциями второго типа являются реакции разложения.
Количество теплоты, выделяемой или поглощаемой при химической реакции, называется тепловым эффектом реакции. Обычно его выражают в килоджоулях (кДж).
Известно, например, что при полном сгорании метана в кислороде с образованием оксида углерода (IV) и воды на каждый моль метана выделяется 891 кДж:

Строго говоря, теплота, выделяемая или поглощаемая в результате химического превращения, является своеобразным «реагентом» или «продуктом» химической реакции. Поэтому для соблюдения закона сохранения и превращения энергии количество теплоты, сопровождающее химическую реакцию, должно быть включено в се уравнение. Уравнения химических реакций, в которых приводятся значения тепловых эффектов, называются термохимическими.
Знак «+» перед значением теплового эффекта в правой части уравнения означает, что теплота выделяется, т. е. реакция является экзотермической. Для эндотермических реакций тепловой эффект должен быть взят со знаком «-»:

Иногда в литературе можно встретить и такие термохимические уравнения, в которых величина теплового эффекта приводится в его левой части:

Легко заметить, что переход от одного типа термохимического уравнения к другому является простой алгебраической операцией.
В термохимических уравнениях, помимо символов химических элементов и теплового эффекта, необходимо указывать агрегатное состояние реагентов и продуктов. Действительно, из сопоставления двух термохимических уравнений:

следует, что величины тепловых эффектов обеих реакций заметно различаются в зависимости от агрегатного состояния воды. При этом разность тепловых эффектов этих реакций, естественно, соответствует теплоте, выделяющейся при конденсации 1 моля воды:

Обратите внимание на то, что значение теплового эффекта в термохимическом уравнении строго соответствует количествам реагентов и продуктов, определяемым стехиометрическими коэффициентами. Наиболее часто встречающейся формой записи термохимических уравнений является такая, согласно которой образуется один моль продукта реакции (поэтому в термохимических уравнениях используются нецелочисленные стехиометрические коэффициенты). Тогда тепловой эффект реакции взаимодействия водорода с кислородом

должен быть удвоен для реакции, в которой используются удвоенные (для получения целочисленных значений) коэффициенты:

Чтобы иметь возможность сравнивать различные химические реакции и производить термохимические расчеты, необходимо относить значения тепловых эффектов к одному и тому же состоянию исходных продуктов и реагентов. В качестве такого состояния, называемого стандартным, обычно выбирают температуру 298 К (25° С) и давление  Па (а также концентрацию 1 моль/л для растворов).
Па (а также концентрацию 1 моль/л для растворов).
Все изложенное выше позволяет сделать вывод, что по экспериментальным данным — массе исходного реагента (простого вещества) и выделяемой (поглощаемой) в протекающей химической реакции теплоте — можно определить тепловой эффект образования более сложного бинарного соединения. Основным условием этого является достаточно высокая точность определения величины как массы, так и теплоты. Именно поэтому в термохимических задачах величины приводятся с достаточно высокой точностью.
Рассмотрим в качестве примера следующую задачу.
Пример №11-1.
При сгорании образца магния массой 6,08 г в кислороде выделяется 150,5 кДж теплоты. Определите тепловой эффект образования оксида магния.
Решение:
Алгоритм решения таких задач в основном сводится к анализу очевидного соотношения между массой реагентов (продуктов) и теплотой, выделяемой (поглошасмой) в химической реакции.
Так, в приведенной выше задаче, рассчитав число молей магния, вступившего в реакцию,  моль, легко оценить величину теплового эффекта образования оксида магния
моль, легко оценить величину теплового эффекта образования оксида магния  протекающего по реакции
протекающего по реакции

Поскольку  , то величина
, то величина  равна 150,5/0,25 = 602 кДж/моль. Ответ:
равна 150,5/0,25 = 602 кДж/моль. Ответ:  = 602 кДж/моль.
= 602 кДж/моль.
В то же время эта же задача может иметь несколько иную формулировку:
Пример №11-2.
При сгорании магния массой 6,08 г в кислороде выделилась теплота в количестве 150,5 кДж. Составьте термохимическое уравнение реакции.
Решение:
В этом случае вычисления, идентичные приведенным выше, требуют записи окончательного решения в виде следующего термохимического уравнения:

Термохимические законы
Рассмотрим основные законы термохимии, которые являются частными проявлениями закона сохранения и превращения энергии.
Первый закон термохимии обычно формулируют следующим образом: Тепловой эффект прямой реакции равен по абсолютному значению и противоположен по знаку тепловому эффекту обратной реакции.
Иначе говоря, осуществив в системе какой-либо химический процесс, а затем ему противоположный, мы возвращаем систему в первоначальное состояние с той же внутренней энергией, какую она имела.
При термохимических расчетах особенно важным является один из видов тепловых эффектов — теплота образования.
Теплотой образования называют тепловой эффект реакции образования одного моля химического соединения из простых веществ, устойчивых при данных условиях.
Например, теплота образования силиката кальция есть тепловой эффект реакции, равный 1635 кДж на 1 моль продукта:

Будем в дальнейшем тепловой эффект реакции образования при стандартных условиях обозначать символом  В табл. 11.1 приведены значения этой величины для некоторых неорганических веществ, что позволит вам провести ряд простейших термохимических расчетов, часть из которых приведена в настоящем пособии. Если вы захотите получить дополнительные сведения о тепловых эффектах реакций образования веществ, то можете обратиться к любому справочнику, содержащему информацию о термодинамических свойствах химических веществ.
В табл. 11.1 приведены значения этой величины для некоторых неорганических веществ, что позволит вам провести ряд простейших термохимических расчетов, часть из которых приведена в настоящем пособии. Если вы захотите получить дополнительные сведения о тепловых эффектах реакций образования веществ, то можете обратиться к любому справочнику, содержащему информацию о термодинамических свойствах химических веществ.
Необходимо помнить, что в термохимии и термодинамике приняты разные исходные положения для учета изменения энергии при химических реакциях. Термохимия, как было указано ранее, рассматривает, сколько энергии приобрела (или отдала) окружающая среда, в которой происходит химическая реакция. Термодинамика, напротив, учитывает изменения энергии, происходящие в самой реакции, т. е. при переходе исходных реагентов в продукты реакции. При этом в термодинамике тепловой эффект реакции образования обозначается символом  . который численно равен, но противоположен по знаку величине
. который численно равен, но противоположен по знаку величине 
Таблица 11.1
Тепловые эффекты реакций образования некоторых веществ при стандартных условиях

Следовательно, эндотермическим процессам (-) в справочнике соответствуют (- ) положительные значения
) положительные значения  , а экзотермическим (+
, а экзотермическим (+ ) отрицательные, т. е. —
) отрицательные, т. е. — Например, эндотермическая реакция паров воды с углем с учетом теплового эффекта может быть выражена двумя способами:
Например, эндотермическая реакция паров воды с углем с учетом теплового эффекта может быть выражена двумя способами:

Оба способа записи термохимического уравнения химической реакции эквивалентны и показывают, что при взаимодействии паров воды с углем происходит поглощение теплоты (в явном виде отражено в первом варианте записи реакции). Это приводит к увеличению теплосодержания в продуктах реакции — в оксиде углерода (II) и в водороде по сравнению с исходными веществами (отражено по втором варианте).
Первый закон термохимии может быть использован для определения теплоты образования соединений, полученных косвенным путем. Например, оксиды хлора  не могут быть получены непосредственным взаимодействием хлора с кислородом, но они легко разлагаются на простые вещества, позволяя измерить тепловой эффект реакции разложения. Очевидно, что теплота образования каждого из этих оксидов равна тепловому эффекту реакции разложении, взятому с обратным знаком.
не могут быть получены непосредственным взаимодействием хлора с кислородом, но они легко разлагаются на простые вещества, позволяя измерить тепловой эффект реакции разложения. Очевидно, что теплота образования каждого из этих оксидов равна тепловому эффекту реакции разложении, взятому с обратным знаком.
Второй термохимический закон, открытий в 1840 г. известным русским химиком Г. И. Гессом, является важнейшим и формулируется следующим образом:
Тепловой эффект химической реакции не зависит от пути ее протекания и определяется только начальным и конечным состоянием системы.
Например, силикат кальция можно получить двумя путями:
1) из простых веществ, сжигая эквимолярные количества кальция и кремния совместно в кислороде:

2) из простых веществ, предварительно превращенных в оксиды:

с их последующим взаимодействием:

В соответствии с законом Гесса получается:

Важным следствием закона Гесса является правило, согласно которому тепловой эффект реакции равен разности суммы тсплот образования продуктов реакции и суммы тсплот образования исходных веществ.
Разумеется, суммирование следует производить с учетом количества вещества, участвующего в реакции, т. е. с учетом стехиометрических коэффициентов в уравнении реакции, например:

В уравнении отсутствует  поскольку железо — простое вещество, а теплота образования всех простых веществ принята равной нулю.
поскольку железо — простое вещество, а теплота образования всех простых веществ принята равной нулю.
Используя значения  ,
, (табл. 11.1), получаем для теплового эффекта реакции (11-5):
(табл. 11.1), получаем для теплового эффекта реакции (11-5):

В заключение отметим, что алгоритм решения задач на следствие из закона Гесса не представляет значительных сложностей. Он требует лишь определенной тренировки в использовании таблиц тсплот образования веществ.
Следствие из закона Гесса, с использованием которого мы познакомились выше, может быть использовано не только для решения «прямой» задачи — определения теплового эффекта реакции, но и для решения «обратной» задачи — определения теплоты образования одного из участников реакции — или реагента, или продукта.
Действительно, в рассмотренной выше реакции (11-5):

уравнение теплового баланса может быть решено относительно теплоты образования любого из компонентов:  :
:

В то же время определение теплоты образования того или иного соединения часто оказывается невозможно выполнить, используя лишь одну химическую реакцию и соответствующее ей уравнение теплового баланса. В этом случае необходим подбор такой системы химических реакций, решение уравнений тепловых балансов которых позволит решить поставленную задачу.
Рассмотрим конкретный пример.
Пример №11-3.
Определить теплоту образования СаО, если известны теплоты следующих реакций:

Решение:
Вычитая из реакции (11-7) реакцию (11-6), получаем формальное соотношение:

Очевидно, что для решения поставленной задачи сформулированные в ней условия должны быть дополнены простейшим уравнением

сложение которого с алгебраической суммой уравнений (11 -6) и (11-7) окончательно дает

Очевидно, что сумма  и представляет собой теплоту образования
и представляет собой теплоту образования 
Закон Гесса часто используют для определения тепловых эффектов, которые трудно или невозможно измерить непосредственно.
Пример 11-4.
Сгорание алмаза и графита в кислороде можно представить уравнениями:

Рассчитать тепловой эффект превращения:

Решение:
Вычитая из уравнения сгорания алмаза в кислороде уравнение сгорания графита, можно определить тепловой эффект реакции (11-9), который невозможно непосредственно измерить из-за низкой скорости реакции 
К термохимическим задачам пятого типа, по-нашему мнению, относятся задачи, близкие к только что рассмотренным. В этих задачах анализируются процессы образования кристаллогидратов из безводных солей и воды. Экспериментальное изучение таких процессов представляет собой большие сложности. В то же время термохимический подход решает эту проблему достаточно просто.
Рассмотрим конкретный пример.
Пример №11-5.
При растворении 1 моля безводной соли  в воде выделяется
в воде выделяется  кДж теплоты, а при растворении в воде 1 моля кристаллогидрата
кДж теплоты, а при растворении в воде 1 моля кристаллогидрата  поглощается
поглощается  кДж теплоты. Определить тепловой эффект процесса образования кристаллогидрата.
кДж теплоты. Определить тепловой эффект процесса образования кристаллогидрата.

Решение:
Алгоритм решения этой задачи сводится к записи следующих двух (в значительной степени формальных) уравнений

Формализм записи обоих уравнений заключается во введении реагента  , который обеспечивает получение в результате реакции одинаковым образом гидратированного продукта
, который обеспечивает получение в результате реакции одинаковым образом гидратированного продукта  . Такая запись помогает легко получить окончательное решение, вычитая из уравнения (11-10) уравнение (11-11). Это дает
. Такая запись помогает легко получить окончательное решение, вычитая из уравнения (11-10) уравнение (11-11). Это дает

для которого 
Готовые задачи по химии по всем темам
- Основные классы неорганических соединений задачи с решением
- Эквивалент. Закон эквивалентов задачи с решением
- Способы выражения состава раствора задачи с решением
- Энергетика химических реакций задачи с решением
- Скорость химических реакций и химическое равновесие задачи с решением
- Физико-химические свойства растворов задачи с решением
- Растворы сильных и слабых электролитов задачи с решением
- Гидролиз солей задачи с решением
- Окислительно — восстановительные реакции (овр) задачи с решением
- Гальванические элементы коррозия металлов задачи с решением
- Электролиз растворов задачи с решением
- Получение и химические свойства металлов задачи с решением
- Комплексные соединения задачи с решением
- Жесткость воды задачи с решением
- Высокомолекулярные соединения задачи с решением
- Металлы III — IV группы задачи с решением
- Металлы V — VI группы задачи с решением
- Металлы VII группы задачи с решением
- Металлы VIII группы задачи с решением


В ходе решения таких задач рекомендуется придерживаться алгоритма:
- внимательно прочитать условие задачи и выяснить, что у вас спрашивают;
- написать соответствующую формулу и проанализировать её;
- найти числовые значения требуемых величин, каждый раз записывая вначале формулу, а затем расчёт, учитывая размерность величин.
Содержание
- Задачи по теме «Газы»
- Задачи для самостоятельного решения
- Задачи по теме «Способы выражения концентрации растворов»
- Задачи для самостоятельного решения
Задачи по теме «Газы»
Известно, что вещества при нормальных условиях (н. у.) могут находиться в трёх агрегатных состояниях: твёрдом, жидком, газообразном. В твёрдом и жидком состояниях между молекулами (атомами) вещества имеются довольно сильные взаимодействия, в результате чего частицы находятся на небольших расстояниях друг от друга (рис. 30).
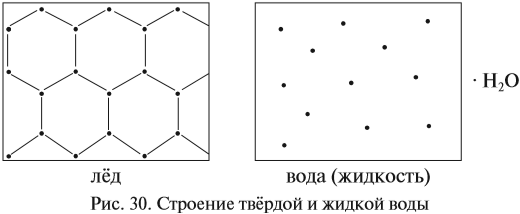
В газах расстояния между частицами очень велики, и силы взаимодействия ничтожны (рис. 31).

Поэтому равные объёмы любых газов содержат одинаковое число молекул. Это формулировка закона АВОГАДРО.
Следствием этого закона является:
1 моль любого газа при нормальных условиях (н. у.) занимает объём 22,4 литра.
Эта величина (22,4 л/моль) является молярным объёмом газа (VМ):
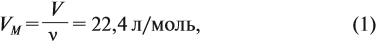
где VM — молярный объём газа, моль/л; V — объём газа, л; ν — количество вещества газа, моль.
Таким образом, зная массу газа, можно определить:
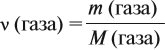
Но для того же газа из формулы (1) имеем:
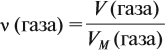
Отсюда для любого газа выполняется соотношение:
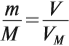
Задача 3. Какую массу имеет кислород объёмом 7 л?

Задача 4. Какой объём занимает азот массой 14 г?
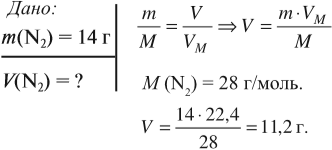
Задача 5. Чему равна молярная масса газа, 1 л которого имеет массу 1,25 г?
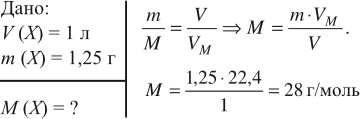
Ответ. Молярная масса неизвестного газа 28 г/моль.
Пользуясь этими формулами, можно рассчитать объём, массу, молярную массу газа, например:

Известно, что

где ρ — плотность газа (г/л), поэтому:

ПОМНИТЕ! Эти формулы можно использовать лишь тогда, когда данные задачи (плотность газа, его объём) измерены при н. у.: 273 К, 1 атм.
Из формулы (3) вытекает понятие об относительной плотности газов (Dx). Эта величина, равная отношению плотностей двух газов:
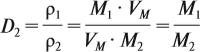
где ρ1 и М1 — плотность и молярная масса одного газа, а ρ2 и М2 — плотность и молярная масса другого газа.
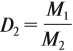
Относительная плотность газа показывает, во сколько раз данный газ тяжелее второго газа. Пользуясь этой формулой, можно легко определить молярную массу данного газа:

Выполняя такие расчёты, следует помнить, что:
- любая смесь газов, например воздух, именуется в задачах словом «газ»;
- средняя молярная масса воздуха, как показывают расчёты, равна 29 г/моль;
- по умолчанию, если не сказано иного, расчёты ведут для н. у.: 273 К, 1 атм.
Задача 6. Определить молярную массу газа, если:
а) плотность его равна 1,25 г/л;
б) плотность его по кислороду равна 0,75.
Решение.

Состав смеси газов, как правило, измеряют в объёмных процентах φ (фи).
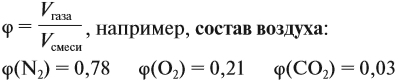
Второе следствие, при помощи которого была экспериментально подтверждена гипотеза Авогадро (гипотеза стала законом уже после смерти автора!), заключается в следующем: объемы реагирующих газов относятся как их коэффициенты в соответствующем уравнении реакции.
Это следствие позволяет решать задачи «в уме», если известны объёмы реагирующих газов или количества вещества для них.
Задача 7. Какой объём кислорода потребуется для сжигания 6 л пропана?
Из уравнения реакции:
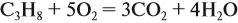
видно, что молярное соотношение пропана и кислорода составляет 1 : 5. Таким образом, объём кислорода в пять раз больше объёма пропана.
Ответ. Требуется 5 · 6 = 30 л кислорода.

Задачи для самостоятельного решения
3. Определить массы газов:
а) хлороводорода, объёмом 56 л;
б) озона О3, объёмом 14 л.
4. Определить объёмы газов:
а) хлороводорода, массой 72 г;
б) аммиака NH3, массой 3,4 г.
5. Определить молярные массы газов, если:
а) 2 л газа имеет массу 2,86 г;
б) 10 г газа занимает объём 7,47 л.
6. Определить молярную массу газа, если:
а) плотность его равна 1,52 г/л;
б) плотность по кислороду равна 1,81.
7. Какой объем занимает смесь, состоящая из 4 г метана и 22 г пропана?
8. Какой газ имеет большую массу: этан, объёмом 56 л или бутан, объёмом 44,8 л?
9. Существуют ли газообразные соединения серы легче воздуха?
10. Определите, не выполняя расчёт, какой из газов тяжелее воздуха: Не, Ar, CO2, CH4, N2, O2.
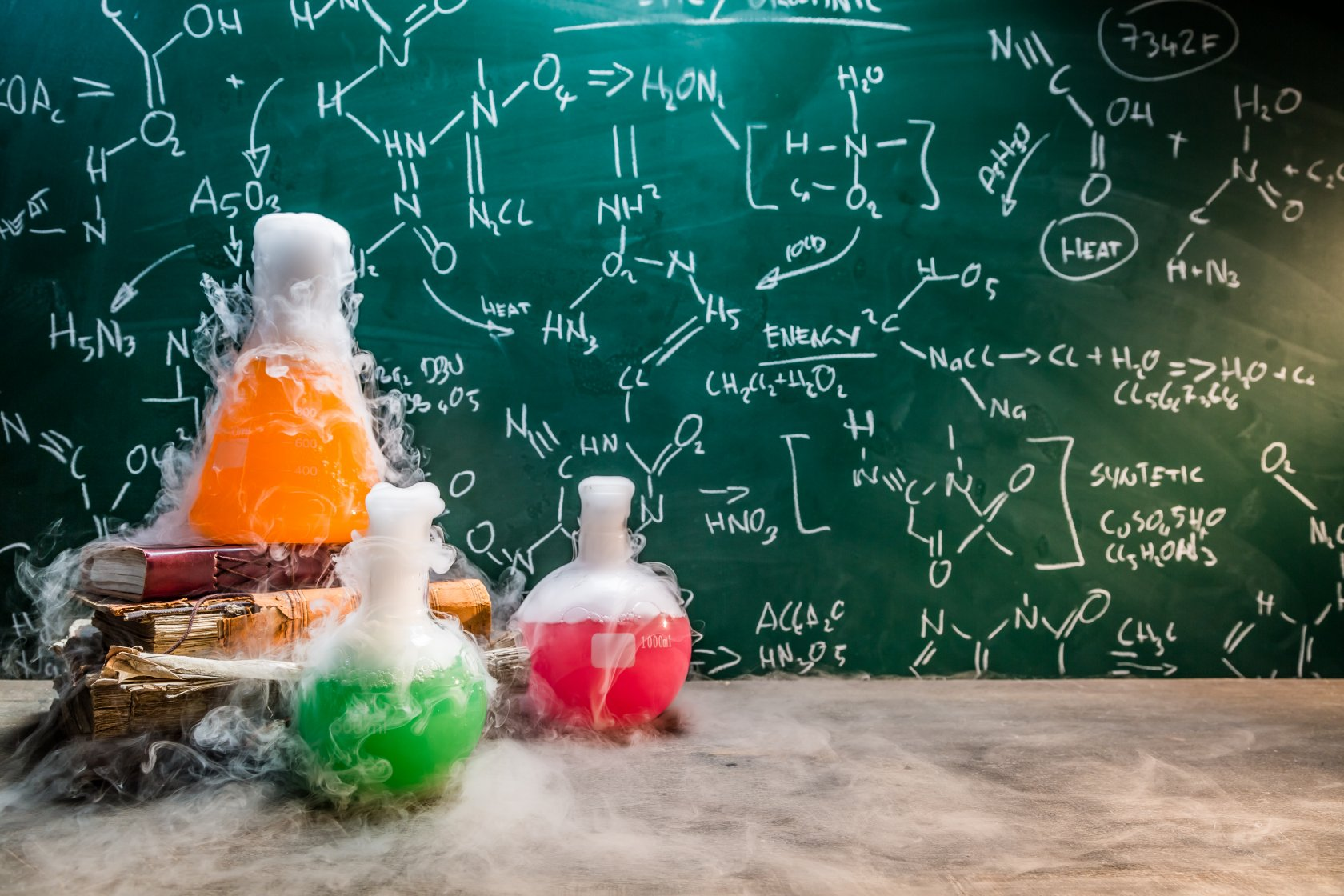
Задачи по теме «Способы выражения концентрации растворов»
Для того чтобы определить массовую долю растворенного вещества, нужно воспользоваться формулой:
Ответ может быть дан в долях (единицы): ω = 0,15; или в процентах: ω% = 15 %.
Задача 8. В 200 г воды растворили 16 г сахара. Определить ω(сахара) в полученном растворе.
Решение. В данном случае масса раствора неизвестна. Но:
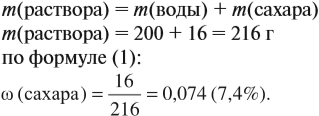
Задача 9. В 300 мл раствора (ρ = 1,2 г/мл) содержится 72 г NаОН. Определить ω(NаОН) в этом растворе.
Решение. В этом случае масса раствора неизвестна, но известен объём. Найдём массу раствора:
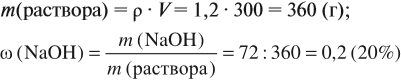
Задача 10. В 20 мл воды растворили 4,48 л хлороводорода. Определить ω(НСl) в соляной кислоте. Плотность раствора равна 1,14 г/мл.
Решение. При растворении хлороводорода в воде получена соляная кислота, её масса равна:
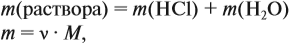
где ν — количество вещества, моль; M — молярная масса вещества, причём для газов
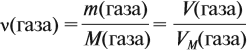
откуда
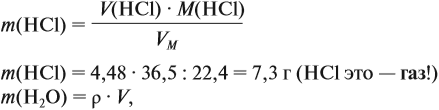
где ρ — плотность воды (1 г/мл); V — объём воды, мл
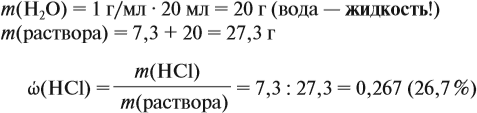
Обратите внимание: в 20 мл воды растворили 4,48 л газа, но суммарный объём отнюдь не равен (4,48 + 0,02), т. е. 4,5 литра! Суммарный объём этого раствора равен:
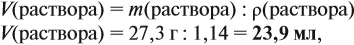
т. е. при растворении более 4 литров газа объём жидкого раствора увеличился менее чем на 4 миллилитра!
Выводы.
- Объёмы жидкостей и объёмы растворяемых газов суммировать нельзя.
- При растворении в жидкости газы сжимаются более чем в 1000 раз.
- Объёмы жидкостей и газов рассчитывают (исходя из значения массы) по-разному:
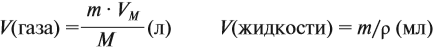
где m — масса, г; М — молярная масса, г/моль; V — объём (жидкости в мл, газа — в л); ρ — плотность жидкости, г/мл.
Пользуясь формулой (1) нетрудно рассчитать и массу раствора, и массу растворённого вещества. Но при этом следует учитывать, что обычно в задачах говорится (упоминается) о «5 %-ном растворе», «16 %-ном растворе» и т. д., т. е. массовая доля вещества выражена в процентах. В этом случае легко видеть, что:
- в 5 %-ном растворе ω(вещества) = 0,05;
- в 16 %-ном растворе ω(вещества)= 0,16 и т. д.
Зная массовую долю вещества в растворе, можно определить:

Задача 11. Сколько граммов соли и воды нужно взять для приготовления 350 мл (ρ = 1,1 г/мл) 12 %-ного раствора?
Решение. Из формулы (1) получаем формулу (2):
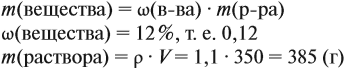
где ρ — плотность раствора (1,1 г/мл); V — объём раствора (350 мл), тогда
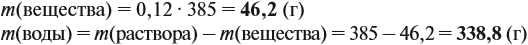
Задача 12. Сколько граммов 8 %-ного раствора можно приготовить, имея 64 г NaCl?
Решение. Из формулы (3):

Такие задачи можно решать, составляя пропорции. При этом следует знать, что массовая доля (в %) вещества показывает, сколько граммов вещества содержится (растворено) в 100 граммах раствора: 5 %-ный раствор ⇒ 5 г вещества в 100 граммах раствора.
Задача 13. Сколько мл 15 %-ного раствора (ρ = 1,1 г/мл) можно приготовить из 22,5 г вещества?

Обратите внимание: в пропорции в одном столбце должны совпадать и размерность, и наименование компонента, о котором идёт речь.
Задача 14. К 200 мл 20 %-ного раствора (ρ = 1,2 г/мл) добавили 30 г того же вещества. Определить массовую долю вещества в полученном растворе.
Решение. Определим в начале массу исходного раствора и растворённого вещества:
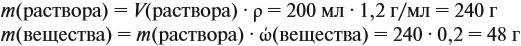
При добавлении новых порций растворяемого вещества, его масса увеличивается:
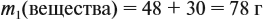
На ту же величину увеличивается масса раствора:
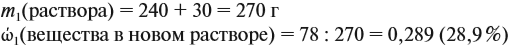
Задача 15. Сколько граммов 19 %-ного раствора и воды нужно взять для получения 380 г 6 %-ного раствора?
Решение. При добавлении воды масса растворённого вещества не меняется. Поэтому рассчитаем массу растворённого вещества в 6 %-ном растворе (столько же его будет и в 19 %-ном растворе):

Теперь можно рассчитать массу 19 %-ного раствора:
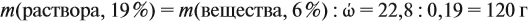
Теперь задумаемся: почему возросла масса исходного 19 %-ного раствора? Потому, что добавили воду. Значит, масса воды равна:
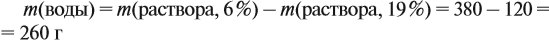
Ответ. Нужно добавить 260 г воды.
В случаях, когда изменяется и масса раствора, и масса вещества, нужно прибегнуть к приёму, когда неизвестная величина (о ней спрашивается в вопросе задачи), принимается за известную, и обозначается А.
Задача 16. Сколько граммов 25 %-ного раствора нужно добавить к 210 г 15 %-ного раствора, чтобы получить 18 %-ный раствор?
Решение. Пусть нужно добавить А граммов 25 %-ного раствора, тогда масса 18 %-ного раствора составит (210 + А) г. Определим массу вещества в 15 %-ном растворе:
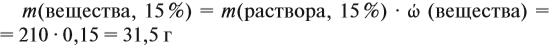
аналогично:
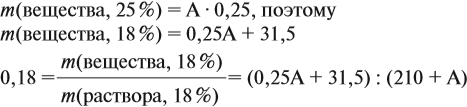
Решим полученное уравнение:
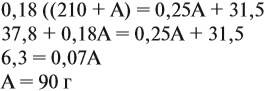
Ответ. Нужно добавить 90 г 25 %-ного раствора.

Задачи для самостоятельного решения
11. В 300 г раствора содержится 45 г поваренной соли. Определить ω (NaСl) в этом растворе.
12. В 300 мл воды растворили 100 г сахара. Определить ω (сахара) в полученном растворе.
13. В 2 л раствора (пл. = 1,05 г/мл) содержится 105 г соли. Определить ω(соли) в этом растворе.
14. В 200 мл воды растворили 56 л аммиака NH3. Определить ω (NH3) в этом растворе.
15. Бромоводород объёмом 5,4 л затрачен на приготовление 8 %-ного раствора (пл. = 1,057 г/мл). Найти объём полученного раствора.
16. Сколько граммов воды и сахара нужно взять для приготовления 3 литров 30 %-ного сиропа? (Пл. = 1,13 г/мл.)
17. Какой объём 25 %-ного раствора можно приготовить из 150 г соли, если плотность раствора равна 1,2 г/мл?
18. К 500 мл 32 %-ной кислоты (ρ = 1,2 г/мл) добавили 1 л воды. Вычислить массовую долю кислоты в полученном растворе.
19. Смешали 25 г 16 %-ного раствора КОН с 30 мл 20 %-ного раствора КОН (плотность 1,2 г/мл). Вычислить массовую долю щёлочи в полученном растворе.
20. К 220 г 20 %-ного раствора поваренной соли добавили 44 мл воды и 36 г этой же соли. Вычислить массовую долю соли в полученном растворе.
21. Определить массу воды, которую нужно выпарить из 1 кг 3 %-ного раствора сульфата меди II для получения 5 %-ного раствора.
22. Сколько граммов воды нужно добавить к 50 г 70 %-ной уксусной кислоты, чтобы получить 5 %-ный уксус?
23. После добавления соды к 200 мл 16 %-ного раствора её (ρ = 1,17 г/мл) массовая доля вещества возросла до 20 %. Определить массу добавленной соды.
24. Какой объём 96 %-ной кислоты (ρ = 1,86 г/мл) необходимо добавить к 5 л 30 %-ной кислоты (ρ = 1,3 г/мл), для того чтобы получить 40 %-ный раствор?
Методика решения задач по химии
При решении задач необходимо руководствоваться несколькими простыми правилами:
- Внимательно прочитать условие задачи;
- Записать, что дано;
- Перевести, если это необходимо, единицы физических величин в единицы системы СИ (некоторые внесистемные единицы допускаются, например литры);
- Записать, если это необходимо, уравнение реакции и расставить коэффициенты;
- Решать задачу, используя понятие о количестве вещества, а не метод составления пропорций;
- Записать ответ.
В целях успешной подготовки по химии следует внимательно рассмотреть решения задач, приводимых в тексте, а также самостоятельно решить достаточное число их. Именно в процессе решения задач будут закреплены основные теоретические положения курса химии. Решать задачи необходимо на протяжении всего времени изучения химии и подготовки к экзамену.
Вы можете использовать задачи на этой странице, а можете скачать хороший сборник задач и упражнений с решением типовых и усложненных задач (М. И. Лебедева, И. А. Анкудимова).
Моль, молярная масса
Молярная масса – это отношение массы вещества к количеству вещества, т.е.
М(х) = m(x)/ν(x), (1)
где М(х) – молярная масса вещества Х, m(x) – масса вещества Х, ν(x) – количество вещества Х. Единица СИ молярной массы – кг/моль, однако обычно используется единица г/моль. Единица массы – г, кг. Единица СИ количества вещества – моль.
Любая задача по химии решается через количество вещества. Необходимо помнить основную формулу:
ν(x) = m(x)/ М(х) = V(x)/Vm = N/NA, (2)
где V(x) – объем вещества Х(л), Vm – молярный объем газа (л/моль), N – число частиц, NA – постоянная Авогадро.
1. Определите массу иодида натрия NaI количеством вещества 0,6 моль.
Дано: ν(NaI)= 0,6 моль.
Найти: m(NaI) =?
Решение. Молярная масса иодида натрия составляет:
M(NaI) = M(Na) + M(I) = 23 + 127 = 150 г/моль
Определяем массу NaI:
m(NaI) = ν(NaI)•M(NaI) = 0,6 • 150 = 90 г.
2. Определите количество вещества атомного бора, содержащегося в тетраборате натрия Na2B4O7 массой 40,4 г.
Дано: m(Na2B4O7)=40,4 г.
Найти: ν(B)=?
Решение. Молярная масса тетрабората натрия составляет 202 г/моль. Определяем количество вещества Na2B4O7:
ν(Na2B4O7)= m(Na2B4O7)/ М( Na2B4O7) = 40,4/202=0,2 моль.
Вспомним, что 1 моль молекулы тетрабората натрия содержит 2 моль атомов натрия, 4 моль атомов бора и 7 моль атомов кислорода (см. формулу тетрабората натрия). Тогда количество вещества атомного бора равно: ν(B)= 4 • ν (Na2B4O7)=4 • 0,2 = 0,8 моль.
Расчеты по химическим формулам. Массовая доля.
Массовая доля вещества – отношение массы данного вещества в системе к массе всей системы, т.е. ω(Х) =m(Х)/m, где ω(X)– массовая доля вещества Х, m(X) – масса вещества Х, m – масса всей системы. Массовая доля – безразмерная величина. Её выражают в долях от единицы или в процентах. Например, массовая доля атомного кислорода составляет 0,42, или 42%, т.е. ω(О)=0,42. Массовая доля атомного хлора в хлориде натрия составляет 0,607, или 60,7%, т.е. ω(Cl)=0,607.
3. Определите массовую долю кристаллизационной воды в дигидрате хлорида бария BaCl2 • 2H2O.
Решение: Молярная масса BaCl2 • 2H2O составляет:
М(BaCl2 • 2H2O) = 137+ 2 • 35,5 + 2 • 18 =244 г/моль
Из формулы BaCl2 • 2H2O следует, что 1 моль дигидрата хлорида бария содержит 2 моль Н2О. Отсюда можно определить массу воды, содержащейся в BaCl2 • 2H2O:
m(H2O) = 2 • 18 = 36 г.
Находим массовую долю кристаллизационной воды в дигидрате хлорида бария BaCl2 • 2H2O.
ω(H2O) = m(H2O)/ m(BaCl2 • 2H2O) = 36/244 = 0,1475 = 14,75%.
4. Из образца горной породы массой 25 г, содержащей минерал аргентит Ag2S, выделено серебро массой 5,4 г. Определите массовую долю аргентита в образце.
Дано: m(Ag )=5,4 г; m = 25 г.
Найти: ω(Ag2S) =?
Решение: определяем количество вещества серебра, находящегося в аргентите: ν(Ag ) =m(Ag )/M(Ag ) = 5,4/108 = 0,05 моль.
Из формулы Ag2S следует, что количество вещества аргентита в два раза меньше количества вещества серебра. Определяем количество вещества аргентита:
ν( Ag2S)= 0,5 • ν (Ag) = 0,5 • 0,05 = 0,025 моль
Рассчитываем массу аргентита:
m(Ag2S) = ν( Ag2S) • М(Ag2S) = 0,025• 248 = 6,2 г.
Теперь определяем массовую долю аргентита в образце горной породы, массой 25 г.
ω(Ag2S) = m(Ag2S)/ m = 6,2/25 = 0,248 = 24,8%.
Вывод формул соединений
5. Определите простейшую формулу соединения калия с марганцем и кислородом, если массовые доли элементов в этом веществе составляют соответственно 24,7, 34,8 и 40,5%.
Дано: ω(K) =24,7%; ω(Mn) =34,8%; ω(O) =40,5%.
Найти: формулу соединения.
Решение: для расчетов выбираем массу соединения, равную 100 г, т.е. m=100 г. Массы калия, марганца и кислорода составят:
m (К) = m ω(К); m (К) = 100 • 0,247= 24,7 г;
m (Mn) = m ω(Mn); m (Mn) =100 • 0,348=34,8 г;
m (O) = m ω(O); m (O) = 100 • 0,405 = 40,5 г.
Определяем количества веществ атомных калия, марганца и кислорода:
ν(К)= m(К)/ М( К) = 24,7/39= 0,63 моль
ν(Mn)= m(Mn)/ М( Mn) = 34,8/ 55 = 0,63 моль
ν(O)= m(O)/ М(O) = 40,5/16 = 2,5 моль
Находим отношение количеств веществ:
ν(К) : ν(Mn) : ν(O) = 0,63 : 0,63 : 2,5.
Разделив правую часть равенства на меньшее число (0,63) получим:
ν(К) : ν(Mn) : ν(O) = 1 : 1 : 4.
Следовательно, простейшая формула соединения KMnO4.
6. При сгорании 1,3 г вещества образовалось 4,4 г оксида углерода (IV) и 0,9 г воды. Найти молекулярную формулу вещества, если его плотность по водороду равна 39.
Дано: m(в-ва) =1,3 г; m(СО2)=4,4 г; m(Н2О)=0,9 г; ДН2 =39.
Найти: формулу вещества.
Решение: Предположим, что искомое вещество содержит углерод, водород и кислород, т.к. при его сгорании образовались СО2 и Н2О. Тогда необходимо найти количества веществ СО2 и Н2О, чтобы определить количества веществ атомарных углерода, водорода и кислорода.
ν(СО2) = m(СО2)/ М(СО2) = 4,4/44 = 0,1 моль;
ν(Н2О) = m(Н2О)/ М(Н2О) = 0,9/18 = 0,05 моль.
Определяем количества веществ атомарных углерода и водорода:
ν(С)= ν(СО2); ν(С)=0,1 моль;
ν(Н)= 2•ν(Н2О); ν(Н)= 2 • 0,05 = 0,1 моль.
Следовательно, массы углерода и водорода будут равны:
m(С) = ν( С) • М(С) = 0,1• 12 = 1,2 г;
m(Н) = ν( Н) • М(Н) = 0,1• 1 =0,1 г.
Определяем качественный состав вещества:
m(в-ва) = m(С) + m(Н) = 1,2 + 0,1 = 1,3 г.
Следовательно, вещество состоит только из углерода и водорода (см. условие задачи). Определим теперь его молекулярную массу, исходя из данной в условии задачи плотности вещества по водороду.
М(в-ва) = 2 • ДН2 = 2 • 39 = 78 г/моль.
Далее находим отношение количеств веществ углерода и водорода:
ν(С) : ν(Н) = 0,1 : 0,1
Разделив правую часть равенства на число 0,1, получим:
ν(С) : ν(Н) = 1 : 1
Примем число атомов углерода (или водорода) за «х», тогда, умножив «х» на атомные массы углерода и водорода и приравняв эту сумму молекулярной массе вещества, решим уравнение:
12х + х = 78. Отсюда х= 6. Следовательно, формула вещества С6Н6 – бензол.
Молярный объем газов. Законы идеальных газов. Объемная доля.
Молярный объем газа равен отношению объема газа к количеству вещества этого газа, т.е.
Vm= V(X)/ ν(x),
где Vm – молярный объем газа – постоянная величина для любого газа при данных условиях; V(X) – объем газа Х; ν(x) – количество вещества газа Х. Молярный объем газов при нормальных условиях (нормальном давлении рн= 101 325 Па ≈ 101,3 кПа и температуре Тн= 273,15 К ≈ 273 К) составляет Vm= 22,4 л/моль.
В расчетах, связанных с газами, часто приходится переходить от данных условий к нормальным или наоборот. При этом удобно пользоваться формулой, следующей из объединенного газового закона Бойля-Мариотта и Гей-Люссака:
pV pнVн
──── = ─── (3)
Т Тн
Где p – давление; V – объем; Т- температура в шкале Кельвина; индекс «н» указывает на нормальные условия.
Состав газовых смесей часто выражают при помощи объемной доли – отношения объема данного компонента к общему объему системы, т.е.
φ(Х) = V(X)/V
где φ(Х) – объемная доля компонента Х; V(X) – объем компонента Х; V – объем системы. Объемная доля – безразмерная величина, её выражают в долях от единицы или в процентах.
7. Какой объем займет при температуре 20оС и давлении 250 кПа аммиак массой 51 г?
Дано: m(NH3)=51 г; p=250 кПа; t=20oC.
Найти: V(NH3) =?
Решение: определяем количество вещества аммиака:
ν(NH3) = m(NH3)/ М(NH3) = 51/17 = 3 моль.
https://5-ege.ru/kak-reshat-zadachi-po-ximii/
Объем аммиака при нормальных условиях составляет:
V(NH3) = Vm • ν(NH3) = 22,4 • 3 = 67,2 л.
Используя формулу (3), приводим объем аммиака к данным условиям [температура Т= (273 +20)К = 293 К]:
pнTVн(NH3) 101,3•293•67,2
V(NH3) =──────── = ───────── = 29,2 л.
pТн 250•273
8. Определите объем, который займет при нормальных условиях газовая смесь, содержащая водород, массой 1,4 г и азот, массой 5,6 г.
Дано: m(N2)=5,6 г; m(H2)=1,4 ; н.у.
Найти: V(смеси)=?
Решение: находим количества вещества водорода и азота:
ν(N2) = m(N2)/ М(N2) = 5,6/28 = 0,2 моль
ν(H2) = m(H2)/ М(H2) = 1,4/ 2 = 0,7 моль
Так как при нормальных условиях эти газы не взаимодействуют между собой, то объем газовой смеси будет равен сумме объемов газов, т.е.
V(смеси)=V(N2) + V(H2)=Vm•ν(N2) + Vm•ν(H2) = 22,4•0,2 + 22,4•0,7 = 20,16 л.
Расчеты по химическим уравнениям
Расчеты по химическим уравнениям (стехиометрические расчеты) основаны на законе сохранения массы веществ. Однако в реальных химических процессах из-за неполного протекания реакции и различных потерь веществ масса образующихся продуктов часто бывает меньше той, которая должна образоваться в соответствии с законом сохранения массы веществ. Выход продукта реакции (или массовая доля выхода) – это выраженное в процентах отношение массы реально полученного продукта к его массе, которая должна образоваться в соответствии с теоретическим расчетом, т.е.
η = [mp(X) •100]/m(X) (4)
Где η– выход продукта, %; mp(X) – масса продукта Х, полученного в реальном процессе; m(X) – рассчитанная масса вещества Х.
В тех задачах, где выход продукта не указан, предполагается, что он – количественный (теоретический), т.е. η=100%.
9. Какую массу фосфора надо сжечь для получения оксида фосфора (V) массой 7,1 г?
Дано: m(P2O5)=7,1 г.
Найти: m(Р) =?
Решение: записываем уравнение реакции горения фосфора и расставляем стехиометрические коэффициенты.
4P+ 5O2 = 2P2O5
Определяем количество вещества P2O5, получившегося в реакции.
ν(P2O5) = m(P2O5)/ М(P2O5) = 7,1/142 = 0,05 моль.
Из уравнения реакции следует, что ν(P2O5)= 2•ν(P), следовательно, количество вещества фосфора, необходимого в реакции равно:
ν(P2O5)= 2•ν(P) = 2• 0,05= 0,1 моль.
Отсюда находим массу фосфора:
m(Р) = ν(Р) • М(Р) = 0,1• 31 = 3,1 г.
10. В избытке соляной кислоты растворили магний массой 6 г и цинк массой 6,5 г. Какой объем водорода, измеренный при нормальных условиях, выделится при этом?
Дано: m(Mg)=6 г; m(Zn)=6,5 г; н.у.
Найти: V(H2) =?
Решение: записываем уравнения реакции взаимодействия магния и цинка с соляной кислотой и расставляем стехиометрические коэффициенты.
Zn + 2 HCl = ZnCl2 + H2↑
Mg + 2 HCl = MgCl2 + H2↑
Определяем количества веществ магния и цинка, вступивших в реакцию с соляной кислотой.
ν(Mg) = m(Mg)/ М(Mg ) = 6/24 = 0,25 моль
ν(Zn) = m(Zn)/ М(Zn) = 6,5/65 = 0,1 моль.
Из уравнений реакции следует, что количество вещества металла и водорода равны, т.е. ν(Mg) = ν(Н2); ν(Zn) = ν(Н2), определяем количество водорода, получившегося в результате двух реакций:
ν(Н2) = ν(Mg) + ν(Zn) = 0,25 + 0,1= 0,35 моль.
Рассчитываем объем водорода, выделившегося в результате реакции:
V(H2) = Vm • ν(H2) = 22,4 • 0,35 = 7,84 л.
11. При пропускании сероводорода объемом 2,8 л (нормальные условия) через избыток раствора сульфата меди (II) образовался осадок массой 11,4 г. Определите выход продукта реакции.
Дано: V(H2S)=2,8 л; m(осадка)= 11,4 г; н.у.
Найти: η =?
Решение: записываем уравнение реакции взаимодействия сероводорода и сульфата меди (II).
H2S + CuSO4 = CuS ↓+ H2SO4
Определяем количество вещества сероводорода, участвующего в реакции.
ν(H2S) = V(H2S) / Vm = 2,8/22,4 = 0,125 моль.
Из уравнения реакции следует, что ν(H2S) = ν(СuS) = 0,125 моль. Значит можно найти теоретическую массу СuS.
m(СuS) = ν(СuS) • М(СuS) = 0,125 • 96 = 12 г.
Теперь определяем выход продукта, пользуясь формулой (4):
η = [mp(X) •100]/m(X)= 11,4 • 100/ 12 = 95%.
12. Какая масса хлорида аммония образуется при взаимодействии хлороводорода массой 7,3 г с аммиаком массой 5,1 г? Какой газ останется в избытке? Определите массу избытка.
Дано: m(HCl)=7,3 г; m(NH3)=5,1 г.
Найти: m(NH4Cl) =? m(избытка) =?
Решение: записываем уравнение реакции.
HCl + NH3 = NH4Cl
Эта задача на «избыток» и «недостаток». Рассчитываем количества вещества хлороводорода и аммиака и определяем, какой газ находится в избытке.
ν(HCl) = m(HCl)/ М(HCl) = 7,3/36,5 = 0,2 моль;
ν(NH3) = m(NH3)/ М(NH3) = 5,1/ 17 = 0,3 моль.
Аммиак находится в избытке, поэтому расчет ведем по недостатку, т.е. по хлороводороду. Из уравнения реакции следует, что ν(HCl) = ν(NH4Cl) = 0,2 моль. Определяем массу хлорида аммония.
m(NH4Cl) = ν(NH4Cl) • М(NH4Cl) = 0,2• 53,5 = 10,7 г.
Мы определили, что аммиак находится в избытке (по количеству вещества избыток составляет 0,1 моль). Рассчитаем массу избытка аммиака.
m(NH3) = ν(NH3) • М(NH3) = 0,1• 17 = 1,7 г.
13. Технический карбид кальция массой 20 г обработали избытком воды, получив ацетилен, при пропускании которого через избыток бромной воды образовался 1,1,2,2 –тетрабромэтан массой 86,5 г. Определите массовую долю СаС2 в техническом карбиде.
Дано: m = 20 г; m(C2H2Br4)=86,5 г.
Найти: ω(СаC2) =?
Решение: записываем уравнения взаимодействия карбида кальция с водой и ацетилена с бромной водой и расставляем стехиометрические коэффициенты.
CaC2 +2 H2O = Ca(OH)2 + C2H2
C2H2 +2 Br2 = C2H2Br4
Находим количество вещества тетрабромэтана.
ν(C2H2Br4) = m(C2H2Br4)/ М(C2H2Br4) = 86,5/ 346 = 0,25 моль.
Из уравнений реакций следует, что ν(C2H2Br4) =ν(C2H2) = ν(СаC2) =0,25 моль. Отсюда мы можем найти массу чистого карбида кальция (без примесей).
m(СаC2) = ν(СаC2) • М(СаC2) = 0,25• 64 = 16 г.
Определяем массовую долю СаC2 в техническом карбиде.
ω(СаC2) =m(СаC2)/m = 16/20 = 0,8 = 80%.
Растворы. Массовая доля компонента раствора
14. В бензоле объемом 170 мл растворили серу массой 1,8 г. Плотность бензола равна 0,88 г/мл. Определите массовую долю серы в растворе.
Дано: V(C6H6) =170 мл; m(S) = 1,8 г; ρ(С6C6)=0,88 г/мл.
Найти: ω(S) =?
Решение: для нахождения массовой доли серы в растворе необходимо рассчитать массу раствора. Определяем массу бензола.
m(С6C6) = ρ(С6C6) •V(C6H6) = 0,88•170 = 149,6 г.
Находим общую массу раствора.
m(р-ра) = m(С6C6) + m(S) =149,6 + 1,8 = 151,4 г.
Рассчитаем массовую долю серы.
ω(S) =m(S)/m=1,8 /151,4 = 0,0119 = 1,19 %.
15. В воде массой 40 г растворили железный купорос FeSO4•7H2O массой 3,5 г. Определите массовую долю сульфата железа (II) в полученном растворе.
Дано: m(H2O)=40 г; m(FeSO4•7H2O)=3,5 г.
Найти: ω(FeSO4) =?
Решение: найдем массу FeSO4 содержащегося в FeSO4•7H2O. Для этого рассчитаем количество вещества FeSO4•7H2O.
ν(FeSO4•7H2O)=m(FeSO4•7H2O)/М(FeSO4•7H2O)=3,5/278=0,0125моль
Из формулы железного купороса следует, что ν(FeSO4)= ν(FeSO4•7H2O)=0,0125 моль. Рассчитаем массу FeSO4:
m(FeSO4) = ν(FeSO4) • М(FeSO4) = 0,0125•152 = 1,91 г.
Учитывая, что масса раствора складывается из массы железного купороса (3,5 г) и массы воды (40 г), рассчитаем массовую долю сульфата железа в растворе.
ω(FeSO4) =m(FeSO4)/m=1,91 /43,5 = 0,044 =4,4 %.
Задачи для самостоятельного решения
- На 50 г йодистого метила в гексане подействовали металлическим натрием, при этом выделилось 1,12 л газа, измеренного при нормальных условиях. Определите массовую долю йодистого метила в растворе. Ответ: 28,4%.
- Некоторый спирт подвергли окислению, при этом образовалась одноосновная карбоновая кислота. При сжигании 13,2 г этой кислоты получили углекислый газ, для полной нейтрализации которого потребовалось 192 мл раствора КОН с массовой долей 28%. Плотность раствора КОН равна 1,25 г/мл. Определите формулу спирта. Ответ: бутанол.
- Газ, полученный при взаимодействии 9,52 г меди с 50 мл 81 % раствора азотной кислоты, плотностью 1,45 г/мл, пропустили через 150 мл 20 % раствора NaOH плотностью 1,22 г/мл. Определите массовые доли растворенных веществ. Ответ: 12,5% NaOH; 6,48% NaNO3; 5,26% NaNO2.
- Определите объем выделившихся газов при взрыве 10 г нитроглицерина. Ответ: 7,15 л.
- Образец органического вещества массой 4,3 г сожгли в кислороде. Продуктами реакции являются оксид углерода (IV) объемом 6,72 л (нормальные условия) и вода массой 6,3 г. Плотность паров исходного вещества по водороду равна 43. Определите формулу вещества. Ответ: С6Н14.
Рекомендуем:
Ключевые слова: решение 25 типовых задач по химии, определение массы, доли, числа,
1
Определение относительной молекулярной массы Мг
Задача
Какова относительная молекулярная масса Мг нитробензола С6Н5NO2? Какова молекулярная масса этого вещества в а.е.м.?

2
Определение массовой доли элемента в соединении
Задача
Какова масса в граммах 1 атома 131I ?

3
Определение числа молекул в порции вещества
Задача
Сколько молекул воды содержится в 1 капле воды массой 0,03 г?

4
Определение массы атома в граммах
Задача
Какова массовая доля фосфора в фосфате кальция Са3(РO4)2 ?

Ответ: ω = 0.2 или 20%
5
Определение молярной массы
Задача
Какова молярная масса вещества, если масса 2.5 моль этого вещества равна 250 г?

6
Определение массового отношения элементов в соединении
Задача
Каково массовое отношение углерода, водорода и кислорода в глюкозе С6Н1206 ?

7
Определение объема, который занимает порция газа при н.у.
Задача
Какой объем (н.у.) занимают 66 г С02?

8
Определение теплового эффекта реакции
Задача
Молярная теплота сгорания угля на воздухе 393.5 кДж/моль. Сколько теплоты выделится при полном сгорании 1 кг угля?

9
Определение максимального выхода продукта реакции
Задача
Сколько максимально литров (н.у.) водорода можно получить, используя 45.5 г цинка и избыток соляной кислоты?

10
Определение реального выхода продукта реакции
Задача
При прокаливании 15,8 г перманганата калия КМnО4 получено 0,896 л (н.у.) кислорода. Каков выход кислорода в данном случае?

11
Определение выхода продукта по стехиометрическим соотношениям
Задача
Сколько граммов азотной кислоты HNO3 максимально можно получить из 44.8 л (н.у.) азота?

12
Определение содержания основного компонента (или содержания примеси) в исходном веществе
Задача
Каково содержание (в процентах) СаСО3 в образце известняка, при длительном прокаливании 400 г которого получено 78,4 л С02 (н.у.)?

13
Определение выхода реакции, когда одно из исходных веществ взято в избытке
Задача
Сколько граммов поваренной соли NaCI можно получить, если смешать два раствора, один из которых содержит 29,2 г HCI, а другой 44 г NaOH?

14
Определение состава газовой смеси (в объемных процентах)
Задача
20 л (н.у.) аммиака пропустили через нагретую до 350°С трубку с железным катализатором. Объем полученной газовой смеси (н.у.) равен 25 л. Каков состав полученной газовой смеси (в объемных процентах) ?

15
Определение объема газа, расходуемого на проведение реакции с другими газами
Задача
Какой минимальный объем кислорода, содержащего 10 объемн. % озона, необходим для полного сжигания 4 л пропана С3Н8 ?

16
Определение молекулярной формулы вещества по относительной плотности его паров
Задача
Относительная плотность паров углеводорода по воздуху 2,69. Массовая доля водорода в соединении 7,69%. Какова молекулярная формула углеводорода?

17
Определение состава газовой смеси
Задача
Относительная плотность 30 л смеси метана СН4 и азота N2 по гелию равна 5. Сколько литров метана и азота взято для приготовления смеси?

18
Определение состава солей в растворе
Задача
В растворе смешали 9,8 г H2S04 и 6,5 г NaOH. Какие соли и в каких количествах образовались?

19
Приготовление раствора с заданной массовой долей растворенного вещества
Задача
Сколько граммов сахарозы надо растворить в 250 г воды, чтобы получить раствор с массовой долей сахарозы 0,3 (30%)?

20
Приготовление раствора с заданной массовой долей растворенного вещества
Задача
: Сколько граммов медного купороса CuS04 • 5Н20 надо добавить к 300 г 2%-го раствора сульфата меди, чтобы получить 5%-ный раствор ?

21
Приготовление раствора с заданной массовой долей растворенного вещества
Задача
Сколько миллилитров воды нужно добавить к 100 мл 30%-го раствора соляной кислоты с плотностью 1,15 г/мл, чтобы получить раствор с массовой долей НCl 5%?

22
Приготовление раствора с заданной массовой долей растворенного вещества
Задача
Сколько граммов ВаО надо добавить к 100 г воды, чтобы получить 5%-ный раствор?

23
Приготовление раствора с заданной молярной концентрацией
Задача
Сколько граммов сульфата натрия Na2S04* 10Н20 необходимо для приготовления 0,5 л раствора с молярной концентрацией 0,02 моль/л?

24
Определение формулы органического вещества по данным о массе продуктов реакции
Задача
При полном сгорании 6,0 г органического вещества получено 8,8 г С02 и 3.6 г воды. Плотность паров органического вещества по водороду равна 30. Какова молекулярная формула вещества?

25
Определение молекулярной формулы органического вещества по данным о продукте реакции
Задача
При обработке 14,8 г одноосновной карбоновой кислоты избытком цинка получено 2,24 л водорода. Какова молекулярная формула кислоты?

Автор задач: С.С.Бердоносов
Решение 25 типовых задач по химии. Выберите дальнейшие действия:
- Перейти к следующей теме:
- Вернуться к списку конспектов по Химии.
- Проверить знания по Химии.
