Задание. Постройте в одной системе координат графики функций у = х² – 6х + 6 при х ≥ 2 и у = х – 3 при х < 2
Определите, при каких значениях m прямая у = m имеет с графиком ровно две общие точки.
Приветствую всех на канале. Меня зовут Любовь. Даю онлайн-консультации по математике для педагогов, родителей, учащихся.
Построение.
Шаг 1. Строим график функции у = х – 3 при х < 2.
Зная, что на графике это часть прямой, можно найти координаты только двух точек для построения. Найдём значение у при выбранных значениях х из промежутка х < 2.
Икс, равное двум, тоже возьмём, но потом эту точку уберём из графика.
При х = 2 у = 2 – 3 = -1
При х = 0 у = 0 – 3 = -3
Строим полупрямую по двум точкам с координатами (2;-1) и (0;-3)
Шаг 2. Строим график функции у = х² – 6х + 6 при
х ≥ 2.
Зная, что на графике это часть параболы, используем определённый алгоритм построения.
1) По формуле х = -b/2а, где а и b коэффициенты уравнения у = х² – 6х + 6, находим первую координату вершины параболы. В нашем случае коэффициенты b =-6, а а=1.
x = -(-6) /2•1 = 3
2) Находим вторую координату вершины параболы, подставив в уравнение у = х² – 6х + 6 вместо х число 3.
у=3² – 6•3 + 6 = 9 -18 + 6=-3
Итак, (3;-3) – координаты вершины параболы.
3) Переносим систему координат в точку с координатами (3;-3) и строим от этой точки как от начала координат часть параболы у =х².
У нас получился график сложной функции с разрывом.
Отвечаем на вопрос: при каких значениях m прямая у = m имеет с графиком ровно две общие точки?
Прямые у = m при разных значениях m – это прямые, параллельные оси х. Их можно провести бесконечно много. Смотрим, какие из них пересекают график ровно в двух точках. Во-первых, это прямая у=-3
Во-вторых, это множество прямых на промежутке от (-2;-1) по оси у
Даём чёткий ответ: Прямая у = m имеет с графиком ровно две общие точки при m =-3 и когда m принадлежит промежутку от (-2:-1).
Была несколько лет экспертом по проверке 2 части экзаменационных работ и знаю, что задание 22 оценивается в 2 балла. Если учащиеся построили верно график – это 1 балл, если ответили правильно на вопрос – ещё 1 балл.
Дорогие девятиклассники!
Успешной сдачи экзаменов в этом году. Удачи и успехов в подготовке!
График кусочно заданной функции
Построить график кусочно заданной функции — один из видов задания 23 из ОГЭ по математике.
Рассмотрим примеры построения таких графиков.
1) Постройте график функции
![Rendered by QuickLaTeX.com [ y = left{ begin{array}{l} 2x - 2,_x < 3; \ - 3x + 13,npu_3 le x le 4; \ 1,5x - 5,npu_x > 4. \ end{array} right, ]](https://www.algebraclass.ru/wp-content/ql-cache/quicklatex.com-424f8d439a602a1dde9dd4e2fb91622b_l3.png)
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
График данной функции состоит из трёх частей.
Значения x=3 и x=4 разбивают числовую прямую на три промежутка, на каждом из которых рассмотрим отдельную функцию.
Соответственно, прямые x=3 и x=4 разбивают координатную плоскость на три области.
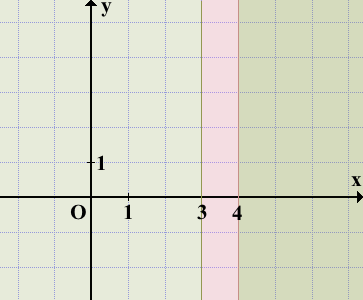
Каждый из графиков строится в своей области и не должен выходить за её пределы.
Чтобы не нарушить это правило, можно прямые x=3 и x=4 (прямые, параллельные оси Oy) выделить на черновике тонкой линией либо пунктиром. В чистовой вариант, разумеется, их переносить не нужно.
Итак, рассмотрим на трёх промежутках три различные функции.
1) Если x<4, y=2x-2.
y=2x-2 — линейная функция. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки.
При x=0 y=2·0-2=-2, получили точку (0;-2).
При x=2 y=2·2-2=2, получили точку (2;2).
Обычно для построения графика оформляют таблицу:
![]()
Значения x можно брать, вообще говоря, любые. Главное, не забыть, что данная прямая не должна выходить правее x=3. Поэтому всё же лучше выбирать x, удовлетворяющие условию x<3.
2) Если 3≤x≤4, y=-3x+13.
y=-3x+13 — линейная функция. График — прямая. Для построения прямой берём две точки.
![]()
3) Если x>4, y=1,5x-5.
y=1,5x-5 — линейная функция. График — прямая. для построения прямой берём две точки.
![]()
Отметим каждую пару точек и проведём через них прямые, не забывая об ограничениях.
Получим график, состоящий их двух лучей и одного отрезка:
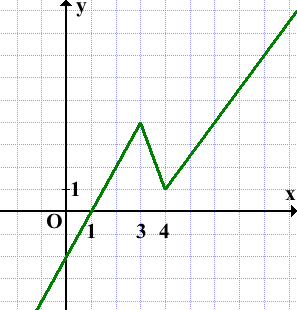
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через точки соединения двух частей графика, то есть при m=1 и m=4:
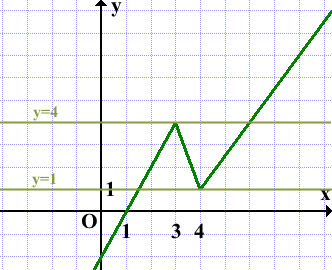
Ответ: 1; 4.
2) Постройте график функции
![]()
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥4, y=x²-10x+27.
y=x²-10x+27 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=1>0).
Ищем координаты вершины параболы.
![]()
![]()
Таким образом, (5;2) — вершина параболы.
Так как a=1, от вершины строим параболу y=x².
(Другой вариант — переписать правую часть формулы в виде y=(x²-10x+25)+2=(x-5)²+2 и построить график параллельным переносом графика y=x² на 5 единиц вправо вдоль оси Ox и на 2 единицы вверх вдоль оси Oy).
2) Если x<4, y=x-1.
y=x-1 — линейная функция. График — прямая. Для построения прямой берём две точки:
![]()
Хотя на x наложено условие x<4, для построения прямой можно брать любые значение. Главное — не забыть, что правее x=4 прямая не должна выходить.
Итак, график данной функции состоит из двух частей. Прямая x=4 разделяет плоскость на две полуплоскости. Справа от неё расположена часть параболы с вершиной в точке (5;2), слева — прямая:
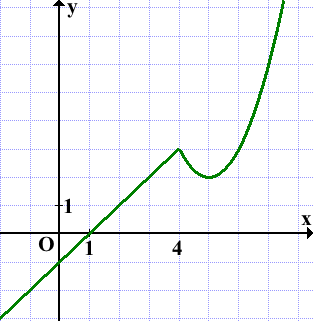
Прямая y=m имеет с графиком ровно две общие точки, если она проходит через вершину параболы и через точку соединения параболы и прямой, то есть при m=2 и m=3:
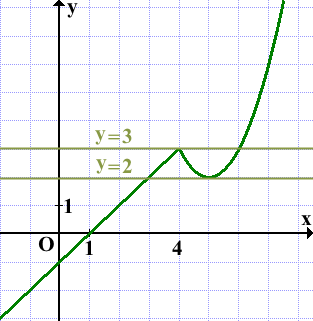
Ответ: 2; 3.
3) Построить график функции
![]()
и определить, при каких значениях m прямая y=m имеет с графиком одну или две общие точки.
Решение:
Область определения функции D(y): x∈R.
1) Если x≥-3, y=x²+4x+4.
y=x²+4x+4 — квадратичная функция. График — парабола ветвями вверх. Можно найти координаты вершины параболы и от вершины построить график функции y=x².
(Если заметить в правой части формулу квадрата суммы и переписать формулу функции y=(x+4)², то можно построить параболу параллельным переносом параболы y=x² на 4 единицы влево вдоль оси Ox).
2) Если x<-3,
![]()
— функция обратной пропорциональности. График — гипербола. Для построения гиперболы нужно взять несколько точек:
![]()
Таким образом, график данной функции состоит из двух частей. Справа от прямой x=-3 строим параболу с вершиной в точке (-2;0), слева — ветвь гиперболы:
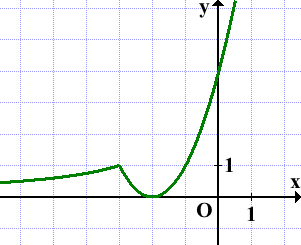
Прямая y=m имеет с графиком одну или две общие точки при m=0 и m≥1:
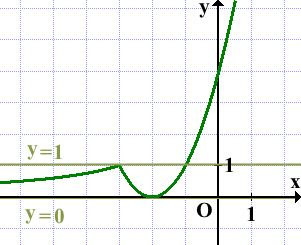
Ответ: m=0 и m∈[1;∞).
Как построить график функции (у = f(x) + n), если известен график функции (у = f(x))
Пусть заданы функций
y=x2
и
y=x2+2
. Выполним построение графиков этих функций в одной системе координат. Составлям таблицу значений функции
y=x2+2
:
| (x) | (0) | (1) | (-1) | (2) | (-2) |
| (y) | (2) | (3) | (3) | (4) | (4) |
Отмечаем точки ((0; 2), (1; 3), (-1; 3), (2; 4), (-2; 4)) на координатной плоскости и соединяем их плавной линией. В результате получится график — парабола.

Обрати внимание!
Получили такую же параболу, как и
y=x2
, но только сдвинутую вдоль оси (y) на (2) единицы масштаба вверх. Вершина параболы сейчас в точке ((0; 2)), а не в точке ((0; 0)), как для параболы
y=x2
. Ось симметрии — прямая (x = 0), как и для графика функции
y=x2
.
При построении в одной системе координат двух графиков функций
y=x2
и
y=x2−3
увидим, что график функции
y=x2−3
получается из графика функции
y=x2
путём параллельного переноса вдоль оси ординат на (3) единицы масштаба вниз.

Аналогичные смещения происходят с графиками других функций. К примеру, для построения графика функции
y=2×2−1
необходимо построить базовую параболу
y=2×2
и сдвинуть её вниз (т. е. параллельно перенести) вдоль оси (y) на (1) единицу масштаба.

Верно утверждение:
для построения графика функции (y = f(x) + n), где (n) — указанное положительное число, необходимо график функции (y= f(x)) поднять вдоль оси (y) на (n) единиц масштаба; для построения графика функции (y = f(x) – n), где (n) — указанное положительное число, необходимо график функции (y = f(x)) опустить вдоль оси (y) на (n) единиц масштаба.
Обрати внимание!
Направление сдвига определяется знаком числа (n): при (n > 0) график сдвигается вверх, а при (n < 0) — вниз.
Прежде чем перейти к разбору квадратичной функции рекомендуем вспомнить, что называют
функцией в математике.
Если вы прочно закрепите общие знания о функции (способы задания, понятие графика)
дальнейшее изучение других
видов функций будет даваться значительно легче.
Что называют квадратичной функцией
Запомните!
![]()
Квадратичная функция — это функция вида
y = ax2 + bx + c,
где a,
b и с — заданные числа.
Другими словами можно сказать, что если в функции старшая (то есть самая большая) степень,
в которой стоит «x» — это «2»,
то перед нами квадратичная функция.
Рассмотрим примеры квадратичных функций и определим, чему в них равны коэффициенты «a»,
«b» и «с».
| Квадратичная функция | Коэффициенты |
|---|---|
| y = 2x2 − 7x + 9 |
|
| y = 3x2 − 1 |
|
| y = −3x2 + 2x |
|
Как построить график квадратичной функции
Запомните!
![]()
График квадратичной функции называют параболой.
Парабола выглядит следующим образом.
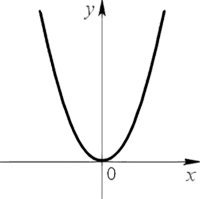
Также парабола может быть перевернутой.
Существует четкий алгоритм действий при построении графика квадратичной функции.
Рекомендуем при построении параболы всегда следовать этому порядку действий, тогда вы сможете избежать ошибок при построении.
Чтобы было проще понять этот алгоритм, сразу разберем его на примере.
Построим график квадратичной функции «y = x2 −7x + 10».
- Направление ветвей параболы
Запомните!

Если «a > 0», то ветви направлены вверх.

Если «a < 0», то ветви направлены вниз.

В нашей функции «a = 1», это означает, что ветви параболы направлены вверх.

- Координаты вершины параболы
Запомните!

Чтобы найти «x0»
(координата вершины по оси «Ox»)
нужно использовать формулу:Найдем «x0» для нашей функции «y = x2 −7x + 10».
Теперь нам нужно найти «y0»
(координату вершины по оси «Oy»).
Для этого нужно подставить найденное значение «x0» в исходную функцию.
Вспомнить, как найти значение функции можно в уроке
«Как решать задачи на функцию» в подразделе
«Как получить значение функции».y0(3,5) =
(3,5)2 − 7 ·3,5 + 10 = 12,25 − 24,5 + 10 =−12,25 + 10 = −2,25
Выпишем полученные координаты вершины параболы.
(·) A (3,5; −2,25) — вершина параболы.
Отметим вершину параболы на системе координат.
Проведем через отмеченную точку ось симметрии, так как парабола — это симметричный график
относительно оси «Oy».
- Нули функции
Для начала давайте разберемся, что называют нулями функции.
Запомните!

Нули функции — это точки пересечения графика функции с осью «Ox»
(осью абсцисс).Наглядно нули функции на графике выглядят так:
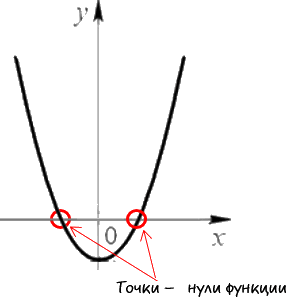
Свое название нули функции получили из-за того, что у этих точек координата
по оси «Oy» равна нулю.Теперь давайте разберемся, как до построения графика функции рассчитать координаты точек нулей функции.
Запомните!

Чтобы найти координаты точек нулей функции, нужно в исходную функцию подставить вместо
«y = 0».Подставим в заданную функцию «y = x2 −7x + 10»
вместо «y = 0» и решим полученное
квадратное уравнение
относительно
«x» .0 = x2 −7x + 10
x2 −7x + 10 = 0x1;2 =
7 ±
√49 − 4 · 1 · 102 · 1 x1;2 =
x1;2 =
x1 = x2 =
x1 = x2 =
x1 = 5 x2 = 2
Мы получили два корня в уравнении, значит, у нас две точки пересечения
с осью «Ox».
Назовем эти точки и выпишем их координаты.- (·) B (5; 0)
- (·) C (2; 0)
Отметим полученные точки («нули функции») на системе координат.

- Дополнительные точки для построения графика
Возьмем четыре произвольные числовые значения для «x».
Целесообразно брать целые числовые значения на оси «Ox»,
которые наиболее близки к оси
симметрии. Числа запишем в таблицу в порядке возрастания.x 1 3 4 6 y Для каждого выбранного значения «x»
рассчитаем «y».- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
4 -
y(3) = 32 − 7 · 3 + 10 = 9 − 21 + 10 =
−2 -
y(4) = 42 − 7 · 4 + 10 = 16 − 28 + 10 =
−2 -
y(6) = 62 − 7 · 6 + 10 = 36 − 42 + 10 =
4
Запишем полученные результаты в таблицу.
x 1 3 4 6 y 4 −2 −2 4 Отметим полученные точки графика на системе координат (зеленые точки).
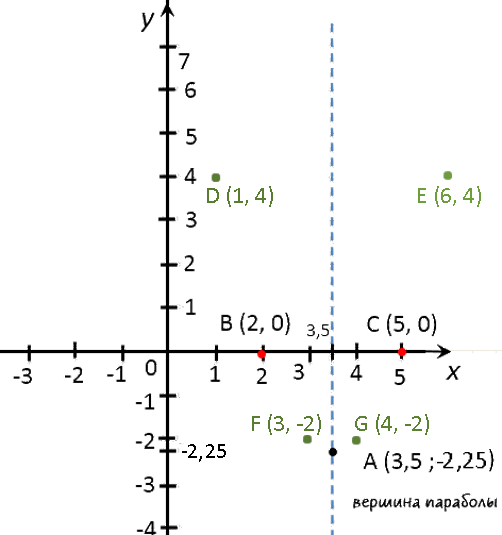
Теперь мы готовы построить график.
На забудьте после построения подписать график функции.
- y(1) = 12 − 7 · 1 + 10 = 1 − 7 + 10 =
Краткий пример построения параболы
Рассмотрим другой пример построения графика квадратичной функции.
Только теперь запишем алгоритм построения коротко без подробностей.
Пусть требуется построить график функции
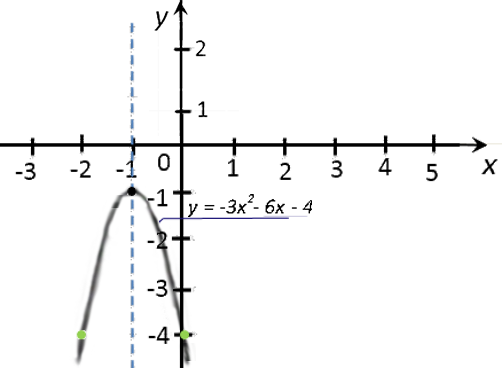
«y = −3x2 − 6x − 4».
- Направление ветвей параболы
- Координаты вершины параболы
x0 =
x0 = == −1
y0(−1) = (−3) · (−1)2 − 6 · (−1) − 4 =
−3 · 1 + 6 − 4 = −1(·) A (−1; −1)
— вершина параболы.
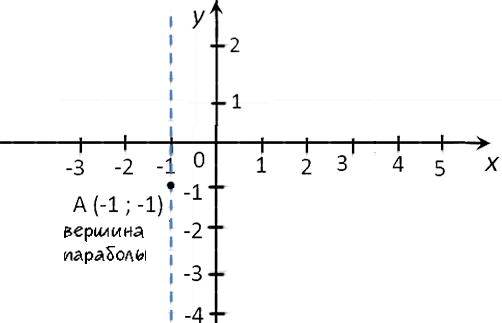
- Нули функции
Точки пересечения с осью «Ox» (y = 0).
0 = −3x2 − 6x − 4
−3x2 − 6x − 4 = 0 |·(−1)
3x2 + 6x + 4 = 0
x1;2 =
−6 ±
√62 − 4 · 3 · 42 · 1 x1;2 =
x1;2 =
Ответ: нет действительных корней.Так как корней нет, значит, график функции не пересекает ось
«Ox». - Вспомогательные точки для: «x = −3»;
«x = −2»;
«x = 0»;
«x = 1». Подставим в исходную функцию
«y = −3x2 − 6x − 4».- y(−3) = −3 · (−3)2 − 6 · (−3) − 4
= −3 · 9 + 18 − 4 = −27 + 14 = −13 -
y(−2) = −3 · (−2)2 − 6 · (−2) − 4
= −3 · 4 + 12 − 4 = −12 + 12 − 4 = −4 -
y(0) = −3 · 02 − 6 · 0 − 4
= −4 -
y(1) = −3 · 12 − 6 · 1 − 4
= −3 −6 − 4 = −13
x −3 −2 0 1 y −13 −4 −4 −13 - y(−3) = −3 · (−3)2 − 6 · (−3) − 4
«a = −3» — ветви параболы направлены вниз.

Отметим вспомогательные точки. Отмечаем на системе координат только те точки, которые
не выходят за масштаб нашей системы координат, то есть точки
«(−2; −4)» и «(0; −4)».
Построим и подпишем график функции.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:

© 2007 – 2023 Сообщество учителей-предметников “Учительский портал”
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.
Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.
Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.
Фотографии предоставлены 
