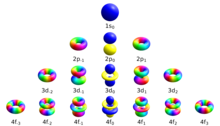| Ароматы в физике элементарных частиц |
|---|
| Ароматы |
|
| Чётность |
|
| Квантовые числа |
|
| Заряды |
|
| Комбинации |
|
| См. также |
|
Магни́тное ква́нтовое число́ (m) — квантовое число, параметр, который вводится при решении уравнения Шрёдингера для электрона в водородоподобном атоме (и вообще для любого движения заряженной частицы). Магнитное квантовое число характеризует ориентацию в пространстве орбитального момента импульса электрона или пространственное расположение атомной орбитали. Оно принимает целые значения от -l до +l, где l — орбитальное квантовое число, то есть имеет ровно столько значений, сколько орбиталей существует на каждом подуровне.
История[править | править код]
В 1896 году голландский физик Питер Зееман поместил в сильное магнитное поле устройство, аналогичное водородной лампе, но наполненное парами раскалённого натрия (Фарадей ставил аналогичный эксперимент в 1862 г. и потерпел неудачу). Обнаружилось, что в магнитном поле число линий в спектрах испускания возрастает. Спектры становятся сложными, но можно показать, что каждая p-линия распадается в магнитном поле на 3 новых линии, каждая d-линия — на 5, каждая f-линия — на 7 линий, а s-линии не изменяются.
Поскольку орбитали атома становятся «видны» только в магнитном поле, очередное квантовое число, записывающее «адрес» орбитали в атоме, назвали магнитным квантовым числом.
Характеристики[править | править код]
Каждое из 2l+1 возможных значений магнитного квантового числа определяет проекцию вектора орбитального момента на данное направление (обычно ось z). Проекция орбитального момента импульса на ось z равна 
Поскольку с орбитальным моментом связан магнитный момент, то магнитное квантовое число, в частности, определяет проекцию орбитального магнитного момента водородоподобного атома на направление магнитного поля и служит причиной расщепления спектральных линий атома в магнитном поле.
Иногда магнитное квантовое число определяют для проекции любого момента частицы (орбитального L, спинового S, суммарного J=L+S). В этом случае оно принимает соответственно 2L+1, 2S+1, 2J+1 значений. Для проекций спинового и суммарного моментов магнитное квантовое число может быть полуцелым.
Магнитное квантовое число в переходах между уровнями может изменяться лишь на определённое значение, устанавливаемое правилами отбора для данного типа перехода.
Олег Лебедь
Эксперт по предмету «Химия»
Задать вопрос автору статьи
Введение
Состояние каждого электрона в атоме описывается волновой функцией, которая называется атомной орбиталью (или уровнем) и характеризуется тремя квантовыми числами. Соответствующие волновые функции выводятся из уравнения Шредингера и должны удовлетворять следующим требованиям: непрерывность, однозначность и конечность каждой волновой функции. При нарушении хотя бы одного из этих требований волновая функция оказывается непригодной для описания состояния электронов в атоме. Следовательно, дискретность энергетических состояний, в которых могут находиться электроны в атоме, является прямым следствием уравнения Шредингера. То же касается и трех квантовых чисел.
Главное квантовое число
Главное квантовое число может принимать любое целочисленное значение:
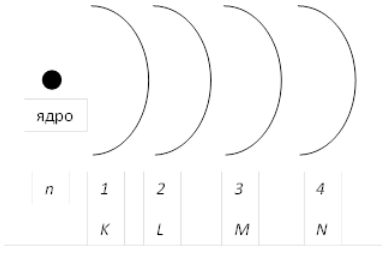
Но атомы известных в настоящее время элементов в стационарном состоянии (т.е. невозбужденные) не содержат электроны, для описания которых необходимы были бы атомные орбитали (уровни) с $n > 7$. Поэтому, в общем случае, реальным верхним пределом изменения главного квантового числа является значение $7$. Главное квантовое число характеризует энергию электрона на соответствующей орбитали. Или, проще говоря, степень удаленности данной орбитали от ядра атома (рис. 1). Чем меньше $n$, тем больше энергия связи электрона с ядром, т.е. тем большее, при прочих равных условиях, количество энергии требуется для удаления этого электрона из атома (эта энергия называется энергией ионизации).
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рисунок 1. Схема раположений орбиталей атома
Забегая вперед, стоит сказать, что иногда для краткости записи электронной конфигурации атома вместо главного квантового числа используется буквенное обозначение соответствующих орбиталей (рис. 1): $K (n = 1)$, $L (n = 2)$, $M (n = 3)$, $N (n = 4)$, и так далее по алфавиту.
Орбитальное квантовое число
Орбитальное квантовое число $l$ может принимать значения от $0 до(n – 1)$:
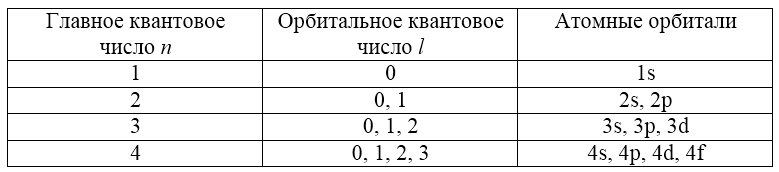
Таким образом, $l$ для первых четырех значений главного квантового числа $n$ принимает следующие значения:
Рисунок 2.
«Квантование» 👇
Орбитальное квантовое число определяет форму соответствующего электронного облака (рис. 4). В записи электронной конфигурации атома оно обозначается по первым буквам английских наименований соответствующих спектральных линий $(sharp – s$, $principal – p$, $diffuse – d$, $fundamental – f$):
Рисунок 3.
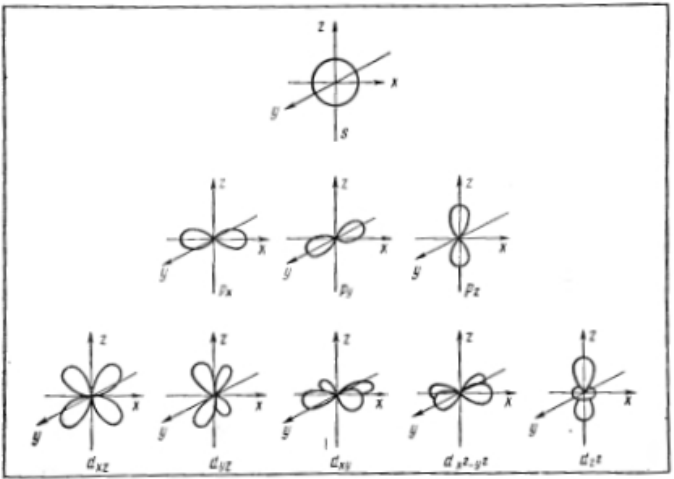
Рисунок 4. Формы электронных облаков атомных $s-$, $p-$, $d-$ орбиталей и их пространственное расположение
Таким образом, для каждого значения $n$ возможны строго определенные (по количеству и характеру) атомные орбитали (подуровни):
Рисунок 5.
Причем значения энергии электронов на соответствующих орбиталях таковы, что подуровень $4s$ расположен ближе к ядру, чем $3d$. Это правило пригодится при решении задач на составление электронных конфигураций атомов.
Магнитное квантовое число
Магнитное квантовое число m может принимать любые целочисленные значения от $+l$ до $-l$, включая $0$, и характеризует расположение соответствующей орбитали в пространстве атома:
Количество значений магнитного квантового числа определяется значением орбитального квантового числа $l$ и равно $(2l + 1)$:
Рисунок 6.
При заданных значениях $n$ и $l$ все возможные атомные орбитали независимо от значений m имеют одинаковую энергию, т.е. являются вырожденными. Кратность вырождения определяется числом атомных орбиталей с одинаковой энергией, т.е. числом значений m при заданном значении $l$. Таким образом, $s$-состояние электрона является вырожденным ($m = 0$), $p$-состояние – трехкратновырожденным ($m = 1$, $0$, $-1$), $d$- состояние – пятикратновырожденным, и.т.д.
Физический смысл магнитного квантового числа схематично представлен на рис. 7, где клетки – это, по сути, места, которые могут быть заняты электронами.
Спиновое квантовое число
Кроме всего прочего, электроны в атоме отличаются собственным моментом количества движения, который условно можно представить как вращение вокруг собственной оси. Это вращение характеризуется спиновым квантовым числом s, которое может иметь лишь два значения $+1/2$ и $-1/2$ (условно говоря, вращение по часовой стрелке и против часовой стрелки).
Примеры решения типовых задач
Пример 1
Записать электронную конфигурацию атома гелия в основном состоянии.
Решение. Главное квантовое число $n = 1$, орбитальное квантовое число $l = n – 1 = 0$, что соответствует s-состоянию. Таким образом, электронная конфигурация атома гелия $1s^2$, где индекс $2$ указывает на число электронов, занимающих орбиталь $1s$.
Пример 2
Записать электронную конфигурацию атома железа с порядковым номером $26$.
Решение. В соответствии с порядком заполнения атомных орбиталей имеем $1s^22s^22p^63s^23p^64s^23d^6$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Материалы портала onx.distant.ru
Квантовые числа
Общая характеристика квантовых чисел
Принцип (запрет) Паули
Правило Хунда
Примеры решения задач
Задачи для самостоятельного решения
Общая характеристика квантовых чисел
Главное квантовое число n характеризует энергию электрона в атоме и размер электронной орбитали. Оно соответствует также номеру электронного слоя, на котором находится электрон. Совокупность электронов в атоме с одинаковым значением главного квантового числа n называют электронным слоем (энергетическим уровнем). n – принимает значения 1, 2, 3, …, ∞ . Энергетические уровни обозначают прописными латинскими буквами:
| Значение n | 1 | 2 | 3 | 4 | 5 | 6 |
| Обозначение слоя | K | L | M | N | O | P |
Различия в энергиях электронов, принадлежащих к различным подуровням данного энергетического уровня, отражает побочное (орбитальное) квантовое число l. Электроны в атоме с одинаковыми значениями n и l составляют энергетический подуровень (электронную оболочку). Максимальное число электронов в оболочке Nl:
Nl = 2(2l + 1). (1)
Побочное квантовое число принимает целые значения 0, 1, … (n – 1). Обычно l обозначается не цифрами, а буквами:
| Значение l | 0 | 1 | 2 | 3 | 4 |
| Обозначение орбитали | s | p | d | f | g |
Орбиталь – пространство вокруг ядра, в котором наиболее вероятно нахождение электрона.
Побочное (орбитальное) квантовое число l характеризует различное энергетическое состояние электронов на данном уровне, форму орбитали, орбитальный момент импульса электрона.
Таким образом, электрон, обладая свойствами частицы и волны, движется вокруг ядра, образуя электронное облако, форма которого зависит от значения l. Так, если l = 0, (s-орбиталь), то электронное облако имеет сферическую симметрию. При l = 1 (p-орбиталь) электронное облако имеет форму гантели. d-орбитали имеют различную форму: dz2 — гантель, расположенная по оси Z с тором в плоскости X – Y, dx2 — y2 — две гантели, расположенные по осям X и Y; dxy, dxz, dyz, — две гантели, расположенные под 45o к соответствующим осям.
- Формы электронных облаков для различных состояний электронов в атомах
Магнитное квантовое число ml характеризует ориентацию орбитали в пространстве, а также определяет величину проекции орбитального момента импульса на ось Z. ml принимает значения от +l до — l, включая 0. Общее число значений ml равно числу орбиталей в данной электронной оболочке.
Магнитное спиновое квантовое число ms характеризует проекцию собственного момента импульса электрона на ось Z и принимает значения +1/2 и –1/2 в единицах h/2p (h – постоянная Планка).
Принцип (запрет) Паули
В атоме не может быть двух электронов со всеми четырьмя одинаковыми квантовыми числами. Принцип Паули определяет максимальное число электронов Nn, на электронном слое с номером n:
Nn = 2n2. (2)
На первом электронном слое может находиться не более двух электронов, на втором – 8, на третьем – 18 и т. д.
Правило Хунда
Заполнение энергетических уровней происходит таким образом, чтобы суммарный спин был максимальным. Например, три р-электрона на орбиталях р-оболочки располагаются следующим образом:
Таким образом, каждый электрон занимает одну р-орбиталь.
Примеры решения задач
Задача 1. Охарактеризуйте квантовыми числами электроны атома углерода в невозбужденном состоянии. Ответ представьте в виде таблицы.
Решение. Электронная формула атома углерода: 1s22s22p2. В первом слое атома углерода находятся два s-электрона с антипараллельными спинами, для которых n = 1. Для двух s-электронов второго слоя n = 2. Спины двух р-электронов второго слоя параллельны; для них m s= +1/2.
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
| 6 | 2 | 1 | 0 | +1/2 |
Задача 2. Охарактеризуйте квантовыми числами внешние электроны атома кислорода в основном состоянии. Ответ представьте в виде таблицы.
Решение. Электронная формула атома кислорода: 1s22s22p4. Во внешнем слое у этого атома находятся 6 электронов 2s22p4. Значения их квантовых чисел приведены в таблице.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 | 0 | 0 | –1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | –1 | +1/2 |
| 6 | 2 | 1 | 1 | –1/2 |
Задача 3. Охарактеризуйте квантовыми числами пять электронов, находящихся в состоянии 4d. Ответ представьте в виде таблицы.
Решение. Согласно правилу Хунда электроны в квантовых ячейках располагаются следующим образом:
Значения главного, побочного и спинового квантовых чисел у электронов одинаковы и равны n=4, l=2, ms=+1/2. Рассматриваемые электроны отличаются значениями квантовых чисел ml.
| № электрона | n | l | ml | ms |
| 1 | 4 | 2 | 2 | +1/2 |
| 2 | 4 | 2 | 1 | +1/2 |
| 3 | 4 | 2 | 0 | +1/2 |
| 4 | 4 | 2 | –1 | +1/2 |
| 5 | 4 | 2 | –2 | +1/2 |
Задача 4. Рассчитайте максимальное число электронов в электронном слое с n = 4.
Решение. Максимальное число электронов, обладающих данным значением главного квантового числа, рассчитываем по формуле (2). Следовательно, в третьем энергетическом уровне может быть не более 32 электронов.
Задача 5. Рассчитайте максимальное число электронов в электронной оболочке с l = 3.
Решение:
Максимальное число электронов в оболочке определяется выражением (1). Таким образом, максимальное число электронов в электронной оболочке с l = 3 равно 14.
Задачи для самостоятельного решения
1. Охарактеризуйте квантовыми числами электроны атома бора в основном состоянии. Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| № электрона | n | l | ml | ms |
| 1 | 1 | 0 | 0 | +1/2 |
| 2 | 1 | 0 | 0 | –1/2 |
| 3 | 2 | 0 | 0 | +1/2 |
| 4 | 2 | 0 | 0 | –1/2 |
| 5 | 2 | 1 | 1 | +1/2 |
2. Охарактеризуйте квантовыми числами d-электроны атома железа в основном состоянии. Ответ представьте в виде таблиц:
Расположение 3d-электронов атома железа на орбиталях:
| ? | ? | ? | ? | ? |
Значения квантовых чисел этих электронов:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
Шесть 3d-электронов атома железа располагаются на орбиталях следующим образом
Квантовые числа этих электронов приведены в таблице
| № электрона | n | l | ml | ms |
| 1 | 3 | 2 | 2 | +1/2 |
| 2 | 3 | 2 | 1 | +1/2 |
| 3 | 3 | 2 | 0 | +1/2 |
| 4 | 3 | 2 | — 1 | +1/2 |
| 5 | 3 | 2 | — 2 | +1/2 |
| 6 | 3 | 2 | 2 | — 1/2 |
3. Каковы возможные значения магнитного квантового числа ml, если орбитальное квантовое число l = 3?
Ответ: ml = +3; +2; +1; 0, — 1, — 2, — 3.
4. Охарактеризуйте квантовыми числами находящиеся во втором электронном слое электроны:
Ответ представьте в виде таблицы:
| № электрона | n | l | ml | ms |
| 1 | ? | ? | ? | ? |
| 2 | ? | ? | ? | ? |
| 3 | ? | ? | ? | ? |
| 4 | ? | ? | ? | ? |
| 5 | ? | ? | ? | ? |
| 6 | ? | ? | ? | ? |
| 7 | ? | ? | ? | ? |
Ответ: Электронная конфигурация 2s22p5. Главное квантовое число для всех электронов равно 2. Для s электронов l = 0, для р-электронов l = 1.
| № электрона | n | l | ml | ms |
| 1 | 2 | 0 | 0 | +1/2 |
| 2 | 2 |
0 |
0 | — 1/2 |
| 3 | 2 | 1 | 1 | +1/2 |
| 4 | 2 | 1 | 0 | +1/2 |
| 5 | 2 | 1 | — 1 | +1/2 |
| 6 | 2 | 1 | 1 | — 1/2 |
| 7 | 2 | 1 | 0 |
— 1/2 |
5. Определите максимальное число электронов на электронном слое, для которого главное квантовое число n = 6.
6. Определите максимальное число электронов на электронной оболочке, для которой побочное квантовое число l = 4.
7. Определите максимальное число электронов на третьем слое.
8. Определите максимальное число электронов на 5d электронной оболочке.
9. Какие значения может принимать орбитальное (побочное) квантовое число l?
Для описания положения электрона в электронной оболочке используют четыре квантовых числа. Здесь мы не будем углубляться в квантово-механические подробности и опишем только утилитарный смысл данных чисел. Набор, состоящий из четырёх квантовых чисел – это «адрес» электрона в электронной оболочке.
Главное квантовое число `n` – определяет полную энергию электрона на энергетическом уровне и показывает, из скольких энергетических уровней состоит электронная оболочка атома. Принимает целочисленные положительные значения от `1` до `oo`. В периодической таблице Д. И. Менделеева `n` равно номеру периода.
Орбитальное квантовое число `l` показывает, сколько энергетических подуровней составляют данный уровень и характеризует форму орбиталей. Принимает значения от `0` до `(n-1)`.
При `n=1`, `l` принимает только одно значение `0` (этому числовому значению соответствует буквенное `s`), следовательно, на первом энергетическом уровне только один подуровень – `s`. Орбиталь `s`-подуровня имеет сферическую форму (рис. 1).
При `n=2`, `l` принимает два значения: `0` `(s)` и `1` `(p)`. Энергетический уровень состоит из двух подуровней – `s` и `p`. Форма `p`-орбитали похожа на объёмную восьмёрку (рис. 1).
При `n=3`, `l` принимает уже три значения: `0` `(s)`; `1` `(p)` и `2` `(d)`. Таким образом, на третьем уровне три подуровня. Орбитали `d`-подуровня имеют форму двух перекрещённых объёмных восьмёрок либо объёмной восьмерки с перемычкой (рис. 1).
При `n=4`, значений `l` уже четыре, следовательно, и подуровней на четвёртом уровне четыре. К перечисленным выше добавляется `3` `(f)`. Орбитали `f`-подуровня имеют более сложную, объёмную, форму.
Магнитное квантовое число `ml` определяет число орбиталей на каждом подуровне и характеризует их взаимное расположение.
Принимает значения `-l` до `+l`, включая `0`.
При `l=0`, `m_l` принимает только одно значение – `0`. Следовательно, орбиталь, находящаяся на данном подуровне (`s`-подуровне), только одна. Мы уже знаем, что она имеет форму сферы с центром в начале координат.
При `l=1`, `m_l` принимает три значения: `−1`; `0`; `+1`. Значит, орбиталей на данном подуровне (`p`-подуровне) три. Так как `p`-орбитали представляют из себя объёмные восьмёрки (то есть линейной структуры), располагаются они в пространстве по осям координат, перпендикулярно друг другу (`p_x`, `p_y`, `p_z`).
При `l=2`, `m_l` принимает уже пять значений: `−2`; `−1`; `0`; `+1`; `+2`. То есть на `d`-подуровне располагаются пять орбиталей. Это плоскостные структуры, в пространстве занимают пять положений.
При `l=3`, то есть на `f`-подуровне, орбиталей становится семь, так как `m_l` – принимает семь значений (от `−3` до `+3` через `0`). Орбитали являются более сложными объёмными структурами, и взаимное их расположение еще более сложно.
Спиновое квантовое число `m_s` характеризует собственный момент количества движения электрона и принимает только два значения: `+1//2` и `-1//2`.
Электронная ёмкость подуровня (максимальное количество электронов на подуровне) может быть рассчитана по формуле `2(2l+1)`, а уровня – по формуле `2n^2`.
Всё вышесказанное можно обобщить в Таблице 2.
Таблица 2. Квантовые числа, атомные орбитали и число электронов на подуровнях (для `n<=4`)
|
`n` |
`l` |
Обозначение орбитали |
`ml` |
Число орбиталей |
Число электронов на подуровне |
|
`1` |
`0` |
`1s` |
`0` |
`1` |
`2` |
|
`2` |
`0` `1` |
`2s` `2p` |
`0` `−1`; `0`; `+1` |
`1` `3` |
`2` `6` |
|
`3` |
`0` `1` `2` |
`3s` `3p` `3d` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` |
`1` `3` `5` |
`2` `6` `10` |
|
`4` |
`0` `1` `2` `3` |
`4s` `4p` `4d` `4f` |
`0` `−1`; `0`; `+1` `−2`; `−1`; `0`; `+1`; `+2` `−3`; `−2`; `−1`; `0`; `+1`; `+2`; `+3` |
`1` `3` `5` `7` |
`2` `6` `10` `14` |
Химические свойства элементов и их соединений определяются электронным строением валентного уровня их атомов. Именно с участием электронов валентного уровня возникают химические связи между атомами и образуется соединение (вещество). Поэтому важно понимать правила заполнения электронных оболочек, строение валентного уровня и составлять электронную конфигурацию атомов элементов.
From Wikipedia, the free encyclopedia
In atomic physics, a magnetic quantum number is a quantum number used to distinguish quantum states of an electron or other particle according to its angular momentum along a given axis in space. The orbital magnetic quantum number (ml or m[a]) distinguishes the orbitals available within a given subshell of an atom. It specifies the component of the orbital angular momentum that lies along a given axis, conventionally called the z-axis, so it describes the orientation of the orbital in space. The spin magnetic quantum number ms specifies the z-axis component of the spin angular momentum for a particle having spin quantum number s. For an electron, s is 1⁄2, and ms is either +1⁄2 or −1⁄2, often called “spin-up” and “spin-down”, or α and β.[1][2] The term magnetic in the name refers to the magnetic dipole moment associated with each type of angular momentum, so states having different magnetic quantum numbers shift in energy in a magnetic field according to the Zeeman effect.[2]
The four quantum numbers conventionally used to describe the quantum state of an electron in an atom are the principal quantum number n, the azimuthal (orbital) quantum number 
, and the magnetic quantum numbers ml and ms. Electrons in a given subshell of an atom (such as s, p, d, or f) are defined by values of (0, 1, 2, or 3). The orbital magnetic quantum number takes integer values in the range from 
to 
, including zero.[3] Thus the s, p, d, and f subshells contain 1, 3, 5, and 7 orbitals each, with values of ml within the ranges 0, ±1, ±2, ±3 respectively. Each of these orbitals can accommodate up to two electrons (with opposite spins), forming the basis of the periodic table.
Other magnetic quantum numbers are similarly defined, such as mj for the z-axis component the total electronic angular momentum j,[1] and mI for the nuclear spin I.[2] Magnetic quantum numbers are capitalized to indicate totals for a system of particles, such as ML or mL for the total z-axis orbital angular momentum of all the electrons in an atom.[2]
Derivation[edit]
These orbitals have magnetic quantum numbers 
from left to right in ascending order. The 
dependence of the azimuthal component can be seen as a color gradient repeating 
times around the vertical axis.
There is a set of quantum numbers associated with the energy states of the atom. The four quantum numbers 
, , , and 
specify the complete quantum state of a single electron in an atom called its wavefunction or orbital. The Schrödinger equation for the wavefunction of an atom with one electron is a separable partial differential equation. (This is not the case for the neutral helium atom or other atoms with mutually interacting electrons, which require more sophisticated methods for solution[4]) This means that the wavefunction as expressed in spherical coordinates can be broken down into the product of three functions of the radius, colatitude (or polar) angle, and azimuth:[5]
The differential equation for 
can be solved in the form 
. Because values of the azimuth angle 
differing by 2
radians (360 degrees) represent the same position in space, and the overall magnitude of does not grow with arbitrarily large as it would for a real exponent, the coefficient 
must be quantized to integer multiples of 
, producing an imaginary exponent: 
.[6] These integers are the magnetic quantum numbers. The same constant appears in the colatitude equation, where larger values of 
tend to decrease the magnitude of 
and values of greater than the azimuthal quantum number do not permit any solution for 
| Relationship between Quantum Numbers | |||
|---|---|---|---|
| Orbital | Values | Number of Values for [7]
|
Electrons per subshell |
| s |  |
1 | 2 |
| p |  |
3 | 6 |
| d |  |
5 | 10 |
| f |  |
7 | 14 |
| g |  |
9 | 18 |
As a component of angular momentum[edit]
Illustration of quantum mechanical orbital angular momentum. The cones and plane represent possible orientations of the angular momentum vector for 
and 
. Even for the extreme values of , the 
-component of this vector is less than its total magnitude.
The axis used for the polar coordinates in this analysis is chosen arbitrarily. The quantum number refers to the projection of the angular momentum in this arbitrarily-chosen direction, conventionally called the -direction or quantization axis. 
, the magnitude of the angular momentum in the -direction, is given by the formula:[7]
.
This is a component of the atomic electron’s total orbital angular momentum 
, whose magnitude is related to the azimuthal quantum number of its subshell by the equation:
- ,
where 
is the reduced Planck constant. Note that this 
for 
and approximates 
for high . It is not possible to measure the angular momentum of the electron along all three axes simultaneously. These properties were first demonstrated in the Stern–Gerlach experiment, by Otto Stern and Walther Gerlach.[8]
Effect in magnetic fields[edit]
The quantum number refers, loosely, to the direction of the angular momentum vector. The magnetic quantum number only affects the electron’s energy if it is in a magnetic field because in the absence of one, all spherical harmonics corresponding to the different arbitrary values of are equivalent. The magnetic quantum number determines the energy shift of an atomic orbital due to an external magnetic field (the Zeeman effect) — hence the name magnetic quantum number. However, the actual magnetic dipole moment of an electron in an atomic orbital arises not only from the electron angular momentum but also from the electron spin, expressed in the spin quantum number.
Since each electron has a magnetic moment in a magnetic field, it will be subject to a torque which tends to make the vector parallel to the field, a phenomenon known as Larmor precession.
Notes[edit]
- ^ m is often used when only one kind of magnetic quantum number, such as ml or mj, is used in a text.
See also[edit]
- Quantum number
- Azimuthal quantum number
- Principal quantum number
- Spin quantum number
- Total angular momentum quantum number
- Electron shell
- Basic quantum mechanics
- Bohr atom
- Schrödinger equation
References[edit]
- ^ a b Martin, W. C.; Wiese, W. L. (2019). “Atomic Spectroscopy – A Compendium of Basic Ideas, Notation, Data, and Formulas”. National Institute of Standards and Technology, Physical Measurement Laboratory. NIST. Retrieved 17 May 2023.
- ^ a b c d Atkins, Peter William (1991). Quanta: A Handbook of Concepts (2nd ed.). Oxford University Press, USA. p. 297. ISBN 0-19-855572-5.
- ^ Griffiths, David J. (2005). Introduction to quantum mechanics (2nd ed.). Upper Saddle River, NJ: Pearson Prentice Hall. pp. 136–137. ISBN 0-13-111892-7. OCLC 53926857.
- ^ “Helium atom”. 2010-07-20.
- ^ “Hydrogen Schrodinger Equation”. hyperphysics.phy-astr.gsu.edu.
- ^ “Hydrogen Schrodinger Equation”. hyperphysics.phy-astr.gsu.edu.
- ^ a b Herzberg, Gerhard (1950). Molecular Spectra and Molecular Structure (2 ed.). D van Nostrand Company. pp. 17–18.
- ^ “Spectroscopy: angular momentum quantum number”. Encyclopædia Britannica.
