Как найти магнитное сопротивление цепи

Как найти магнитное сопротивление цепи


Расчет сопротивления проводника. Удельное сопротивление. Реостаты | Физика 8 класс #16 | Инфоурок

Видео: Расчет сопротивления проводника. Удельное сопротивление. Реостаты | Физика 8 класс #16 | Инфоурок

Содержание

  • Формулы и единицы измерения
  • Как рассчитывается магнитное сопротивление?
  • Разница с электрическим сопротивлением
  • Примеры
  • Соленоиды
  • Катушка намотана на прямоугольный железный сердечник
  • Решенные упражнения
  • – Упражнение 1
  • Решение
  • – Упражнение 2.
  • Решение
  • Ссылки

В магнитное сопротивление или магнитное сопротивление – это противодействие, которое среда представляет прохождению магнитного потока: чем выше сопротивление, тем сложнее установить магнитный поток. В магнитной цепи сопротивление играет ту же роль, что и электрическое сопротивление в электрической цепи.

Катушка, переносимая электрическим током, является примером очень простой магнитной цепи. Благодаря току создается магнитный поток, который зависит от геометрического расположения катушки, а также от силы тока, проходящего через нее.

Формулы и единицы измерения

Обозначив магнитный поток как Φм, у нас есть:

Φм = N.i / (ℓc / мкАc)

Куда:

-N – количество витков катушки.

-Сила тока составляет я.

-ℓc представляет длину цепи.

–Кc – площадь поперечного сечения.

-μ – проницаемость среды.

Фактор в знаменателе, который объединяет геометрию плюс влияние среды, и есть магнитное сопротивление цепи, скалярная величина, которая обозначается буквой, чтобы отличить ее от электрического сопротивления. Так:

ℜ = ℓc / мкАc

В Международной системе единиц (СИ) измеряется как величина, обратная генри (умноженная на количество витков N). В свою очередь, Генри – это единица измерения магнитной индукции, эквивалентная 1 тесла (Тл) x квадратный метр / ампер. Таким образом:

1 ЧАС-1 = 1 А /Т.м2

 Как 1 T.m2 = 1 Вебер (Wb), сопротивление также выражается в A / Wb (ампер / Вебер или, чаще, ампер-виток / Вебер).

Как рассчитывается магнитное сопротивление?

Поскольку магнитное сопротивление играет ту же роль, что и электрическое сопротивление в магнитной цепи, можно расширить аналогию с помощью эквивалента закона Ома V = IR для этих цепей.

Хотя он не циркулирует должным образом, магнитный поток Φм занимает место тока, а вместо напряжения V, определяет магнитное напряжение или магнитодвижущая сила, аналог электродвижущей силы илиf.e.m в электрических цепях.

Магнитодвижущая сила отвечает за поддержание магнитного потока. Сокращенно f.m.m и обозначается как ℱ. Таким образом, мы наконец получили уравнение, которое связывает три величины:

ℱ = Φм . ℜ

И сравнивая с уравнением Φм = N.i / (ℓc / мкАc), сделан вывод, что:

 ℱ = N.i

Таким образом, сопротивление может быть вычислено, зная геометрию контура и проницаемость среды, а также зная магнитный поток и магнитное напряжение, благодаря этому последнему уравнению, называемому Закон Гопкинсона.

Разница с электрическим сопротивлением

Уравнение магнитного сопротивления ℜ = ℓc / мкАc похож на R = L / σA на электрическое сопротивление. В последнем случае σ представляет собой проводимость материала, L – длину провода, а A – площадь его поперечного сечения.

Эти три величины: σ, L и A постоянны. Однако проницаемость среды μ, в общем, оно непостоянно, поэтому магнитное сопротивление цепи тоже непостоянно, в отличие от его электрического аналога.

Если происходит изменение среды, например, при переходе от воздуха к железу или наоборот, происходит изменение проницаемости с последующим изменением сопротивления. А также магнитные материалы проходят через циклы гистерезиса.

Это означает, что приложение внешнего поля заставляет материал сохранять часть магнетизма даже после того, как поле снято.

По этой причине каждый раз, когда рассчитывается магнитное сопротивление, необходимо тщательно определять, где материал находится в цикле, и, таким образом, знать его намагниченность.

Примеры

Хотя сопротивление сильно зависит от геометрии контура, оно также зависит от проницаемости среды. Чем выше это значение, тем меньше сопротивление; так обстоит дело с ферромагнитными материалами. С другой стороны, воздух имеет низкую проницаемость, поэтому его магнитное сопротивление выше.

Соленоиды

Соленоид – это обмотка длинойℓ сделано с N витками, через которые пропускается электрический ток I. Обычно витки намотаны по кругу.

Внутри него создается интенсивное и однородное магнитное поле, а снаружи поле становится примерно нулевым.

Если обмотке придать круглую форму, имеется тор. Внутри может быть воздух, но если поместить железный сердечник, магнитный поток будет намного выше, благодаря высокой проницаемости этого минерала.

Катушка намотана на прямоугольный железный сердечник

Магнитную цепь можно построить, намотав катушку на прямоугольный железный сердечник. Таким образом, когда через провод проходит ток, можно создать интенсивный поток поля, ограниченный внутри железного сердечника, как показано на рисунке 3.

Сопротивление зависит от длины цепи и площади поперечного сечения, указанной на рисунке. Показанная схема является однородной, так как сердечник выполнен из одного материала, а поперечное сечение остается однородным.

Решенные упражнения

– Упражнение 1

Найдите магнитное сопротивление прямолинейного соленоида с 2000 витками, зная, что, когда через него протекает ток 5 А, генерируется магнитный поток 8 мВт.

Решение

Уравнение используется ℱ = N.i для расчета магнитного натяжения, так как сила тока и количество витков в катушке доступны. Просто умножается:

ℱ = 2000 x 5 A = 10000 ампер-виток

Тогда используется ℱ = Φм . ℜ, стараясь выразить магнитный поток в Вебере (приставка «m» означает «милли», поэтому она умножается на 10 -3:

Φм = 8 х 10 -3 Wb

Теперь сопротивление очищено и подставлены значения:

ℜ = ℱ/ Φм = 10 000 ампер-витков / 8 x 10-3 Wb = 1,25 х 106 ампер-поворот / Вб

– Упражнение 2.

Рассчитайте магнитное сопротивление цепи, показанной на рисунке, с указанными размерами в сантиметрах. Проницаемость керна составляет μ = 0,005655 Тм / А, а площадь поперечного сечения постоянна, 25 см.2.

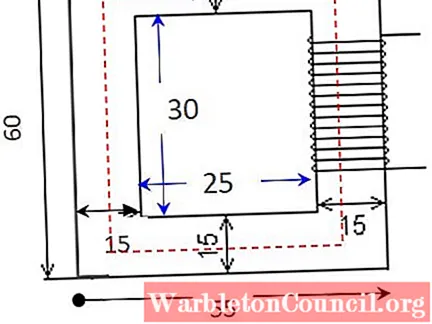
Решение

Применим формулу:

ℜ = ℓc / мкАc

Проницаемость и площадь поперечного сечения доступны как данные в отчете. Осталось найти длину контура, которая является периметром красного прямоугольника на рисунке.

Для этого длину горизонтальной стороны усредняют, добавляя большую длину и меньшую длину: (55 + 25 см) / 2 = 40 см. Затем действуйте таким же образом для вертикальной стороны: (60 + 30 см) / 2 = 45 см.

Наконец, складываются средние длины четырех сторон:

ℓc = 2 х 40 см + 2 х 45 см = 170 см 

Вычтите подставляемые значения в формуле сопротивления, но не раньше, чем выразите длину и площадь поперечного сечения, указанные в заявлении, в единицах СИ:

ℜ = 170 х 10 -2м / (0,005655 Tm / A x 0,0025 м2) = 120 248 ампер-оборот / Вб

Ссылки

  1. Алеман, М. Ферромагнитный сердечник. Получено с: youtube.com.
  2. Магнитная цепь и сопротивление. Получено с: mse.ndhu.edu.tw.
  3. Спинадел, Э. 1982. Электрические и магнитные цепи. Новая библиотека.
  4. Википедия. Магнитодвижущая сила. Получено с: es.wikipedia.org.
  5. Википедия. Магнитное сопротивление. Получено с: es.wikipedia.org.
Источник

From Wikipedia, the free encyclopedia

Magnetic reluctance

Common symbols

 {mathcal {R}}, {mathcal {S}}
SI unit H−1

Derivations from
other quantities

 {displaystyle {frac {1}{mathcal {P}}}}, {displaystyle {frac {mathcal {F}}{Phi }}}, {displaystyle {frac {l}{mu _{0}mu _{r}A}}}
Dimension M–1 L–2 T2 I2

Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.

Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm’s law in this respect. However, magnetic flux passing through a reluctance does not give rise to dissipation of heat as it does for current through a resistance. Thus, the analogy cannot be used for modelling energy flow in systems where energy crosses between the magnetic and electrical domains. An alternative analogy to the reluctance model which does correctly represent energy flows is the gyrator–capacitor model.

Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.

History[edit]

The term reluctance was coined in May 1888 by Oliver Heaviside.[1] The notion of “magnetic resistance” was first mentioned by James Joule in 1840.[2] The idea for a magnetic flux law, similar to Ohm’s law for closed electric circuits, is attributed to Henry Augustus Rowland in an 1873 paper.[3] Rowland is also responsible for coining the term magnetomotive force in 1880,[4] also coined, apparently independently, a bit later in 1883 by Bosanquet.[5]

Reluctance is usually represented by a cursive capital {displaystyle {mathcal {R}}}.

Definitions[edit]

In both AC and DC fields, the reluctance is the ratio of the magnetomotive force (MMF) in a magnetic circuit to the magnetic flux in this circuit. In a pulsating DC or AC field, the reluctance also pulsates (see phasors).

The definition can be expressed as follows:

{displaystyle {mathcal {R}}={frac {mathcal {F}}{Phi }}}

where

It is sometimes known as Hopkinson’s law and is analogous to Ohm’s Law with resistance replaced by reluctance, voltage by MMF and current by magnetic flux.

Permeance is the inverse of reluctance:

{displaystyle {mathcal {P}}={frac {1}{mathcal {R}}}}

Its SI derived unit is the henry (the same as the unit of inductance, although the two concepts are distinct).

Magnetic flux always forms a closed loop, as described by Maxwell’s equations, but the path of the loop depends on the reluctance of the surrounding materials. It is concentrated around the path of least reluctance. Air and vacuum have high reluctance, while easily magnetized materials such as soft iron have low reluctance. The concentration of flux in low-reluctance materials forms strong temporary poles and causes mechanical forces that tend to move the materials towards regions of higher flux so it is always an attractive force (pull).

The reluctance of a uniform magnetic circuit can be calculated as:

{displaystyle {mathcal {R}}={frac {l}{mu _{0}mu _{r}A}}={frac {l}{mu A}}}

where

Applications[edit]

  • Constant air gaps can be created in the core of certain transformers to reduce the effects of saturation. This increases the reluctance of the magnetic circuit, and enables it to store more energy before core saturation. This effect is also used in the flyback transformer.
  • Variable air gaps can be created in the cores by a movable keeper to create a flux switch that alters the amount of magnetic flux in a magnetic circuit without varying the constant magnetomotive force in that circuit.
  • Variation of reluctance is the principle behind the reluctance motor (or the variable reluctance generator) and the Alexanderson alternator. Another way of saying this is that the reluctance forces strive for a maximally aligned magnetic circuit and a minimal air gap distance.
  • Multimedia loudspeakers are typically shielded magnetically, in order to reduce magnetic interference caused to televisions and other CRTs. The speaker magnet is covered with a material such as soft iron to minimize the stray magnetic field.

Reluctance can also be applied to:

  • Reluctance motors
  • Variable reluctance (magnetic) pickups
  • Magnetic capacitance
  • Magnetic circuit
  • Magnetic complex reluctance

References[edit]

  1. ^ Heaviside O. (1892) Electrical Papers, Vol 2 – L.; N.Y.: Macmillan, p. 166
  2. ^ Joule J. (1884) Scientific Papers, vol 1, p.36
  3. ^ Rowland, Henry A. (1873). “XIV. On magnetic permeability, and the maximum of magnetism of iron, steel, and nickel”. Philosophical Magazine. Series 4. 46 (304): 140–159. doi:10.1080/14786447308640912.
  4. ^ Rowland, Henry A, “On the general equations of electro-magnetic action, with application to a new theory of magnetic attractions, and to the theory of the magnetic rotation of the plane of polarization of light” (part 2), American Journal of Mathematics, vol. 3, nos. 1–2, pp. 89–113, March 1880.
  5. ^ Bosanquet, R.H.M. (1883). “XXVIII.On magnetomotive force”. Philosophical Magazine. Series 5. 15 (93): 205–217. doi:10.1080/14786448308628457.
Источник

ТОЭ › Магнитные цепи

Магнитной цепью называется устройство, отдельные участки которого выполнены из ферромагнитных материалов, по которым замыкается магнитный поток. Примерами простейших цепей могут служить магнитопроводы кольцевой катушки и электромагнита, изображенного на рис. 6.11, а. Электрические машины и трансформаторы, электромагнитные аппараты и приборы имеют обычно магнитные цепи более сложной формы.

Если магнитная цепь выполнена из одного и того же материала и имеет по всей длине одинаковое сечение, то цепь называется однородной.

Если же отдельные участки цепи изготовлены из различных ферромагнитных материалов и имеют различные длины и сечения, то цепь — неоднородная.

Магнитные цепи, так же как и электрические, бывают разветвленные (рис. 6.11,6) и неразветвленные (рис. 6.11,а).

В неразветвленных цепях магнитный поток Ф во всех сечениях имеет одно и то же значение.

Разветвленные цепи могут быть симметричными и несимметричными. Цепь, представленная на рис. 6.11,6, считается симметричной, если правая и левая части ее имеют одинаковые размеры, выполнены из одного и того же материала и если МДС I1W1 и I2W2 одинаковы. При невыполнении хотя бы одного из указанных условий цепь будет несимметричной.

Разобьем неразветвленную магнитную цепь, например, на рис 6.11, а на ряд однородных участков, каждый из которых выполнен из определенного материала и имеет одинаковое поперечное сечение S вдоль всей своей длины. Длину каждого участка L будем считать равной длине средней магнитной линии в пределах этого участка. Из сказанного выше следует, что магнитные потоки всех участков неразветвленной цепи равны, т. е.

Ф1=Ф2=Ф3=…=Фn,

и поле на каждом участке можно считать однородным, т. е. Ф= BS; поэтому

B1S1=B2S2=B3S3=…=BnSn

Где n — число участков цепи. Магнитное напряжение на любом из участков магнитной цепи

Где H — Напряженность, (измеряется в ампер на метр А/М).

B — Магнитная индукция (измеряется в теслах Тл).

L — Длинна средне силовой линии проходящей через центр поперечного сечения магнитопровода.

S — площадь поперечного сечения магнитопровода.

— Магнитная постоянная.

μr — Магнитная проницаемость ферромагнетиков.

При заданном направлении тока в обмотке направление потока и МДС IW определяется по правилу буравчика.

Магнитное сопротивление и закон Ома для магнитной цепи.

По аналогии с электрической цепью величину

называют магнитным сопротивлением участка магнитной цепи (измеряется в 1/Гн).

Таким образом, магнитное напряжениеВыражение (3) по аналогии с электрической цепью часто называют законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μr ферромагнетиков, оно практически не применяется для расчета магнитных цепей.

9.1.3. Свойства ферромагнитных материалов

Магнитное состояние любой точки изотропной среды, т. е. среды с одинаковыми свойствами во всех направлениях, вполне определяется вектором напряженности магнитного поля Н

и вектором магнитной индукции
В
, которые совпадают друг с другом по направлению.

Основная единица магнитной индукции в системе СИ называется тесла (Тл): 1 Тл = 1 Вб/м2 = 1 В·с/м2. Это индукция такого однородного магнитного поля, в котором магнитный поток Ф

через поверхность площадью 1 м2, перпендикулярную направлению магнитных линий поля, равен одному веберу (Вб).

В вакууме индукция и напряженность магнитного поля связаны простым соотношением: В = m0Н, где m 0 = 4p·10-7 Гн/м — магнитная постоянная. Для ферромагнитных материалов зависимость индукции от напряженности магнитного поля В(H)

в общем случае нелинейная.

Для того чтобы экспериментально исследовать магнитные свойства ферромагнитного материала, необходимо все измерения производить на образце, в котором магнитное поле однородное. Таким образцом может быть тороид, изготовленный из исследуемого ферромагнитного материала (рис. 9.5), длина магнитных линий в котором много больше его поперечных размеров (тонкостенный тороид). На тороиде находится равномерно навитая обмотка с числом витков w

.

Можно считать, что в тороиде из ферромагнитного изотропного материала с плотно намотанными витками все магнитные линии — окружности, а векторы напряженности и индукции магнитного поля направлены по касательной к соответствующей окружности. Так, на рис. 9.5 показаны средняя магнитная линия и векторы Н

и
В
в одной из ее точек.

При расчете напряженности и индукции магнитного поля в тонкостенном тороиде можно считать, что все магнитные линии имеют одинаковую длину, равную длине средней линии 2p
r
.

Предположим, что ферромагнитный материал тонкостенного тороида полностью размагничен и тока I

в обмотке нет (
В
= 0 и
Н
= 0). Если теперь плавно увеличивать постоянный ток
I
в обмотке катушки, то в ферромагнитном материале возникнет магнитное поле, напряженность которого определяется законом полного тока (9.1):

H
=Iw/2pr.
(9.3)

Каждому значению напряженности H

магнитного поля в тонкостенном тороиде соответствует определенная намагниченность ферромагнитного материала, а следовательно, и соответствующее значение магнитной индукции
В
.

Если начальное магнитное состояние материала тонкостенного тороида характеризуется значениями Н

= 0,
В
= 0, то при плавном нарастании тока получим нелинейную зависимость
В(Н),
которая называется кривой первоначального намагничивания (рис. 9.5, штриховая линия). Начиная с некоторых значений напряженности
H
магнитного поля индукция
В
в тонкостенном ферромагнитном тороиде практически перестает увеличиваться и остается равной
Вmax
. Эта область зависимости
В(Н)
называется областью технического насыщения.

Если, достигнув насыщения, начать плавно уменьшать постоянный ток в обмотке, т. е. уменьшать напряженность поля (9.3), то индукция также начнет уменьшаться. Однако зависимость В(Н)

уже не совпадает с кривой первоначального намагничивания. Изменив направление тока в обмотке и увеличив его значение, получим новый участок зависимости
В(Н).
При значительных отрицательных значениях напряженности магнитного поля снова наступит техническое насыщение ферромагнитного материала. Если теперь продолжить эксперимент: сначала уменьшать ток обратного направления, затем увеличивать ток прямого направления до насыщения и т. д., то после нескольких циклов перемагничивания для зависимости
В(Н)
будет получена симметричная кривая (рис. 9.5, сплошная линия). Этот замкнутый цикл
В(Н)
называется предельной статической петлей гистерезиса (или предельным статическим циклом гистерезиса) ферромагнитного материала. Если во время симметричного перемагничивания область технического насыщения не достигается, то симметричная кривая
В(Н)
называется симметричной частной петлей гистерезиса ферромагнитного материала.

Предельный статистический цикл гистерезиса ферромагнитных материалов характеризуется следующими параметрами:

Нс

— коэрцитивной силой,
Вr
— остаточной индукцией и
k=Br/BH—l0Hc
— коэффициентом прямоугольности.

По значению параметра Hс

предельного статического цикла гистерезиса ферромагнитные материалы делятся на группы:

1) магнитные материалы с малыми значениями коэрцитивной силы (Hс

<� 0,05…0,01 А/м) называются магнитно-мягкими;

2) магнитные материалы с большими значениями коэрцитивной силы (Hс

> 20…30 кА/м) называются магнитно-твердыми.

Магнитно-твердые материалы используются для изготовления постоянных магнитов, а магнитно-мягкие — для изготовления магнитопроводов электротехнических устройств, работающих в режиме перемагничивания по предельному или частым циклам.

Магнитно-мягкие материалы в свою очередь делятся на три типа: магнитные материалы с прямоугольной предельной статической петлей гистерезиса, у которых коэффициент прямоугольности k

> 0,95 (рис. 9.6, а); магнитные материалы с округлой предельной статической петлей гистерезиса, у которых коэффициент прямоугольности 0,4 < <
k
< 0,7 (рис. 9.6, б); магнитные материалы с линейными свойствами, у которых зависимость
В(H)
практически линейная:
В =mrm0Н
(рис. 9.6, в), где
mr
— относительная магнитная проницаемость.

Все типы магнитных характеристик ферромагнитных материалов могут быть получены на образцах, изготовленных либо из различных ферромагнитных сплавов, либо из ферромагнитной керамики (ферриты). Ценное свойство ферритов в отличие от ферромагнитных сплавов — их высокое удельное электрическое сопротивление.

Магнитопроводы из ферромагнитных материалов с прямоугольным предельным статическим циклом гистерезиса применяются в оперативной памяти цифровых ЭВМ, магнитных усилителях и других устройствах автоматики. Ферромагнитные материалы с округлым предельным статическим циклом гистерезиса используются при изготовлении магнитопроводов электрических машин и аппаратов. Магнитопроводы этих устройств обычно работают в режиме перемагничивания по симметричным частным циклам. При основных расчетах магнитопроводов таких электротехнических устройств симметричные частные циклы заменяют основной кривой намагничивания ферромагнитного материала, которая представляет собой геометрическое место вершин симметричных частных циклов тонкостенного ферромагнитного тороида (рис. 9.7), полученных при синусоидальном токе низкой частоты в обмотке.

По основной кривой намагничивания ферромагнитного материала определяют зависимость абсолютной магнитной проницаемости

ma

=
mrm0
=
В/Н
(9.4)

от напряженности Н

магнитного поля, которая показана на рис. 9.7 штриховой линией.

На рис. 9.8 приведены основные кривые намагничивания некоторых электротехнических сталей, используемых в электрических машинах, трансформаторах и других устройствах, а также чугуна и пермаллоя.

Из ферромагнитных материалов с линейными свойствами изготовляют участки магнитопроводов для катушек индуктивности колебательных контуров с высокой добротностью. Такие контуры применяются в различных радиотехнических устройствах (приемниках, передатчиках), в малогабаритных антеннах средств связи и т. д.

Если на участке магнитопровода с площадью поперечного сечения S

магнитное поле неоднородное, то часто расчет можно вести, пользуясь средним значением индукции
Вср = Ф/S
и напряженностью
Нср
на средней магнитной линии. Например, для тороида с прямоугольной формой поперечного сечения, внутренним радиусом
rt,
внешним радиусом
r2
и высотой
h
, изготовленного из магнитного материала с линейными свойствами
В = mrm0H
при
mr
= const (рис. 9.6, в),

где

Из полученных выражений следует, что

В дальнейшем для упрощения расчетов неоднородность магнитного поля в поперечном сечении каждого участка магнитопровода учитывать не будем, и будем считать, что поле в каждом участке однородное и определяется значениями напряженности и индукции на средней магнитной линии.

Физический смысл сопротивления

Электрический ток — это движение заряженных частиц в определенном направлении, которое инициируется разницей напряжения на концах проводника. Проводящие ток материалы обладают сопротивлением, которое можно наглядно представить как силу трения. Чем тем больше препятствий электроны встречают на своем пути, тем быстрее теряют энергию.

Значение сопротивления зависит от свойств материала проводника, его длины и площади сечения. Лучшей проводимостью среди доступных металлов характеризуется медь, поэтому современные ЛЭП и электропроводка изготавливаются из медных жил. Энергопотери таких линий гораздо меньше, чем алюминиевых или стальных.

На сопротивление оказывает влияние условия среды. Некоторые материалы при достижении критической температуры порядка -200°С обладают сверхпроводимостью, то есть нулевым сопротивлением. Это позволяет использовать их для изготовления сложной аппаратуры и мощных турбогенераторов.

В элементах типа ТЭН или греющих кабелях, наоборот, сопротивление очень большое. За счет передачи части энергии от заряженных частиц материалу проводника устройство нагревается и сообщает тепло окружающему пространству.

Сопротивлением обладают не только проводники, но и источники тока, измерительные приборы, конденсаторы, катушки, контакты в соединениях. Существует 3 вида сопротивлений:

  • активное при постоянном и переменном токе;
  • индуктивное;
  • емкостное.

По величине оно может быть малым, средним и большим. Чем меньше значение, тем сильнее влияет на результат измерений сопротивление самого прибора и его контактов.

Закон Ома для переменного и постоянного тока

Для цепи постоянного тока правильными будут уже озвученные нами взаимосвязи основных параметров электроцепи:

Закон Ома для постоянного тока

При подключении к электроцепи источника переменного тока, сила электротока в цепи будет определяться по формуле:

где (Z) — полное сопротивление или импеданс, который состоит из активной ((R)) и реактивных составляющих ( (X_C) — сопротивление емкости и (X_L) — сопротивление индуктивности).

Реактивное сопротивление цепи зависит:

  • от значений реактивных элементов,
  • от частоты электротока;
  • от формы тока в цепи.

Прозвонка проводов

В режиме прозвонки можно проверить провода на обрыв на любом участке цепи. На шкале мультиметра она обозначена значком «звуковой микшер». При неповрежденной проводке и контактах будет слышен сигнал — тонкое попискивание. Если проводимости нет, звук прекращается.

  1. Выбрать переключателем режим прозвонки.
  2. Щупы вставить в базу СОМ и средний разъем VΩmA.
  3. Прикоснуться мультиметром к контактам исследуемого участка, замкнув цепь.

По наличию или отсутствию звука делаются выводы о целостности проводов. Рекомендуется предварительно прозвонить сами щупы, чтобы исключить их повреждение. Они соединяются наконечниками друг с другом, при этом должен слышаться непрерывный звук.

Сопротивление заземления

Для снижения напряжения прикосновения до безопасной величины в случае короткого замыкания используется заземлитель. Это устройство обладает небольшим сопротивлением, позволяющим электричеству через токопроводящие элементы перетекать в грунт. Отсюда и происходит название этой важной компоненты системы электробезопасности.

Сопротивление заземления нормируется в зависимости от типа объекта и энергопотребления. Так в трехфазных сетях с напряжением 380 В оно не должно превышать 4 Ом, в однофазных на 220 В — 8 Ом.

Проверка работоспособности контура производится специальными измерителями параметров заземления — М-416, MRU-105, Мetrel и другими. В отличие от бытовых мультиметров они гораздо мощнее, имеют длинные щупы, используют в качестве источника питания батарейки, линии электропередач или встроенный генератор. Напряжение в цепи может достигать 1000 В. С помощью таких установок можно измерять сопротивление заземление, удельное сопротивление грунта, а также шаговое и контактное напряжение.

Для проведения работ понадобятся 2 штыря и комплект проводов. Предварительно нужно снять окислы с контактов заземлителя, для этого пригодится рашпиль или напильник.

Потенциальный электрод забивается на расстоянии 15 м от здания, токовый — 30 м, затем соединяются проводами с тестером по схеме. При касании щупом зачищенного контакта заземлителя прибор пропускает ток через электроды, определяет напряжение и силу тока. Он самостоятельно проводит вычисления и выдает показания в Омах.

Еще один способ, который позволяет найти сопротивление заземления, — измерение токовыми клещами. При этом не нужно использовать дополнительные провода и электроды или частично отключать заземлители при сложной схеме подключения. Провода просто охватываются разъемными щечками прибора, внутри которых расположены магнитопроводы. Прилегание проводников и контактов измерителя должно быть максимально плотным, чтобы снизить погрешности. После снятия показаний в одной точке сразу же можно переходить для работы в другое место.

Как измерить сопротивление мультиметром: порядок действий

Испытания проводятся без подключения к сети. Батарейка подает на контакты небольшое напряжение, поэтому другой источник тока не нужен. Благодаря этому измерение не представляет угрозы человеку и считается безопасным.

Установка режима и выбор диапазона

Для проверки сопротивления на шкале мультиметра выделен сектор, обозначенный буквой Ω (омега). Чтобы задать нужный регистр точности, требуется определить ожидаемый порядок величины:

  • до 200 Ом;
  • до 2000 Ом (2К);
  • до 20К;
  • до 200К;
  • до 2000К (2М).

В некоторых приборах можно измерять сопротивления до 200 мегаОм (200м). Они используются для проверки резисторов с большой емкостью. Плохо проводящие ток диэлектрики, из которых изготавливается изоляция проводов, исследуются с помощью мегаомметров. Мультиметры для этой цели не подходят, поскольку не могут генерировать большие токи, а диапазон их ограничивается максимумом в 200 мОм.

Подключение щупов

Для проведения измерений нужно вставить щупы в разъемы на корпусе прибора:

  • черный — в гнездо СОМ;
  • красный — в VΩmА.

При таком расположении «минус» будет подаваться на черный проводник, «плюс» — на красный. Обычные резисторы не имеют полярности, их можно подключать к проводникам в любой последовательности.

Измерения

Несмотря на то, что удар током вам не грозит, пальцами желательно контактов не касаться. Иначе мультиметр покажет данные с погрешностью. Поскольку сопротивление человеческого тела от 3 до 100 Ом, ошибка может быть очень большой.

Перед началом измерений концы щупов рекомендуется соединить и проверить непосредственно сами проводники. Особенно это важно, если исследуются резисторы с небольшим R, где десятые доли Ом могут иметь значение.

После определения сопротивления щупов эту цифру надо запомнить, чтобы вычитать из всех дальнейших результатов.

Измерения проводятся при соприкосновении наконечников с контактами элемента. Данные считываются с дисплея и при необходимости переводятся в Омы с учетом учитывая приставки к числу:

Если диапазон выставлен правильно, значение будет отличным от 0. Для более точного измерения можно повернуть переключатель на меньшую цифру.

Если на экране высветился 0, предел постепенно снижают до получения численного результата. Когда на приборе видна только цифра 1, это значит, что сопротивление бесконечно. Из-за обрыва ток в цепи отсутствует.

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 31 марта 2020 года; проверки требуют 2 правки.

Эта статья — о законе магнитной цепи. Об основном законе электрической цепи см. Закон Ома; об акустическом законе Ома см. Акустический закон Ома.

Классическая электродинамика
VFPt Solenoid correct2.svg
Электричество · Магнетизм

Электростатика

Закон Кулона
Теорема Гаусса
Электрический дипольный момент
Электрический заряд
Электрическая индукция
Электрическое поле
Электростатический потенциал

Магнитостатика

Закон Био — Савара — Лапласа
Закон Ампера
Магнитный момент
Магнитное поле
Магнитный поток
Магнитная индукция

Электродинамика

Векторный потенциал
Диполь
Потенциалы Лиенара — Вихерта
Сила Лоренца
Ток смещения
Униполярная индукция
Уравнения Максвелла
Электрический ток
Электродвижущая сила
Электромагнитная индукция
Электромагнитное излучение
Электромагнитное поле

Электрическая цепь

Закон Ома
Законы Кирхгофа
Индуктивность
Радиоволновод
Резонатор
Электрическая ёмкость
Электрическая проводимость
Электрическое сопротивление
Электрический импеданс

Ковариантная формулировка

Тензор электромагнитного поля
Тензор энергии-импульса
4-потенциал
4-ток

См. также: Портал:Физика

Зако́н О́ма для магни́тной цепи́ (зако́н Го́пкинсона) — физический закон для магнитной цепи, аналогичный закону Ома для электрической цепи. Определяет связь между магнитодвижущей силой, магнитным сопротивлением и магнитным потоком в магнитной цепи.

Формулировка[править | править код]

В неразветвлённой магнитной цепи магнитный поток прямо пропорционален магнитодвижущей силе и обратно пропорционален полному магнитному сопротивлению[1].

Вывод[править | править код]

Рассмотрим неразветвлённую магнитную цепь, состоящую из ярма с площадью поперечного сечения S из материала c магнитной проницаемостью mu и зазора из другого материала, имеющего то же сечение и магнитную проницаемость mu _{{1}}. На ярмо надета катушка с числом витков N, по которой идёт ток i. Рассмотрим среднюю линию магнитной цепи и применим теорему о циркуляции магнитного поля.

{displaystyle Hl+H_{1}l_{1}={frac {4pi Ni}{c}}.qquad (1)}

Здесь H — напряжённость магнитного поля внутри ярма, {displaystyle H_{1}} — напряжённость магнитного поля внутри зазора, l — длина ярма, измеренная вдоль средней линии индукции, {displaystyle l_{1}} — длина зазора, с – скорость света в вакууме. Так как линии индукции непрерывны, то значения магнитного потока Phi внутри ярма и внутри зазора одинаковы. Из соотношений {displaystyle Phi =BS,B=mu H} выражаем напряжённость магнитного поля через поток {displaystyle H=Phi /(mu S),} {displaystyle H_{1}=Phi /(mu _{1}S).} Подставляя эти выражения в формулу (1), получаем из неё значение магнитного потока Phi :

{displaystyle Phi ={frac {frac {4pi Ni}{c}}{{frac {l}{mu S}}+{frac {l_{1}}{mu 1S}}}}.}

Полученная формула подобна закону Ома для замкнутой электрической цепи. При этом величина {displaystyle F_{m}={frac {4pi Ni}{c}}} играет роль электродвижущей силы и поэтому по аналогии она получила название магнитодвижущей силы. Её отличие от электродвижущей силы состоит в том, что в магнитном потоке не движутся никакие частицы. Сумма {displaystyle R_{m}={frac {l}{mu S}}+{frac {l_{1}}{mu _{1}S}}} входит в формулу так же, как полное сопротивление электрической цепи в законе Ома, и поэтому её называют полным магнитным сопротивлением цепи. Итак, закон Ома для магнитной цепи можно записать в виде {displaystyle Phi ={frac {F_{m}}{R_{m}}}.} В неразветвлённой магнитной цепи магнитный поток равен частному от деления магнитодвижущей силы на полное магнитное сопротивление.

История[править | править код]

Идею о том, что величину магнитного потока в магнитной цепи можно записать аналогично закону Ома для электрической цепи, первым высказал американский физик Генри Роуланд в 1873 году[2]. Закон часто называют формулой Гопкинсона или законом Гопкинсона в честь английского физика и инженера Джона Гопкинсона (Хопкинсона), который вместе со своим братом Эдвардом в 1886 году разработал формализм для расчёта магнитных цепей.

Примечания[править | править код]

  1. ↑ Калашников, 1956, с. 289.
  2. ↑ Rowland, Henry A. XIV. On magnetic permeability, and the maximum of magnetism of iron, steel, and nickel (англ.) // Philosophical Magazine : journal. — 1873. — Vol. 46, no. 304. — P. 140—159.

Литература[править | править код]

  • Калашников С. Г. Электричество. — М.: ГИТТЛ, 1956. — 664 с.
Источник

Магнитное сопротивление (МС) – один из важнейших параметров «магнитопроводов», характеризующий их реакцию на изменения э/м поля. На их практическом применении основывается работа большинства электротехнических устройств, начиная от простейших датчиков и кончая мощными электрическими агрегатами.

Что собой представляет магнитное сопротивление

Прежде необходимо ознакомиться с некоторыми особенностями использования ферромагнитных материалов (другое их название – «ферромагнетики»). Эти вещества позволяют повысить напряженность магнитного поля, действующего в пределах данной системы, а также придать силовым линиям нужную ориентацию. Ферромагнитные материалы, обладающие магнитной проводимостью, входят в состав различных приборов, широко используемых в электротехнике.

Магнитопроводы – это вещества особой структуры, которым при производстве придается определенная форма и размеры. С точки зрения передачи потоков электромагнитной энергии через такие тела они аналогичны электрическим цепям. Отличие состоит в том, что одни из них описываются активным электрическим сопротивлением, а другие – его магнитным аналогом.

Магнитное сопротивление представляет собой параметр, характеризующий ферромагнитные материалы с точки зрения их способности препятствовать или способствовать распространению потоков э/м полей. Этот показатель помогает оценивать полевые структуры, образующиеся в магнитопроводах при эксплуатации промышленного и бытового электротехнического оборудования.

МС – одна из важнейших характеристик магнитной цепи, представляемая в виде соотношения двух связанных с ней величин. В формуле для их выражения используются магнитодвижущая сила МДС, обозначаемая как «F», и создаваемый ей магнитный поток «Ф»:

F= ФхRm
При необходимости связать МС с геометрическими размерами магнитопровода применяется формула:
Rm = L/mm0S

В этом представлении L и S – это длина и поперечное сечение участка магнитопровода, а m – магнитная проницаемость ферромагнитного материала цепи. Второй сомножитель в знаменателе, обозначаемый как «m0» – это так называемая «магнитная постоянная», характеризующая особенности используемого материала. При неоднородной магнитной цепи, состоящей из различных частей с отличными один от других показателей L, S и m, ее МС находится как сумма отдельных составляющих.

Как появилось понятие «магнитное сопротивление» в измерительной практике
Понять, когда и в связи с чем появилось это понятие поможет исследование простейшей магнитной цепи, образующейся в магнитопроводе неразветвленного сердечника определенного сечения. Обязательно учитываются следующие важные моменты:
  • Магнитопровод изготавливается из специального материала с проницаемостью, обозначаемой значком «m» (читается, как «мю»).
  • В нем обязательно наличие зазора той же площади, что и у основания (двухполюсного ярма).
  • Полая часть между полюсами, как правило, заполняется изоляционным материалом.
  • Магнитная проницаемость диэлектрика в зазоре отлична от того же показателя для самого ферромагнетика.

При выполнении всех перечисленных условий подавляющее количество силовых линий замыкается в зоне, где расположен зазор магнитного сердечника. При оценке рабочих параметров системы достаточно учитывать только эту их часть, не принимая во внимание все остальные. Добавим к этому, что такая конструкция вполне может быть описана с помощью закона о магнитном напряжении.

В чем проявляется сходство с электрическими цепями

Поскольку в ферромагнитном материале силовые линии непрерывны во всей его площади и объему – магнитный поток «Ф» распределяется равномерно как в самом ярме, так и в его зазоре. Далее следует воспользоваться известным определением магнитной индукции, (она обозначается как «B»), которое учитывает интенсивность силовых линий. На следующем этапе проводимых преобразований через физическую величину потока «Ф» выражается напряженность электрического поля «H», в полученное соотношение подставляется в формулу для «B».

В результате этих преобразований получится выражение, внешне очень похожее на хорошо известный закон Ома для участка электрической цепи:
U=IR – Электрическая.
F=Фℜ – Магнитная.

В качестве ЭДС в этой формуле выступает магнитодвижущая сила (МДС), по своей природе сходная с известным из электротехники электрическим аналогом. А второй сомножитель в правой части ℜ – это ни что иное, как аналог электрического сопротивления, которое в данном случае называется «магнитным».

Формулировку закона, определяющего соотношение между тремя рабочими величинами, применительно к магнитным цепям можно представить следующим образом. В магнитопроводах без ответвлений магнитный поток «Ф» находится как результат деления МДС на их МС.

Из приведенной выше формулы становится понятным, что в системе СИ магнитное сопротивление должно измеряться в амперах на вебер. Вместе с тем справедливо утверждение, что этот показатель для общей магнитной цепи равен сумме тех же величин для каждой ее части. Это правило действительно для последовательного соединения отдельных участков магнитопровода.

При параллельном их соединении складываться будут величины, обратные МС (аналоги электрической проводимости). Соотношение между магнитным сопротивлением, МДС и потоком полностью аналогично тому, как связаны между собой 1/R, напряжение U и ток I в электрических цепях.

При выражении рассматриваемого показателя через геометрические размеры магнитопровода хорошо видно, что сопротивление более протяженной ферромагнитной заготовки с длиной ярма L имеет большее значение. С другой стороны МС магнитопровода с большей площадью поперечного сечения S при прочих равных условиях будет меньше:
R=ρ*1/S – Электрическое.
R=1/µS – Магнитное.

Основная сложность при оценке рассматриваемых параметров состоит в том, что магнитная проводимость не постоянна в пределах исследуемой системы. Ее величина зависит от множества факторов, включая концентрацию силовых линий исследуемого потока. Указанная проблема объясняется нелинейностью магнитных цепей, что существенно усложняет их теоретические расчеты (в сравнении с электрическими аналогами).

От чего зависит МС
Магнитное сопротивление зависит от целого ряда факторов, среди которых выделим следующие характеристики исследуемого материала:
  • Длина и форма магнитопровода.
  • Площадь его поперечного сечения.
  • Количество составляющих частей.
  • Величина магнитной проницаемости.

Влияние первых трех факторов автоматически учтено в формулах и рассуждениях. Последний показатель учитывается по аналогии с удельной электропроводностью, используемой при формулировке закона Ома для электрического сопротивления.

Более доступно разъяснить влияние этих факторов удается на примере эксперимента, проводимого с использованием комплексного магнитопровода, состоящего из нескольких частей.

Доказательство связи магнитного сопротивления частей с общим значением
Для получения подтверждения такой зависимости специалистами проводился эксперимент, для проведения которого потребовалось приготовить следующие детали и измерительные приборы:
  • U-образное ярмо (образец магнитопровода).
  • Специальная намагничивающая обмотка.
  • Источник переменного тока (электрическая сеть 220 В).
  • Понижающий трансформатор.
  • Реостат, вольтметр и амперметр.

При проведении этого опыта амперметр, реостат и намагничивающая катушка включались последовательно, после чего всю эту цепочку подсоединяли к источнику переменного тока.

После того, как на первичную обмотку через понижающий трансформатор подавался ток – во вторичной обмотке наводилась ЭДС, которая измерялась посредством вольтметра. Показания измерительного прибора были пропорциональны величине магнитного потока в ярме.

Далее экспериментаторы переходили к следующей последовательности действий:
  • Сначала ток в цепи выставлялся по амперметру на фиксированном уровне.
  • Затем бралась объемная металлическая пластина и прижималась к поверхности магнитопровода.
  • Это приводило к тому, что общее магнитное сопротивление системы заметно изменялось.
  • Обнаруживалось данное отличие по показанию вольтметра, которое резко возрастало при приближении стальной заготовки.
Физическую суть этого эксперимента проще всего понять, если учесть следующие моменты:
  • Магнитные свойства веществ определяются микроскопическими молекулярными токами, в огромном количестве присутствующими в их структуре.
  • При приближении и прижатии к магнитопроводу тел, обладающих магнитными свойствами, общее количество таких вращающихся систем заметно увеличивается.
  • Это приводит к возрастанию общего магнитного потока, а также напряженности э/м поля.

Такие непривычные сочетания, как «магнитодвижущая сила» и «магнитное сопротивление» со временем стали широко применяться при описании процессов, происходящих в ферромагнетиках. Несмотря на то, что они были введены по аналогии с электрическими величинами – эти понятия оказались очень удобными при решении многих электротехнических задач.

Похожие темы:
  • Законы Фарадея. Для эл/м индукции и в электролизе
  • Эффект Джозефсона. Работа и применение. Особенности
  • Сверхпроводящие магниты. Устройство и работа. Применение
Источник

Добавить комментарий