Содержание:
Магнитные цепи:
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т. д.) входят магнитные цепи.
Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют неразветвленными и разветвленными; применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Расчет неразветвленной однородной магнитной цепи
В неразветвленной магнитной цепи (рис. 9.1, 9.2) магнитный поток во всех участках один и тот же.
При расчете и конструировании магнитной цепи электромагнитного устройства решаются вопросы, связанные с выбором размеров, формы, материалов. Эти вопросы изучают в специальных курсах.
Здесь рассмотрим расчет для существующей или сконструированной магнитной цепи, размеры и материалы которой, а также расположение обмоток с токами известны. При этом решают задачи двух типов.
Прямая задача:
По заданному магнитному потоку в цепи требуется определить намагничивающую силу, необходимую для создания этого потока.
Рассмотрим решение этой задачи для неразветвленной однородной магнитной цепи (см. рис. 9.1) без учета потоков рассеяния.
1. По заданному магнитному потоку и известной площади S поперечного сечения сердечника находят магнитную индукцию:
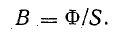
2. Определяют напряженность магнитного поля Н в сердечнике. Зависимость В(Н) — характеристика намагничивания — для стали нелинейная, а магнитная проницаемость 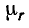
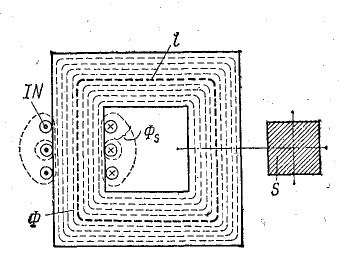
Рис. 9.1. Неразветвленная однородная магнитная цепь
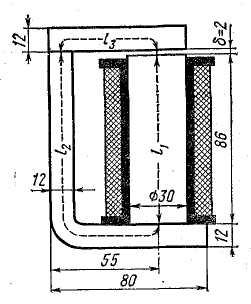
Рис. 9.2. Неразветвленная неоднородная магнитная цепь
Обычно напряженность магнитного поля определяют по кривой намагничивания данного сорта стали (см. рис. 8.30 и приложение 4).
3. Находят намагничивающую силу по закону полного тока [см. формулу (8.41)]:
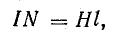
где l — длина магнитопровода, подсчитанная по средней линии без учета закруглений, причем условно принимается, что эта средняя линия во всех точках совпадает с линией магнитной индукции.
Обратная задача:
По заданной намагничивающей силе требуется найти магнитный поток в магнитопроводе.
1. Определяют напряженность магнитного поля в сердечнике:
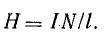
2. По кривой намагничивания данного сорта стали находят магнитную индукцию В.
3. Определяют магнитный поток:
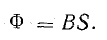
Для конкретных величин В и Н, определенных в ходе решения задачи, можно подсчитать статическую магнитную проницаемость данного сорта стали по формуле (8.37):
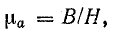
тогда магнитная индукция
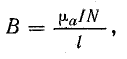
магнитный поток
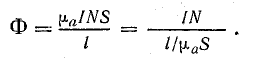
Обозначив знаменатель этого выражения через Rм:
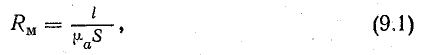
получим
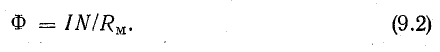
Магнитное сопротивление
Выражение (9.2) по форме напоминает закон Ома для электрической цепи: на месте тока стоит магнитный поток, на месте э. д. с. — намагничивающая сила (ее называют еще магнитодвижущей силой — м. д. с.). Величину Rм называют магнитным сопротивлением. Выражение магнитного сопротивления сердечника по форме аналогично выражению для определения сопротивления проводника электрическому току. Нужно отметить, что формулы для электрической и магнитной цепей похожи только написанием. Никакого физического подобия явлений в электрической и магнитной цепях не существует.
Расчет магнитных цепей обычно проводят без определения магнитного сопротивления. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Пользуясь им, найдем, как должна измениться намагничивающая сила катушки, если в стальном сердечнике (см. рис. 9.1) сделать хотя бы незначительный воздушный зазор, а магнитный поток при этом должен остаться таким же.
Предположим, что в стальном сердечнике длиной l = 100 мм имеется воздушный зазор δ = 1 мм.
Магнитное сопротивление сердечника
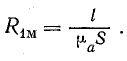
Магнитное сопротивление сердечника с воздушным зазором равно сумме сопротивлений двух участков.
Сопротивление стальной части магнитной цепи при той же магнитной индукции останется практически без изменения, так как уменьшение длины ее очень незначительно (≈ 1 %).
Сопротивление воздушного зазора
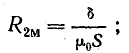
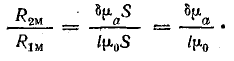
Предположим, что относительная магнитная проницаемость стали 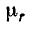 = 1000, тогда
= 1000, тогда
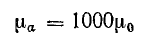
и
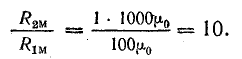
Магнитное сопротивление воздушного зазора оказывается в 10 раз больше сопротивления стального сердечника.
Отсюда следует, что для обеспечения того же магнитного потока при наличии воздушного зазора в 1 мм нужно иметь намагничивающую силу примерно в 10 раз большую, чем при его отсутствии. Эта разница оказывается во много раз большей для сердечников из специальных сплавов, для которых величина 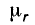 достигает сотен тысяч.
достигает сотен тысяч.
Поэтому во всех случаях, когда по условиям работы электромагнитного устройства без воздушного зазора обойтись нельзя, следует по возможности его сокращать.
Задача 9.1.
В сердечнике кольцевой формы из электротехнической стали нужно получить магнитный поток Ф = 2 • 10-3 Вб. Определить: 1) ток в обмотке, имеющей N = 100 витков; 2) магнитную проницаемость стали при заданном потоке в сердечнике; 3) индуктивность катушки.
Размеры сердечника заданы в миллиметрах на рис. 9.3.
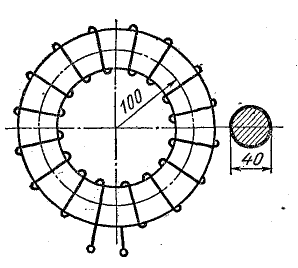
Рис. 9.3. К задаче 9.1
Решение. Площадь сечения сердечника
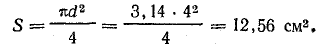
Считая магнитную индукцию по сечению сердечника постоянной, найдем ее величину по заданному потоку:
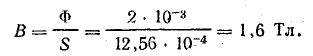
По кривой намагничивания (см.рис. 8.30) определим напряженность магнитного поля: H = 50 А/см = 5000 А/м.
Намагничивающая сила, необходимая для создания заданного потока,
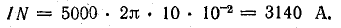
Ток в обмотке
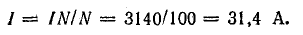
Магнитная проницаемость стали при найденных величинах В и H
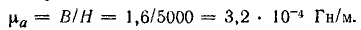
Относительная магнитная проницаемость
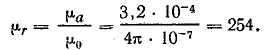
Индуктивность катушки
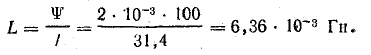
Задача 9.3.
Определить магнитный поток и магнитное сопротивление сердечника (рис. 9.4), размеры которого заданы в миллиметрах, если в катушке с числом витков N = 200 ток I = 6 А. Сердечник изготовлен из электротехнической стали 1511, причем 10% его сечения занимает изоляция между листами.
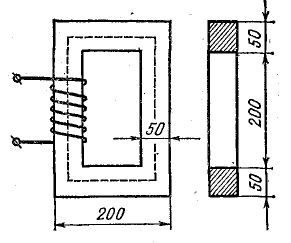
Рис. 9.4. К задаче 9.3
Решение. Намагничивающая сила и напряженность поля
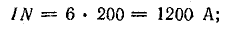
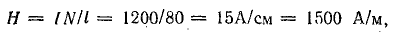
где I — длина замкнутого сердечника по средней линии; согласно размерам, указанным на чертеже, l = 80 см = 0,8 м.
Магнитная индукция по характеристике намагничивания электротехнической стали 1511 В = 1,42 Тл.
Полная площадь сечения сердечника
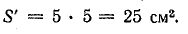
Активная площадь
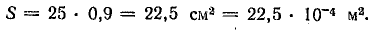
Магнитный поток
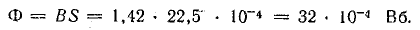
Магнитная проницаемость при заданной величине намагничивающей силы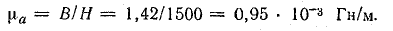
Магнитное сопротивление
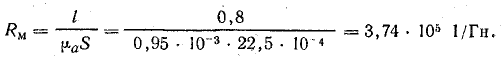
Расчет неразветвленной неоднородной магнитной цепи
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых кроме участков из ферромагнитных материалов имеются воздушные зазоры.
Прямая задача:
При решении прямой задачи размеры и материалы каждого участка цепи известны, а магнитный поток задан; определяют намагничивающую силу. Порядок решения прямой задачи такой же, как и для однородной цепи, но магнитную индукцию и напряженность поля определяют для каждого участка; при этом потоки рассеяния в расчет не принимают.
Магнитная индукция k-го участка
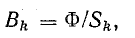
где Sk — площадь поперечного сечения k-го участка.
По магнитной индукции определяют напряженность поля: для участков из ферромагнитных материалов — по кривым намагничивания; для воздушных зазоров и других участков из неферромагнитных материалов — по формуле 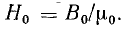
Далее составляют уравнение согласно закону полного тока:

где Нk — напряженность магнитного поля k-го участка (принимают ее одинаковой во всех точках этого участка); lk — длина k-то участка, взятая по средней линии; Нklk — магнитное напряжение к-то участка (далее магнитное напряжение будем обозначать Um); 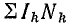 — алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
— алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
Намагничивающую силу считают положительной в левой части уравнения (9.3), если ее направление, определенное по правилу буравчика, совпадает с направлением обхода магнитного контура. Магнитное напряжение в правой части уравнения считают положительным, если направление магнитного потока совпадает с направлением обхода контура.
Для магнитной цепи (см. рис. 9.2) развернутое уравнение (9.3) имеет вид
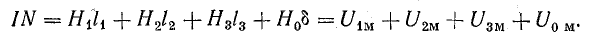
Обратная задача:
Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как нельзя сразу установить распределение магнитного напряжения между участками.
Нельзя воспользоваться формулой (9.2), так как магнитное сопротивление участка из ферромагнитного материала зависит от величины 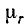 , которая определяется не известной еще магнитной индукцией.
, которая определяется не известной еще магнитной индукцией.
Задачу можно решить методом последовательных приближений.
При наличии в цепи воздушного зазора первое значение магнитного потока можно взять, считая магнитное сопротивление воздушного зазора равным сопротивлению всей магнитной цепи.
Основанием для такого выбора является то, что даже малый воздушный зазор имеет магнитное сопротивление, значительно большее, чем вся остальная часть цепи, выполненная из ферромагнитных материалов.
Пренебрегая в первом приближении магнитным сопротивлением ферромагнитной части цепи, получим поток
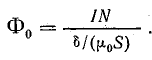
Определить магнитный поток можно, построив кривую намагничивания цепи в целом. Для этого нужно задаться произвольно несколькими величинами магнитного потока и определить соответствующие им величины намагничивающей силы.
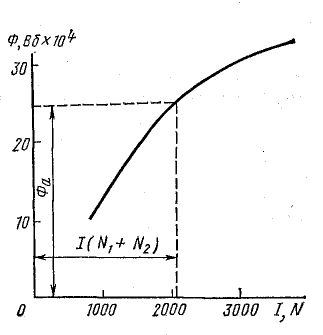
Рис. 9.5. Кривая намагничивания магнитной цепи
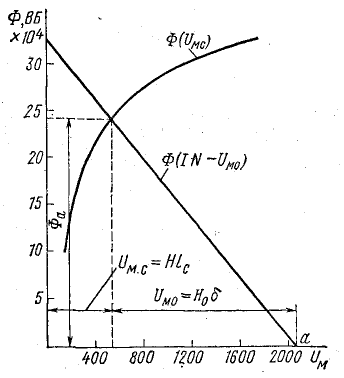
Рис. 9.6. К расчету неразветвленной неоднородной магнитной цепи (обратная задача)
По результатам расчета строится кривая намагничивания цепи (рис. 9.5). По кривой находят магнитный поток, соответствующий заданной намагничивающей силе.
Возможен и другой путь графо-аналитического решения обратной задачи (рис. 9.6). По взятым произвольно нескольким величинам магнитного потока находят величины 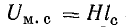 (для стальной части цепи) и
(для стальной части цепи) и 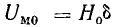 (для воздушного зазора). Затем из начала координат строят кривую
(для воздушного зазора). Затем из начала координат строят кривую 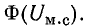
На оси абсцисс находят точку a, соответствующую заданной намагничивающей силе IN, из которой влево проводят прямую Ф(IN — Uм0).
В точке пересечения этих графиков по оси ординат находят искомый поток, а по оси абсцисс — величины Uм.с = Нlс и Uм0 = Н0δ.
Задача 9.5.
Магнитная цепь электромагнитного реле клапанного типа, изготовленная из стали, имеет поток Ф = 1,2 • 10-3 Вб. Определить число витков катушки реле, необходимое для возбуждения созданного магнитного потока при токе в катушке 0,2 А. Ярмо и якорь реле прямоугольного сечения 7,5 x 1,2 см, сердечник круглого сечения диаметром 3 см. Другие размеры показаны на рис. 9.2.
Решение. Магнитная цепь реле делится на однородные участки:
а) сердечник круглого сечения
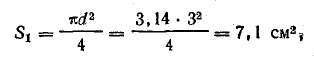
длина l1 = 8,6 см;
б) ярмо прямоугольного сечения
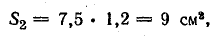
длина l2 = 14,9 см (см. рис. 9.2);
в) якорь прямоугольного сечения
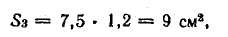
длина l3 = 6,1 см;
г) воздушный зазор, сечение которого принимаем равным сечению сердечника, пренебрегая некоторым увеличением его за счет выпучивания линий магнитной индукции:
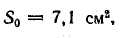
длина δ = 0,2 см.
Магнитная индукция в участках цепи:
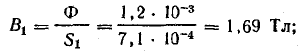
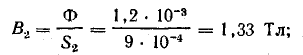
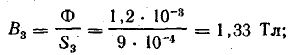
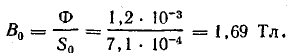
Напряженность магнитного поля в стальных участках определена по кривой намагничивания литой стали, которая принята такой же и для кованой стали: Н1 = 57 А/см; Н2 = 18 А/см; Нз = 18 А /см.
В воздушном зазоре
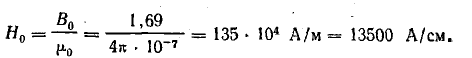
Составляем уравнение по закону полного тока:
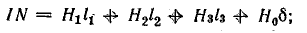
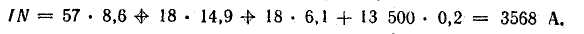
Число витков обмотки
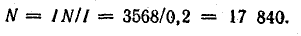
Задача 9.7.
Две катушки N1 = 2000 и N2 = 600 витков насажены на стержни сердечника из электротехнической стали 1211. Размеры магнитной цепи показаны на рис. 9.7. Определить магнитный поток при токе в катушках I = 0,8 А и при соединении концов катушек по схеме: К1 соединен с К2 напряжение приложено к зажимам Н1 и Н2.
Решение. Магнитная цепь рис. 9.7 имеет шесть участков, размеры которых найдены из чертежа:
а) воздушный зазор — δ01 = 0,09 см, S01 = 5 • 4,5 = 22,5 см2;
б) стержень А — l1 = 20 см, S1 = 22,5 см2;
в) ярмо Б — l2 = 25 см, S2 = 22,5 см2;
г) стержень В — lз = 20 см, S3 = 22,5 см2;
д) воздушный зазор — δ02 = 0,09 см, S02 = 22,5 см2;
е) якорь Д — l0 = 25 см, S6 = 22,5 см2.
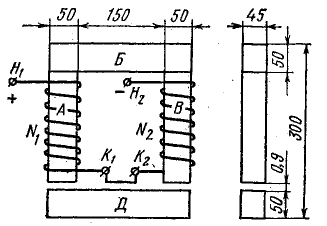
Рис. 9.7. К задаче 9.7
Задаемся несколькими величинами магнитного потока, причем наибольший возможный поток найдем в предположении, что магнитное сопротивление создают только воздушные зазоры [см. формулы (9.1), (9.2)]:
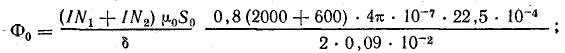
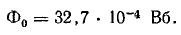
При определении потока учтено, что катушки включены согласно, поэтому их намагничивающие силы сложены.
Для полученного потока найдем намагничивающую силу с учетом стальной части магнитной цепи. Последовательность решения та же, что и при решении задачи 9.5. Результаты расчета для Ф0 и других величин потока сведены в табл. 9.1.
Таблица 9.1
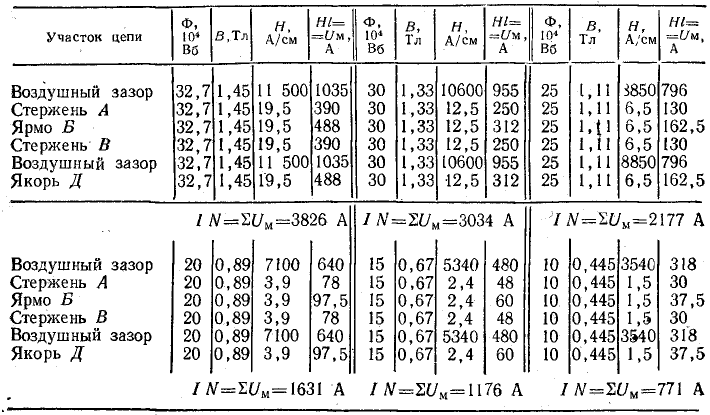
Зависимость Ф(IN) построена на рис. 9.5.
По этой кривой определяем искомый поток, соответствующий намагничивающей силе:
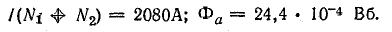
Для графо-аналитического способа определения потока по типу рис. 9.6 из табл. 9.1 выпишем величины Ф и Нlc в табл. 9.2.
Таблица 9.2

Зависимости Ф(Um.c) и Ф(IN — Um0) показаны на рис. 9.6, причем прямая Ф(IN — Um0) построена по двум точкам. При IN — Um0 = 0
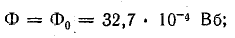
при Ф = 0
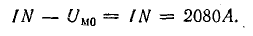
В точке пересечения графиков определяем искомый магнитный поток, а также величины Hlc = Um.c и H0δ = Um0, соответствующие этому потоку:
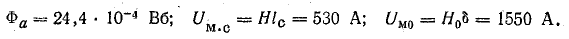
Расчет разветвленной магнитной цепи
В разветвленной магнитной цепи магнитные потоки в общем случае различны в разных ветвях (рис. 9.8).
Разветвленные магнитные цепи делятся на симметричные и несимметричные.
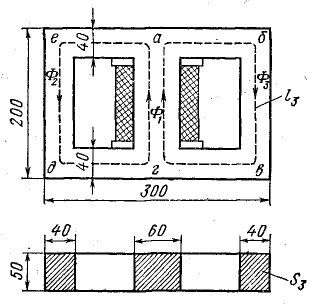
Рис. 9.8. Разветвленная симметричная магнитная цепь
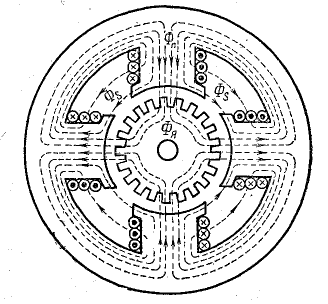
Рис. 9.9. Магнитная цепь четырехполюсной электрической машины
Симметричную магнитную цепь мысленно можно разделить на неразветвленные цепи таким образом, что во всех участках выделенной цепи магнитный поток будет один и тот же. Кроме того, предполагается симметричное расположение намагничивающих сил (рис. 9.8, 9.9).
Если указанные условия симметрии не соблюдаются, то магнитная цепь относится к несимметричным (рис. 9.10).
Узловые и контурные уравнения магнитной цепи
Симметричная магнитная цепь (см. рис. 9.8) состоит из двух одинаковых контуров. Средний стержень вместе с катушкой (источником намагничивающей силы) входит в оба контура.
Место соединения среднего стержня с ярмом является узлом магнитной цепи, в котором магнитный поток Ф1, делится на два равных потока, если магнитное сопротивление обоих контуров одинаково:
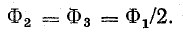
Расчет разветвленной симметричной цепи из-за равенств потоков симметричных контуров сводится к расчету одного контура, который выполняют в том же порядке, что и расчет неразветвленной цепи.
В аналогичной несимметричной магнитной цепи поток в узле делится на неравные части, но для любого узла пригодно уравнение
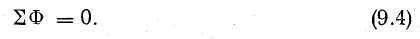
Для схемы рис. 9.8 это уравнение в развернутом виде записывают так:
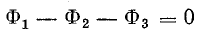 или
или 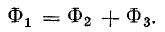
При составлении такого уравнения учитывают направления потоков: направленные к узлу и направленные от узла потоки берутся с разными знаками.
Для каждого контура магнитной цепи можно также составить уравнение по закону полного тока.
Предположим, что все участки магнитной цепи выполнены из материалов с постоянными значениями магнитной проницаемости. Каждый участок и вся цепь имеют линейную зависимость магнитного потока от магнитного напряжения Ф(Uм).
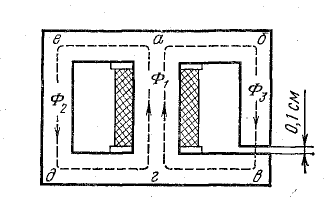
Рис. 9.10. Разветвленная несимметричная магнитная цепь
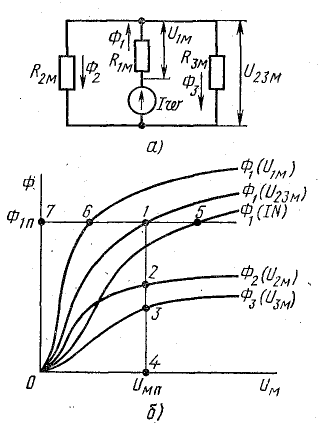
Рис. 9.11. К расчету разветвленной магнитной цепи графическим методом
Определив для каждого участка магнитное сопротивление Rм, магнитную цепь можно представить соответствующей схемой замещения, в которую войдут постоянные магнитные сопротивления участков и намагничивающие силы.
На рис. 9.11, а показана схема замещения магнитной цепи (см. рис. 9.8). Пренебрегая потоками рассеяния, расчет магнитной цепи можно выполнить аналогично расчету электрической цепи, решая систему линейных уравнений, составленных для узлов (см. формулу (9.4)] и контуров [см. формулу (9.3)].
Графический расчет разветвленной цепи
Элементы схем замещения магнитных цепей, осуществляемых на практике (кроме элементов, соответствующих воздушным зазорам), имеют нелинейные характеристики Ф(Uм), так как магнитная проницаемость ферромагнитных материалов зависит от напряженности поля. Нелинейными являются и магнитные цепи в целом.
Аналогия с электрической цепью указывает на возможность графического расчета нелинейной магнитной цепи в порядке. Первый этап расчета состоит в построении характеристик Ф(Uм) для каждого участка цепи в общей системе координат. Для этого используются характеристики намагничивания материалов, из которых изготовлена магнитная цепь. Например, чтобы построить характеристику Ф3(U3м), нужно ряд величин напряженности поля Н3, взятых из характеристики намагничивания материала третьего участка магнитной цепи, умножить на длину этого участка (H3l3 = U3м), а соответствующие им величины магнитной индукции умножить на площадь S3 этого участка (В3S3 = Ф3).
По полученным значениям U3м и Ф3 строят график Ф3(U3м) (рис. 9.11, б). Магнитные сопротивления R2м и R3м соединены параллельно. Поэтому магнитные напряжения второго и третьего участков одинаковы: U2м = U3м = U2.3м.
Сумма магнитных потоков этих участков равна магнитному потоку первого участка (сопротивление R1м): Ф1 = Ф2 + Ф3.
Складывая магнитные потоки Ф2 и Ф3 для ряда значений магнитного напряжения, получим кривую Ф1 (U2.3м).
На рис. 9.11, б это показано для одного значения Uм.п.Отрезки 4-3 и 4-2 в масштабе магнитных потоков выражают потоки Ф3 и Ф2. Сумма этих отрезков, равная отрезку 4-1, выражает магнитный поток Ф1П. Магнитное сопротивление R1м и сопротивление, эквивалентное R2м и R3м, соединены последовательно. Поэтому намагничивающая сила всей цепи IN равна сумме магнитных напряжений U1м и U2.3м: IN = U1м + U2.3м. Магнитные же потоки участков цепи с сопротивлениями R1м и R2.3м одинаковы.
Складывая магнитные напряжения U1м и U2.3м для ряда значений магнитного потока, получим кривую Ф1(IN). На рис. 9.11, б это показано для одного значения Ф1п. Отрезки 7-6 и 7-1 в масштабе магнитных напряжений выражают магнитные напряжения U1м и U2.3м. Сумма этих отрезков дает отрезок 7-5, выражающий намагничивающую силу IN.
Выполнив указанные построения, нетрудно решить различные задачи расчета магнитной цепи.
Задача 6.9.
Катушка, имеющая 500 витков, расположена на среднем стержне магнитопровода, изготовленного из стали 1511 (см. рис. 9.8). Определить ток в катушке, если в крайнем стержне поток Ф2 = Ф3 = 2 • 10-3Вб. Рассеяние потока не учитывается.
Решение. В данной симметричной цепи можно наметить два одинаковых в магнитном отношении контура: а-б-в-г-а и а-е-д-г-а. В каждом из них по два участка:
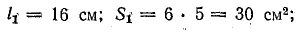
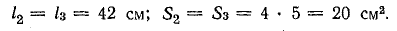
Рассматривая один из контуров, решим задачу в порядке, принятом для неразветвленной цепи:
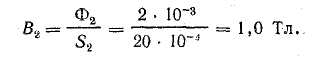
Магнитный поток в среднем стержне в два раза больше, чем в крайних:
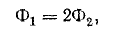
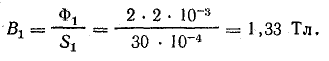
По кривым намагничивания стали 1511 находим:
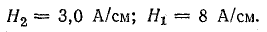
По закону полного тока,
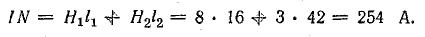
Ток в катушке
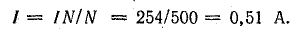
Задача 9.10.
В крайнем стержне магнитопровода, взятого по условию задачи 9.9, имеется воздушный зазор δ = 0,1 см. Определить, как нужно изменить ток в катушке, чтобы сохранить прежнюю величину потока в этом стержне (см. рис. 9.10).
Решение. При наличии воздушного зазора в одном крайнем стержне магнитная цепь становится несимметричной.
В контуре а-е-д-г-а сохранились те же участки; в контуре а-б-в-г-а: l1 = 16 см; l3 = 41,9 см; δ = 0,1 см; S1 = 30 см2;
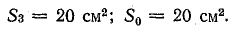
Магнитная индукция в воздушном зазоре и крайнем стержне 6-в
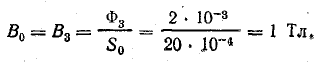
Напряженность поля
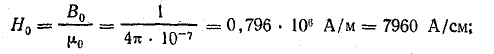
по кривой намагничивания стали 1511 Н3 = 3 А/см.
В магнитной цепи можно наметить третий контур (а-б-в-г-д-е-а). Для этого контура, по закону полного тока,
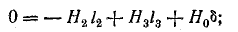
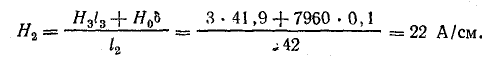
Магнитная индукция на участке l2 по кривой намагничивания В2 = 1,48 Тл. Магнитный поток на участке l2
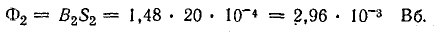
Магнитный поток в среднем стержне (участок l1) определим на основании первого закона Кирхгофа для узла а:
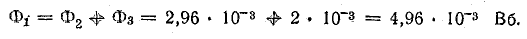
Магнитная индукция на этом участке
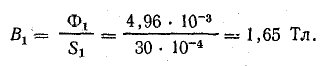
Напряженность поля Н1 = 69,5 А/см.
Для одного из контуров, включающего средний стержень, например а-б-в-г-а, по закону полного тока,
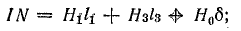
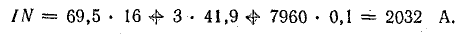
Ток в катушке
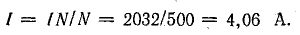
Вывод. Для того чтобы сохранить в крайнем стержне такой же магнитный поток при наличии воздушного зазора δ = 0,1 см, требуется увеличить ток в катушке почти в восемь раз по сравнению с тем случаем, когда зазор отсутствует.
Постоянные магниты
В измерительных приборах, электрической аппаратуре и других устройствах в качестве источников намагничивающей силы широко применяют постоянные магниты.
На рис. 9.12 схематично изображены магнитные системы магнито-электрического измерительного прибора (а) и поляризованного реле (б).
Эти системы, как и большинство им подобных, имеют несколько участков: 1) из магнитно-твердого материала— постоянного магнита 1; 2) из магнитно-мягкого материала 2, служащего магнитопроводом, и воздушного зазора 3, форма и размеры которого определяются конструкцией и назначением устройства.
При расчете магнитной цепи с постоянным магнитом требуется определить магнитный поток и индукцию в воздушном зазоре или по заданному потоку найти оптимальные размеры постоянного магнита (наименьшие объем и габариты).
Характеристики размагничивания постоянных магнитов
Величины остаточной магнитной индукции Вг и коэрцитивной силы Hс характеризуют материал постоянного магнита: чем они больше, тем выше его качество. Как известно, на петле гистерезиса Вг соответствует Н = 0, а при В = 0 Н = Нс.
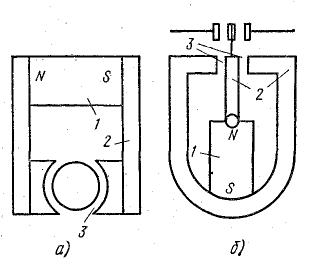
Рис. 9.12. Магнитные цепи с постоянными магнитами
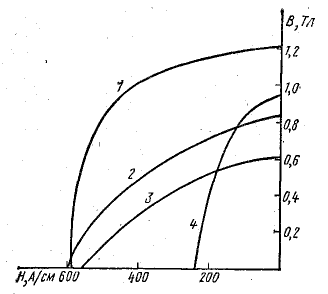
Рис. 9.13. Характеристики размагничивания постоянных магнитов:
1 — АНКО-4; 2 — АНКО-2; З-АН-2; 4 — сталь с 30% СО
Промежуточные магнитные состояния определяются частью петли магнитного гистерезиса, лежащей во второй четверти, — характеристикой размагничивания (рис. 9.12). Эта характеристика используется при расчете постоянных магнитов.
Согласно закону полного тока, сумма магнитных напряжений участков магнитной цепи (рис. 9.12) равна нулю, так как внешняя намагничивающая сила (ампер-витки) отсутствует:
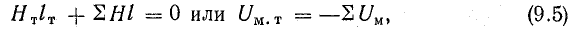
где Uм.т — магнитное напряжение постоянного магнита; 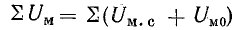 — сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
— сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
Левая и правая части равенства (9.5) связаны с магнитной индукцией и потоком определенными зависимостями: Фт(Uм.т) — кривая размагничивания постоянного магнита (по форме повторяет кривую размагничивания материала, из которого выполнен постоянный магнит); Фм(Uм.с) — кривая намагничивания части конструкции устройства, изготовленной из магнитно-мягкого материала; Ф0(Uм0) — прямая, проходящая через начало координат и повторяющая в других масштабах зависимость 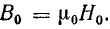
Определение магнитного потока в магнитной цепи с постоянным магнитом
Пренебрегая потоком рассеяния 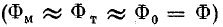 и магнитным напряжением в участках из магнитно-мягкого материала (
и магнитным напряжением в участках из магнитно-мягкого материала (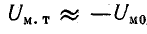 ), можно построить в общей системе координат зависимости
), можно построить в общей системе координат зависимости 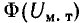 и
и 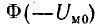 .
.
В этом случае искомый магнитный поток Ф0 определяется точкой их пересечения (рис. 9.14).
Магнитная индукция в воздушном зазоре
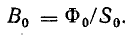
Из равенства (9.5) следует, что напряженности поля в воздушном зазоре и магните направлены в противоположные стороны.
При отсутствии воздушного зазора (постоянный магнит замкнут) остаточная индукция имеет величину Вг, а при наличии зазора будет меньше Вг (рис. 9.14). Воздушный зазор создает эффект размагничивания магнита.
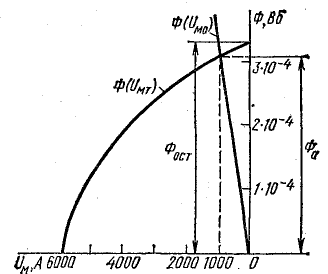
Рис. 9.14. К расчету магнитной цепи с постоянным магнитом
Задача 9.12.
Определить магнитный поток и индукцию в воздушном зазоре постоянного магнита (см. рис. 9.12, а), если магнит, изготовленный из сплава АНКО-2, имеет длину lт = 10 см; SТ = 4 см2. Полюса и цилиндрический сердечник изготовлены из магнитно-мягкой стали, имеют общую длину lм = 15 см; воздушный зазор между полюсом и сердечником δ = 0,2 см с каждой стороны и площадь S = 10 см2. Характеристика размагничивания сплава АНКО-2 представлена на рис. 9.13.
Решение. Построим зависимость магнитного потока в магните от магнитного напряжения Ф(Uм.т).
Для этого, согласно кривой 2 на рис. 9.13, берем величины В и Н, подсчитываем Ф и Uм.т и результаты подсчета сводим в табл. 9.3.
Для тех же величин магнитного потока определим Uм0 = Н0δ для воздушного зазора. Величинами Hсlс для участков из стали пренебрегаем из-за их незначительной величины.
Т а б л и ц а 9.3

Для потока Ф = 3,28 • 10-4 Вб
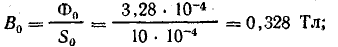
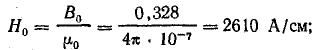
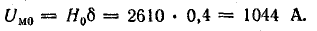
Результаты подсчетов сводим в табл. 9.4.
Таблица 9.4
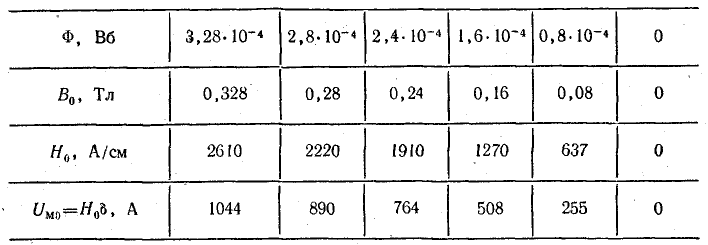
Зависимости Ф(Uм.т) и Ф(Uм0) построены на рис. 9.14. В точке пересечения этих графиков находим магнитный поток:
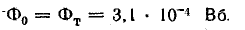
Магнитная индукция в воздушном зазоре
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
Ток или поток? Магнитные цепи и их основные характеристики
Время на прочтение
6 мин
Количество просмотров 13K
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это… а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции – а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель – рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову – провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи – ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
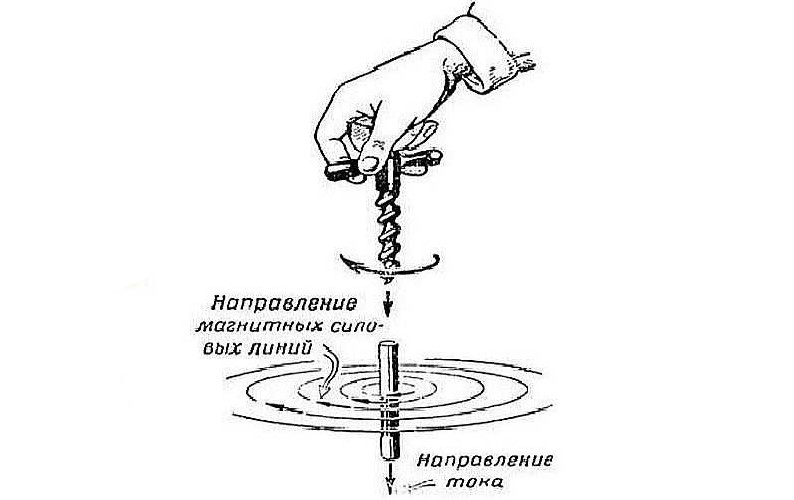
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
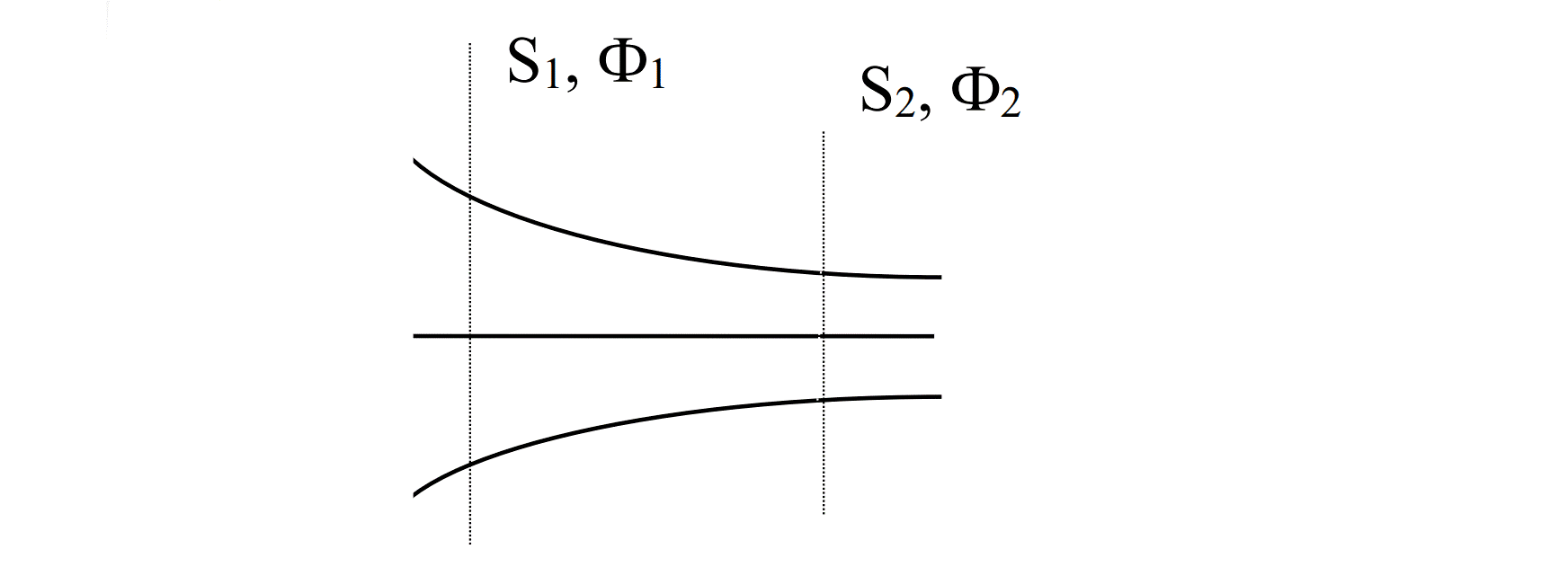
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю… Мне одному это что-то напоминает?
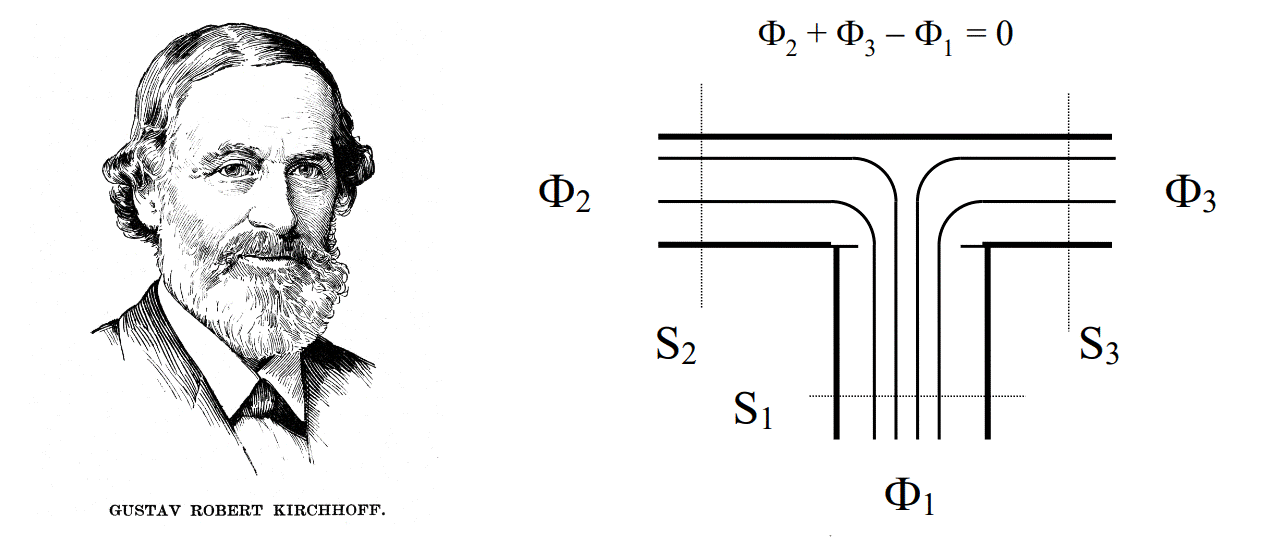
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае – магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи – силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
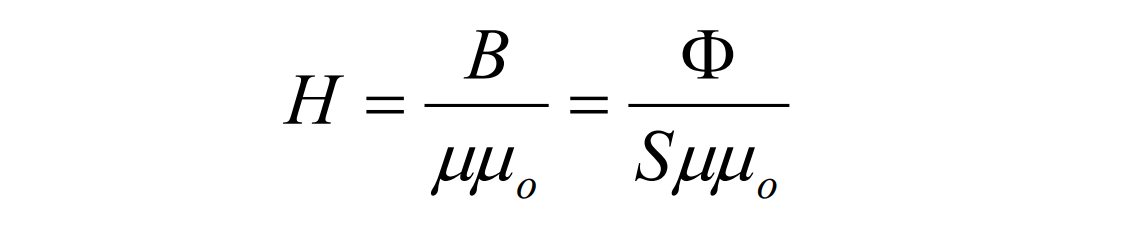
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
-
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
-
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
-
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
-
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь – нет. А по ссылке – да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора – подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
From Wikipedia, the free encyclopedia
| Magnetic reluctance | |
|---|---|
|
Common symbols |
 , ,  |
| SI unit | H−1 |
|
Derivations from |
 , ,  , ,  |
| Dimension | M–1 L–2 T2 I2 |
Magnetic reluctance, or magnetic resistance, is a concept used in the analysis of magnetic circuits. It is defined as the ratio of magnetomotive force (mmf) to magnetic flux. It represents the opposition to magnetic flux, and depends on the geometry and composition of an object.
Magnetic reluctance in a magnetic circuit is analogous to electrical resistance in an electrical circuit in that resistance is a measure of the opposition to the electric current. The definition of magnetic reluctance is analogous to Ohm’s law in this respect. However, magnetic flux passing through a reluctance does not give rise to dissipation of heat as it does for current through a resistance. Thus, the analogy cannot be used for modelling energy flow in systems where energy crosses between the magnetic and electrical domains. An alternative analogy to the reluctance model which does correctly represent energy flows is the gyrator–capacitor model.
Magnetic reluctance is a scalar extensive quantity. The unit for magnetic reluctance is inverse henry, H−1.
History[edit]
The term reluctance was coined in May 1888 by Oliver Heaviside.[1] The notion of “magnetic resistance” was first mentioned by James Joule in 1840.[2] The idea for a magnetic flux law, similar to Ohm’s law for closed electric circuits, is attributed to Henry Augustus Rowland in an 1873 paper.[3] Rowland is also responsible for coining the term magnetomotive force in 1880,[4] also coined, apparently independently, a bit later in 1883 by Bosanquet.[5]
Reluctance is usually represented by a cursive capital 
Definitions[edit]
In both AC and DC fields, the reluctance is the ratio of the magnetomotive force (MMF) in a magnetic circuit to the magnetic flux in this circuit. In a pulsating DC or AC field, the reluctance also pulsates (see phasors).
The definition can be expressed as follows:
where
It is sometimes known as Hopkinson’s law and is analogous to Ohm’s Law with resistance replaced by reluctance, voltage by MMF and current by magnetic flux.
Permeance is the inverse of reluctance:
Its SI derived unit is the henry (the same as the unit of inductance, although the two concepts are distinct).
Magnetic flux always forms a closed loop, as described by Maxwell’s equations, but the path of the loop depends on the reluctance of the surrounding materials. It is concentrated around the path of least reluctance. Air and vacuum have high reluctance, while easily magnetized materials such as soft iron have low reluctance. The concentration of flux in low-reluctance materials forms strong temporary poles and causes mechanical forces that tend to move the materials towards regions of higher flux so it is always an attractive force (pull).
The reluctance of a uniform magnetic circuit can be calculated as:
where
Applications[edit]
- Constant air gaps can be created in the core of certain transformers to reduce the effects of saturation. This increases the reluctance of the magnetic circuit, and enables it to store more energy before core saturation. This effect is also used in the flyback transformer.
- Variable air gaps can be created in the cores by a movable keeper to create a flux switch that alters the amount of magnetic flux in a magnetic circuit without varying the constant magnetomotive force in that circuit.
- Variation of reluctance is the principle behind the reluctance motor (or the variable reluctance generator) and the Alexanderson alternator. Another way of saying this is that the reluctance forces strive for a maximally aligned magnetic circuit and a minimal air gap distance.
- Multimedia loudspeakers are typically shielded magnetically, in order to reduce magnetic interference caused to televisions and other CRTs. The speaker magnet is covered with a material such as soft iron to minimize the stray magnetic field.
Reluctance can also be applied to:
- Reluctance motors
- Variable reluctance (magnetic) pickups
- Magnetic capacitance
- Magnetic circuit
- Magnetic complex reluctance
References[edit]
- ^ Heaviside O. (1892) Electrical Papers, Vol 2 – L.; N.Y.: Macmillan, p. 166
- ^ Joule J. (1884) Scientific Papers, vol 1, p.36
- ^ Rowland, Henry A. (1873). “XIV. On magnetic permeability, and the maximum of magnetism of iron, steel, and nickel”. Philosophical Magazine. Series 4. 46 (304): 140–159. doi:10.1080/14786447308640912.
- ^ Rowland, Henry A, “On the general equations of electro-magnetic action, with application to a new theory of magnetic attractions, and to the theory of the magnetic rotation of the plane of polarization of light” (part 2), American Journal of Mathematics, vol. 3, nos. 1–2, pp. 89–113, March 1880.
- ^ Bosanquet, R.H.M. (1883). “XXVIII.On magnetomotive force”. Philosophical Magazine. Series 5. 15 (93): 205–217. doi:10.1080/14786448308628457.

Содержание
- Формулы и единицы измерения
- Как рассчитывается магнитное сопротивление?
- Разница с электрическим сопротивлением
- Примеры
- Соленоиды
- Катушка намотана на прямоугольный железный сердечник
- Решенные упражнения
- – Упражнение 1
- Решение
- – Упражнение 2.
- Решение
- Ссылки
В магнитное сопротивление или магнитное сопротивление – это противодействие, которое среда представляет прохождению магнитного потока: чем выше сопротивление, тем сложнее установить магнитный поток. В магнитной цепи сопротивление играет ту же роль, что и электрическое сопротивление в электрической цепи.
Катушка, переносимая электрическим током, является примером очень простой магнитной цепи. Благодаря току создается магнитный поток, который зависит от геометрического расположения катушки, а также от силы тока, проходящего через нее.

Формулы и единицы измерения
Обозначив магнитный поток как Φм, у нас есть:
Φм = N.i / (ℓc / мкАc)
Куда:
-N – количество витков катушки.
-Сила тока составляет я.
-ℓc представляет длину цепи.
–Кc – площадь поперечного сечения.
-μ – проницаемость среды.
Фактор в знаменателе, который объединяет геометрию плюс влияние среды, и есть магнитное сопротивление цепи, скалярная величина, которая обозначается буквой, чтобы отличить ее от электрического сопротивления. Так:
ℜ = ℓc / мкАc
В Международной системе единиц (СИ) измеряется как величина, обратная генри (умноженная на количество витков N). В свою очередь, Генри – это единица измерения магнитной индукции, эквивалентная 1 тесла (Тл) x квадратный метр / ампер. Таким образом:
1 ЧАС-1 = 1 А /Т.м2
Как 1 T.m2 = 1 Вебер (Wb), сопротивление также выражается в A / Wb (ампер / Вебер или, чаще, ампер-виток / Вебер).
Как рассчитывается магнитное сопротивление?
Поскольку магнитное сопротивление играет ту же роль, что и электрическое сопротивление в магнитной цепи, можно расширить аналогию с помощью эквивалента закона Ома V = IR для этих цепей.
Хотя он не циркулирует должным образом, магнитный поток Φм занимает место тока, а вместо напряжения V, определяет магнитное напряжение или магнитодвижущая сила, аналог электродвижущей силы илиf.e.m в электрических цепях.
Магнитодвижущая сила отвечает за поддержание магнитного потока. Сокращенно f.m.m и обозначается как ℱ. Таким образом, мы наконец получили уравнение, которое связывает три величины:
ℱ = Φм . ℜ
И сравнивая с уравнением Φм = N.i / (ℓc / мкАc), сделан вывод, что:
ℱ = N.i
Таким образом, сопротивление может быть вычислено, зная геометрию контура и проницаемость среды, а также зная магнитный поток и магнитное напряжение, благодаря этому последнему уравнению, называемому Закон Гопкинсона.
Разница с электрическим сопротивлением
Уравнение магнитного сопротивления ℜ = ℓc / мкАc похож на R = L / σA на электрическое сопротивление. В последнем случае σ представляет собой проводимость материала, L – длину провода, а A – площадь его поперечного сечения.
Эти три величины: σ, L и A постоянны. Однако проницаемость среды μ, в общем, оно непостоянно, поэтому магнитное сопротивление цепи тоже непостоянно, в отличие от его электрического аналога.
Если происходит изменение среды, например, при переходе от воздуха к железу или наоборот, происходит изменение проницаемости с последующим изменением сопротивления. А также магнитные материалы проходят через циклы гистерезиса.
Это означает, что приложение внешнего поля заставляет материал сохранять часть магнетизма даже после того, как поле снято.
По этой причине каждый раз, когда рассчитывается магнитное сопротивление, необходимо тщательно определять, где материал находится в цикле, и, таким образом, знать его намагниченность.
Примеры
Хотя сопротивление сильно зависит от геометрии контура, оно также зависит от проницаемости среды. Чем выше это значение, тем меньше сопротивление; так обстоит дело с ферромагнитными материалами. С другой стороны, воздух имеет низкую проницаемость, поэтому его магнитное сопротивление выше.
Соленоиды
Соленоид – это обмотка длинойℓ сделано с N витками, через которые пропускается электрический ток I. Обычно витки намотаны по кругу.
Внутри него создается интенсивное и однородное магнитное поле, а снаружи поле становится примерно нулевым.

Если обмотке придать круглую форму, имеется тор. Внутри может быть воздух, но если поместить железный сердечник, магнитный поток будет намного выше, благодаря высокой проницаемости этого минерала.
Катушка намотана на прямоугольный железный сердечник
Магнитную цепь можно построить, намотав катушку на прямоугольный железный сердечник. Таким образом, когда через провод проходит ток, можно создать интенсивный поток поля, ограниченный внутри железного сердечника, как показано на рисунке 3.
Сопротивление зависит от длины цепи и площади поперечного сечения, указанной на рисунке. Показанная схема является однородной, так как сердечник выполнен из одного материала, а поперечное сечение остается однородным.

Решенные упражнения
– Упражнение 1
Найдите магнитное сопротивление прямолинейного соленоида с 2000 витками, зная, что, когда через него протекает ток 5 А, генерируется магнитный поток 8 мВт.
Решение
Уравнение используется ℱ = N.i для расчета магнитного натяжения, так как сила тока и количество витков в катушке доступны. Просто умножается:
ℱ = 2000 x 5 A = 10000 ампер-виток
Тогда используется ℱ = Φм . ℜ, стараясь выразить магнитный поток в Вебере (приставка «m» означает «милли», поэтому она умножается на 10 -3:
Φм = 8 х 10 -3 Wb
Теперь сопротивление очищено и подставлены значения:
ℜ = ℱ/ Φм = 10 000 ампер-витков / 8 x 10-3 Wb = 1,25 х 106 ампер-поворот / Вб
– Упражнение 2.
Рассчитайте магнитное сопротивление цепи, показанной на рисунке, с указанными размерами в сантиметрах. Проницаемость керна составляет μ = 0,005655 Тм / А, а площадь поперечного сечения постоянна, 25 см.2.
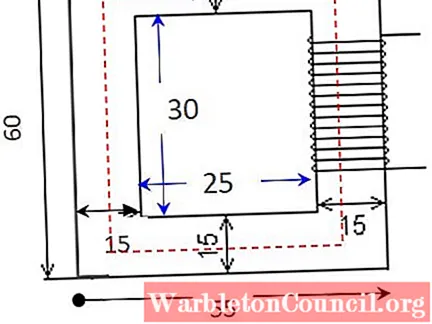
Решение
Применим формулу:
ℜ = ℓc / мкАc
Проницаемость и площадь поперечного сечения доступны как данные в отчете. Осталось найти длину контура, которая является периметром красного прямоугольника на рисунке.
Для этого длину горизонтальной стороны усредняют, добавляя большую длину и меньшую длину: (55 + 25 см) / 2 = 40 см. Затем действуйте таким же образом для вертикальной стороны: (60 + 30 см) / 2 = 45 см.
Наконец, складываются средние длины четырех сторон:
ℓc = 2 х 40 см + 2 х 45 см = 170 см
Вычтите подставляемые значения в формуле сопротивления, но не раньше, чем выразите длину и площадь поперечного сечения, указанные в заявлении, в единицах СИ:
ℜ = 170 х 10 -2м / (0,005655 Tm / A x 0,0025 м2) = 120 248 ампер-оборот / Вб
Ссылки
- Алеман, М. Ферромагнитный сердечник. Получено с: youtube.com.
- Магнитная цепь и сопротивление. Получено с: mse.ndhu.edu.tw.
- Спинадел, Э. 1982. Электрические и магнитные цепи. Новая библиотека.
- Википедия. Магнитодвижущая сила. Получено с: es.wikipedia.org.
- Википедия. Магнитное сопротивление. Получено с: es.wikipedia.org.
Макеты страниц
По определению, падение магнитного напряжения  но
но

где S — площадь поперечного сечения участка.
Следовательно,

откуда
 (14.15)
(14.15)
Уравнение (14.14) называют законом Ома для магнитной цепи. Это уравнение устанавливает связь между падением магнитного напряжения  и потоком Ф;
и потоком Ф;  называют магнитным сопротивлением участка магнитной цепи. Величину, обратную магнитному сопротивлению, называют магнитной проводимостью:
называют магнитным сопротивлением участка магнитной цепи. Величину, обратную магнитному сопротивлению, называют магнитной проводимостью:
 (14.16)
(14.16)
Из предыдущего известно, что вебер-амперная характеристика участка магнитной цепи в общем случае нелинейна. Следовательно, в общем случае  и
и  являются функциями магнитного потока (непостоянными величинами). Поэтому практически понятиями
являются функциями магнитного потока (непостоянными величинами). Поэтому практически понятиями  и
и  при расчетах пользуются в тех случаях, когда магнитная цепь в целом или ее участок, для которых определяются
при расчетах пользуются в тех случаях, когда магнитная цепь в целом или ее участок, для которых определяются  и
и  , не насыщены. Чаще всего это бывает, когда в магнитной цепи имеется достаточно большой воздушный зазор, спрямляющий вебер-амперную характеристику магнитной цепи в целом или ее участка.
, не насыщены. Чаще всего это бывает, когда в магнитной цепи имеется достаточно большой воздушный зазор, спрямляющий вебер-амперную характеристику магнитной цепи в целом или ее участка.
Магнитное сопротивление участка цепи  можно сопоставить со статическим сопротивлением нелинейного резистора
можно сопоставить со статическим сопротивлением нелинейного резистора  (см. § 13.10) и так же, как последнее,
(см. § 13.10) и так же, как последнее,  можно использовать при качественном рассмотрении различных вопросов, например вопроса об изменении потоков двух параллельных ветвей при изменении потока в неразветвленной части магнитной цепи (как в § относительно электрической цепи).
можно использовать при качественном рассмотрении различных вопросов, например вопроса об изменении потоков двух параллельных ветвей при изменении потока в неразветвленной части магнитной цепи (как в § относительно электрической цепи).
Пример 146. Найти  воздушного зазора постоянного магнита и магнитный поток, если
воздушного зазора постоянного магнита и магнитный поток, если  , площадь поперечного сечения воздушного зазора
, площадь поперечного сечения воздушного зазора  .
.
Решение:

где 
В заключение отметим, что если воспользоваться понятием магнитного сопротивления, то второй закон Кирхгофа [см. формулу (14.9)] для любого контура магнитной цепи, содержащей  участков, может быть записан так:
участков, может быть записан так:
 (14.17)
(14.17)

Рис. 14.19
Практически формулой (14.17) как расчетной удается воспользоваться, когда магнитная цепь не насыщена и  не является функцией
не является функцией  Если же имеет место насыщение, то является функцией (т. е. неизвестно
Если же имеет место насыщение, то является функцией (т. е. неизвестно  ) и при использовании формулы (14.17) возникают известные трудности.
) и при использовании формулы (14.17) возникают известные трудности.



