| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Электромагни́тная инду́кция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле[1]. Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года[2]. Он обнаружил, что электродвижущая сила (ЭДС), возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.
Закон Фарадея[править | править код]
Согласно закону электромагнитной индукции Фарадея (в СИ):
где
— электродвижущая сила, действующая вдоль произвольно выбранного контура,
— магнитный поток через поверхность, ограниченную этим контуром.
Знак «минус» в формуле отражает правило Ленца , названное так по имени физика Э. Х. Ленца:
- Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.
Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:
где
— электродвижущая сила,
— число витков,
— магнитный поток через один виток,
— потокосцепление катушки.
Векторная форма[править | править код]
Закон Фарадея можно записать либо в дифференциальной форме:
(в системе СИ)
или
(в системе СГС),
либо в эквивалентной интегральной форме:
(СИ)
или
(СГС).
Здесь 




Закон Фарадея в такой форме описывает лишь ту часть ЭДС, которая возникает при изменении магнитного потока через контур за счёт изменения со временем самого поля без изменения (движения) границ контура (об учёте последнего см. ниже).
- В этом виде закон Фарадея входит в систему уравнений Максвелла для электромагнитного поля (в дифференциальной или интегральной форме соответственно)[3].
Если же, магнитное поле постоянно, а магнитный поток изменяется вследствие движения границ контура (например, при увеличении его площади), то возникающая ЭДС порождается силами, удерживающими заряды на контуре (в проводнике) и силой Лоренца, порождаемой прямым действием магнитного поля на движущиеся (с контуром) заряды. При этом равенство 

- Некоторые авторы, например, М. Лившиц в журнале «Квант» за 1998 год[4] отрицают корректность применения термина закон Фарадея или закон электромагнитной индукции и т. п. к формуле
в случае подвижного контура (оставляя для обозначения этого случая или его объединения со случаем изменения магнитного поля, например, термин правило потока)[5]. В таком понимании закон Фарадея — это закон, касающийся лишь циркуляции электрического поля (но не ЭДС, создаваемой с участием силы Лоренца), и в этом понимании понятие закон Фарадея в точности совпадает с содержанием соответствующего уравнения Максвелла.
- Однако возможность (пусть с некоторыми оговорками, уточняющими область применимости) совпадающей формулировки «правила потока» с законом электромагнитной индукции нельзя назвать чисто случайной. Дело в том, что, по крайней мере для определённых ситуаций, это совпадение оказывается очевидным проявлением принципа относительности. А именно, например, для случая относительного движения катушки с присоединённым к ней вольтметром, измеряющим ЭДС, и источника магнитного поля (постоянного магнита или другой катушки с током), в системе отсчёта, связанной с первой катушкой, ЭДС оказывается равной именно циркуляции электрического поля, тогда как в системе отсчёта, связанной с источником магнитного поля (магнитом), происхождение ЭДС связано с действием силы Лоренца на движущиеся с первой катушкой носители заряда. Однако та и другая ЭДС обязаны совпадать, поскольку вольтметр показывает одну и ту же величину, независимо от того, для какой системы отсчёта мы её рассчитали.
Потенциальная форма[править | править код]
При выражении магнитного поля через векторный потенциал закон Фарадея принимает вид:
(в случае отсутствия безвихревого поля, то есть тогда, когда электрическое поле порождается полностью только изменением магнитного, то есть электромагнитной индукцией).
В общем случае, при учёте и безвихревого (например, электростатического) поля имеем:
Подробнее
Поскольку вектор магнитной индукции по определению выражается через векторный потенциал так:
то можно подставить это выражение в
получая
и, поменяв местами дифференцирование по времени и пространственным координатам (ротор):
Отсюда, поскольку 

То есть в случае отсутствия безвихревой части можно записать
а в общем случае
История[править | править код]
В 1820 году Ханс Кристиан Эрстед показал, что протекающий по цепи электрический ток вызывает отклонение магнитной стрелки. Если электрический ток порождает магнетизм, то с магнетизмом должно быть связано появление электрического тока. Эта мысль захватила английского ученого М. Фарадея. «Превратить магнетизм в электричество», — записал он в 1822 году в своём дневнике. Многие годы он настойчиво ставил различные опыты, но безуспешно, и только 29 августа 1831 года наступил триумф: он открыл явление электромагнитной индукции. Установка, на которой Фарадей сделал своё открытие, состояла из кольца из мягкого железа примерно 2 см шириной и 15 см диаметром. На каждой половине кольца было намотано много витков медной проволоки. Цепь одной обмотки замыкала проволока, в её витках находилась магнитная стрелка, удаленная настолько, чтобы не сказывалось действие магнетизма, созданного в кольце. Через вторую обмотку пропускался ток от батареи гальванических элементов. При включении тока магнитная стрелка совершала несколько колебаний и успокаивалась; когда ток прерывали, стрелка снова колебалась. Выяснилось, что стрелка отклонялась в одну сторону при включении тока и в другую, когда ток прерывался. М. Фарадей установил, что «превращать магнетизм в электричество» можно и с помощью обыкновенного магнита.
В это же время американский физик Джозеф Генри также успешно проводил опыты по индукции токов, но пока он собирался опубликовать результаты своих опытов, в печати появилось сообщение М. Фарадея об открытии им электромагнитной индукции.
М. Фарадей стремился использовать открытое им явление, чтобы получить новый источник электричества.
См. также[править | править код]
- Взаимоиндукция
- Самоиндукция
- Индуктивность
- Закон электромагнитной индукции Фарадея
Примечания[править | править код]
- ↑ Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- ↑ Faraday, Michael; Day, P. The philosopher’s tree: a selection of Michael Faraday’s writings (англ.). — CRC Press, 1999. — P. 71. — ISBN 978-0-7503-0570-9.
- ↑
Это уравнение Максвелла может быть переписано в эквивалентном виде(здесь просто производная по t внесена под знак интеграла). В таком виде уравнение также может быть включено в систему уравнений Максвелла, причем оговорка о неподвижности контура интегрирования теряет актуальность, так как производная теперь не действует на границу области (на пределы интегрирования), а само интегрирование в любом случае полагается «мгновенным». В принципе, в таком виде это уравнение также могут называть законом Фарадея (чтобы отличить его от других уравнений Максвелла), пусть в таком виде оно и не совпадает прямо с его обычной формулировкой (но эквивалентно ей в своей области применимости).
- ↑ М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- ↑ Такой отказ объясняется тем, что, в отличие от закона для циркуляции электрического поля, выполняющегося всегда, «правило» корректно работает лишь для случаев, когда контур, в котором вычисляется ЭДС, совпадает физически с проводником (то есть совпадает их движение; в противном же случае правило может не работать (самый известный пример — униполярная машина Фарадея; контур, который в этом случае трудно определить, но кажется довольно очевидным, что он не меняется; во всяком случае, довольно затруднительно указать разумное определение для контура, который бы в этом случае менялся), то есть проявляется парадокс, что для «закона природы» недопустимо.
Ссылки[править | править код]
- Про электромагнитную индукцию в «Школе для электрика»
- Электромагнитная индукция (учебный видеофильм)
Явление электромагнитной индукции знакомо нам ещё со школы, однако далеко не каждый запомнил что это такое или смог в своё время разобраться в мудреном определении. Возможно вы изучаете физику прямо сейчас и ищете более понятное изложение традиционно сложного описания. Тогда эта статья прекрасно вам подойдет и нужно дочитать её до самого конца.
Электромагнитная индукция – одно из главных физических явлений, с которым нам приходится иметь дело чуть ли не ежесекундно. Виноваты многочисленные электронные устройства вокруг нас. Но что это такое и где мы можем встретиться с индукцией?
Давайте посмотрим, как на википедии описывается электромагнитная индукция:
Электромагнитная индукция — явление возникновения электрического тока, электрического поля или электрической поляризации при изменении магнитного поля во времени или при движении материальной среды в магнитном поле.
Спасибо! Теперь-то всё ясно! Мы уже не запутаемся и прекрасно поняли, что такое электромагнитная индукция.
Давайте разбираться в сложном для большинства читателей определении также, как мы это делали с законом ома или законами Ньютона на нашем канале.
Читаем поэтапно:
“Возникновение электрического тока” – вроде вопрос возникать не должен. Где-то и почему-то возникает электрический ток. Что такое электрический ток мы уже знаем. Теперь мы понимаем, что иногда он может возникать из-за чего-то и наверное тут оно как-то связано с индукцией.
“Электрического поля и электрической поляризации…” – важное дополнение, но для базового понимания не требуется. Достаточно просто понять, что может возникать электрический ток. Электрическое поле – понятие связанное. Поляризация – вообще скорее как связанное явление.
“При изменении магнитного поля…” – тут нужно вспомнить, что магнитным полем называется особый вид материи, существующий вокруг магнитов будь-то постоянных или переменных. Также оно существует и вокруг проводников с током. Уместно вспомнить картинку с линиями магнитной индукции вокруг магнитика.
Под изменением магнитного поля понимается изменение размера (значения) вектора магнитной индукции (В) или напряженности магнитного поля. Про напряженность магнитного поля чаще говорят применительно к вакууму, а вот про вектор магнитной индукции отметим дополнительно. Это численная силовая характеристика магнитного поля. Чем мощнее поле, тем больше этот вектор.
По сути дела вектор магнитной индукции – это величина, показывающая с какой силой (обозначаем F) действует магнитное поле на внесенный в него проводник с током (обозначено I) и определенной длиной (l). Это приведенная характеристика, которая используется для удобства и возможности описания силы магнитного поля.
Или, соотношение силы, действующей на проводник к произведению его длины на силу тока в этом проводнике.
Вектор магнитной индукции направлен следующим образом (при этом основная сплошная линия – это силовая магнитная линия магнитного поля):
Так вот под изменением магнитного поля в основном определении подразумевается изменение параметров этого вектора магнитной индукции.
“…во времени…” – тут всё ясно. Вся изложенная выше канитель меняется во времени. Сейчас вектор был равен 1, а через две минуты значение стало равным 2. Вот и изменилось магнитное поле во времени.
“…при движении материальной среды в магнитном поле…” – ну тут есть отличный пример. Катались ли вы на велосипеде под линиями электропередач? А било ли вас током от движущегося велосипеда под линиями электромагнитных передач? Если да, то привет! Вы на практике познали электромагнитную индукцию. Высоковольтные провода окружены магнитным полем или линиями магнитной индукции. Когда вы заезжаете в зону его действия, вы являетесь той самой материальной средой, которая движется в магнитном поле. На вас появляется электрический ток. Он и лупит по рукам, а иногда и по пятой точке от сиденья. Такой электрический ток называется индукционным током.
Правда есть тут одно важное уточнение – эта материальная среда должна быть замкнутым контуром, как рама велосипеда. Почему-то в определении из википедии это важнейшее обстоятельство опущено. Но Фарадей когда-то обнаружил рассматриваемое явление именно в экспериментах с замкнутым контуром. Да и в тех же электродвигателях мы имеем дело с короткозамкнутым ротором.
Поэтому, гораздо чаще в учебниках мы встречаем такое определение:
Электромагнитная индукция – это явление возникновения тока в замкнутом проводнике при прохождении через него магнитного потока, изменяющегося со временем.
Вроде всё и проще, и понятнее. Кроме новой фразы магнитный поток.
Магнитный поток – это поток вектора магнитной индукции, о котором мы говорили выше, через поверхность. Ну а упрощая эту фразу – это то, сколько раз линии магнитной индукции пронизывают некоторую площадь или даже СКОЛЬКО векторов магнитной индукции проходят через площадь.
Также было сказано, что магнитного потока “изменяющегося во времени“. Обратите внимание, что под изменением понимается как количество векторов В в контуре (уменьшение напряженности поля) так и изменение направления и угла В относительно нормали к этому контуру. Ведь формула магнитного потока:
Значит, любое изменение параметров, входящих в состав формулы, вызовет и изменение магнитного потока.
Значит, простое определение электромагнитной индукции выглядит так:
Если в магнитном поле крутить замкнутую рамку, то в ней появится электрический ток. А ещё можно менять магнитное поле разными способами. И тоже появится ток. Это и будет электромагнитная индукция.
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
→
2.1 Методы расчета магнитных цепей постоянного тока
2.1 Методы расчета магнитных цепей постоянного тока
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
Расчет магнитных цепей при постоянных токах
Основанием к расчету магнитных цепей служат: первый закон Кирхгофа для магнитных цепей и закон полного тока — второй закон Кирхгофа для магнитных цепей.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи и имеет вид:
∫ H → ⋅ dl → = ∑ I⋅w ,
где
∫ H → ⋅ dl → = ∑ H⋅l — падение магнитного напряжения UM = H·l в контуре;
F= ∑ I⋅w — магнитодвижущая сила контура (м. д. с.).
Второй закон Кирхгофа для магнитных цепей сформулируем следующим образом: алгебраическая сумма магнитных напряжений UM = H·l в замкнутом контуре магнитной цепи ( ∑ U M = ∑ H⋅l ) равна алгебраической сумме магнитодвижущих сил F = I·w в том же контуре ( ∑ F = ∑ I⋅w ) :
∑ U M = ∑ F
или
∑ H⋅l = ∑ I⋅w .
Задачи на расчет магнитной цепи могут быть двух видов: прямая задача на расчет магнитной цепи — когда задан поток и требуется рассчитать магнитодвижущую силу (м. д. с.) и обратная задача на расчет магнитной цепи — когда по заданной м. д. с. требуется рассчитать магнитный поток.
В обоих случаях должны быть известны геометрические размеры магнитной цепи и заданы кривые намагничивания ее материалов.
Алгоритм прямой задачи расчета неразветвленной магнитной цепи
Дана конфигурация и геометрические размеры неразветвленной магнитной цепи, кривая (или кривые) намагничивания магнитного материала и магнитный поток или индукция магнитного поля в каком-либо сечении. Требуется найти магнитодвижущую силу, ток или число витков намагничивающей обмотки.
Расчет проводим в соответствии с алгоритмом:
1. Разбиваем магнитную цепь на однородные (из одного магнитного материала) участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков (в метрах) берем по средней силовой линии.
2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке:
B k = Ф S k .
Если задана магнитная индукция на каком-либо участке магнитной цепи, то магнитный поток вдоль всей неразветвленной цепи
Ф = Bk·Sk.
3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала k-го участка цепи (например, рис. 2.1, табл. 2.1) определяем напряженности поля Hk на каждом участке магнитной цепи.
Напряженность поля в воздушном зазоре находим по формуле
H возд = B возд μ 0 = B возд 4π⋅ 10 −7 .
4. Подсчитаем сумму падений магнитных напряжений UMk = Hk·lk вдоль всей магнитной цепи ∑ U Mk = ∑ H k ⋅ l k и на основании второго закона Кирхгофа для магнитной цепи приравниваем сумме магнитодвижущих сил Fk = Ik·wk вдоль всей магнитной цепи:
∑ H k ⋅ l k = ∑ I k ⋅ w k .
Основным допущением при расчете является то, что магнитный поток вдоль всей неразветвленной магнитной цепи полагаем неизменным. В действительности не большая часть потока всегда замыкается, минуя основной путь. Этот поток называют потоком рассеяния.
Единицы измерения магнитных величин
B — индукция магнитного поля, Тл (Тесла);
H — напряженность магнитного поля, А/м (Ампер/метр);
Ф — поток индукции магнитного поля, Вб (Вебер);
F = I·w — магнитодвижущая сила (м. д. с.), А (Ампер);
UM = H·l — магнитное напряжение, А (Ампер!).
Константы
μ 0 =4π⋅ 10 −7 Гн/м — магнитная постоянная.
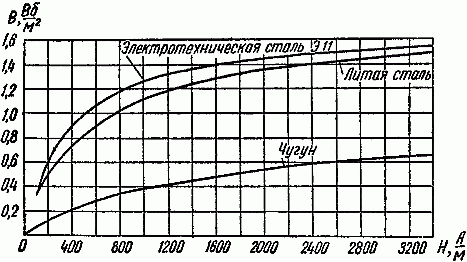
Рис. 2.1 Кривые намагничивания стали и чугуна
Таблица 2.1 — Данные основной кривой намагничивания листовой электротехнической стали Э11
|
B, Вб/м2 |
H, А/м |
|||||||||
|
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
0,4 |
140 |
143 |
146 |
149 |
152 |
155 |
158 |
161 |
164 |
167 |
|
0,5 |
171 |
175 |
179 |
183 |
187 |
191 |
195 |
199 |
203 |
207 |
|
0,6 |
211 |
216 |
221 |
226 |
231 |
236 |
241 |
246 |
251 |
256 |
|
0,7 |
261 |
266 |
271 |
276 |
281 |
287 |
293 |
299 |
306 |
312 |
|
0,8 |
318 |
324 |
330 |
337 |
344 |
352 |
360 |
369 |
378 |
387 |
|
0,9 |
397 |
407 |
417 |
427 |
437 |
447 |
458 |
469 |
480 |
491 |
|
1,0 |
502 |
514 |
527 |
541 |
555 |
570 |
585 |
600 |
615 |
631 |
|
1,1 |
647 |
664 |
682 |
701 |
720 |
739 |
759 |
779 |
800 |
821 |
|
1,2 |
843 |
866 |
891 |
918 |
946 |
976 |
1010 |
1040 |
1070 |
1100 |
|
1,3 |
1140 |
1180 |
1220 |
1260 |
1300 |
1340 |
1380 |
1430 |
1480 |
1530 |
|
1,4 |
1580 |
1640 |
1710 |
1780 |
1860 |
1950 |
2050 |
2150 |
2260 |
2380 |
|
1,5 |
2500 |
2640 |
2790 |
2950 |
3110 |
3280 |
3460 |
3660 |
3880 |
4120 |
|
1,6 |
4370 |
4630 |
4910 |
5220 |
5530 |
5880 |
6230 |
6600 |
6980 |
7370 |
|
1,7 |
7780 |
8200 |
8630 |
9070 |
9630 |
10100 |
10600 |
11100 |
11600 |
12200 |
|
1,8 |
12800 |
13400 |
14000 |
14600 |
15200 |
15900 |
16600 |
17300 |
18000 |
18800 |
|
1,9 |
19700 |
20600 |
21600 |
22 600 |
23600 |
24600 |
25600 |
26800 |
28200 |
29600 |
|
2,0 |
31000 |
32500 |
34300 |
36500 |
39000 |
42000 |
45500 |
49500 |
54500 |
59500 |
Примеры пользования таблицей:
1) При B = 0,80 Вб/м2: H = 318 А/м; при B = 0,85 Вб/м2: H = 352 А/м.
2) При B = 1,13 Вб/м2: H = 701 А/м.
Решение задач на расчет магнитных цепей при постоянных токах
Задача 2.1. На рис. 2.2 изображен разрез трех катушек, по которым проходят токи I1 = 8 А, I2=10 А и I3 = 5 А.
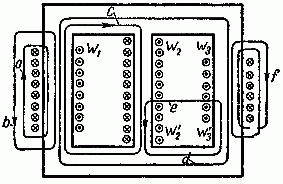
Рис. 2.2
Катушки размещены на стальном сердечнике. Первая катушка (левая) w1 имеет 8 витков, вторая (средняя) w2 — 10 витков и третья (правая) w3 — 6 витков. Определить полную магнитодвижущую силу (м. д. с.) по замкнутым контурам а, b, с, d, е, f, показанным на рис. 2.2. Контур е охватывает катушки w’2 с 4 витками и w’3 с 2 витками.
Изменится ли результат решения задачи, если при тех же данных катушки разместить на сердечнике из другого магнитного материала?
Решение
Воспользуемся законом полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
∫ H → ⋅ dl → = ∑ I⋅w .
Пользуясь законом полного тока, найдем:
∫ a H → ⋅ dl → = w 1 ⋅ I 1 =8⋅8=64 А; ∫ b H → ⋅ dl → =− w 1 ⋅ I 1 =−8⋅8=−64 А; ∫ c H → ⋅ dl → = w 2 ⋅ I 2 − w 1 ⋅ I 1 =10⋅10−8⋅8=36 А; ∫ d H → ⋅ dl → = w 1 ⋅ I 1 − w 2 ⋅ I 2 + w 2 ⋅ I 2 + w 3 ⋅ I 3 =8⋅8+6⋅5=94 А; ∫ e H → ⋅ dl → = w ′ 2 ⋅ I 2 − w ′ 3 ⋅ I 3 =4⋅10+2⋅5=50 А; ∫ f H → ⋅ dl → =2 w 3 ⋅ I 3 =2⋅6⋅5=60 А.
В правой части последнего выражения коэффициент 2 учитывает то обстоятельство, что витки w3 охватываются контуром интегрирования (циркуляции) дважды.
Следует заметить, что при пользовании правилом винта необходимо всегда сопоставлять направление обхода по контуру циркуляции с направлениями токов, пронизывающих поверхность, ограниченную контуром циркуляции.
Результаты решения задачи не изменятся, если катушки разместить на сердечнике из другого магнитного материала, так как м. д. с. определяется только величиной полного тока и не зависит от магнитных свойств вещества.
Задача 2.2. Определить магнитодвижущую силу (прямая задача расчета одноконтурной магнитной цепи), необходимую для получения магнитного потока в 5,9·10–4 Вб в кольцеобразном сердечнике, сечением S = 5 см2. Длина средней линии магнитной индукции l = 25 см.
Определить Н (напряженность магнитного поля в сердечнике) и μ r (относительная магнитная проницаемость материала сердечника). Материал сердечника — слаболегированная электротехническая листовая сталь Э11.
Решение
Найдем магнитную индукцию
B= Ф S = 5,9⋅ 10 −4 5⋅ 10 −4 =1,18 Вб м 2 .
По кривой намагничивания для стали Э11 найдем, что индукции B = 1,18 Вб/м2 соответствует H = 800 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H·l = 800·0,25 = 200 А.
Определим абсолютную магнитную проницаемость:
μ a = B H = 1,18 800 =1475⋅ 10 −6 Гн м .
Магнитная проницаемость (относительная магнитная проницаемость)
μ r = μ a μ 0 = 1475⋅ 10 −6 4π⋅ 10 −7 =1175.
Задача 2.3. На рис. 2.3 изображен электромагнит, сердечник которого изготовлен из слаболегированной листовой электротехнической стали Э11, а якорь — из литой стали.
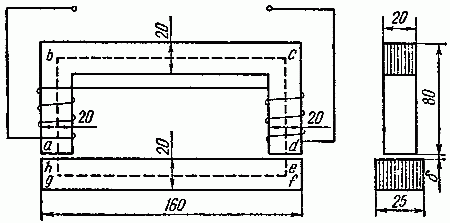
Рис. 2.3
Какой ток должен быть пропущен через обмотку электромагнита (прямая задача расчета одноконтурной магнитной цепи), состоящую из w = 500 витков, для того, чтобы в якоре была создана магнитная индукция в 0,84 Вб/м2. Размеры на рис. 2.3 даны в миллиметрах. Длина воздушного зазора δ = 1 мм. Площадь сечения воздушного зазора считать равной площади сечения сердечника (пренебрегаем потоком рассеяния). Чему равна статическая индуктивность электромагнита?
Решение
Это пример прямой задачи на расчет магнитной цепи. На рис. 2.3 пунктиром проведена средняя линия магнитной индукции (приближенно). Длина проходящей вдоль сердечника части средней линии магнитной индукции abсd = l1 = 0,28 м. Сечение сердечника S1 = 2·2 = 4 см2 = 4·10–4 м2.
Сечение якоря S2 = 2·2,5 = 5 см2 = 5·10–4 м2, длина проходящей через него части средней линии магнитной индукции efgh = l2 = 0,16 м. Магнитная индукция в якоре B2 = 0,84 Вб/м2 (по условию задачи).
Из условия равенства магнитных потоков в якоре и в сердечнике (одноконтурная магнитная цепь, потоком рассеяния пренебрегаем)
Ф1 = B1·S1 = B2·S2
найдем магнитную индукцию в сердечнике:
B 1 = B 2 ⋅ S 2 S 1 = 0,84⋅5⋅ 10 −4 4⋅ 10 −4 =1,05 Вб м 2 .
Сечение воздушного зазора, длина проходящей в нем части линии магнитной индукции и магнитная индукция равны:
S 3 =4⋅ 10 −4 м 2 ; l 3 =2δ=2⋅ 10 −3 м; B 3 =1,05 Вб м 2 ,
напряженность магнитного поля в воздухе:
H 3 = B 3 μ 0 = 1,05 4π⋅ 10 −7 =84⋅ 10 4 А м .
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H1·l1 + H2·l2 + H3·l3.
В целях большей наглядности расчеты удобно свести в таблицу, в которой данные для напряженности магнитного поля в отдельных элементах магнитопровода взяты по соответствующим кривым намагничивания. Так, для сердечника, изготовленного из стали Э11, находим, что индукции B1 = 1,05 Вб/м2 соответствует значение напряженности магнитного поля H1 = 570 А/м, а для якоря, изготовленного из литой стали, имеем, что величине B2 = 0,84 Вб/м2 соответствует значение H2 = 540 А/м.
|
Название участка |
Материал |
S, м2 |
l, м |
B, Вб/м2 |
H, А/м |
H·l, А |
|
Сердечник |
Сталь Э11 |
4·10–4 |
0,28 |
1,05 |
570 |
160 |
|
Якорь |
Литая сталь |
5·10–4 |
0,16 |
0,84 |
540 |
85 |
|
Воздушный зазор |
Воздух |
4·10–4 |
0,002 |
1,05 |
84·104 |
1680 |
F= ∑ H k ⋅ l k =160+85+1680=1925 А.
Искомый ток найдем, пользуясь формулой F = I·w:
I= F w = 1925 500 =3,85 А.
Статическая индуктивность электромагнита равна отношению потокосцепления (полного магнитного потока) к току:
L ст = Ψ I = w⋅Ф I = 500⋅4,2⋅ 10 −4 3,85 =0,053 Гн=053 мГн.
Задача 2.4. Найти магнитную индукцию в якоре электромагнита (обратная задача расчета одноконтурной магнитной цепи), изображенном на рис. 2.3, если на электромагнит намотано w = 250 витков, по которым проходит ток I = 4,4 А. Сердечник изготовлен из листовой электротехнической стали Э11, а якорь — из литой стали. Размеры сердечника и якоря те же, что и в предыдущей задаче. Длина воздушного зазора 0,5 мм. Площадь сечения воздушного зазора считать равной площади сердечника.
Решение
Это пример обратной задачи на расчет магнитной цепи. Для ее решения надо построить кривую зависимости магнитного потока Ф в функции магнитодвижущей силы F и на кривой найти рабочую точку.
Чтобы построить кривую Ф = f (F) будем задаваться различными величинами магнитных потоков Ф, по которым вычисляем соответствующие им значения магнитной индукции B в каждом из участков магнитной цепи. Затем по кривым намагничивания находим напряженность поля H, соответствующую каждому значению индукции B, и, наконец, вычисляем магнитодвижущую силу по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F= ∑ H k ⋅ l k .
Так, например, примем Ф = 3,2·10–4 Вб. Тогда
B серд = Ф S серд = 3,2⋅ 10 −4 4⋅ 10 −4 =0,8 Вб м 2 ; B як = Ф S як = 3,2⋅ 10 −4 5⋅ 10 −4 =0,64 Вб м 2 ; B заз = B серд =0,8 Вб м 2 .
По кривым намагничивания находим напряженности магнитного поля:
H серд =318 А м ; H як =330 А м ; H заз = B заз μ 0 = 0,8 4π⋅ 10 −7 =64⋅ 10 4 А м .
Магнитодвижущая сила
F= H серд ⋅ l серд + H як ⋅ l як + H заз ⋅ l заз = =318⋅0,28+330⋅0,16+64⋅ 10 4 ⋅ 10 −3 =780 А.
Эта магнитодвижущая сила меньше заданной, которая равна
I·w = 4,4·250 = 1100 А.
Аналогично проводим расчеты для больших значений Ф, которые сведены в следующую таблицу:
|
Ф, Вб |
Bсерд, Вб/м2 |
Нсерд, А/м |
lсерд, м |
Bяк, Вб/м2 |
Hяк, А/м |
lяк, м |
Bзаз, Вб/м2 |
Hзаз, А/м |
lзаз, м |
F, А |
|
3,2·10–4 |
0,8 |
318 |
0,28 |
0,64 |
330 |
0,16 |
0,8 |
64·104 |
1·10–3 |
780 |
|
3,6·10–4 |
0,9 |
397 |
0,28 |
0,72 |
400 |
0,16 |
0,9 |
72·104 |
1·10–3 |
895 |
|
4,0·10–4 |
1,0 |
502 |
0,28 На http://www.online-invest.org проекты хайп. |
0,80 |
490 |
0,16 |
1,0 |
80·104 |
1·10–3 |
1020 |
|
4,4·10–4 |
1,1 |
647 |
0,28 |
0,88 |
600 |
0,16 |
1,1 |
88·104 |
1·10–3 |
1160 |
Мы остановились на величине Ф = 4,4·10–4 Вб потому, что для этого значения магнитного потока суммарная магнитодвижущая сила равна 1160 А, что больше заданных 1100 А. По данным расчетов построена кривая Ф = f (F) и на ней определена рабочая точка, которая при F = 1100 А соответствует значению магнитного потока в 4,24·10–4 (рис. 2.4).
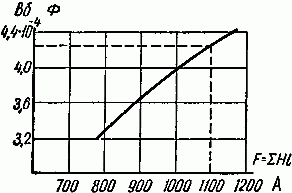
Рис. 2.4
Следовательно, искомая индукция в якоре электромагнита
B як = Ф S як = 4,24⋅ 10 −4 5⋅ 10 −4 =0,848 Вб м 2 .
Обычно в технических расчетах значения магнитной индукции округляют до сотых долей Вб/м2 (целые сотни гауссов); поэтому считаем Bяк = 0,85 Вб/м2.
Укажем, что задача могла бы быть решена и другим путем — методом проб: суть его состоит в том, что так же, как и выше, задаются некоторым значением магнитного потока Ф, для которого подсчитывают магнитодвижущую силу F. Если она окажется меньше заданной, то берут большие значения Ф до тех пор, пока не получат F больше заданной величины. После этого значения Ф, соответствующие большим и меньшим против заданного значениям F сужают до тех пор, пока для одного из сечений магнитной цепи полученные значения магнитной индукции будут различаться друг от друга не более чем на 0,1 Вб/м2 (1000 Гс). Искомое значение Ф можно затем найти путем интерполирования.
Так, например, задаемся величиной Ф = 3,2·10–4 Вб, которой соответствует магнитодвижущая сила F = 780 А, что меньше заданного значения Fзад = 1100 А. Теперь зададимся Ф’ = 4,4·10–4 Вб, для которого найдем F’ = 1160 А; это больше заданной величины Fзад. Уменьшаем значение Ф, принимая его, например, равным 4·10–4 Вб; ему соответствует значение F” = 1020 А, что вновь меньше заданной величины магнитодвижущей силы. Итак, при Ф” = 4·10–4 Вб: B”як = 0,8 Вб/м2, а при Ф’ = 4,4·10–4 Вб: B’як = 0,88 Вб/м2.
Таким образом, значения магнитной индукции B в одном из сечений (в данном случае в якоре) отличаются одно от другого менее, чем на 0,1 Вб/м2 (0,88 — 0,8 = 0.08 Вб/м2).
Окончательное значение магнитного потока найдем линейным интерполированием.
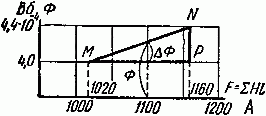
Рис. 2.5
Из треугольника MNP (рис. 2.5) имеем:
ΔФ 4,4⋅ 10 −4 −4⋅ 10 −4 = 1100−1020 1160−1020 ,
отсюда
ΔФ=0,23⋅ 10 −4 Вб, а Ф=4⋅ 10 −4 +0,23⋅ 10 −4 =4,23⋅ 10 −4 Вб.
Искомая индукция в якоре
B як = Ф S як = 4,23⋅ 10 −4 5⋅ 10 −4 ≈0,85 Вб м 2 .
Задача 2.5. Найти магнитную индукцию в воздушном зазоре тороида (обратная задача расчета одноконтурной магнитной цепи), изготовленного из литой стали (рис. 2.6), если на тороид намотано w = 400 витков, по которым проходит ток I = 4 А. Воздушный зазор = 2 мм. Размеры тороида на рисунке даны в мм.
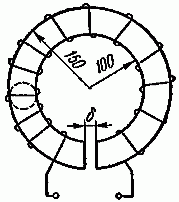
Рис. 2.6
Решение
Задача может быть решена аналогично предыдущей. Мы здесь укажем, как быстрее всего найти первое приближенное значение магнитного потока. Для этого предполагаем, что вся заданная магнитодвижущая сила F = I·w расходуется на ту часть магнитопровода, которая предполагается имеющей наибольшее магнитное сопротивление. Получаемое при этом значение магнитного потока будет завышено по сравнению с фактическим, ибо в расчете не были учтены магнитные сопротивления других участков цепи.
Полагая в нашем случае, что вся магнитодвижущая сила падает на магнитном сопротивлении воздушного зазора, запишем по второму закону Кирхгофа для магнитной цепи (закону полного тока):
F=I⋅w= H возд ⋅δ= B μ 0 ⋅δ,
откуда
B= I⋅w⋅ μ 0 δ = 4⋅400⋅4π⋅ 10 −7 2⋅ 10 −3 =1,0 Вб м 2 .
Так как это значение индукции, как указано выше, явно завышено, проведем новый расчет для меньшего значения магнитной индукции, например, для 0,8 Вб/м2. По кривой намагничивания для литой стали этой индукции соответствует величина напряженности магнитного поля Hст = 490 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока) при этом будет равна
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,8 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1650 А,
что превышает заданную величину 1600 А.
Теперь проведем расчет для еще меньшей индукции B = 0,7 Вб/м2. Для нее по кривой намагничивания напряженность Hст = 380 А/м. Общая магнитодвижущая сила в этом случае будет
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,7 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1410 А,
что меньше заданной величины 1600 А.
Таким образом, истинная величина индукции находится в пределах от 0,7 до 0,8 Вб/м2. Ее мы найдем интерполированием (рис. 2.7).
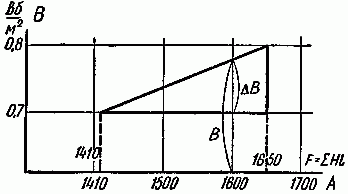
Рис. 2.7
Искомая индукция B=0,7+ΔB, где ΔB находится из соотношения
ΔB 0,1 = 1600−1410 1650−1410 = 190 240 ,
откуда
ΔB= 190 240 ⋅0,1≈0,08 Вб м 2 .
Итак, искомая индукция равна 0,78 Вб/м2 (7800 Гс).
Задача 2.6. Определить все магнитные потоки и ток, проходящий через катушку, расположенную на среднем стержне сердечника, если в левом стержне имеется магнитная индукция в 0,95 Вб/м2. Размеры магнитопровода на рис. 2.8 даны в миллиметрах. Материал сердечника — листовая сталь Э11. Число витков катушки w = 500.
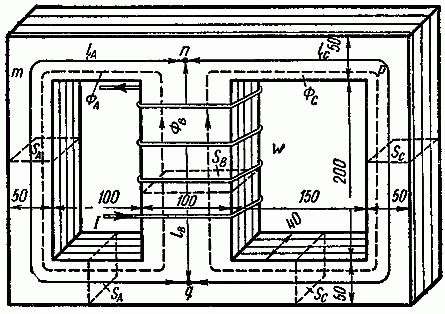
Рис. 2.8
Решение
Покажем на рисунке средние линии магнитной индукции. По данным задачи найдем их длины:
lA = 60 см; lB = 25 см; lC = 70 см.
Задачи на сложную разветвленную несимметричную магнитную цепь решаются на основании первого и второго законов Кирхгофа для магнитной цепи:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
В уравнениях (2) и (3) HA, HB и HC соответственно напряженности магнитного поля в стержнях A, B и C.
Для магнитной индукции в левом стержне BA = 0,95 Вб/м2 по кривой намагничивания для листовой стали найдем HA = 447 А/м.
Из уравнения (3) получим
H C = H A ⋅ l A l C = 447⋅60 70 =384 А м .
По кривой намагничивания находим, что H = 384 А/м соответствует индукция BC = 0,89 Вб/м2.
По уравнению (1) получим
Ф B = Ф A + Ф C = B A ⋅ S A + B C ⋅ S C = =0,95⋅20⋅ 10 −4 +0,89⋅20⋅ 10 −4 =36,8⋅ 10 −4 Вб.
Следовательно,
B B = Ф B S B = 36,8⋅ 10 −4 40⋅ 10 −4 =0,92 Вб м 2 .
Этой индукции по кривой намагничивания соответствует HB = 417 А/м. По уравнению (2) найдем
I·w = HB·lB + HC·lC = 417·0,25 + 384·0,7 = 373 А.
Искомый ток
I= F w = 373 500 ≈0,75 А.
Задача 2.7. Магнитная цепь изготовлена из листовой электротехнической стали Э11. На средний стержень сердечника намотана катушка, содержащая w = 930 витков, по которым проходит ток I = 1 А (рис. 2.8). На всем участке A сечение магнитной цепи считать SA = 20 см2, на участке B — SB = 40 см2, на участке С — SC = 20 см2. Длины средних линий магнитной индукции каждого из участков считать равными: lA = 55 см, lB = 25 см, lC = 80 см.
Найти значения магнитной индукции во всех стержнях.
Решение
Выберем на рис. 2.8 пути средних линий магнитной индукции и запишем уравнения:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
Построим кривые зависимостей
ФA = f1 (HA·lA) = f1 (UMnq);
ФB = f2 (I·w — HB·lB) = f2 (UMnq);
ФC = f3 (HC·lC) = f3 (UMnq).
Здесь UMnq — разность скалярных магнитных потенциалов точек n и q, или магнитодвижущая сила между теми же точками.
Для построения кривой f1 задаемся различными величинами магнитных потоков ФA, по которым находим соответствующие им значения магнитной индукции BA, для которых по кривой намагничивания определяем напряженность магнитного поля HA. Беря произведение HA·lA, находим для различных потоков значения магнитных напряжений на участке A. Результаты вычислений сводим в таблицу. Таким же путем производим расчет для построения кривой на участке C. Наконец, для построения кривой f2 (участок B) задаемся значениями ФB и по ним находим BB, HB, HB·lB и разность I·w — HB·lB. Указанные вычисления сведены в таблицу.
|
ФА, 10–4 Вб |
BA, Вб/м2 |
HA, А/м |
HAlA, А |
ФC, 10–4 Вб |
BC, Вб/м2 |
HC, А/м |
HClC, А |
ФB, 10–4 Вб |
BB, Вб/м2 |
HB, А/м |
HBlB, А |
Iw–HBlB, Смотрите на сайте tłumacz Warszawa. Вкусы одноразок. А |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
930 |
|
10 |
0,5 |
171 |
94 |
10 |
0,5 |
171 |
137 |
20 |
0,5 |
171 |
43 |
887 |
|
12 |
0,6 |
211 |
116 |
12 |
0,6 |
211 |
169 |
24 |
0,6 |
211 |
53 |
877 |
|
14 |
0,7 |
261 |
143 |
14 |
0,7 |
261 |
209 |
28 |
0,7 |
261 |
65 |
865 |
|
16 |
0,8 |
318 |
175 |
16 |
0,8 |
318 |
254 |
32 |
0,8 |
318 |
80 |
850 |
|
18 |
0,9 |
397 |
218 |
18 |
0,9 |
397 |
318 |
36 |
0,9 |
397 |
99 |
831 |
|
20 |
1,0 |
502 |
276 |
20 |
1,0 |
502 |
402 |
40 |
1,0 |
502 |
126 |
804 |
|
22 |
1,1 |
647 |
356 |
22 |
1,1 |
647 |
518 |
44 |
1,1 |
647 |
162 |
768 |
|
24 |
1,2 |
843 |
463 |
24 |
1,2 |
843 |
675 |
48 |
1,2 |
843 |
210 |
720 |
|
26 |
1,3 |
1140 |
626 |
26 |
1,3 |
1140 |
913 |
52 |
1,3 |
1140 |
285 |
645 |
|
28 |
1,4 |
1580 |
870 |
28 |
1,4 |
1580 |
1265 |
56 |
1,4 |
1580 |
395 |
535 |
|
30 |
1,5 |
2500 |
1375 |
30 |
1,5 |
2500 |
2000 |
60 |
1,5 |
2500 |
625 |
305 |
По этим данным построены кривые ФA, ФB, ФC (рис. 2.9).
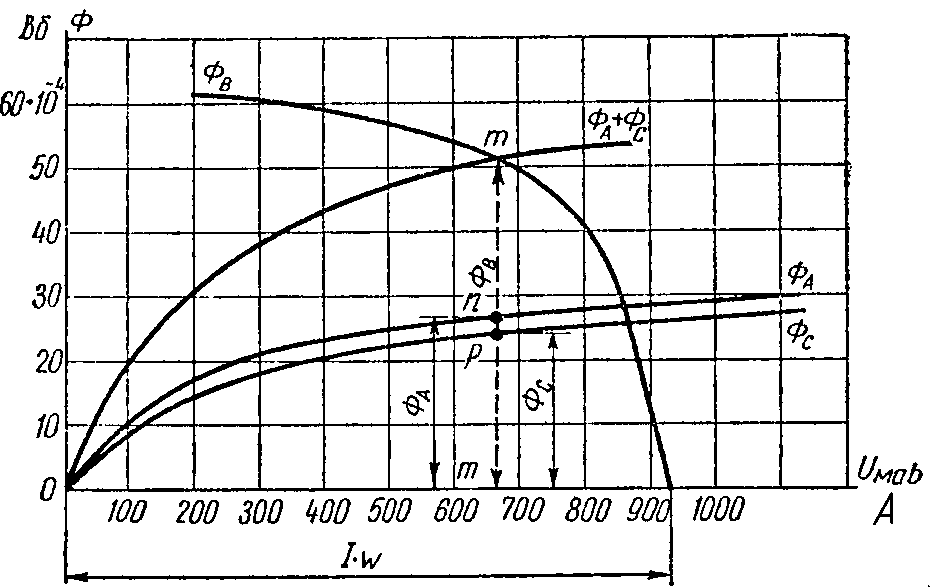
Рис. 2.9
Так как величины магнитных потоков должны удовлетворять уравнению (1), то проводим еще одну вспомогательную кривую ФB = ФA + ФC; она строится путем суммирования ординат кривых ФA и ФC для одних и тех же значений абсцисс. Точка m ее пересечения с кривой ФB = f2 (I·w — HB·lB) определяет величину искомого потока
ФB = 50,4·10–4 Вб.
Перпендикуляр mm’, опущенный из m на ось абсцисс, пересечет кривую ФA в точке n, а кривую ФC — в точке p, отрезок nm’ выражает искомый магнитный поток в стержне A:
ФA = 26,4·10–4 Вб, а отрезок pm’ — поток ФC = 24·10–4 Вб.
По найденным потокам находим магнитные индукции в каждом из стержней:
B A = Ф A S A = 26,4⋅ 10 −4 20⋅ 10 −4 =1,32 Вб м 2 ; B B = Ф B S B = 50,4⋅ 10 −4 40⋅ 10 −4 =1,26 Вб м 2 ; B C = Ф C S C = 24,0⋅ 10 −4 20⋅ 10 −4 =1,20 Вб м 2 .
Проверка. Можно убедиться, что при найденных значениях магнитных индукций удовлетворяются уравнения (1) — (3). Для этого по кривой намагничивания надо найти для каждого значения B соответствующее значение H и подставить в указанные уравнения.
Задача 2.8. Сердечник собран из листов электротехнической стали марки Э11. Форма и размеры сердечника (в мм) указаны на рис. 2.10.
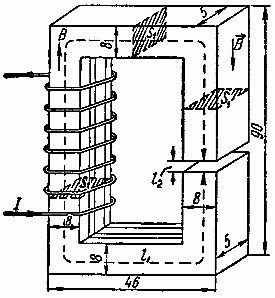
Рис. 2.10
Обмотка имеет w = 400 витков, по которым проходит ток I = 3,5 А. Длина воздушного зазора составляет 1 мм. Определить магнитный поток в сердечнике. При расчете следует считать, что сечение воздушного зазора равно сечению сердечника.
Задачу решить следующими аналитическими методами: а) линейной аппроксимации, б) кусочно-линейной аппроксимации, в) дробно-линейной аппроксимации.
Результаты, полученные для каждого из случаев, сравнить с теми, какие получаются при решении задачи обычным способом.
Решение
Найдем длину средней линии магнитной индукции и сечение стального сердечника (рис. 2.10):
l1 = 2· (90 — 8) + 2· (46 — 8) = 240 мм = 0,24 м;
S1 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Длина средней линии магнитной индукции в воздушном зазоре и его сечение равны:
l2 = 1 мм = 1·10–3 м;
S2 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Решая задачу способом, указанным в решении задачи 2.4, найдем магнитную индукцию B = 1,35 Вб/м2 и соответствующий магнитный поток
Ф = B·S = 1,35·0,4·10–4 = 0,54·10–4 Вб.
а) Расчет магнитной цепи методом линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания прямой линией в некоторой области изменения магнитной индукции. Примем, например, что магнитная индукция изменяется в пределах от нуля до 1,5 Вб/м2. Заменим кривую намагничивания (рис. 2.11) прямой линией 0b.
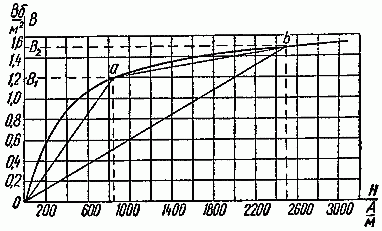
Рис. 2.11
Ее уравнение B = k1·H, здесь коэффициент k1 равен тангенсу угла наклона прямой 0b к оси абсцисс и выражает приближенное значение абсолютной магнитной проницаемости стали в рассматриваемом интервале
μ a1 = μ r1 ⋅ μ 0 = k 1 = B H = 1,5 2500 =6⋅ 10 −4 Гн м .
Искомый магнитный поток определяем по уравнению:
Ф= I⋅w R M1 + R M2 ,
где
R M1 = l 1 μ a1 ⋅ S 1 = l 1 μ r1 μ 0 ⋅ S 1 ; R M2 = l 2 μ 0 ⋅ S 2 — магнитные сопротивления, соответственно стальной части и воздушного зазора.
Производим вычисления:
R M1 = l 1 μ a1 ⋅ S 1 = 0,24 6⋅ 10 −4 ⋅0,4⋅ 10 −4 =1,0⋅ 10 7 1 Гн ; R M2 = l 2 μ 0 ⋅ S 2 = 1⋅ 10 −3 4π⋅ 10 −7 ⋅0,4⋅ 10 −4 =1,98⋅ 10 7 1 Гн ; Ф= I⋅w R M1 + R M2 = 3,5⋅400 1,0⋅ 10 7 +1,98⋅ 10 7 =0,47⋅ 10 −7 Вб.
Ошибка в сравнении с результатами, полученными обычным способом, составляет
0,54⋅ 10 −4 −0,47⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈13%.
б) Расчет магнитной цепи методом кусочно-линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания отрезками прямых линий, например, из двух прямых отрезков 0a и ab (рис. 2.11).
Предполагается, что рабочий режим лежит в области индукций между B1 и B2, соответствующих точкам a и b.
Уравнение прямой ab, выражающей зависимость магнитной индукции от напряженности магнитного поля в стали, имеет вид:
B ст = B 1 + k 2 ⋅ ( H ст − H 1 ), (1)
где k2 — тангенс угла наклона прямой ab с осью абсцисс:
k 2 = B 2 − B 1 H 2 − H 1 . (2)
Напряженность магнитного поля в воздухе может быть выражена следующим образом:
H в = B в μ 0 = Ф μ 0 ⋅ S 2 = B ст ⋅ S 1 μ 0 ⋅ S 2 = B ст μ ′ 0 , (3)
где ради краткости обозначено
μ ′ 0 = μ 0 ⋅ S 2 S 1 . (4)
Подставляя в уравнение (3) вместо Bст его значение из уравнения (1), получим:
H в =[ B 1 + k 2 ⋅ ( H ст − H 1 ) ]⋅ 1 μ ′ 0 . (5)
Для определения Hст воспользуемся уравнением второго закона Кирхгофа для магнитной цепи (законом полного тока)
Hст·l1 + Hв·l2 = I·w. (6)
Подставляя в уравнение (6) значение Нв из уравнения (5), будем иметь:
H ст ⋅ l 1 + B 1 ⋅ l 2 μ ′ 0 + k 2 ⋅ l 2 μ ′ 0 ⋅ ( H ст − H 1 )=I⋅w.
Решая это алгебраическое уравнение относительно Hст, найдем:
H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (7)
где
B ′ = B 1 − k 2 ⋅ H 1 . (8)
Величина магнитной индукции в стали находится путем подстановки найденного значения Hс в уравнение (1):
B ст = μ ′ 0 ⋅ I⋅w⋅ k 2 + B ′ ⋅ l 1 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (9)
Для нашей задачи выберем ломаную так, что:
в точке a
B1 = 1,2 Вб/м2, соответствующее H1 = 843 А/м,
в точке b
B2 = 1,5 Вб/м2, соответствующее H2 = 2500 А/м.
По формулам (2), (4), (8), (7) и (1) находим:
k 2 = B 2 − B 1 H 2 − H 1 = 1,5−1,2 2500−843 =18,15⋅ 10 −5 Гн м ; μ ′ 0 = μ 0 ⋅ S 2 S 1 = μ 0 ⋅ 0,4⋅ 10 −4 0,4⋅ 10 −4 = μ 0 =4π⋅ 10 −7 Гн м ; B ′ = B 1 − k 2 ⋅ H 1 =1,2−18,15⋅ 10 −5 ⋅843=1,05 Вб м 2 ; H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 = 3,5⋅400⋅4π⋅ 10 −7 −1,05⋅1⋅ 10 −3 4π⋅ 10 −7 ⋅0,24+18,15⋅ 10 −5 ⋅1⋅ 10 −3 =1470 А м ; B ст = B 1 + k 2 ⋅ ( H ст − H 1 )=1,2+18,15⋅ 10 −5 ⋅ ( 1470−843 )=1,314 Вб м 2 .
И, наконец, искомый поток
Ф = Bст·S1 = 1,314·0,4·10–4 = 0,525·10–4 Вб.
Ошибка по сравнению с обычным способом расчета составляет
0,54⋅ 10 −4 −0,525⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈3%.
в) Расчет магнитной цепи методом дробно-линейной аппроксимации кривой намагничивания
Дробно-линейная аппроксимация делается посредством уравнения:
B ст = H ст α+β⋅ H ст . (10)
Входящие сюда коэффициенты α и β находятся из известных значений магнитной индукции и напряженности магнитного поля в двух выбранных точках кривой намагничивания, между которыми ожидается действительный режим работы стального участка магнитной цепи.
Для определения Нст поступим следующим образом: из уравнения (10) значение Вст подставим в уравнение (3), тогда получим:
H в = B ст μ ′ 0 = H ст μ ′ 0 ⋅ ( α+β⋅ H ст ) .
Это значение Нв подставим в уравнение (6) второго закона Кирхгофа для магнитной цепи (закона полного тока):
H ст ⋅ l 1 + H ст ⋅ l 2 μ ′ 0 ⋅ ( α+β⋅ H ст ) =I⋅w.
Решая относительно Нст это квадратное уравнение, найдем:
H ст = 1 2 ( I⋅w l 1 − 1+p q )+ 1 4 ( I⋅w l 1 − 1+p q ) 2 + I⋅w q⋅ l 1 . (11)
Второй корень квадратного уравнения, как не имеющий физического смысла, ввиду того что Нст должна выражаться положительным числом, опущен.
В уравнении (11) введены ради краткости обозначения:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α ; q= β α . (12)
Проведем числовые расчеты для нашей задачи, принимая для B и H те числовые значения, какие они имеют на границах рассматриваемого интервала в указанных выше точках a и b. По уравнению (10) имеем:
1,2= 843 α+β⋅843 ; 1,5= 2500 α+β⋅2500 .
Решая эти два уравнения, найдем:
α=213 м Гн ; β=0,581 м 2 Вб .
Далее по формулам (12), (13), (11) и (10) получим:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α = 1⋅ 10 −3 ⋅0,4⋅ 10 −4 0,24⋅0,4⋅ 10 −4 ⋅4π⋅ 10 −7 ⋅α 213=15,6; q= β α = 0,581 213 =2,73⋅ 10 −3 м А ; I⋅w q⋅ l 1 = 3,5⋅400 2,73⋅ 10 −3 ⋅0,24 =2,14⋅ 10 6 А 2 м 2 ; 1 2 ( I⋅w l 1 − 1+p q )= 1 2 ( 3,5⋅400 0,24 − 16,6 2,73⋅ 10 −3 )=−125; H ст = 1 2 ( I⋅w l 1 − 1+p q )+ [ 1 2 ( I⋅w l 1 − 1+p q ) ] 2 + I⋅w q⋅ l 1 = =−125+ 125 2 +2,14⋅ 10 6 =−125+1515=1390 А м ; B ст = H ст α+β⋅ H ст = 1390 213+0,581⋅1390 =1,363 Вб м 2 .
Искомый магнитный поток равен:
Ф = Bст·S1 = 1,363·0,4·10–4 = 0,545·10–4 Вб.
Ошибка в сравнении с обычным методом расчета магнитных цепей составляет:
0,545⋅ 10 −4 −0,54⋅ 10 −4 0,545⋅ 10 −4 ⋅100%≈0,9%.
Отметим, что расчет при помощи дробно-линейной аппроксимации приводит к удовлетворительным результатам даже в тех случаях, когда велико расстояние между граничными точками.
 закон полного тока,
закон полного тока,
магнитная цепь,
расчет магнитной цепи,
методы расчета магнитных цепей,
решение задач магнитные цепи
Явление электромагнитной индукции заключается в том, что в результате изменения во времени магнитного потока, который пронизывает замкнутый проводящий контур, в контуре возникает электрический ток. Открыто это явление было физиком из Великобритании Максом Фарадеем в 1831 году.
Формула магнитного потока
Введем обозначения, необходимые нам для записи формулы. Для обозначения магнитного потока используем букву Ф, площади контура – S, модуля вектора магнитной индукции – B, α – это угол между вектором B→ и нормалью n→ к плоскости контура.
Магнитный поток, который проходит через площадь замкнутого проводящего контура, можно задать следующей формулой:
Φ=B·S·cos α,
Проиллюстрируем формулу.
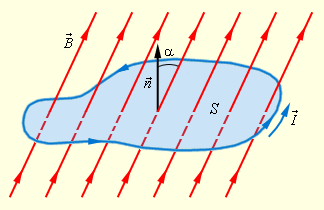
Рисунок 1.20.1. Магнитный поток через замкнутый контур. Направление нормали n→ и выбранное положительное направление l→ обхода контура связаны правилом правого буравчика.
За единицу магнитного потока в СИ принят 1 вебер (Вб). Магнитный поток, равный 1 Вб, может быть создан в плоском контуре площадью 1 м2 под воздействием магнитного поля с индукцией 1 Тл, которое пронизывает контур по направлению нормали.
1 Вб=1 Тл·м2
Закон Фарадея
Изменение магнитного потока приводит к тому, что в проводящем контуре возникает ЭДС индукции δинд. Она равна скорости, с которой происходит изменение магнитного потока через ограниченную контуром поверхность, взятой со знаком минус. Впервые экспериментально установил это Макс Фарадей. Он же записал свое наблюдение в виде формулы ЭДС индукции, которая теперь носит название Закона Фарадея:
Закон Фарадея:
δинд=-∆Φ∆t
Правило Ленца
Согласно результатам опытов, индукционный ток, который возникает в замкнутом контуре в результате изменения магнитного потока, всегда направлен определенным образом. Создаваемое индукционным током магнитное поле препятствует изменению вызвавшего этот индукционный ток магнитного потока. Ленц сформулировал это правило в 1833 году.
Проиллюстрируем правило Ленца рисунком, на котором изображен неподвижный замкнутый проводящий контур, помещенный в однородное магнитное поле. Модуль индукции увеличивается во времени.
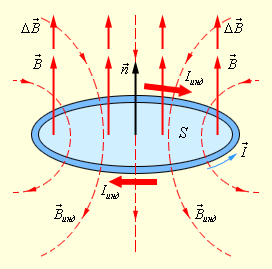
Рисунок 1.20.2. Правило Ленца
Здесь ∆Φ∆t>0, а δинд<0 < 0. Индукционный ток Iинд протекает навстречу выбранному положительному направлению l→ обхода контура.
Благодаря правилу Ленца мы можем обосновать тот факт, что в формуле электромагнитной индукции δинд и ∆Φ∆t противоположны по знакам.
Если задуматься о физическом смысле правила Ленца, то это частный случай Закона сохранения энергии.
Причины возникновения индукционного тока в движущихся и неподвижных проводниках
Причин, по которым может происходить изменение магнитного потока, пронизывающего замкнутый контур, две:
- Изменение магнитного потока вследствие перемещения всего контура или отдельных его частей в магнитном поле, которое не изменяется со временем;
- Изменение магнитного поля при неподвижном контуре.
Перейдем к рассмотрению этих случаев подробнее.
Перемещение контура или его частей в неизменном магнитном поле
При движении проводников и свободных носителей заряда в магнитном поле возникает ЭДС индукции. Объяснить возникновение δинд можно действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца здесь – это сторонняя сила.
На рисунке мы изобразили пример индукции, когда прямоугольный контур помещен в однородное магнитное поле B→ направленное перпендикулярно плоскости контура. Одна из сторон контура перемещается по двум другим сторонам с некоторой скоростью.
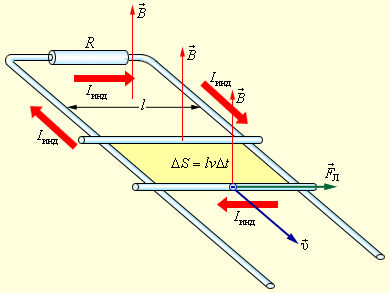
Рисунок 1.20.3. Возникновение ЭДС индукции в движущемся проводнике. Отражена составляющая силы Лоренца, которая действует на свободный электрон
На свободные заряды подвижной части контура воздействует сила Лоренца. Основная составляющая силы Лоренца в данном случае направлена вдоль проводника и связана с переносной скоростью зарядов υ→. Модуль этой сторонней силы равен:
FЛ=eυ→B.
Работа силы FЛ на пути l равна:
A=FЛ·l=eυBl.
По определению ЭДС:
δинд=Ae=υBl.
Значение сторонней силы для неподвижных частей контура равно нулю. Для соотношения δинд можно записать другой вариант формулы. Площадь контура с течением времени изменяется на ΔS=lυΔt. Соответственно, магнитный поток тоже будет с течением времени изменяться: ΔΦ=BlυΔt.
Следовательно,
δинд=∆Φ∆t.
Знаки в формуле, которая связывает δинд и ∆Φ∆t, можно установить в зависимости от того, какие направления нормали и направления контура будут выбраны. В случае выбора согласованных между собой по правилу правого буравчика направлений нормали n→ и положительного направления обхода контура l→ можно прийти к формуле Фарадея.
При условии, что сопротивление всей цепи – это R, то по ней будет протекать индукционный ток, который равен Iинд=δиндR. За время Δt на сопротивлении R выделится джоулево тепло:
∆Q=RIинд2∆t=υ2B2l2R∆t
Парадокса здесь нет. Мы просто не учли воздействие на систему еще одной силы. Объяснение заключается в том, что при протекании индукционного тока по проводнику, расположенному в магнитном поле, на свободные заряды действует еще одна составляющая силы Лоренца, которая связана с относительной скоростью движения зарядов вдоль проводника. Благодаря этой составляющей появляется сила Ампера FА→.
Для рассмотренного выше примера модуль силы Ампера равен FA =IBl. Направление силы Ампера таково, что она совершает отрицательную механическую работу Aмех. Вычислить эту механическую работу за определенный период времени можно по формуле:
Aмех=-Fυ∆t=-IBlυ∆t=-υ2B2l2R∆t
Проводник, перемещающийся в магнитном поле, испытывает магнитное торможение. Это приводит к тому, что полная работа силы Лоренца равна нулю. Джоулево тепло может выделяться либо за счет уменьшения кинетической энергии движущегося проводника, либо за счет энергии, которая поддерживает скорость перемещения проводника в пространстве.
Изменение магнитного поля при неподвижном контуре
Вихревое электрическое поле – это электрическое поле, которое вызывается изменяющимся магнитным полем.
В отличие от потенциального электрического поля работа вихревого электрического поля при перемещении единичного положительного заряда по замкнутому проводящему контуру равна δинд в неподвижном проводнике.
В неподвижном проводнике электроны могут приводиться в движение только под действием электрического поля. А возникновение δинд нельзя объяснить действием силы Лоренца.
Первым, кто ввел понятие вихревого электрического поля, был английский физик Джон Максвелл. Случилось это в 1861 году.
Фактически, явления индукции в подвижных и неподвижных проводниках протекают одинаково. Так что в этом случае мы тоже можем использовать формулу Фарадея. Отличия касаются физической причины возникновения индукционного тока: в движущихся проводниках δинд обусловлена силой Лоренца, в неподвижных – действием на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
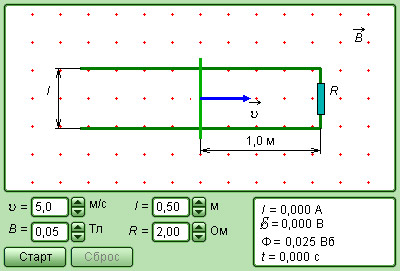
Рисунок 1.20.4. Модель электромагнитной индукции
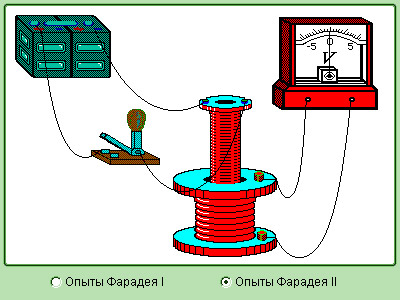
Рисунок 1.20.5. Модель опытов Фарадея
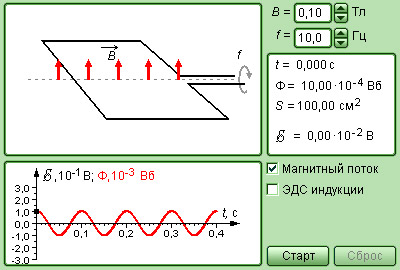
Рисунок 1.20.6. Модель генератора переменного тока
Электромагнитная индукция — это очень важное физическое явление, используемое в работе многих устройств, таких как трансформатор, генератор переменного напряжения, индукционная плита. Оно также имело большое теоретическое значение — привело к открытию электромагнитной волны.
Фарадея, первооткрывателя явления электромагнитной индукции, посетил в своей лаборатории министр финансов Великобритании и спросил:
- » Какую пользу человечество получит от вашего исследования? «
Фарадей ответил:
- » Трудно судить, но я уверен, что вы будете собирать с этого налоги. «
Он не ошибся — НДС в той же Великобритании добавляется к цене электроэнергии, поставляемой в дом.
Приведенный выше список применений, хотя и неполный, впечатляет. Они, безусловно, присутствуют в нашей жизни и являются инженерными разработками явления электромагнитной индукции.
В чем заключается явление электромагнитной индукции?
В общем смысле явление электромагнитное индукции заключается в генерации электрического тока с помощью магнитного поля.
Скажем точнее, явление электромагнитной индукции заключается в образовании электродвижущей силы (ЭДС) в проводнике в результате изменения потока магнитного поля, пронизывающего поверхность, охватывающую проводник. В замкнутой цепи электродвижущая сила (ЭДС) вызывает протекание электрического тока.
В приведенном выше определении явления могут быть неясными два понятия — ЭДС индукции и магнитный поток.
ЭДС индукции.
Абсолютная величина электродвижущей силы ( ЭДС индукции с символом εинд ) есть работа внешней силы Az, которая вызывает перемещение единичного заряда по цепи. Следовательно: | εинд | = Az / q .
Как видите, в определении мы использовали абсолютное значение ЭДС индукции. Это потому, что оно может быть отрицательным, при определенных ситуациях. С другой стороны, работа внешних сил, согласно принципу сохранения энергии, всегда, при генерации электрического тока, должна быть положительной.
Определение потока магнитной индукции.
Поток магнитной индукции B через поверхность S называется скалярным произведением векторов B и S: dФ = B * S * cos α , где α — угол между двумя векторами, а S — вектор, перпендикулярный поверхности S с величиной, равной площади этой поверхности.
Магнитный поток будет меняться при изменении любой величины, входящей в формулу — площади поверхности, значения магнитной индукции, угла между площадью поверхности и вектором индукции — при сохранении постоянства остальных переменных. Конечно, все эти величины могут изменяться одновременно, но таким образом, что их произведение не остается постоянным.
О том, что электрический ток является источником магнитного поля, было известно с 1820 года (работа Орстеда). Фарадей задался вопросом, не верно ли и обратное — не может ли магнитное поле быть источником (причиной) электрического тока. Однако дело оказалось не таким простым. Только в 1831 году ученый наблюдал это явление при определенных особых обстоятельствах. Оказалось, что при стабильных условиях электрический ток не возникает.
Почему это происходит? Даже в очень сильном, но постоянном во времени магнитном поле электрический ток не будет течь в замкнутой цепи «сам по себе». Он течет только тогда, когда мы соответствующим образом перемещаем контур или изменяем магнитное поле, в котором находится контур.
Когда Фарадей обратил внимание на условия, при которых в присутствии магнитного поля возникает электрический ток, он провел десятки экспериментов, которые обобщил и из которых сделал количественные выводы в виде закона электромагнитной индукции. Мы не будем здесь говорить об этом законе, а сосредоточимся только на сути явления электромагнитной индукции. Мы попытаемся увидеть двойственность этого явления, т.е. то, что оно имеет две разновидности, и ответить на вопрос, почему электрический ток течет при определенных условиях.
Мы рассмотрим, какие силы вызывают индукционный ток, т.е. какие силы действуют на свободные заряды в проводнике, заставляя их двигаться.
Эксперимент Фарадея 1831 года, демонстрирующий электромагнитную индукцию между двумя катушками (см. рисунок 1).
Справа находится аккумулятор, питающий меньшую из двух катушек (A), которая создает магнитное поле. Когда эта катушка находится в состоянии покоя, индукционный ток не наблюдается. Однако если переместить его внутрь большей катушки (B), переменный магнитный поток индуцирует в ней ток. Мы обнаруживаем это, наблюдая за колебаниями стрелки гальванометра (G) слева.

Закон электромагнитной индукции Фарадея
Явление электромагнитной индукции описывается законом Фарадея, первооткрывателя и исследователя этого явления.
Представьте себе простейший контур с подвижной стороной, помещенный в магнитное поле так, чтобы поверхность контура была перпендикулярна линиям магнитного поля (рис. 2.).

Мы перемещаем контур со скоростью v вправо. Это изменяет поток магнитной индукции, пронизывающий поверхность, охватываемую контуром, обозначенным на рисунке более темным цветом.
Вспоминая определение магнитного потока индукции, мы можем понять, почему изменяется поток ФB (рис. 2) — потому что, значение площади S поверхности увеличивается .
Вследствие изменения потока магнитной индукции в рассматриваемой цепи возникнет электродвижущая сила индукции и, следовательно, потечет электрический ток.

В рассматриваемом нами случае легко вычислить работу внешней силы, предполагая постоянную скорость движения контура. Внешняя сила Fz действует в соответствии со смещением контура (и вектором скорости) и в любой момент уравновешивает электродинамическую силу (силу Ампера) Fed, действующую в противоположном направлении (рис. 3.). Согласно определению работы Az = F * Δx где Δx — смещение контура во времени Δt.
Величина силы Fz равна величине электродинамической силы (силе Ампера) Fed, действующей на контур. Поэтому Az = I * L * B * Δx, где — I сила индукционного тока, протекающего в цепи (и в контуре), L — длина контура (той части, где протекает электрический ток), B — величина магнитной индукции. Давайте введем наше выражение в определение ЭДС индукции. Зная, что q = I * Δt, получаем:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * ΔS / Δt = dФB / dt.
Мы получили интересный результат. Абсолютное значение ЭДС индукции равно скорости изменения потока магнитной индукции.
В рассматриваемом здесь случае поток магнитной индукции изменяется равномерно во времени. В общем случае это совсем не обязательно. Вот почему мы пишем: εинд = ΔФB / Δt , где Δt → 0, который в сокращенном виде записывается как dФB / dt . Это производная магнитного потока по времени.
Хотя наш вывод формулы относится к одному примеру, оказывается, что выведенное отношение является общим. Необходимо сделать лишь небольшую поправку. Это знак минус, который связан с определенной условностью и принципом сохранения энергии.
Таким образом, закон электромагнитной индукции Фарадея записывается следующим образом: εинд = — dФB / dt и формулируется так:
Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.
Википедия
Знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт отражён в правиле Ленца.
Этот закон верен независимо от того, как изменяется поток магнитного поля; когда изменение вызвано относительным движением источника магнитного поля и контура, или когда движения вообще нет, но значение магнитной индукции меняется.
Закон Фарадея — это универсальный, всеобъемлющий и полный математический отчет о явлении электромагнитной индукции.
Вернемся на мгновение к нашему примеру и отметим, что скорость изменения потока, а значит и абсолютное значение ЭДС индукции, в данном случае равна произведению B*L*v. Это следует из ранее написанных соотношений, а именно:
| εинд | = Az / q = I * L * B * Δx / I * Δt = B * L * Δx / Δt = B * L * ( Δx / Δt ) = B * L * v .
Правило Ленца.
Правило Ленца позволяет быстро и легко определить направление индукционного тока. Это действительно одна из форм принципа сохранения энергии. Правило гласит, что индукционный ток, наведенный в проводнике под действием переменного потока магнитной индукции, всегда имеет такое направление, что магнитное поле, создаваемое этим индукционным током, противодействует причине (т.е. изменению потока магнитного поля), которая его вызвала.
Пример задачи
Дано:
Контур в форме квадрата со стороной d = 0,5 м «втягивается» с постоянной скоростью v = 4 м/с в область однородного магнитного поля, величина индукции которого B = 1 Тл (см. рис. 4). Электрическое сопротивление цепи равно R = 2 Ом.

Нам нужно найти ответы на следующие вопросы:
a) Когда (в какой момент/моменты) в рамке будет протекать электрический ток?
б) Определите направление этого электрического тока.
(в) Вычислите значение силы, действующей на рамку при ее перемещении в соответствии с направлением вектора скорости. Предположите отсутствие механического сопротивления движению.
Решение.
(a) Индукционный ток протекает при изменении потока магнитной индукции через поверхность, охваченную контуром. В ситуации, показанной на рисунке 4, магнитный поток равен нулю и будет оставаться таковым до тех пор, пока правый край контура не коснется границы области магнитного поля. Затем, по мере движения контура, он будет все больше и больше заполняться магнитным полем — магнитный поток будет увеличиваться. Поэтому выполняется условие электромагнитной индукции, т.е. начинает протекать индукционный ток. Как долго? Это легко вычислить, поскольку движение рамы равномерно:
t = d / v = 0,5 / 2 = 0,25 секунд
Ток будет течь до тех пор, пока весь квадрат не войдет в магнитное поле. Тогда поток будет ненулевым, но больше не будет меняться.
б) Воспользуемся правилом Ленца. Мы уже заметили, что поток магнитной индукции при «втягивании» контура в магнитное поле увеличивается. Поэтому индукционный ток будет протекать в таком направлении, чтобы противодействовать увеличению потока.
Магнитное поле, создаваемое индукционным током с вектором индукции Bинд, будет противоположно вектору B.
Таким образом, вектор Bинд направлен в нашу сторону. Если расположить таким образом большой палец правой руки, остальные согнутые пальцы покажут направление индукционного тока. Ток будет течь против часовой стрелки.
(в) Снова воспользуемся равномерностью движения рамы. Обратите внимание, что сила, которая действует на рамку при ее перемещении по вектору скорости (например, сила моей руки), не может быть единственной силой, действующей на квадрат. Если бы это было так, он бы двигался с ускорением. Поскольку движение равномерное, это означает, что в каждый момент времени существует сила, которая уравновешивает силу моей руки. Это и есть электродинамическая сила. Ведь теперь в рамке течет ток, и часть его протекает в магнитном поле (см. рис. 5).

Красная стрелка показывает направление электрического тока. Электродинамическая сила (сила Ампера) действует слева (я определил ее с помощью правила трех пальцев). На верхнюю часть рамки и нижнюю часть также действуют электродинамические силы, но они аннулируют друг друга.
Подведем итог: электродинамическая сила уравновешивает силу моей руки. Таким образом, я могу сравнить значения обеих сил, то есть F = Fed = B * I * d, где I — сила индукционного тока. Теперь достаточно рассчитать значение силы этого тока. Мы будем использовать закон Фарадея и закон Ома для участка цепи. Давайте начнем с последнего: поскольку нас интересует только значение I, мы напишем
I = εинд / R .
| εинд | = ΔФB / Δt = Δx * d * B / Δt = ( Δx / Δt ) * d * B = v * d * B .
После подстановки в I получаем: I = εинд / R = v * d * B / R .
В конечном итоге искомое значение силы будет выражено через: Fed = B * I * d = ( B * d * v * d * B ) / R = ( B2 * d2 * v ) / R .
Подставляя численные значения получим: Fed = F = ( 12 * 0,52 * 4 ) / 2 = 0,5 Н .
Список использованной литературы
- Миллер М. А., Пермитин Г. В. Электромагнитная индукция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1999. — Т. 5: Стробоскопические приборы — Яркость. — С. 537—538. — 692 с. — 20 000 экз. — ISBN 5-85270-101-7.
- М. Лившиц. Закон электромагнитной индукции или «правило потока»? // Квант. — 1998. — № 3. — С. 37—38.
- Физика, базовый уровень, 11 класс, учебник — Пурышева Н.С., Важеевская Н.Е., Исаев Д.А., Чаругин В.М











