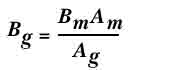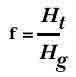Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 мая 2021 года; проверки требуют 16 правок.
| Магнитная индукция | |
|---|---|
 |
|
| Размерность | MT−2I−1 |
| Единицы измерения | |
| СИ | Тл |
| СГС | Гс |
| Примечания | |
| Векторная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела.
Стандартное обозначение: ; единица измерения в СИ — тесла (Тл), в СГС — гаусс (Гс) (связь: 1 Тл = 104 Гс).
Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла.
Для измерения магнитной индукции используются магнитометры-тесламетры. Также она может быть найдена расчётным путём — в статической ситуации для этого достаточно знать пространственное распределение токов.
Вектор в общем случае зависит от координат рассматриваемой точки и времени 
. Он не инвариантен относительно преобразований Лоренца и изменяется при смене системы отсчёта.
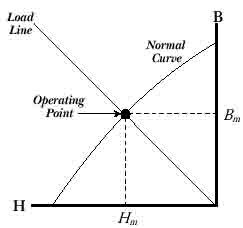
Физический смысл[править | править код]
Магнитная индукция — это такой вектор, что сила Лоренца 
, действующая со стороны магнитного поля[1] на заряд 
, движущийся со скоростью 
, равна
![{displaystyle {vec {F}}=q^{*}left[{vec {v}}times {vec {B}}right]}](data:image/svg+xml,%3Csvg%20xmlns='http://www.w3.org/2000/svg'%20viewBox='0%200%200%200'%3E%3C/svg%3E)
- (по величине ).
![{displaystyle {vec {F}}=q^{*}left[{vec {v}}times {vec {B}}right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eaf19b61520d51d208329c484d386ffbf8e9977)
Косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор перпендикулярен им обоим и направлен по правилу левой руки).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока 
в рамке на её площадь. Момент сил зависит от ориентации рамки и достигает максимального значения при каких-то определённых углах. Звёздочка у символа указывает на то, что заряд или ток являются «пробными», то есть используемыми именно для регистрации поля, в отличие от тех же величин без звёздочки.
Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля 
.
Способы расчёта[править | править код]
Общий случай[править | править код]
В общем случае расчёт магнитной индукции проводится совместно с расчётом электрической составляющей электромагнитного поля посредством решения системы уравнений Максвелла:
- ,
где 
— магнитная постоянная, 
— магнитная проницаемость, 
— диэлектрическая проницаемость, а 
— скорость света в вакууме. Через 
обозначена плотность заряда (Кл/м3) и через 
плотность тока (А/м2).
Магнитостатика[править | править код]
В магнитостатическом пределе[3] расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу 
током 
и когда оно создаётся объёмным распределением тока:
- .
В магнитостатике эта формула играет ту же роль, что закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени).
Если заранее очевидна геометрия поля, помогает теорема Ампера о циркуляции магнитного поля[4] (эта запись является интегральной формой уравнения Максвелла для 
в вакууме):
- .
Здесь 
— произвольная поверхность, натянутая на выбранный замкнутый контур 
.
- Простые примеры
Вектор магнитной индукции прямого провода с током на расстоянии 
от него составляет
- ,
где 
— единичный вектор вдоль окружности, по оси симметрии которой проложен провод. Предполагается, что среда однородна.
Вектор магнитной индукции прямого внутри соленоида с током и числом витков на единицу длины 
равен
- ,
где 
— единичный вектор вдоль оси соленоида. Здесь также предполагается однородность магнетика, которым заполнен соленоид.
Связь с напряжённостью[править | править код]
Магнитная индукция и напряжённость магнитного поля связаны через соотношение
- ,
где — магнитная проницаемость среды (вообще говоря, это тензорная величина, но в большинстве реальных случаев её можно считать скаляром, то есть просто константой конкретного материала).
Основные уравнения[править | править код]
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.
Некоторые из уравнений:
- из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для плотности энергии магнитного поля
- .
- Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
Типичные значения[править | править код]
| объект |  , Тл |
объект | , Тл
|
|---|---|---|---|
| магнитоэкранируемая комната | 10-14 | солнечное пятно | 0,15 |
| межзвёздное пространство | 10-10 | небольшой магнит (Nd-Fe-B) | 0,2 |
| магнитное поле Земли | 5*10-5 | большой электромагнит | 1,5 |
| 1 см от провода с током 100 А | 2*10-3 | сильный лабораторный магнит | 10 |
| небольшой магнит (феррит) | 0,01 | поверхность нейтронной звезды | 108 |
Примечания[править | править код]
См. также[править | править код]
- Векторный потенциал
- Уравнения Максвелла
- Электромагнитное поле
- Тензор электромагнитного поля
- Напряжённость магнитного поля
Магнитная индукция
Магнитная индукция — это силовая характеристика магнитного поля в выбранной точке пространства. Она определяет силу, с которой магнитное поле воздействует на заряженную частицу, что движется внутри него. Магнитная индукция считается фундаментальной характеристикой магнитного поля (как напряжённость для электрического поля).
Магнитная индукция описывает магнитную силу (вектор) на тестовом объекте (например, на куске железа) в каждой точке пространства. Простыми словами: если естественный магнит поднести к магнитным веществам (таким, как железо, никель, кобальт и т. д.), это вызовет в них магнитные свойства, которые называются “магнитной индукцией”. Магнитная индукция используется для создания искусственных магнитов.
Магнитная индукция также называется плотностью магнитного потока.
Магнитная индукция измеряется:
- в системе СИ единицей тесла (Тл),
- в системе СГС единицей гаусс (Гс).
Соотношение между Тл и Гс: 1 Тл = 10 000 Гс.
Магнитная индукция — это векторная величина и обозначается буквой B со стрелочкой:
Индукция (от лат. inducere — вводить, наведение) — производство токов в цепи под действием магнита или другого тока.
Формулы вычисления магнитной индукции
Формула магнитной индукции:
Где:
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Где:
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:
Где:
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Где:
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Электромагнитная индукция и магнитная индукция: какая между ними разница?
Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.
Магнитная индукция может производить постоянный магнит, но может и не производить.
Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.
В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.
Узнайте также про:
- Магнитное поле,
- Магнитное поле Земли,
- Уравнения Максвелла
- Напряженность электрического поля.
Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B = F A m a x I l . .
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
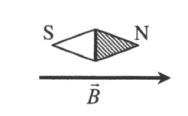
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.
μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
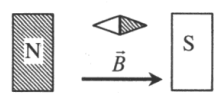
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.
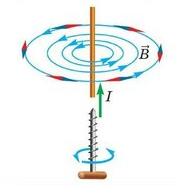
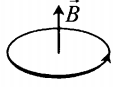
Отсюда следует, что:
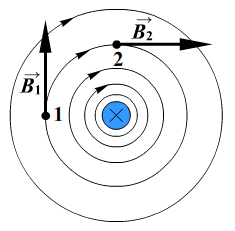
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.
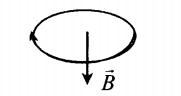
Способы обозначения направлений векторов:
| Вверх |  |
| Вниз |  |
| Влево |  |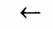
| Вправо |  |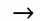
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
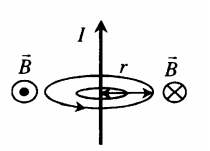
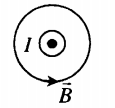
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
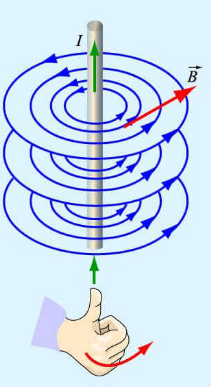
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B = μ μ 0 I 2 π r . .
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
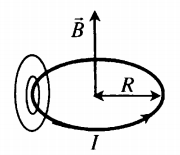
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
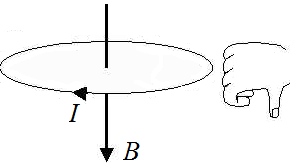
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
Модуль напряженности в центре витка:
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
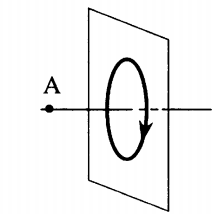
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
Магнитное поле электромагнита (соленоида)
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
l — длина соленоида, d — диаметр проволоки.
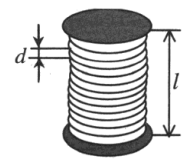
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B = μ μ 0 I N l . . = μ μ 0 I d . .
Модуль напряженности магнитного поля в центральной части соленоида:
H = I N l . . = I d . .
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
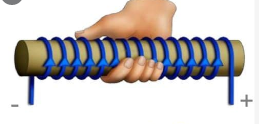
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
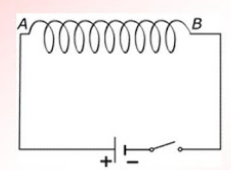
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
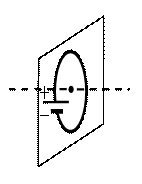На рисунке изображён круглый проволочный виток, по которому течёт электрический ток. Виток расположен в вертикальной плоскости. В центре витка вектор индукции магнитного поля тока направлен
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
pазбирался: Алиса Никитина | обсудить разбор | оценить
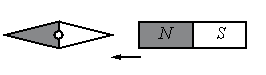Магнитная стрелка компаса зафиксирована на оси (северный полюс затемнён, см. рисунок). К компасу поднесли сильный постоянный полосовой магнит и освободили стрелку. В каком положении установится стрелка?
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
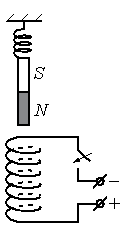Непосредственно над неподвижно закреплённой проволочной катушкой вдоль её оси на пружине подвешен полосовой магнит (см. рисунок). Куда начнёт двигаться магнит сразу после замыкания ключа? Ответ поясните, указав, какие физические явления и законы Вы использовали для объяснения.
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Вектор магнитной индукции: формула
Один из параметров магнитного поля – его силовая характеристика. Она обозначает, с какой силой поле влияет на движущиеся в нём заряженные частицы. Это значение из разряда векторных величин, носит название магнитная индукция B→.
Физический смысл магнитной индукции (МИ)
Возможность действовать на предмет магнитным полем (МП) определяет сущность настоящей индукции. Она появляется в момент перемещения в катушке индуктивности магнита постоянной природы. Результатом такого движения является появление тока, с одновременным увеличением магнитного потока. Поскольку обмотка у катушки металлическая, а структура металла – кристаллическая решётка, то можно объяснить физические свойства этого явления.
Электроны, находящиеся в этой решётке, при отсутствии магнитного воздействия находятся в покое. Движения никакого нет. Оно начинается в тот момент, когда электроны попадают под воздействие переменного МП (поле изменяется при перемещении постоянного магнита).
Значение возникающего в катушке тока зависит от диаметра жилы и количества витков, физических характеристик магнита и скорости его движения.
Единица размерности в системе Си рассматриваемой характеристики – тесла. Она обозначается буквами Тл.
Важно! Электроны в решётке, после попадания катушки в МП, разворачиваются под некоторым углом и выстраиваются вдоль силовых линий МП. Количество ориентированных частиц и однородность их размещения зависимы от величины поля.
Вектор – это вектор индукции магнитного поля (градиентный параметр МП).
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Модуль вектора магнитной индукции
Чтобы определить величину вектора МИ, нужно узнать его модуль. Как определяется модуль вектора магнитной индукции (градиент)? Это можно понять на примере небольшой модели. Если поместить в поле подковообразного магнита горизонтально подвешенный проводник, то МП магнита будет действовать только на участок, расположенный в междуполюсном промежутке. Сила F→, действующая на этот участок, будет направлена под прямым углом к линиям индукции и самому проводнику. Она достигает своего максимума, когда орт МИ располагается перпендикулярно проводнику.
Значение модуля B→ будет равно отношению максимального значения этой силы F→ к произведению длины отрезка ∆L на силу движения зарядов (I), а именно:
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон Био-Савара-Лапласа
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
где:
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
Для кругового движения она выглядит так:
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
Теорема о циркуляции
Изначально в 1826 году Андре Ампер сформулировал данную теорему. Он разобрал случай с постоянными электрическими полями, его теорема применима к магнитостатике. Теорема гласит: циркуляция МП постоянного электричества по любому контуру соразмерна сумме сил всех токов, которые пронизывают этот контур.
Стоит знать! Тридцать пять лет спустя Д. Максвелл обобщил это утверждение, проведя параллели с гидродинамикой.
Другое название теоремы – закон Ампера, описывающий циркуляцию МП.
Математически теорема записывается следующим образом.
где:
- B→– вектор магнитной индукции;
- j→ – плотность движения электронов.
Это интегральная форма записи теоремы. Здесь в левой части интегрируют по некоторому замкнутому контуру, в правой части – по натянутой поверхности на полученный контур.
Магнитный поток
Одна из физических величин, характеризующих уровень МП, пересекающего любую поверхность, – магнитный поток. Обозначается буквой φ и имеет единицу измерения вебер (Вб). Эта единица характерна для системы СИ. В СГС магнитный поток измеряется в максвеллах (Мкс):
Магнитный поток φ определяет величину МП, пронизывающую определённую поверхность. Поток φ зависит от угла, под которым поле пронизывает поверхность, и силы поля.
Формула для расчёта имеет вид:
где:
- В – скалярная величина градиента магнитной индукции;
- S – площадь пересекаемой поверхности;
- α – угол, образованный потоком Ф и перпендикуляром к поверхности (нормалью).
Внимание! Поток Ф будет наибольшим, когда B→ совпадёт с нормалью по направлению (угол α = 00). Аналогично Ф = 0, когда он проходит параллельно нормали (угол α = 900).
Вектор магнитной индукции, или магнитная индукция, указывает направление поля. Применяя простые методы: правило буравчика, свободно ориентирующуюся магнитную стрелку или контур с током в магнитном поле, можно определить направление действия этого поля.
Видео
Магнитная индукция, магнитный поток: определение, формулы, смысл
Физический смысл магнитной индукции
Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся.
Васильев Дмитрий ПетровичПрофессор электротехники СПбГПУ Если же металл попадает под действие переменного магнитного поля (из-за перемещения постоянного магнита внутри катушки – именно перемещения), то заряды начинают двигаться под действием этого магнитного поля.
В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого.
При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля.
Чем выше сила магнитного поля, тем больше количество частиц поворачиваются и тем более однородным будет являться их расположение.
Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле.
Формула магнитной индукции
где, В — вектор магнитной индукции, F — максимальная сила действующая на проводник с током, I — сила тока в проводнике, l — длина проводника.
Формула магнитной индукции:
Формула магнитной индукции: B = Mmax/IS
- B — индукция магнитного поля (в Тл)
- Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
- l — длина проводника (в м)
- S — площадь рамки (в м²)
Другие формулы, где встречается B
Эти формулы также можно использовать для её расчёта.
Сила Ампера:
Сила Ампера: Fa=IBL sinα
- Fa — сила Ампера (в Н — ньютон)
- I — сила тока (в А — ампер)
- B — индукция магнитного поля (в Тл)
- L — длина проводника (в м)
- α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)
Сила Лоренца:
Сила Лоренца: Fл = qvB sinα
- Fл — сила Лоренца (в Н — ньютон)
- q — заряд частицы (в Кл — кулон)
- v — скорость (в м/с)
- B — индукция (в Тл)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток:
Магнитный поток: Ф = BS cosα
- Ф — магнитный поток (в Вб – вебер)
- B — индукция (в Тл)
- S — площадь рамки (в м²)
- α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))
Магнитный поток
Магнитный поток это скалярная величина, которая характеризует действие магнитной индукции на некий металлический контур.
Магнитная индукция определяется числом силовых линий, проходящих через 1 см2 сечения металла.
Магнитометры, используемые для ее измерения, называют теслометрами.
Абрамян Евгений ПавловичДоцент кафедры электротехники СПбГПУ Единицей измерения магнитной индукции в системе СИ является Тесла (Тл).
После прекращения движение электронов в катушке сердечник, если он выполнен из мягкого железа, теряет магнитные качества. Если он изготовлен из стали, то он имеет способность некоторое время сохранять свои магнитные свойства.
Взаимодействие магнитов
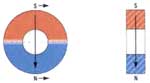
Постоянный магнит (или магнитная стрелка) ориентируется вдоль магнитного меридиана Земли. Тот его конец, который указывает на север, называется северным полюсом (N), а противоположный конец — южным полюсом (S). Приближая два магнита друг к другу, заметим, что одноименные их полюсы отталкиваются, а разноименные — притягиваются (рис. 1).
Если разделить полюса, разрезав постоянный магнит на две части, то мы обнаружим, что каждая из них тоже будет иметь два полюса, т. е. будет постоянным магнитом (рис. 2). Оба полюса — северный и южный, — неотделимые друг от друга, равноправны.
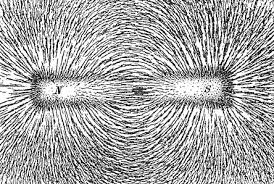
Магнитное поле, создаваемое Землей или постоянными магнитами, изображается, подобно электрическому полю, магнитными силовыми линиями. Картину силовых линий магнитного поля какого-либо магнита можно получить, помещая над ним лист бумаги, на котором насыпаны равномерным слоем железные опилки. Попадая в магнитное поле, опилки намагничиваются — у каждой из них появляется северный и южный полюсы. Противоположные полюсы стремятся сблизиться друг с другом, но этому мешает трение опилок о бумагу. Если постучать по бумаге пальцем, трение уменьшится и опилки притянутся друг к другу, образуя цепочки, изображающие линии магнитного поля.
На рис. 3 показано расположение в поле прямого магнита опилок и маленьких магнитных стрелок, указывающих направление линий магнитного поля. За это направление принято направление северного полюса магнитной стрелки.
Направление вектора МИ
Направление магнитных полей может указать стрелка магнита, помещаемая в эти поля. Она будет крутиться до тех пор, пока не остановится. Северный конец стрелки покажет, куда ориентирован B→ орт того или иного поля.
Линии магнитной индукции
Таким же образом ведёт себя рамка с током, имеющая возможность без помех ориентироваться в МП. Направленность вектора индукции указывает ориентацию нормали к такому замкнутому электромагнитному контуру.
Внимание! Здесь используют правило буравчика (правого винта). Если винт вращать так, как направлен ток в рамке, то поступательное продвижение винта совпадёт с направлением положительной нормали.
В некоторых случаях, чтобы найти направление, применяют правило правой руки.
Наглядное отображение линий МИ
Линию, к которой можно провести касательную, совпадающую с B→, называют линией магнитной индукции (МИ). С помощью таких линий можно визуально отобразить магнитное поле. Это сомкнутые контурные чёрточки, которые охватывают токи. Их густота всегда пропорциональна величине B→ в конкретной точке МП.
Информация. Когда имеют дело с МП прямого движения заряженных частиц, то эти линии изображаются в виде концентрических окружностей. Они имеют свой центр, расположенный на прямой линии с током, и находятся в плоскостях, расположенных под прямым углом к нему.
С направлением магнитных линий также можно определиться, пользуясь правилом буравчика.
Основные формулы для вычисления вектора МИ
Вектор магнитной индукции, формула которого B = Fm/I*∆L, можно находить, применяя другие математические вычисления.
Закон электромагнитной индукции
Закон электромагнитной индукции (закон Фарадея) звучит так:
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром.
Математически его можно описать формулой:
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре всегда направлен так, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из N витков (то есть он — катушка), то ЭДС индукции будет вычисляться следующим образом.
Закон Фарадея для контура из N витков
Ɛi — ЭДС индукции [В]
ΔФ/Δt — скорость изменения магнитного потока [Вб/с]
N — количество витков [-]
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением R:
Закон Ома для проводящего контура
Ɛi — ЭДС индукции [В]
I — сила индукционного тока [А]
R — сопротивление контура [Ом]
Если проводник длиной l будет двигаться со скоростью v в постоянном однородном магнитном поле с индукцией B ЭДС электромагнитной индукции равна:
ЭДС индукции для движущегося проводника
Ɛi — ЭДС индукции [В]
B — магнитная индукция [Тл]
v — скорость проводника [м/с]
l — длина проводника [м]
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле
- вследствие изменения во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Закон Био-Савара-Лапласа
Формула ЭДС индукции
Описывает правила нахождения B→ магнитного поля, которое создаёт постоянный электроток. Это экспериментально установленная закономерность. Био и Савар в 1820 году выявили её на практике, Лапласу удалось сформулировать. Этот закон является основополагающим в магнитостатике. При практическом опыте рассматривался неподвижный провод с малым сечением, через который пропускали электроток. Для изучения выбирался малый участок провода, который характеризовался вектором dl. Его модуль соответствовал длине рассматриваемого участка, а направление совпадало с направлением тока.
Интересно. Лаплас Пьер Симон предложил считать током даже движение одного электрона и на этом утверждении, с помощью данного закона, доказал возможность определения МП продвигающегося точечного заряда.
Согласно этому физическому правилу, каждый сегмент dl проводника, по которому протекает электрический ток I, образовывает в пространстве вокруг себя на промежутке r и под углом α магнитное поле dB:
dB = µ0 *I*dl*sin α /4*π*r2,
- dB – магнитная индукция, Тл;
- µ0 = 4 π*10-7 – магнитная постоянная, Гн/м;
- I – сила тока, А;
- dl – отрезок проводника, м;
- r – расстояние до точки нахождения магнитной индукции, м;
- α – угол, образованный r и вектором dl.
Важно! Согласно закону Био-Савара-Лапласа, суммируя векторы магнитных полей отдельных секторов, можно определить МП нужного тока. Оно будет равно векторной сумме.
Существуют формулы, описывающие этот закон для отдельных случаев МП:
- поля прямого перемещения электронов;
- поля кругового движения заряженных частиц.
Формула для МП первого типа имеет вид:
Для кругового движения она выглядит так:
В этих формулах µ – это магнитная проницаемость среды (относительная).
Рассматриваемый закон вытекает из уравнений Максвелла. Максвелл вывел два уравнения для МП, случай, где электрическое поле постоянно, как раз рассматривают Био и Савар.
Принцип суперпозиции
Для МП существует принцип, согласно которому общий вектор магнитной индукции в определённой точке равен векторной сумме всех векторов МИ, созданных разными токами в данной точке:
Правило Ленца
Чтобы определить направление индукционного тока, нужно воспользоваться правилом Ленца.
Академически это правило звучит следующим образом: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
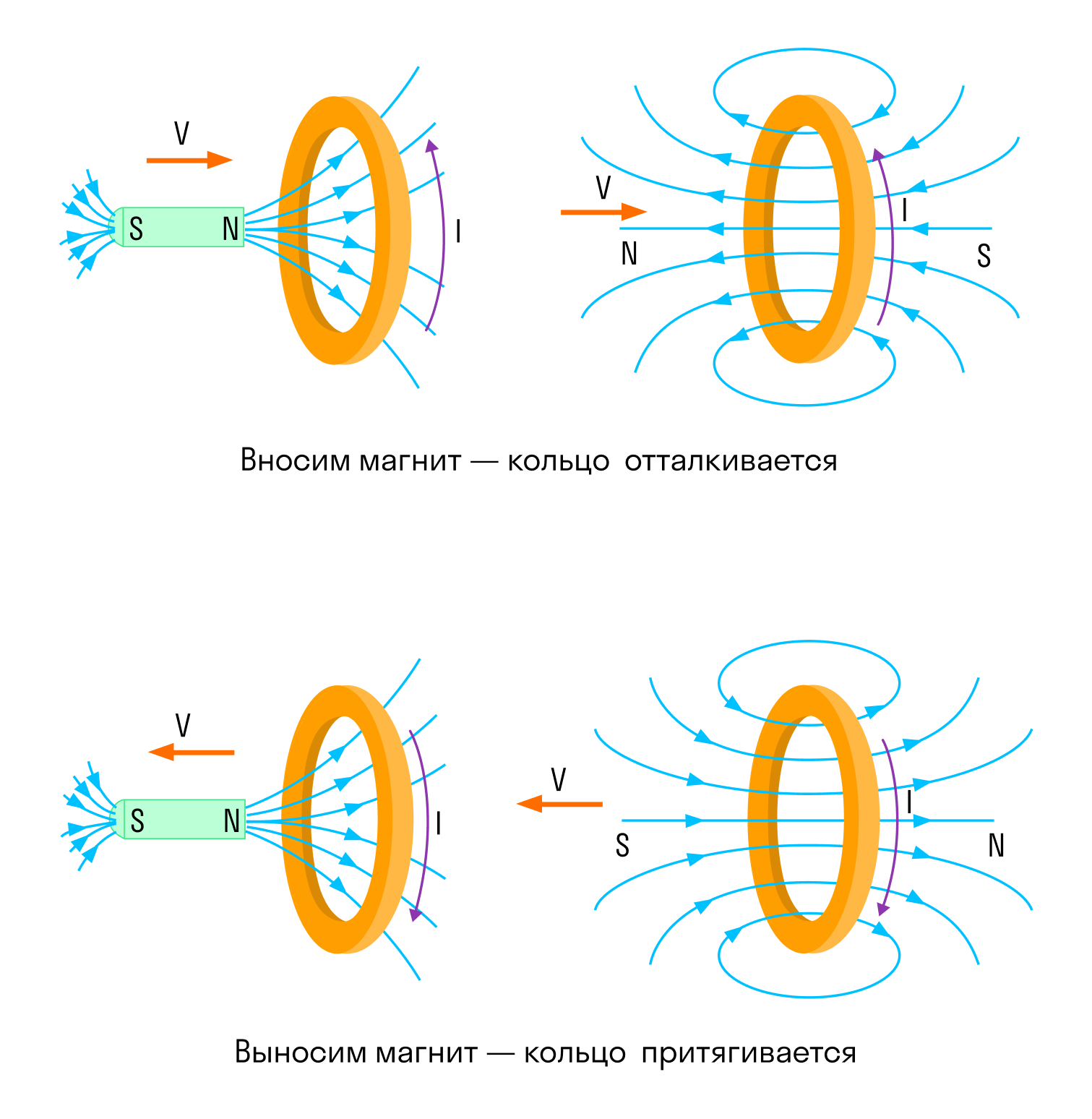
Давайте попробуем чуть проще: катушка в данном случае — это недовольная бабуля. Забирают у нее магнитный поток — она недовольна и создает магнитное поле, которое этот магнитный поток хочет обратно отобрать.
Дают ей магнитный поток, забирай, мол, пользуйся, а она такая — «Да зачем сдался мне ваш магнитный поток!» и создает магнитное поле, которое этот магнитный поток выгоняет.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Майкл Фарадей провел ряд опытов, которые помогли открыть явление электромагнитной индукции.
Опыт раз. На одну непроводящую основу намотали две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушка замкнута на гальванометр, а магнит движется вдвигается (выдвигается) относительно катушки
Вот, что показали эти опыты:
-
Индукционный ток возникает только при изменении линий магнитной индукции.
Направление тока будет различно при увеличении числа линий и при их уменьшении.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС.
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
[spoiler title=”источники:”]
http://amperof.ru/teoriya/vektor-magnitnoj-indukcii-formula.html
[/spoiler]
О постоянных магнитах
для простого инженера
Издревле,
магниты
считались вещью загадочной. Древние греки называли
магнитный железняк – камнем Геркулеса. Да и сейчас
обсуждается много идей разного рода вечных
двигателей и т.п. Но мы в данной заметке
постараемся рассмотреть сугубо утилитарную сторону
применения постоянных магнитов.
1. Введение в постоянные магниты
Постоянный магнит оказал огромное влияние на
историю человечества. В первую очередь это касается
магнитного компаса, остающегося и поныне надежным
средством морской и воздушной навигации.
Во-вторых, постоянный магнит стал одним из главных
факторов, повлиявших на исследования
электродинамических процессов и приведших в итоге к
созданию электродинамики, как науки, так и всей
многообразной электродинамической техники.
Однако, до последнего времени практическое применение
постоянных магнитов в области техники ограничивалось в
основном следующими отдельными, хотя и весьма
важными, применениями:
– телефон
и динамический громкоговоритель
– микроэлектродвигатель
– системы возбуждения небольших электрогенераторов
– поляризованные реле
– измерительные, научные и медицинские приборы
– маломощные держатели (магнитные защелки, ловители,
сепараторы и т.п.)
Эти устройства характеризуются, как правило,
небольшими мощностями, усилиями и моментами. Везде, где
нужно было увеличивать силу или мощность устройства,
конструкторская мысль обращалась к
использованию электромагнитов (соленоидов),
распространившихся в технике куда более широко, но имеющих
и свои ограничения и особенности.
Однако, за последние 30 лет свойства постоянных магнитов
революционным образом изменились, что хорошо видно из
приведенной ниже диаграммы.
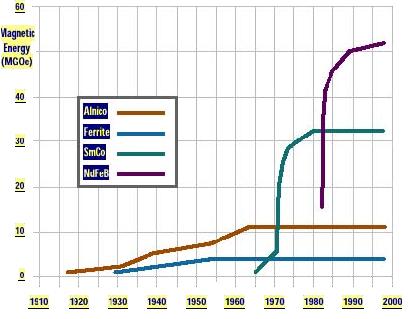
Нижняя голубая линия показывает динамику развития свойств
ферритовых
магнитов, именно тех, которые мы используем
обычно в защелках, динамиках и т.п.
Следующая красная – магнитные сплавы типа Альнико (
алюминиево-никелиевые),
применяемые
обычно в радио и телевизионной аппаратуре.
А вот зеленая и фиолетовая – соответствуют новому виду
магнитов, изготавливаемых на основе редкоземельных
элементов:
– зеленая линия – Самарий- кобальтовые магниты,
– фиолетовая линия – Неодим – железо – боровые.
Как видно из диаграммы магнитная энергия самариевых
магнитов в 6 раз выше, а неодимовых в 10 раз выше , чем у
привычных нам ферритовых (керамических) изделий. На
практике это означает, что неодимовый магнитик, размером
c куриное яйцо, неосторожно взятый в руки, –
способен раздробить пальцы. Т.е. механические усилия ,
которые могут создаваться современными постоянными
магнитами уже не являются силами игрушечными или
приборными, а вполне соответствуют усилиям, характерным
для обычных машин и механизмов, т.е – десятки и сотни
килограммов.
Такие свойства делают
возможным, например, изготовление различных малогабаритных
механических и электромеханических удерживающих устройств
с высоким усилием фиксации, например станочных
приспособлений, грузоподъемных устройств и т.п.
Естественно, что опыта использования мощных магнитов
в нашей обычной мебельной технологии пока нет,
исключая магнитные сепараторы для древесной стружки
на плитных заводах. Эти знания остаются пока
достоянием специалистов – электромехаников.
Поэтому представляется, что конструктор, механик или
технолог любого предприятия, в том числе и мебельного или
деревообрабатывающего, должны знать больше о
редкоземельных магнитах, как об одном из важных и
перспективных направлений развития современной техники и
технологии.
По закону Ампера ( в простой скалярной форме F = I х L х
B) , на проводник с током, помещенный в магнитное поле
действует сила F, пропорциональная длине проводника L,
силе тока I и величине магнитной индукции B. Поэтому,
электромеханические устройства ( электрические двигатели,
реле и т.п. приводные и др. элементы техники ) основанные
на явлении электромагнитной индукции и в которых применены
магниты нового типа при сохранении своих размеров
становятся значительно сильнее. Т.е. пропорционально
увеличению величины магнитной индукции возрастает крутящий
момент или тяговое усилие или скорость движения
(вращения). Или же, при сохранении мощности
устройства соответственно уменьшаются его габариты и
вес. В некоторых случаях применение новых магнитов
позволяет существенно снизить расход электроэнергии и это
не противоречит законам физики.
Примечание . Цена машины, станка
или др. устройства, в том числе и шкафа, прямо
связана с его материалоемкостью. Во многих случаях
эта зависимость – едва ли не прямая пропорция, что,
впрочем, когда нибудь станет понятным и
мебельщикам.Более подробно и с картинками
можно посмотреть закон Ампера и др. основные понятия
электромагнетизма в любом школьном учебнике
или справочнике по физике.
Производство магнитов на основе редкоземельных элементов
(самария, неодима) давно миновало лабораторную стадию и в
последние несколько лет развивается быстрыми темпами
по достаточно гибким технологиям, в том числе и в нашей
стране, и они доступны любому заказчику. Хотя
магниты называются редкоземельными, но фактически,
природные ресурсы ( руды и рудные концентраты ) в нашей
странеи для их производства весьма велики.
По данным ООО “Химсталькомплект”
постоянные магниты NdFeB, из известных в настоящее время
систем, занимают уникальное положение по соотношению
характеристики/стоимость, что объясняет бурный рост их
производства и внедрение в различные отрасли. Так, в
1989г. их было произведено 190 т, в 1999г. 13500 т, а
2000г.-17500 т металлокерамических магнитов и
магнитопластов. По прогнозам аналитиков к 2005г. будет
произведено около 40000 тонн магнитов NdFeB.
Современные технологии позволяют
изготавливать магниты самых разнообразных простых и
сложных геометрических форм. Ниже в таблицах показаны
различные магнитные элементы и характеристики
магнитных материалов (взяты со страницы ООО
“Химсталькомплект” http://www.metalopt.ru)
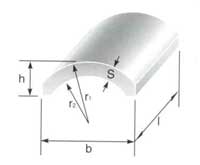
Сегменты различной
геометрии и
направленности поля:
радиальной намагниченности
h, b, l,s, R1, R2 — геометрические
параметры сегмента
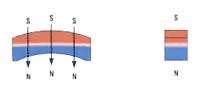
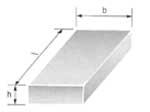
параллельной намагниченностиПризмы
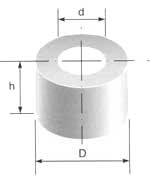
h, b, l — геометрические параметры призмыКольца — с
различным
количеством
полюсов и направлением поля
2-х полюсное кольцо
4-х полюсное кольцо
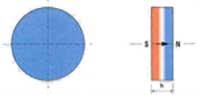
Цилиндры
Магниты
сложных
форм2. Свойства современных постоянных
магнитов
Основные
характеристики магнитных материалов
| Материал | (BH) max, МГс*Э | B r , Гс | H c , Э | Цена, $ за 1 кг на российском рынке |
Цена, $ на единицу (BH)max |
Гибкие магнитные материалы |
1.6 | 1725 | 1325 | 5-10 | 3.1- 6.2 |
Керамика ( феррит) |
3 | 4000 | 2400 | 1-2.5 | 0.3-0.85 |
Альнико |
9 | 13500 |
1400 | 44.1 | 4.3 |
Sm-Co |
20 | 10500 |
9200 | 250 -500 |
12.5 |
Спеченные Nd-Fe-B |
50 | 14200 |
12500 |
70-150 |
1.4-3.7 |
Br – остаточная индукция,
т.е. основная силовая характеристика постоянного
магнита , BHmax – энергетическое произведение
3. Формулы для расчета постоянных
магнитов
Ниже приведены методы и формулы для
приблизительного расчета несложных магнитных систем на
основе постоянных магнитов, рекомендуемые английской
фирмой Dexter,
вполне доступные для понимания пожилого
дровосека. Все последующие формулы, комментарии
и картинки взяты непосредственно со страницы фирмы ,
правда не могу поручиться за абсолютную точность моего
перевода.
Расчет магнитной
индукции аксиально-намагниченных
цилиндрических магнитов с радиусом (r)
и длиной (l ), в точке
расположенной на расстоянии (d)
от повехности, вдоль оси производится по
формуле:
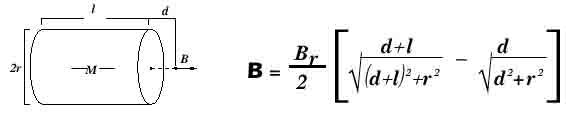
Пример:
r=0.5″, l=1″,d=0.25″, B r
=12200 Gauss, B=2935.7Gauss
Расчет методом граничных элементов ( МГЭ),
B=2788.7 GaussРасчет магнитной индукции
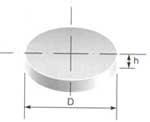
для призматических магнитов намагниченных
по длине , толщиной (2t), шириной
(2w ) и длиной ( l),
для точки расположенной на расстоянии (d)
от поверхности вдоль магнитной оси производится по формуле:
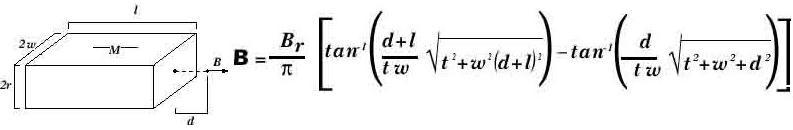
Пример:
2t=1″, 2w=1″,l=0.5″, d=0.25″,
Br=12200, B=2386.5
Gauss
Используя МГЭ, B=2238
GaussРасчет магнитной индукции
в точке вдоль осей этих геометрий более
комплексный. Есть три компонента магнитной
индукции, которые должны быть приняты во
внимание . но принцип остается тем же.
Подобные формулы приемлемы для
прямоугольных магнитов. Цилиндрические
магниты труднее поддаются расчету, для них
рекомендуются компьютерные методы расчета.При использовании принципа
совмещения, могут быть подвергнуты анализу
магниты и более сложных геометрических
форм. Для примера , мы можем рассчитать
магнитную индукцию вдоль оси
цилиндрической трубы
по формуле:
Вычитая магнитную
индукцию внутреннего цилиндра с диаметром (2
ri ) из магнитной
индукции цилиндра с внешним диаметром (2r0
), мы получаем магнитную индукцию трубы (
которая обычно используется в Фарадеевых
поворотных устройствах).Подобная логика может быть
приложима и к другим магнитам симметричной
формы:
Используя принцип
суперпозиции , можно определить магнитную
индукцию в промежутке между двумя соосно
расположенными магнитами:
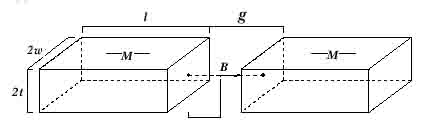
Индукция
между двумя призмами на расстоянии (d)
определяется по формуле B = B
1 + B 2 ,
где B 2 –
индукция от призмы на расстоянии (g-d).Приближенно, результаты
таких расчетов могут быть применимы к
магнитам, размещенным в ненасыщенной
стальной цепи. Когда используются подобные
формулы, обычно исходят из предположения ,
что распределение индукции в стали
соответствует индукции магнита двойной
длины. Если большая часть магнитного
потока проходит через зазор ( т.е. без
потерь в стали), то результат расчета
имеет хорошую точность.Для двух магнитов
размещенных на C-образной скобе расчет производится по формуле:
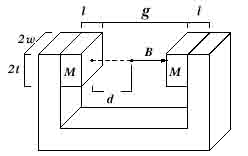
B= B1 +
B 2 , где B1
– индукция прямоугольного блока длиной (2l)
на расстоянии ( d). B
2 – индукция
прямоугольного блока длиной (2l
) на расстоянии ( g-d).Пример: l=1″,
2w=1″, 2t=1″,
B r=12200 Gauss,
g =1″, d=0.3″,
B 1=3033 Gauss, B2
B 1 + B 2
=4243 Gauss, используя МГЭ, B
=4121 Gauss =1210 Gauss,Дальнейшие вариации на эту
тему бесконечны. Для большей точности
рекомендуются компьютерные расчетыРасчет магнитных цепей
Эмпирический подход
пригоден для анализа цепи со стальным
сердечником или другими проницаемыми
материалами. Начиная с идеальной цепи не
имеющей потерь и сопротивления в стали,
этот метод используется для эмпирического
определения отношений в точных моделях
магнитных цепей.Рисунок идеальной цепи см.
ниже
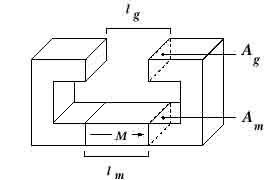
Используя закон Ампера для
цепи, допускаем , что в стали отсутствуют
потери магнитодвижущей силы:
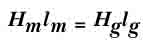
где Hm=MMF
магнита, lm =длинамагнита, Hg = MMF
поперек зазора, lg
= длина зазора.Допуская , что весь поток
индукции проходит полностью через зазор (
т.е. без потерь) мы можем написать
следующее соотношение:
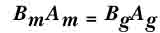
Где Bm
– индукция магнита, Am
– поперечное сечение магнита, Bg
– поток через зазор , Ag
– поперечное сечение зазора. Если
мы допустим B m
и Hm и
возьмем их соотношение , то мы получим
коэффициент проницаемости
(PC).
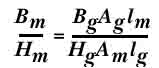
Проницаемость материала
определяется как µ=B/H. В
системе CGS проницаемость воздуха равна
единице, таким образом Bg=Hg
. Тогда соотношение для коэффициента
проницаемости :
|
 |
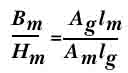
Этот подсчет является
приблизительным , потому что не учитывает
потерь индукции или MMF в цепи. Фактор
потерь (ó) и фактор сопротивления (f
) определяются эмпирически в соответствии
с упомянутыми выше отношениями ( для
большей точности) .
Фактор потерь есть
соотношение общего магнитного потока к
потоку в зазоре. Он определяется
проницаемостью, и аналогичен проводимости
электрической цепи. A magnetic circuit can
usually be broken up into basic leakage
paths. Для каждой потерянной магнитной
линии эмпирически определяется формула для
магнитной проводимости , которая может
быть использована. Обычно используются
формулы из книги ( “Electromagnetic
Devices ” ( Электромагнитные
устройства) написанной Herbert C. Roters
(New York: John Wiley & Sons, Inc.,
1941).
Фактор потерь определяется по фомуле
:
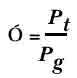
Где P t
– сумма проницаемости всех потерянных
магнитных линий ( включая зазор) цепи,
Pg –
проницаемость зазора.Фактор сопротивления (f)
считается для потерь MMF
в несущих магнитный поток элементах цепи (
т.е. стали) и небольших зазорах между
деталями. Этот фактор определяется
эмпирически и находится в пределах от 1,1
до 1.5 для большинства цепей. Большие
значения относятся к цепям близким к
уровню насыщению стали. Фактор
сопротивления:
Где Ht
– суммарная MMF и H
g – MMF
поперек зазораРасчет
магнитных силОбычно
импользуется следующая формула для расчета
удерживающей силы магнита :F=0.577B2A
где B
– индукция в килогауссах, A –
площадь полюса в квадратных дюймах. Для
магнитов, конструкция которых показана
ниже используется следующая формула:
|
 |
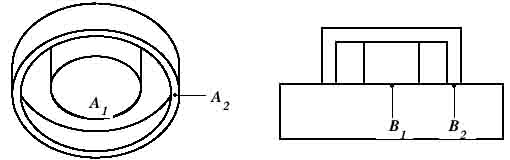Для
простых магнитов отделенных от стальной
пластины воздушным промежутком (d),с хорошей точностью для B
может быть рассчитано через текущие
соотношения.
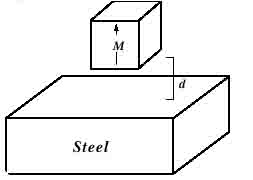
Для
магнита непосредственно соприкасающегося
со сталью , могут быть использованы
следующие два метода. Если магнит имеет
форму подобную диску или пластинке ( малое
отношение длина/диаметр) , используется
следующая формула:
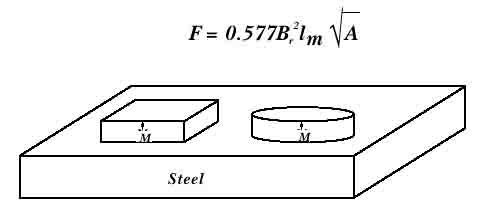
где Br=
остаточная индукция, lm
= длина магнита и A=площадьполюса.
Для
магнитов имеющих кубическую или
призматическую форму или для тех, у
которых соотношение длины к диаметру равно
1 или более, результат может быть получен
с хорошей точностью. Допуская, что индукция в стали
приблизительно эквивалентна индукции
магнита двойной длины, мы можем вычислить
магнитную индукцию в центре используя
следующее уравнение:
| Calculate B@d=-l
|
F=0.577B2A |
Примечание . Облегчить эти
расчеты можно используя, например,
стандартные способы из программы ”
Excel” пакета “Windows” или
несколько специальных магнитных
калькуляторов, расположенных на
сайте фирмы “Dexter ”
>>>
Для самостоятельного анализа и
расчета магнитных систем можно рекомендовать
так же очень интересный отечественный
комплекс программ для инженерного
моделирования электромагнитных, тепловых и
механических задач методом конечных
элементов ELCUT™ . Дружественный
пользовательский интерфейс, простота
описания даже самых сложных моделей, широкие
аналитические возможности комплекса и
высокая степень автоматизации всех операций
позволяют разработчику полностью
сосредоточиться на своей задаче не
отвлекаясь на изучение математических основ
вычислительных алгоритмов и особенностей их
реализации. Ознакомиться с возможностями
комплекса, пройти обучение и получить
бесплатно демоверсию программы можно
непосредственно на сервере
ELCUT Для начала освоения программы
требуется всего несколько часов.
Достоинством программы является то,
что выдаваемая цветная графика очень удобна
для понимания существа, т.е физики
процесса.По вопросам производства и применения
современных постоянных магнитов в сети
имеется значительное количество
источников на русском и иностранном языках.
Для меня впрочем будет достаточно, если
данная заметка вызовет интерес к магнитной
технике и у наших рационализаторов –
мебельщиков. Каждый может легко сделать
поиск в сети и сам. Для справки – по
имеющейся информации, в столь
консервативной, до недавнего
времени, штуке – как автомобиль,
японцы используют уже до 2-3 килограммов
редкоземельных магнитовА. Абушенко
26 июля 2002 года
Дополнительно
для
чтения о постоянных магнитах
рекомендуется
рекомендуется
1. Перспективные
материалы для постоянных магнитов, А.С. Мищенко и А.М. Тишин
>>>
2. Информационные ресурсы
Магнитного технологического центра группы
“Arnold” >>>
в том числе “Перечень научно-технической
литературы по магнитной тематике” ,
“Алфавитный перечень фирм, связанных с
производством магнитов” и много др.
полезной информации
3. Расчет и проектирование
магнитных систем с постоянными магнитами.
Р.Р. Арнольд, М. изд. Энергия, 1969 г.,
скачать можно по ссылке
http://www.knigka.info/engine/download.php?id=430
Некоторые отечественные и
зарубежные предприятия – изготовители
постоянных магнитовПолимагнит, ОАО,
Москва
>>>
Редмаг, Калуга >>>
Химсталькомплект,ООО, г. Озерск,
Челябинская обл.
>>>
Group Arnold. The magnetic products group of
SPS technologies
>>>
Dexter magnetic
technologies
>>> последнее изм.
24.07.03
Электромагнитная индукция
Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.33%) 96 votes
