Как найти магнитную индукцию прямого тока - Сайт, где вы сможете решить свои вопросы

Виталий Викторович Карабут

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Любой электрический ток можно представить в виде совокупности элементарных токов. Следовательно, можно рассчитать характеристики магнитного поля, порождаемого любыми токами, если использовать:

Закон Био – Савара – Лапласа:

$dvec{B}=frac{mu_{0}}{4pi }frac{I}{r^{3}}left[ dvec{l}vec{r}right]left( 1 right)$

где $dvec{l}$ – элементарный участок проводника, по которому течет ток $I$; $vec{r}$ – радиус-вектор, который проводится от элемента $dl$ с током к точке, в которой исследуется поле; $mu_{0}$– магнитная постоянная.
Принцип суперпозиции магнитных полей. Магнитная индукция поля, которое создают несколько элементов с токами, – это векторная сумма индукций полей, каждого элементарного тока отдельно. Для непрерывных токов:

$vec{B}=intlimits_l {dvec{B}} left( 2 right)$.

Замечание 1

В выражении (2) следует учитывать, что суммирование является векторным.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Закон Био-Савара-Лапласа дает возможность рассчитывать магнитные поля, которые создают токи, распределенные в пространстве. Плотность этих токов может изменяться в зависимости от координаты (или радиус-вектора, определяющего положение точки) ($vec{j}(vec{r})$).

Около избранной точки пространства, в котором находится магнитное поле, выберем бесконечно малую трубку тока, с длиной $dl$, сечением $dS$. В точке $C$, которая находится на расстоянии $r$ от трубки тока, создаваемое ей поле равно:

$dvec{B}=frac{mu_{0}}{4pi }frac{left[ vec{j, }left( vec{r}right)vec{r} right]}{r^{3}}dldSleft( 3 right)$.

где $dV=dldS.$

Результирующее поле находят интегрированием выражения (3) по объему в котором текут токи.

Применение закона Био-Савара – Лапласа для нахождения магнитного поля прямого тока

Пусть по очень длинному, тонкому проводу, течет постоянный то $I$ (рис.1). Рассчитаем поле, которое создает этот проводник в некоторой токе $C$, находящейся на расстоянии $R$ от него.

Рисунок 1. Магнитное поле прямого тока. Автор24 — интернет-биржа студенческих работ

«Магнитное поле прямого тока» 👇

По закону Био-Савара – Лапласа в точке $C$ элемент $dl$ с током $I$ создает магнитное поле:

$dB=frac{mu_{0}}{4pi }frac{Idlsin beta }{r^{2}}left( 4 right)$.

где $beta$ – угол между направлением течения тока и $vec{r}$.

Все элементы нашего проводника с током в точке $C$ создают магнитные поля, направленные вдоль одной прямой, и направлены они перпендикулярно плоскости рисунка к нам. Учтем следующие простые соотношения (см. рис.1):

$r=frac{R}{cos alpha };l=R, tg, alpha ;dl=frac{R, dalpha}{{cos}^{2}alpha };sin {beta =cos {alpha (5).}}$

Принимая во внимание формулы (5) закон (4) приведем к виду:

$dB=frac{mu_{0}}{4pi }frac{Isin alpha dalpha }{R}left( 6 right)$

Применим принцип суперпозиции, для этого выражение (6) проинтегрируем, учтем, что $-frac{pi }{2}le alpha le frac{pi }{2},$ получим:

$B=frac{mu_{0}}{4pi }frac{I}{R}intlimits_{-frac{pi }{2}}^frac{pi}{2} sin alpha dalpha =frac{mu_{0}}{2pi }frac{I}{R}left( 7 right)$

Закон полного тока и его применение для нахождения магнитного поля прямого тока

Допустим, что токи, создающие магнитное поле и контур, по которому мы будем рассматривать интегрирование, находятся в однородном магнитоизотропном веществе, тогда закон полного тока (или закон циркуляции вектора магнитной индукции) запишем в виде:

$ointlimits_L {vec{B}dvec{r}=mu mu_{0}I, left( 8 right),}$

где $mu $ – магнитная проницаемость вещества; $I$ – алгебраическая сумма токов, охватываемых контуром $L$.

Теорема о циркуляции (или закон полного тока), в теории магнетизма, играет роль аналогичную теореме Гаусса для вектора напряженности в электростатике. Если в распределении токов имеется симметрия, то этот закон упрощает процедуру поиска вектора магнитной индукции.

Рассмотрим магнитное поле, которое создается прямым длинным тонким проводом (рис.1). Условия, как и представленные выше. Найдем поле в точке $C$. Применяя закон полного тока.

Магнитное поле прямого тока имеет осевую симметрию (силовые линии поля – окружности с центрами на оси провода). Величина вектора индукции одинакова для всех точек одной такой силовой линии. В качестве контура $L$ возьмем окружность радиуса $R$, тогда циркуляция вектора индукции равна:

$ointlimits_L {vec{B}d} vec{r}=BL=2pi R B, left( 9 right)$.

Поскольку контур $L$ охватывает только ток $I$, то результат правой части (9) приравняем к величине этого тока, умноженному на магнитную постоянную и магнитную проницаемость вещества:

$2pi RB=mu mu_{0}I, , left( 10 right)$,

считая, что проводник находится в вакууме ($mu=1$), получаем:

$B=mu_{0}frac{I}{2pi R}, left( 11 right)$.

Сравнивая формулы (7) и (11), мы видим, что результаты одинаковые.

Магнитное поле прямого тока в проводе, имеющем конечную длину

Допустим, что у нас имеется прямой тонкий провод, конечной длины по которому течет неизменяющийся ток $I$ (рис.2). Определим, какова магнитная индукция поля в точке $C$, создаваемая этим проводом.

Рисунок 2. Магнитное поле прямого тока в проводе, имеющем конечную длину. Автор24 — интернет-биржа студенческих работ

Полярные углы, соответствующие концам проводника будем считать равными $varphi_{1}=a$ и $varphi_{2}=b$.

Вектор магнитной индукции перпендикулярен плоскости рисунка. Силовые линии – это окружности, как и у бесконечного проводника.

Модуль элементарного магнитного поля ($dB$), которое создает малый участок $dl$ (рис.2) по закону Био-Савара-Лапласа запишем так:

$dB=frac{mu_{0}}{4pi }frac{Idlsin alpha }{r^{2}}=frac{mu_{0}I}{4pi R}cos {varphi dvarphi }left( 12 right)$

где из рис.2 видно, что:

$sin {alpha =cos {varphi ;}, }$
$dlcos {varphi =rdvarphi ;, }$
$r=frac{R}{cos varphi }.$

Воспользуемся принципом суперпозиции и получим магнитное поле в точке $C$, создаваемое всеми участками проводника с током:

$B=intlimits_a^b {frac{mu_{0}I}{4pi R}cos {varphi dvarphi }=}frac{mu_{0}I}{4pi R}left( sin left( b right)-sin left( a right)right)left( 13 right)$

Если рассматривать бесконечно длинный проводник, как частный случай прямого проводника с током, то следует учесть, что для него:

$a=-frac{pi }{2};, b=frac{pi }{2}$,

тогда из (13) следует:

$B=frac{mu_{0}I}{2pi R}left( 14 right)$

Результат (14) снова совпал с (7) и (11).

Магнитное поле внутри прямого тока

Рассмотрим длинный прямой проводник радиуса $R$. Пусть материалом этого проводника будет парамагнетик, магнитная проницаемость которого $mu$. Материал провода будем считать однородным. Плотность тока, текущего в проводнике при этом может быть представлена:

$j=frac{I}{pi R^{2}}, left( 15 right)$.

где $j$ – постоянная величина.

Задачу будем решать, используя закон о циркуляции вектора магнитной индукции (8). Кривую, по которой будем рассматривать циркуляцию совместим с силовой линией магнитного поля. Внутри проводника, магнитное поле так же имеет осевую симметрию. Силовые линии представлены окружностями, с центрами на оси провода. Радиус рассматриваемой силовой линии будем считать равным $r$, тогда

$ointlimits_L {vec{B}d} vec{r}=B 2pi r, left( 16 right)$.

Из закона полного тока следует, что:

$2pi rB=I_{1}=mu mu_{0}jpi r^{2}to $$B=frac{1}{2}mu mu_{0}rj$ при $rle R(17).$

Для бесконечно длинного провода мы видим:

что внутри проводника индукция магнитного поля прямо пропорциональна расстоянию от оси провода, до точки рассмотрения.
вне провода индукция обратно пропорциональна расстоянию.
у поверхности проводника вектор магнитной индукции претерпевает разрыв, поскольку для внутреннего материала проводника $mu >1$, для вакуума $mu =1$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Всем доброго времени суток. В прошлой статье я рассказал о магнитном поле и немного остановился на его параметрах. Данная статья продолжает тему магнитного поля и посвящена такому параметру как магнитная индукция. Для упрощения темы я буду рассказывать о магнитном поле в вакууме, так как различные вещества имеют разные магнитные свойства, и как следствие необходимо учитывать их свойства.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Закон Био – Савара – Лапласа

В результате исследования магнитных полей создаваемых электрическим током, исследователи пришли к таким выводам:

магнитная индукция, создаваемая электрическим током пропорциональна силе тока;
магнитная индукция имеет зависимость от формы и размеров проводника, по которому протекает электрический ток;
магнитная индукция в любой точке магнитного поля зависит от расположения данной точки по отношению к проводнику с током.

Французские учёные Био и Савар, которые пришли к таким выводам обратились к великому математику П. Лапласу для обобщения и вывода основного закона магнитной индукции. Он высказал гипотезу, что индукция в любой точке магнитного поля, создаваемое проводником с током можно представить в виде суммы магнитных индукций элементарных магнитных полей, которые создаются элементарным участком проводника с током. Данная гипотеза и стала законом магнитной индукции, называемого законом Био – Савара – Лапласа. Для рассмотрения данного закона изобразим проводник с током и создаваемую им магнитную индукцию

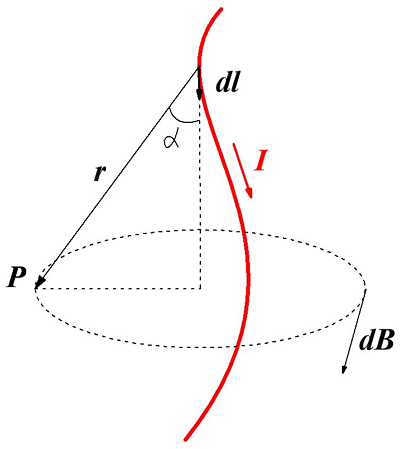
Магнитная индукция dB, создаваемая элементарным участком проводника dl.

Тогда магнитная индукция dB элементарного магнитного поля, которое создается участком проводника dl, с током I в произвольной точке Р будет определяться следующим выражением

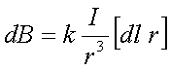
где I – сила тока, протекающая по проводнику,

r – радиус-вектор, проведённый от элемента проводника к точке магнитного поля,

dl – минимальный элемент проводника, который создает индукцию dB,

k – коэффициент пропорциональности, зависящий от системы отсчёта, в СИ k = μ₀/(4π)

Так как [dl r] является векторным произведением, тогда итоговое выражение для элементарной магнитной индукции будет выглядеть следующим образом

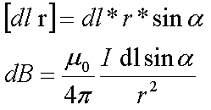
Таким образом, данное выражение позволяет найти магнитную индукцию магнитного поля, которое создается проводником с током произвольной формы и размеров при помощи интегрирования правой части выражения

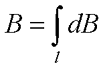
где символ l обозначает, что интегрирование происходит по всей длине проводника.

Магнитная индукция прямолинейного проводника

Как известно простейшее магнитное поле создает прямолинейный проводник, по которому протекает электрический ток. Как я уже говорил в предыдущей статье, силовые линии данного магнитного поля представляют собой концентрические окружности расположенные вокруг проводника.

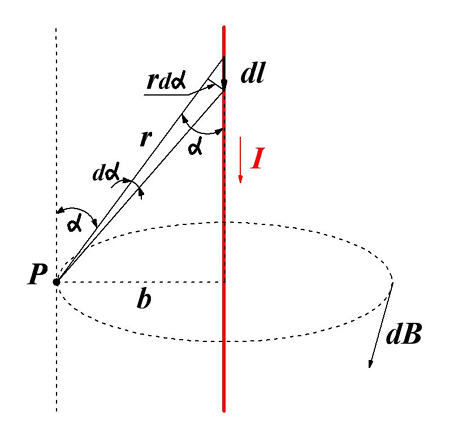
Магнитная индукция магнитного поля создаваемого прямолинейным проводником с током.

Для определения магнитной индукции В прямого провода в точке Р введем некоторые обозначения. Так как точка Р находится на расстоянии b от провода, то расстояние от любой точки провода до точки Р определяется как r = b/sinα. Тогда наименьшую длину проводника dl можно вычислить из следующего выражения

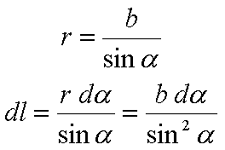
В итоге закон Био – Савара – Лапласа для прямолинейного провода бесконечной длины будет иметь вид

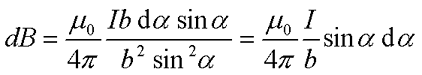
где I – ток, протекающий по проводу,

b – расстояние от центра провода до точки, в которой рассчитывается магнитная индукция.

Теперь просто проинтегрируем получившееся выражение по dα в пределах от 0 до π.

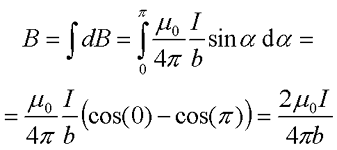
Таким образом, итоговое выражение для магнитной индукции прямолинейного провода бесконечной длины будет иметь вид

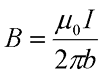
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – ток, протекающий по проводу,

b – расстояние от центра проводника до точки, в которой измеряется индукция.

Магнитная индукция кольца

Индукция прямого провода имеет небольшое значение и уменьшается при удалении от проводника, поэтому в практических устройствах практически не применяется. Наиболее широко используются магнитные поля созданные проводом, намотанным на какой либо каркас. Поэтому такие поля называются магнитными полями кругового тока. Простейшим таким магнитным поле обладает электрический ток, протекающий по проводнику, который имеет форму окружности радиуса R.

В данном случае практический интерес представляет два случая: магнитное поле в центре окружности и магнитное поле в точке Р, которое лежит на оси окружности. Рассмотрим первый случай.

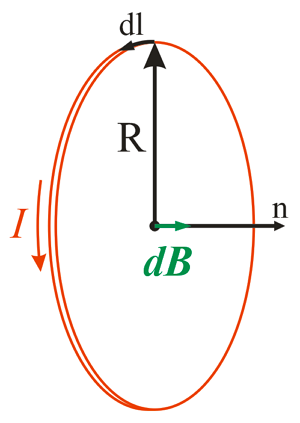
Магнитная индукция в центре кругового тока.

В данном случае каждый элемент тока dl создаёт в центре окружности элементарную магнитную индукцию dB, которая перпендикулярна к плоскости контура, тогда закон Био-Савара-Лапласа будет иметь вид

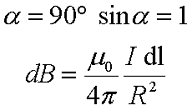
Остается только проинтегрировать полученное выражение по всей длине окружности

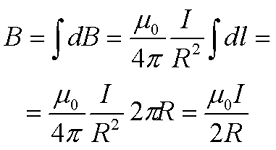
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник.

Рассмотрим второй случай, когда точка, в которой вычисляется магнитная индукция, лежит на прямой х, которая перпендикулярна плоскости ограниченной круговым током.

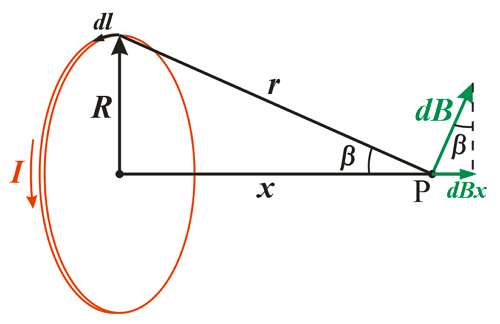
Магнитная индукция в точке, лежащей на оси окружности.

В данном случае индукция в точке Р будет представлять собой сумму элементарных индукций dB_X, которые в свою очередь представляет собой проекцию на ось х элементарной индукции dB

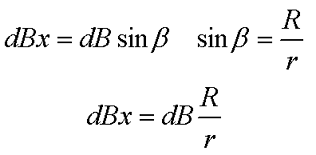
Применив закон Био-Савара-Лапласа вычислим величину магнитной индукции

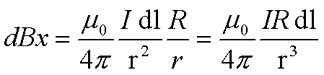
Теперь проинтегрируем данное выражение по всей длине окружности

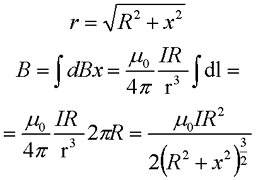
где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м,

I – сила тока в проводнике,

R – радиус окружности, в которое свернут проводник,

х – расстояние от точки, в которой вычисляется магнитная индукция, до центра окружности.

Как видно из формулы при х = 0, получившееся выражение переходит в формулу для магнитной индукции в центре кругового тока.

Циркуляция вектора магнитной индукции

Для расчёта магнитной индукции простых магнитных полей достаточно закона Био-Савара-Лапласа. Однако при более сложных магнитных полях, например, магнитное поле соленоида или тороида, количество расчётов и громоздкость формул значительно увеличится. Для упрощения расчётов вводится понятие циркуляции вектора магнитной индукции.

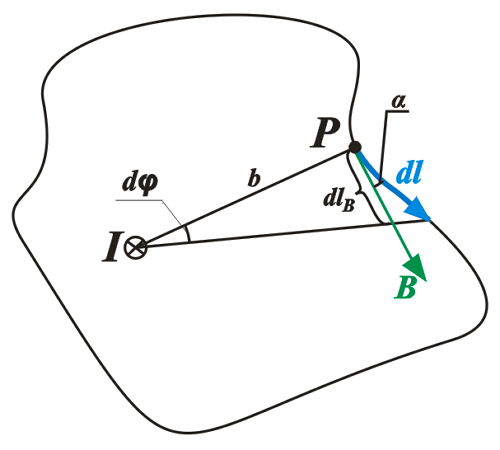
Циркуляция вектора магнитной индукции по произвольному контуру.

Представим некоторый контур l, который перпендикулярный току I. В любой точке Р данного контура, магнитная индукция В направлена по касательной к данному контуру. Тогда произведение векторов dl и В описывается следующим выражением

Так как угол dφ достаточно мал, то векторов dl_В определяется, как длина дуги

Таким образом, зная магнитную индукцию прямолинейного проводника в данной точке, можно вывести выражение для циркуляции вектора магнитной индукции

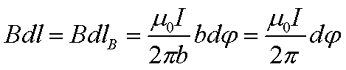
Теперь остаётся проинтегрировать получившееся выражение по всей длине контура

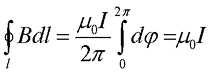
В нашем случае вектор магнитной индукции циркулирует вокруг одного тока, в случае же нескольких токов выражение циркуляции магнитной индукции переходит в закон полного тока, который гласит:

Циркуляция вектора магнитной индукции по замкнутому контуру пропорциональна алгебраической сумме токов, которые охватывает данный контур.

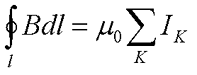
Магнитное поле соленоида и тороида

С помощью закона полного тока и циркуляции вектора магнитной индукции достаточно легко определить магнитную индукцию таких сложных магнитных полей как у соленоида и тороида.

Соленоидом называется цилиндрическая катушка, которая состоит из множества витков проводника, намотанных виток к витку на цилиндрический каркас. Магнитное поле соленоида фактически состоит из множества магнитных полей кругового тока с общей осью, перпендикулярной к плоскости каждого кругового тока.

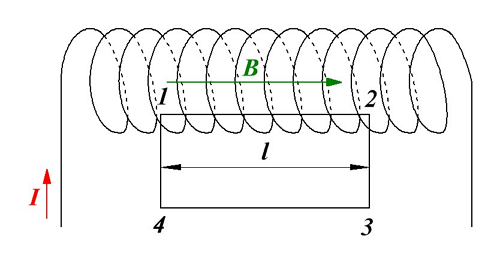
Магнитная индукция соленоида.

Воспользуемся циркуляцией вектора магнитной индукции и представим циркуляцию по прямоугольному контуру 1-2-3-4. Тогда циркуляция вектора магнитной индукции для данного контура будет иметь вид

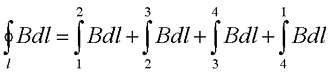
Так как на участках 2-3 и 4-1 вектор магнитной индукции перпендикулярен к контуру, то циркуляция равна нулю. На участке 3-4, который значительно удалён от соленоида, то его так же можно не учитывать. Тогда с учётом закона полного тока магнитная индукция в соленоиде достаточно большой длины будет иметь вид

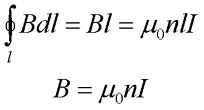
где n – число витков проводника соленоида, которое приходится на единицу длины,

I – ток, протекающий по соленоиду.

Тороид образуется путём намотки проводника на кольцевой каркас. Данная конструкция эквивалентна системе из множества одинаковых круговых токов, центры которых расположены на окружности.

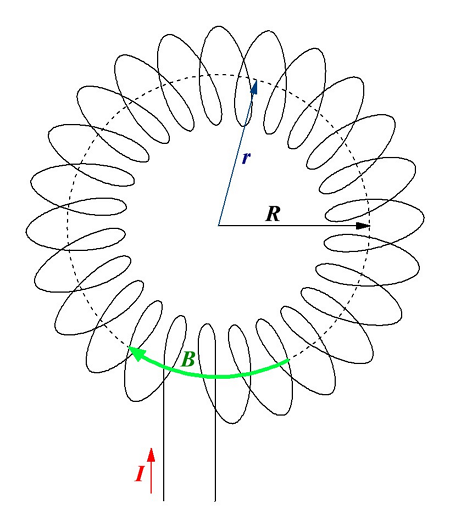
Магнитная индукция тороида.

В качестве примера рассмотрим тороид радиуса R, на который намотано N витков провода. Вокруг каждого витка провода возьмём контур радиуса r, центр данного контура совпадает в центром тороида. Так как вектор магнитной индукции B направлен по касательной к контуру в каждой точке контура, то циркуляция вектора магнитной индукции будет иметь вид

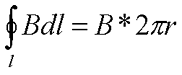
где r – радиус контура магнитной индукции.

Контур проходя внутри тороида охватывает N витков провода с током I, тогда закон полного тока для тороида будет иметь вид

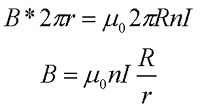
где n – число витков проводника, которое приходится на единицу длины,

r – радиус контура магнитной индукции,

R – радиус тороида.

Таким образом, используя закон полного тока и циркуляцию вектора магнитной индукции можно рассчитать сколь угодно сложное магнитное поле. Однако закон полного тока дает правильные результаты только лишь в вакууме. В случае расчёта магнитной индукции в веществе необходимо учитывать так называемые молекулярные токи. Об этом пойдёт речь в следующей статье.

Источник

Магнитное поле прямого тока — создается током, текущего по тонкому прямому бесконечному проводу

$Large B=int dB=frac{mu mu _0I}{4pi R}int_{0}^{pi }{sinalpha dalpha }=frac{mu mu _02I}{4pi R}$

Вывод формулы для магнитного поля прямого тока :

За постоянную интегрирования возьмем угол α (угол между векторами dl и r) и выразим через него все остальные величины

$Large r=frac{R}{sinalpha } ; dl=frac{rdalpha }{sinalpha }$

Магнитная индукция, которая создавается одним элементом проводника, равна

$Large dB=frac{mu mu _0}{4pi R}sinalpha dalpha$

Поскольку угол α для всех элементов прямого тока изменяется в пределах от 0 до π, то

$Large B=frac{mu mu _0I}{4pi R}int_{0}^{pi }{sinalpha dalpha }$

Посчитаем интеграл, и получим формулу Магнитной индукции поля прямого тока

$Large B=frac{mu mu _02I}{4pi R}$

Так же есть :

Магнитное поле кругового тока: $large B=int dB=frac{mu mu _0I}{4pi R^2}int{dl }=frac{mumu _0 I }{2pi R}$

В Формуле мы использовали :

— Магнитная индукция прямого тока

— Магнитная проницаемость среды

$mu _0=1.2566times 10^{−6}$ — Магнитная постоянная

— Сила тока

— Расстояние от провода до точки, где мы вычисляем магнитную индукцию

— Угол между вектором dl и r

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 мая 2021 года; проверки требуют 16 правок.

Магнитная индукция

Размерность	MT⁻²I⁻¹
Единицы измерения
СИ	Тл
СГС	Гс
Примечания
Векторная величина

Классическая электродинамика

Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела.

Стандартное обозначение: ; единица измерения в СИ — тесла (Тл), в СГС — гаусс (Гс) (связь: 1 Тл = 10⁴ Гс).

Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла.

Для измерения магнитной индукции используются магнитометры-тесламетры. Также она может быть найдена расчётным путём — в статической ситуации для этого достаточно знать пространственное распределение токов.

Вектор в общем случае зависит от координат рассматриваемой точки и времени . Он не инвариантен относительно преобразований Лоренца и изменяется при смене системы отсчёта.

Физический смысл[править | править код]

Магнитная индукция — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд ${displaystyle q^{*}}$ , движущийся со скоростью , равна

${displaystyle {vec {F}}=q^{*}left[{vec {v}}times {vec {B}}right]}$

(по величине ${displaystyle F=q^{*}vBsin alpha }$

Косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор перпендикулярен им обоим и направлен по правилу левой руки).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока I^* в рамке на её площадь. Момент сил зависит от ориентации рамки и достигает максимального значения при каких-то определённых углах. Звёздочка у символа указывает на то, что заряд или ток являются «пробными», то есть используемыми именно для регистрации поля, в отличие от тех же величин без звёздочки.

Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля .

Способы расчёта[править | править код]

Общий случай[править | править код]

В общем случае расчёт магнитной индукции проводится совместно с расчётом электрической составляющей электромагнитного поля посредством решения системы уравнений Максвелла:

${displaystyle mathrm {div} ,(varepsilon {vec {E}})={frac {rho }{varepsilon _{0}}}, mathrm {rot} ,{vec {E}}=-{frac {partial {vec {B}}}{partial t}},}$

${displaystyle mathrm {div} ,{vec {B}}=0, ,mathrm {rot} ,{frac {vec {B}}{mu }}=mu _{0}{vec {j}}+{frac {varepsilon }{c^{2}}}{frac {partial {vec {E}}}{partial t}}}$

где $mu _{0}$ — магнитная постоянная, — магнитная проницаемость, — диэлектрическая проницаемость, а — скорость света в вакууме. Через rho обозначена плотность заряда (Кл/м³) и через vec{j} плотность тока (А/м²).

Магнитостатика[править | править код]

В магнитостатическом пределе^[3] расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу $L_{1}$ током и когда оно создаётся объёмным распределением тока:

${displaystyle {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int limits _{L_{1}}{frac {Ileft({vec {r}}_{1}right)d{vec {l}}_{1}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}},qquad {vec {B}}left({vec {r}}right)={mu _{0} over 4pi }int {frac {{vec {j}}left({vec {r}}_{1}right)dV_{1}times left({vec {r}}-{vec {r}}_{1}right)}{left|{vec {r}}-{vec {r}}_{1}right|^{3}}}}$

В магнитостатике эта формула играет ту же роль, что закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени).

Если заранее очевидна геометрия поля, помогает теорема Ампера о циркуляции магнитного поля^[4] (эта запись является интегральной формой уравнения Максвелла для в вакууме):

${displaystyle oint limits _{L}{vec {B}}cdot d{vec {l}}=mu _{0}int limits _{S}{vec {j}}cdot d{vec {S}}}$

Здесь — произвольная поверхность, натянутая на выбранный замкнутый контур .

Простые примеры

Вектор магнитной индукции прямого провода с током на расстоянии от него составляет

${displaystyle {vec {B}}={frac {mu _{0}mu I}{2pi a}}cdot {vec {e}}_{varphi }}$

где ${displaystyle {vec {e}}_{varphi }}$ — единичный вектор вдоль окружности, по оси симметрии которой проложен провод. Предполагается, что среда однородна.

Вектор магнитной индукции прямого внутри соленоида с током и числом витков на единицу длины равен

${displaystyle {vec {B}}=mu _{0}mu nIcdot {vec {e}}_{z}}$

где ${displaystyle {vec {e}}_{z}}$ — единичный вектор вдоль оси соленоида. Здесь также предполагается однородность магнетика, которым заполнен соленоид.

Связь с напряжённостью[править | править код]

Магнитная индукция и напряжённость магнитного поля связаны через соотношение

${displaystyle {vec {B}}=mu _{0}mu {vec {H}}}$

где — магнитная проницаемость среды (вообще говоря, это тензорная величина, но в большинстве реальных случаев её можно считать скаляром, то есть просто константой конкретного материала).

Основные уравнения[править | править код]

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.

Некоторые из уравнений:

из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,

Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

${displaystyle {vec {F}}=K{frac {q_{m}^{*}{vec {r}}}{r^{3}}}.}$

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

Выражение для плотности энергии магнитного поля

${displaystyle w={frac {B^{2}}{2mu _{0}mu }}}$ .

Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Типичные значения[править | править код]

характерные значения магнитной индукции

объект	, Тл	объект	, Тл
магнитоэкранируемая комната	10^-14	солнечное пятно	0,15
межзвёздное пространство	10^-10	небольшой магнит (Nd-Fe-B)	0,2
магнитное поле Земли	5*10^-5	большой электромагнит	1,5
1 см от провода с током 100 А	2*10^-3	сильный лабораторный магнит	10
небольшой магнит (феррит)	0,01	поверхность нейтронной звезды	10⁸

Примечания[править | править код]

См. также[править | править код]

Векторный потенциал
Уравнения Максвелла
Электромагнитное поле
Тензор электромагнитного поля
Напряжённость магнитного поля

Источник

Линии,
вдоль которых в магнитном поле
располагаются оси маленьких магнитных
стрелок, называют магнитными
линиями магнитного поля.

Направление,
которое указывает северный полюс
магнитной стрелки в каждой точке поля,
принято за направление магнитной линии
магнитного поля.

Цепочки,
которые образуют в магнитном поле
железные опилки, показывают форму
магнитных линий магнитного поля

Если
прямой проводник пропустить сквозь
лист картона, на который насыпан тонкий
слой железных опилок, включить ток и
опилки слегка встряхнуть, то под действием
магнитного поля тока железные опилки
расположатся вокруг проводника не
беспорядочно, а по концентрическим
окружностям

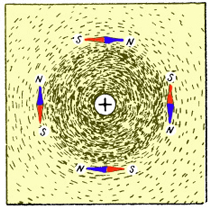
На
рисунке показано расположение
магнитных стрелок вокруг проводника с
током, расположенного перпендикулярно
плоскости чертежа, ток в нём направлен
от нас, что условно обозначено кружком
с крестиком. Оси этих стрелок устанавливаются
вдоль магнитных линий магнитного поля
прямого тока (рис. а).

При
изменении направления тока в проводнике
на противоположное (к нам), что условно
обозначено кружком с точкой, все магнитные
стрелки поворачиваются на 180°
(рис. б).

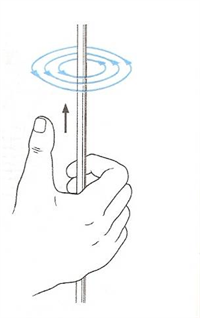
Направление
линий магнитного поля можно определить
с помощью правила правой руки:

если
обхватить проводник с током ладонью
правой руки так, чтобы отставленный
большой палец был сонаправлен с током,
то согнутые четыре пальца укажут
направление линий магнитного поля.

27. Магнитное поле кругового тока

Определим
магнитную индукцию на оси проводника
с током на расстоянии х от
плоскости кругового тока.
Векторы   перпендикулярны
плоскостям, проходящим через
соответствующие   и  .
Следовательно, они образуют симметричный
конический веер. Из соображения симметрии
видно, что результирующий вектор   направлен
вдоль оси кругового тока. Каждый из
векторов   вносит
вклад равный ,
а   взаимно
уничтожаются. Но , ,
а т.к. угол между   и   α
– прямой, то   тогда
получим

Подставив
и,
проинтегрировав по всему контуру ,
получим выражение для нахождения магнитной
индукции кругового тока:

При ,
получим магнитную
индукцию в центре кругового тока:

Заметим,
что в числителе –
магнитный момент контура. Тогда, на
большом расстоянии от контура, при ,
магнитную индукцию можно рассчитать
по формуле:

28. Теорема о циркуляции вектора b

Интеграл
вида
–
циркуляция вектора B→ по замкнутому
контуру L.

Циркуляция
B
равна
сумме токов, проходящих через площадь,
ограниченную контуром l:

Вначале
рассмотрим случай, когда контур лежит
в плоскости перпендикулярно потоку
(ток I направлен
за чертеж). В каждой точке контура
вектор направлен по касательной
к окружности, проходящей через эту точку
(линии прямого тока – окружности).

Воспользуемся
свойствами скалярного произведения
векторов.

         где   –
проекция dl на
вектор  ,
но  ,
где R –
расстояние от прямой тока I до
dl.