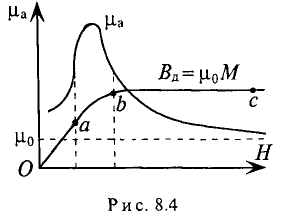
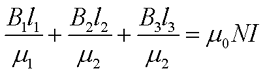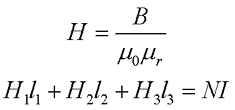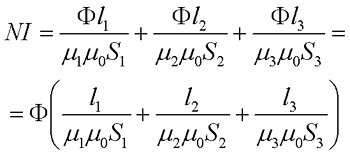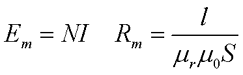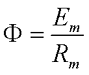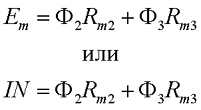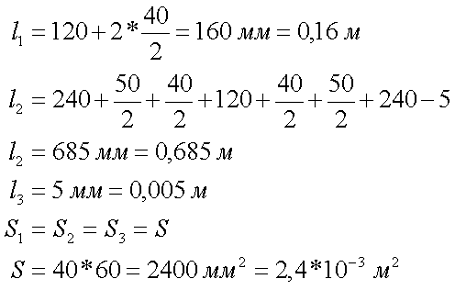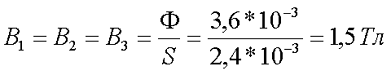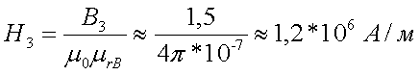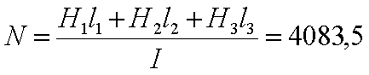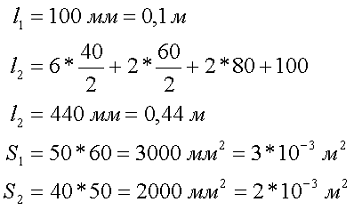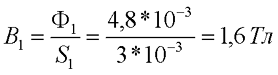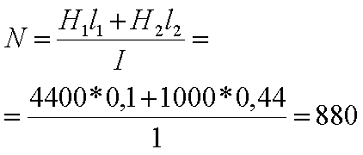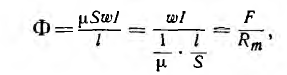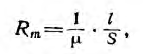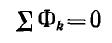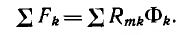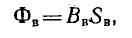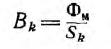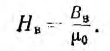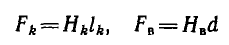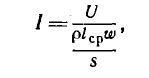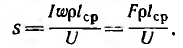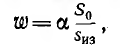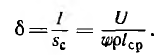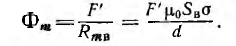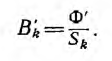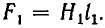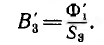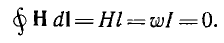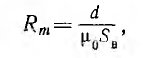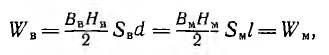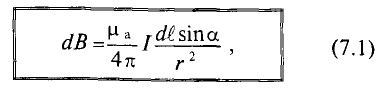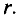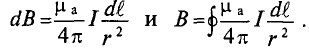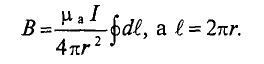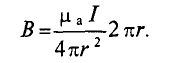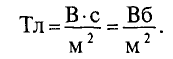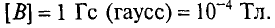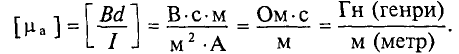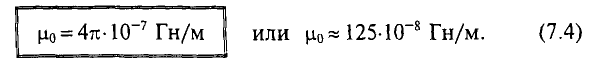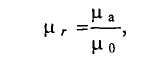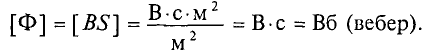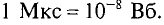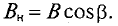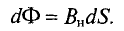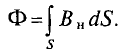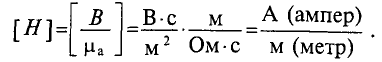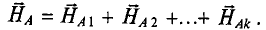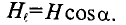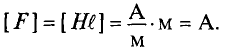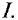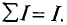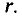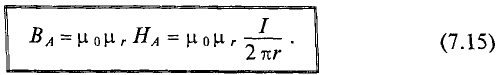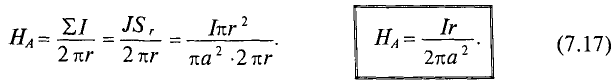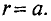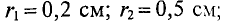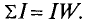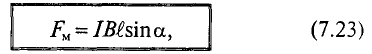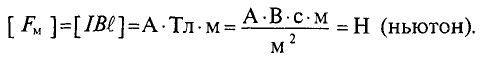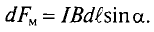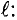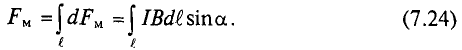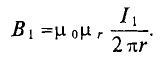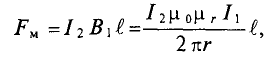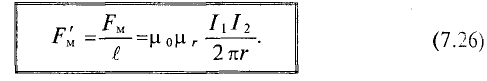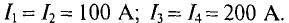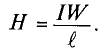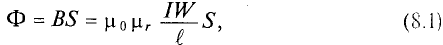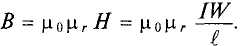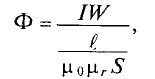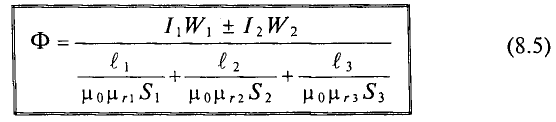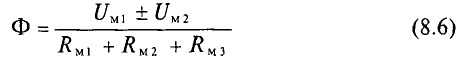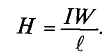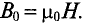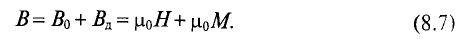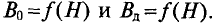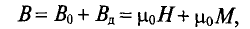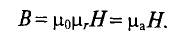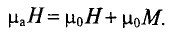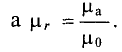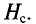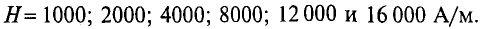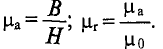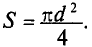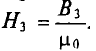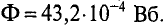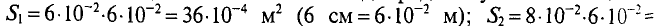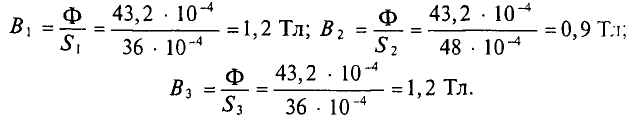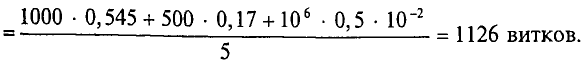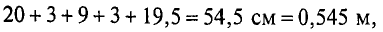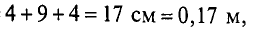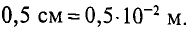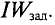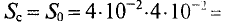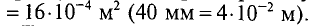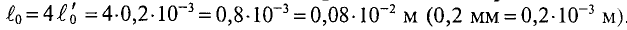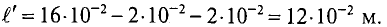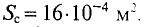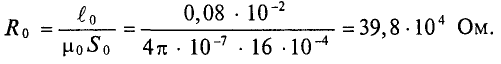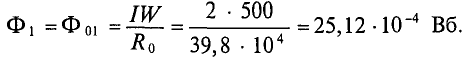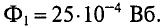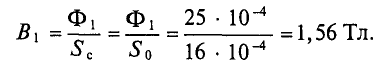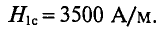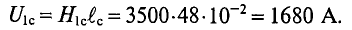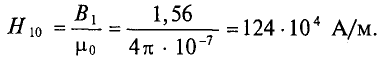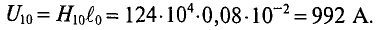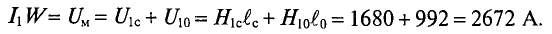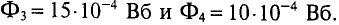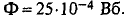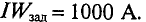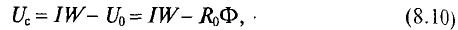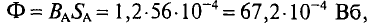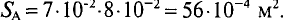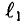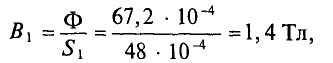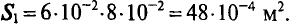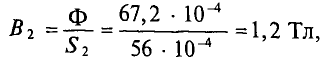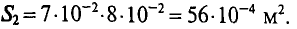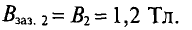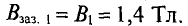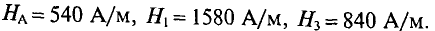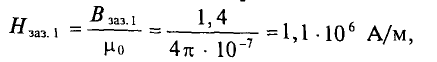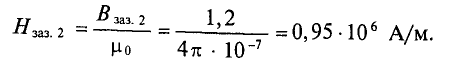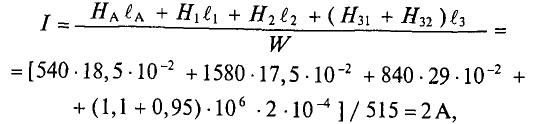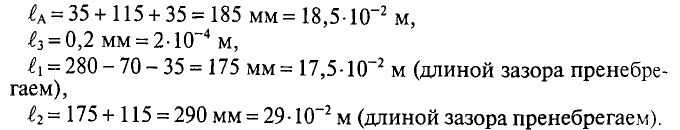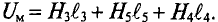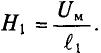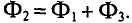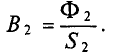Всем доброго времени суток. В прошлой статье я начал рассказывать о магнитном поле в веществе и затронул вопросы напряженности магнитного поля, магнитной проницаемости и восприимчивости, а также рассказал о намагничивании и гистерезисе в ферромагнетиках. Однако магнитное поле зависит не только от свойств веществ, но и от их формы. Об этом я и расскажу в статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Что такое магнитная цепь?
Магнитной цепью называется, соединение магнетиков, по которым замыкается магнитный поток. То есть сердечник, на который намотан любой дроссель, трансформатор, катушка индуктивности и т.д. является магнитной цепью. Более того если веществом такого сердечника является воздух (то есть катушки индуктивности не имеющие каркаса), то и он является магнитной цепью. Очень часто магнитную цепь называют магнитопроводом, что по сути так и есть, сердечник проводит магнитное поле, также как и проводник проводит электрический ток. Более того на магнитные цепи распространяются законы электрического тока: закон Ома, правила Кирхгофа и так далее, но об этом ниже.
Магнитные цепи бывают однородные и неоднородные. Однородными называют магнитные цепи, которые на протяжении всей своей длины изготовлены из одного материала (то есть имеет одинаковую магнитную проницаемость) и одинаковое поперечное сечение. Если хотя бы одно из этих условий не выполняется, то такая магнитная цепь называется неоднородной.
Также различают разветвлённые и неразветвлённые магнитные цепи. То есть не разветвлённые цепи состоят из одного контура, а разветвлённые, соответственно, состоят из нескольких контуров, по которым замыкается магнитный поток. Разветвлённые цепи могут быть симметричные и несимметричные. У симметричных цепей магнитный поток каждого контура одинаков.
Параметры магнитных цепей
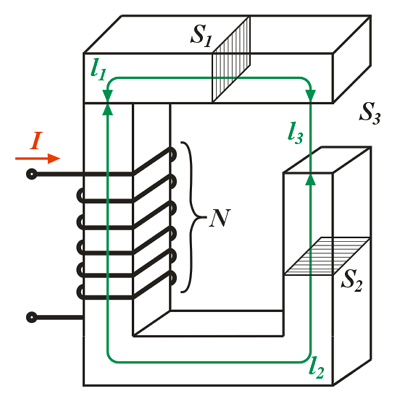
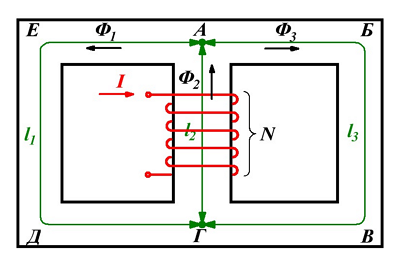
Как я уже говорил многие законы для электрических цепей подходят и для магнитных. Для обобщения этих законов необходимо ввести некоторые параметры, характеризующие магнитные цепи. Представим неоднородную и неразветвлённую магнитную цепь
Неоднородная и неразветвлённая магнитная цепь.
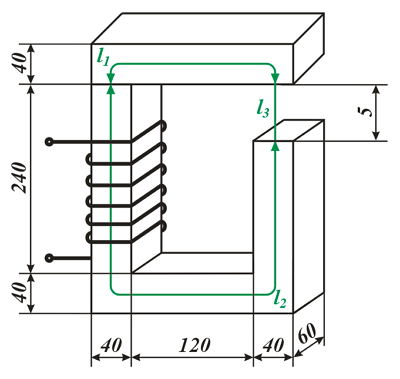
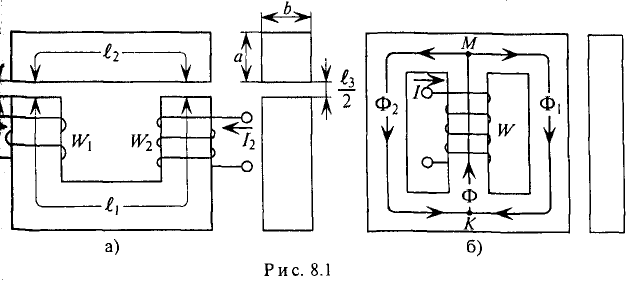
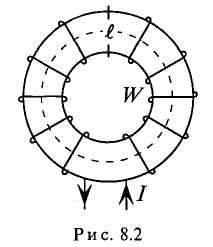
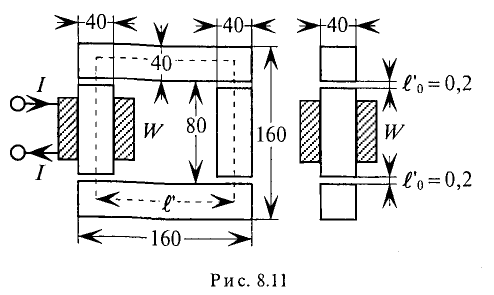
Данная цепь состоит из трёх участков длиной l1, l2, l3, имеющих поперечное сечение S1, S2, S3, причем магнитное поле создается током I, протекающим по соленоиду, содержащему N витков. Так как линии магнитного поля в основном замыкаются через магнитопровод, то магнитный поток Φ, можно считать одинаковым на всём протяжении магнитной цепи и определяется следующим выражением
где В – магнитная индукция,
S – площадь поперечного сечения, которую пронизывает магнитный поток.
Таким образом, магнитный поток является аналогом силы тока в электрических цепях.
Согласно закона полного тока и циркуляции вектора магнитной индукции составим уравнение
где В1, В2, В3 – соответственно магнитная индукция на участках l1, l2, l3 магнитной цепи;
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м;
μ1, μ2, μ3 – соответственно относительная магнитная проницаемость участков l1, l2, l3 сердечника;
N – количество витков провода;
I – ток, протекающий по проводу.
При использовании ферромагнетиков определение относительной магнитной проницаемость составляет некоторые трудности, поэтому вместо магнитной индукции в данном законе используют напряженность магнитного поля, следовательно для данной магнитной цепи закон полного тока можно представить следующим образом
Выражая магнитную индукцию через магнитный поток, получим следующее выражение
где S1, S2, S3 – соответственно, площадь поперечного сечения участков l1, l2, l3 магнитной цепи.
Таким образом, проводя аналогию с электрической цепью, получим следующие параметры магнитной цепи
где Em – магнитодвижущая сила,
Rm – магнитное сопротивление цепи.
Следовательно, вышеописанное выражение можно представить следующим выражением
где Rm1, Rm1, Rm1 – соответственно магнитные сопротивления участков l1, l2, l3 магнитной цепи.
Законы магнитной цепи
Как я писал выше многие законы электрических цепей подходят и для магнитных цепей. Например, закон Ома для магнитной цепи звучит следующим образом: магнитный поток Φ прямо пропорционален магнитодвижущей силе Em и обратно пропорционален полному сопротивлению магнитной цепи Rm. И выражается он следующей формулой, называемой также формулой Гопкинсона
Кроме закона Ома для магнитных цепей действуют правила Кирхгофа. Так первый закон Киргхофа для магнитных цепей звучит следующим образом: алгебраическая сумма магнитных потоков ∑Φ в узле магнитной цепи равна нулю. Для пояснения данного правила изобразим разветвлённую магнитную цепь
Разветвлённая магнитная цепь.
Данная магнитная цепь состоит из двух контуров АБВГ и АГДЕ. Ветвь АГ создает магнитный поток Φ2, который в точке А делится на два потока Φ1 и Φ3. Таким образом, в точке А алгебраическая сумма магнитных потоков равна нулю
Аналогично второй закон Кирхгофа для магнитной цепи звучит следующим образом: в контуре магнитной цепи алгебраическая сумма магнитодвижущижся сил ∑Еm равна алгебраической сумме магнитных напряжений на отдельных участках.
Магнитное напряжение на участке цепи определяется произведение магнитного потока Φ на магнитное сопротивление участка Rm, следовательно, второй закон Кирхгофа будет иметь вид
тогда для магнитной цепи изображённой выше второе правило Кирхгофа будет иметь вид
Использую данные соотношения достаточно просто рассчитать необходимые геометрические размеры магнитопроводов для различных магнитных систем, например, трансформаторы, дроссели, катушки индуктивности и так далее, чем мы и займёмся ниже.
Расчёт магнитных цепей
Теория без практического приложения мало интересна радиолюбителям, поэтому приступим к практическому применению теории магнитных цепей. Практический расчёты магнитный цепей сводится к определению магнитодвижущей силы Em (или как вариант определению количества витков провода N при некотором токе I), которая создает заданную магнитную индукцию B (или магнитный поток Φ). Для данных расчётов необходимо знать геометрические размеры магнитной цепи и магнитную проницаемость материала.
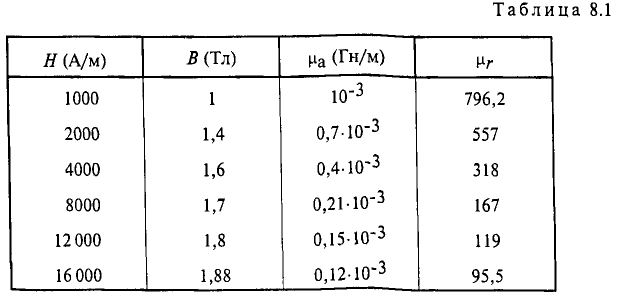
Для начала рассчитаем неразветвлённую магнитную цепь, пример которой дан на рисунке ниже
Расчёт неразветвлённой магнитной цепи (магнитопровода).
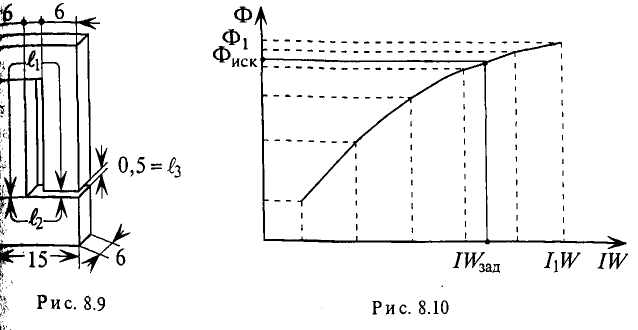
Данная магнитная цепь состоит из трех частей l1, l2, l3 выполненных из различных материалов. Где участок l1 – литая сталь, l2 – электротехническая сталь, l3 – воздушный разрыв.
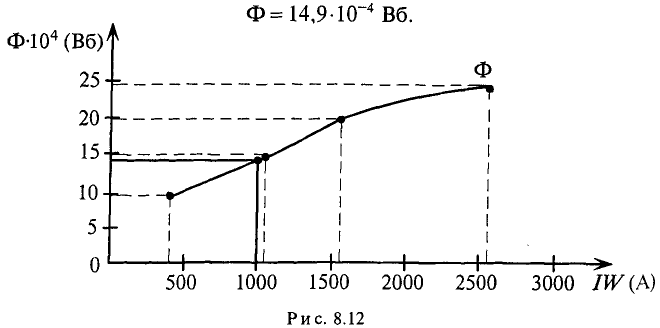
Необходимо рассчитать число витков N обмотки для создания магнитного потока Φ = 3,6 * 10-3 Вб, если сила тока протекающего по обмоткам составляет I = 2 A.
Так как магнитная цепь у нас неоднородная, то для начала необходимо рассчитать среднюю длину магнитных силовых линий l1, l2, l3, которая проходит по центру магнитной цепи, а также сечение магнитной цепи S.
Далее рассчитываем магнитную индукцию заданных участков l1, l2, l3
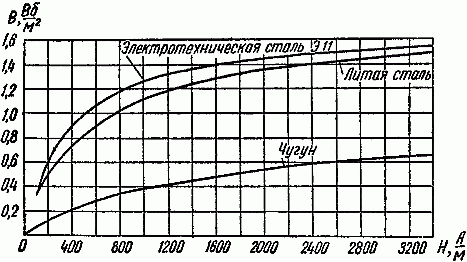
Найдём значение напряженности магнитного поля. Так как часть магнитопровода представлена ферромагнетиками, то магнитную индукцию для них находим с помощью графической зависимости магнитной индукции от напряженности магнитного поля
Зависимость индукции от напряженности магнитного поля электротехнической и листовой стали.
Так l1 – литая сталь, то при В1 = 1,5 Тл, напряженность магнитного поля Н1 ≈ 7 А/см = 700 А/м;
l2 – электротехническая сталь, про В2 = 1,5 Тл, напряженность магнитного поля Н2 ≈ 30 А/см = 3000 А/м;
l3 – воздушный разрыв, напряженность магнитного поля определяется как
где μ0 = 4π*10-7 – магнитная постоянная,
μrB – относительная магнитная проницаемость воздуха, μrB ≈ 1.
Теперь используя закон полного тока, в котором магнитную индукцию выразим через напряженность магнитного поля, можно рассчитать количество витков провода N
В итоге получаем количество витков N = 4083,5.
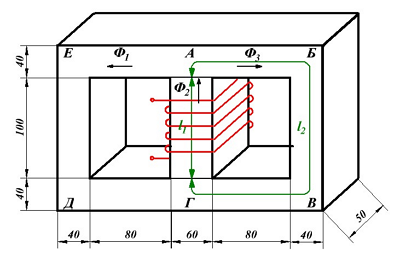
Кроме неразветвленных магнитных цепей часто встречаются разветвлённые магнитные цепи, пример которой представлен на рисунке ниже
Расчёт разветвлённой магнитной цепи (магнитопровода).
В качестве примера рассчитаем количество витков провода N, который намотан на центральном стержне, при котором в крайних стержнях создается магнитная индукция B2 = 1,2 Тл. При этом сила тока, протекающая по виткам провода I = 1 А, а материал магнитопровода – электротехническая сталь.
Первоначально разобьем контур АБВГА на два участка l1 и l2, для который вычислим длину и поперечное сечение
Затем вычислим, какой магнитный поток необходимо создать в правом стержне
Согласно первому закону Кирхгофа для магнитных цепей магнитный поток центрального стержня Φ1 будет равен сумме потоков из крайних стержней. Ввиду того, что данная разветвлённая магнитная цепь является симметричной, то
Тогда магнитная индукция в центральном стержне составит
Теперь определим напряженность магнитного поля по графику зависимости от магнитной индукции:
при В1 = 1,6 Тл, напряженность составит Н1 = 44 А/см = 4400 А/м;
при В2 = 1,2 Тл, напряженность составит Н1 = 10 А/см = 1000 А/м;
В итоге можно рассчитать количество витков провода, необходимых по условию задачи
На сегодня всё, в следующей статье я расскажу о таком явлении как электромагнитная индукция и самоиндукция, а также важнейшем параметре электромагнитных элементов – индуктивности.
Большой практический интерес представляет собой магнитное поле катушки с током. Вообще по своей форме катушка напоминает пружину. Но в то время, если пружина важна в каких-либо механических системах, то катушка используется в магнетизме. Все потому что мы пропускаем электрический ток через катушку и это позволяет получить магнитное поле, сосредоточенное в основном внутри катушки и на её концах.
Посмотрите, как проходят линии магнитного поля внутри и снаружи катушки (рис. 1).
На рис. 1. представлена фотография с изображением формы силовых линий магнитного поля, полученного с помощью железных опилок. Мы видим, что линии поля внутри практически параллельны друг другу и оси катушки. На концах катушки они расходятся.
С другой стороны, в области вне соленоида, вдали от его краёв, железные опилки практически никак не упорядочены, что доказывает, что магнитная индукция там мала — магнитное поле слабое. Напоминает ли вам что-нибудь такое расположение линий магнитного поля? Такое расположение линий магнитного поля обуславливает множество применений катушки в технике.
Магнитные линии магнитного поля катушки с током являются также замкнутыми кривыми. Принято считать, что вне катушки они направлены от северного полюса катушки к южному.
Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
Напомним: характерной величиной магнитного поля является поток вектора магнитной индукции B, который присваивается каждой точке в пространстве. Значение вектора B является мерой «силы» магнитного поля. Удобным и наглядным представлением магнитного поля являются линии поля. Векторы индукции B являются касательными к этим линиям.
На рис. 2 показаны силовые линии, источником которых является катушка, состоящая из пяти витков проводника с электрическим током, а на рис. 3 показаны силовые линии, возникающие из кругового тока. Здесь аналогичный характер линий. Мы предполагаем, что в случае с катушкой мы имеем дело с суммированием полей, исходящих от отдельных катушек, в результате чего внутри катушки образуется почти однородное поле.

Обратите внимание, что чем плотнее (ближе друг к другу) намотаны катушки, тем больше они напоминают круги (окружности), и тогда мы практически имеем дело с сильным и однородным полем внутри катушки. Такое поле показано на рисунке 4. А соответствующая этой фигуре реальная катушка с несколько иным числом витков показана на рис. 5.
На практике мы используем катушки с еще более плотно намотанными витками (см. рисунок 6). Можно использовать даже несколько слоев катушек. Все это делается для того, чтобы получить максимально возможное значение магнитной индукции внутри катушки. Она прямо пропорциональна плотности намотки, т.е. количеству витков на единицу длины катушки.
Для плотно намотанной катушки с малым диаметром по отношению к её длине зависимость магнитной индукции внутри неё выражается следующим образом: B = ( μ0 * μr * I * N ) / L , где
где μ0 — магнитная постоянная, μr — магнитная проницаемость среды внутри катушки, I — значение силы тока, протекающего в обмотке, N — число витков, L — длина катушки.
Из вышеприведенной формулы можно, например, сделать следующий выводы:
- Если выполнить замену имеющейся катушки на другую катушку с бóльшим количеством витков проволоки, то она будет притягивать больше железных предметов при той же силе тока. Это говорит о том, что магнитное действие катушки с электрическим током тем сильнее, чем больше число витков в ней.
- При увеличении силы электрического тока действие магнитного поля катушки с током становится сильнее, при уменьшении — слабее.
- Магнитное действие катушки с током может быть значительно увеличено без изменения числа витков и силы тока протекающего в катушке. Это можно сделать, вставив железный стержень (сердечник) внутрь катушки. Железо, вставленное внутрь катушки, усиливает её магнитное действие. Этот момент в приведенной выше формуле отражает переменная μr.
Обратим внимание на еще один, очень важный аспект магнитного поля, создаваемого катушкой. А именно, сходство силовых линий этого поля с силовыми линиями постоянного магнита в форме стержня. Смотрите рисунки 7а. и 7б., где оба поля показаны символически.
Электромагниты и их применение
Обратите внимание на направление электрического тока в катушке. Согласно правилу правой руки, электрический ток создает магнитное поле, силовые линии которого направлены так же, как у магнита. Таким образом, мы можем назначить магнитные полюса катушке с электрическим током, что и у магнита. Поэтому такую катушку с электрическим током можно назвать электромагнитом.
Важно! Катушка с железным сердечником внутри называется электромагнитом.
Электромагниты находят бóльшее применение в технике, чем постоянные магниты. Это происходит в основном по двум причинам:
- Они создают более сильное магнитное поле, потому что мы можем использовать в них ферромагнитный сердечник, который в 1000-чи раз усилит магнитное поле, создаваемое электрическим током, протекающим в катушке.
- Вы можете управлять ими — увеличивать или уменьшать значение индукции, потому что она прямо пропорциональна электрическому току, протекающему в обмотке.
Отметим широкое применение электромагнитов, которые используются, например, в:
- электрические машины (двигатели и генераторы);
- громкоговорители, реле, контакторы и т.д.;
- магнитные железные дороги;
- устройства, использующие ядерный магнитный резонанс (МРТ). Основной частью МРТ является сверхпроводящий электромагнит, который генерирует очень сильное магнитное поле с индукцией = 3 Тесла. Внутрь этого электромагнита помещается пациент, подлежащий тестированию;
- электромагнитные краны (сталелитейные заводы, верфи, цеха);
- круговые ускорители (например, в ЦЕРНе, где работает сверхпроводящий электромагнит);
- замки для ворот и дверей.
Конечно, не во всех случаях применения электромагнит похож на так называемый стержневой магнит, очень часто он напоминает подковообразный магнит. Например, электромагнит, используемый для подъема железного лома, модель которого показана на рис. 8. или электромагнит, который используется для электрического звонка (рис. 9.).
Наконец, интересный факт. Можно пойти еще дальше и соединить оба конца катушки. Тогда мы получим так называемую тороидальную катушку (см. рис. 10). Это важный компонент электрических систем переменного тока; он служит для хранения энергии магнитного поля и может иметь высокую индуктивность (L).
Список использованных источников
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. Физика 8 / Под ред. Орлова В.А., Ройзена И.И. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- https://ru.wikipedia.org/wiki/Электрический_звонок
Магнитное поле играет очень большую роль в электротехнике и электронике. Без магнитного поля не функционировали бы герконы, электромагнитные реле, соленоиды, катушки индуктивности, дроссели, трансформаторы, двигатели, динамики, генераторы электрической энергии да и вообще много чего.
Природа магнетизма
Согласно одной из легенд, когда-то давным-давно жил в Греции пастух по имени Магнес. И вот шел он как-то со своим стадом овец, присел на камень и обнаружил, что конец его посоха, сделанный из железа, стал притягиваться к этому камню. С тех пор стали называть этот камень магнетит в честь Магнеса. Этот камень представляет из себя оксид железа.
Если такой камень положить на деревянную доску на воду или подвесить на нитке, то он всегда выстраивался в определенном положении. Один его конец всегда показывал на СЕВЕР, а другой — на ЮГ.
Этим свойством камня пользовались древние цивилизации. Поэтому, это был своего рода первый компас. Потом уже стали обтачивать такой камень и делать из разные фигурки. Например, так выглядел китайский древний компас, ложка которого была сделана из того самого магнетита. Ручка у этой ложки всегда показывала на ЮГ.
Ну а далее дело шло за практичностью и маленькими габаритами. Из магнетита вытачивали маленькие стрелки, которые подвешивали на тонкую иглу посередине. Так стали появляться первые малогабаритные компасы.
Древние цивилизации, конечно, не знали еще что такое север и юг. Поэтому, одну сторону магнетита они назвали северным полюсом (North), а противоположный конец — южным (South). Названия на английском очень легко запомнить, если кто смотрел американский мультфильм «Южный парк», он же Сауз (South) парк).
Магнитные линии и магнитный поток
Вокруг магнита экспериментальным путем были обнаружены магнитные силовые линии. Эти магнитные линии создают так называемое магнитное поле.
Как вы могли заметить на рисунке, концентрация магнитных силовых линий на самых краях магнита намного больше, чем в его середине. Это говорит о том, что магнитное поле является более сильным именно на краях магнита, а в его середине практически равна нулю. Направлением магнитных силовых линий считается направление от севера к югу.
Ошибочно считать, что магнитные силовые линии начинают свое движение от северного полюса и заканчивают свой век на южном. Это не так. Магнитные линии — они замкнуты и непрерывны. В магните это будет выглядеть примерно так.
Если приблизить два разноименных полюса, то произойдет притягивание магнитов
Если же приблизить одноименными полюсами, то произойдет их отталкивание
Итак, ниже важные свойства магнитных силовых линий.
- Магнитные линии не поддаются гравитации.
- Никогда не пересекаются между собой.
- Всегда образуют замкнутые петли.
- Имеют определенное направление с севера на юг.
- Чем больше концентрация силовых линий, тем сильнее магнитное поле.
- Слабая концентрация силовых линий указывает на слабое магнитное поле.
Магнитные силовые линии, которые образуют магнитное поле, называют также магнитным потоком.
Итак, давайте рассмотрим два рисунка и ответим себе на вопрос, где плотность магнитного потока будет больше? На рисунке «а» или на рисунке «б»?
Видим, что на рисунке «а» мало силовых магнитных линий, а на рисунке «б» их концентрация намного больше. Отсюда можно сделать вывод, что плотность магнитного потока на рисунке «б» больше, чем на рисунке «а».
В физике формула магнитного потока записывается как
где
Ф — магнитный поток, Вебер
В — плотность магнитного потока, Тесла
а — угол между перпендикуляром n (чаще его зовут нормалью) и плоскостью S, в градусах
S — площадь, через которую проходит магнитный поток, м2
Что же такое 1 Вебер? Один вебер — это магнитный поток, который создается полем индукцией 1 Тесла через площадку 1м2 расположенной перпендикулярно направлению магнитного поля.
Напряженность магнитного поля
Формула напряженности
Слышали ли вы когда-нибудь такое выражение: «напряженность между ними все росла и росла». То есть по сути напряженность — это что-то невидимое, какая-то сдерживающая сила, энергия. Здесь почти все то же самое. Напряженностью магнитного поля также часто называют силой магнитного поля. Напряженность магнитного поля напрямую зависит от плотности магнитного потока и выражается формулой
где
H — напряженность магнитного поля, Ампер/метр
B — плотность магнитного потока, Тесла
μ0 — магнитная постоянная = 4π × 10-7 Генри/метр или если написать по человечески 1,2566 × 10-6 Генри/метр.
PS.
Эта формула работает только тогда, когда между витками катушки находится воздух, либо вакуум. Более крутая формула выглядит вот так.
где
μ — это относительная магнитная проницаемость.
У разных веществ она разная
Напряженность магнитного поля проводника с током
Итак, имеем какой-либо проводник, по которому течет электрический ток.
Для того, чтобы вычислить напряженность магнитного поля на каком-то расстоянии от проводника при условии, что проводник находится в воздушном пространстве либо в вакууме, достаточно воспользоваться формулой
где
H — напряженность магнитного поля, Ампер/метр
I — сила тока, текущая через проводник, Ампер
r — расстояние до точки, в которой измеряется напряженность, метр
Магнитное поле проводника с током
Оказывается, если через какой-либо проводник пропустить электрический ток, то вокруг проводника образуется магнитное поле.
Здесь можно вспомнить знаменитое правило буравчика, но для наглядности я лучше буду использовать правило самореза, так как почти все хоть раз в жизни ввинчивали либо болт, либо саморез.
Ввинчиваем по часовой стрелке — саморез идет вниз. В нашем случае он показывает направление электрического тока. Движение наших рук показывает направление линий магнитного поля. Все то же самое, когда мы начинаем откручивать саморез. Он начинает вылазить вверх, то есть в нашем случае показывает направление электрического тока, а наша рука в этом время рисует в воздухе направление линий магнитного поля.
Также часто в учебниках физики можно увидеть, что направление электрического тока от нас рисуют кружочком с крестиком, а к нам — кружочком с точкой. В этом случае опять представляем себе саморез и уже в голове увидим направление магнитного поля.
Как думаете, что будет если мы сделаем вот такую петельку из провода? Что изменится в этом случае?
Давайте же рассмотрим этот случай более подробно. Так в этой плоскости оба проводника создают магнитное поле, то по идее они должны отталкиваться друг от друга. Но если они хорошо закреплены, то начинается самое интересное. Давайте рассмотрим вид сверху, как это выглядит.
Как вы можете заметить, в области, где суммируются магнитные силовые линии плотность магнитного потока прям зашкаливает.
Соленоид
А что если сделать много-много таких петелек? Взять какую-нибудь круглую бобину, намотать на нее провод и потом убрать бобину. У нас должно получится что-то типа этого.
Если подать постоянное напряжение на такую катушку, магнитные силовые линии будут выглядеть вот так.
Вы только посмотрите, какая бешеная плотность магнитного потока внутри такой катушки! Получается, что от каждой петельки магнитное поле суммируется, что в итоге дает такую плотность магнитного потока. Такую катушку также называют катушкой индуктивности или соленоидом.
Вот также схема, показывающая как магнитные силовые линии складываются в соленоиде.
Плотность магнитного потока зависит от того, какая сила тока проходит через соленоид. Чтобы увеличить плотность магнитного потока, достаточно поверх витков намотать еще больше витков и вставить сердечник из специального материала — феррита.
Если в электрических цепях есть такое понятие, как ЭДС — электродвижущая сила, то и в магнитных цепях есть свой аналог — МДС — магнитодвижущая сила. Магнитодвижущая сила выражается в виде тока, протекающего через катушку из N витков и выражается в Амперах-витках.
где
I — это сила тока в катушке, Амперы
N — количество витков катушки, штуки)
Также советую посмотреть очень простое и интересное видео про магнитное поле.
Похожие статьи по теме «магнитное поле»
Катушка индуктивности
Трансформатор
Электромагнитное реле
Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
→
2.1 Методы расчета магнитных цепей постоянного тока
2.1 Методы расчета магнитных цепей постоянного тока
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
2 Магнитное поле и магнитные цепи при постоянных токах
Расчет магнитных цепей при постоянных токах
Основанием к расчету магнитных цепей служат: первый закон Кирхгофа для магнитных цепей и закон полного тока — второй закон Кирхгофа для магнитных цепей.
Первый закон Кирхгофа для магнитных цепей гласит: алгебраическая сумма магнитных потоков в узле магнитной цепи равна нулю.
Закон полного тока применяется к замкнутому контуру, образованному средними магнитными линиями магнитной цепи и имеет вид:
∫ H → ⋅ dl → = ∑ I⋅w ,
где
∫ H → ⋅ dl → = ∑ H⋅l — падение магнитного напряжения UM = H·l в контуре;
F= ∑ I⋅w — магнитодвижущая сила контура (м. д. с.).
Второй закон Кирхгофа для магнитных цепей сформулируем следующим образом: алгебраическая сумма магнитных напряжений UM = H·l в замкнутом контуре магнитной цепи ( ∑ U M = ∑ H⋅l ) равна алгебраической сумме магнитодвижущих сил F = I·w в том же контуре ( ∑ F = ∑ I⋅w ) :
∑ U M = ∑ F
или
∑ H⋅l = ∑ I⋅w .
Задачи на расчет магнитной цепи могут быть двух видов: прямая задача на расчет магнитной цепи — когда задан поток и требуется рассчитать магнитодвижущую силу (м. д. с.) и обратная задача на расчет магнитной цепи — когда по заданной м. д. с. требуется рассчитать магнитный поток.
В обоих случаях должны быть известны геометрические размеры магнитной цепи и заданы кривые намагничивания ее материалов.
Алгоритм прямой задачи расчета неразветвленной магнитной цепи
Дана конфигурация и геометрические размеры неразветвленной магнитной цепи, кривая (или кривые) намагничивания магнитного материала и магнитный поток или индукция магнитного поля в каком-либо сечении. Требуется найти магнитодвижущую силу, ток или число витков намагничивающей обмотки.
Расчет проводим в соответствии с алгоритмом:
1. Разбиваем магнитную цепь на однородные (из одного магнитного материала) участки постоянного сечения и определяем длины lk и площади поперечного сечения Sk участков. Длины участков (в метрах) берем по средней силовой линии.
2. Исходя из постоянства потока вдоль всей неразветвленной магнитной цепи, по заданному магнитному потоку Ф и сечениям Sk участков находим магнитные индукции на каждом участке:
B k = Ф S k .
Если задана магнитная индукция на каком-либо участке магнитной цепи, то магнитный поток вдоль всей неразветвленной цепи
Ф = Bk·Sk.
3. По найденным магнитным индукциям Bk участков цепи и кривой намагничивания материала k-го участка цепи (например, рис. 2.1, табл. 2.1) определяем напряженности поля Hk на каждом участке магнитной цепи.
Напряженность поля в воздушном зазоре находим по формуле
H возд = B возд μ 0 = B возд 4π⋅ 10 −7 .
4. Подсчитаем сумму падений магнитных напряжений UMk = Hk·lk вдоль всей магнитной цепи ∑ U Mk = ∑ H k ⋅ l k и на основании второго закона Кирхгофа для магнитной цепи приравниваем сумме магнитодвижущих сил Fk = Ik·wk вдоль всей магнитной цепи:
∑ H k ⋅ l k = ∑ I k ⋅ w k .
Основным допущением при расчете является то, что магнитный поток вдоль всей неразветвленной магнитной цепи полагаем неизменным. В действительности не большая часть потока всегда замыкается, минуя основной путь. Этот поток называют потоком рассеяния.
Единицы измерения магнитных величин
B — индукция магнитного поля, Тл (Тесла);
H — напряженность магнитного поля, А/м (Ампер/метр);
Ф — поток индукции магнитного поля, Вб (Вебер);
F = I·w — магнитодвижущая сила (м. д. с.), А (Ампер);
UM = H·l — магнитное напряжение, А (Ампер!).
Константы
μ 0 =4π⋅ 10 −7 Гн/м — магнитная постоянная.
Рис. 2.1 Кривые намагничивания стали и чугуна
Таблица 2.1 — Данные основной кривой намагничивания листовой электротехнической стали Э11
|
B, Вб/м2 |
H, А/м |
|||||||||
|
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
|
0,4 |
140 |
143 |
146 |
149 |
152 |
155 |
158 |
161 |
164 |
167 |
|
0,5 |
171 |
175 |
179 |
183 |
187 |
191 |
195 |
199 |
203 |
207 |
|
0,6 |
211 |
216 |
221 |
226 |
231 |
236 |
241 |
246 |
251 |
256 |
|
0,7 |
261 |
266 |
271 |
276 |
281 |
287 |
293 |
299 |
306 |
312 |
|
0,8 |
318 |
324 |
330 |
337 |
344 |
352 |
360 |
369 |
378 |
387 |
|
0,9 |
397 |
407 |
417 |
427 |
437 |
447 |
458 |
469 |
480 |
491 |
|
1,0 |
502 |
514 |
527 |
541 |
555 |
570 |
585 |
600 |
615 |
631 |
|
1,1 |
647 |
664 |
682 |
701 |
720 |
739 |
759 |
779 |
800 |
821 |
|
1,2 |
843 |
866 |
891 |
918 |
946 |
976 |
1010 |
1040 |
1070 |
1100 |
|
1,3 |
1140 |
1180 |
1220 |
1260 |
1300 |
1340 |
1380 |
1430 |
1480 |
1530 |
|
1,4 |
1580 |
1640 |
1710 |
1780 |
1860 |
1950 |
2050 |
2150 |
2260 |
2380 |
|
1,5 |
2500 |
2640 |
2790 |
2950 |
3110 |
3280 |
3460 |
3660 |
3880 |
4120 |
|
1,6 |
4370 |
4630 |
4910 |
5220 |
5530 |
5880 |
6230 |
6600 |
6980 |
7370 |
|
1,7 |
7780 |
8200 |
8630 |
9070 |
9630 |
10100 |
10600 |
11100 |
11600 |
12200 |
|
1,8 |
12800 |
13400 |
14000 |
14600 |
15200 |
15900 |
16600 |
17300 |
18000 |
18800 |
|
1,9 |
19700 |
20600 |
21600 |
22 600 |
23600 |
24600 |
25600 |
26800 |
28200 |
29600 |
|
2,0 |
31000 |
32500 |
34300 |
36500 |
39000 |
42000 |
45500 |
49500 |
54500 |
59500 |
Примеры пользования таблицей:
1) При B = 0,80 Вб/м2: H = 318 А/м; при B = 0,85 Вб/м2: H = 352 А/м.
2) При B = 1,13 Вб/м2: H = 701 А/м.
Решение задач на расчет магнитных цепей при постоянных токах
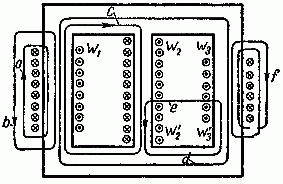
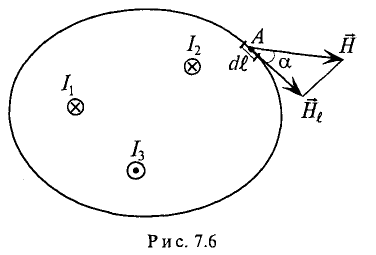
Задача 2.1. На рис. 2.2 изображен разрез трех катушек, по которым проходят токи I1 = 8 А, I2=10 А и I3 = 5 А.
Рис. 2.2
Катушки размещены на стальном сердечнике. Первая катушка (левая) w1 имеет 8 витков, вторая (средняя) w2 — 10 витков и третья (правая) w3 — 6 витков. Определить полную магнитодвижущую силу (м. д. с.) по замкнутым контурам а, b, с, d, е, f, показанным на рис. 2.2. Контур е охватывает катушки w’2 с 4 витками и w’3 с 2 витками.
Изменится ли результат решения задачи, если при тех же данных катушки разместить на сердечнике из другого магнитного материала?
Решение
Воспользуемся законом полного тока. Линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, проходящих сквозь поверхность, ограничиваемую контуром интегрирования,
∫ H → ⋅ dl → = ∑ I⋅w .
Пользуясь законом полного тока, найдем:
∫ a H → ⋅ dl → = w 1 ⋅ I 1 =8⋅8=64 А; ∫ b H → ⋅ dl → =− w 1 ⋅ I 1 =−8⋅8=−64 А; ∫ c H → ⋅ dl → = w 2 ⋅ I 2 − w 1 ⋅ I 1 =10⋅10−8⋅8=36 А; ∫ d H → ⋅ dl → = w 1 ⋅ I 1 − w 2 ⋅ I 2 + w 2 ⋅ I 2 + w 3 ⋅ I 3 =8⋅8+6⋅5=94 А; ∫ e H → ⋅ dl → = w ′ 2 ⋅ I 2 − w ′ 3 ⋅ I 3 =4⋅10+2⋅5=50 А; ∫ f H → ⋅ dl → =2 w 3 ⋅ I 3 =2⋅6⋅5=60 А.
В правой части последнего выражения коэффициент 2 учитывает то обстоятельство, что витки w3 охватываются контуром интегрирования (циркуляции) дважды.
Следует заметить, что при пользовании правилом винта необходимо всегда сопоставлять направление обхода по контуру циркуляции с направлениями токов, пронизывающих поверхность, ограниченную контуром циркуляции.
Результаты решения задачи не изменятся, если катушки разместить на сердечнике из другого магнитного материала, так как м. д. с. определяется только величиной полного тока и не зависит от магнитных свойств вещества.
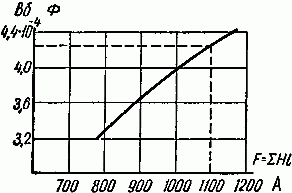
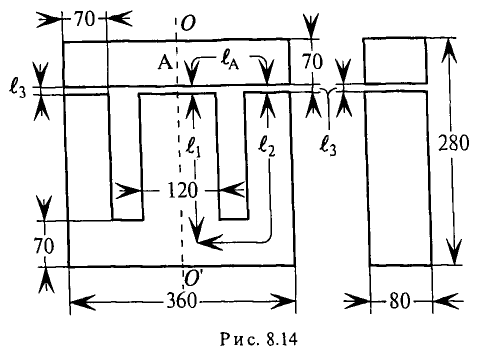
Задача 2.2. Определить магнитодвижущую силу (прямая задача расчета одноконтурной магнитной цепи), необходимую для получения магнитного потока в 5,9·10–4 Вб в кольцеобразном сердечнике, сечением S = 5 см2. Длина средней линии магнитной индукции l = 25 см.
Определить Н (напряженность магнитного поля в сердечнике) и μ r (относительная магнитная проницаемость материала сердечника). Материал сердечника — слаболегированная электротехническая листовая сталь Э11.
Решение
Найдем магнитную индукцию
B= Ф S = 5,9⋅ 10 −4 5⋅ 10 −4 =1,18 Вб м 2 .
По кривой намагничивания для стали Э11 найдем, что индукции B = 1,18 Вб/м2 соответствует H = 800 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H·l = 800·0,25 = 200 А.
Определим абсолютную магнитную проницаемость:
μ a = B H = 1,18 800 =1475⋅ 10 −6 Гн м .
Магнитная проницаемость (относительная магнитная проницаемость)
μ r = μ a μ 0 = 1475⋅ 10 −6 4π⋅ 10 −7 =1175.
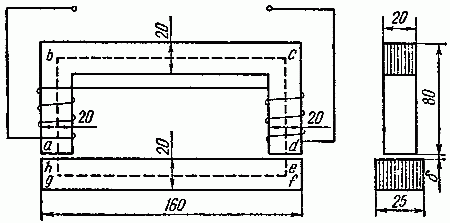
Задача 2.3. На рис. 2.3 изображен электромагнит, сердечник которого изготовлен из слаболегированной листовой электротехнической стали Э11, а якорь — из литой стали.
Рис. 2.3
Какой ток должен быть пропущен через обмотку электромагнита (прямая задача расчета одноконтурной магнитной цепи), состоящую из w = 500 витков, для того, чтобы в якоре была создана магнитная индукция в 0,84 Вб/м2. Размеры на рис. 2.3 даны в миллиметрах. Длина воздушного зазора δ = 1 мм. Площадь сечения воздушного зазора считать равной площади сечения сердечника (пренебрегаем потоком рассеяния). Чему равна статическая индуктивность электромагнита?
Решение
Это пример прямой задачи на расчет магнитной цепи. На рис. 2.3 пунктиром проведена средняя линия магнитной индукции (приближенно). Длина проходящей вдоль сердечника части средней линии магнитной индукции abсd = l1 = 0,28 м. Сечение сердечника S1 = 2·2 = 4 см2 = 4·10–4 м2.
Сечение якоря S2 = 2·2,5 = 5 см2 = 5·10–4 м2, длина проходящей через него части средней линии магнитной индукции efgh = l2 = 0,16 м. Магнитная индукция в якоре B2 = 0,84 Вб/м2 (по условию задачи).
Из условия равенства магнитных потоков в якоре и в сердечнике (одноконтурная магнитная цепь, потоком рассеяния пренебрегаем)
Ф1 = B1·S1 = B2·S2
найдем магнитную индукцию в сердечнике:
B 1 = B 2 ⋅ S 2 S 1 = 0,84⋅5⋅ 10 −4 4⋅ 10 −4 =1,05 Вб м 2 .
Сечение воздушного зазора, длина проходящей в нем части линии магнитной индукции и магнитная индукция равны:
S 3 =4⋅ 10 −4 м 2 ; l 3 =2δ=2⋅ 10 −3 м; B 3 =1,05 Вб м 2 ,
напряженность магнитного поля в воздухе:
H 3 = B 3 μ 0 = 1,05 4π⋅ 10 −7 =84⋅ 10 4 А м .
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F = H1·l1 + H2·l2 + H3·l3.
В целях большей наглядности расчеты удобно свести в таблицу, в которой данные для напряженности магнитного поля в отдельных элементах магнитопровода взяты по соответствующим кривым намагничивания. Так, для сердечника, изготовленного из стали Э11, находим, что индукции B1 = 1,05 Вб/м2 соответствует значение напряженности магнитного поля H1 = 570 А/м, а для якоря, изготовленного из литой стали, имеем, что величине B2 = 0,84 Вб/м2 соответствует значение H2 = 540 А/м.
|
Название участка |
Материал |
S, м2 |
l, м |
B, Вб/м2 |
H, А/м |
H·l, А |
|
Сердечник |
Сталь Э11 |
4·10–4 |
0,28 |
1,05 |
570 |
160 |
|
Якорь |
Литая сталь |
5·10–4 |
0,16 |
0,84 |
540 |
85 |
|
Воздушный зазор |
Воздух |
4·10–4 |
0,002 |
1,05 |
84·104 |
1680 |
F= ∑ H k ⋅ l k =160+85+1680=1925 А.
Искомый ток найдем, пользуясь формулой F = I·w:
I= F w = 1925 500 =3,85 А.
Статическая индуктивность электромагнита равна отношению потокосцепления (полного магнитного потока) к току:
L ст = Ψ I = w⋅Ф I = 500⋅4,2⋅ 10 −4 3,85 =0,053 Гн=053 мГн.
Задача 2.4. Найти магнитную индукцию в якоре электромагнита (обратная задача расчета одноконтурной магнитной цепи), изображенном на рис. 2.3, если на электромагнит намотано w = 250 витков, по которым проходит ток I = 4,4 А. Сердечник изготовлен из листовой электротехнической стали Э11, а якорь — из литой стали. Размеры сердечника и якоря те же, что и в предыдущей задаче. Длина воздушного зазора 0,5 мм. Площадь сечения воздушного зазора считать равной площади сердечника.
Решение
Это пример обратной задачи на расчет магнитной цепи. Для ее решения надо построить кривую зависимости магнитного потока Ф в функции магнитодвижущей силы F и на кривой найти рабочую точку.
Чтобы построить кривую Ф = f (F) будем задаваться различными величинами магнитных потоков Ф, по которым вычисляем соответствующие им значения магнитной индукции B в каждом из участков магнитной цепи. Затем по кривым намагничивания находим напряженность поля H, соответствующую каждому значению индукции B, и, наконец, вычисляем магнитодвижущую силу по второму закону Кирхгофа для магнитной цепи (закону полного тока)
F= ∑ H k ⋅ l k .
Так, например, примем Ф = 3,2·10–4 Вб. Тогда
B серд = Ф S серд = 3,2⋅ 10 −4 4⋅ 10 −4 =0,8 Вб м 2 ; B як = Ф S як = 3,2⋅ 10 −4 5⋅ 10 −4 =0,64 Вб м 2 ; B заз = B серд =0,8 Вб м 2 .
По кривым намагничивания находим напряженности магнитного поля:
H серд =318 А м ; H як =330 А м ; H заз = B заз μ 0 = 0,8 4π⋅ 10 −7 =64⋅ 10 4 А м .
Магнитодвижущая сила
F= H серд ⋅ l серд + H як ⋅ l як + H заз ⋅ l заз = =318⋅0,28+330⋅0,16+64⋅ 10 4 ⋅ 10 −3 =780 А.
Эта магнитодвижущая сила меньше заданной, которая равна
I·w = 4,4·250 = 1100 А.
Аналогично проводим расчеты для больших значений Ф, которые сведены в следующую таблицу:
|
Ф, Вб |
Bсерд, Вб/м2 |
Нсерд, А/м |
lсерд, м |
Bяк, Вб/м2 |
Hяк, А/м |
lяк, м |
Bзаз, Вб/м2 |
Hзаз, А/м |
lзаз, м |
F, А |
|
3,2·10–4 |
0,8 |
318 |
0,28 |
0,64 |
330 |
0,16 |
0,8 |
64·104 |
1·10–3 |
780 |
|
3,6·10–4 |
0,9 |
397 |
0,28 |
0,72 |
400 |
0,16 |
0,9 |
72·104 |
1·10–3 |
895 |
|
4,0·10–4 |
1,0 |
502 |
0,28 На http://www.online-invest.org проекты хайп. |
0,80 |
490 |
0,16 |
1,0 |
80·104 |
1·10–3 |
1020 |
|
4,4·10–4 |
1,1 |
647 |
0,28 |
0,88 |
600 |
0,16 |
1,1 |
88·104 |
1·10–3 |
1160 |
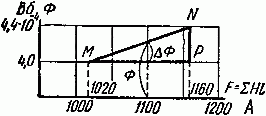
Мы остановились на величине Ф = 4,4·10–4 Вб потому, что для этого значения магнитного потока суммарная магнитодвижущая сила равна 1160 А, что больше заданных 1100 А. По данным расчетов построена кривая Ф = f (F) и на ней определена рабочая точка, которая при F = 1100 А соответствует значению магнитного потока в 4,24·10–4 (рис. 2.4).
Рис. 2.4
Следовательно, искомая индукция в якоре электромагнита
B як = Ф S як = 4,24⋅ 10 −4 5⋅ 10 −4 =0,848 Вб м 2 .
Обычно в технических расчетах значения магнитной индукции округляют до сотых долей Вб/м2 (целые сотни гауссов); поэтому считаем Bяк = 0,85 Вб/м2.
Укажем, что задача могла бы быть решена и другим путем — методом проб: суть его состоит в том, что так же, как и выше, задаются некоторым значением магнитного потока Ф, для которого подсчитывают магнитодвижущую силу F. Если она окажется меньше заданной, то берут большие значения Ф до тех пор, пока не получат F больше заданной величины. После этого значения Ф, соответствующие большим и меньшим против заданного значениям F сужают до тех пор, пока для одного из сечений магнитной цепи полученные значения магнитной индукции будут различаться друг от друга не более чем на 0,1 Вб/м2 (1000 Гс). Искомое значение Ф можно затем найти путем интерполирования.
Так, например, задаемся величиной Ф = 3,2·10–4 Вб, которой соответствует магнитодвижущая сила F = 780 А, что меньше заданного значения Fзад = 1100 А. Теперь зададимся Ф’ = 4,4·10–4 Вб, для которого найдем F’ = 1160 А; это больше заданной величины Fзад. Уменьшаем значение Ф, принимая его, например, равным 4·10–4 Вб; ему соответствует значение F” = 1020 А, что вновь меньше заданной величины магнитодвижущей силы. Итак, при Ф” = 4·10–4 Вб: B”як = 0,8 Вб/м2, а при Ф’ = 4,4·10–4 Вб: B’як = 0,88 Вб/м2.
Таким образом, значения магнитной индукции B в одном из сечений (в данном случае в якоре) отличаются одно от другого менее, чем на 0,1 Вб/м2 (0,88 — 0,8 = 0.08 Вб/м2).
Окончательное значение магнитного потока найдем линейным интерполированием.
Рис. 2.5
Из треугольника MNP (рис. 2.5) имеем:
ΔФ 4,4⋅ 10 −4 −4⋅ 10 −4 = 1100−1020 1160−1020 ,
отсюда
ΔФ=0,23⋅ 10 −4 Вб, а Ф=4⋅ 10 −4 +0,23⋅ 10 −4 =4,23⋅ 10 −4 Вб.
Искомая индукция в якоре
B як = Ф S як = 4,23⋅ 10 −4 5⋅ 10 −4 ≈0,85 Вб м 2 .
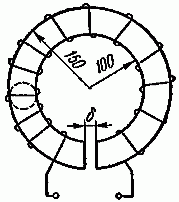
Задача 2.5. Найти магнитную индукцию в воздушном зазоре тороида (обратная задача расчета одноконтурной магнитной цепи), изготовленного из литой стали (рис. 2.6), если на тороид намотано w = 400 витков, по которым проходит ток I = 4 А. Воздушный зазор = 2 мм. Размеры тороида на рисунке даны в мм.
Рис. 2.6
Решение
Задача может быть решена аналогично предыдущей. Мы здесь укажем, как быстрее всего найти первое приближенное значение магнитного потока. Для этого предполагаем, что вся заданная магнитодвижущая сила F = I·w расходуется на ту часть магнитопровода, которая предполагается имеющей наибольшее магнитное сопротивление. Получаемое при этом значение магнитного потока будет завышено по сравнению с фактическим, ибо в расчете не были учтены магнитные сопротивления других участков цепи.
Полагая в нашем случае, что вся магнитодвижущая сила падает на магнитном сопротивлении воздушного зазора, запишем по второму закону Кирхгофа для магнитной цепи (закону полного тока):
F=I⋅w= H возд ⋅δ= B μ 0 ⋅δ,
откуда
B= I⋅w⋅ μ 0 δ = 4⋅400⋅4π⋅ 10 −7 2⋅ 10 −3 =1,0 Вб м 2 .
Так как это значение индукции, как указано выше, явно завышено, проведем новый расчет для меньшего значения магнитной индукции, например, для 0,8 Вб/м2. По кривой намагничивания для литой стали этой индукции соответствует величина напряженности магнитного поля Hст = 490 А/м.
Общая магнитодвижущая сила по второму закону Кирхгофа для магнитной цепи (закону полного тока) при этом будет равна
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,8 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1650 А,
что превышает заданную величину 1600 А.
Теперь проведем расчет для еще меньшей индукции B = 0,7 Вб/м2. Для нее по кривой намагничивания напряженность Hст = 380 А/м. Общая магнитодвижущая сила в этом случае будет
F= H ст ⋅ l ст + H возд ⋅δ=490⋅0,785+ 0,7 4π⋅ 10 −7 ⋅2⋅ 10 −3 =1410 А,
что меньше заданной величины 1600 А.
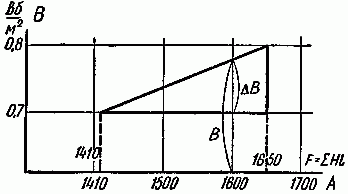
Таким образом, истинная величина индукции находится в пределах от 0,7 до 0,8 Вб/м2. Ее мы найдем интерполированием (рис. 2.7).
Рис. 2.7
Искомая индукция B=0,7+ΔB, где ΔB находится из соотношения
ΔB 0,1 = 1600−1410 1650−1410 = 190 240 ,
откуда
ΔB= 190 240 ⋅0,1≈0,08 Вб м 2 .
Итак, искомая индукция равна 0,78 Вб/м2 (7800 Гс).
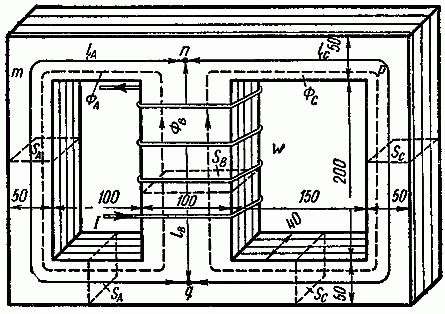
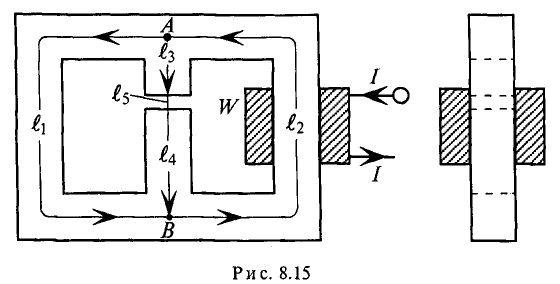
Задача 2.6. Определить все магнитные потоки и ток, проходящий через катушку, расположенную на среднем стержне сердечника, если в левом стержне имеется магнитная индукция в 0,95 Вб/м2. Размеры магнитопровода на рис. 2.8 даны в миллиметрах. Материал сердечника — листовая сталь Э11. Число витков катушки w = 500.
Рис. 2.8
Решение
Покажем на рисунке средние линии магнитной индукции. По данным задачи найдем их длины:
lA = 60 см; lB = 25 см; lC = 70 см.
Задачи на сложную разветвленную несимметричную магнитную цепь решаются на основании первого и второго законов Кирхгофа для магнитной цепи:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
В уравнениях (2) и (3) HA, HB и HC соответственно напряженности магнитного поля в стержнях A, B и C.
Для магнитной индукции в левом стержне BA = 0,95 Вб/м2 по кривой намагничивания для листовой стали найдем HA = 447 А/м.
Из уравнения (3) получим
H C = H A ⋅ l A l C = 447⋅60 70 =384 А м .
По кривой намагничивания находим, что H = 384 А/м соответствует индукция BC = 0,89 Вб/м2.
По уравнению (1) получим
Ф B = Ф A + Ф C = B A ⋅ S A + B C ⋅ S C = =0,95⋅20⋅ 10 −4 +0,89⋅20⋅ 10 −4 =36,8⋅ 10 −4 Вб.
Следовательно,
B B = Ф B S B = 36,8⋅ 10 −4 40⋅ 10 −4 =0,92 Вб м 2 .
Этой индукции по кривой намагничивания соответствует HB = 417 А/м. По уравнению (2) найдем
I·w = HB·lB + HC·lC = 417·0,25 + 384·0,7 = 373 А.
Искомый ток
I= F w = 373 500 ≈0,75 А.
Задача 2.7. Магнитная цепь изготовлена из листовой электротехнической стали Э11. На средний стержень сердечника намотана катушка, содержащая w = 930 витков, по которым проходит ток I = 1 А (рис. 2.8). На всем участке A сечение магнитной цепи считать SA = 20 см2, на участке B — SB = 40 см2, на участке С — SC = 20 см2. Длины средних линий магнитной индукции каждого из участков считать равными: lA = 55 см, lB = 25 см, lC = 80 см.
Найти значения магнитной индукции во всех стержнях.
Решение
Выберем на рис. 2.8 пути средних линий магнитной индукции и запишем уравнения:
для узла n
ФB = ФA + ФC; (1)
для контура npqn
HB·lB + HC·lC = I·w; (2)
для контура npqmn
HC·lC — HA·lA = 0. (3)
Построим кривые зависимостей
ФA = f1 (HA·lA) = f1 (UMnq);
ФB = f2 (I·w — HB·lB) = f2 (UMnq);
ФC = f3 (HC·lC) = f3 (UMnq).
Здесь UMnq — разность скалярных магнитных потенциалов точек n и q, или магнитодвижущая сила между теми же точками.
Для построения кривой f1 задаемся различными величинами магнитных потоков ФA, по которым находим соответствующие им значения магнитной индукции BA, для которых по кривой намагничивания определяем напряженность магнитного поля HA. Беря произведение HA·lA, находим для различных потоков значения магнитных напряжений на участке A. Результаты вычислений сводим в таблицу. Таким же путем производим расчет для построения кривой на участке C. Наконец, для построения кривой f2 (участок B) задаемся значениями ФB и по ним находим BB, HB, HB·lB и разность I·w — HB·lB. Указанные вычисления сведены в таблицу.
|
ФА, 10–4 Вб |
BA, Вб/м2 |
HA, А/м |
HAlA, А |
ФC, 10–4 Вб |
BC, Вб/м2 |
HC, А/м |
HClC, А |
ФB, 10–4 Вб |
BB, Вб/м2 |
HB, А/м |
HBlB, А |
Iw–HBlB, Смотрите на сайте tłumacz Warszawa. Вкусы одноразок. А |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
930 |
|
10 |
0,5 |
171 |
94 |
10 |
0,5 |
171 |
137 |
20 |
0,5 |
171 |
43 |
887 |
|
12 |
0,6 |
211 |
116 |
12 |
0,6 |
211 |
169 |
24 |
0,6 |
211 |
53 |
877 |
|
14 |
0,7 |
261 |
143 |
14 |
0,7 |
261 |
209 |
28 |
0,7 |
261 |
65 |
865 |
|
16 |
0,8 |
318 |
175 |
16 |
0,8 |
318 |
254 |
32 |
0,8 |
318 |
80 |
850 |
|
18 |
0,9 |
397 |
218 |
18 |
0,9 |
397 |
318 |
36 |
0,9 |
397 |
99 |
831 |
|
20 |
1,0 |
502 |
276 |
20 |
1,0 |
502 |
402 |
40 |
1,0 |
502 |
126 |
804 |
|
22 |
1,1 |
647 |
356 |
22 |
1,1 |
647 |
518 |
44 |
1,1 |
647 |
162 |
768 |
|
24 |
1,2 |
843 |
463 |
24 |
1,2 |
843 |
675 |
48 |
1,2 |
843 |
210 |
720 |
|
26 |
1,3 |
1140 |
626 |
26 |
1,3 |
1140 |
913 |
52 |
1,3 |
1140 |
285 |
645 |
|
28 |
1,4 |
1580 |
870 |
28 |
1,4 |
1580 |
1265 |
56 |
1,4 |
1580 |
395 |
535 |
|
30 |
1,5 |
2500 |
1375 |
30 |
1,5 |
2500 |
2000 |
60 |
1,5 |
2500 |
625 |
305 |
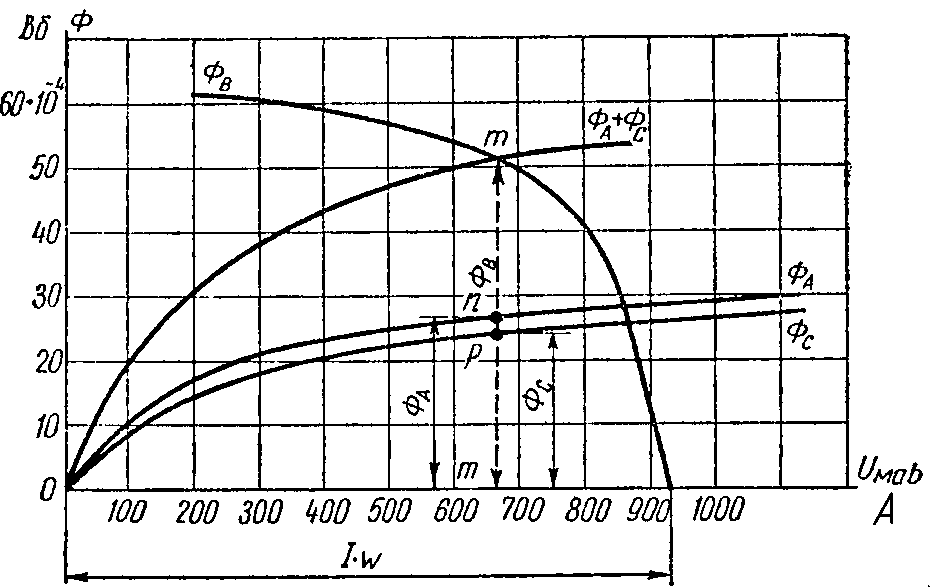
По этим данным построены кривые ФA, ФB, ФC (рис. 2.9).
Рис. 2.9
Так как величины магнитных потоков должны удовлетворять уравнению (1), то проводим еще одну вспомогательную кривую ФB = ФA + ФC; она строится путем суммирования ординат кривых ФA и ФC для одних и тех же значений абсцисс. Точка m ее пересечения с кривой ФB = f2 (I·w — HB·lB) определяет величину искомого потока
ФB = 50,4·10–4 Вб.
Перпендикуляр mm’, опущенный из m на ось абсцисс, пересечет кривую ФA в точке n, а кривую ФC — в точке p, отрезок nm’ выражает искомый магнитный поток в стержне A:
ФA = 26,4·10–4 Вб, а отрезок pm’ — поток ФC = 24·10–4 Вб.
По найденным потокам находим магнитные индукции в каждом из стержней:
B A = Ф A S A = 26,4⋅ 10 −4 20⋅ 10 −4 =1,32 Вб м 2 ; B B = Ф B S B = 50,4⋅ 10 −4 40⋅ 10 −4 =1,26 Вб м 2 ; B C = Ф C S C = 24,0⋅ 10 −4 20⋅ 10 −4 =1,20 Вб м 2 .
Проверка. Можно убедиться, что при найденных значениях магнитных индукций удовлетворяются уравнения (1) — (3). Для этого по кривой намагничивания надо найти для каждого значения B соответствующее значение H и подставить в указанные уравнения.
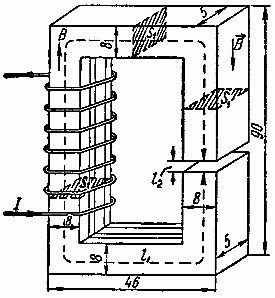
Задача 2.8. Сердечник собран из листов электротехнической стали марки Э11. Форма и размеры сердечника (в мм) указаны на рис. 2.10.
Рис. 2.10
Обмотка имеет w = 400 витков, по которым проходит ток I = 3,5 А. Длина воздушного зазора составляет 1 мм. Определить магнитный поток в сердечнике. При расчете следует считать, что сечение воздушного зазора равно сечению сердечника.
Задачу решить следующими аналитическими методами: а) линейной аппроксимации, б) кусочно-линейной аппроксимации, в) дробно-линейной аппроксимации.
Результаты, полученные для каждого из случаев, сравнить с теми, какие получаются при решении задачи обычным способом.
Решение
Найдем длину средней линии магнитной индукции и сечение стального сердечника (рис. 2.10):
l1 = 2· (90 — 8) + 2· (46 — 8) = 240 мм = 0,24 м;
S1 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Длина средней линии магнитной индукции в воздушном зазоре и его сечение равны:
l2 = 1 мм = 1·10–3 м;
S2 = 8·5 = 40 мм2 = 0,4·10–4 м2.
Решая задачу способом, указанным в решении задачи 2.4, найдем магнитную индукцию B = 1,35 Вб/м2 и соответствующий магнитный поток
Ф = B·S = 1,35·0,4·10–4 = 0,54·10–4 Вб.
а) Расчет магнитной цепи методом линейной аппроксимации кривой намагничивания
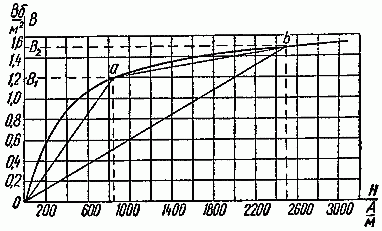
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания прямой линией в некоторой области изменения магнитной индукции. Примем, например, что магнитная индукция изменяется в пределах от нуля до 1,5 Вб/м2. Заменим кривую намагничивания (рис. 2.11) прямой линией 0b.
Рис. 2.11
Ее уравнение B = k1·H, здесь коэффициент k1 равен тангенсу угла наклона прямой 0b к оси абсцисс и выражает приближенное значение абсолютной магнитной проницаемости стали в рассматриваемом интервале
μ a1 = μ r1 ⋅ μ 0 = k 1 = B H = 1,5 2500 =6⋅ 10 −4 Гн м .
Искомый магнитный поток определяем по уравнению:
Ф= I⋅w R M1 + R M2 ,
где
R M1 = l 1 μ a1 ⋅ S 1 = l 1 μ r1 μ 0 ⋅ S 1 ; R M2 = l 2 μ 0 ⋅ S 2 — магнитные сопротивления, соответственно стальной части и воздушного зазора.
Производим вычисления:
R M1 = l 1 μ a1 ⋅ S 1 = 0,24 6⋅ 10 −4 ⋅0,4⋅ 10 −4 =1,0⋅ 10 7 1 Гн ; R M2 = l 2 μ 0 ⋅ S 2 = 1⋅ 10 −3 4π⋅ 10 −7 ⋅0,4⋅ 10 −4 =1,98⋅ 10 7 1 Гн ; Ф= I⋅w R M1 + R M2 = 3,5⋅400 1,0⋅ 10 7 +1,98⋅ 10 7 =0,47⋅ 10 −7 Вб.
Ошибка в сравнении с результатами, полученными обычным способом, составляет
0,54⋅ 10 −4 −0,47⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈13%.
б) Расчет магнитной цепи методом кусочно-линейной аппроксимации кривой намагничивания
Здесь расчет магнитной цепи основан на замене рабочей части кривой намагничивания отрезками прямых линий, например, из двух прямых отрезков 0a и ab (рис. 2.11).
Предполагается, что рабочий режим лежит в области индукций между B1 и B2, соответствующих точкам a и b.
Уравнение прямой ab, выражающей зависимость магнитной индукции от напряженности магнитного поля в стали, имеет вид:
B ст = B 1 + k 2 ⋅ ( H ст − H 1 ), (1)
где k2 — тангенс угла наклона прямой ab с осью абсцисс:
k 2 = B 2 − B 1 H 2 − H 1 . (2)
Напряженность магнитного поля в воздухе может быть выражена следующим образом:
H в = B в μ 0 = Ф μ 0 ⋅ S 2 = B ст ⋅ S 1 μ 0 ⋅ S 2 = B ст μ ′ 0 , (3)
где ради краткости обозначено
μ ′ 0 = μ 0 ⋅ S 2 S 1 . (4)
Подставляя в уравнение (3) вместо Bст его значение из уравнения (1), получим:
H в =[ B 1 + k 2 ⋅ ( H ст − H 1 ) ]⋅ 1 μ ′ 0 . (5)
Для определения Hст воспользуемся уравнением второго закона Кирхгофа для магнитной цепи (законом полного тока)
Hст·l1 + Hв·l2 = I·w. (6)
Подставляя в уравнение (6) значение Нв из уравнения (5), будем иметь:
H ст ⋅ l 1 + B 1 ⋅ l 2 μ ′ 0 + k 2 ⋅ l 2 μ ′ 0 ⋅ ( H ст − H 1 )=I⋅w.
Решая это алгебраическое уравнение относительно Hст, найдем:
H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (7)
где
B ′ = B 1 − k 2 ⋅ H 1 . (8)
Величина магнитной индукции в стали находится путем подстановки найденного значения Hс в уравнение (1):
B ст = μ ′ 0 ⋅ I⋅w⋅ k 2 + B ′ ⋅ l 1 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 , (9)
Для нашей задачи выберем ломаную так, что:
в точке a
B1 = 1,2 Вб/м2, соответствующее H1 = 843 А/м,
в точке b
B2 = 1,5 Вб/м2, соответствующее H2 = 2500 А/м.
По формулам (2), (4), (8), (7) и (1) находим:
k 2 = B 2 − B 1 H 2 − H 1 = 1,5−1,2 2500−843 =18,15⋅ 10 −5 Гн м ; μ ′ 0 = μ 0 ⋅ S 2 S 1 = μ 0 ⋅ 0,4⋅ 10 −4 0,4⋅ 10 −4 = μ 0 =4π⋅ 10 −7 Гн м ; B ′ = B 1 − k 2 ⋅ H 1 =1,2−18,15⋅ 10 −5 ⋅843=1,05 Вб м 2 ; H ст = I⋅w⋅ μ ′ 0 − B ′ ⋅ l 2 μ ′ 0 ⋅ l 1 + k 2 ⋅ l 2 = 3,5⋅400⋅4π⋅ 10 −7 −1,05⋅1⋅ 10 −3 4π⋅ 10 −7 ⋅0,24+18,15⋅ 10 −5 ⋅1⋅ 10 −3 =1470 А м ; B ст = B 1 + k 2 ⋅ ( H ст − H 1 )=1,2+18,15⋅ 10 −5 ⋅ ( 1470−843 )=1,314 Вб м 2 .
И, наконец, искомый поток
Ф = Bст·S1 = 1,314·0,4·10–4 = 0,525·10–4 Вб.
Ошибка по сравнению с обычным способом расчета составляет
0,54⋅ 10 −4 −0,525⋅ 10 −4 0,54⋅ 10 −4 ⋅100%≈3%.
в) Расчет магнитной цепи методом дробно-линейной аппроксимации кривой намагничивания
Дробно-линейная аппроксимация делается посредством уравнения:
B ст = H ст α+β⋅ H ст . (10)
Входящие сюда коэффициенты α и β находятся из известных значений магнитной индукции и напряженности магнитного поля в двух выбранных точках кривой намагничивания, между которыми ожидается действительный режим работы стального участка магнитной цепи.
Для определения Нст поступим следующим образом: из уравнения (10) значение Вст подставим в уравнение (3), тогда получим:
H в = B ст μ ′ 0 = H ст μ ′ 0 ⋅ ( α+β⋅ H ст ) .
Это значение Нв подставим в уравнение (6) второго закона Кирхгофа для магнитной цепи (закона полного тока):
H ст ⋅ l 1 + H ст ⋅ l 2 μ ′ 0 ⋅ ( α+β⋅ H ст ) =I⋅w.
Решая относительно Нст это квадратное уравнение, найдем:
H ст = 1 2 ( I⋅w l 1 − 1+p q )+ 1 4 ( I⋅w l 1 − 1+p q ) 2 + I⋅w q⋅ l 1 . (11)
Второй корень квадратного уравнения, как не имеющий физического смысла, ввиду того что Нст должна выражаться положительным числом, опущен.
В уравнении (11) введены ради краткости обозначения:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α ; q= β α . (12)
Проведем числовые расчеты для нашей задачи, принимая для B и H те числовые значения, какие они имеют на границах рассматриваемого интервала в указанных выше точках a и b. По уравнению (10) имеем:
1,2= 843 α+β⋅843 ; 1,5= 2500 α+β⋅2500 .
Решая эти два уравнения, найдем:
α=213 м Гн ; β=0,581 м 2 Вб .
Далее по формулам (12), (13), (11) и (10) получим:
p= l 2 ⋅ S 1 l 1 ⋅ S 2 ⋅ μ 0 ⋅α = 1⋅ 10 −3 ⋅0,4⋅ 10 −4 0,24⋅0,4⋅ 10 −4 ⋅4π⋅ 10 −7 ⋅α 213=15,6; q= β α = 0,581 213 =2,73⋅ 10 −3 м А ; I⋅w q⋅ l 1 = 3,5⋅400 2,73⋅ 10 −3 ⋅0,24 =2,14⋅ 10 6 А 2 м 2 ; 1 2 ( I⋅w l 1 − 1+p q )= 1 2 ( 3,5⋅400 0,24 − 16,6 2,73⋅ 10 −3 )=−125; H ст = 1 2 ( I⋅w l 1 − 1+p q )+ [ 1 2 ( I⋅w l 1 − 1+p q ) ] 2 + I⋅w q⋅ l 1 = =−125+ 125 2 +2,14⋅ 10 6 =−125+1515=1390 А м ; B ст = H ст α+β⋅ H ст = 1390 213+0,581⋅1390 =1,363 Вб м 2 .
Искомый магнитный поток равен:
Ф = Bст·S1 = 1,363·0,4·10–4 = 0,545·10–4 Вб.
Ошибка в сравнении с обычным методом расчета магнитных цепей составляет:
0,545⋅ 10 −4 −0,54⋅ 10 −4 0,545⋅ 10 −4 ⋅100%≈0,9%.
Отметим, что расчет при помощи дробно-линейной аппроксимации приводит к удовлетворительным результатам даже в тех случаях, когда велико расстояние между граничными точками.

магнитная цепь,
расчет магнитной цепи,
методы расчета магнитных цепей,
решение задач магнитные цепи
Содержание:
Расчет магнитных цепей:
Большинство электротехнических устройств (машины, трансформаторы, реле и др.) основано на использовании магнитного поля. Главной частью этих устройств является магнитная цепь, т. е. совокупность тел, большей частью ферромагнитных, в которых создается магнитный поток намагничивающей силой обмоток, обтекаемых током, или с помощью постоянных магнитов.
Расчет магнитной цепи заключается в установлении связи между магнитным потоком, током в обмотках, числом витков и геометрическими размерами цепи с учетом магнитных свойств материалов, из которых она выполнена. Если магнитная цепь состоит из участков с постоянными сечениями по их длине, применяется приближенный метод, основанный на допущении равномерного распределения потока по сечению магнитной цепи.
Самой простой магнитной цепью этого типа является тороид, средний диаметр которого значительно больше поперечных размеров магнитопровода (см. рис. 1.14). Поток тороида
где F —wl — намагничивающая сила (н. с.), l — длина средней линии, а величина
Подобно направлениям
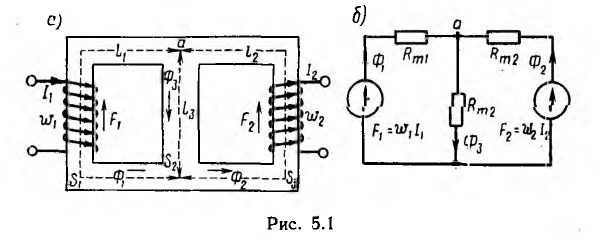
Для разветвленной магнитной цепи, например цепи рис. 5.1, а, могут быть получены зависимости, аналогичные законам Кирхгофа, если заменить токи I на потоки Ф, э. д. с. 
выражает принцип непрерывности магнитного потока. Для контуров по аналогии со вторым законом Кирхгофа
Здесь также должны быть учтены направления Fk и Фk.
Расчетная аналогия между электрическими и магнитными цепями не распространяется на физические процессы. В отличие от э. д. с., которая движет в проводниках элементарные заряды, н. с. движения не вызывает. В соответствии с законом Джоуля — Ленца в электрической цепи происходит непрерывная затрата электрической энергии; постоянное магнитное поле, раз созданное, не требует энергии для своего поддержания. В электрической цепи возможно существование э. д.с. без тока, когда цепь разомкнута, т.е. R =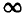
Для магнитных цепей представляет интерес как прямая задача — нахождение потока по заданной н. с., так и обратная задача — определение потребных н. с. по заданному потоку в одном из участков.
Расчет линейных магнитных цепей
В ряде устройств их магнитные цепи работают на практически прямолинейном участке основных кривых намагничивания, т. е. могут рассматриваться как линейные.
В линейной магнитной цепи магнитная проницаемость участков постоянна и, следовательно, их магнитное сопротивление также является величиной постоянной. Решение как прямой, так и обратной задачи требует предварительного определения магнитного сопротивления участков цепи.
Расчет неразветвленной магнитной цепи постоянного сечения выполняется аналогично тороиду ; здесь l — также длина средней линии. Необходимо отметить, что наличие магнитного рассеяния приводит к неравномерному распределению потока вдоль магнитной цепи и расчет крайне затрудняется. В дальнейшем рассматривается только приближенный учет рассеяния.
Если разветвленная магнитная цепь (рис. 5.1, а и 5.2, а) представляет собой соединение призматических или цилиндрических участков, выполненных из материалов с различной ц, вычисление магнитных сопротивлений участков производится однозначно. Если материал всей цепи один и тот же, разделение ее на участки в известных пределах произвольно; средние линии показаны пунктиром.
После определения сопротивлений участков можно весьма наглядно
изобразить магнитную цепь наподобие электрической, как это сделано
на рис. 5.1, б для магнитной цепи рис. 5.1, а с двумя н. с. и на рис. 5.2, б для магнитной цепи рис. 5.2, а с одной н. с.
В таких цепях должны быть указаны положительные направления н. с. и магнитных потоков. Если не все направления известны, ими следует задаться с тем, чтобы в результате расчета определить правильные направления.
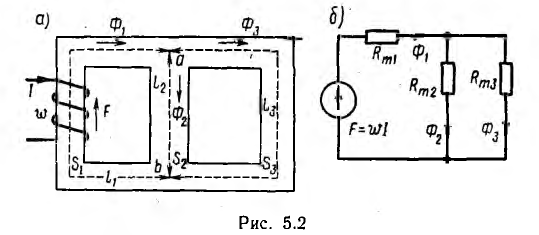
Расчет линейной цепи как для прямой, так и для обратной задачи выполняется подобно расчету электрической цепи аналогичными методами — по зависимостям, аналогичным законам Кирхгофа, методами преобразования магнитных цепей, контурных потоков, наложения, взаимности и узловых магнитных напряжений. Так, для цепи рис. 5.2, пользуясь методом преобразования, можно написать:
Расчет нелинейных магнитных цепей
Неразватвленная нелинейная (ферромагнитная) цепь:
В электротехнике самое широкое применение нашли магнитные цепи из ферромагнитных материалов, так как они имеют относительно малое магнитное сопротивление. Это позволяет при заданном магнитном потоке соответственно уменьшить н. с. при тех же размерах магнитопровода или размеры магнитопровода при той же н. с. Ферромагнитные цепи нелинейны, так как их магнитная проницаемость 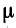
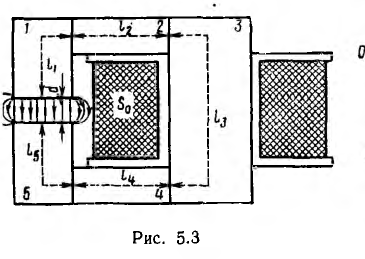
Далее рассматривается наиболее простой, но весьма важный для практики графо-аналитический метод расчета обратной задачи, для неразветвленной магнитной цепи. Пусть задана та индукция Вв, которую надо получить в воздушном зазоре электромагнита с участками магнитопровода, выполненными из разных материалов (рис. 5.3). Требуется найти необходимую н. с.
По заданным размерам магнитопронода проводится средняя линия пути потока во всех участках и определяется длина каждого из них. Длина d воздушного зазора должна быть задана.
Затем определяется полезный поток в воздушном зазоре
где SB — его сечение, принимаемое равным сечению полюсов, т. е. участков l и 5.
Поток Фм в магнитопроводе за счет рассеяния у краев воздушного зазора несколько больше:
Фм = σФВ,
где σ — коэффициент рассеяния; величина его зависит от формы
магнитопровода и лежит в пределах от 1,1 до 1,4.
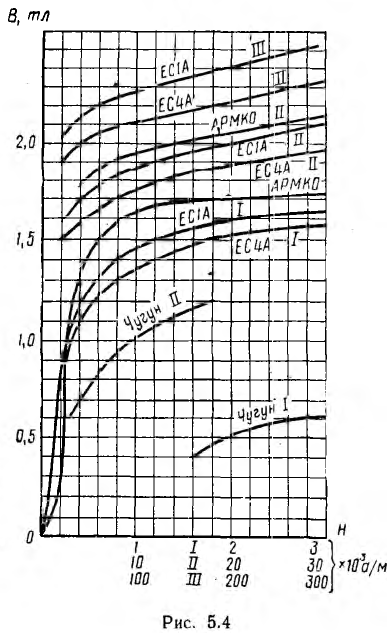
По индукции в каждом из k участков магнитопровода
находят напряженность поля Нк для каждого из участков по основным кривым намагничивания В (Н) соответствующих материалов (рис. 5.4).
Для воздушного зазора напряженность поля
Затем для отдельных участков магнитопровода и для воздушного зазора находят н. с.
и их суммированием — полную н. с. 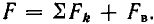
По найденной н. с. и по заданному напряжению U, питающему обмотку, приближенно может быть найдено число витков w. Так как длина витков обмотки различна — внутренних меньше, наружных больше, то расчет начинается с определения длины среднего витка lср по известным размерам магнитопровода и выбранному расположению обмотки. Тогда из закона Ома
(где р — удельное сопротивление материала обмотки) определяется сечение провода
По сортаменту проводов выбирают ближайшее большее сечение Sc провода и определяют сечение провода с изоляцией Sиз. После этого можно найти число витков по отношению площади окна (за вычетом сечения каркаса катушки и пр.) к сечению провода с изоляцией S0
где а — коэффициент заполнения, учитывающий воздушные промежутки, остающиеся между проводами при намотке катушки; его величина лежит в пределах от 0,7 до 0,85 и зависит от формы сечения провода (для круглого меньше, для прямоугольного больше). Затем из приведенного выражения определяется плотность тока в обмотке:
Если полученная плотность тока превышает допустимую по нагреву, то это значит, что размеры магнитной цепи (площадь окна) не позволяют получить заданную индукцию.
Прямая задача расчета этой магнитной цепи — нахождение индукции в воздушном зазоре по заданной н. с. — решается графическим методом. В соответствии с указанной в аналогией, вольтамперным характеристикам U (I) электрических цепей соответствуют ампервеберные характеристики F (Ф) магнитных цепей.
Построение характеристик Fk(Фk) для отдельных участков магнитной цепи производят по кривым намагничивания Вк(Нк) материала участка. Для этого ординаты Вк кривой намагничивания умножают на площадь сечения участка Sk и откладывают BkSk = Фk по оси абсцисс; абсциссы кривой намагничивания Нк умножают на длину участка Iк и откладывают Hklk = Fk по оси ординат.
Для воздушного зазора получается прямая линия, в уравнении которой учитывается, что рассеяние увеличивает реальное сечение потока по сравнению с сечением SB полюсов, примерно в σ раз, т. е. ординаты прямой Вв = 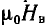
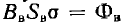
Для магнитной цепи рис. 5.3 по ампервеберным характеристикам отдельных участков (одинаковые участки l и 5, а также 2 и 4 можно объединить), суммированием н. с. F (ординат) для разных значений потока (абсцисс) строится ампервеберная характеристика F (Ф) всей цепи (рис. 5.5).
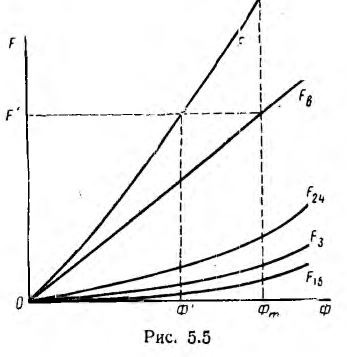
При этом целесообразно начать построение для предельного значения потока Фm, которое можно вычислить для заданной н. с. F’, если пренебречь магнитным сопротивлением магнитопровода по сравнению с магнитным сопротивлением RmB воздушного зазора:
Затем по кривой F(Ф) для заданного значения н. с. F’ находится значение Ф’, а затем искомая индукция в воздушном зазоре
а также индукция в любом участке цепи:
Разветвленная нелинейная (ферромагнитная) цепь
Пренебрегая рассеянием, решается обратная и прямая задачи расчета разветвленной магнитной цепи, изображенной на рис. 5.2, а. Каждый из трех участков этой цепи имеет свое сечение Sk, среднюю длину 1к и выполнен из своего материала. Выбранные направления потоков показаны на рис. 5.2, а.
Пусть в обратной задаче необходимо найти н. с. F, обеспечивающую заданное значение индукции В3 в третьем участке намагничивания поля.
Сначала находят поток Ф3 = B3S3, а по кривой намагничивания В3 (Н3) для материала третьего участка определяют напряженность поля Н3 и н. с. F3 = H3l3. Так как участки 2 и 3 соединены параллельно, то F3 = F2 = H2l2; отсюда вычисляют 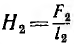
Затем по аналогу первого закона Кирхгофа определяют поток Ф1 = Ф2 + Ф3, индукцию 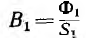
На основании аналога второго закона Кирхгофа искомая н. с. F = F1 + F2.
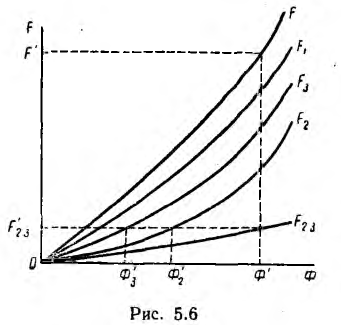
Прямая задача нахождения В3 по заданной н. с. F’ решается построением ампервеберной характеристики всей цепи по характеристикам отдельных участков Fk (Фк) (рис. 5.6), построенных аналогично указанному в п. 1 этого
параграфа. Сначала сложением потоков Ф2 и Ф3 (абсцисс) параллельно соединенных участков для одинаковых значений н. с. (ординат) строят кривую F2з (Ф).
Затем для последовательно соединенных участков l и 2, 3 складывают н. с. (ординаты) F1 и F23, что дает амперментную характеристику F (Ф) всей цепи. По этой кривой для заданной н. с. F’ находят поток Ф ‘, которому на кривой F23(Ф) соответствует н. с. F23 = F3, а для нее по кривой F3(Ф) определяется поток Ф3, откуда искомая индукция
Аналогия с электрическими цепями может быть использована и для расчета более сложных магнитных цепей, например цепей с последовательно параллельным соединением участков, имеющих несколько обмоток с токами (см. рис. 5.1). В этом случае должны быть применены построения, изложенные для электрических цепей, содержащих источники напряжения.
Расчет потоков рассеяния можно выполнить для некоторых простых случаев методами теории электромагнитного поля (см. ч. IV).
Расчет цепи с постоянным магнитом
Постоянные магниты применяются в измерительных приборах, магнето, электрических машинах без возбуждения постоянным током, поляризованных реле, устройствах автоматики и телемеханики и т.д.
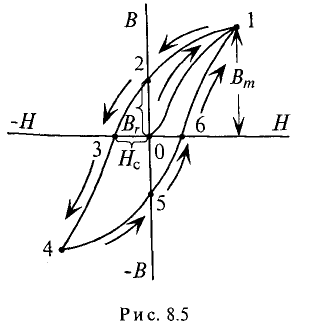
Широкому применению постоянных магнитов способствуют большие успехи, достигнутые мировой техникой в деле изготовления высоко качественных магнитнотвердых материалов, имеющих большую коэрцитивную силу Нс и остаточную индукцию Вr.
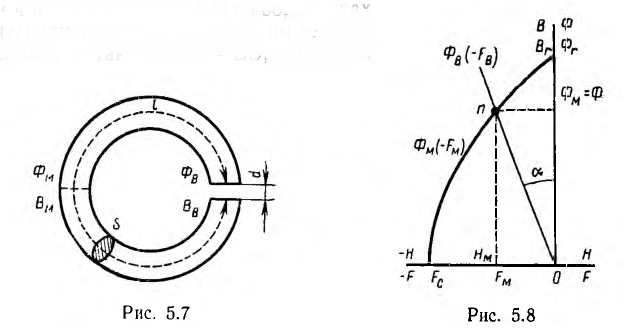
При изготовлении тороидального магнита после снятия с ферромагнитного тороида намагничивающей его обмотки, в нем создают зазор d, получая таким образом постоянный магнит длиной I и сечением 5 (рис. 5 7). Основной характеристикой магнита является часть петли гистерезиса, лежащая во втором квадранте, — кривая размагничивания (рис. 5.8) в координатах В (Н) или пропорциональных им величинах Ф (F), так как Ф = BS, a F= HI.
При отсутствии зазора остаточный поток и индукция в тороиде равны соответственно Ф, и Вг, а напряженность поля Н = 0, так как при отсутствии обмотки с током по закону полного тока
При наличии воздушного зазора также
где FM — н. с. магнита, FB — н. с. воздушного зазора.
Предполагая сохранение однородности поля в магните и зазоре,
Тогда
Магнитное сопротивление при появлении зазора увеличивается.
Из-за этого магнитный поток и индукция должны уменьшиться по сравнению с Ф, и Вг, т. е. рабочая точка на кривой размагничивания должна несколько опуститься, где ей будут соответствовать отрицательные значения н. с. FM и напряженности поля НM в сердечнике магнита.
Из-за постоянства магнитного сопротивления зазора
где SB — сечение зазора; зависимость потока ФB в нем от величины н. с.
FB = RMФв изображается прямой линией, проходящей через начало координат (см. рис. 5.8) и образующей угол а с осью ординат, определяемый соотношением
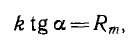
больше зазор d. При пренебрежении рассеянием потоки Фв и Фм равны между собой и рабочая точка п, определяющая искомый поток магнита, лежит на пересечении прямой Фв (— Fв) с кривой размагничивания Фм(—Фм).
Таким образом, поток магнита тем меньше остаточного потока Фr, чем больше зазор d.
Энергия магнитного поля в зазоре, учитывая соотношение между
т. е. равна энергии внутри магнита.
Вопрос о наивыгоднейшем положении рабочей точки n на кривой размагничивания определяется энергетическими соображениями — магнит должен работать в таком режиме, чтобы энергия магнитного поля в зазоре была максимальной.
Эта энергия, пропорциональная в каждой точке кривой размагничивания произведению ее ординаты на ее абсциссу, графически представлена как функция индукции в первом квадранте рис. 5.9, где по оси абсцисс отложена энергия. Для всех магнитнотвердых материалов по данным опыта с достаточной степенью точности можно принять, что рабочая точка m, соответствующая максимуму энергии, лежит на пересечении кривой размагничивания с диагональю прямоугольника, построенного на Вr и Hc.
В технике применяются также магниты сложной формы с неоднородным полем и большим рассеянием, из-за чего их расчет значительно усложняется. В реальных условиях использования постоянного магнита в его зазор вводятся дополнительные детали из магнитномягкого материала.
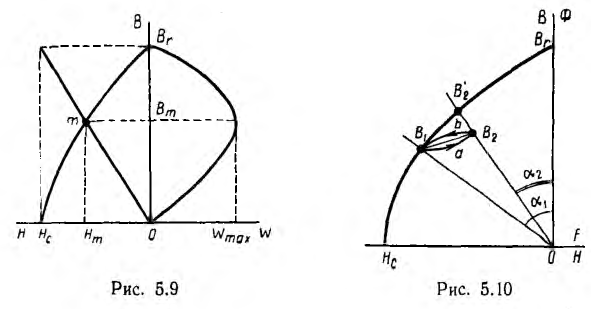
Так, например, в зазоре постоянного магнита в измерительном приборе
магнитоэлектрической системы (см. рис. 2.12) расположены ферромагнитные полюсные наконечники и цилиндрический сердечник.
Введение этих деталей вызывает уменьшение зазора и его магнитного
сопротивления. Магнитным сопротивлением самих деталей можно пренебречь.
Если магниту без деталей соответствовала индукция В1 (рис. 5.10) при 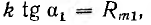
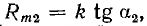
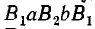
Так ка практически эта петля очень узка, то ее часто заменяют прямой возврата B1B2.
Такие переходы имеют место в электрических машинах с постоянными магнитами, в телефонных индукторах, магнето и т. п. Магнитное сопротивление воздушного зазора этих машин изменяется при вращении ротора, так как последний имеет сложную форму.
Магнитное поле и его параметры
Если магнитную стрелку поместить около проводника, по которому проходит ток, то на стрелку будут действовать силы, заставляющие стрелку установиться в определенном направлении. Если проводник с током вращать вокруг оси, перпендикулярной оси проводника, то и стрелка будет вращаться вместе с проводником.
Пространство, в котором обнаруживается действие сил на магнитную стрелку или ток, называется магнитным полем, магнитное поле создается электрическим током. Следовательно, магнитное поле и электрический ток неразрывно связаны. Магнитное поле не может существовать без электричекого тока.
За направление магнитного поля принимается направление, в котором устанавливается северный конец магнитной стрелки, расположенной в этом магнитном поле.
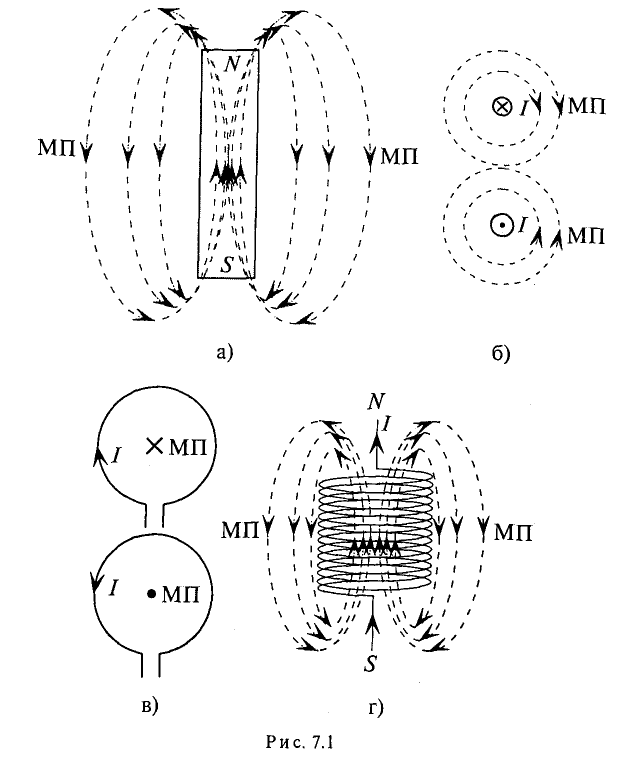
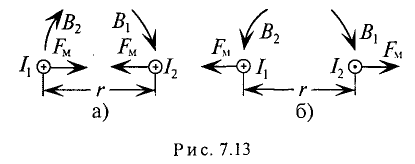
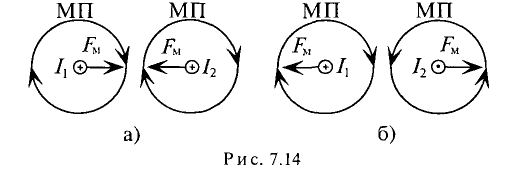
Для наглядности магнитное поле изображается магнитными линиями, которые в отличие от электрических линий всегда замкнуты. В качестве примера на рис. 7.1а приведены магнитные линии постоянного магнита прямоугольной формы.
Направление магнитных линий, т.е. направление магнитного (МП), и направление тока 
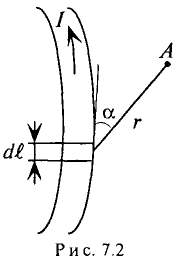
Для кругового тока: если вращательное движение буравчика совпадает с направлением кругового тока, то поступательное движение буравчика при этом указывает направление магнитного поля. Поле кругового тока изображено на рис. 7.1 в.
На рис. 7.1г изображено магнитное поле, созданное током 
В проводнике с током и вокруг него магнитное поле обусловлено этим током. Внутри постоянного магнита или намагниченного тела магнитное поле обусловлено внутренним и внутримолекулярным направленным движением элементарных заряженных частиц.
В атоме любого вещества вокруг ядра направленно, по определенным орбитам вращаются электроны (круговой ток). Следовательно, атомы любого вещества являются элементарными магнитными, которые называются доменами. Домены имеют северный полюс. Полярность домена зависит от направления тока нейтронов вокруг ядра. Направление тока электронов вокруг атома противоположно направлению вращения электрона.
Под влиянием внешних факторов (внешнего магнитного поля) магнитики-домены могут ориентироваться, т. е. поворачиваться в определенном направлении. Ориентация в определенном направлении обуславливает намагничивание. Все материалы обладают различной способностью намагничивания (магнитная проницаемость). Таким образом, намагнитить данный материал — значит сориентировать элементарные магнитики этого материала в определенном направлении, ограниченный материал, как и постоянный магнит, создает внешнее магнитное поле.
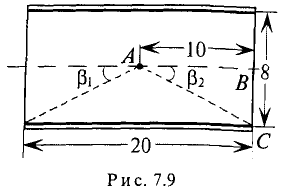
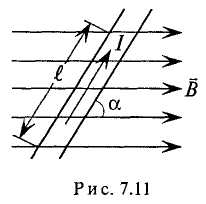
Магнитная индукция
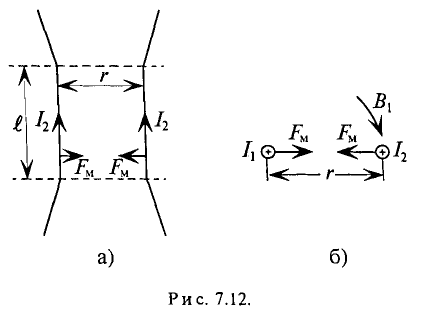
Для характеристики интенсивности магнитного поля вводится понятие магнитной индукции. Магнитная индукция характеризуется силой, действующей на движущийся в магнитном поле электрический заряд (ток). Обозначается магнитная индукция кривой В.
Элементарная магнитная индукция 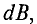
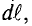
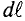
Где: 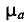
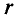
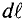
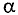
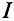
Для определения магнитной индукции В, которая создается всем проводником длиной 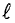
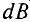
Магнитная индукция – величина векторная. Вектор магнитной индукции в каждой точке магнитного поля направлен по касательной к магнитной линии в этой точке.
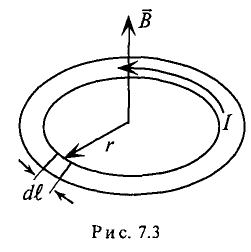
В качестве примера определяется магнитная индукция в центре кольцевого проводника радиусом 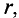
Величина магнитной индукции определяется по выражению (7.2), т.е.
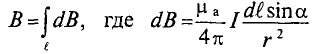
Так как радиус окружности 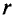
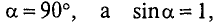
Вынося постоянные величины за знак интеграла, получим
Тогда
Иначе
где 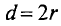
Таким образом, магнитная индукция в магнитном поле пропорциональна величине тока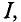
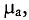
Магнитное поле, магнитная индукция в каждой точке которого нет одинаковое значение и магнитные линии параллельны друг другу, называется однородным.
Основной единицей измерения магнитной индукции является 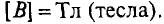
Кроме того, иногда пользуются единицей магнитной индукции:
Магнитная проницаемость
Из выражений (7.1) и (7.3) следует, что магнитная индукция в магнитном поле зависит от абсолютной магнитной проницаемость 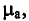
Абсолютная магнитная проницаемость среды характеризует спорность среды намагничиваться. Единицей абсолютной магнитной проницаемости является (из (7.3))
Абсолютная магнитная проницаемость вакуума 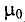
Абсолютную магнитную проницаемость любой среды 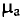
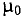
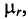
тогда
Иногда 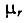
В зависимости от магнитной проницаемости все вещества делятся на диамагнитные, парамагнитные и ферромагнитные.
1. Магнитная проницаемость диамагнитных (противомагнитных) веществ 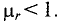
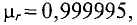
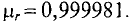
2. Магнитная проницаемость парамагнитных веществ 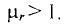
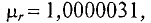
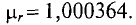
Магнитная проницаемость диамагнитных и парамагнитных материалов – величина постоянная и в технических расчетах принимаются равной единице
3. Магнитная проницаемость ферромагнитных материалов во много раз больше единицы 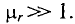
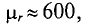
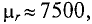
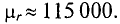
Магнитный поток
Магнитный поток Ф сквозь площадку S, перпендикулярную вектору магнитной индукции 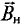
Магнитный поток измеряется в веберах (основная единица):
В практических расчетах встречается единица магнитного потока максвелл, которая в 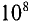
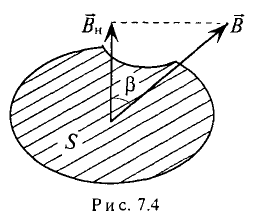
Если вектор магнитной индукции 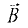
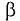
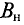
В общем случае при определении магнитного потока через произвольную поверхность в неоднородном магнитном поле площадку S разбивают на бесконечно малые площадки 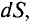
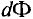
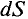
Магнитный поток Ф через всю поверхность площадью S определется суммированием (интегрированием) элементарных магнитных потоков 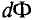
Магнитный поток сквозь замкнутую поверхность равен нулю 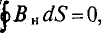
Магнитный поток, как один из параметров магнитного поля, необходимо знать или определять при анализе и расчете режима работы различных электротехнических приборов, устройств и установок (магнитных цепей, электрических машин, трансформаторов, электромагнитов различного назначения, электроизмерительных приборов и др.).
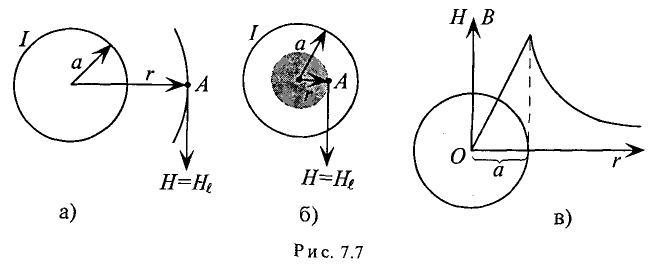
Напряженность магнитного поля
Напряженность в каждой точке магнитного поля — это расчетная величина, характеризующая интенсивность магнитного поля в точке, созданного током, без учета среды, в которой создается поле.
Обозначается напряженность магнитного поля буквой Н. Если в катушку, по которой проходит ток 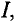
Разница между напряженностью Н и индукцией В в какой-либо точке магнитного поля (хотя обе величины характеризуют интенсивность магнитного поля) заключается в том, что напряженность в точке магнитного поля характеризует интенсивность поля й точке, созданного током без учета магнитной проницаемость среды, в которой создается поле, а индукция в этой точке характеризует интенсивность магнитного поля, созданного током, которая намагничивается и изменяет его интенсивность; т.е напряженность является расчетной величиной, не имеющей физического смысла, так как физически невозможно представить обе, что интенсивность поля не зависит от среды.
Таким образом, соотношение между В и Н в какой-либо точке магнитного поля выглядит следующим образом:
так как 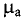
Из выражения (7.8) определяем единицу измерения напряженности в любой точке магнитного поля:
В практических расчетах можно встретить единицу напряженности эрстед (Э).
Напряженность — величина векторная, причем направление вектора напряженности в каждой точке совпадает с направлением магнитного поля в этой точке (касательная к магнитной линии в этой точке).
Если магнитное поле создано несколькими токами, то напряженность в каждой точке этого поля определяется геометрической суммой напряженностей, созданных каждым током в этой точке (рис. 7.5):
Очевидно, для каждой точки магнитного поля напряженность имеет определенную величину и направление.
Закон полного тока
Допустим, что в точке А вектор напряженности Н составляет угол 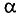
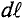
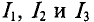
Проекцию вектора напряженности Яна элемент длины контура 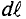
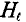
Сумма (интеграл) произведений элементов длины 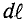
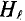
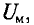
Выражение 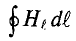
Магнитное напряжение 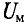
Алгебраическая сумма токов, пронизывающих площадь, ограниченную замкнутым контуром(рис. 7.6), называется полным током сквозь поверхность, ограниченную этим контуром.
Это и есть математическое выражение полного тока для площади, ограниченной контуром (рис. 7.6).
Для определения знака каждого тока (7.10), пронизывающего площадь, ограниченную замкнутым контуром, задаются направлением обхода контура (по или против часовой стрелки). Тогда ток, совпадающий с поступательным движением буравчика, рукоятка которого вращается в заданном направлении обхода контура, в алгебраической сумме берется со знаком «плюс».
Установлено, что магнитное напряжение (магнитодвижущая сила) поля по замкнутому контуру равно полному току, пронизывающему поверхность, ограниченную этим контуром:
Формула (7.11) и есть математическое выражение закона полностью тока.
Если напряженность имеет одинаковую величину по всему контуру и направлена по магнитной линии 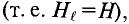
Закон полного тока нашел широкое применение для расчета магнитных цепей, магнитных полей, прямого тока, тока катушки и др.
Магнитное поле прямолинейного проводника с током
Напряженность в каждой точке магнитного поля, созданного током прямолинейного проводника, и индукцию в этой точке легко определить, воспользовавшись законом полного тока. То есть закон полного тока позволяет определить интенсивность магнитного поля (Н и В) в любой точке А магнитного поля, расположенной на расстоянии 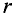
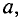
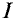
Можно определить Н и В, созданные током 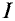
1) вне проводника с током и
2) внутри проводника с током.
1. Напряженность в точке А, расположенной вне проводника с током, т. е. 
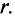
Таким образом, полный ток
Тогда
При этом напряженность 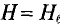
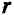
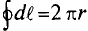
Таким образом, величина напряженности в точке А, расположенной вне проводника, будет равна
Величина магнитной индукции в точке А согласно выражению (7.15)
Если магнитное поле создается в воздухе, т.е. 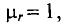
Интенсивность магнитного поля в любой точке А, расположенной проводника с током, обратно пропорциональна расстоянию 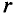
Напряженность в точке А, расположенной внутри проводника с током, 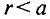
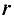
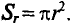
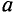
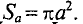
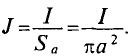
Величина магнитной индукции в той же точке А внутри проводка будет равна ,
Интенсивность магнитного поля в любой его точке, расположенной внутри проводника с током, пропорциональна расстоянию 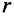
Зависимость интенсивности магнитного поля внутри 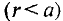
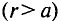
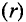
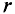
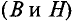
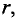
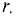
Пример 7.1
По медному проводнику радиусом 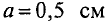
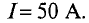
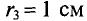
Решение
Вычисление значений Ни В производят по выражениям (7.14), (7.15), (7.17) и (7.18), учитывая, что 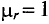
Таким образом, пример 7.1 подтверждает, что наибольшая интенсивность магнитного поля имеет место на поверхности проводника с током. Кроме того, напряженность магнитного поля на поверхности проводника можно определить по формулам (7.14) или (7.17) — результат получается одинаковым.
Магнитное поле кольцевой и цилиндрической катушек
Напряженность магнитного поля кольцевой катушки с числом токов W, по которым проходит ток I (рис. 7.8а), определяется е по закону полного тока.
Точка А находится на окружности радиусом 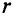
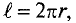
Напряженность поля Н во всех точках замкнутого контура одинакова и направлена по касательной в каждой точке окружности (рис. 7.8а).
Для определения напряженности Н в любой точке этой окружности можно воспользоваться выражением (7.12):
Произведение тока 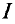
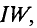
Таким образом, напряженность магнитного поля в любой точке кольцевой катушки определяется ампер-витками 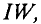
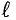
На расстоянии 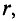
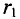
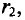
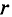
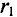
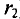
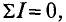
Напряженность в любой точке кольцевой катушки можно определить выражением (7.19), если воспользоваться частью кольцевой катушки длиной 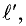
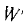
Цилиндрическую катушку (рис. 7.8в) можно рассматривать как часть кольцевой катушки (рис. 7.86) с бесконечно большим радиусом. Поэтому и для цилиндрической катушки справедливо выражение
Используя это уравнение, можно определить напряженность в точке А, расположенной на осевой линии цилиндрической катушки длиной 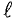
Ошибка в определении напряженности в цилиндрической катушке будет тем меньше, чем больше длина катушки, меньше ее сечение и исследуемая точка лежит ближе к центру цилиндра.
Более точным выражением для определения величины напряженности в точке А на осевой линии цилиндрической катушки является выражение
Величина магнитной индукции в точке А цилиндрической катушки
Пример 7.2
Определить напряженность в точке А на оси катушки (рис. 7.9), если ток в катушке 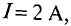
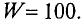
Решение
Определяется напряженность магнитного поля в точке по приближенному выражению:
Для определения напряженности в точке А по более точному напряжению определяется 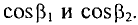
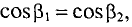
Тогда
Погрешность, полученная при определении напряженности по приближенному выражению:
Электромагнитная сила
В однородное магнитное поле с индукцией В помещен проводник длиной 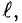
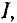
Вокруг проводника с током создается магнитное поле 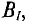
Направление поля 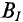
Эта сила 
Направление электромагнитной силы определяется по правилу левой руки:
Левую руку располагают так, чтобы магнитные линии входили в ладонь, вытянутые четыре пальца совпадали с направлением тока в проводнике, тогда отогнутый большой палец укажет направление электромагнитной силы.
Направление электромагнитной силы 
Очевидно, на проводник длиной 
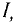
Электромагнитная сила, т. е. сила взаимодействия тока I, проходящего по проводнику длиной 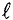
Если же проводник с током 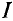
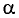
В общем случае для однородного магнитного поля и прямолинейного проводника с током, расположенного в этом поле, величина электромагнитной силы определяется выражением
где 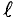
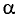
Единица силы ньютон связана с единицей магнитной индукции тесла следующим соотношением:
Если в неоднородное магнитное поле помешен криволинейный проводник с током 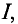
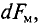
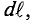
Для вычисления электромагнитной силы, действующей на весь проводник, элементарные электромагнитные силы 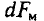
Взаимодействие тока с магнитным полем широко используется электрических машинах, электроизмерительных приборах, тяговых и подъемных электромагнитах, контакторах и др.
Электромагнитные силы приходится учитывать при расчете электрических аппаратов, распределительных устройств электростанций, линий электропередачи, сетей и в других случаях.
Взаимодействие проводников с токами
Параллельное расположение проводников стоками на практике встречается часто, например в линиях электропередачи, при установлении шин распределительных устройств электрических станций и подстанций, в кабелях и др. Для того чтобы правильно выдать провода, шины, изоляторы, на которых они закреплены, приходится определять электромагнитные силы взаимодействия проводников или шин.
Сила взаимодействия проводников с токами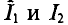
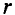
Индукция 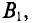
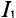
Тогда электромагнитная сила 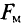
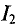
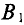
где 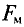
Выражение (7.25) позволяет определить силу взаимодействия двух проводников с током с большой степенью точности, если длина параллельно расположенных проводников 
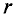
Выражение (7.25) является математическим выражением закона Ампера для определения силы взаимодействия проводников с током.
На практике удобно рассчитывать силу взаимодействия проводников с токами 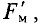
Направление силы взаимодействия двух проводников с током можно определить по правилу левой руки, определив предварительно направление магнитной индукции каждого проводника в центре другого проводника (рис. 7.13).
Определить направление силы взаимодействия двух проводников с токами можно иначе — определив направления магнитных полей каждого проводника по правилу буравчика (рис. 7.14). Как видно на рис. 7.14а, магнитное поле между проводниками ослаблено, а на рис. 7.14б -усилено. Электромагнитные силы направлены в сторону ослабленного поля. В любом из предложенных методов определения направления электромагнитных сил (рис. 7.13 и 7.14) легко увидеть, что при одинаковом направлении взаимодействующих токов проводники притягивается (рис. 7.13а и 7.14а), а при разных направлениях — отталкивается (рис. 7.13б и 7.14б).
Пример 7.3
Определить величину и направление сил, действующих на единицу длины проводов 1, 2, 3 и 4, расположенных на расстояниях, показанных в сантиметрах на рис. 7.15а, если по проводам проходят токи:
Решение
Для решения примера 7.3 необходимо определить расстояние между проводами (1-4) и (2—3), т.е. расстояние 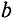
Расстояние между проводами 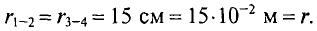
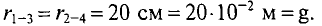
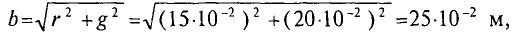
Силы взаимодействия между проводами с указанными токами, приходящиеся на единицу длины этих проводов, определяются выражению (7.26):
При расчете учтено, что 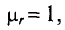
Направления сил взаимодействия указаны на рис. 7.15б.
Магнитные цепи и их расчет
В состав многих электротехнических устройств входят магнитные цепи.
Магнитная цепь представляет собой сочетание тел преимущественно из ферромагнитных материалов, в которых замыкается магнитный поток.
Простейшей магнитной цепью является сердечник кольцевой катушки (рис. 7.8а), в котором замыкается магнитный поток, соединенный током этой катушки. Магнитные цепи трансформатор, электрических машин, измерительных приборов и других электрических аппаратов имеют более сложную форму.
Отдельные участки магнитных цепей могут изготавливаться из различных ферромагнитных материалов различной формы и размеров. Одним из участков магнитной цепи может быть воздушный зазор.
Конструктивно различают неразветвленные и разветвленные магнитные цепи (рис. 8.1).
Характерной особенностью неразветвленной магнитной цепи (рис 8.1а) является то, что магнитный поток Ф, созданный токами моток для всех участков и сечений магнитной цепи, имеет одинаковое значение (как ток в неразветвленной электрической цепи). Для разветвленной магнитной цепи (рис. 8.1б) характерно то, что созданный током магнитный поток Ф разветвляется, при этом его величина определяется алгебраической суммой магнитных потоков в разветвлениях 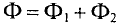
Разветвленная магнитная цепь может быть симметричной или несимметричной. Цепь считается симметричной, если правая и левая ее части имеют одинаковые размеры, выполнены из одинакового материала (включая воздушные зазоры) и действующие в каждой части магнитодвижущие силы 
Магнитные цепи могут быть однородными и неоднородными. Однородная магнитная цепь представляет собой замкнутый сердечник (рис. 7.8а), который по всей длине 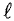
Неоднородная магнитная цепь (рис. 8.1а) состоит из нескольких однородных участков, каждый из которых по всей своей длине имеет одинаковое сечение и выполнен из определенного материала.
На рис. 8.1а изображена неразветвленная неоднородная магнитная цепь, состоящая из трех однородных участков длиной 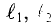
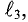
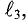
Закон Ома для магнитной цепи
Если по кольцевой катушке с числом витков 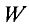
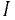
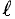
На рис. 7.8а изображена однородная неразветвленная магнитная цепь, сердечник которой по всей длине 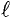
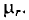
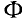
где
Это же уравнение (8.1) можно записать иначе:
где числитель 
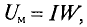
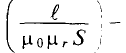
Тогда магнитный поток магнитной цепи
Это и есть математическое выражение закона Ома для разветвленной однородной магнитной цепи, изображенной на рис. 7.8а, т. е. магнитный поток в рассматриваемой магнитной и пропорционален магнитному напряжению 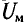
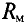
Если неразветвленная цепь неоднородна и на сердечнике имеются две обмотки, т.е. две магнитодвижущие силы и три однородных участка (рис. 8.1а), то закон Ома для такой магнитной цепи:
и иначе:
Как и ток в неразветвленной электрической цепи с несколькими источниками и несколькими сопротивлениями).
В выражениях (8.5) и (8.6) знак «плюс» между магнитными напряжениями ставят тогда, когда обмотки 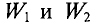
Из выражений (8.3) и (8.5) следует, что наибольшим сопротивлением в магнитной цепи обладает воздушный зазор 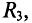
Как видно, законы в магнитной цепи для определения магнитного потока во многих случаях аналогичны законам в электрических цепях для определения электрического тока, что в значительной степени помогает при расчетах магнитных цепей.
Однако пользоваться законом Ома с использованием выражений (8.4) и (8.5) для расчета магнитных цепей не представляется возможным, так как магнитная цепь нелинейная. Нелинейность магнитной цепи обусловлена тем, что магнитное сопротивление ферромагнитных участков магнитной цепи, определяющее магнитный поток, само зависит от магнитного потока.
Тем не менее законы Ома для однородной и неоднородной цепи решают качественную задачу расчета цепей, т. е. зависимость параметров магнитных цепей друг от друга.
Расчет магнитных цепей производится с использованием закона полного тока.
Намагничивание ферромагнитных материалов
Так как ферромагнитный материал является основой магнитных цепей, то для исследования и расчета магнитных цепей необходимо изучить свойства и характеристики ферромагнитных материалов.
Если по катушке с числом витков W, расположенной на замкнутом магнитопроводе длиной 
Если магнитопровод выполнен из неферромагнитного материала, то индукция в магнитном поле магнитопровода
Если же магнитопровод катушки выполнен из ферромагнитного материала, то этот материал намагничивается, т. е. происходит ориентация доменов ферромагнитного материала в направлении внешнего магнитного поля, созданного магнитодвижущей силой катушки IW. Тем самым создается добавочная магнитная индукция 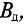
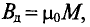
Таким образом, магнитная индукция В в магнитопроводе катушки складывается из двух компонентов — магнитной индукции внешнего поля, созданной МДС катушки 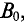
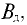
Зависимость магнитных индукций 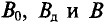
Зависимость 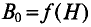
Характер изменения добавляемой индукции 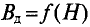
Участок 
Участок 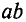
Участок 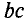
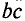
Суммарная кривая 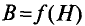
Суммарная кривая 3 зависимости индукции ферромагнитного материала от напряженности магнитного поля 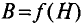
Ферромагнитные материалы относятся к нелинейным средам, поэтому магнитные цепи, в которых они используются, являются нелинейными.
Магнитная проницаемость ферромагнитных материалов – величина непостоянная и зависит от предварительного намагничивания, т. е. от напряженности поля, созданного в материале. Характер этой зависимости представлен кривой 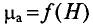
Из выражения (7.7)
Тогда
Если левую и правую части этого уравнения разделить на Н то получается
Из уравнения видно, что изменение 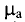
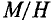
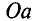
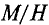
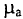
Максимального значения абсолютная магнитная проницаемость 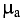
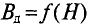
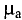
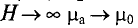
Определить магнитную проницаемость ферромагнитного материала при определенной напряженности Н или индукции В можно, воспользовавшись кривой намагничивания данного ферромагнитного материала:
Циклическое перемагничивание
Изменение тока в катушке (рис. 8.2) и соответственно напряженности Н магнитного поля в ней не только по величине, но и по направлению приводит к изменению индукции в ферромагнитном сердечнике катушки по величине и направлению (рис. 8.5).
Зависимость магнитной индукции В в сердечнике от напряженности Н при изменении тока 
Если в катушке находится полностью размагниченный сердечник, то при токе 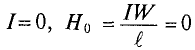
Увеличение тока приводит к увеличению напряженности Н, а следовательно, и индукции В в ферромагнитном материале до насыщения по кривой 0-1, т.е. по кривой намагничивания данного ферромагнитного материала (рис. 8.5). Если уменьшать ток до нуля, то и напряженность Я уменьшается до нуля, а индукция при этом уменьшается от величины 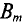
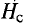
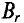
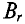
Если изменить направление тока в катушке, а следовательно, и направление напряженности в сердечнике и увеличивать эту напряженность (в обратном направлении), то можно добиться уменьшения индукции до нуля (кривая 2-3), т. е. сердечник полностью размагнитится. Напряженность 0—3, которая потребность для того, чтобы размагнитить ферромагнитный материал, полностью дезориентировать домены, называется задерживающей, или коэрцитивной, силой
Если продолжить увеличение напряженности, то индукция изменит свое направление и ее значение будет увеличиваться в новом направлении от нуля до насыщения по кривой 3-4.
Если уменьшать напряженность до нулевого значения, то ин-уменьшится по кривой 4-5, где отрезок 0-5 – остаточная индукция 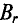
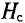
Циклическое перемагничивание имеет место в магнитопроводах (сердечниках) электрических машин, трансформаторов, электроизмерительных приборов, дросселей и др., по обмоткам которых проходит переменный ток.
Циклическое перемагничивание сопровождается затратой электрической энергии, которая преобразуется в тепловую и в большинстве случаев рассеивается в пространстве. Такие тепловые потери относят к магнитным потерям 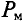
Искусственно циклическое перемагничивание можно применить для размагничивания ферромагнитного материала, т. е. для уменьшения остаточной индукции до нулевого значения. Для этого по катушке, расположенной на магнитопроводе из ферромагнитного материала, пропускают изменяющийся по величине и направлению ток (переменный ток), величину которого постепенно уменьшают до нулевого значения.
Ферромагнитные материалы
Свойства большинства ферромагнитных материалов являются одинаковыми, однако проявляются они по-разному в зависимости от химического состава материала. В этой связи различают две основные группы ферромагнитных материалов: а) магнитно-мягкие и б) магнитно-твердые.
А. Магнитно-мягкие ферромагнитные материалы обладают высокой магнитной проницаемостью 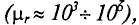
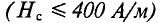
Магнитно-мягкие ферромагнитные материалы легко намагничиваются и размагничиваются.
К магнитно-мягким материалам относятся металлы и сплавы: электролитическое железо, электротехническая сталь, пермаллой, ферриты, магнитодиэлектрики и др.
Железо и электротехническая сталь нашли широкое применение для магнитных цепей электрических машин, аппаратов, трансформаторов, электроизмерительных приборов, т.е. там, где необходимо создать сильное магнитное поле при относительно больших магнитодвижущих силах (IW).
Ферриты и магнитодиэлектрики применяются в качестве магнитопроводов в аппаратуре проводной и радиосвязи, в магнитных удлинителях, вычислительных машинах и других видах техники.
Дермаллой используется при изготовлении сердечников, предназченных для работы в высокочастотных устройствах до 10000 кГц. Магнитные свойства пермаллоев в значительной степени зависят от технологии их изготовления.
Магнитно-твердые ферромагнитные материалы обладают значительной магнитной проницаемостью 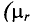
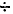
Из магнитно-твердых материалов изготавливаются постоянные магниты, применяемые в технике связи, электроизмерительной сфере и т. п.
Магнитно-твердым материалам, обладающим лучшими магнитными свойствами, относятся такие сплавы, как альни, альнипальнико и др.
Пример 8.1
Определить и изобразить изменение относительной магнитной проницаемости 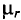
Решение
Результаты расчета заносятся в таблицу 8.1, воспользовавшись живой намагничивания электротехнической стали (Приложение 6) и следующими выражениями:
Расчет неоднородной магнитной цепи
Прямая задача расчета неразветвленной неоднородной магнитной цепи (рис. 8.9) решается в следующей последовательности.
1. По заданному магнитному потоку Ф, который для всех участков неразветвленной цепи имеет одинаковое значение, определяют магнитную индукцию В каждого участка 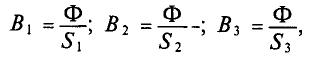
Для прямоугольного сечения (рис. 8.7) 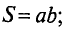
Если задана магнитная индукция какого-либо участка 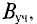
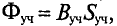
2. По кривым намагничивания материалов (Приложение 5 или 6) определяют напряженности ферромагнитных участков 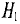
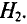
3. Определив длину средней линии каждого участка, по закону полного тока (второй закон Кирхгофа для магнитной цепи) вычисляют намагничивающую силу рассчитываемой магнитной цепи 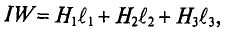
Пример 8.2
Определить число витков обмотки, расположенной на сердечнике из электротехнической листовой стали, размеры которого указаны на рис. 8.9. в см, если по обмотке проходит ток 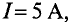
Решение
Магнитная цепь состоит из 3-х однородных участков сечением 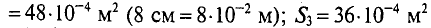
1. По заданному потоку определяется магнитная индукция в каждом однородном участке:
По кривой намагничивания для листовой электротехнической стали (Приложение 5 или 6) определяются напряженности первого – 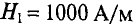
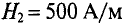
Составляется уравнение по закону полного тока для магнитной цепи: 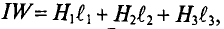
Предварительно вычисляется длина средней линии каждого участка:
- 1.
- 2.
- 3.
Обратная задача расчета неоднородной неразветвленной магнитной цепи, т.е. определение магнитного потока по заданной магнитодвижущей силе (МДС), может быть решена методом последовательных приближений. Для этого задаются несколькими значениями магнитного потока и для каждого из них решают данную задачу расчета магнитной цепи. По результатам расчетов замагничивающих сил для разных магнитных потоков строят зависимость 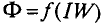
Пример 8.3
Определить магнитный поток в замкнутом сердечнике из листовой электротехнической стали, размеры которого указаны на рис. 8.11 в мм, если на сердечнике расположена обмотка (катушка) с числом витков W= 500, по которой проходит ток 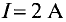
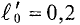
Решение
Сечение сердечника магнитной цепи при указанных размерах будет равно
Длина четырех воздушных зазоров на стыках сердечника:
Длина средней линии сердечника: 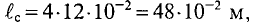
Как видно, длина воздушного зазора 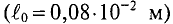
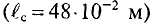
Магнитная цепь в рассматриваемом примере состоит из двух однородных участков — сердечника из листовой электротехнической стали длиной 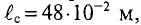
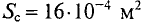
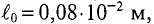
Для выбора одного из магнитных потоков на графике зависимости 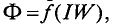
Это предположение обусловлено тем, что сопротивление воздушного зазора 
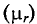
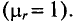
Таким образом по закону Ома для магнитной цепи
Тогда
Магнитный поток
Магнитодвижущая сила (IW), необходимая для создания магнитного потока 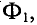
Магнитная индукция в магнитопроводе и воздушном зазоре будет равна
Напряженность магнитного поля в сердечнике из листовой электро-технической стали (Приложение 6)
При этом магнитное напряжение
А напряженность в воздушном зазоре
Магнитное напряжение при этом
Следовательно, магнитодвижущая сила для создания магнитного потока 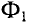
Так как заданные ампер-витки 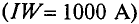
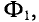
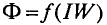
Магнитодвижущая сила для каждого из выбираемых магнитных потоков 
Результаты расчетов заносят в таблицу 8.2 и график 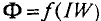
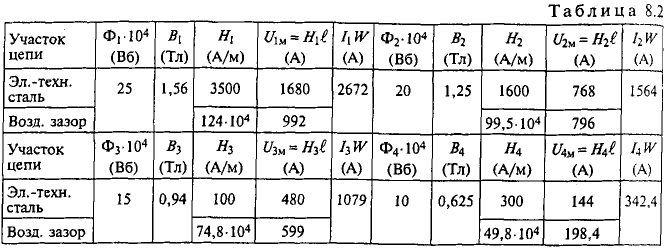
Примечание. Если по таблице 8.2 значение 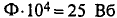
По этому графику определяется магнитный поток Ф, созданный заданными ампер-витками
Как видно (рис. 8.12), заданная 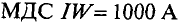
Такой же результат можно получить при расчете той же магнитной цепи графо-аналитическим методом пересечений (рис. 8.13).
Как указывалось выше, магнитная цепь является нелинейной цепью, так как кривая намагничивания любого ферромагнитного материала, из которого состоит магнитная цепь, — кривая линия (см. рис. 8.3 и Приложение 6).
Таким образом, рассматриваемая в примере 8.3 (рис. 8.11) неответвленная магнитная цепь состоит из двух однородных участков. участок, выполненный из листовой электротехнической стали нелинейный участок и воздушный зазор — линейный участок
Следовательно, расчет нелинейной неразветвленной магнитной цепи можно осуществить графо-аналитическим методом пересечений аналогично методу расчета нелинейных неразветвленных электрических цепей постоянного тока (см. рис. 5.36, 5.6, 5.86). я нелинейного участка неразветвленной магнитной цепи строится кривая зависимости Ф =f(Uc) по результатам, полученным при расчете обратной задачи примера 8.3 (таблица 8.2). Кривая зависимости Ф =f(Uc) называется магнитной характеристикой магнитной цепи.
Для построения магнитной характеристики выписываются значения величины магнитного потока Ф и магнитного напряжения ферромагнитных участках 
Согласно второму закону Кирхгофа для магнитной цепи, изображенной на рис. 8.11, в соответствии с законом полного тока:
откуда
где 
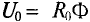
Зависимость (8.10) 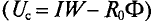
Точка А откладывается на оси абсцисс 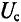
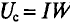
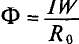
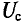
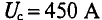
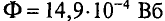
Как видно, результат получился таким же, как при расчете цепи (рис. 8.11) методом последовательных приближений.
Расчет разветвленных магнитных цепей
Расчет симметричной разветвленной магнитной цепи рассматривается на примере 8.4 (прямая задача).
Пример 8.4
На среднем стержне Ш-образного сердечника, выполненного из электротехнической стали Э21 (1311), расположена обмотка с числом витков W=515 (рис. 8.14). Якорь А этой разветвленной магнитной цепи выполнен из стали Э42 (1512). Между якорем А и сердечником находится воздушный зазор 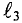
Определить величину тока в обмотке, расположенной на среднем стержне, при котором в якоре А создается магнитная индукция ВА = 1,2 Тл.
Решение
Магнитная цепь по оси симметрии (00′) делится на две равные части. Каждая часть рассчитывается отдельно как неоднородная неразветвленная магнитная цепь. Магнитный поток Ф в каждой части определяется по заданной магнитной индукции в якоре
где
В каждой части (половине) вычисленный магнитный поток зачтен через якорь, воздушные зазоры и участок Ш-образного сердечника.
По вычисленному потоку Ф определяется магнитная индукция в однородных участках.
На участке
На участке
В зазоре бокового стержня
В зазоре среднего стержня
В якоре – ВА= 1,2 Тл.
Напряженность магнитного поля для ферромагнитных участков (Приложение 5):
Напряженность в воздушных зазорах:
3. Величина тока определяется из уравнения, составленного по закону полного тока:
где длина средней линии каждого участка магнитной цепи соответственно равна:
Таким образом, индукцию ВА=1,2 Тл в якоре разветвленной магнитной цепи (рис. 8.14) создает ток 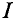
Расчет несимметричной разветвленной магнитной цепи рассматривается на примере 8.5 (прямая задача).
Пример 8.5
Для разветвленной несимметричной магнитной цепи (рис. 8.15) известны длины пяти участков, их поперечные сечения и магнитный поток Ф5 в воздушном зазоре длиной 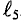
Определить магнитодвижущую силу 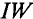
Решение произвести в общем виде. Стрелками указано направление магнитного потока участков цепи.
Решение
Магнитные потоки участков 3, 4 и 5 одинаковы, т. е. 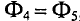
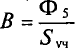
Для участков 3 и 4, выполненных из ферромагнитного материала, по кривой намагничивания определяется напряженность поля, а напряженность в воздушном зазоре определяется по формуле
Магнитное напряжение на участках 3, 4, 5, между точками А и В, определяется соотношением
Такое же магнитное напряжение будет на участке 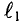
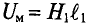
По кривой намагничивания для материала участка определяется индукция 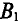
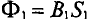
Магнитный поток согласно первому закону Кирхгофа для разветвленной магнитной цепи будет равен
Величина магнитной индукции вычисляется отношением
По кривой намагничивания определяется 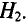
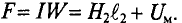
Расчеты всех магнитных цепей произведены с учетом отсутствия рассеяния магнитного потока.
- Цепи переменного тока
- Символический метод расчета цепей
- Четырехполюсники
- Линейные диаграммы
- Индуктивность и ее расчет
- Энергия в электрических цепях
- Линейные электрические цепи
- Нелинейные электрические цепи