Как найти магнитную проницаемость сердечника соленоида

Здравствуйте

Прошу помощи в решении задачи. Чувству, что хожу где-то рядом, но что-то делаю не то. Какая-то формула что ли вылетает…

Условие задачи:
Площадь поперечного сечения соленоида, намотанного на металлический сердечник, S = 1 см2, его длина l = 10 см, диаметр проволки – d = 3мм. Найти магнитную проницаемость μ материала сердечника, если индуктивность соленоида L= 0,44 Гн.

Мое решение:
Индуктивность соленоида определяется по формуле

Вот далее начинаются уже мои рассуждения и домыслы
В данной формуле неизвестных две величины. Число витков N и собственно магнитная проницаемость
Из какого материала выполнен сердечник соленоида не сказано, сказано лишь, что это металл.
Поскольку соотношение l/d = 0,1/0,003 =33 много больше 1, то это позволяет считать соленоид длинным и пользоваться соответствующими ему формулами индуктивности. формула указана выше. Из нее выражаю μ

Пробую найти число витков N. Но его можно найти предположив, что витки намотаны в один слой и прилегают плотно друг к другу. Тогда можно из этого условия найти, что
N = l/d = 0,1/0,003 =33 витка. Подставляем в формулу. И получаем просто невероятный ответ:

Подскажите пож-та, как правильно решить задачу…

Спасибо заранее

Магнитное поле соленоида

Соленоидом
называется совокупность N
одинаковых витков изолированного
проводящего провода, равномерно
намотанных на общий каркас или сердечник.
По виткам проходит одинаковый ток.
Магнитные поля, созданные каждым витком
в отдельности, складываются по принципу
суперпозиции. Индукция магнитного поля
внутри соленоида велика, а вне его –
мала. Для бесконечно длинного соленоида
индукция магнитного поля вне соленоида
стремится к нулю. Если длина соленоида
во много раз больше диаметра его витков,
то соленоид можно практически считать
бесконечно
длинным.
Магнитное
поле такого соленоида целиком сосредоточено
внутри него и является однородным
(рис.6).

Величину
индукции магнитного поля внутри
бесконечно длинного соленоида можно
определить, используя теорему
о циркуляции вектора
:циркуляция
вектора
по произвольному замкнутому контуру
равна алгебраической сумме токов,
охватываемых контуром, умноженной на
магнитную постоянную μ_о:

,
(20)

где
μ₀ =
4π 10^-7
Гн/м.

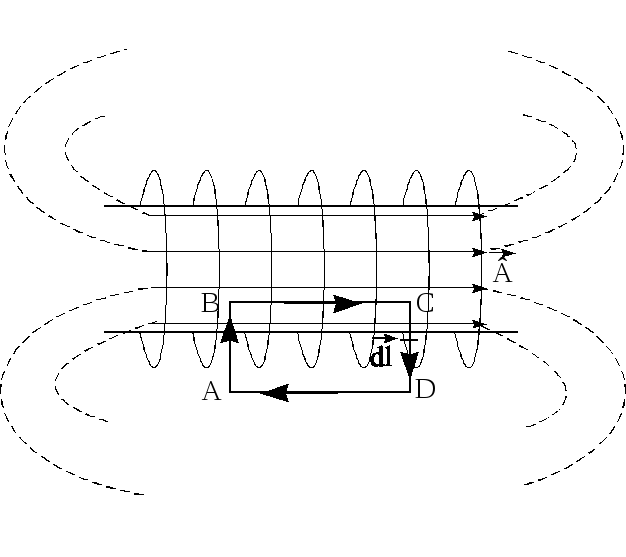
Рис.6.
Магнитное поле соленоида

Для
определения величины магнитной индукции
В внутри соленоида выберем замкнутый
контур ABCD
прямоугольной формы, где
– элемент длины контура, задающий
направление обхода (рис.6). При этом длиныAB
и CD
будем считать бесконечно малыми.

Тогда
циркуляция вектора
по замкнутому контуруABCD,
охватывающему N
витков, равна:

(21)

На
участках AB
и CD
произведение
,
так как вектораивзаимно перпендикулярны. Поэтому

.
(22)

На
участке DA
вне соленоида интеграл,
так как магнитное поле вне контура
равно нулю.

Тогда формула (21)
примет вид:

,
(23)

где
l
– длина участка BC.
Сумма токов, охватываемых контуром,
равна

,
(24)

где
I_c
– сила
тока соленоида; N – число
витков, охватываемых контуром ABCD.

Подставив (23) и
(24) в (20), получим:

. (25)

Из
(25) получим выражение для индукции
магнитного поля бесконечно длинного
соленоида:

.
(26)

Так
как число витков на единицу длину
соленоида n
равно:

(27)

то
окончательно получим:

.
(28)

Если внутрь
соленоида помещен сердечник, то формула
(28) для В примет вид:

.
(29),

где

– магнитная проницаемость материала
сердечника.

Таким
образом, индукция
В магнитного поля соленоида определяется
током соленоида I_c,
числом витком n
на единицу длины соленоида и магнитной
проницаемостью материала сердечника.

Цилиндрический магнетрон

Магнетроном
называется двухэлектродная электронная
лампа (диод), содержащая накаливаемый
катод и холодный анод и помещенная во
внешнее магнитное поле.

Анод
диода имеет форму цилиндра радиусом
.
Катод представляет собой полый цилиндр
радиусом,
вдоль оси которого расположена нить
накала, как правило, изготавливаемая
из вольфрама (рис.7).

Раскалённый
катод в результате явления термоэлектронной
эмиссии испускает термоэлектроны,
которые образуют вокруг катода электронное
облако. При подаче анодного напряжения
(рис.8),
электроны начинают перемещаться от
катода к аноду вдоль радиусов, что
приводит к возникновению анодного тока.
Анодный ток регистрируется миллиамперметром.

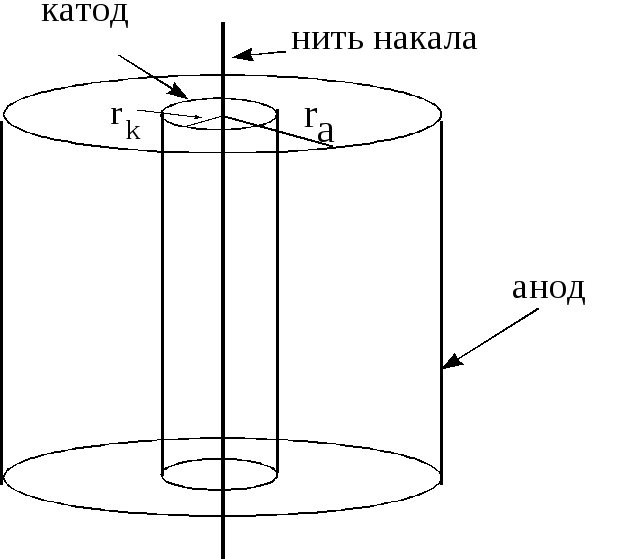
Рис.7.
Схема диода

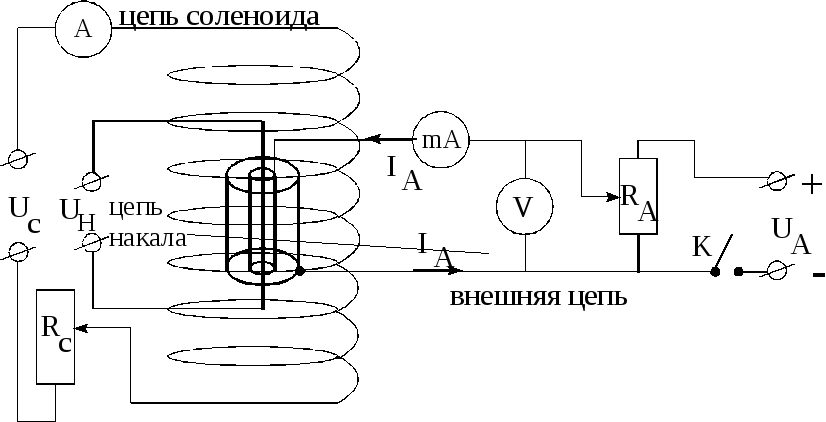Рис.8.
Электрическая схема цепи

Величина
анодного напряжения регулируется
потенциометром R_A.
Чем больше анодное напряжение, тем
большее количество электронов за единицу
времени достигает анода, следовательно,
тем больше анодный ток.

Напряжённость
электрического поля Е между катодом и
анодом такая же, как и в цилиндрическом
конденсаторе:

,
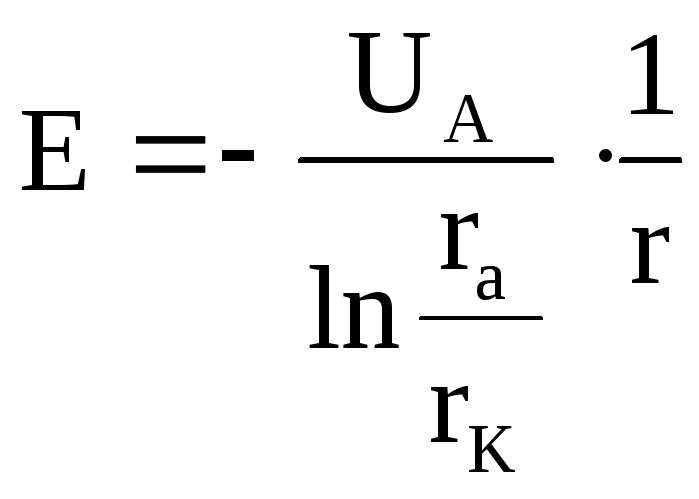(30)

где
r
– расстояние от оси катода до данной
точки пространства между катодом и
анодом.

Из
формулы (30) следует, что напряжённость
поля Е обратно пропорциональна расстоянию
r
до оси катода. Следовательно, напряженность
поля максимальна у катода.

Так как

r_к <<r_a,

(31)

то
значение логарифма ln
стремится к большой величине. Тогда с
увеличением расстояния r
напряженность электрического поля
между катодом и анодом снижается до
нуля. Поэтому, можно считать, что электроны
приобретают скорость под действием
поля только вблизи катода, и дальнейшее
их движение к аноду происходит с
постоянной по величине скоростью.

Внешнее
магнитное поле, в которое помещён диод,
создаётся соленоидом (рис.8). Длина
соленоида l
много больше диаметра его витков, поэтому
поле внутри соленоида можно считать
однородным. Ток в цепи соленоида
изменяется с помощью потенциометра R_C
(рис.8) и регистрируется амперметром.

Характер
движения электронов в зависимости от
величины поля соленоида показан на
рис.9. Если ток в цепи соленоида отсутствует,
то индукция магнитного поля В = 0.
Тогда электроны движутся от катода к
аноду практически по радиусам.

Увеличение
тока в цепи соленоида приводит к
возрастанию величины В. При этом,
траектории движения электронов начинают
искривляться, однако все электроны
достигают анода. В анодной цепи будет
течь ток такой же, как и в отсутствии
магнитного поля.

Рис.9.
Зависимость анодного тока I_A
от величины тока соленоида I_c
в идеальном (1) и реальном (2) случаях, а
также характер движения электронов в
зависимости от величины поля соленоида.

При
некотором значении тока в соленоиде
радиус окружности, по которой движется
электрон, становится равным половине
расстояния между катодом и анодом:

..
(32)

Электроны
в этом случае касаются анода и уходят
к катоду (рис.9). Такой режим работы диода
называется критическим.
При этом по соленоиду течёт критический
ток I_кр,
которому соответствует критическое
значение индукции магнитного поля В =
В_кр.

При
В = В_кр
анодный ток в идеальном случае должен
скачком уменьшиться до нуля. При В > В_кр
электроны не попадают на анод (рис.9), и
анодный ток также будет равен нулю
(рис.9, кривая 1).

Однако
на практике, вследствие некоторого
разброса скоростей электронов и нарушения
соосности катода и соленоида, анодный
ток уменьшается не скачком, а плавно
(рис.9, кривая 2). При этом значение силы
тока соленоида, соответствующее точке
перегиба на кривой 2, считается критическим
I_кр.
Критическому значению тока соленоида
соответствует анодный ток, равный:

,
(33)

где
– максимальное значение анодного тока
при В = 0.

Зависимость
анодного тока I_A
от величины индукции магнитного поля
В (или от тока в соленоиде) при постоянном
анодном напряжении и постоянном накале
называется сбросовой
характеристикой магнетрона.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

      Предлагаемая методика и соответствующая ей программа (MUCalculator.exe) предназначены для измерения и расчета магнитной проницаемости материалов магнитопроводов импульсных блоков питания. Это позволяет использовать магнитопроводы без маркировки или с неизвестной маркировкой.

На страницах сайта и на страницах радиолюбительских журналов опубликовано множество описаний импульсных блоков питания. Один из основных элементов такого устройства — импульсный трансформатор, от правильного расчета которого зависят работоспособность, надежность и долговечность блока и питаемого прибора. В описаниях этих устройств указаны материал и типоразмер магнитопровода, а также намоточные данные трансформатора, поэтому проблем с изготовлением устройства не возникает. А как быть радиолюбителю, который решил повторить устройство, но не может найти нужный магнитопровод? На помощь приходят методики и программы расчета импульсного трансформатора [1, 2]. Зачастую у радиолюбителя накапливаются трансформаторы от различных блоков питания телевизоров, компьютеров и прочей бытовой техники. Если магнитопровод имеет маркировку, то нужную для расчета информацию находят в справочниках [3, 4] или на сайтах в Интернете (особенно для зарубежных ферритов). Эти параметры подставляют в формулы или вводят в программы. Но попадаются магнитопроводы, которые не имеют никаких опознавательных знаков (а если и имеют, то что-либо определить по ним трудно). Предлагаемая методика была разработана именно для таких магнитопроводов.

      Она основана на известной формуле расчета индуктивности тороидальной обмотки

      где L — индуктивность, Гн; w — число витков; µo = 4 pi -10-7 Гн/м — абсолютная магнитная проницаемость вакуума; µ— магнитная проницаемость материала магнитопровода; l — средняя длина магнитной силовой линии в магнито-проводе, м; S—площадь поперечного сечения магнитопровода, м2.
Из (1) получаем формулу для расчета магнитной проницаемости

      Для практических расчетов более удобна формула, полученная из (2), в которой индуктивность выражена в микрогенри, а размеры — в миллиметрах:

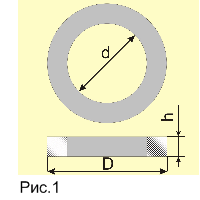
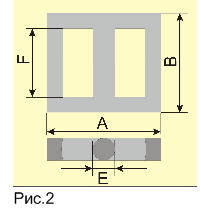
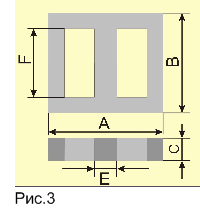
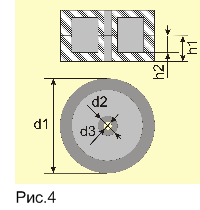
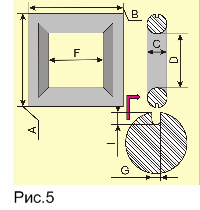
      Кроме индуктивности, для расчета магнитной проницаемости материала магнитопровода нужно еще знать параметры l и S. Следует учесть, что формула (3) приближенная и дает наиболее точный результат для тороидальных (кольцевых) магнитопроводов. Для других типов (Ш-образный, П-образный, броневой), которые имеют разветвленную магнитную цепь, сложно вывести точные формулы, связывающие индуктивность, магнитную проницаемость и размеры магнитопровода. Поэтому расчеты ведут, используя так называемые эквивалентные размеры l и S ([5], с. 20—36), которые подставляют в формулу (3). Для радиолюбительской практики такой точности достаточно. В таблице перечислены формулы для определения l и S для наиболее распространенных типов магнитопроводов [5].

            Работу ведут в определенной последовательности.

      1. На исследуемый магнитопровод наматывают пробную обмотку, например, из 10…20 витков провода диаметром 0,3…0,4 мм (их число и диаметр роли не играют). Важно, чтобы витки равномерно по всей длине разместились на магнитопроводе. Для удобства расчета по формуле (3) лучше намотать 10 витков. Затем измеряют индуктивность пробной обмотки в микрогенри. Если магнитопровод состоит из нескольких частей (Ш-образный, П-образный, броневой), то его нужно сжать, чтобы устранить или минимизировать немагнитный зазор, который уменьшает индуктивность пробной обмотки и занижает вычисленное значение магнитной проницаемости материала. Также следует учесть влияние инструментов, стягивающих болтов и шпилек, поэтому желательно, чтобы они были изготовлены из немагнитных материалов.

      2. Далее из таблицы выбирают тип исследуемого магнитопровода и по соответствующему чертежу делают все необходимые измерения в миллиметрах. Измерять лучше штангенциркулем, чтобы результаты были как можно точнее. Затем по соответствующим формулам вычисляют среднюю длину магнитной линии ? в миллиметрах и площадь поперечного сеченияS в квадратных миллиметрах.

      3. Измеренную в микрогенри индуктивность, число витков w, а также значения l и S подставляют в формулу (3) и определяют магнитную проницаемость материала магнитопровода.

 

      Для упрощения расчетов и экономии времени разработана программа «? -Калькулятор» для ПК, которая по предлагаемой методике рассчитывает магнитную проницаемость магнитопроводов распространенных типов. Программа написана в среде Visual Studio 2008 фирмы Microsoft на языке Visual Basic 2008 ЕЕ. Она также определяет сечение магнитопровода и среднюю длину магнитной линии, которые тоже нужны для дальнейших расчетов импульсного трансформатора. Зная магнитную проницаемость материала магнитопровода, можно по справочникам найти ближайший аналог и определить необходимые параметры (индукцию насыщения, удельные потери и др.).
      Папка с программой может иметь любое удобное имя и храниться на любом носителе или разделе жесткого диска. В ней имеются исполняемый файл MUCalculator.exe и файл справки Help.chm (его можно запустить отдельно, чтобы изучить работу с программой до ее использования).

      После запуска программы MUCalculator.exe открывается ее окно (рис. 6). В его верхней части расположена строка меню, содержащая два пункта: Файл и Справка. Пункт меню Файл состоит из команд: Сохранить — сохраняет текущий расчет в текстовом файле внутри папки с программой, Печать — печатает текущий расчет на системном принтере, Рассчитать — выполняет расчет магнитной проницаемости выбранного магнитопровода, Выход — выход из программы без сохранения текущего расчета. Пункт меню Справка информирует пользователя о программе и ее авторе.
      Часть окна программы ниже строки меню состоит из пяти панелей (рис. 6):

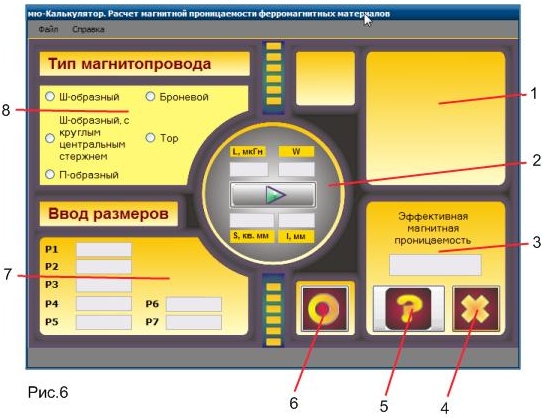
      8 — выбор типа магнитопровода, 7 — ввод его размеров, 1 — вывод изображения чертежа магнитопровода, 2 — расчет, 3 — вывод результата расчета. Последняя панель имеет три кнопки: 6 — очистка полей ввода, 5 — вызов справки, 4 — выход из программы.

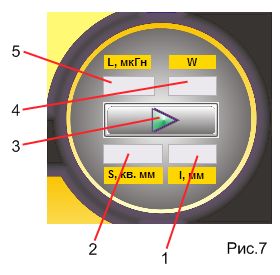
      Панель расчета, показанная с увеличением на рис. 7, содержит элементы: 5 и 4 — поля для ввода индуктивности L и числа витков w пробной обмотки; 3 — кнопка Рассчитать, 2 и 1 — поля для вывода вычисленных значений S и ? .

      На панели выбора типа магнитопровода щелчком левой кнопки мыши выбирают тип исследуемого магнитопровода. После этого в правом верхнем углу панели появляется чертеж выбранного магнитопровода с указаниями необходимых размеров, а также надписи возле полей. Далее как можно точнее измеряют в миллиметрах все необходимые размеры исследуемого магнитопровода и записывают их в соответствующие поля.
      На панели расчета вводят измеренную в микрогенри индуктивность пробной обмотки и число ее витков. При наличии дробной части ее вводят после разделительной точки (не запятой). После ввода всей информации нажимают на кнопку Рассчитать или выполняют команду меню Файл -> Рассчитать. После этого в полях вывода появятся вычисленные значения ? и S, а также ? — магнитной проницаемости материала магнитопровода.

      Для проведения нового расчета нужно очистить все поля нажатием на кнопку Очистить. Для удобства программа показывает всплывающие подсказки при наведении указателя мыши на основные объекты панелей и сообщения об ошибках, если какой-нибудь параметр не введен или введен неверно, с указанием названия этого параметра.
      Распечатку результатов расчета выполняют командой меню Файл—>Печать. По этой команде системный принтер печатает стандартную страницу А4 с результатами текущего расчета и чертежом магнитопровода.
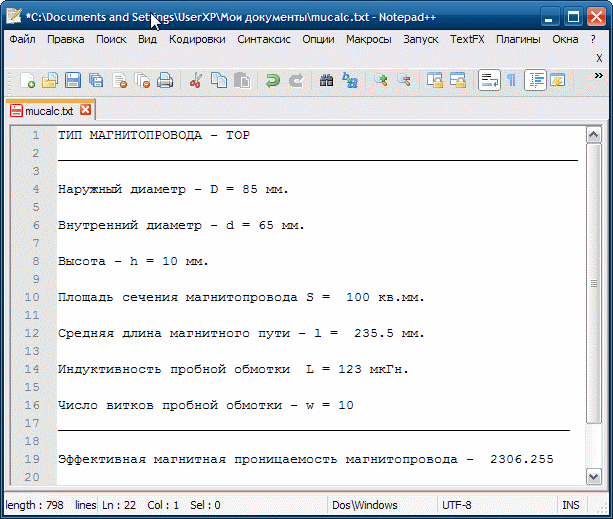
      Для сохранения результатов расчета в текстовый файл следует выполнить команду меню Файл—>Сохранить. При этом откроется стандартное окно сохранения файла. В поле Имя файла нужно ввести имя сохраняемого файла (расширение .txt программа добавляет автоматически) и нажать на кнопку Сохранить. Если файла с таким именем не существует, программа спросит, нужно ли его создать На этот вопрос надо ответить утвердительно (нажать на кнопку ОК). В результате будет создан текстовый файл с информацией об исследуемом магнитопроводе, результатами и датой расчета. Если файл с таким именем существует, программа об этом предупредит и спросит, нужно ли его создать. Если на этот вопрос также ответить утвердительно, программа дописывает новые результаты расчета в конец этого файла, не стирая ранее сделанные записи.
      Сохраненный файл можно прочитать, удалить в нем ненужные записи и распечатать с помощью любого подходящего текстового редактора, например, Notepad++ (рис. 8).

Ю. ИЛИТИЧ, пгт. Верховина Ивано-Франковской обл., Украина

Радио, №4 2011г стр. 30-32

      ЛИТЕРАТУРА
      1. Косенко С. Расчет импульсного трансформатора двухтактного преобразователя Радио, 2005, № 4. с. 35-37, 44.
      2. Москатов Е, Методика и программа расчета импульсного трансформатора двухтактного преобразователя. — Радио, 2006, № 6, с. 35-37
      3. Куневич А. В., Сидоров И. Н. Индуктивные элементы на ферритах. Ферритовые сердечники в узлах радиоаппаратуры. Справочник домашнего мастера. — Л.: Лениздат, 1997.
      4. Сидоров И. Н., Христинин А. А., Скорняков С. В. Малогабаритные магнитопрово-ды и сердечники. — М.: Радио и связь, 1989.
      5. Гликман И. Я., Русин Ю. С, Горский А. Н. Электромагнитные элементы радиоэлектронной аппаратуры. Справочник. — М.: Радио и связь, 1991.

СКАЧАТЬ ПРОГРАММУ

      Программа для определения проницаемости проверялась на WIN XP SP3, необходим Net framework 3.0

Решение:
На проводник действуют: две одинаковые силы натяжения нитей Т, сила тяжести mg и сила

со стороны магнитного поля, где α — угол между направлениями тока I и магнитной индукции (в нашем случае α = 90° и sinα = 1). Подразумевается, что направления тока и магнитной индукции таковы, что сила F направлена вниз (рис. 140). В противном случае силы натяжения нитей при пропускании тока не возрастают, а уменьшаются, и нити не оборвутся.
Если проводник находится в равновесии, то

отсюда

Для разрыва одной из нитей необходимо выполнение условия

или

6 На прямой проводник длины l=0,5 м, расположенный перпендикулярно к линиям индукции магнитного поля, действует сила F=0,15 Н. Найти ток I, протекающий в проводнике, если магнитная индукция B = 20 мТл.

Решение:
Если проводник расположен перпендикулярно к направлению магнитной индукции, то F=BIl, где I-ток в проводнике; отсюда I=F/Bl=15 А.

7 Между полюсами магнита подвешен горизонтально на двух невесомых нитях прямой проводник длины l=0,2 м и массы m=10 г. Индукция однородного магнитного поля B = 49 мТл и перпендикулярна к проводнику. На какой угол α от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток I=2 А?

Решение: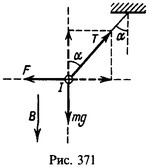
На проводник действуют: силы натяжения двух нитей Т, сила тяжести mg и сила F=BIl со стороны магнитного поля (рис. 371). При равновесии проводника суммы проекций сил (с учетом их знаков) на вертикальное и горизонтальное направления равны нулю:

отсюда

8 Найти напряженность Н и индукцию B магнитного поля прямого тока в точке, находящейся на расстоянии r=4м от проводника, если ток I=100 А.

Решение:

9 ГОСТ 8.417—81 дает такое определение единицы силы тока — ампера: «Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожной малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длины 1 м силу взаимодействия, равную ». Исходя из этого определения, вычислить магнитную постоянную mo.

Решение:
Вокруг бесконечно длинного прямолинейного проводника, по которому течет ток I1 образуется магнитное поле, напряженность которого на расстоянии r от проводника

а индукция

При этом векторы Н и В направлены одинаково и лежат в плоскости, перпендикулярной к проводнику. На отрезок второго проводника длины l, по которому течет ток I₂, магнитное поле действует с силой

где α — угол между направлениями отрезка проводника и магнитной индукции. Так как второй проводник параллелен первому, то α = 90° и sinα = 1. Таким образом,

Подставив значения

найдем

10 Индукция однородного магнитного поля B=0,5 Тл. Найти магнитный поток через площадку S=25 см², расположенную перпендикулярно к линиям индукции. Чему будет равен магнитный поток, если площадку повернуть на угол α = 60° от первоначального положения?

Решение: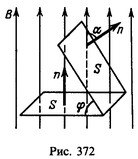
На рис. 372 показано направление магнитной индукции и положение площадки в обоих случаях. По определению магнитный поток

где α — угол между нормалью n к площадке и направлением магнитной индукции В. В первом случае

во втором случае α=φ (углы с взаимно перпендикулярными сторонами) и

11 Найти магнитную индукцию и магнитный поток через поперечное сечение никелевого сердечника соленоида (рис. 141), если напряженность однородного магнитного поля внутри соленоида H=25 кА/м. Площадь поперечного сечения сердечника S=20 см², магнитная проницаемость никеля μ = 200.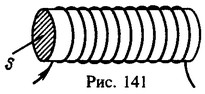

Решение:

12 Магнитный поток через поперечное сечение катушки, имеющей n=1000 витков, изменился на величину ΔФ = 2 мВб в результате изменения тока в катушке от I₁ = 4 А до I₂ = 20А. Найти индуктивность L катушки.

Решение:

13 Виток площади S = 2 см² расположен перпендикулярно к линиям индукции однородного магнитного поля. Найти индуцируемую в витке э.д.с, если за время Δt = 0,05 с магнитная индукция равномерно убывает от B₁=0,5Тл до В₂ = 0,1 Тл.

Решение:

14 Какой магнитный поток пронизывал каждый виток катушки, имеющей n =1000 витков, если при равномерном исчезновении магнитного поля в течение времени Δt = 0,1 с в катушке индуцируется э.д.с. ε = 10 В?

Решение:

15 Рамка в форме равностороннего треугольника помещена в однородное магнитное поле с напряженностью H=64кА/м. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 30°. Найти длину стороны рамки а, если в рамке при выключении поля в течение времени Δt = 0,03 с индуцируется э. д. с. ε = 10 мВ.

Решение:
Начальный магнитный поток через рамку

где
площадь рамки и B=µ₀H-магнитная индукция. Конечный магнитный поток Ф₂=0. Изменение магнитного потока

Э.д.с. индукции

отсюда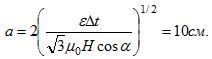


16 Квадратная рамка со стороной а=10см помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 60°. Найти магнитную индукцию В этого поля, если в рамке при выключении поля в течение времени Δt = 0,01 с индуцируется э.д.с. ε = 50 мВ.

Решение:

17 Плоский виток площади S= 10 см² помещен в однородное магнитное поле перпендикулярно к линиям индукции. Сопротивление витка R=1 Ом. Какой ток I протечет по витку, если магнитная индукция поля будет убывать со скоростью ΔB/Δt = 0,01 Тл/с?

Решение:

18 Плоский виток площади S= 10 см² помещен в однородное магнитное поле с напряженностью H=80 кА/м, перпендикулярное к линиям индукции. Сопротивление витка R = 1 Ом. Какой заряд протечет по витку, если поле будет исчезать с постоянной скоростью?

Решение:

19 Какова индуктивность катушки с железным сердечником, если за время Δt = 0,5 с ток в цепи изменился от I₁ = 10 А до I₂ = 5 А, а возникшая при этом э.д.с. самоиндукции ε = 25 В?

Решение:
Э.д.с. самоиндукции

отсюда

20 Проводник длины l=2 м движется в однородном магнитном поле со скоростью v = 5 м/с, перпендикулярной к проводнику и линиям индукции поля. Какая э. д. с. индуцируется в проводнике, если магнитная индукция B=0,1 Тл?
Решение: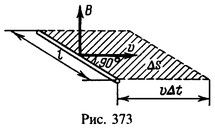
Э.д.с. индукции

магнитный поток через площадь ΔS, «заметаемую» проводником за время Δt (рис. 373). Опуская знак минус, найдем

21 Самолет летит горизонтально со скоростью v = 900 км/ч. Найти разность потенциалов, возникающую между концами крыльев самолета, если вертикальная составляющая индукции земного магнитного поля Bo = 0,5 мкТл и размах крыльев самолета l=12 м.

Решение:
Крылья самолета за время Δt «заметают» площадь

Магнитный поток через эту площадь равен

где

вертикальная составляющая индукции земного магнитного поля (α — угол между вертикалью и направлением магнитной индукции). Разность потенциалов V между концами крыльев самолета равна э.д.с. ε, индуцируемой в металлических крыльях и корпусе самолета при его движении в магнитном поле Земли:

22 С какой скоростью должен двигаться проводник длины l=10 см перпендикулярно к линиям индукции однородного магнитного поля, чтобы между концами проводника возникла разность потенциалов V=0,01 В? Скорость проводника составляет с направлением самого проводника угол α = 30°. Линии индукции перпендикулярны к проводнику, индукция B = 0,2 Тл.

Решение: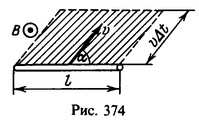
Площадь, «заметаемая» за время Δt проводником, скорость которого v направлена под углом а к самому проводнику, представляет собой площадь параллелограмма (рис.374):

Магнитный поток через эту площадь

Разность потенциалов V между концами проводника равна э.д.с. ε, индуцируемой в этом проводнике:

23 Какой ток идет через гальванометр, присоединенный к железнодорожным рельсам, при приближении к нему поезда со скоростью v = 60 км/ч? Вертикальная составляющая индукции земного магнитного поля Bо=50 мкТл. Сопротивление гальванометра R=100 Ом. Расстояние между рельсами l=1,2 м; рельсы считать изолированными друг от друга и от земли.

Решение:

24 Квадратная рамка со стороной l=2 см помещена в однородное магнитное поле с индукцией B = 100 Тл. Плоскость рамки перпендикулярна к линиям индукции поля. Сопротивление рамки R=1 Ом. Какой ток протечет по рамке, если ее выдвигать из магнитного поля со скоростью ν = 1 см/с, перпендикулярной к линиям индукции? Поле имеет резко очерченные границы, и стороны рамки параллельны этим границам.

Решение: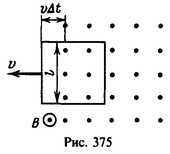
Пока рамка находится в области, где имеется магнитное поле, магнитный поток через поверхность, ограниченную рамкой,
при движении рамки не изменяется. Поэтому э.д.с. индукции в рамке не возникает. После того как одна из сторон рамки вышла за границу поля (рис. 375), магнитный поток через поверхность, ограниченную рамкой, будет изменяться. За время Δt рамка перемещается на расстояние νΔt и часть площади рамки, которую пересекает магнитное поле, уменьшается на величину
Магнитный поток за это время изменяется на величину

Индуцируемая в рамке э.д.с.

и по рамке протечет ток

Когда рамка выйдет из области, где имеется магнитное поле, э.д.с. индукции снова станет равной нулю.

25 Проволочный виток площади S= 1 см², имеющий сопротивление R = 1 мОм, пронизывается однородным магнитным полем, линии индукции которого перпендикулярны к плоскости витка. Магнитная индукция изменяется со скоростью ΔB/Δt = 0,01 Тл/с. Какое количество теплоты выделяется в витке за единицу времени?

Решение: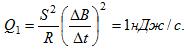

26 Прямоугольная рамка, подвижная сторона которой имеет длину l, помещена в однородное магнитное поле с индукцией B. Плоскость рамки перпендикулярна к линиям индукции магнитного поля. Подвижную сторону, которая вначале совпадает с противоположной ей неподвижной, начинают двигать равномерно со скоростью ν. Найти зависимость тока I в рамке от времени t. Сопротивление единицы длины проводника равно Rl.

Решение:


27 Два параллельных, замкнутых на одном конце провода, расстояние между которыми l=50 см, находятся в однородном магнитном поле с индукцией B = 5 мТл. Плоскость, в которой расположены провода, перпендикулярна к линиям индукции поля. На провода положен металлический мостик, который может скользить по проводам без трения. Мостик под действием силы F=0,1 мН движется со скоростью ν=10м/с. Найти сопротивление R мостика. Сопротивлением проводов пренебречь.

Решение:

28 Рамка из n = 1000 витков, имеющих площадь S = 5 см², замкнута на гальванометр с сопротивлением R=10 кОм и помещена в однородное магнитное поле с индукцией B=10мТл, причем линии индукции поля перпендикулярны к ее плоскости. Какой заряд q протечет по цепи гальванометра, если направление индукции магнитного поля плавно изменить на обратное?

Решение:
При плавном изменении магнитной индукции в рамке индуцируется э.д.с.

где ΔФ-изменение магнитного потока, Δt — время, в течение которого происходило это изменение. Ток в рамке

Заряд, протекший по цепи за время Δt,

Начальный поток магнитной индукции

При изменении направления магнитного поля на обратное магнитный поток изменяет знак. Поэтому конечный магнитный поток

Изменение магнитного потока

Таким образом,

29 Замкнутая катушка диаметра D с числом витков n помещена в однородное магнитное поле с индукцией В. Плоскость катушки перпендикулярна к линиям индукции поля. Какой заряд q протечет по цепи катушки, если ее повернуть на 180? Проволока, из которой намотана катушка, имеет площадь сечения S и удельное сопротивление ρ.

Решение:

30 В цепь включены последовательно источник тока с э.д.с. ε = 1,2 В, реостат с сопротивлением R=1 Ом и катушка с индуктивностью L=1 Гн. В цепи протекал постоянный ток I₀. С некоторого момента сопротивление реостата начинают менять так, чтобы ток уменьшался с постоянной скоростью ΔI/Δt = 0,2 А/с. Каково сопротивление R, цепи спустя время t = 2 с после начала изменения тока?

Решение:
Сумма э.д.с. источника тока и э.д.с, индуцируемой в цепи при равномерном изменении тока, равна

Ток изменяется
по закону

Сопротивление цепи в любой момент времени

В момент времени t= 2 с искомое сопротивление Rt= 1,75 0м.

31 Какой ток I покажет амперметр в схеме, изображенной на рис. 142, если индукция перпендикулярного к плоскости рисунка однородного магнитного поля меняется с течением времени по закону B = kt? Точки с и d лежат на концах диаметра проволочного кольца. Сопротивление единицы длины проволоки равно Rl; диаметр кольца равен D.

 

Определив из условий задачи либо напряженность поля, либо
магнитную индукцию, нужно по графику для данного материала определить
недостающую из этих двух величин и затем найти

μ = B/(μ₀H).

Пример.Найти индуктивность соленоида с железным сердечником,
если обмотка соленоида выполнена в один слой из проволоки диаметром 0,4 мм,
витки плотно прилегают друг к другу. По соленоиду идет ток 1 А. Объем соленоида
1500 с³ .

Решение. Индуктивность
соленоида можно определить по формуле (1.4.3). Так как соленоид имеет магнитный
сердечник, то сначала определим  магнитную проницаемость последнего, как
отношение B/(μ₀H). Для этого находим напряженность поля  на оси соленоида 
по формуле H = In , где n (число витков на единицу длины) подсчитывается следующим
образом: витки плотно прилегают друг к другу и общее число витков равно N = l/d  ( d – диаметр
проволоки), n = N/l = 1/d .

Тогда напряженность 

                                            H = I/d = 1/(0,4·10^-3
) = 2500 А/м.

Из графика (рис. 14) следует, что этому значению для железа
соответствует магнитная индукция 1,4 Тл. Этих данных достаточно для
определения  дтносительной магнитной проницаемости сердечника и далее
индуктивности. Подставив их в формулу (1.4.3) , получим

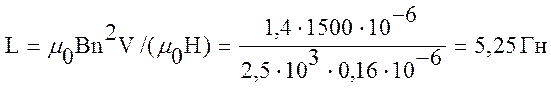
   Ответ: L = 5,25 Гн.

5.  ЭНЕРГИЯ И ПЛОТНОСТЬ ЭНЕРГИИ
МАГНИТНОГО ПОЛЯ.

МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА

Энергия магнитного поля, созданного проводником с током,
определяется формулой

W = LI²/2.

Плотность энергии (энергия единицы объема) вычисляют как ω = dW/dV или для
однородного поля ω = W/V. Подставив в формулу выражения (3.5.1) , (3.4.3) и (3.2.4),
получим

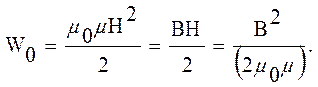                                                                        (3.5.2)

При вычислении энергии следует учитывать магнитные свойства
среды.

      Пример.  Определить энергию и плотность энергии катушки длиной  l = 10 см и диаметром d = 4 см, если по ней течет ток I =  1,5 А. Число витков на каждый
сантиметр длины равно 10, сердечник стальной.

    Решение. Найдем плотность энергии  Напряженность
определяем по формуле

                          А / м.

По графику (рис.14) найдем, что магнитная индукция для стали
В = 1,25 Тл. Тогда :

                                                   

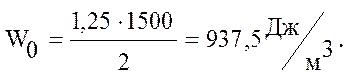
Энергия магнитного поля :

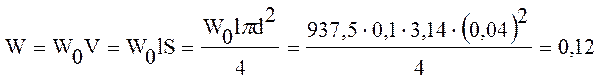                    Дж

    Ответ:  W = 0,12 Дж; W₀ = 937,5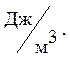

Если во внешнее поле вносится ферромагнетик, то он
намагничивается. Магнитные свойства вещества характеризуется магнитной
проницаемостью μ и магнитной восприимчивостью χ, связанными между собой соотношением :

                                           μ = 1 + χ                                            (3.5.3)

Величины χ и μ
безразмерные. Состояние намагниченности характеризуется вектором J – намагниченность, определяемой
магнитным моментом единицы объема магнетика : 

                                                    

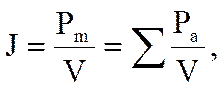
где P_m = ∑ p_a  – магнитный момент магнетика, равный
векторной сумме магнитных моментов отдельных атомов ( молекул).

Единица измерения намагниченности в СИ –  А/м. В слабых
магнитных полях намагниченность прямо пропорциональна напряженности намагничивающего
поля:

J = χ H.

НИЖЕ ПРИВЕДЕНЫ НЕКОТОРЫЕ  ИЗ ТИПОВЫХ ЗАДАНИЙ ДЛЯ ПОДГОТОВКИ К
ЭКЗАМЕНУ.

1.ОБЩИЕ ВОПРОСЫ. ЗАКОН БИО-САВАРА – ЛАПЛПСА И ЕГО
ПРИМЕНЕНИЕ К ПРОВОДНИКАМ РАЗЛИЧНОЙ ФОРМЫ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ.

1.  Чем
порождаются магнитные поля?

2.  Магнитное
поле можно создать с помощью  А) проводников с током  Б) покоящихся зарядов В)
движущихся зарядов

1) А и В      2)
А)         3) Б          4) Б и В

3.   Какие
силовые поля существуют вокруг движущегося протона (электрона, нейтрона…)?

4.  Характеристиками
магнитных полей являются физические величины … .

5.   Закон
Био-Савара- Лапласа в общем виде.

6.   Физический
смысл формул   В = µµ₀ Н ;  В
=µµ₀I/r;  
В =µµ₀I/2r;

7.   Единица
измерения магнитного потока (магнитной индукции, напряженность магнитного поля,
индуктивность и т,д…).

8.   Какая
физическая величина измеряется в теслах (Тл)?

9.    Два
тока  I₁=I₂ 
ткут в одном направлении (от нас). Результирующий вектор магнитной индукции в
точке А, лежащей посредине между токами направлен

1)  вниз;     2)  вверх;     3)  к току I₂.   
4) равен нулю.

10. 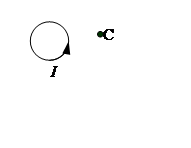 По круговому
витку течет ток I. Указать направление напряженность
магнитного поля в точке С.

1) вправо  2)
влево        3) на нас         4) от нас

11.  α – частица (β –
частица, электрон) вращается по круговой орбите радиуса о,5 мкм с частотой 100
об/с. Найти напряженность поля в центре окружности.

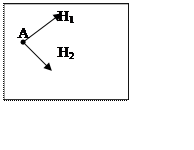
12.  Два магнита создают 
магнитные поля  Н₁   и  Н₂  , направленные
перпендикулярно друг другу.  Как расположится стрелка компаса, помещенного в точку 
А?

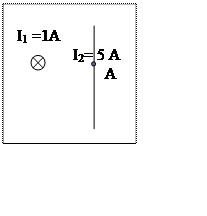
13.   Бесконечно
длинные проводники с токами расположены на расстоянии 5 см так, как показано на
рисунке. Определить напряженность магнитного поля в точке А.

14.   В центре
проволочного кругового  витка  ток  силой 5 А создает магнитное поле 
напряженностью  50 А/м. Найти радиус витка.

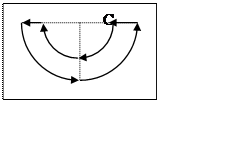
15.   Найти индукцию
магнитного поля в центре неполной окружности радиуса  R
= 20 см при силе тока I =3 А. Указать
направление вектора магнитной индукции.

16.  По квадратной
рамке течет ток  5А Напряженность магнитного поля в центре рамки 5 А/м.
Определить сторону рамки.

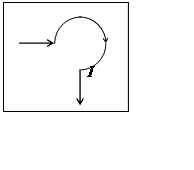
17.   По проводнику с
током приведенной формы протекает ток силой  1,5 А. Определить напряженность
магнитного поля в точке С, если радиусы полуокружностей равны 10 и 7 см.

18.   Прямолинейный
бесконечный ток I₁ = 1 А  проходит через середину
радиуса       (R =50 см) кругового тока I₂
= 5 А перпендикулярно плоскости последнего. Определить напряженность
магнитного поля в центре кругового тока.

19.   По проводнику,
согнутому в виде прямоугольника со сторонами  8 и  12 см  течёт ток силой  5 А.
Определить напряженность  и  индукцию магнитного поля в точке пересечения
диагоналей.