§ 144. Магнитная проницаемость железа. До сих пор мы
рассматривали
только магнитное поле в вакууме или,
что практически почти то же самое, в
воздухе. Теперь мы переходим к рассмотрению
магнитного поля в различных веществах
и в первую очередь в железе и сходных с
ним сильно намагничивающихся материалах.
Рассмотрим
опыт, схема которого показана на рис.
274. На длинный соленоид I надета индукционная
катушка II,
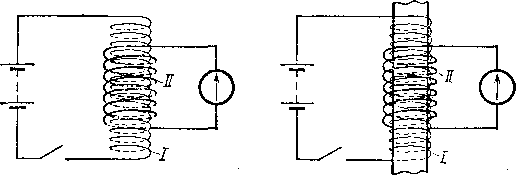
Рис.
274. В надетой на соленоид I катушке II при
замыкании ключа в цепи соленоида
индуцируется ток. Индукционный ток
меньше в отсутствие железного сердечника
в соленоиде (а),
чем с сердечником (б)
а)
б)
в
цепь которой включен так называемый
баллистический гальванометр, т. е.
гальванометр с большим периодом колебаний
подвижной части. Особенность этого
прибора заключается в том, что при
прохождении через него импульсов
тока, длительность которых значительно
(по крайней мере в 10
раз) меньше периода колебаний подвижной
части, максимальное отклонение (отброс)
подвижной части от положения равновесия
оказывается пропорциональным заряду
q,
прошедшему
через гальванометр.
Когда
через соленоид течет ток определенной
силы, сквозь катушку II проходит
определенный магнитный поток Ф. При
выключении тока магнитный поток
уменьшается до нуля, так что изменение
магнитного потока ЛФ— =Ф, т. е. равно
начальному значению магнитного потока.
Это изменение происходит за некоторый
промежуток времени Д/. При этом в катушке
II индуцируется’э.д. с., среднее значение
которой
о
ДФ Ф
Если
сопротивление цепи, в которую включена
катушка II (т. е. общее сопротивление
катушки, гальванометра и соединительных
проводов), равно R,
то
в течение времени Д/ через гальванометр
будет течь ток, среднее значение которого
l-ii-LJ®.
R
~
R
At
‘
В
результате через гальванометр пройдет
заряд
q
= Ibt
= %, (144.1)
который
можно определить по отбросу стрелки
гальванометра (см. упражнения 141.4 и
141.5). Из сказанного вытекает, что, измеряя
отброс стрелки баллистического
гальванометра при включении тока в
соленоиде, можно определять начальное
значение магнитного потока (поток Ф
пропорционален отбросу стрелки).
Проделаем
описанный опыт дважды. Ток в соленоиде
I в обоих случаях установим одинаковый,
но во втором опыте введем предварительно
в соленоид I железный сердечник (рис.
274, б).
Мы обнаружим, что во втором опыте (при
наличии сердечника) отброс стрелки
гальванометра, а следовательно, и
начальное значение магнитного потока
Ф оказываются гораздо большими, чем в
первом опыте (когда железный сердечник
отсутствует). Чтобы без железного
сердечника получить такой же отброс
стрелки гальванометра, как и при наличии
сердечника, нужно было бы во много
раз усилить первичный ток в соленоиде
I. Но усиление первичного тока в соленоиде
I означает, что мы увеличиваем начальное
значение магнитного потока внутри этого
соленоида, а следовательно, и сквозь
катушку II. Таким образом, внесение
железного сердечника сильно увеличивает
начальное значение магнитного потока.
Повторяя наш опыт с сердечниками
различной толщины, мы убедимся, что
увеличение магнитного потока будет
тем больше, чем большая часть do-
леноида
заполняется железом. Наибольшее
увеличение наблюдается, когда весь
соленоид заполнен железом, т. е. когда
обмотка плотно навита на железньщ
сердечник.
Строго
говоря, полное увеличение магнитного
потока достигается лишь тогда, когда
все линии магнитного поля
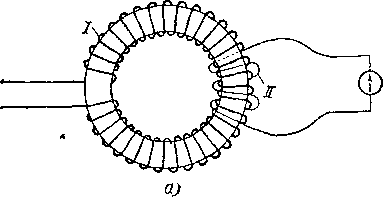
поток
соленоида: а) наибольшее увеличение
магнитного потока достигается в
кольцеобразном сердечнике; б)
большое увеличение магнитного потока
получается также у длинного и тонкого
соленоида с выступающими концами
сердечника. Первичная катушка I в обоих
случаях должна плотно обвивать
сердечник
проходят
в веществе сердечника. Это бывает,
например, у соленоида, плотно навитого
на замкнутый в виде кольца сердечник
(рис. 275, а).
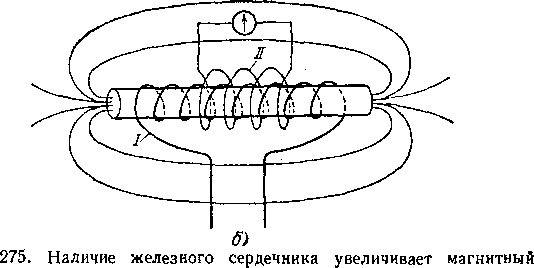
Однако, »если соленоид достаточно длинен
по сравнению со своими поперечными
размерами и плотно навит на длинный
выступающий сердечник, то индукционная
катушка, помещенная в средней части
соленоида (рис. 275, б), будет пронизываться
практически полным потоком.
В
этом случае отношение магнитных потоков
в соленоиде, навитом на сердечник, и
в том же соленоиде без сердечника’
зависит только от материала сердечника,
конечно, при условии, что начальный ток
в обмотке имеет одно и
то
же значение. Для разных сортов железа
и стали это отношение различно. Обозначая
его греческой буквой ^ (мю), мы можем
написать:
Ф
= ^Ф0,
где
Ф — магнитный поток в катушке с
сердечником, а Ф0
— магнитный поток в катушке без
сердечника.
Величину
р., характеризующую магнитные свойства
железа, использованного для сердечника,
называют его магнитной
проницаемостью
1).
Как уже упоминалось,
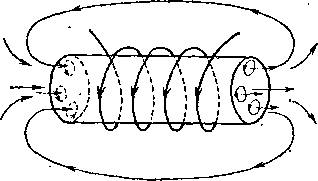
Рис.
276. Под влиянием магнитного поля соленоида
амперовы токи в железном сердечнике
ориентируются так, что направление их
совпадает с током в соленоиде
измерения
показывают, что наличие железного
сердечника увеличивает магнитный поток
весьма значительно, иногда в тысячи
раз. Мы можем, следовательно, сказать,
что магнитная
проницаемость железа весьма велит
и в некоторых случаях может достигать
значения нескольких тысяч.
Возрастание
магнитного потока при введении в
соленоид железа нетрудно понять с точки
зрения представлений об амперовых
молекулярных токах. Под влиянием
магнитного поля соленоида амперовы
токи в железе ориентируются, стремясь
стать параллельно токам обмотки
соленоида (рис. 276). Этим объясняется
намагничивание железа и усиление
магнитного поля во внешнем пространстве.
Этим же объясняется и увеличение
магнитного потока сквозь соленоид при
введении в него сердечника: к магнитному
потоку, создаваемому током в обмотке
соленоида, добавляется магнитный поток,
создаваемый совокупностью ориентированных
амперовых токов.
В
опыте, изображенном на рис. 274, поток
через один виток катушки II равен BS,
где
В
— магнитная индукция поля в соленоиде,
a
S
—
площадь поперечного сечения соленоида.
Поток Ф, фигурирующий в формуле (144.1),
равен NBS
(N
—
число витков катушки II). Отсюда следует,
что увеличение потока Ф в ц раз означает,
что’магнитная индукция В
в железном сердечнике в р. раз больше,
чем
магнитная индукция Вв
(при том же токе в соленоиде) в случае,
когда вместо железа был вакуум. Таким
образом, заполнение железом пространства,
в котором было поле с индукцией Во,
увеличивает индукцию поля в р. раз:
B
= xB0. (144.2)
В
§ 126 мы отмечали, что наряду с магнитной
индукцией В,
которая является основной силовой
1)
характеристикой магнитного поля, в
некоторых случаях оказывается полезной
вспомогательная
характеристика Н,
связанная с В
соотношением (см. формулу (126.4))
Б
= рц,0Я (144.3)
и
называемая напряженностью
магнитного поля (напомним, что р0
— магнитная постоянная, см. формулу
(126.2)).
В
применении к рассматриваемому опыту
формула
-
дает
50=1ЛоЯ0
(в отсутствие сердечника, когда |Д,=1) и
5=рр0Я
(при наличии сердечника). Поскольку
В=р.В0,
имеем
рр0Я
= рр0Я0,
или Н
= Я0.
Таким
образом, напряженность магнитного поля
не зависит от того, заполнен соленоид
каким-либо материалом или нет. В случае,
когда все пространство, в котором поле
отлично от нуля, заполнено однородным
веществом, напряженность поля не зависит
от свойств этого вещества 2).
§
145. Магнитная проницаемость различных
веществ. Вещества парамагнитные и
диамагнитные. Если в описанных выше
опытах вместо сердечника из железа
брать сердечники из других материалов,
то также можно обнаружить изменение
магнитного потока. Естественнее всего
ждать, что наиболее заметный эффект
дадут материалы, подобные по своим
магнитным свойствам железу, т. е. никель,
кобальт и некоторые магнитные сплавы.
Действительно, при введении в катушку
сердечника из этих материалов увеличение
магнитного потока оказывается довольно
значительным. Иными словами, можно
сказать, что магнитная проницаемость
их велика; у никеля, например, р. может
достигать значения 50, у кобальта 100. Все
эти материалы с большими значениями р.
объединяют в одну группу ферромагнитных
материалов.
Однако
и все остальные «немагнитные» материалы
также оказывают некоторое влияние на
магнитный поток, хотя влияние это
значительно меньше, чем у материалов
ферромагнитных. С помощью очень тщательных
измерений можно это изменение
обнаружить и определить магнитную
проницаемость различных материалов.
При этом, однако, нужно иметь в виду, что
в опыте, описанном выше, мы сравнивали
магнитный поток в катушке, полость
которой заполнена железом, с потоком
в катушке, внутри _ которой имеется
воздух. Пока речь шла о таких сильно
магнитных материалах, как железо, никель,
кобальт, это не имело значения, так как
наличие воздуха очень мало влияет на
магнитный поток. Но при исследовании
магнитных свойств других веществ, в
частности самого воздуха, мы должны,
конечно, вести сравнение с катушкой,
внутри которой воздуха нет (вакуум).
Таким образом, за магнитную
проницаемость мы принимаем отношение
магнитных потоков в исследуемом
веществе и в вакууме
(ц= =Ф/Ф0).
Иными словами, за
единицу мы принимаем магнитную
проницаемость для вакуума
(если
Ф=Ф0,
то
|л.=1).
Измерения
показывают, что магнитная проницаемость
всех веществ отлична от единицы, хотя
в большинстве случаев это отличие очень
мало. Но особенно замечательным
оказывается тот факт, что у одних веществ
магнитная проницаемость р, больше
единицы, а у других она меньше единицы,
т. е. заполнение катушки одними веществами
увеличивает магнитный поток, а заполнение
катушки другими веществами уменьшает
этот поток. Первые из э_тих веществ
называются парамагнитными
(pOl),
а
вторые — диамагнитными
((*<!). Как показывает табл. 7, отличие
проницаемости ц от единицы как у
парамагнитных, так и у диамагнитных
веществ невелико,.
Нужно
особенно подчеркнуть, что для парамагнитных
и диамагнитных тел магнитная проницаемость
р. не > зависит от магнитной индукции
внешнего, намагничивающего поля, т.
е. представляет собой постоянную
величину, характеризующую данное
вещество. Как мы увидим § 149, это не имеет
места для железа и других сходных с ним
(ферромагнитных) тел.
Таблица
7.
Магнитная проницаемость для
некоторых
парамагнитных и
диамагнитных
веществ
|
Парамагнитные |
Диамагнитные |
||
|
Азот |
1,000013 |
Водород |
0,999937 |
|
Воздух |
1,000038 |
ный) |
|
|
Кислород |
1,000017 |
Вода |
0,999991 |
|
Кислород |
1,0034 |
Стекло |
0,999987 |
|
Эбонит |
1,000014 |
Цинк |
0,999991 |
|
Алюминий |
1,000023 |
Серебро |
0,999981 |
|
Вольфрам |
1,000175 |
Золото |
0,999963 |
|
Платина |
1,000253 |
Медь |
0,999912 |
|
Висмут |
0,999824 |
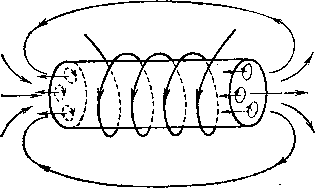
Рис.
277. Диамагнитные вещества внутри катушки
ослабляют магнитное поле соленоида.
Элементарные токи в них направлены
противоположно току « соленоиде
Влияние
парамагнитных и диамагнитных веществ
на магнитный поток объясняется, так же
как и влияние веществ ферромагнитных,
тем, что к магнитному потоку, создаваемому
током в обмотке катушки, присоединяется
поток, исходящий из элементарных
амперовых токов. Парамагнитные
вещества увеличивают магнитный
поток катушки.
Это
увеличение потока при заполнении
катушки парамагнитным веществом
указывает на то, что и в
парамагнитных веществах под действием
внешнего магнитного поля элементарные
токи ориентируются так, что направление
их совпадает с направлением тока
обмотки
(рис. 276). Небольшое отличие р. от единицы
указывает лишь на то, чт;о в случае
парамагнитных веществ этот добавочный
магнитный поток очень невелик, т. е.
что парамагнитные вещества намагничиваются
очень слабо.
Уменьшение
магнитного потока при заполнении
катушки диамагнитным веществом
означает, что в этом случае магнитный
поток от элементарных амперовых токов
направлен противоположно магнитному
потоку катушки, т. е. что в
диамагнитных веществах под действием
внешнего магнитного поля возникают
элементарные токи, направ
ленные
противоположно токам обмотки
(рис. 277). Малость отклонений (J.
от
единицы и в этом случае указывает на
то, что дополнительный поток этих
элементарных токов невелик.
§
146. Движение парамагнитных и диамагнитных
тел в магнитном поле. Опыты Фарадея.
Притяжение
железных предметов к магнитам является
наиболее простым и бросающимся в
глаза проявлением магнитного поля и
исторически послужило основой всего
развития учения о магнетизме. Оно
сводится к воздействию магнитного поля
на ориентированные молекулярные токи
намагнитившегося железа. Так же, но
только значительно слабее должно
действовать магнитное поле и
на
парамагнитные тела,
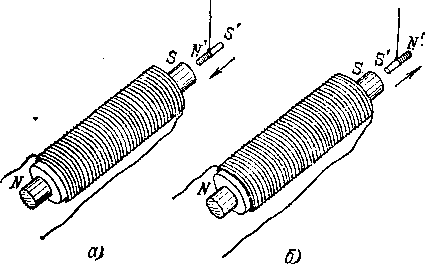
Рис.
278. а)
При намагничивании парамагнитного или
ферромагнитного тела на ближайшем
к магниту конце возникает полюс,
разноименный с полюсом намагничивающего
магнита; парамагнитное тело притягивается
к магниту, б)
В тех же условиях на ближайшем к магниту
конце диамагнитного тела возникает
полюс одноименный; диамагнитное
тело отталкивается от магнита
потому
что, как мы могли судить по опытам,
описанным в предыдущем параграфе, и в
парамагнитных телах ориентация
элементарных токов происходит так же,
как в ферромагнитных: магнитный поток
элементарных токов усиливает, хотя и
незначительно, магнитный поток
ориентирующего поля и, следовательно,
парамагнитные
тела притягиваются к магниту
(рис. 278, а).
В
отличие от тел парамагнитных, диамагнитные
тела уменьшают магнитный поток катушки.
Это означает, что в диамагнитном теле
под действием внешнего поля возникают
элементарные токи такого направления,
что их магнитное поле противоположно
направлению внешнего магнитного
поля. Следовательно, и действие внешнего
магнитного поля на диамагнитные тела
противоположно по направлению
действию его на тела ферро- и парамагнитные,
т. е. диамагнитные
тела отталкиваются от магнита
(рис. 278, б). ч
Мы
можем выразить этот факт и несколько
иначе. Когда мы подносим к магниту
какое-нибудь железное тело, то оно
намагничивается так, что на той стороне
его, которая обращена к магниту, возникает
полюс, разноименный с полюсом магнита;
то же имеет место и в случае парамагнитного
тела (рис. 278, а).
Напротив, в случае диамагнитного
тела на стороне, ближайшей к полюсу
намагничивающего магнита, возникает
полюс, одноименный с этим полюсом магнита
(рис. 278, б). Рис. 276 и 277 поясняют, почему
парамагнитные тела притягиваются к
магниту, а диамагнитные отталкиваются
от него.
Именно
такие действия и были обнаружены
Фарадеем. В 1845 г., использовав сильный
электромагнит, Фарадей установил
способность всех
тел намагничиваться и открыл, что одни
тела, притягиваются к магниту, а другие
отталкиваются от него. Он предложил
для первых название парамагнитных, для
вторых название диамагнитных. Индукционные
опыты с пара- и диамагнитными телами,
подобные описанным в § 144, были
произведены значительно позже, когда
магнитные свойства диамагнитных и
парамагнитных тел были уже установлены
на основании исследований Фарадея.
По
силе притяжения или отталкивания можно
судить и количественно о способности
тела намагничиваться, т. е. можно
определить магнитную проницаемость ц.
для данного вещества. Этот метод
измерения ц, основанный на изучении
притяжения илн отталкивания маленького
тела из данного вещества, теоретически
более сложен, чем описанный нами в §
145 метод, основанный на измерении
магнитного потока. Но зато он гораздо
чувствительнее и, кроме того, пригоден
для измерения в маленьком образчике
вещества, тогда как для измерения ц по
индукционному способу нужно заполнить
изучаемым веществом всю полость катушки.
В тех случаях, когда удается измерить
ц
и тем и другим способом, получаются
согласующиеся результаты.
л
146.1. Полюсы сильного
электромагнита
на рис. 279 срезаны не-
-
параллельно
друг другу, так что внизу расстояние
между ними значительно меньше, чем
наверху. Между ними подвешивается на
нити шарик из различных испытуемых
материалов. Верхний конец нити прикреплен
к спиральной пружинке, растяжение
которой позволяет измерить силу,
действующую со стороны магнитного
поля на шарик (пружинные весы). Оказывается,
что если шарик изготовлен из алюминия,
вольфрама или платины, то эта сила
направлена вниз (пружинка растягивается),
а в случае серебра, золота, меди или
висмута она направлена вверх (пружинка
сокращается). Объясните этот опыт.
-
При
исследовании магнитной проницаемости
жидких веществ часто поступают так.
Жидкость наливают в коленчатую
Рис.
280. К упражнению 146.2
Рис.
279. К упражнению 146.1
трубку
и одно из колен помещают между полюсами
сильного электромагнита (рис. 280). Жидкость
в этом колене поднимается или опускается
в зависимости от того, является ли она
парамагнитной или диамагнитной.
Объясните это явление.
§
147. Молекулярная теория магнетизма.
Теория, объясняющая различие в
магнитных свойствах веществ на основе
изучения строения отдельных частиц
этих веществ — их атомов или молекул,—
получила название молекулярной
теории магнетизма.
Эта теория очень сложна и во многом еще
не завершена. Поэтому здесь мы не можем
разбирать ее сколько-нибудь подробно.
Укажем лишь на основные причины различия
между свойствами парамагнитных и
диамагнитных тел.
Каждое
тело, и парамагнитное и диамагнитное,
представляется нам в целом ненамагниченным
до тех пор, пока на него не действует
внешнее магнитное поле. Но обусловливается
это в телах парамагнитных и в телах
диамагнитных разными причинами.
Диамагнитными являются тела, каждая
частица которых — атом или молекула,—
находясь вне магнитного поля, не обладает
магнитными свойствами. Только внешнее
магнитное поле превращает их в элементарные
магниты (вызывает элементарные токи),
определенным образом направленные.
Напротив, частицы парамагнитных
веществ уже сами по себе, еще до того,
как на них начало действовать внешнее
поле, представляют собой элементарные
магниты (элементарные токи). Здесь роль
внешнего магнитного поля сводится
к определенной ориентации, упорядочению
расположения этих магнитиков. Пока поле
не действовало, все они были расположены
беспорядочно, хаотически, и вещество
в целом представлялось нам ненамагниченным.
В магнитном же поле эти элементарные
магниты выстраиваются в большей или
меньшей мере параллельными цепочками,
и вещество в целом намагничивается.
В
чем же состоит различие между строением
частиц диамагнитных и парамагнитных
веществ? В атомах всех тёл есть большое
число движущихся электронов. Каждый
из них и представляет собой амперов
элементарный круговой ток. Но в атомах
диамагнитных веществ до внесения их
в магнитное поле магнитные действия
этих отдельных токов взаимно
компенсируют друг друга, так что атом
в целом не является элементарным
магнитом. Когда мы вносим такое вещество
в магнитное поле, то на кансдый движущийся
электрон действует сила Лоренца, и
совокупное действие всех этих сил,
как показывает расчет, приводит к тому,
что в атоме индуцируется определенный
ток, т. е. атом приобретает свойства
элементарного магнита. Так как эти токи
являются индукцион
ными,
то направление их, согласно правилу
Ленца, должно быть противоположно
направлению тока в катушке, создающего
внешнее магнитное поле, т. е. магнитный
поток от этих токов должен ослаблять
поток внешнего поля, и диамагнитное
тело отталкивается от магнита.’
В
атомах парамагнитных веществ магнитные
действия отдельных электронов не
полностью компенсируют друг друга, так
что атом в целом и сам по себе является
элементарным магнитом. Действие внешнего
магнитного поля упорядочивает расположение
этих элементарных токов, причем токи
ориентируются так, что их направление
преимущественно совпадает с направлением
тока катушки, создающего внешнее
магнитное поле. Поэтому магнитный
поток от элементарных токов в этом
случае усиливает поток катушки, и
парамагнитное тело притягивается к
магниту.
Строго
говоря, диамагнетизм есть общее свойство
всех веществ. Внешнее магнитное поле
производит и на атомы парамагнитных
веществ такое же индуцирующее
действие, как на атомы диамагнитных
веществ. Но в парамагнитных веществах
это действие перекрывается более сильным
ориентирующим действием внешнего
магнитного поля, которое упорядочивает
собственные элементарные токи атомов.
Мы
видим, таким образом, что диамагнетизм
и парамагнетизм объясняются различиями
в строении самих атомов или молекул
вещества.

Рис.
281. Изменение магнитного поля при
внесении в него куска железа
§
148. Магнитная защита. Само собой разумеется,
что намагничивание ферромагнитных,
парамагнитных и диамагнитных тел
происходит не только тогда, когда мы
помещаем их внутрь соленоида, но и
вообще всегда, когда вещество помещается
в магнитное поле. Во всех этих случаях
к магнитному полю, которое существовало
до внесения в него вещества, добавляется
магнитное поле, обусловленное
намагничиванием этого вещества, в
результате чего магнитное поле
изменяется. Из сказанного в предыдущих
параграфах ясно, что наиболее сильные
изменения поля происходят при внесении
в него ферромагнитных тел, в частности
железа изменение магнитного поля
вокруг ферромагнитных тел очень удобно
наблюдать, пользуясь картиной линий
поля, получаемой
при
помощи железных опилок. На рис. 281
изображены, ’ . например, изменения,
наблюдающиеся при внесении куска
железа прямоугольной формы в магнитное
поле, которое раньше было однородным.
Как видим, поле перестает быть
однородным и приобретает сложный
характер; в одних местах оно усиливается,
в других — ослабляетея.
-
Когда
на современных судах устанавливают и
выверяют
-
компасы,
тр вводят поправки к показаниям компаса,
зависящие
от
формы и расположения частей судна и от
положения компаса не нем. Объясните,
почему это необходимо. Зависят ли
поправки от сорта стали, примененной
при постройке судна?
-
Почему
суда, снаряжаемые экспедициями для
исследования магнитного поля Земли,
строят не стальные, а деревянные и для
скрепления обшивки променяют медные
винты?
Очень
интересна и практически важна картина,
которая наблюдается при внесении в
магнитное поле замкнутого железного
сосуда, например полого шара. Как видно
из рис. 282, в результате сложения внешнего
магнитного

Рис.
282. Полый железный шар внесен в однородное
магнитное поле
поля
с полем намагнитившегося железа поле
во внутренней области шара почти
исчезает. Этим пользуются для
В
Рис.
283. Линии магнитного поля сосредоточены
в железном кольце, внесенном в магнитное
поле
создания
магнйтной
защиты
или магнитной
экранировки, т.
е. для защиты тех или иных приборов от
действия внешнего магнитного поля.
Картина,
которую мы наблюдаем при создании
магнитной защиты, внешне напоминает
создание электростатической защиты
при помощи проводящей оболочки. Однако
между этими явлениями есть глубокое
принципиальное различие. В случае
электростатической защиты металлические
стенки могут1
быть сколь угодно тонкими. До
статочно,
например, посеребрить поверхность
стеклянного сосуда, помещенного в
электрическое поле, чтобы внутри сосуда
не оказалось поля, которое обрывается
на поверхности металла. В случае же
магнитного поля тонкие железные
стенки не являются защитой для внутреннего
пространства: магнитные поля проходят
сквозь железо, и внутри сосуда оказывается
некоторое магнитное поле. Лишь при
достаточно толстых железных стенках
ослабление поля внутри полости может
сделаться настолько сильным, что
магнитная, защита приобретает практическое
значение, хотя и в этом, случае поле
внутри не уничтожается полностью. И
в этом случае ослабление поля не есть
результат обрыва его на поверхности
железа; линии магнитного поля отнюдь
не обрываются, но по-прежнему остаются
замкнутыми, проходя сквозь железо.
Изображая .графически распределение
линий магнитного поля в толще железа и
в полости, получим картину (рис. 283),
которая . .и показывает, что ослабление
поля внутри полости есть результат
изменения направления линий поля, а не
их обрыва.
353
§
149. Особенности ферромагнитных тел.
Бросающейся в глаза особенностью
ферромагнитных тел является их способность
к сильному намагничиванию, вследствие
которой магнитная проницаемость
этих тел имеет очень большие значения.
У железа, например, магнитная проницаемость
(J.
достигает
значений, которые в тысячи раз превосходят
значения ц у парамагнитных и диамагнитных
веществ. Намагничивание ферромагнитных
тел было изучено в опытах А. Г. Столетова
и других ученых. Эти опыты показали,
сверх того, что, в отличие от парамагнитных
и диамагнитных веществ, магнитная
проницаемость ферромагнитных веществ
сильно зависит от напряженности 1)
магнитного поля,
при которой производят ее измерение.
Так, например, в слабых полях магнитная
проницаемость |х железа достигает
значений шести тысяч, а в сильных полях
значения (А падают до нескольких сот и
ниже.
В
§§ 118 и 119 для характеристики магнитных
свойств контуров с током была введена
векторная величина рт,
называемая
магнитным
моментом
тока (см. формулу – (118.1)). Молекулярные
токи также обладают магнитным
моментом.
Когда вещество не намагничено, магнитные
моменты отдельных молекулярных токов
ориентированы хаотически (беспорядочно),
вследствие чего их векторная сумма
равна нулю, вещество в целом магнитным
моментом не обладает.
Под
действием внешнего магнитного поля
магнитные моменты молекулярных токов
приобретают в большей или меньшей
степени преимущественную ориентацию
в направлении поля (в случае ферро-
и парамагнетиков) либо возникают
индукционные молекулярные токи, магнитные
моменты которых ориентированы против
поля (в случае диамагнетиков, § 147). В
результате суммарный магнитный
момент молекулярных токов становится
отличным от нуля, и тело оказывается
намагниченным. Естественно в качестве
меры намагниченности вещества принять
суммарный
магнитный момент молекулярных токов,
заключенных в единице объема вещества.
В соответствии с этим вводится векторная
величина J,
называемая
намагничен-
нос/пью
вещества и определяемая выражением
У=
2
Рт, (149.1)
по
единице объема
где
Рт
—
магнитный момент отдельного молекулярного
тока.
.
Можно показать, что намагниченность J
связана
с магнитной индукцией В
в веществе и напряженностью магнитного
поля Н
соотношением, которое имеет вид
•/
= £—Н. (149.2)
С
учетом того, что B—ii0H,
получается
формула
У
= (}г—1)//. (149.3)
Заменим
в формуле (149.2) векторы их модулями и
напишем получившееся соотношение в
виде
В
= -j-
[i0«/
=
~1~ М’о*^ =
В0
4″
(напомним,
что в рассматриваемом случае Н=Нй,
а ц-0Я0=
—Во
— магнитной индукции поля соленоида в
отсутствие вещества). Теперь умножим
это соотношение на площадь поперечного
сечения соленоида S:
BS
=
B0Si0JS.
Произведение
BS
равно
Ф — магнитному потоку через сечеНие
соленоида, B0S
равно
Ф0
— магнитному потоку в
отсутствие
вещества. Следовательно, мы приходим к
формуле
Ф
= Ф„ + ^ = Ф0
+ Ф’, (149.4)
где
через Ф’ обозначено выражение ц0</5,
которое можно рассматривать как
добавочный поток магнитной индукции,
создаваемый намагниченным веществом:
Ф’
= [А„ JS. (149.5)
В
случае ферромагнитных и парамагнитных
веществ этот поток положителен (Ф>Фо),
в
случае диамагнитных веществ —
отрицателен (Ф<Ф0).
Таким
образом, намагниченность J
пропорциональна
добавочному потоку, который создается
намагниченным веществом.
Учтя,
что Ф=}лФ0,
из формулы (149.4) легко получить соотношение
Ф’
= = (ц— 1) Ф0. (149.6)
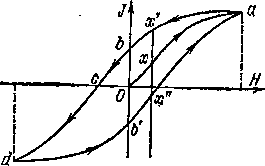
Рис.
284.
Зависимость намагниченности J
от
напряженности внешнего магнитного
поля Н.
Стрелки
указывают направление процесса
Изучение
зависимости намагниченности железа и
других ферромагнитных материалов
от напряженности внешнего магнитного
поля обнаруживает ряд особенностей
этих веществ, имеющих важное
практическое значение.
Возьмем
кусок ненамагничен- ного железа, поместим
его в магнитное поле и будем измерять
намагниченность железа J,
постепенно
увеличивая напряженность внешнего
магнитного поля Н.
Намагниченность J
возрастает
сначала резко, затем все медленнее и,
наконец, при значениях Н
около
нескольких десятков тысяч ампер на метр
намагниченность перестает возрастать:
все элементарные токи уже ориентированы,
железо достигло магнитного
насыщения. Графически
зависимость У от Я в описываемом опыте
изображается кривой Оа
на рис. 284. Горизонтальная часть этой
кривой вблизи точки а
соответствует магнитному насыщению.
Достигнув
насыщения, начнем ослаблять внешнее
магнитное поле. При этом намагниченность
железа уменьшается, но убывание это
идет медленнее, нем раньше шло
ее
возрастание. Зависимость между J
и
Н
в этом случае изображается ветвью кривой
аЬ
на рис. 284. Мы видим, таким образом, -что
одному и тому же значению Н
могуТ соответствовать различные значения
намагниченности (точки х,
х’
и х”
на рис. 284) в зависимости от того, подходим
ли мы к .этому значению со стороны малых
или со стороны больших значений Н.
Намагниченность железа зависит,
стало быть, не только от того, в каком
поле данный кусок находится, но и от
предыдущей истории этого куска. Это
явление получило название магнитного
гистерезиса.
Когда
внешнее магнитное поле становится
равным нулю, железо продолжает сохранять
некоторую остаточную
намагниченность
(§ 112),
которая характеризуется отрезком ОЬ
графика. В этом и заключается причина
того, что из железа или стали можно
изготовлять постоянные магниты.
Для
дальнейшего размагничивания железа
нужно приложить внешнее магнитное
поле, направленное в противоположную
сторону. Ход изменения намагниченности
J
при
возрастании напряженности Н
этого противоположно направленного
поля изображается ветвью кривой bed.
Лишь
когда напряженность этого поля достигнет
определенного значения (в нашем опыте
значения, изображаемого отрезком Ос),
железо будет полностью размагничено
(точка с).
Таким образом, напряженность
размагничивающего поля (отрезок Ос)
является мерой того, насколько прочно
удерживается состояние намагничивания
железа. Ее называют коэрцитивной
силой.
При уменьшении напряженности поля
обратного направления и затем при
возрастании напряженности поля
первоначального направления ход
изменения намагниченности железа
изображается ветвью кривой db‘a.
При
новом повторении всего цикла
размагничивания, перем’агничивания и
повторного намагничивания железа в
первоначальном направлении форма этой
кривой повторяется *). Из рис. 284 видно,
что эта кривая, изображающая ход
зависимости намагниченности железа J
от
напряженности внешнего поля Н,
имеет вид петли. Ее называют петлей
гистерезиса
для данного сорта железа или стали.
Форма петли гистерезиса является
важнейшей
*)■
Ветвь Оа
изображает ход намагничивания исходного
ненамаг- ничённого материала и не
повторяется при повторных циклах. Для
того чтобы вновь воспроизвести ветвь
Оа,
необходимо привести материал в
первоначальное ненам^гниченное состояние.
Для этого достаточно, например, сильно
нагреть его.
характеристикой
магнитных свойств того или иного
ферромагнитного материала. В частности,
зная ее, мы можем определить такие важные
характеристики этого материала, как
его магнитное насыщение, остаточную
намагниченность и коэрцитивную силу.
Процесс
намагничивания вещества можно
характеризовать не только кривой
зависимости У от Я (рис. 284), но и кривой
зависимости В
от Я. Обе зависимости закономерно
связаны друг с другом. Первая из них
имеет
В,
Тл
И,
А/и
Рис.
285. Кривые намагничивания для различных
сортов железа и стали: 1
— мягкое железо,’ 2
— закаленная сталь. 3
— незакаленная сталь

вид
•/= (ц—1 )Я (см. фор мулу (149.3)), вторая —
5=(хцоЯ.
На рис. 285 по- ^ казана зависимость В
от ‘
Я
для различных сортов 1,2.
железа
и стали. По форме этой петли можно выбрать
^8
материал,
который наилуч- q
4
шим
образом подходит для той или иной
практичес- О
кой
задачи. Так, для изго-_^^
товления
постоянных маг-. ’ нитов необходим
материал-<7,8 с большой коэрцитивной
силой (сталь и особенно ’
специальные
сорта кобаль- -%в
товой
стали); для электри- _9
п
ческих
машин и особенно -£ш7
‘-та
о зооо ‘ Ш для
трансформаторов выгодны материалы
с очень малой площадью петли гистерезиса,
ибо они, как оказывается, меньше всего
нагреваются при перемаг-
ничивании
1);
для некоторых специальных приборов
важны материалы, магнитное насыщение
которых достигается при малых полях, и
т. д.
В
отличие от парамагнетиков и диамагнетиков
(§ 145) у ферромагнетиков магнитная
проницаемость ц не остается постоянной,
а зависит от напряженности внешнего
намагничивающего поля Я. Эта зависимость
для магнит
ного
сплава (пермаллоя) и для мягкого железа
показана на рис. 286. Как мы видим, магнитная
проницаемость ц. имеет малые начальные
значения в слабых полях, затем нарастает
до максимального значения и при дальнейшем
увеличении поля снова уменвшается.
Важно
отметить, что при достижении определенной
температуры магнитная проницаемость
ферромагнитных
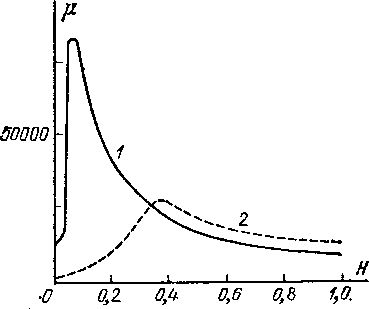
Рис.
286. Зависимость fi
от
Н:
1
— у магнитного сплава (пермаллоя)^ 2
— у мягкого железа
тел
резко падает до значения, близкого к
единице. Эта температура, характерная
для каждого ферромагнитного вещества,
носит название точки
Кюри
по имени французского физика Пьера
Кюри (1859—1906). При температурах
выше точки Кюри
все ферромагнитные тела становятся
парамагнитными.
У железа точка Кюри равна 767 °С, у никеля
— 360 °С, у кобальта — около 1130 °С. У
некоторых ферромагнитных сплавов
точка Кюри лежит вблизи 100 °С.
•f
149.1.
Какой из ферромагнитных материалов,
приведенных на
-
рис.
285, наиболее пригоден для постоянных
магнитов? Какой из них наиболее пригоден
для электромагнитов с выстрой
регулировкой подъемной силы?
-
Можно
ли электромагнитным краном переносить
раскаленные стальные болванки?
его
кристаллической структуры. Атомы железа,
если взять их, например, в парообразном
состоянии, сами по себе диамагнитны или
лишь слабо парамагнитны. Ферромагнетизм
есть свойство железа в твердом состоянии,
т. е. свойство ^кристаллов железа.
В
этом нас убеждает ряд фактов. Прежде
всего на это указывает зависимость
магнитных свойств железа и других
ферромагнитных материалов от обработки,
изменяющей их кристаллическое строение
(закалка, отжиг). Далее оказывается, что
из парамагнитных и диамагнитных металлов
можно изготовить сплавы, обладающие
высокими ферромагнитными свойствами.
Таков, например, сплав’ Гейслера, почти
не уступающий по своим магнитным
свойствам железу, хотя он состоит из
таких слабомагнйт- ных металлов, как
медь (60 %), марганец (25 %)
и алюминий (15 %).
С другой стороны, некоторые сплавы из
ферромагнитных материалов, например1
сплав из 75 % железа и 25 % никеля, почти не
магнитны. Наконец, самым веским
подтверждением является то, что при
достижении определенной температуры
(точки Кюри) все ферромагнитные
вещества теряют свои ферромагнитные
свойства.
Ферромагнитные
вещества отличаются от парамагнитных
не только весьма большим значением
магнитной проницаемости ц и ее
зависимостью от напряженности поля,
но и весьма своеобразной связью между
намагниченностью и напряженностью
намагничивающего поля. Эта особенность
находит свое выражение в явлении
гистерезиса со всеми его следствиями:
наличием остаточной намагниченности
и коэрцитивной силы.
В
чем причина гистерезиса? Вид кривых на
рис. 284 и 285 — различие между ходом
нарастания намагничивания ферромагнетика
при увеличении Н
и ходом его размагничивания при уменьшении
Н
— показывает, что при изменении
намагниченности ферромагнетика, т. е.
при увеличении или уменьшении напряженности
внешнего поля, ориентация и дезориентация
элементарных магнитов не сразу следует
за полем, а происходит с известным
отставанием.
Подробное
изучение процессов намагничивания и
размагничивания железа и других
ферромагнитных веществ показало, что
ферромагнитные свойства вещества
определяются не магнитными свойствами
отдельных атомов или молекул, которые
сами по себе парамагнитны, а намагничиванием
целых областей, называемых доменами
*),— небольших участков вещества,
содержащих очень большое число атомов.
Взаимодействие магнитных моментов
отдельных атомов ферромагнетика
приводит к созданию чрезвычайно
сильных внутренних магнитных полей,
действующих в пределах каждой такой
области и выстраивающих в пределах этой
области все атомные магнитики параллельно
друг другу, как показано на рис. 287. Таким
образом, даже в отсутствие внешнего
поля ферромагнитное вещество состоит
из ряда отдельных областей, каждая из
которых самопроизвольно намагничена
до насыщения. Но
направление
намагниченности для разных областей
различно, так что вследствие хаотичности
распределения этих областей тело в
целом оказывается в отсутствие
внешнего поля ненамагниченным.
k
A »
КОТОрЫХ
параллельна внешнему по-
* лю,
и вещество в целом оказывается
I
|
f
t
f I t t t M ft M t ft
Под.
влиянием внешнего поля происходит
перестройка и перегруппировка таких
областей самопроизвольного намагничивания,
в результате которой получают
преимуще- Z ство
те области, намагниченность
намагниченным.
а)
|
н
f
f t t t
-
i
и
I
t
M ft Hill
-
tt
t
б)
Рис.
287. Схема ориентации молекулярных
магнитов в областях самопроизвольного
намагничивания 1
и 2:
а)
внешнее магнитное поле отсутствует;
б)
под действием внешнего магнитного поля
области 1
и 2
перестраиваются
Один
из примеров такой перестройки областей
самопроизвольного намагничивания
показан на рис. 287. Здесь условно изображены
две смежные области, направления
намагниченности которых перпендикулярны
друг к другу. При наложении внешнего
поля часть атомов области 2,
в которой намагниченность перпендикулярна
к полю, на границе ее с областью 1,
в которой намагниченность параллельна
полю, поворачивается, так что направление
их магнитного момента становится
параллельным полю. В результате область
1,
намагниченная параллельно внешнему
полю, расширяется за счет тех областей,
в которых направление намагниченности
образует большие углы с направлением
поля, и возникает преимущественное
намагничивание тела по направлению
внешнего поля. В очень сильных внешних
полях возможны и повороты направления
ориентации всех атомов в пределах целой
области.
При
снятии (уменьшении) внешнего поля
происходит обратный процесс распада
и дезориентации этих областей, т. е.
размагничивание тела. Ввиду больших по
сравнению с атомами размеров областей
самопроизвольного намагничивания
как процесс ориентации их, так и обратный
процесс дезориентации происходят с
гораздо большими затруднениями, чем
установление ориентации или дезориентации
отдельных молекул или атомов, имеющее
место в парамагнитных и диамагнитных
телах. Этим и объясняется отставание
намагничивания и размагничивания
от изменения внешнего поля, т. е. гистерезис
ферромагнитных тел.
Решение:
На проводник действуют: две одинаковые силы натяжения нитей Т, сила тяжести mg и сила![]()
со стороны магнитного поля, где α — угол между направлениями тока I и магнитной индукции (в нашем случае α = 90° и sinα = 1). Подразумевается, что направления тока и магнитной индукции таковы, что сила F направлена вниз (рис. 140). В противном случае силы натяжения нитей при пропускании тока не возрастают, а уменьшаются, и нити не оборвутся.
Если проводник находится в равновесии, то![]()
отсюда![]()
Для разрыва одной из нитей необходимо выполнение условия![]()
или![]()
6 На прямой проводник длины l=0,5 м, расположенный перпендикулярно к линиям индукции магнитного поля, действует сила F=0,15 Н. Найти ток I, протекающий в проводнике, если магнитная индукция B = 20 мТл.
Решение:
Если проводник расположен перпендикулярно к направлению магнитной индукции, то F=BIl, где I-ток в проводнике; отсюда I=F/Bl=15 А.
7 Между полюсами магнита подвешен горизонтально на двух невесомых нитях прямой проводник длины l=0,2 м и массы m=10 г. Индукция однородного магнитного поля B = 49 мТл и перпендикулярна к проводнику. На какой угол α от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток I=2 А?
Решение: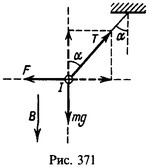 На проводник действуют: силы натяжения двух нитей Т, сила тяжести mg и сила F=BIl со стороны магнитного поля (рис. 371). При равновесии проводника суммы проекций сил (с учетом их знаков) на вертикальное и горизонтальное направления равны нулю:
На проводник действуют: силы натяжения двух нитей Т, сила тяжести mg и сила F=BIl со стороны магнитного поля (рис. 371). При равновесии проводника суммы проекций сил (с учетом их знаков) на вертикальное и горизонтальное направления равны нулю:![]()
отсюда![]()
8 Найти напряженность Н и индукцию B магнитного поля прямого тока в точке, находящейся на расстоянии r=4м от проводника, если ток I=100 А.
Решение:![]()
9 ГОСТ 8.417—81 дает такое определение единицы силы тока — ампера: «Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожной малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длины 1 м силу взаимодействия, равную ![]() ». Исходя из этого определения, вычислить магнитную постоянную mo.
». Исходя из этого определения, вычислить магнитную постоянную mo.
Решение:
Вокруг бесконечно длинного прямолинейного проводника, по которому течет ток I1 образуется магнитное поле, напряженность которого на расстоянии r от проводника![]()
а индукция![]()
При этом векторы Н и В направлены одинаково и лежат в плоскости, перпендикулярной к проводнику. На отрезок второго проводника длины l, по которому течет ток I2, магнитное поле действует с силой![]()
где α — угол между направлениями отрезка проводника и магнитной индукции. Так как второй проводник параллелен первому, то α = 90° и sinα = 1. Таким образом,![]()
Подставив значения![]()
найдем![]()
10 Индукция однородного магнитного поля B=0,5 Тл. Найти магнитный поток через площадку S=25 см2, расположенную перпендикулярно к линиям индукции. Чему будет равен магнитный поток, если площадку повернуть на угол α = 60° от первоначального положения?
Решение: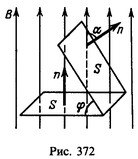 На рис. 372 показано направление магнитной индукции и положение площадки в обоих случаях. По определению магнитный поток
На рис. 372 показано направление магнитной индукции и положение площадки в обоих случаях. По определению магнитный поток![]()
где α — угол между нормалью n к площадке и направлением магнитной индукции В. В первом случае![]()
во втором случае α=φ (углы с взаимно перпендикулярными сторонами) и ![]()
11 Найти магнитную индукцию и магнитный поток через поперечное сечение никелевого сердечника соленоида (рис. 141), если напряженность однородного магнитного поля внутри соленоида H=25 кА/м. Площадь поперечного сечения сердечника S=20 см2, магнитная проницаемость никеля μ = 200.
Решение:![]()
12 Магнитный поток через поперечное сечение катушки, имеющей n=1000 витков, изменился на величину ΔФ = 2 мВб в результате изменения тока в катушке от I1 = 4 А до I2 = 20А. Найти индуктивность L катушки.
Решение:![]()
13 Виток площади S = 2 см2 расположен перпендикулярно к линиям индукции однородного магнитного поля. Найти индуцируемую в витке э.д.с, если за время Δt = 0,05 с магнитная индукция равномерно убывает от B1=0,5Тл до В2 = 0,1 Тл.
Решение:![]()
14 Какой магнитный поток пронизывал каждый виток катушки, имеющей n =1000 витков, если при равномерном исчезновении магнитного поля в течение времени Δt = 0,1 с в катушке индуцируется э.д.с. ε = 10 В?
Решение:![]()
15 Рамка в форме равностороннего треугольника помещена в однородное магнитное поле с напряженностью H=64кА/м. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 30°. Найти длину стороны рамки а, если в рамке при выключении поля в течение времени Δt = 0,03 с индуцируется э. д. с. ε = 10 мВ.
Решение:
Начальный магнитный поток через рамку![]()
где ![]()
площадь рамки и B=µ0H-магнитная индукция. Конечный магнитный поток Ф2=0. Изменение магнитного потока![]()
Э.д.с. индукции ![]()
отсюда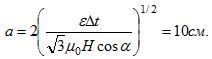
16 Квадратная рамка со стороной а=10см помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 60°. Найти магнитную индукцию В этого поля, если в рамке при выключении поля в течение времени Δt = 0,01 с индуцируется э.д.с. ε = 50 мВ.
Решение:![]()
17 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле перпендикулярно к линиям индукции. Сопротивление витка R=1 Ом. Какой ток I протечет по витку, если магнитная индукция поля будет убывать со скоростью ΔB/Δt = 0,01 Тл/с?
Решение:![]()
18 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле с напряженностью H=80 кА/м, перпендикулярное к линиям индукции. Сопротивление витка R = 1 Ом. Какой заряд протечет по витку, если поле будет исчезать с постоянной скоростью?
Решение:![]()
19 Какова индуктивность катушки с железным сердечником, если за время Δt = 0,5 с ток в цепи изменился от I1 = 10 А до I2 = 5 А, а возникшая при этом э.д.с. самоиндукции ε = 25 В?
Решение:
Э.д.с. самоиндукции![]()
отсюда![]()
20 Проводник длины l=2 м движется в однородном магнитном поле со скоростью v = 5 м/с, перпендикулярной к проводнику и линиям индукции поля. Какая э. д. с. индуцируется в проводнике, если магнитная индукция B=0,1 Тл?
Решение: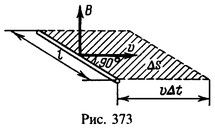 Э.д.с. индукции
Э.д.с. индукции![]()
магнитный поток через площадь ΔS, «заметаемую» проводником за время Δt (рис. 373). Опуская знак минус, найдем![]()
21 Самолет летит горизонтально со скоростью v = 900 км/ч. Найти разность потенциалов, возникающую между концами крыльев самолета, если вертикальная составляющая индукции земного магнитного поля Bo = 0,5 мкТл и размах крыльев самолета l=12 м.
Решение:
Крылья самолета за время Δt «заметают» площадь![]()
Магнитный поток через эту площадь равен![]()
где![]()
вертикальная составляющая индукции земного магнитного поля (α — угол между вертикалью и направлением магнитной индукции). Разность потенциалов V между концами крыльев самолета равна э.д.с. ε, индуцируемой в металлических крыльях и корпусе самолета при его движении в магнитном поле Земли:![]()
22 С какой скоростью должен двигаться проводник длины l=10 см перпендикулярно к линиям индукции однородного магнитного поля, чтобы между концами проводника возникла разность потенциалов V=0,01 В? Скорость проводника составляет с направлением самого проводника угол α = 30°. Линии индукции перпендикулярны к проводнику, индукция B = 0,2 Тл.
Решение: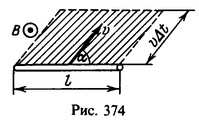 Площадь, «заметаемая» за время Δt проводником, скорость которого v направлена под углом а к самому проводнику, представляет собой площадь параллелограмма (рис.374):
Площадь, «заметаемая» за время Δt проводником, скорость которого v направлена под углом а к самому проводнику, представляет собой площадь параллелограмма (рис.374):![]()
Магнитный поток через эту площадь![]()
Разность потенциалов V между концами проводника равна э.д.с. ε, индуцируемой в этом проводнике:![]()
23 Какой ток идет через гальванометр, присоединенный к железнодорожным рельсам, при приближении к нему поезда со скоростью v = 60 км/ч? Вертикальная составляющая индукции земного магнитного поля Bо=50 мкТл. Сопротивление гальванометра R=100 Ом. Расстояние между рельсами l=1,2 м; рельсы считать изолированными друг от друга и от земли.
Решение:![]()
24 Квадратная рамка со стороной l=2 см помещена в однородное магнитное поле с индукцией B = 100 Тл. Плоскость рамки перпендикулярна к линиям индукции поля. Сопротивление рамки R=1 Ом. Какой ток протечет по рамке, если ее выдвигать из магнитного поля со скоростью ν = 1 см/с, перпендикулярной к линиям индукции? Поле имеет резко очерченные границы, и стороны рамки параллельны этим границам.
Решение: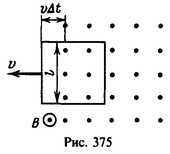 Пока рамка находится в области, где имеется магнитное поле, магнитный поток через поверхность, ограниченную рамкой,
Пока рамка находится в области, где имеется магнитное поле, магнитный поток через поверхность, ограниченную рамкой,
при движении рамки не изменяется. Поэтому э.д.с. индукции в рамке не возникает. После того как одна из сторон рамки вышла за границу поля (рис. 375), магнитный поток через поверхность, ограниченную рамкой, будет изменяться. За время Δt рамка перемещается на расстояние νΔt и часть площади рамки, которую пересекает магнитное поле, уменьшается на величину ![]()
Магнитный поток за это время изменяется на величину ![]()
Индуцируемая в рамке э.д.с.![]()
и по рамке протечет ток![]()
Когда рамка выйдет из области, где имеется магнитное поле, э.д.с. индукции снова станет равной нулю.
25 Проволочный виток площади S= 1 см2, имеющий сопротивление R = 1 мОм, пронизывается однородным магнитным полем, линии индукции которого перпендикулярны к плоскости витка. Магнитная индукция изменяется со скоростью ΔB/Δt = 0,01 Тл/с. Какое количество теплоты выделяется в витке за единицу времени?
Решение: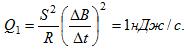
26 Прямоугольная рамка, подвижная сторона которой имеет длину l, помещена в однородное магнитное поле с индукцией B. Плоскость рамки перпендикулярна к линиям индукции магнитного поля. Подвижную сторону, которая вначале совпадает с противоположной ей неподвижной, начинают двигать равномерно со скоростью ν. Найти зависимость тока I в рамке от времени t. Сопротивление единицы длины проводника равно Rl.
Решение:![]()
27 Два параллельных, замкнутых на одном конце провода, расстояние между которыми l=50 см, находятся в однородном магнитном поле с индукцией B = 5 мТл. Плоскость, в которой расположены провода, перпендикулярна к линиям индукции поля. На провода положен металлический мостик, который может скользить по проводам без трения. Мостик под действием силы F=0,1 мН движется со скоростью ν=10м/с. Найти сопротивление R мостика. Сопротивлением проводов пренебречь.
Решение:![]()
28 Рамка из n = 1000 витков, имеющих площадь S = 5 см2, замкнута на гальванометр с сопротивлением R=10 кОм и помещена в однородное магнитное поле с индукцией B=10мТл, причем линии индукции поля перпендикулярны к ее плоскости. Какой заряд q протечет по цепи гальванометра, если направление индукции магнитного поля плавно изменить на обратное?
Решение:
При плавном изменении магнитной индукции в рамке индуцируется э.д.с.![]()
где ΔФ-изменение магнитного потока, Δt — время, в течение которого происходило это изменение. Ток в рамке![]()
Заряд, протекший по цепи за время Δt,![]()
Начальный поток магнитной индукции![]()
При изменении направления магнитного поля на обратное магнитный поток изменяет знак. Поэтому конечный магнитный поток![]()
Изменение магнитного потока![]()
Таким образом,![]()
29 Замкнутая катушка диаметра D с числом витков n помещена в однородное магнитное поле с индукцией В. Плоскость катушки перпендикулярна к линиям индукции поля. Какой заряд q протечет по цепи катушки, если ее повернуть на 180? Проволока, из которой намотана катушка, имеет площадь сечения S и удельное сопротивление ρ.
Решение:![]()
30 В цепь включены последовательно источник тока с э.д.с. ε = 1,2 В, реостат с сопротивлением R=1 Ом и катушка с индуктивностью L=1 Гн. В цепи протекал постоянный ток I0. С некоторого момента сопротивление реостата начинают менять так, чтобы ток уменьшался с постоянной скоростью ΔI/Δt = 0,2 А/с. Каково сопротивление R, цепи спустя время t = 2 с после начала изменения тока?
Решение:
Сумма э.д.с. источника тока и э.д.с, индуцируемой в цепи при равномерном изменении тока, равна![]()
Ток изменяется
по закону![]()
Сопротивление цепи в любой момент времени![]()
В момент времени t= 2 с искомое сопротивление Rt= 1,75 0м.
31 Какой ток I покажет амперметр в схеме, изображенной на рис. 142, если индукция перпендикулярного к плоскости рисунка однородного магнитного поля меняется с течением времени по закону B = kt? Точки с и d лежат на концах диаметра проволочного кольца. Сопротивление единицы длины проволоки равно Rl; диаметр кольца равен D.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 января 2020 года; проверки требуют 11 правок.
Магни́тная проница́емость — физическая величина, коэффициент (зависящий от свойств среды), характеризующий связь между магнитной индукцией 

Для разных сред этот коэффициент различен, поэтому говорят о магнитной проницаемости конкретной среды (подразумевая её состав, состояние, температуру и т. д.).
Обычно обозначается греческой буквой 
История[править | править код]
Впервые этот термин встречается в работе Вернера Сименса «Beiträge zur Theorie des Elektromagnetismus» («Вклад в теорию электромагнетизма») опубликованной в 1881 году[1].
Определения[править | править код]
Соотношение между магнитной индукцией и напряжённостью магнитного поля через магнитную проницаемость вводится как:
,
и 
.
Для изотропных веществ запись 
Через 

Магнитная проницаемость 


Смысл[править | править код]
Величина магнитной проницаемости отражает, насколько массово магнитные моменты отдельных атомов или молекул данной среды ориентируются параллельно приложенному внешнему магнитному полю некоей стандартной напряжённости и насколько велики эти моменты. Значениям 
Есть аналогия с содержанием понятия «диэлектрическая проницаемость» как показателя меры реагирования электрических дипольных моментов молекул на электрическое поле.
Свойства[править | править код]
Магнитная проницаемость в СИ связана с магнитной восприимчивостью χ соотношением:
,
а в гауссовой системе аналогичное соотношение выглядит как
.
Вообще говоря, магнитная проницаемость зависит как от свойств вещества, так и от величины и направления магнитного поля для анизотропных веществ (и, кроме того, от температуры, давления и т. д.).
Также она зависит от скорости изменения поля со временем, в частности, для синусоидального изменения поля — зависит от частоты этого колебания (в этом случае для описания намагничивания вводят комплексную магнитную проницаемость, чтобы описать влияние вещества на сдвиг фазы B относительно H). При достаточно низких частотах — небольшой быстроте изменения поля, её можно обычно считать в этом смысле независимой от частоты.
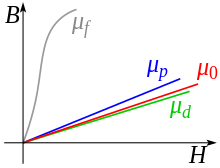
Схематический график зависимости ‘B’ от ‘H’ (кривая намагничивания) для ферромагнетиков, парамагнетиков и диамагнетиков, а также для вакуума, иллюстрирующий различие магнитной проницаемости (представляющей собою наклон графика) для: ферромагнетиков (μf), парамагнетиков (μp), вакуума(μ0) и диамагнетиков (μd)

Магнитная проницаемость сильно зависит от величины поля для нелинейных по магнитной восприимчивости сред (типичный пример — ферромагнетики, для которых характерен магнитный гистерезис). Для таких сред магнитная проницаемость, как независящее от поля число, может указываться приближенно, в линейном приближении.
Для неферромагнитных сред линейное приближение 
Классификация веществ по значению магнитной проницаемости[править | править код]
Подавляющее большинство веществ относятся либо к классу диамагнетиков (

Для ферромагнетиков, вследствие гистерезиса, понятие магнитной проницаемости, строго говоря, неприменимо. Однако, в определённом диапазоне изменения намагничивающего поля (в тех случаях, когда можно было пренебречь остаточной намагниченностью, но до насыщения) можно, в лучшем или худшем приближении, всё же представить эту зависимость как линейную (а для магнитомягких материалов ограничение снизу может быть и не слишком практически существенно), и в этом смысле величина магнитной проницаемости бывает измерена и для них.
Сверхпроводники в ряде деталей ведут себя так, как если бы их магнитная проницаемость равнялась нулю: материал выталкивает магнитное поле при переходе в сверхпроводящее состояние. Иногда формально говорят, что сверхпроводники — идеальные диамагнетики, хотя ситуация более сложна.
Магнитная проницаемость воздуха примерно равна магнитной проницаемости вакуума и в технических расчетах принимается равной единице[3].
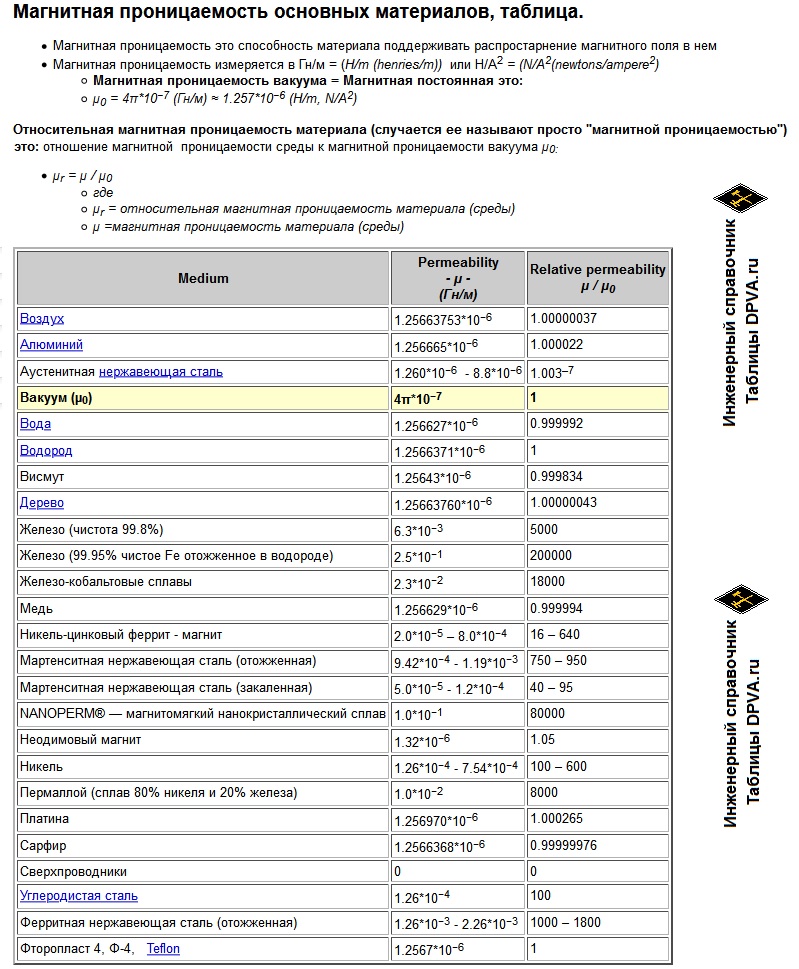
Таблицы значений[править | править код]
В двух таблицах ниже приведены значения магнитной проницаемости некоторых[4] веществ.
Примечание о пользовании первой таблицей:
- берем значение парамагнетика, например, воздуха – 0,38, умножаем его на
и прибавляем единицу, получаем
= 1,00000038,
- берем значение диамагнетика, например, воды – 9, умножаем его на
и вычитаем из единицы, получаем
= 0,999991.
Парамагнетики, |
 |
Диамагнетики, |

|
|---|---|---|---|
| Азот | 0,013 | Водород | 0,063 |
| Воздух | 0,38 | Бензол | 7,5 |
| Кислород | 1,9 | Вода | 9 |
| Эбонит | 14 | Медь | 10,3 |
| Алюминий | 23 | Стекло | 12,6 |
| Вольфрам | 176 | Каменная соль | 12,6 |
| Платина | 360 | Кварц | 15,1 |
| Жидкий кислород | 3400 | Висмут | 176 |
| Medium | Восприимчивость  (объемная, СИ) |
Абсолютная проницаемость  , Гн/м , Гн/м
|
Относительная проницаемость 
|
Магнитное поле | Максимум частоты |
|---|---|---|---|---|---|
| Метглас (англ. Metglas) | 1,25 | 1 000 000[5] | при 0,5 Тл | 100 кГц | |
| Наноперм (англ. Nanoperm) | 10⋅10-2 | 80 000[6] | при 0,5 Тл | 10 кГц | |
| Мю-металл | 2,5⋅10-2 | 20 000[7] | при 0,002 Тл | ||
| Мю-металл | 50 000[8] | ||||
| Пермаллой | 1,0⋅10-2 | 8000[7] | при 0,002 Тл | ||
| Электротехническая сталь | 5,0⋅10-3 | 4000[7][нет в источнике] | при 0,002 Тл | ||
| Никель-цинковый Феррит | 2,0⋅10-5 — 8,0⋅10-4 | 16-640 | от 100 кГц до 1 МГц[источник не указан 4122 дня] | ||
| Марганец-цинковый Феррит | >8,0⋅10-4 | 640 (и более) | от 100 кГц до 1 МГц | ||
| Сталь | 1,26⋅10-4 | 100[7] | при 0,002 Тл | ||
| Никель | 1,25⋅10-4 | 100[7] — 600 | при 0,002 Тл | ||
| Неодимовый магнит | 1,05[9] | до 1,2—1,4 Тл | |||
| Платина | 1,2569701⋅10-6 | 1,000265 | |||
| Алюминий | 2,22⋅10-5[10] | 1,2566650⋅10-6 | 1,000022 | ||
| Дерево | 1,00000043[10] | ||||
| Воздух | 1,00000037[11] | ||||
| Бетон | 1[12] | ||||
| Вакуум | 0 | 1,2566371⋅10-6 (μ0) | 1[13] | ||
| Водород | −2,2⋅10-9[10] | 1,2566371⋅10-6 | 1,0000000 | ||
| Фторопласт | 1,2567⋅10-6[7] | 1,0000 | |||
| Сапфир | −2,1⋅10-7 | 1,2566368⋅10-6 | 0,99999976 | ||
| Медь | −6,4⋅10-6 или −9,2⋅10-6[10] |
1,2566290⋅10-6 | 0,999994 | ||
| Вода | −8,0⋅10-6 | 1,2566270⋅10-6 | 0,999992 | ||
| Висмут | −1,66⋅10-4 | 1 | 0,999834 | ||
| Сверхпроводники | −1 | 0 | 0 |
См. также[править | править код]
- Магнитная восприимчивость
- Диэлектрическая проницаемость
Примечания[править | править код]
- ↑ Werner von Siemens, Lebenserinnerungen
- ↑ Подразумевается суммирование по повторяющемуся индексу (j), то есть запись следует понимать так:
. Эта запись, как легко видеть, означает умножение вектора слева на матрицу по правилам матричного умножения.
- ↑ Намагничивание стали. Магнитная проницаемость. Дата обращения: 16 июля 2011. Архивировано из оригинала 19 марта 2011 года.
- ↑ Магнитная проницаемость. Магнитная проницаемость среды. Относительная магнитная проницаемость. Магнитная проницаемость вещества. Дата обращения: 16 июля 2011. Архивировано из оригинала 12 февраля 2012 года.
- ↑ “Metglas Magnetic Alloy 2714A”, ”Metglas” (недоступная ссылка — история). Metglas.com. Дата обращения: 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ “Typical material properties of NANOPERM”, ”Magnetec” (PDF). Дата обращения: 8 ноября 2011.
- ↑ 1 2 3 4 5 6 “Relative Permeability”, ”Hyperphysics”. Hyperphysics.phy-astr.gsu.edu. Дата обращения: 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Nickel Alloys-Stainless Steels, Nickel Copper Alloys, Nickel Chromium Alloys, Low Expansion Alloys. Nickel-alloys.net. Дата обращения: 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ Juha Pyrhönen, Tapani Jokinen, Valéria Hrabovcová. Design of Rotating Electrical Machines (неопр.). — John Wiley and Sons, 2009. — С. 232. — ISBN 0-470-69516-1.
- ↑ 1 2 3 4 Richard A. Clarke. Clarke, R. ”Magnetic properties of materials”, surrey.ac.uk. Ee.surrey.ac.uk. Дата обращения: 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ B. D. Cullity and C. D. Graham (2008), Introduction to Magnetic Materials, 2nd edition, 568 pp., p.16
- ↑ NDT.net. Determination of dielectric properties of insitu concrete at radar frequencies. Ndt.net. Дата обращения: 8 ноября 2011. Архивировано 3 июня 2012 года.
- ↑ точно, по определению.
Магнитная проницаемость среды железа, стали и ферромагнитных тел (Таблица)
Магнитная проницаемость ферромагнитных тет
Магнитная проницаемость μ ферромагнитных тел определяется выражением:
μ = B/H
где В обозначает магнитную индукцию в теле, а H — напряженность внешнего намагничивающего поля.
В справочной таблице даны значения В и μ при изменении Н в пределах от 1 до 6000 эрстед для: 1) электролитического железа (Fe); 2) никеля (Ni), кобальта (Со) и сплава Гейслера (75,6% Си + 14,25% Mn + 10,15% Al)
|
H |
Fe |
Ni |
Co |
Сплав Гейслера |
||||
|
В |
μ |
В |
μ |
В |
μ |
В |
μ |
|
|
1,0 |
5800 |
5800 |
650 |
650 |
— |
— |
— |
— |
|
1,5 |
7500 |
5000 |
1350 |
900 |
— |
— |
— |
— |
|
2,5 |
9200 |
3680 |
2800 |
1120 |
210 |
84 |
120 |
48 |
|
5,0 |
11000 |
2200 |
4330 |
865 |
570 |
114 |
400 |
80 |
|
10 |
12300 |
1230 |
4940 |
494 |
1700 |
170 |
720 |
72 |
|
20 |
13450 |
673 |
5400 |
270 |
3400 |
170 |
1070 |
54 |
|
50 |
14850 |
297 |
5850 |
117 |
5960 |
119 |
1540 |
31 |
|
100 |
16000 |
160 |
6200 |
62 |
7840 |
78 |
1970 |
20 |
|
150 |
16860 |
112 |
6400 |
43 |
9000 |
60 |
2250 |
15 |
|
300 |
18400 |
61,3 |
6700 |
22 |
— |
— |
2800 |
9,3 |
|
500 |
19200 |
38,4 |
6910 |
14 |
— |
— |
3120 |
6,2 |
|
1000 |
20000 |
20,0 |
7370 |
7,4 |
— |
— |
3670 |
3,7 |
|
2000 |
21060 |
10,5 |
8400 |
4,2 |
_ |
_ |
4710 |
2,4 |
|
3000 |
22100 |
7,4 |
9380 |
3,1 |
— |
— |
5750 |
1,9 |
|
4000 |
23130 |
5,8 |
1040 |
2,6 |
— |
— |
6780 |
1,7 |
|
5000 |
24120 |
4,8 |
— |
— |
— |
— |
7790 |
1,6 |
|
6000 |
25130 |
4,2 |
— |
— |
— |
— |
8790 |
1,5 |
Магнитная проницаемость железа и стали в слабых полях
Значения магнитной проницаемости μ даны при изменении H в пределах от 0,01 до 0,2 эрстед для: 1) электролитического железа неотожженного; 2) стали динамомашинной неотожженной, отожженной один раз и отожженной два раза.
|
H |
Значения магнитной проницаемости μ |
|||
|
Железо неотожженное |
Сталь |
|||
|
неотожж. |
отожж. 1 раз |
отожж. 2 раза |
||
|
0,01 |
300 |
413 |
522 |
351 |
|
0,03 |
420 |
437 |
586 |
433 |
|
0,05 |
560 |
463 |
650 |
540 |
|
0,10 |
975 |
532 |
786 |
872 |
|
0 15 |
1500 |
590 |
912 |
1390 |
|
0,20 |
2100 |
638 |
1040 |
3030 |
_______________
Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, – М.: 1960.


Таблицы DPVA.ru – Инженерный Справочник
Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Магнитная проницаемость. Магнитная постоянная. / / Магнитная проницаемость основных материалов, таблица.
главная страница / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Магнитная проницаемость. Магнитная постоянная. / / Магнитная проницаемость основных материалов, таблица.
Магнитная проницаемость основных материалов, таблица.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск в инженерном справочнике DPVA. Введите свой запрос: |
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
![]()