§ 144. Магнитная проницаемость железа. До сих пор мы
рассматривали
только магнитное поле в вакууме или,
что практически почти то же самое, в
воздухе. Теперь мы переходим к рассмотрению
магнитного поля в различных веществах
и в первую очередь в железе и сходных с
ним сильно намагничивающихся материалах.
Рассмотрим
опыт, схема которого показана на рис.
274. На длинный соленоид I надета индукционная
катушка II,
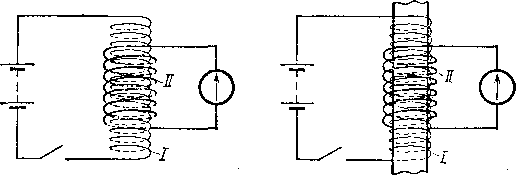
Рис.
274. В надетой на соленоид I катушке II при
замыкании ключа в цепи соленоида
индуцируется ток. Индукционный ток
меньше в отсутствие железного сердечника
в соленоиде (а),
чем с сердечником (б)
а)
б)
в
цепь которой включен так называемый
баллистический гальванометр, т. е.
гальванометр с большим периодом колебаний
подвижной части. Особенность этого
прибора заключается в том, что при
прохождении через него импульсов
тока, длительность которых значительно
(по крайней мере в 10
раз) меньше периода колебаний подвижной
части, максимальное отклонение (отброс)
подвижной части от положения равновесия
оказывается пропорциональным заряду
q,
прошедшему
через гальванометр.
Когда
через соленоид течет ток определенной
силы, сквозь катушку II проходит
определенный магнитный поток Ф. При
выключении тока магнитный поток
уменьшается до нуля, так что изменение
магнитного потока ЛФ— =Ф, т. е. равно
начальному значению магнитного потока.
Это изменение происходит за некоторый
промежуток времени Д/. При этом в катушке
II индуцируется’э.д. с., среднее значение
которой
о
ДФ Ф
Если
сопротивление цепи, в которую включена
катушка II (т. е. общее сопротивление
катушки, гальванометра и соединительных
проводов), равно R,
то
в течение времени Д/ через гальванометр
будет течь ток, среднее значение которого
l-ii-LJ®.
R
~
R
At
‘
В
результате через гальванометр пройдет
заряд
q
= Ibt
= %, (144.1)
который
можно определить по отбросу стрелки
гальванометра (см. упражнения 141.4 и
141.5). Из сказанного вытекает, что, измеряя
отброс стрелки баллистического
гальванометра при включении тока в
соленоиде, можно определять начальное
значение магнитного потока (поток Ф
пропорционален отбросу стрелки).
Проделаем
описанный опыт дважды. Ток в соленоиде
I в обоих случаях установим одинаковый,
но во втором опыте введем предварительно
в соленоид I железный сердечник (рис.
274, б).
Мы обнаружим, что во втором опыте (при
наличии сердечника) отброс стрелки
гальванометра, а следовательно, и
начальное значение магнитного потока
Ф оказываются гораздо большими, чем в
первом опыте (когда железный сердечник
отсутствует). Чтобы без железного
сердечника получить такой же отброс
стрелки гальванометра, как и при наличии
сердечника, нужно было бы во много
раз усилить первичный ток в соленоиде
I. Но усиление первичного тока в соленоиде
I означает, что мы увеличиваем начальное
значение магнитного потока внутри этого
соленоида, а следовательно, и сквозь
катушку II. Таким образом, внесение
железного сердечника сильно увеличивает
начальное значение магнитного потока.
Повторяя наш опыт с сердечниками
различной толщины, мы убедимся, что
увеличение магнитного потока будет
тем больше, чем большая часть do-
леноида
заполняется железом. Наибольшее
увеличение наблюдается, когда весь
соленоид заполнен железом, т. е. когда
обмотка плотно навита на железньщ
сердечник.
Строго
говоря, полное увеличение магнитного
потока достигается лишь тогда, когда
все линии магнитного поля
поток
соленоида: а) наибольшее увеличение
магнитного потока достигается в
кольцеобразном сердечнике; б)
большое увеличение магнитного потока
получается также у длинного и тонкого
соленоида с выступающими концами
сердечника. Первичная катушка I в обоих
случаях должна плотно обвивать
сердечник
проходят
в веществе сердечника. Это бывает,
например, у соленоида, плотно навитого
на замкнутый в виде кольца сердечник
(рис. 275, а).
Однако, »если соленоид достаточно длинен
по сравнению со своими поперечными
размерами и плотно навит на длинный
выступающий сердечник, то индукционная
катушка, помещенная в средней части
соленоида (рис. 275, б), будет пронизываться
практически полным потоком.
В
этом случае отношение магнитных потоков
в соленоиде, навитом на сердечник, и
в том же соленоиде без сердечника’
зависит только от материала сердечника,
конечно, при условии, что начальный ток
в обмотке имеет одно и
то
же значение. Для разных сортов железа
и стали это отношение различно. Обозначая
его греческой буквой ^ (мю), мы можем
написать:
Ф
= ^Ф0,
где
Ф — магнитный поток в катушке с
сердечником, а Ф0
— магнитный поток в катушке без
сердечника.
Величину
р., характеризующую магнитные свойства
железа, использованного для сердечника,
называют его магнитной
проницаемостью
1).
Как уже упоминалось,
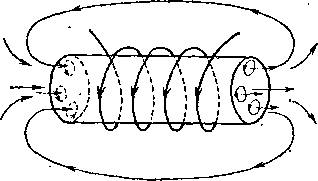
Рис.
276. Под влиянием магнитного поля соленоида
амперовы токи в железном сердечнике
ориентируются так, что направление их
совпадает с током в соленоиде
измерения
показывают, что наличие железного
сердечника увеличивает магнитный поток
весьма значительно, иногда в тысячи
раз. Мы можем, следовательно, сказать,
что магнитная
проницаемость железа весьма велит
и в некоторых случаях может достигать
значения нескольких тысяч.
Возрастание
магнитного потока при введении в
соленоид железа нетрудно понять с точки
зрения представлений об амперовых
молекулярных токах. Под влиянием
магнитного поля соленоида амперовы
токи в железе ориентируются, стремясь
стать параллельно токам обмотки
соленоида (рис. 276). Этим объясняется
намагничивание железа и усиление
магнитного поля во внешнем пространстве.
Этим же объясняется и увеличение
магнитного потока сквозь соленоид при
введении в него сердечника: к магнитному
потоку, создаваемому током в обмотке
соленоида, добавляется магнитный поток,
создаваемый совокупностью ориентированных
амперовых токов.
В
опыте, изображенном на рис. 274, поток
через один виток катушки II равен BS,
где
В
— магнитная индукция поля в соленоиде,
a
S
—
площадь поперечного сечения соленоида.
Поток Ф, фигурирующий в формуле (144.1),
равен NBS
(N
—
число витков катушки II). Отсюда следует,
что увеличение потока Ф в ц раз означает,
что’магнитная индукция В
в железном сердечнике в р. раз больше,
чем
магнитная индукция Вв
(при том же токе в соленоиде) в случае,
когда вместо железа был вакуум. Таким
образом, заполнение железом пространства,
в котором было поле с индукцией Во,
увеличивает индукцию поля в р. раз:
B
= xB0. (144.2)
В
§ 126 мы отмечали, что наряду с магнитной
индукцией В,
которая является основной силовой
1)
характеристикой магнитного поля, в
некоторых случаях оказывается полезной
вспомогательная
характеристика Н,
связанная с В
соотношением (см. формулу (126.4))
Б
= рц,0Я (144.3)
и
называемая напряженностью
магнитного поля (напомним, что р0
— магнитная постоянная, см. формулу
(126.2)).
В
применении к рассматриваемому опыту
формула
-
дает
50=1ЛоЯ0
(в отсутствие сердечника, когда |Д,=1) и
5=рр0Я
(при наличии сердечника). Поскольку
В=р.В0,
имеем
рр0Я
= рр0Я0,
или Н
= Я0.
Таким
образом, напряженность магнитного поля
не зависит от того, заполнен соленоид
каким-либо материалом или нет. В случае,
когда все пространство, в котором поле
отлично от нуля, заполнено однородным
веществом, напряженность поля не зависит
от свойств этого вещества 2).
§
145. Магнитная проницаемость различных
веществ. Вещества парамагнитные и
диамагнитные. Если в описанных выше
опытах вместо сердечника из железа
брать сердечники из других материалов,
то также можно обнаружить изменение
магнитного потока. Естественнее всего
ждать, что наиболее заметный эффект
дадут материалы, подобные по своим
магнитным свойствам железу, т. е. никель,
кобальт и некоторые магнитные сплавы.
Действительно, при введении в катушку
сердечника из этих материалов увеличение
магнитного потока оказывается довольно
значительным. Иными словами, можно
сказать, что магнитная проницаемость
их велика; у никеля, например, р. может
достигать значения 50, у кобальта 100. Все
эти материалы с большими значениями р.
объединяют в одну группу ферромагнитных
материалов.
Однако
и все остальные «немагнитные» материалы
также оказывают некоторое влияние на
магнитный поток, хотя влияние это
значительно меньше, чем у материалов
ферромагнитных. С помощью очень тщательных
измерений можно это изменение
обнаружить и определить магнитную
проницаемость различных материалов.
При этом, однако, нужно иметь в виду, что
в опыте, описанном выше, мы сравнивали
магнитный поток в катушке, полость
которой заполнена железом, с потоком
в катушке, внутри _ которой имеется
воздух. Пока речь шла о таких сильно
магнитных материалах, как железо, никель,
кобальт, это не имело значения, так как
наличие воздуха очень мало влияет на
магнитный поток. Но при исследовании
магнитных свойств других веществ, в
частности самого воздуха, мы должны,
конечно, вести сравнение с катушкой,
внутри которой воздуха нет (вакуум).
Таким образом, за магнитную
проницаемость мы принимаем отношение
магнитных потоков в исследуемом
веществе и в вакууме
(ц= =Ф/Ф0).
Иными словами, за
единицу мы принимаем магнитную
проницаемость для вакуума
(если
Ф=Ф0,
то
|л.=1).
Измерения
показывают, что магнитная проницаемость
всех веществ отлична от единицы, хотя
в большинстве случаев это отличие очень
мало. Но особенно замечательным
оказывается тот факт, что у одних веществ
магнитная проницаемость р, больше
единицы, а у других она меньше единицы,
т. е. заполнение катушки одними веществами
увеличивает магнитный поток, а заполнение
катушки другими веществами уменьшает
этот поток. Первые из э_тих веществ
называются парамагнитными
(pOl),
а
вторые — диамагнитными
((*<!). Как показывает табл. 7, отличие
проницаемости ц от единицы как у
парамагнитных, так и у диамагнитных
веществ невелико,.
Нужно
особенно подчеркнуть, что для парамагнитных
и диамагнитных тел магнитная проницаемость
р. не > зависит от магнитной индукции
внешнего, намагничивающего поля, т.
е. представляет собой постоянную
величину, характеризующую данное
вещество. Как мы увидим § 149, это не имеет
места для железа и других сходных с ним
(ферромагнитных) тел.
Таблица
7.
Магнитная проницаемость для
некоторых
парамагнитных и
диамагнитных
веществ
|
Парамагнитные |
Диамагнитные |
||
|
Азот |
1,000013 |
Водород |
0,999937 |
|
Воздух |
1,000038 |
ный) |
|
|
Кислород |
1,000017 |
Вода |
0,999991 |
|
Кислород |
1,0034 |
Стекло |
0,999987 |
|
Эбонит |
1,000014 |
Цинк |
0,999991 |
|
Алюминий |
1,000023 |
Серебро |
0,999981 |
|
Вольфрам |
1,000175 |
Золото |
0,999963 |
|
Платина |
1,000253 |
Медь |
0,999912 |
|
Висмут |
0,999824 |
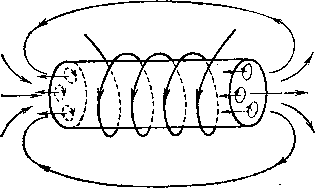
Рис.
277. Диамагнитные вещества внутри катушки
ослабляют магнитное поле соленоида.
Элементарные токи в них направлены
противоположно току « соленоиде
Влияние
парамагнитных и диамагнитных веществ
на магнитный поток объясняется, так же
как и влияние веществ ферромагнитных,
тем, что к магнитному потоку, создаваемому
током в обмотке катушки, присоединяется
поток, исходящий из элементарных
амперовых токов. Парамагнитные
вещества увеличивают магнитный
поток катушки.
Это
увеличение потока при заполнении
катушки парамагнитным веществом
указывает на то, что и в
парамагнитных веществах под действием
внешнего магнитного поля элементарные
токи ориентируются так, что направление
их совпадает с направлением тока
обмотки
(рис. 276). Небольшое отличие р. от единицы
указывает лишь на то, чт;о в случае
парамагнитных веществ этот добавочный
магнитный поток очень невелик, т. е.
что парамагнитные вещества намагничиваются
очень слабо.
Уменьшение
магнитного потока при заполнении
катушки диамагнитным веществом
означает, что в этом случае магнитный
поток от элементарных амперовых токов
направлен противоположно магнитному
потоку катушки, т. е. что в
диамагнитных веществах под действием
внешнего магнитного поля возникают
элементарные токи, направ
ленные
противоположно токам обмотки
(рис. 277). Малость отклонений (J.
от
единицы и в этом случае указывает на
то, что дополнительный поток этих
элементарных токов невелик.
§
146. Движение парамагнитных и диамагнитных
тел в магнитном поле. Опыты Фарадея.
Притяжение
железных предметов к магнитам является
наиболее простым и бросающимся в
глаза проявлением магнитного поля и
исторически послужило основой всего
развития учения о магнетизме. Оно
сводится к воздействию магнитного поля
на ориентированные молекулярные токи
намагнитившегося железа. Так же, но
только значительно слабее должно
действовать магнитное поле и
на
парамагнитные тела,
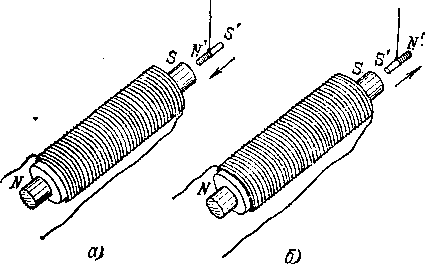
Рис.
278. а)
При намагничивании парамагнитного или
ферромагнитного тела на ближайшем
к магниту конце возникает полюс,
разноименный с полюсом намагничивающего
магнита; парамагнитное тело притягивается
к магниту, б)
В тех же условиях на ближайшем к магниту
конце диамагнитного тела возникает
полюс одноименный; диамагнитное
тело отталкивается от магнита
потому
что, как мы могли судить по опытам,
описанным в предыдущем параграфе, и в
парамагнитных телах ориентация
элементарных токов происходит так же,
как в ферромагнитных: магнитный поток
элементарных токов усиливает, хотя и
незначительно, магнитный поток
ориентирующего поля и, следовательно,
парамагнитные
тела притягиваются к магниту
(рис. 278, а).
В
отличие от тел парамагнитных, диамагнитные
тела уменьшают магнитный поток катушки.
Это означает, что в диамагнитном теле
под действием внешнего поля возникают
элементарные токи такого направления,
что их магнитное поле противоположно
направлению внешнего магнитного
поля. Следовательно, и действие внешнего
магнитного поля на диамагнитные тела
противоположно по направлению
действию его на тела ферро- и парамагнитные,
т. е. диамагнитные
тела отталкиваются от магнита
(рис. 278, б). ч
Мы
можем выразить этот факт и несколько
иначе. Когда мы подносим к магниту
какое-нибудь железное тело, то оно
намагничивается так, что на той стороне
его, которая обращена к магниту, возникает
полюс, разноименный с полюсом магнита;
то же имеет место и в случае парамагнитного
тела (рис. 278, а).
Напротив, в случае диамагнитного
тела на стороне, ближайшей к полюсу
намагничивающего магнита, возникает
полюс, одноименный с этим полюсом магнита
(рис. 278, б). Рис. 276 и 277 поясняют, почему
парамагнитные тела притягиваются к
магниту, а диамагнитные отталкиваются
от него.
Именно
такие действия и были обнаружены
Фарадеем. В 1845 г., использовав сильный
электромагнит, Фарадей установил
способность всех
тел намагничиваться и открыл, что одни
тела, притягиваются к магниту, а другие
отталкиваются от него. Он предложил
для первых название парамагнитных, для
вторых название диамагнитных. Индукционные
опыты с пара- и диамагнитными телами,
подобные описанным в § 144, были
произведены значительно позже, когда
магнитные свойства диамагнитных и
парамагнитных тел были уже установлены
на основании исследований Фарадея.
По
силе притяжения или отталкивания можно
судить и количественно о способности
тела намагничиваться, т. е. можно
определить магнитную проницаемость ц.
для данного вещества. Этот метод
измерения ц, основанный на изучении
притяжения илн отталкивания маленького
тела из данного вещества, теоретически
более сложен, чем описанный нами в §
145 метод, основанный на измерении
магнитного потока. Но зато он гораздо
чувствительнее и, кроме того, пригоден
для измерения в маленьком образчике
вещества, тогда как для измерения ц по
индукционному способу нужно заполнить
изучаемым веществом всю полость катушки.
В тех случаях, когда удается измерить
ц
и тем и другим способом, получаются
согласующиеся результаты.
л
146.1. Полюсы сильного
электромагнита
на рис. 279 срезаны не-
-
параллельно
друг другу, так что внизу расстояние
между ними значительно меньше, чем
наверху. Между ними подвешивается на
нити шарик из различных испытуемых
материалов. Верхний конец нити прикреплен
к спиральной пружинке, растяжение
которой позволяет измерить силу,
действующую со стороны магнитного
поля на шарик (пружинные весы). Оказывается,
что если шарик изготовлен из алюминия,
вольфрама или платины, то эта сила
направлена вниз (пружинка растягивается),
а в случае серебра, золота, меди или
висмута она направлена вверх (пружинка
сокращается). Объясните этот опыт.
-
При
исследовании магнитной проницаемости
жидких веществ часто поступают так.
Жидкость наливают в коленчатую
Рис.
280. К упражнению 146.2
Рис.
279. К упражнению 146.1
трубку
и одно из колен помещают между полюсами
сильного электромагнита (рис. 280). Жидкость
в этом колене поднимается или опускается
в зависимости от того, является ли она
парамагнитной или диамагнитной.
Объясните это явление.
§
147. Молекулярная теория магнетизма.
Теория, объясняющая различие в
магнитных свойствах веществ на основе
изучения строения отдельных частиц
этих веществ — их атомов или молекул,—
получила название молекулярной
теории магнетизма.
Эта теория очень сложна и во многом еще
не завершена. Поэтому здесь мы не можем
разбирать ее сколько-нибудь подробно.
Укажем лишь на основные причины различия
между свойствами парамагнитных и
диамагнитных тел.
Каждое
тело, и парамагнитное и диамагнитное,
представляется нам в целом ненамагниченным
до тех пор, пока на него не действует
внешнее магнитное поле. Но обусловливается
это в телах парамагнитных и в телах
диамагнитных разными причинами.
Диамагнитными являются тела, каждая
частица которых — атом или молекула,—
находясь вне магнитного поля, не обладает
магнитными свойствами. Только внешнее
магнитное поле превращает их в элементарные
магниты (вызывает элементарные токи),
определенным образом направленные.
Напротив, частицы парамагнитных
веществ уже сами по себе, еще до того,
как на них начало действовать внешнее
поле, представляют собой элементарные
магниты (элементарные токи). Здесь роль
внешнего магнитного поля сводится
к определенной ориентации, упорядочению
расположения этих магнитиков. Пока поле
не действовало, все они были расположены
беспорядочно, хаотически, и вещество
в целом представлялось нам ненамагниченным.
В магнитном же поле эти элементарные
магниты выстраиваются в большей или
меньшей мере параллельными цепочками,
и вещество в целом намагничивается.
В
чем же состоит различие между строением
частиц диамагнитных и парамагнитных
веществ? В атомах всех тёл есть большое
число движущихся электронов. Каждый
из них и представляет собой амперов
элементарный круговой ток. Но в атомах
диамагнитных веществ до внесения их
в магнитное поле магнитные действия
этих отдельных токов взаимно
компенсируют друг друга, так что атом
в целом не является элементарным
магнитом. Когда мы вносим такое вещество
в магнитное поле, то на кансдый движущийся
электрон действует сила Лоренца, и
совокупное действие всех этих сил,
как показывает расчет, приводит к тому,
что в атоме индуцируется определенный
ток, т. е. атом приобретает свойства
элементарного магнита. Так как эти токи
являются индукцион
ными,
то направление их, согласно правилу
Ленца, должно быть противоположно
направлению тока в катушке, создающего
внешнее магнитное поле, т. е. магнитный
поток от этих токов должен ослаблять
поток внешнего поля, и диамагнитное
тело отталкивается от магнита.’
В
атомах парамагнитных веществ магнитные
действия отдельных электронов не
полностью компенсируют друг друга, так
что атом в целом и сам по себе является
элементарным магнитом. Действие внешнего
магнитного поля упорядочивает расположение
этих элементарных токов, причем токи
ориентируются так, что их направление
преимущественно совпадает с направлением
тока катушки, создающего внешнее
магнитное поле. Поэтому магнитный
поток от элементарных токов в этом
случае усиливает поток катушки, и
парамагнитное тело притягивается к
магниту.
Строго
говоря, диамагнетизм есть общее свойство
всех веществ. Внешнее магнитное поле
производит и на атомы парамагнитных
веществ такое же индуцирующее
действие, как на атомы диамагнитных
веществ. Но в парамагнитных веществах
это действие перекрывается более сильным
ориентирующим действием внешнего
магнитного поля, которое упорядочивает
собственные элементарные токи атомов.
Мы
видим, таким образом, что диамагнетизм
и парамагнетизм объясняются различиями
в строении самих атомов или молекул
вещества.

Рис.
281. Изменение магнитного поля при
внесении в него куска железа
§
148. Магнитная защита. Само собой разумеется,
что намагничивание ферромагнитных,
парамагнитных и диамагнитных тел
происходит не только тогда, когда мы
помещаем их внутрь соленоида, но и
вообще всегда, когда вещество помещается
в магнитное поле. Во всех этих случаях
к магнитному полю, которое существовало
до внесения в него вещества, добавляется
магнитное поле, обусловленное
намагничиванием этого вещества, в
результате чего магнитное поле
изменяется. Из сказанного в предыдущих
параграфах ясно, что наиболее сильные
изменения поля происходят при внесении
в него ферромагнитных тел, в частности
железа изменение магнитного поля
вокруг ферромагнитных тел очень удобно
наблюдать, пользуясь картиной линий
поля, получаемой
при
помощи железных опилок. На рис. 281
изображены, ’ . например, изменения,
наблюдающиеся при внесении куска
железа прямоугольной формы в магнитное
поле, которое раньше было однородным.
Как видим, поле перестает быть
однородным и приобретает сложный
характер; в одних местах оно усиливается,
в других — ослабляетея.
-
Когда
на современных судах устанавливают и
выверяют
-
компасы,
тр вводят поправки к показаниям компаса,
зависящие
от
формы и расположения частей судна и от
положения компаса не нем. Объясните,
почему это необходимо. Зависят ли
поправки от сорта стали, примененной
при постройке судна?
-
Почему
суда, снаряжаемые экспедициями для
исследования магнитного поля Земли,
строят не стальные, а деревянные и для
скрепления обшивки променяют медные
винты?
Очень
интересна и практически важна картина,
которая наблюдается при внесении в
магнитное поле замкнутого железного
сосуда, например полого шара. Как видно
из рис. 282, в результате сложения внешнего
магнитного

Рис.
282. Полый железный шар внесен в однородное
магнитное поле
поля
с полем намагнитившегося железа поле
во внутренней области шара почти
исчезает. Этим пользуются для
В
Рис.
283. Линии магнитного поля сосредоточены
в железном кольце, внесенном в магнитное
поле
создания
магнйтной
защиты
или магнитной
экранировки, т.
е. для защиты тех или иных приборов от
действия внешнего магнитного поля.
Картина,
которую мы наблюдаем при создании
магнитной защиты, внешне напоминает
создание электростатической защиты
при помощи проводящей оболочки. Однако
между этими явлениями есть глубокое
принципиальное различие. В случае
электростатической защиты металлические
стенки могут1
быть сколь угодно тонкими. До
статочно,
например, посеребрить поверхность
стеклянного сосуда, помещенного в
электрическое поле, чтобы внутри сосуда
не оказалось поля, которое обрывается
на поверхности металла. В случае же
магнитного поля тонкие железные
стенки не являются защитой для внутреннего
пространства: магнитные поля проходят
сквозь железо, и внутри сосуда оказывается
некоторое магнитное поле. Лишь при
достаточно толстых железных стенках
ослабление поля внутри полости может
сделаться настолько сильным, что
магнитная, защита приобретает практическое
значение, хотя и в этом, случае поле
внутри не уничтожается полностью. И
в этом случае ослабление поля не есть
результат обрыва его на поверхности
железа; линии магнитного поля отнюдь
не обрываются, но по-прежнему остаются
замкнутыми, проходя сквозь железо.
Изображая .графически распределение
линий магнитного поля в толще железа и
в полости, получим картину (рис. 283),
которая . .и показывает, что ослабление
поля внутри полости есть результат
изменения направления линий поля, а не
их обрыва.
353
§
149. Особенности ферромагнитных тел.
Бросающейся в глаза особенностью
ферромагнитных тел является их способность
к сильному намагничиванию, вследствие
которой магнитная проницаемость
этих тел имеет очень большие значения.
У железа, например, магнитная проницаемость
(J.
достигает
значений, которые в тысячи раз превосходят
значения ц у парамагнитных и диамагнитных
веществ. Намагничивание ферромагнитных
тел было изучено в опытах А. Г. Столетова
и других ученых. Эти опыты показали,
сверх того, что, в отличие от парамагнитных
и диамагнитных веществ, магнитная
проницаемость ферромагнитных веществ
сильно зависит от напряженности 1)
магнитного поля,
при которой производят ее измерение.
Так, например, в слабых полях магнитная
проницаемость |х железа достигает
значений шести тысяч, а в сильных полях
значения (А падают до нескольких сот и
ниже.
В
§§ 118 и 119 для характеристики магнитных
свойств контуров с током была введена
векторная величина рт,
называемая
магнитным
моментом
тока (см. формулу – (118.1)). Молекулярные
токи также обладают магнитным
моментом.
Когда вещество не намагничено, магнитные
моменты отдельных молекулярных токов
ориентированы хаотически (беспорядочно),
вследствие чего их векторная сумма
равна нулю, вещество в целом магнитным
моментом не обладает.
Под
действием внешнего магнитного поля
магнитные моменты молекулярных токов
приобретают в большей или меньшей
степени преимущественную ориентацию
в направлении поля (в случае ферро-
и парамагнетиков) либо возникают
индукционные молекулярные токи, магнитные
моменты которых ориентированы против
поля (в случае диамагнетиков, § 147). В
результате суммарный магнитный
момент молекулярных токов становится
отличным от нуля, и тело оказывается
намагниченным. Естественно в качестве
меры намагниченности вещества принять
суммарный
магнитный момент молекулярных токов,
заключенных в единице объема вещества.
В соответствии с этим вводится векторная
величина J,
называемая
намагничен-
нос/пью
вещества и определяемая выражением
У=
2
Рт, (149.1)
по
единице объема
где
Рт
—
магнитный момент отдельного молекулярного
тока.
.
Можно показать, что намагниченность J
связана
с магнитной индукцией В
в веществе и напряженностью магнитного
поля Н
соотношением, которое имеет вид
•/
= £—Н. (149.2)
С
учетом того, что B—ii0H,
получается
формула
У
= (}г—1)//. (149.3)
Заменим
в формуле (149.2) векторы их модулями и
напишем получившееся соотношение в
виде
В
= -j-
[i0«/
=
~1~ М’о*^ =
В0
4″
(напомним,
что в рассматриваемом случае Н=Нй,
а ц-0Я0=
—Во
— магнитной индукции поля соленоида в
отсутствие вещества). Теперь умножим
это соотношение на площадь поперечного
сечения соленоида S:
BS
=
B0Si0JS.
Произведение
BS
равно
Ф — магнитному потоку через сечеНие
соленоида, B0S
равно
Ф0
— магнитному потоку в
отсутствие
вещества. Следовательно, мы приходим к
формуле
Ф
= Ф„ + ^ = Ф0
+ Ф’, (149.4)
где
через Ф’ обозначено выражение ц0</5,
которое можно рассматривать как
добавочный поток магнитной индукции,
создаваемый намагниченным веществом:
Ф’
= [А„ JS. (149.5)
В
случае ферромагнитных и парамагнитных
веществ этот поток положителен (Ф>Фо),
в
случае диамагнитных веществ —
отрицателен (Ф<Ф0).
Таким
образом, намагниченность J
пропорциональна
добавочному потоку, который создается
намагниченным веществом.
Учтя,
что Ф=}лФ0,
из формулы (149.4) легко получить соотношение
Ф’
= = (ц— 1) Ф0. (149.6)
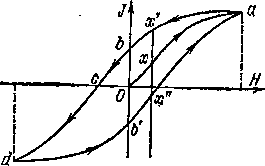
Рис.
284.
Зависимость намагниченности J
от
напряженности внешнего магнитного
поля Н.
Стрелки
указывают направление процесса
Изучение
зависимости намагниченности железа и
других ферромагнитных материалов
от напряженности внешнего магнитного
поля обнаруживает ряд особенностей
этих веществ, имеющих важное
практическое значение.
Возьмем
кусок ненамагничен- ного железа, поместим
его в магнитное поле и будем измерять
намагниченность железа J,
постепенно
увеличивая напряженность внешнего
магнитного поля Н.
Намагниченность J
возрастает
сначала резко, затем все медленнее и,
наконец, при значениях Н
около
нескольких десятков тысяч ампер на метр
намагниченность перестает возрастать:
все элементарные токи уже ориентированы,
железо достигло магнитного
насыщения. Графически
зависимость У от Я в описываемом опыте
изображается кривой Оа
на рис. 284. Горизонтальная часть этой
кривой вблизи точки а
соответствует магнитному насыщению.
Достигнув
насыщения, начнем ослаблять внешнее
магнитное поле. При этом намагниченность
железа уменьшается, но убывание это
идет медленнее, нем раньше шло
ее
возрастание. Зависимость между J
и
Н
в этом случае изображается ветвью кривой
аЬ
на рис. 284. Мы видим, таким образом, -что
одному и тому же значению Н
могуТ соответствовать различные значения
намагниченности (точки х,
х’
и х”
на рис. 284) в зависимости от того, подходим
ли мы к .этому значению со стороны малых
или со стороны больших значений Н.
Намагниченность железа зависит,
стало быть, не только от того, в каком
поле данный кусок находится, но и от
предыдущей истории этого куска. Это
явление получило название магнитного
гистерезиса.
Когда
внешнее магнитное поле становится
равным нулю, железо продолжает сохранять
некоторую остаточную
намагниченность
(§ 112),
которая характеризуется отрезком ОЬ
графика. В этом и заключается причина
того, что из железа или стали можно
изготовлять постоянные магниты.
Для
дальнейшего размагничивания железа
нужно приложить внешнее магнитное
поле, направленное в противоположную
сторону. Ход изменения намагниченности
J
при
возрастании напряженности Н
этого противоположно направленного
поля изображается ветвью кривой bed.
Лишь
когда напряженность этого поля достигнет
определенного значения (в нашем опыте
значения, изображаемого отрезком Ос),
железо будет полностью размагничено
(точка с).
Таким образом, напряженность
размагничивающего поля (отрезок Ос)
является мерой того, насколько прочно
удерживается состояние намагничивания
железа. Ее называют коэрцитивной
силой.
При уменьшении напряженности поля
обратного направления и затем при
возрастании напряженности поля
первоначального направления ход
изменения намагниченности железа
изображается ветвью кривой db‘a.
При
новом повторении всего цикла
размагничивания, перем’агничивания и
повторного намагничивания железа в
первоначальном направлении форма этой
кривой повторяется *). Из рис. 284 видно,
что эта кривая, изображающая ход
зависимости намагниченности железа J
от
напряженности внешнего поля Н,
имеет вид петли. Ее называют петлей
гистерезиса
для данного сорта железа или стали.
Форма петли гистерезиса является
важнейшей
*)■
Ветвь Оа
изображает ход намагничивания исходного
ненамаг- ничённого материала и не
повторяется при повторных циклах. Для
того чтобы вновь воспроизвести ветвь
Оа,
необходимо привести материал в
первоначальное ненам^гниченное состояние.
Для этого достаточно, например, сильно
нагреть его.
характеристикой
магнитных свойств того или иного
ферромагнитного материала. В частности,
зная ее, мы можем определить такие важные
характеристики этого материала, как
его магнитное насыщение, остаточную
намагниченность и коэрцитивную силу.
Процесс
намагничивания вещества можно
характеризовать не только кривой
зависимости У от Я (рис. 284), но и кривой
зависимости В
от Я. Обе зависимости закономерно
связаны друг с другом. Первая из них
имеет
В,
Тл
И,
А/и
Рис.
285. Кривые намагничивания для различных
сортов железа и стали: 1
— мягкое железо,’ 2
— закаленная сталь. 3
— незакаленная сталь

вид
•/= (ц—1 )Я (см. фор мулу (149.3)), вторая —
5=(хцоЯ.
На рис. 285 по- ^ казана зависимость В
от ‘
Я
для различных сортов 1,2.
железа
и стали. По форме этой петли можно выбрать
^8
материал,
который наилуч- q
4
шим
образом подходит для той или иной
практичес- О
кой
задачи. Так, для изго-_^^
товления
постоянных маг-. ’ нитов необходим
материал-<7,8 с большой коэрцитивной
силой (сталь и особенно ’
специальные
сорта кобаль- -%в
товой
стали); для электри- _9
п
ческих
машин и особенно -£ш7
‘-та
о зооо ‘ Ш для
трансформаторов выгодны материалы
с очень малой площадью петли гистерезиса,
ибо они, как оказывается, меньше всего
нагреваются при перемаг-
ничивании
1);
для некоторых специальных приборов
важны материалы, магнитное насыщение
которых достигается при малых полях, и
т. д.
В
отличие от парамагнетиков и диамагнетиков
(§ 145) у ферромагнетиков магнитная
проницаемость ц не остается постоянной,
а зависит от напряженности внешнего
намагничивающего поля Я. Эта зависимость
для магнит
ного
сплава (пермаллоя) и для мягкого железа
показана на рис. 286. Как мы видим, магнитная
проницаемость ц. имеет малые начальные
значения в слабых полях, затем нарастает
до максимального значения и при дальнейшем
увеличении поля снова уменвшается.
Важно
отметить, что при достижении определенной
температуры магнитная проницаемость
ферромагнитных
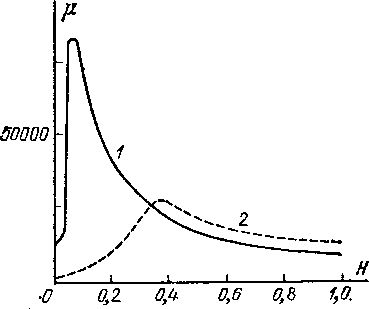
Рис.
286. Зависимость fi
от
Н:
1
— у магнитного сплава (пермаллоя)^ 2
— у мягкого железа
тел
резко падает до значения, близкого к
единице. Эта температура, характерная
для каждого ферромагнитного вещества,
носит название точки
Кюри
по имени французского физика Пьера
Кюри (1859—1906). При температурах
выше точки Кюри
все ферромагнитные тела становятся
парамагнитными.
У железа точка Кюри равна 767 °С, у никеля
— 360 °С, у кобальта — около 1130 °С. У
некоторых ферромагнитных сплавов
точка Кюри лежит вблизи 100 °С.
•f
149.1.
Какой из ферромагнитных материалов,
приведенных на
-
рис.
285, наиболее пригоден для постоянных
магнитов? Какой из них наиболее пригоден
для электромагнитов с выстрой
регулировкой подъемной силы?
-
Можно
ли электромагнитным краном переносить
раскаленные стальные болванки?
его
кристаллической структуры. Атомы железа,
если взять их, например, в парообразном
состоянии, сами по себе диамагнитны или
лишь слабо парамагнитны. Ферромагнетизм
есть свойство железа в твердом состоянии,
т. е. свойство ^кристаллов железа.
В
этом нас убеждает ряд фактов. Прежде
всего на это указывает зависимость
магнитных свойств железа и других
ферромагнитных материалов от обработки,
изменяющей их кристаллическое строение
(закалка, отжиг). Далее оказывается, что
из парамагнитных и диамагнитных металлов
можно изготовить сплавы, обладающие
высокими ферромагнитными свойствами.
Таков, например, сплав’ Гейслера, почти
не уступающий по своим магнитным
свойствам железу, хотя он состоит из
таких слабомагнйт- ных металлов, как
медь (60 %), марганец (25 %)
и алюминий (15 %).
С другой стороны, некоторые сплавы из
ферромагнитных материалов, например1
сплав из 75 % железа и 25 % никеля, почти не
магнитны. Наконец, самым веским
подтверждением является то, что при
достижении определенной температуры
(точки Кюри) все ферромагнитные
вещества теряют свои ферромагнитные
свойства.
Ферромагнитные
вещества отличаются от парамагнитных
не только весьма большим значением
магнитной проницаемости ц и ее
зависимостью от напряженности поля,
но и весьма своеобразной связью между
намагниченностью и напряженностью
намагничивающего поля. Эта особенность
находит свое выражение в явлении
гистерезиса со всеми его следствиями:
наличием остаточной намагниченности
и коэрцитивной силы.
В
чем причина гистерезиса? Вид кривых на
рис. 284 и 285 — различие между ходом
нарастания намагничивания ферромагнетика
при увеличении Н
и ходом его размагничивания при уменьшении
Н
— показывает, что при изменении
намагниченности ферромагнетика, т. е.
при увеличении или уменьшении напряженности
внешнего поля, ориентация и дезориентация
элементарных магнитов не сразу следует
за полем, а происходит с известным
отставанием.
Подробное
изучение процессов намагничивания и
размагничивания железа и других
ферромагнитных веществ показало, что
ферромагнитные свойства вещества
определяются не магнитными свойствами
отдельных атомов или молекул, которые
сами по себе парамагнитны, а намагничиванием
целых областей, называемых доменами
*),— небольших участков вещества,
содержащих очень большое число атомов.
Взаимодействие магнитных моментов
отдельных атомов ферромагнетика
приводит к созданию чрезвычайно
сильных внутренних магнитных полей,
действующих в пределах каждой такой
области и выстраивающих в пределах этой
области все атомные магнитики параллельно
друг другу, как показано на рис. 287. Таким
образом, даже в отсутствие внешнего
поля ферромагнитное вещество состоит
из ряда отдельных областей, каждая из
которых самопроизвольно намагничена
до насыщения. Но
направление
намагниченности для разных областей
различно, так что вследствие хаотичности
распределения этих областей тело в
целом оказывается в отсутствие
внешнего поля ненамагниченным.
k
A »
КОТОрЫХ
параллельна внешнему по-
* лю,
и вещество в целом оказывается
I
|
f
t
f I t t t M ft M t ft
Под.
влиянием внешнего поля происходит
перестройка и перегруппировка таких
областей самопроизвольного намагничивания,
в результате которой получают
преимуще- Z ство
те области, намагниченность
намагниченным.
а)
|
н
f
f t t t
-
i
и
I
t
M ft Hill
-
tt
t
б)
Рис.
287. Схема ориентации молекулярных
магнитов в областях самопроизвольного
намагничивания 1
и 2:
а)
внешнее магнитное поле отсутствует;
б)
под действием внешнего магнитного поля
области 1
и 2
перестраиваются
Один
из примеров такой перестройки областей
самопроизвольного намагничивания
показан на рис. 287. Здесь условно изображены
две смежные области, направления
намагниченности которых перпендикулярны
друг к другу. При наложении внешнего
поля часть атомов области 2,
в которой намагниченность перпендикулярна
к полю, на границе ее с областью 1,
в которой намагниченность параллельна
полю, поворачивается, так что направление
их магнитного момента становится
параллельным полю. В результате область
1,
намагниченная параллельно внешнему
полю, расширяется за счет тех областей,
в которых направление намагниченности
образует большие углы с направлением
поля, и возникает преимущественное
намагничивание тела по направлению
внешнего поля. В очень сильных внешних
полях возможны и повороты направления
ориентации всех атомов в пределах целой
области.
При
снятии (уменьшении) внешнего поля
происходит обратный процесс распада
и дезориентации этих областей, т. е.
размагничивание тела. Ввиду больших по
сравнению с атомами размеров областей
самопроизвольного намагничивания
как процесс ориентации их, так и обратный
процесс дезориентации происходят с
гораздо большими затруднениями, чем
установление ориентации или дезориентации
отдельных молекул или атомов, имеющее
место в парамагнитных и диамагнитных
телах. Этим и объясняется отставание
намагничивания и размагничивания
от изменения внешнего поля, т. е. гистерезис
ферромагнитных тел.
Предлагаемая методика и соответствующая ей программа (MUCalculator.exe) предназначены для измерения и расчета магнитной проницаемости материалов магнитопроводов импульсных блоков питания. Это позволяет использовать магнитопроводы без маркировки или с неизвестной маркировкой.
На страницах сайта и на страницах радиолюбительских журналов опубликовано множество описаний импульсных блоков питания. Один из основных элементов такого устройства — импульсный трансформатор, от правильного расчета которого зависят работоспособность, надежность и долговечность блока и питаемого прибора. В описаниях этих устройств указаны материал и типоразмер магнитопровода, а также намоточные данные трансформатора, поэтому проблем с изготовлением устройства не возникает. А как быть радиолюбителю, который решил повторить устройство, но не может найти нужный магнитопровод? На помощь приходят методики и программы расчета импульсного трансформатора [1, 2]. Зачастую у радиолюбителя накапливаются трансформаторы от различных блоков питания телевизоров, компьютеров и прочей бытовой техники. Если магнитопровод имеет маркировку, то нужную для расчета информацию находят в справочниках [3, 4] или на сайтах в Интернете (особенно для зарубежных ферритов). Эти параметры подставляют в формулы или вводят в программы. Но попадаются магнитопроводы, которые не имеют никаких опознавательных знаков (а если и имеют, то что-либо определить по ним трудно). Предлагаемая методика была разработана именно для таких магнитопроводов.
Она основана на известной формуле расчета индуктивности тороидальной обмотки
![]()
где L — индуктивность, Гн; w — число витков; µo = 4 pi -10-7 Гн/м — абсолютная магнитная проницаемость вакуума; µ— магнитная проницаемость материала магнитопровода; l — средняя длина магнитной силовой линии в магнито-проводе, м; S—площадь поперечного сечения магнитопровода, м2.
Из (1) получаем формулу для расчета магнитной проницаемости
![]()
Для практических расчетов более удобна формула, полученная из (2), в которой индуктивность выражена в микрогенри, а размеры — в миллиметрах:
![]()
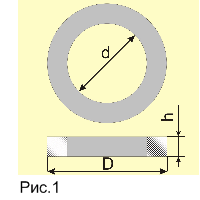
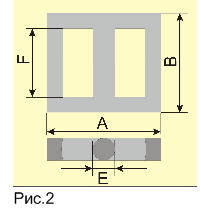
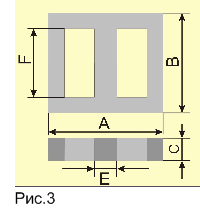
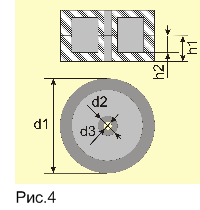
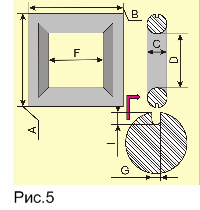
Кроме индуктивности, для расчета магнитной проницаемости материала магнитопровода нужно еще знать параметры l и S. Следует учесть, что формула (3) приближенная и дает наиболее точный результат для тороидальных (кольцевых) магнитопроводов. Для других типов (Ш-образный, П-образный, броневой), которые имеют разветвленную магнитную цепь, сложно вывести точные формулы, связывающие индуктивность, магнитную проницаемость и размеры магнитопровода. Поэтому расчеты ведут, используя так называемые эквивалентные размеры l и S ([5], с. 20—36), которые подставляют в формулу (3). Для радиолюбительской практики такой точности достаточно. В таблице перечислены формулы для определения l и S для наиболее распространенных типов магнитопроводов [5].
Работу ведут в определенной последовательности.
1. На исследуемый магнитопровод наматывают пробную обмотку, например, из 10…20 витков провода диаметром 0,3…0,4 мм (их число и диаметр роли не играют). Важно, чтобы витки равномерно по всей длине разместились на магнитопроводе. Для удобства расчета по формуле (3) лучше намотать 10 витков. Затем измеряют индуктивность пробной обмотки в микрогенри. Если магнитопровод состоит из нескольких частей (Ш-образный, П-образный, броневой), то его нужно сжать, чтобы устранить или минимизировать немагнитный зазор, который уменьшает индуктивность пробной обмотки и занижает вычисленное значение магнитной проницаемости материала. Также следует учесть влияние инструментов, стягивающих болтов и шпилек, поэтому желательно, чтобы они были изготовлены из немагнитных материалов.
2. Далее из таблицы выбирают тип исследуемого магнитопровода и по соответствующему чертежу делают все необходимые измерения в миллиметрах. Измерять лучше штангенциркулем, чтобы результаты были как можно точнее. Затем по соответствующим формулам вычисляют среднюю длину магнитной линии ? в миллиметрах и площадь поперечного сеченияS в квадратных миллиметрах.
3. Измеренную в микрогенри индуктивность, число витков w, а также значения l и S подставляют в формулу (3) и определяют магнитную проницаемость материала магнитопровода.

Для упрощения расчетов и экономии времени разработана программа «? -Калькулятор» для ПК, которая по предлагаемой методике рассчитывает магнитную проницаемость магнитопроводов распространенных типов. Программа написана в среде Visual Studio 2008 фирмы Microsoft на языке Visual Basic 2008 ЕЕ. Она также определяет сечение магнитопровода и среднюю длину магнитной линии, которые тоже нужны для дальнейших расчетов импульсного трансформатора. Зная магнитную проницаемость материала магнитопровода, можно по справочникам найти ближайший аналог и определить необходимые параметры (индукцию насыщения, удельные потери и др.).
Папка с программой может иметь любое удобное имя и храниться на любом носителе или разделе жесткого диска. В ней имеются исполняемый файл MUCalculator.exe и файл справки Help.chm (его можно запустить отдельно, чтобы изучить работу с программой до ее использования).
После запуска программы MUCalculator.exe открывается ее окно (рис. 6). В его верхней части расположена строка меню, содержащая два пункта: Файл и Справка. Пункт меню Файл состоит из команд: Сохранить — сохраняет текущий расчет в текстовом файле внутри папки с программой, Печать — печатает текущий расчет на системном принтере, Рассчитать — выполняет расчет магнитной проницаемости выбранного магнитопровода, Выход — выход из программы без сохранения текущего расчета. Пункт меню Справка информирует пользователя о программе и ее авторе.
Часть окна программы ниже строки меню состоит из пяти панелей (рис. 6):
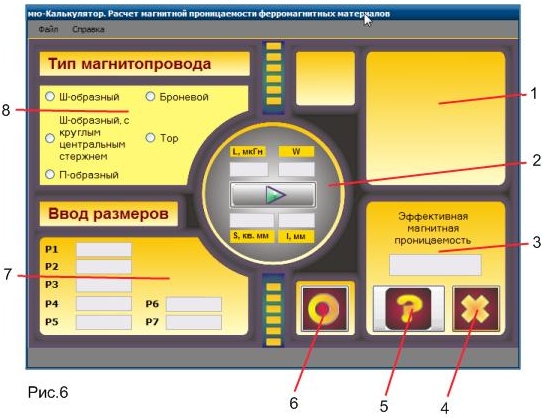
8 — выбор типа магнитопровода, 7 — ввод его размеров, 1 — вывод изображения чертежа магнитопровода, 2 — расчет, 3 — вывод результата расчета. Последняя панель имеет три кнопки: 6 — очистка полей ввода, 5 — вызов справки, 4 — выход из программы.
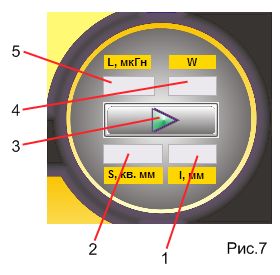
Панель расчета, показанная с увеличением на рис. 7, содержит элементы: 5 и 4 — поля для ввода индуктивности L и числа витков w пробной обмотки; 3 — кнопка Рассчитать, 2 и 1 — поля для вывода вычисленных значений S и ? .
На панели выбора типа магнитопровода щелчком левой кнопки мыши выбирают тип исследуемого магнитопровода. После этого в правом верхнем углу панели появляется чертеж выбранного магнитопровода с указаниями необходимых размеров, а также надписи возле полей. Далее как можно точнее измеряют в миллиметрах все необходимые размеры исследуемого магнитопровода и записывают их в соответствующие поля.
На панели расчета вводят измеренную в микрогенри индуктивность пробной обмотки и число ее витков. При наличии дробной части ее вводят после разделительной точки (не запятой). После ввода всей информации нажимают на кнопку Рассчитать или выполняют команду меню Файл -> Рассчитать. После этого в полях вывода появятся вычисленные значения ? и S, а также ? — магнитной проницаемости материала магнитопровода.
Для проведения нового расчета нужно очистить все поля нажатием на кнопку Очистить. Для удобства программа показывает всплывающие подсказки при наведении указателя мыши на основные объекты панелей и сообщения об ошибках, если какой-нибудь параметр не введен или введен неверно, с указанием названия этого параметра.
Распечатку результатов расчета выполняют командой меню Файл—>Печать. По этой команде системный принтер печатает стандартную страницу А4 с результатами текущего расчета и чертежом магнитопровода.
Для сохранения результатов расчета в текстовый файл следует выполнить команду меню Файл—>Сохранить. При этом откроется стандартное окно сохранения файла. В поле Имя файла нужно ввести имя сохраняемого файла (расширение .txt программа добавляет автоматически) и нажать на кнопку Сохранить. Если файла с таким именем не существует, программа спросит, нужно ли его создать На этот вопрос надо ответить утвердительно (нажать на кнопку ОК). В результате будет создан текстовый файл с информацией об исследуемом магнитопроводе, результатами и датой расчета. Если файл с таким именем существует, программа об этом предупредит и спросит, нужно ли его создать. Если на этот вопрос также ответить утвердительно, программа дописывает новые результаты расчета в конец этого файла, не стирая ранее сделанные записи.
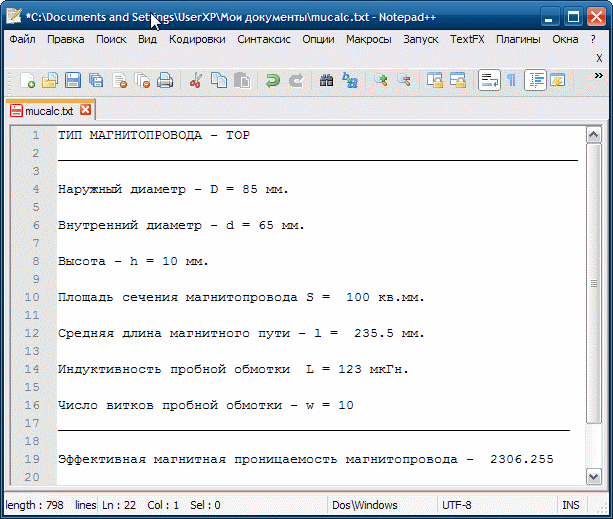
Сохраненный файл можно прочитать, удалить в нем ненужные записи и распечатать с помощью любого подходящего текстового редактора, например, Notepad++ (рис. 8).
Ю. ИЛИТИЧ, пгт. Верховина Ивано-Франковской обл., Украина
Радио, №4 2011г стр. 30-32
ЛИТЕРАТУРА
1. Косенко С. Расчет импульсного трансформатора двухтактного преобразователя Радио, 2005, № 4. с. 35-37, 44.
2. Москатов Е, Методика и программа расчета импульсного трансформатора двухтактного преобразователя. — Радио, 2006, № 6, с. 35-37
3. Куневич А. В., Сидоров И. Н. Индуктивные элементы на ферритах. Ферритовые сердечники в узлах радиоаппаратуры. Справочник домашнего мастера. — Л.: Лениздат, 1997.
4. Сидоров И. Н., Христинин А. А., Скорняков С. В. Малогабаритные магнитопрово-ды и сердечники. — М.: Радио и связь, 1989.
5. Гликман И. Я., Русин Ю. С, Горский А. Н. Электромагнитные элементы радиоэлектронной аппаратуры. Справочник. — М.: Радио и связь, 1991.
СКАЧАТЬ ПРОГРАММУ
Программа для определения проницаемости проверялась на WIN XP SP3, необходим Net framework 3.0
До сих пор мы рассматривали только магнитное поле в вакууме или, что практически почти то же самое, в воздухе. Теперь мы переходим к рассмотрению магнитного поля в различных веществах и в первую очередь в железе и сходных с ним сильно намагничивающихся материалах.
Рассмотрим опыт, схема которого показана на рис. 274. На длинный соленоид I надета индукционная катушка II, в цепь которой включен так называемый баллистический гальванометр, т. е. гальванометр с большим периодом колебаний подвижной части. Особенность этого прибора заключается в том, что при прохождении через него импульсов тока, длительность которых значительно (по крайней мере в 10 раз) меньше периода колебаний подвижной части, максимальное отклонение (отброс) подвижной части от положения равновесия оказывается пропорциональным заряду ![]() , прошедшему через гальванометр.
, прошедшему через гальванометр.
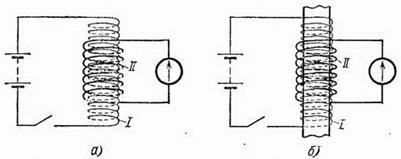
Рис. 274. В надетой на соленоид I катушке II при замыкании ключа в цепи соленоида индуцируется ток. Индукционный ток меньше в отсутствие железного сердечника в соленоиде (а), чем с сердечником (б)
Когда через соленоид течет ток определенной силы, сквозь катушку II проходит определенный магнитный поток ![]() . При выключении тока магнитный поток уменьшается до нуля, так что изменение магнитного потока
. При выключении тока магнитный поток уменьшается до нуля, так что изменение магнитного потока ![]() , т. е. равно начальному значению магнитного потока. Это изменение происходит за некоторый промежуток времени
, т. е. равно начальному значению магнитного потока. Это изменение происходит за некоторый промежуток времени ![]() . При этом в катушке II индуцируется э. д. с., среднее значение которой
. При этом в катушке II индуцируется э. д. с., среднее значение которой
![]() .
.
Если сопротивление цепи, в которую включена катушка II (т. е. общее сопротивление катушки, гальванометра и соединительных проводов), равно ![]() , то в течение времени
, то в течение времени ![]() через гальванометр будет течь ток, среднее значение которого
через гальванометр будет течь ток, среднее значение которого
![]() .
.
В результате через гальванометр пройдет заряд
![]() , (144.1)
, (144.1)
который можно определить по отбросу стрелки гальванометра (см. упражнения 141.4 и 141.5). Из сказанного вытекает, что, измеряя отброс стрелки баллистического гальванометра при включении тока в соленоиде, можно определять начальное значение магнитного потока (поток ![]() пропорционален отбросу стрелки).
пропорционален отбросу стрелки).
Проделаем описанный опыт дважды. Ток в соленоиде I в обоих случаях установим одинаковый, но во втором опыте введем предварительно в соленоид I железный сердечник (рис. 274, б). Мы обнаружим, что во втором опыте (при наличии сердечника) отброс стрелки гальванометра, а следовательно, и начальное значение магнитного потока ![]() оказываются гораздо большими, чем в первом опыте (когда железный сердечник отсутствует). Чтобы без железного сердечника получить такой же отброс стрелки гальванометра, как и при наличии сердечника, нужно было бы во много раз усилить первичный ток в соленоиде I. Но усиление первичного тока в соленоиде I означает, что мы увеличиваем начальное значение магнитного потока внутри этого соленоида, а следовательно, и сквозь катушку II. Таким образом, внесение железного сердечника сильно увеличивает начальное значение магнитного потока. Повторяя наш опыт с сердечниками различной толщины, мы убедимся, что увеличение магнитного потока будет тем больше, чем большая часть соленоида заполняется железом. Наибольшее увеличение наблюдается, когда весь соленоид заполнен железом, т. е. когда обмотка плотно навита на железный сердечник.
оказываются гораздо большими, чем в первом опыте (когда железный сердечник отсутствует). Чтобы без железного сердечника получить такой же отброс стрелки гальванометра, как и при наличии сердечника, нужно было бы во много раз усилить первичный ток в соленоиде I. Но усиление первичного тока в соленоиде I означает, что мы увеличиваем начальное значение магнитного потока внутри этого соленоида, а следовательно, и сквозь катушку II. Таким образом, внесение железного сердечника сильно увеличивает начальное значение магнитного потока. Повторяя наш опыт с сердечниками различной толщины, мы убедимся, что увеличение магнитного потока будет тем больше, чем большая часть соленоида заполняется железом. Наибольшее увеличение наблюдается, когда весь соленоид заполнен железом, т. е. когда обмотка плотно навита на железный сердечник.
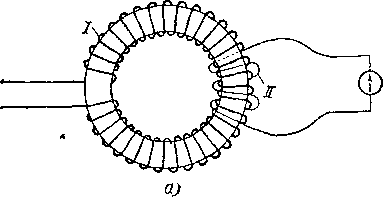
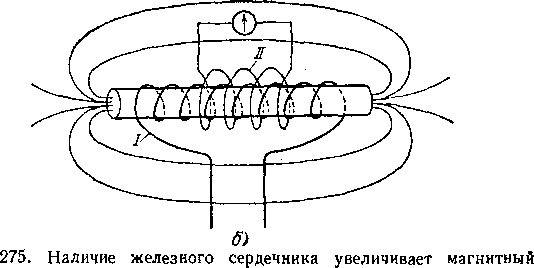
Строго говоря, полное увеличение магнитного потока достигается лишь тогда, когда все линии магнитного поля проходят в веществе сердечника. Это бывает, например, у соленоида, плотно навитого на замкнутый в виде кольца сердечник (рис. 275, а). Однако, если соленоид достаточно длинен по сравнению со своими поперечными размерами и плотно навит на длинный выступающий сердечник, то индукционная катушка, помещенная в средней части соленоида (рис. 275, б), будет пронизываться практически полным потоком.
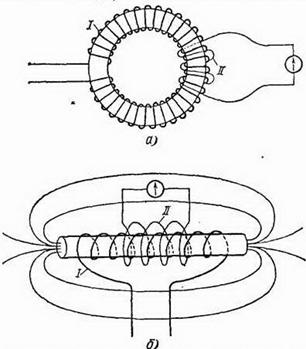
Рис. 275. Наличие железного сердечника увеличивает магнитный поток соленоида: а) наибольшее увеличение магнитного потока достигается в кольцеобразном сердечнике; б) большое увеличение магнитного потока получается также у длинного и тонкого соленоида с выступающими концами сердечника. Первичная катушка I в обоих случаях должна плотно обвивать сердечник
В этом случае отношение магнитных потоков в соленоиде, навитом на сердечник, и в том же соленоиде без сердечника зависит только от материала сердечника, конечно, при условии, что начальный ток в обмотке имеет одно и то же значение. Для разных сортов железа и стали это отношение различно. Обозначая его греческой буквой ![]() (мю), мы можем написать:
(мю), мы можем написать:
![]() ,
,
где ![]() – магнитный поток в катушке с сердечником, а
– магнитный поток в катушке с сердечником, а ![]() – магнитный поток в катушке без сердечника.
– магнитный поток в катушке без сердечника.
Величину ![]() , характеризующую магнитные свойства железа, использованного для сердечника, называют его магнитной проницаемостью. Как уже упоминалось, измерения показывают, что наличие железного сердечника увеличивает магнитный поток весьма значительно, иногда в тысячи раз. Мы можем, следовательно, сказать, что магнитная проницаемость железа весьма велика и в некоторых случаях может достигать значения нескольких тысяч.
, характеризующую магнитные свойства железа, использованного для сердечника, называют его магнитной проницаемостью. Как уже упоминалось, измерения показывают, что наличие железного сердечника увеличивает магнитный поток весьма значительно, иногда в тысячи раз. Мы можем, следовательно, сказать, что магнитная проницаемость железа весьма велика и в некоторых случаях может достигать значения нескольких тысяч.
Возрастание магнитного потока при введении в соленоид железа нетрудно понять с точки зрения представлений об амперовых молекулярных токах. Под влиянием магнитного поля соленоида амперовы токи в железе ориентируются, стремясь стать параллельно токам обмотки соленоида (рис. 276). Этим объясняется намагничивание железа и усиление магнитного поля во внешнем пространстве. Этим же объясняется и увеличение магнитного потока сквозь соленоид при введении в него сердечника: к магнитному потоку, создаваемому током в обмотке соленоида, добавляется магнитный поток, создаваемый совокупностью ориентированных амперовых токов.
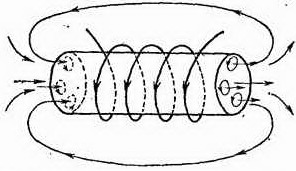
Рис. 276. Под влиянием магнитного поля соленоида амперовы токи в железном сердечнике ориентируются так, что направление их совпадает с током в соленоиде
В опыте, изображенном на рис. 274, поток через один виток катушки II равен ![]() , где
, где ![]() – магнитная индукция поля в соленоиде, a
– магнитная индукция поля в соленоиде, a ![]() – площадь поперечного сечения соленоида. Поток
– площадь поперечного сечения соленоида. Поток ![]() , фигурирующий в формуле (144.1), равен
, фигурирующий в формуле (144.1), равен ![]() (
( ![]() – число витков катушки II). Отсюда следует, что увеличение потока
– число витков катушки II). Отсюда следует, что увеличение потока ![]() в
в ![]() раз означает, что магнитная индукция
раз означает, что магнитная индукция ![]() в железном сердечнике в
в железном сердечнике в ![]() раз больше, чем магнитная индукция
раз больше, чем магнитная индукция ![]() (при том же токе в соленоиде) в случае, когда вместо железа был вакуум. Таким образом, заполнение железом пространства, в котором было поле с индукцией
(при том же токе в соленоиде) в случае, когда вместо железа был вакуум. Таким образом, заполнение железом пространства, в котором было поле с индукцией ![]() , увеличивает индукцию поля в
, увеличивает индукцию поля в ![]() раз:
раз:
![]() . (144.2)
. (144.2)
В § 126 мы отмечали, что наряду с магнитной индукцией ![]() , которая является основной силовой характеристикой магнитного поля, в некоторых случаях оказывается полезной вспомогательная характеристика
, которая является основной силовой характеристикой магнитного поля, в некоторых случаях оказывается полезной вспомогательная характеристика ![]() , связанная с
, связанная с ![]() соотношением (см. формулу (126.4))
соотношением (см. формулу (126.4))
![]() (144.3)
(144.3)
и называемая напряженностью магнитного поля (напомним, что ![]() – магнитная постоянная, см. формулу (126.2)).
– магнитная постоянная, см. формулу (126.2)).
В применении к рассматриваемому опыту формула (144.3) дает ![]() (в отсутствие сердечника, когда
(в отсутствие сердечника, когда ![]() ) и
) и ![]() (при наличии сердечника). Поскольку
(при наличии сердечника). Поскольку ![]() , имеем
, имеем
![]() , или
, или ![]() .
.
Таким образом, напряженность магнитного поля не зависит от того, заполнен соленоид каким-либо материалом или нет. В случае, когда все пространство, в котором поле отлично от нуля, заполнено однородным веществом, напряженность поля не зависит от свойств этого вещества.
Форум РадиоКот • Просмотр темы – Вычисление магнитной проницаемости ферритового сердечника с
Сообщения без ответов | Активные темы
| ПРЯМО СЕЙЧАС: |
| Автор | Сообщение |
|---|---|
|
|
Заголовок сообщения: Вычисление магнитной проницаемости ферритового сердечника с
|
|
Первый раз сказал Мяу!
Зарегистрирован: Вт янв 24, 2023 00:34:39 Рейтинг сообщения: 0
|
Приветствую всех многоуважаемых радиокотов. Столкнулся с проблемой… для начала предистория: |
| Вернуться наверх |
Профиль
|
| Реклама | |
|
|
|
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
1. Есть куча калькуляторов для расчёта проницаемости сердечника, нужно только намотать пробную обмотку и измерить индуктивность. И нужно определять проницаемость без зазора для вставки в программу. mobilandser писал(а): Ну если будет совсем беда плюну и соберу опять на ирке Ну если не умеешь готовит обратно-ходы кто тебе не дает, делай на ИРках. |
||
| Вернуться наверх | |||
| Реклама | |
|
|
|
|
electroget |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Зарегистрирован: Ср сен 30, 2020 16:51:47 Рейтинг сообщения: 0
|
как правильно рассчитать магнитную проницаемость сердечника Вопрос не совсем понятен. |
||
| Вернуться наверх | |||
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
Он сам не знает чего хочет. |
||
| Вернуться наверх | |||
| Реклама | |

|
25.05.2023 Вебинар «Источники питания MORNSUN: новинки для промавтоматики и оптимальные решения для телекоммуникации»
Приглашаем на вебинар, посвященный новой продукции MORNSUN для промышленной автоматизации и телекоммуникационных приложений. Подробнее>> |
|
Agaev |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 11 Рейтинг сообщения: 0
|
Если магнитопровод аналогичен комповому БП, то можно выбрать материал N27 и сравнить результат расчета с предыдущим. Хорошо бы ещё схему и фото посмотреть. |
||
| Вернуться наверх | |||
| Реклама | |
|
|
|
|
mobilandser |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
|
Зарегистрирован: Вт янв 24, 2023 00:34:39 Рейтинг сообщения: 0
|
Ребята, все это понятно, намотать некоторое количество витков, заключить в сердечник, сжать его как следует и замерять индуктивность, а там есть и программы и формулы для расчета проницаемости. Все это я знаю. Вопрос в том, как измерять проницаемость в сердечнике в коротом УЖЕ ЕСТЬ зазор. Я ж не могу его замазать чем-то магнитопроницаемым что бы получить сердечник БЕЗ зазора. У меня все сердечники с УЖЕ установленным зазором. Как мне измерять в таком случае магнитную проницаемость??? Ну как вам еще пояснить чего мне нужно…? |
| Вернуться наверх | |
|
vlasovzloy |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 52 Рейтинг сообщения: 0
|
Ток пускать повышать и смотреть когда перестанет дросселем быть Добавлено after 41 second: |
||
| Вернуться наверх | |||
|
mobilandser |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
|
Зарегистрирован: Вт янв 24, 2023 00:34:39 Рейтинг сообщения: 0
|
Если магнитопровод аналогичен комповому БП, то можно выбрать материал N27 и сравнить результат расчета с предыдущим. Хорошо бы ещё схему и фото посмотреть. Сердечник с каркасом был взят с какого-то блока питания (тоже обратноходовой). Был разобран для своих целей. Вообще-то говоря нужен был сердечник без зазора, но блок питания был таковым, поэтому он с зазором уже был изначально. Добавлено after 2 minutes 36 seconds: Ток пускать повышать и смотреть когда перестанет дросселем быть Добавлено after 41 second: Такую методику не слышал и не знаю даже как ею воспользоваться. |
| Вернуться наверх | |
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
Для особо одарённых. Телекот писал(а): Проницаемость сердечника для обратно-хода практически не важна если она более 1000, там главное зазор, поскольку индуктивность определяет именно он. К примеру берём сердечник с проницаемостью 1000 с длинной магнитной линии 80мм и зазором 1мм, и второй такой же сердечник с проницаемостью 2000. Так магнитная проницаемость обоих сердечников с зазором будет отличаться на 3-4%. Добавлено after 3 minutes 22 seconds: Последний раз редактировалось Телекот Вт янв 24, 2023 12:56:04, всего редактировалось 1 раз. |
||
| Вернуться наверх | |||
|
electroget |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Зарегистрирован: Ср сен 30, 2020 16:51:47 Рейтинг сообщения: 0
|
Неужели с существующим зазором вообще никак не посчитать проницаемость? Не брать же ее с балды а-ля пальцем в небо. Должны же существовать специальные формулы (более / менее понятные) для расчета этой заразы? Именно чтоб посчитать, можно только для замкнутого сердечника. Последний раз редактировалось electroget Вт янв 24, 2023 12:56:39, всего редактировалось 1 раз. |
||
| Вернуться наверх | |||
|
vlasovzloy |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 52 Рейтинг сообщения: 0
|
К старичку постучись, он должен знать методику. Я чото быстрым гуглением не могу найти. Там смысл что через намотаную катушку пускают импульс тока и по наклону вычисляют максимальное чтото потом чтото кудато умножают делят и вычисляют магнитную проницаемость. Чтото такое вобщем |
||
| Вернуться наверх | |||
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
Методики нет, потому как индуктивность мало зависит от проницаемости сердечника, она в основном зависит от зазора. Телекот писал(а): К примеру берём сердечник с проницаемостью 1000 с длинной магнитной линии 80мм и зазором 1мм, и второй такой же сердечник с проницаемостью 2000. Так магнитная проницаемость обоих сердечников с зазором будет отличаться на 3-4%. Едиственно собрать сердечник без зазора. |
||
| Вернуться наверх | |||
|
Agaev |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 11 Рейтинг сообщения: 0
|
Разделите длину магнитной линии на толщину зазора и получите проницаемость. Это в общем случае. Зачастую магнитопроводов для ОХ это тоже касается. |
||
| Вернуться наверх | |||
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||||
Карма: 135 Рейтинг сообщения: 0
|
А нечего что изменения проницаемости сердечника в 2 раза приводит к изменению обшей проницаемости на 4%, а изменения зазора на 10% изменяет общию проницаемость в 2-3 раза. Телекот писал(а): 2. Проницаемость сердечника для обратно-хода практически не важна если она более 1000, там главное зазор, поскольку индуктивность определяет именно он. Хочется измерить проницаемость сложи сердечники так как на нижнем рисунке, катушку намотай на левой половинке.
|
||||
| Вернуться наверх | |||||
|
vlasovzloy |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 52 Рейтинг сообщения: 0
|
Ахаха, телекот самое лучшее решение))) |
||
| Вернуться наверх | |||
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
Но не нужное. |
||
| Вернуться наверх | |||
|
electroget |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Зарегистрирован: Ср сен 30, 2020 16:51:47 Рейтинг сообщения: 0
|
Сильное решение, согласен. |
||
| Вернуться наверх | |||
|
сэм |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
|
Карма: 10 Рейтинг сообщения: 0
|
Где- то недавно попадался расчет эффект проницаемости с зазором в инете, через магнитное сопротивление, длинну магнитной линии и толщину зазора |
| Вернуться наверх | |
|
Телекот |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 135 Рейтинг сообщения: 0
|
А что здесь такого. |
||
| Вернуться наверх | |||
|
Starichok51 |
Заголовок сообщения: Re: Вычисление магнитной проницаемости ферритового сердечник
|
||
Карма: 152 Рейтинг сообщения: 0
|
Телекот писал(а): магнитное сопротивление сердечника берём 1 делённое на проницаемость и поэтому, как уже говорил Телекот, в сердечнике с зазором собственная проницаемость феррита становится пофую. |
||
| Вернуться наверх | |||
Кто сейчас на форуме |
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 20 |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |

Магнитная проницаемость — железо
Индуктивность L катушки с железным сердечником значительно больше, чем у катушки без сердечника, так как магнитная проницаемость железа в тысячи раз больше, чем у воздуха. Катушку с железным сердечником и большой индуктивностью называют дросселем. [16]
Действительно, магнитный скалярный потенциал таких полей в пространстве между полюсами удовлетворяет уравнению Лапласа, а на поверхности полюсов при большом значении магнитной проницаемости железа может считаться постоянным. [17]
Выражения (7.175) и (7.176) показывают, что если обмотка занимает всю высоту окна ( h k), ноток рассеяния будет отсутствовать, так как магнитная проницаемость железа предполагается бесконечной. [18]
А — толщина железного листа в см, / — частота в пер / ск. Q-см, П — магнитная проницаемость железа , выраженная в Н / см и равная 0 4 п 10 — 8 л ( ft — относительная магнитная проницаемость), Втах — наибольшее среднее значение магнитной индукции. [19]
Магнитное состояние сердечника, несущего обмотки переменного тока, может быть значительно изменено подмагничиванием постоянным током. Таким образом, изменяется не только магнитная проницаемость железа , но также и полное сопротивление обмоток. [20]
Предположим теперь, что средой с меньшей магнитной проницаемостью является воздух, средой же с большей проницаемостью является железо. Картина поля, изображенного на рис. 105, относится при этом к случаю тока, расположенного в воздухе. Она ясно показывает, что магнитные линии в воздухе будут почти нормальны к поверхности железа, даже если магнитная проницаемость железа только в девять раз превосходит проницаемость воздуха. В действительности магнитная проницаемость железа во много раз больше проницаемости воздуха, и условие перпендикулярности к поверхности железа магнитных линий в воздухе соблюдается с весьма высокой точностью. Однако это условие не имеет места в случае, когда ток проходит внутри железа, как это. [21]
Предположим теперь, что средой с меньшей магнитной проницаемостью является воздух, средой же с большей проницаемостью является железо. Картина поля, изображенного на рис. 105, относится при этом к случаю тока, расположенного в воздухе. Она ясно показывает, что магнитные линии в воздухе будут почти нормальны к поверхности железа, даже если магнитная проницаемость железа только в девять раз превосходит проницаемость воздуха. В действительности магнитная проницаемость железа во много раз больше проницаемости воздуха, и условие перпендикулярности к поверхности железа магнитных линий в воздухе соблюдается с весьма высокой точностью. Однако это условие не имеет места в случае, когда ток проходит внутри железа, как это. [22]
В каждом разложении остается произвольным ряд производных второго и высших порядков. Таким образом, поля определяются не полностью. Оставшаяся некоторая степень произвола может быть использована для улучшения фокусировки более высоких порядков. Подробнее этот вопрос будет исследован в случае наличия только электрического поля. Найдя по заданному характеру пучка те поля, в которых эти пучки должны получаться, можно определить конфигурацию электродов и магнитов, которыми такие поля будут созданы. В случае электрического поля поверхности электродов должны иметь форму и расположение любой пары эквипотенциальных поверхностей, в случае магнитного поля то же будет относиться к внешним поверхностям полюсных башмаков, если принять, что магнитная проницаемость железа бесконечно велика. [23]
Следует еще учесть время нарастания тока в обмотке реле до тока срабатывания. Вспомните, как зависит индуктивность катушки от магнитной проницаемости магнитопровода. В следящей системе входной сигнал изменяется произвольным образом. Учтите, что токи в симметричных половинах схемы увеличились одинаково. Можно однозначно сказать, какой из токов больше. Необходима более сложная схема. В самом принципе работы магнитного усилителя заложена необходимость питания его переменным током. Обратная связь в усилителях как дроссельного, так трансформаторного типа используется для увеличения коэффициента усиления и делается положительной. Правильно, в двухтактных ( дифференциальных) схемах ток нагрузки пропорционален току управления. В таком случае ток в нагрузке всегда был бы равен нулю. Ток управления на фазу рабочего тока не влияет. Правильно, при увеличении этого сопротивления возрастают ток смещения и нулевой ток. Этих данных для определения коэффициента усиления по мощности недостаточно. Это объясняется тем, что магнитная проницаемость воздуха значительно меньше магнитной проницаемости железа . Правильно, регулирующий орган ( например, руль) относится к регулируемому объекту. [24]
Магнитная проницаемость ферромагнитных тет
Магнитная проницаемость μ ферромагнитных тел определяется выражением:
μ = B/H
где В обозначает магнитную индукцию в теле, а H — напряженность внешнего намагничивающего поля.
В справочной таблице даны значения В и μ при изменении Н в пределах от 1 до 6000 эрстед для: 1) электролитического железа (Fe); 2) никеля (Ni), кобальта (Со) и сплава Гейслера (75,6% Си + 14,25% Mn + 10,15% Al)
Итак, мы решили поразвлечься и всерьёз сваять что-нибудь стоящее своими руками, как то: индуктивный фильтр для блока питания, дроссель для усилительного каскада, выходной трансформатор для однотактного УНЧ, или фиг его знает — чего ещё похуже.
Что объединяет этих жертв нашего волеизъявления?
Каждое из перечисленных моточных изделий содержит магнитомягкий магнитопровод, и через каждое из них протекает постоянный ток. И если к переменному току, даже значительных величин, магнитопровод относится сдержанно-положительно, то к постоянке питает явную антипатию и может резко войти в насыщение от её переизбытка.
При насыщении сердечника его относительная магнитная проницаемость резко уменьшается, что влечёт за собой пропорциональное уменьшение индуктивности изделия.
На этой странице порассуждаем о тороидальных магнитопроводах из ферритов, распылённого железа, электротехнической стали и их способности противостоять постоянному току.
Для наглядности рассмотрим график зависимости B от H , называемый петлёй гистерезиса, для распространённого, где-то даже народного, феррита марки N87 фирмы EPCOS.
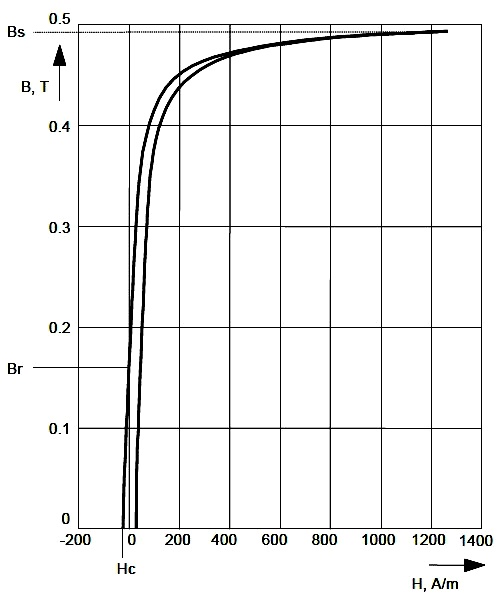 Здесь:
Здесь:
H — напряжённость магнитного поля, а
B — магнитная индукция в сердечнике.
Зависимость приведена при температуре изделия +25 гр.С.
Интересующие нас параметры из datasheet-а производителя:
Начальная магнитная проницаемость —
µ = 2200 ,
Магнитная индукция насыщения при H=1200 А/м — Bнас = 0,490 Т .
Если внимательно присмотреться к графику, то легко заметить, что в области малых и средних индукций зависимость практически линейна и её наклон примерно равен µ . Именно на этот участок в большинстве случаев и должен приходиться диапазон рабочих индукций.
При дальнейшем повышении напря- жённости магнитного поля магнитная проницаемость начинает быстро падать, пока не наступает момент, при котором дальнейший рост магнитной индукции в сердечнике стопорится на определённой величине. В спецификациях это величина приводится, как значение магнитной индукции насыщения — Bнас , или Bs , т.е. величина, при которой значение магнитной проницаемости падает до неприлично малых значений.
Так что давайте без лишних прелюдий и телодвижений сделаем фундаментальный вывод — для нормальной работы катушки, намотанной на магнитопроводе, рабочие значения магнитной индукция в сердечнике не должны превышать величину 0,75 — 0,8 от значения справочной характеристики Bнас (Bs) .
Переходим к незамысловатым формулам!
Магнитная индукция в сердечнике равна:
B = µ×µ0×n×I/l , где:
µ — магнитная проницаемость сердечника,
µ0 = 4π×10 -7 (Гн/м) — физическая константа, называемая магнитной постоянной,
n — количество витков обмотки,
I — ток в обмотке,
l — средняя длина магнитного контура.
Поскольку рабочий режим магнитопровода мы выбираем в линейной области петли гестерезиса, то в качестве значения µ можно использовать паспортную характеристику начальной магнитной проницаемости сердечника.
Теперь можно рисовать калькулятор для расчёта магнитной индукции в катушке с учетом выбранного типа сердечника и конкретного количества витков обмотки.
Для удобства восприятия, помещу сюда и значение индуктивности полученного моточного изделия. Формулы для вычислений этого параметра выглядят следующим образом:
L=0,0002×µ×h×n 2 ×ln(Dвнешн/Dвнутр) при соблюдении условия Dвнешн/Dвнутр>1,75 ,
L=0,0004×µ×h×n 2 ×(Dвнешн-Dвнутр)/(Dвнешн+Dвнутр) при Dвнешн/Dвнутр
ТАБЛИЦА РАСЧЁТА МАГНИТНОЙ ИНДУКЦИИ В КАТУШКЕ С ТОРОИДАЛЬНЫМ СЕРДЕЧНИКОМ.
Увы, но значительных токов через катушки на ферритовых кольцах, или торах из трансформаторной стали нам пропустить не удастся — нужны танцы с бубнами в виде немагнитных воздушных зазоров.
Другое дело — сердечники из распылённого железа, представляющие собой магнитопровод с немагнитными зазорами, технологически распределёнными по всему объёму магнитопровода. Их очевидный плюс — высокая индукция насыщения, минус — малые величины магнитной проницаемости.
В связи с этим, в некоторых случаях (в основном на низких частотах) предпочтительным является использование именно сердечников из ферритов (или железа) с пропилом для создания малого воздушного зазора. Данная мера позволяет в значительной мере увеличить величину допустимых токов через катушку без ввода магнитопровода в режим насыщения. Длина этого воздушного зазора позволяет регулировать как величину максимально-допустимой напряжённости магнитного поля в сердечнике, так и параметр изменившейся магнитной проницаемости, называемой эквивалентной магнитной проницаемостью сердечника с зазором — µэф . Значение этого параметра вычисляется по формуле:
µэф = µ/(1+lз×µ/l) , где:
µ — начальная магнитная проницаемость сердечника,
l — средняя длина магнитного контура,
lз — длина воздушного зазора (толщина пропила).
Давайте посчитаем этот параметр.
РАСЧЁТ ЭКВИВАЛЕНТНОЙ МАГНИТНОЙ ПРОНИЦАЕМОСТИ СЕРДЕЧНИКА С ЗАЗОРОМ.
Таблица даёт приблизительную, но, в большинстве своём, приемлемую точность расчёта при величинах длины воздушного зазора 0,2-2 мм.
Для Ш-образных сердечников в качестве внутреннего и внешнего диаметров следует вводить справочную характеристику длины магнитного контура le .
Определив ниже магнитную проницаемость сердечника с зазором, следует ввести это значение в предыдущий калькулятор и заново произвести вычисления магнитной индукции и индуктивности катушки.
Для наглядности приведу два графика петли гистерезиса Ш-образного ферритового сердечника марки N87 без немагнитного воздушного зазора и с зазором около 1 мм. Феррит ETD 59/31/22, достаточно крупный, с средней длиной магнитного контура le = 139 мм.
Механизмы влияния зазора у Ш-образных и тороидальных сердечников абсолютно идентичны.
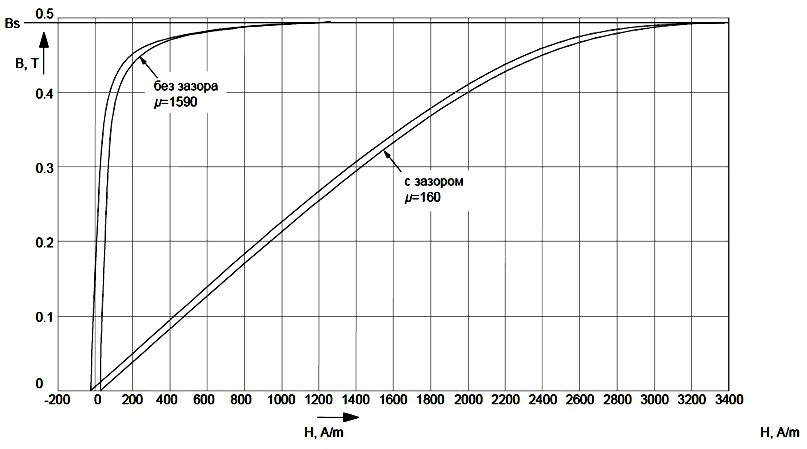
Эквивалентная магнитная проницаемость сердечника с зазором уменьшилась и составила величину 160 единиц. Соответственно, уменьшился и наклон петли, позволяя сердечнику работать при гораздо больших значениях напряжённости магнитного поля вдали от области магнитной индукции насыщения сердечника.
А учитывая то, что значение напряжённости H прямо пропорционально, протекающему через катушку току, можно с уверенностью сказать, что область безопасных индукций теперь соответствует более чем на порядок большим токам в обмотке.
Линейная область петли гистерезиса также заметно увеличилась, что позволяет увеличить максимальные рабочие значения магнитной индукция в сердечнике вплоть до 0,85-0,9 от значения справочной характеристики Bнас (Bs).




