Как найти магнитный момент альфа частицы

Решение задач – обязательная практика в жизни всех студентов-технарей. В сегодняшней статье разберемся, как решать задачи на силу Лоренца. 

Если вам скучно читать про решение задач, переходите в наш телеграм-канал. Там найдется интересная информация и новости для всех специальностей. А еще, у нас есть второй канал, где мы рассказываем об акциях нашего сервиса и дарим приятные скидки. Проверьте — и не упустите выгоду!

Задачи по теме «сила Лоренца»

Даже если вы не новичок, прежде чем решать задачи, прочтите общую памятку и на всякий случай держите под рукой полезные формулы. 

Задача на силу Лоренца №1

Условие 

Электрон с энергией 300 эВ движется перпендикулярно линиям индукции однородного магнитного поля напряженностью 465 А/м. Определить силу Лоренца, скорость и радиус траектории электрона.

Решение

Скорость электрона можно найти из формулы кинетической энергии:

Eк=m·v22v=2Eкm

Сила Лоренца является центростремительной силой, значит, по второму закону Ньютона, можно записать:

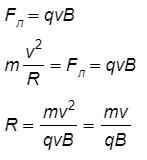
Магнитная индукция равна напряженности, умноженной на магнитную постоянную. Подставив ранее найденное выражение для скорости в формулу для радиуса и силы Лоренца, запишем:

R=m2Eктqμ0H=2Eктqμ0HFл=q2Eктμ0H​

Теперь осталось только подставить значения и вычислить:

v=2·4,8·10-169,1·10-31=3,25·107 мсFл=4·3,14·10-7·465·1,6·10-19·3,25·107=3·10-15НR=2·4,8·10-16·9,1·10-314·3,14·10-7·465·1,6·10-19=0,32 м

Ответ: v=3,25·107 мс; Fл=3·10-15Н; R=0,32 м.

Задача на силу Лоренца №2

Условие

Альфа-частица влетает в магнитное поле с индукцией 1 Тл перпендинулярно силовым линиям. Найти момент импульса частицы относительно центра окружности, по которой она будет двигаться.

Решение

Когда частица влетает в поле перпендикулярно силовым линиям, на нее начинает действовать сила Лоренца, которая выполняет роль центростремительной силы. Радиус окружности, по которой будет двигаться частица:

R=mvQBm=6,65·10-27 кг – масса альфа частицыQ=2e=3,2·10-19Кл – заряд альфа частицы

Момент импульса частицы относительно центра окружности найдем по формуле:

L=mvR=m2v2QB=6,65·10-272·0,35·10723,2·10-19·1=5,42·10-21кг·м2с

Ответ: 5,42·10-21 кг·м2с.

Задача на силу Лоренца №3

Условие

В однородном магнитном поле с индукцией  В = 0,5 Тл вращается с частотой n = 10 с-1 стержень длиной l = 20 см. Ось вращения параллельна линиям индукции и проходит через один из концов стержня перпендикулярно его оси. Определите разность потенциалов U на концах стержня.

Решение

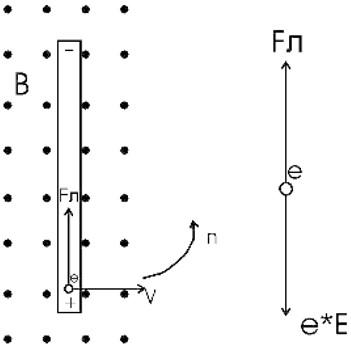
Рассмотрим физическую суть процессов, проходящих в стержне. Когда стержень движется в магнитном поле, в нем возникает ЭДС индукции, которая обусловлена действием силы Лоренца на заряды стержня.

Под действием этой силы в стержне происходит разделение зарядов: свободные электроны перемещаются вверх и между концами стержня возникает разность потенциалов.

Заряды на концах стержня создают поле E, препятствующее дальнейшему разделению зарядов. В какой-то момент сила Лоренца уравновесится с силой возникающего поля:

Fл=e·ЕЕ=Fле=evBe=vB

Скорость нижнего конца стержня, а значит, и скорость электронов в нем, можно найти, зная частоту вращения и длину стержня:

v=2π·n·l

C учетом этого, перепишется выражения для напряженности электрического поля:

 Е=2πnlB

Индуцируемая разность потенциалов, по определению, равна:

U=Е·lU=2πnl2B=2·3,14·10-1·0,22·0,5=1,3В

Ответ: 1,3 В.

Задача на силу Лоренца №4

Условие

Какая сила действует на заряд 0,005 Кл, движущийся в магнитном поле с индукцие 0,5 Тл со скоростью 150 м/с под углом 45 градусов к вектору магнитной индукции?

Решение

Это простейшая задача на определение силы Лоренца. Вспомним формулу и запишем, что на заряд действует сила Лоренца, равная:

F=q·v·B·sinα

Подставим значения и вычислим:

F=0,005·150·0,5·22=0,26 Н

Ответ: 0,26 Н.

Задача на силу Лоренца №5

Условие

На тело с зарядом 0,8 мКл, движущееся в магнитном поле, со стороны поля действует сила, равная 32Н. Какова скорость тела, если вектор магнитного поля перпендикулярен ей?

Решение

Это классическая задача на применение формулы силы Лоренца. Так как векторы скорости и магнитной индукции перпендикулярны, можно записать:

F=qvBsinα=qvBv=FqB=320,8·10-3·2=20·103 мс

Ответ: 20000 м/с.

Проходите магнитостатику? Вам также может быть интересно:

1. Задачи на закон Био-Савара-Лапласа.
2. Задачи на теорему о циркуляции магнитного поля.

Вопросы на тему «Сила Лоренца»

Вопрос 1. Что такое сила Лоренца?

Ответ. Сила Лоренца — это сила, с которой магнитное поле действует на заряженную частицу, движущуюся в нем.

Сила Лоренца действует только на движущиеся заряды.

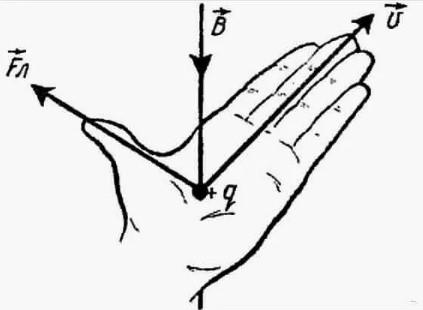
Вопрос 2. Как определить направление силы Лоренца?

Ответ. Направление силы Лоренца определяется по правилу левой руки:

Если левую руку расположить так, чтобы составляющая вектора В, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движении положительного заряда (= против движения отрицательного заряда), то отогнутый на 90 градусов большой палец покажет направление действующей на заряд силы Лоренца.

Вопрос 3. Зависит ли сила Лоренца от знака заряда?

Ответ. Да, зависит. Для противоположных зарядов сила Лоренца будет направлена в противоположные стороны.

Вопрос 4. Совершает ли сила Лоренца работу?

Ответ. Нет. Сила Лоренца не совершает работу, т.к., являясь перпендикулярной вектору скорости частицей, может изменить лишь направление скорости, но не ее значение. Работа силы Лоренца всегда равна нулю!

Вопрос 5. По какой траектории движется частица, попадающая в магнитное поле, перпендикулярное вектору скорости?

Ответ. Частица, влетающая в магнитное поле перпендикулярно линиям магнитной индукции, будет двигаться в этом поле по окружности определенного радиуса под действием силы Лоренца.

Нужна помощь в решении задач и других заданий по учебе? Профессиональный сервис для студентов посодействует, обращайтесь в любое время!

Движение альфа частицы по окружности

Задание 17. α-частица движется по окружности в однородном магнитном поле между полюсами магнита под действием силы Лоренца. После замены магнита по таким же траекториям стали двигаться протоны, обладающие той же скоростью. Как изменились индукция магнитного поля и модуль силы Лоренца?

Для каждой величины определите соответствующий характер изменения:

3) не изменилась

На α-частицу со стороны магнитного поля действует сила Лоренца , где q – заряд частицы; v – скорость частицы; B – модуль магнитной индукции магнитного поля. Так как α-частица движется по окружности, то магнитное поле направлено перпендикулярно его движению, то есть и сила Лоренца в данном случае запишется в виде

.

В соответствии со вторым законом Ньютона, силу Лоренца также можно записать как

,

где – центростремительное ускорение. Получаем значение индукции напряженности магнитного поля:

.

Альфа-частица имеет в своем составе два протона и два нейтрона, то есть ее масса в 4 раза больше массы протона, а заряд в 2 раза больше заряда протона.

Следовательно, сила Лоренца в случае протонов, станет равной:

(уменьшится в 4 раза), а индукция магнитного поля:

Движение альфа частицы по окружности

Альфа-частица движется по окружности в однородном магнитном поле. Как изменятся ускорение альфа-частицы и частота её обращения, если уменьшить её кинетическую энергию?

Для каждой величины определите соответствующий характер изменения:

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Ускорение α-частицы

Частота обращения α-частицы

При движении заряженной частицы в однородном магнитном поле по окружности параметры системы связаны между собой соотношениями

При уменьшении кинетической энергии уменьшается и скорость частицы. Если скорость частицы уменьшится, то ускорение частицы тоже уменьшится.

Рассмотрим второе уравнение ещё раз и выразим из него радиус обращения частицы:

Частота обращения частицы обратно пропорциональна периоду: Радиус обращения частицы прямо пропорционален её скорости, следовательно, при изменении скорости отношение скорости и радиуса остаётся неизменным, то есть частота обращения частицы не изменяется.

Движение заряженной частицы в магнитном поле: формулы. Движение заряженных частиц в однородном магнитном поле

Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы F_B, которую поле оказывает на частицу при ее движении в нем со скоростью v.

Общие свойства магнитной силы

Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:

• Величина F_B магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
• Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
• Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, F_B перпендикулярна плоскости, образованной v и B (см.рис. ниже).
• Величина и направление F_B зависит от скорости частицы и от величины и направления магнитного поля B.
• Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
• Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.

Сила Лоренца

Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде F_B = qv х B.

Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца F_B при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.

Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно F_Л = qE + qv х В. Его принято называть так: полная сила Лоренца.

Движение заряженных частиц в однородном магнитном поле

Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.

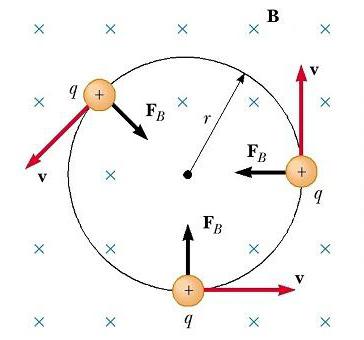
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила F_B направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и F_B изменяются непрерывно, как показано на рисунке. Так как F_B всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.

Динамика кругового движения частицы

Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем F_B центробежной силе, требуемой для сохранения круговой траектории движения:

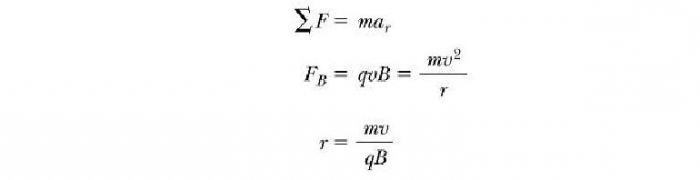
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы

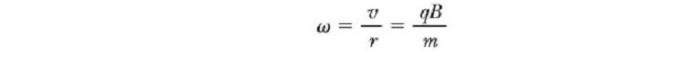
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:

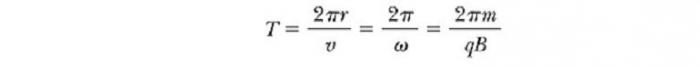
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.

Движение частицы под углом к вектору магнитного поля

Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы F_B в этом направлении. В результате составляющая ускорения a_x= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила F_B = qv х В вызывает изменение во времени компонентов скорости v_y и v_z. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν_⊥ = √(ν_у 2 + ν_z 2 ).

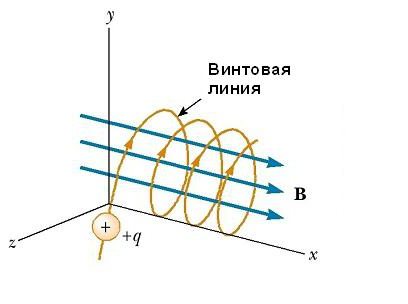
Неоднородное магнитное поле: как в нем движутся частицы

Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.

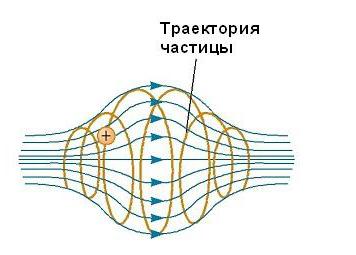
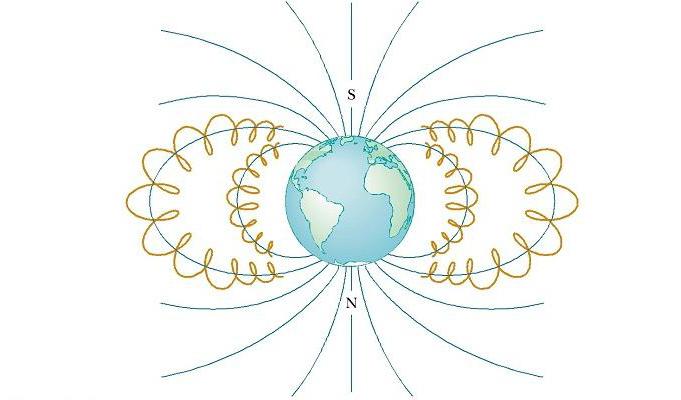
Как Земля влияет на движение космических частиц

Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.

Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.

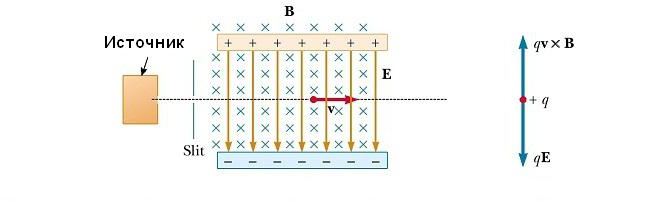
Селектор скоростей

Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).

Масс-спектрометр

Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B₀, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q

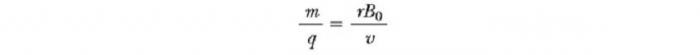
и затем, используя уравнение v=E/B, мы находим, что

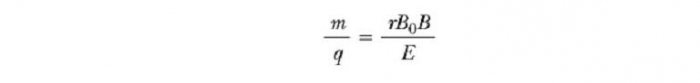
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B₀, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/m_е для электронов.

Циклотрон

Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.

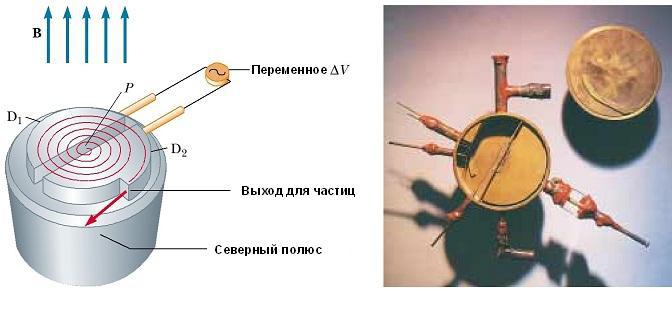
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).

Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т – время одного полного оборота внутри двух дуантов.

Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D₂ получает более низкий электрический потенциал, чем D₁ на величину qΔV, то ион ускоряется в зазоре перед входом в D₂, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D₂ по полукруглой траектории большего радиуса (потому что его скорость увеличилась).

Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один “удар” через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы – ν = qBR /m. Следовательно, ее кинетическая энергия

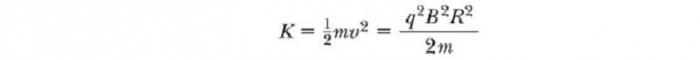
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.

Эффект Холла

Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.

Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.

[spoiler title=”источники:”]

http://phys-ege.sdamgia.ru/problem?id=11940

http://www.syl.ru/article/203046/new_dvijenie-zaryajennoy-chastitsyi-v-magnitnom-pole-formulyi-dvijenie-zaryajennyih-chastits-v-odnorodnom-magnitnom-pole

[/spoiler]

Сила Лоренца .

Сила Лоренца действует на заряженную частицу, движущуюся в магнитном поле.

( F_л=Bqv cdot sin alpha )

(B) -магнитная индукция, единица измерения Тесла [Тл]

(q) – заряд частицы, единица измерения Кулон [Кл] )

(v) – скорость частицы

( alpha )- угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы ( vec{v} )

---

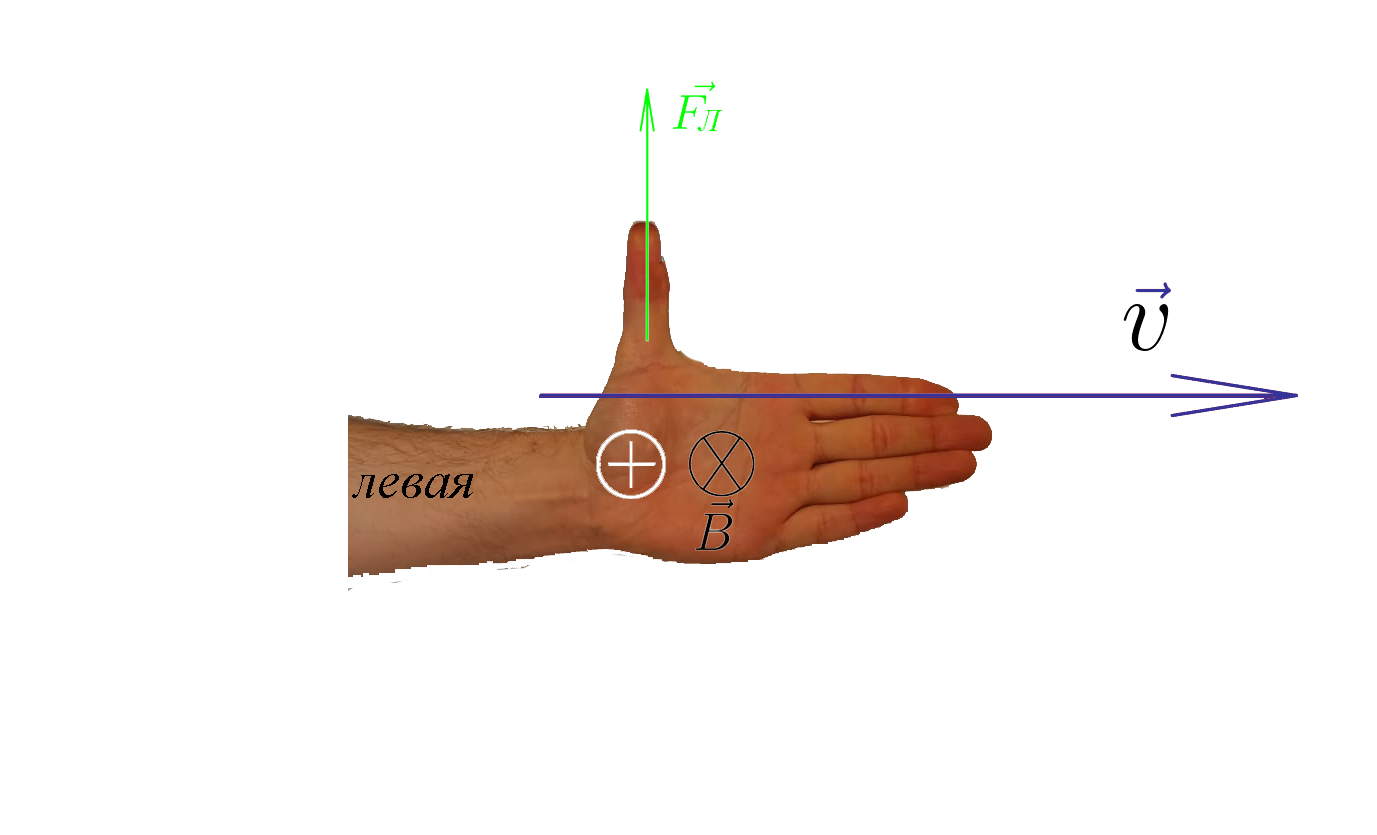
Направление силы Лоренца, действующей на положительно заряженную частицу .

Если вектор магнитной индукциии входит в ладонь левой руки, а четыре пальца сонаправлены с
направлением вектора скорости положительно заряженной частицы, то отогнутый на ( 90^0 )
большой палец показывает направление силы Лоренца действующей на эту частицу.

---

Задача 1. (Сила Лоренца)

Пылинка, имеющая заряд (q=10^{-6} Кл) движется в магнитном поле с индукцией
(B=20 Тл) . Скорость пылинки перпендикулярна линиям магнитной индукции и равна

(100 м/с )

Вычислить значение силы Лоренца, действующей на пылинку со стороны магнитного поля.
Дать ответ в миллиньютонах.

Показать ответ
Показать решение
Видеорешение

Задача 2.

Шарик с зарядом (q=100 мкКл) влетает в магнитное поле с
индукцией (B=100 Тл) со скоростью (v=30 м/с .)

Угол между вектором магнитной индукции ( vec{B} ) и вектором скорости частицы
( vec{v} ) составляет ( alpha=30^0 . )

Найти значение силы Лоренца, действующей на шарик со стороны поля.

Показать ответ
Показать решение
Видеорешение

---

---

Задача 3. (Сила Лоренца)

Электрон движется в магнитном поле с индукцией
(B=1 Тл) перпендикулярно линиям магнитного поля со скоростью (v=10^8 м/с . )

Вычислить значение силы Лоренца, действующей на электрон со стороны магнитного поля.

Заряд электрона ( q=1,6 cdot 10^{-19} Кл . )

Дать ответ в пиконьютонах.

1 пН ( = 10^{-12} Н . )

Показать ответ
Показать решение
Видеорешение

---

Задача 4. (Сила Лоренца)

С какой скоростью двигался протон в магнитном поле с индукцией (B=10^{-2} Тл) перпендикулярно линиям поля,
если на него действовала сила Лоренца (F_л=3,2 cdot 10^{-17 } Н ? )
Заряд протона ( q=1,6 cdot 10^{-19} Кл . )

Дать ответ в километрах в секунду.

Показать ответ
Показать решение
Видеорешение

---

Задача 5. (Сила Лоренца)

Альфа-частица движется в магнитном поле с индукцией (B=10^{-3} Тл) перпендикулярно линиям поля, при этом на нее действует сила Лоренца (F_л=6,4 cdot 10^{-15 } Н . )
Вычислить скорость альфа-частицы, если ее заряд (q=3,2 cdot 10^{-19} Кл . )

Дать ответ в километрах в секунду.

Показать ответ
Показать решение
Видеорешение

---

Задача 8. (Сила Лоренца)

Протон влетает в магнитное поле со скоростью (v= 10^{5} м/с ) перпендикулярно линиям индукции,
после чего он движется по окружности.Найти радиус этой окружности, если индукция поля
(B=0,01 Тл . )
Заряд протона (q=1,6 cdot 10^{-19} Кл )
Масса протона (m=1,6 cdot 10^{-27} кг )

Показать ответ
Показать решение
Видеорешение

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 декабря 2020 года; проверки требуют 7 правок.

Магнитный момент
Размерность	L2I
Единицы измерения
СИ	А⋅м2
Примечания
векторная величина

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная физическая величина, характеризующая магнитные свойства вещества, то есть способность создавать и воспринимать магнитное поле. Вычисляется как

где — плотность тока в элементе объёма , а — радиус-вектор этого элемента объёма.

Магнитный момент измеряется в А⋅м², или в Вб·м, или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10⁻³ Дж/Тл. Специфическими единицами элементарного магнитного момента являются магнетон Бора и ядерный магнетон.

Объекты, обладающие магнитным моментом[править | править код]

Магнитными свойствами обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Как показала квантовая механика, магнитный момент электронов, протонов, нейтронов и других частиц обусловлен наличием у них собственного момента импульса — спина. Он обычно представляется как вращение частицы вокруг своей оси, однако это сугубо модельная картина, служащая лишь для демонстрации аналогии с явлениями макромира.

Среда, состоящая из частиц (например, молекул), индивидуальные магнитные моменты которых ориентированы не хаотично, будет обладать магнитным моментом и характеризоваться намагниченностью.

Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки; элементарным источником магнетизма считают замкнутый ток.

Формулы для вычисления магнитного момента[править | править код]

В случае плоского контура с электрическим током магнитный момент вычисляется как

где — сила тока в контуре, — площадь контура,
— единичный вектор нормали к плоскости контура. Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Для произвольного замкнутого контура магнитный момент равен

где — радиус-вектор, проведенный из начала координат до элемента длины контура .

В общем случае произвольного распределения токов в среде:

где — плотность тока в элементе объёма .

Магнитный момент во внешнем поле[править | править код]

Потенциальная энергия магнитного диполя в магнитном поле:

Минимизации энергии отвечает сонаправленность момента и поля. Поэтому, скажем, рамка с током «стремится» расположиться в плоскости, ортогональной к , и так, чтобы оказалось (не ).

Момент силы, действующий со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

Эти выражения аналогичны соответствующим выражениям для электрического дипольного момента во внешнем электрическом поле.

Создание магнитного поля самим моментом[править | править код]

Магнитный момент создаёт в точке, задаваемой радиус-вектором , магнитное поле

.

Предполагается, что начало координат произвольно выбрано в области токов, формирующих магнитный момент, а расстояние до точки, где ищется поле, достаточно велико по сравнению с размерами данной области. Через обозначена магнитная постоянная.

Приведённое выражение также имеет аналог для электрического поля, создаваемого электрическим дипольным моментом на большом расстоянии от него.

См. также[править | править код]

• Электрический дипольный момент
• Аномальный магнитный момент

Литература[править | править код]

• Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.

В
начало на лист изменений

Опыт
Резерфода. Радиоактивный распад.

Знаменитый опыт. В данном разделе
доказывается ошибочность принятого сегодня толкования этого эффекта, ставшего
основанием фундамента теоретической ядерной физики.

Сегодня понятие излучения включает в
себя и испускание каких либо частиц и собственно
электромагнитное излучение. И между ними, как правило, не делается разницы, что
само по себе уже неверно, даже если иметь в виду фотон. По теории фотон тоже
частица,  безмассовая,
абсолютно нейтральная!!!!  ( в энциклопедиях пишут, даже истинно нейтральная), и
следовательно,  не подчиняется закону
Кулона – не взаимодействует с электрическими зарядами и полями. Для данной
частицы даже не свойственен магнитный момент. И в то же время фотон участвует
за счет мултипольности и в магнитном,
и в электрическом и даже в гравитационном взаимодействиях. Подобный наворот заставляет задуматься о
научной компетенции авторов понятий зарядовой четности и зарядового сопряжения.
То есть путем множества оговорок противоречащих одна другой все-таки приходится признать, что фотон вовсе не нейтрален. Бывают
кванты – фотоны электрического и магнитного типа.

Ну что сказать, ну что сказать, устроены
так люди…

Противоречия при помощи таких же
противоречий и составляют основу претендующей на звание абсолюта
ядерно-квантовой физики.

Так в чем разница между излучением
частицы и излучением света. Да в том, что материальная частица без каких либо
оговорок взаимодействует со всеми полями по одному закону, а излучение по
другому.

К примеру, возьмем частицу вещества, атом
или молекулу. В опытах Штерна-Герлаха
и Раби такая частица,
обладающая магнитным «»моментом»»
притягивается к полюсам  магнита в
зависимости от ориентации и положения относительно полюсов. На основе этого
эффекта построены все принятые сегодня  квантовые стандарты частоты.

О магнитном моменте далее будем говорить как о способности намагничиваться.

В опытах с электрическими полями, Милликен, Иоффе сами не подозревая того, доказали
существование электрического дипольного момента у атомов, молекул и даже
пылинок вещества. То есть атомы не нейтральны в принципе. У них в любом
состоянии существует потенциал отличный от нуля. И находясь
между двумя потенциалами он должны принять потенциал равный
напряженности электрического поля в данной 
наблюдаемой точке. А если быть совсем точным, то напряжению или разнице
потенциалов, поскольку любая среда имеет сопротивление.

Иначе не имеет смысла говорить о потоках
и самой напряженности.

Частицы атома в этом плане ничем не
должны отличаться от самого атома в плане магнитного и электрического
взаимодействия. То есть частица должна будет притягиваться (отклонятся) к
полюсам магнита.

 Сравним с опытом,  приписываемым Резерфорду.

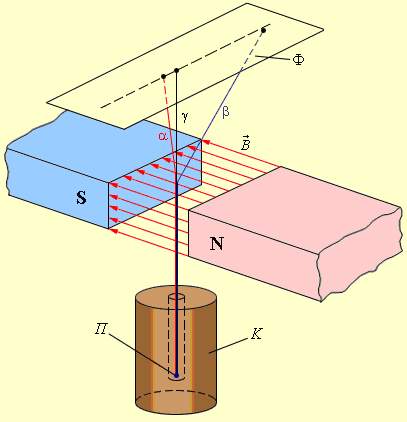
Рис1.  Схема опыта по обнаружению α-, β– и γ–излучений.
К – свинцовый контейнер, П – радиоактивный препарат, Ф
– фотопластинка, В – магнитное поле.

Наблюдения показали, что одновременно a-и b-излучения испускаются
только веществами, содержащими несколько различных радиоактивных элементов.
Чистые радиоактивные элементы испускают или a–излучение или b-излучение, каждому их которых сопутствует g-излучение. Радиоактивность возникает вследствие самопроизвольного
распада ядер одних элементов и превращения их в ядра других. Превращения ядер
бывают двух типов: a-распад и b-распад. Они
подчиняются определенным закономерностям, называемым правилами радиоактивного
смещения. Эти правила установил Содди.

Э. Резерфорд экспериментально установил (1899), что соли урана
испускают лучи трёх типов, которые по-разному отклоняются в магнитном поле:

http://ru.wikipedia.org/wiki/%D0%A0%D0%B0%D0%B4%D0%B8%D0%BE%D0%B0%D0%BA%D1%82%D0%B8%D0%B2%D0%BD%D1%8B%D0%B9_%D1%80%D0%B0%D1%81%D0%BF%D0%B0%D0%B4

Хотя
оба естественных изотопа урана  U238 U235 только
альфа и гамма активны. Картинка явно
врет, так как и Радий испускает только два вида радиоактивного излучения:
гамма-лучи с энергией 0.188 МЭв и альфа-частицы с
энергией 4.777 МЭв. Полоний 210  и торий 226 также не являются бета активными.
Только  они были открыты к моменту опыта.

Вывод: сама схема
опыта синтезирована и гораздо позже. Либо это был другой элемент.

Но все-таки
рассмотрим эту схему, поскольку именно она тиражируется во всех учебниках.

Здесь частицы a  и  b  излучения отклоняются не к полюсам, а
перпендикулярно к направлению вектора магнитной индукции. То есть
выталкиваются  магнитным полем в
плоскости перпендикулярной магнитному потоку. Точно также ведет себя и
проводник с током. Он выталкивается полем в сторону уменьшения напряженности,
независимо от того с какой стороны он в это поле вносится. Важен только угол
между вектором магнитной индукции и проводником.

Объяснить
такое выталкивание силой Лоренца не получается потому что мешает магнитный
момент.  Если квантовая механика
позволяет намагничивание частиц, то это касается как частиц, так и атомов в
целом.  Должно присутствовать отклонение
к полюсам.  И у атомов оно имеется и
доказано в опытах с молекулярно-атомными пучками. В противном случае, при
отсутствии в опытах отклонения частиц по направлению к полюсам говорит об
отсутствии и магнитного момента и намагничиваемости
частиц,  что в свою очередь ставит под
сомнение весь аппарат квантовой механики…. 
То есть и с самой силой Лоренца проблема номер раз!!!! Нет учета
магнитного момента электрона…..  а его и
не было во времена Лоренца!!!!!!!!!!!

Обнаруженная особенность
говорит об отсутствии «магнитного 
момента» у якобы излучаемых 
частиц.

Второе это положительность
заряда альфа частицы. Никто опытов с ядрами?????  Гелия в поле конденсатора не проводил.

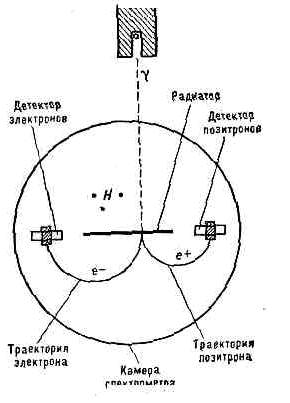
Электрон-позитронная пара.  Различие отклонений никак не комментируется. да и спиральность треков тоже.

Зато все  прекрасно согласуется с опытами Дж. Томсона в
1897 г.
с катодными лучами и подтверждено в опыте Иоффе.

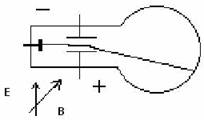
Они, то есть
 только электроны,  отклонялись к электроду конденсатора
расположенному перпендикулярно вектору магнитной индукции.

В классической
электродинамике такое взаимодействие с электрическим и магнитным полем имеет
только электрический ток в проводнике. А о токе и переносчике тока уже
говорилось в более ранних статьях.  А с
позитронами и любыми другими положительно заряженными частицами таких опытов не
ставилось…

Обнаруженное противоречие
между поведением атомов и уже якобы атомных частиц заставляет задуматься о том,
что такие элементарные частицы (прежде всего электрон) не являются на самом
деле материальными (с заметной массой) частицами, а являются истинным
излучением.   И носитель этого излучения
не электрон – элементарная частица.

Эти три вида радиоактивных излучений сильно
отличаются друг от друга по проникающей способности. Наименьшей проникающей
способностью обладает α-излучение. В воздухе при
нормальных условиях α-лучи проходят путь в
несколько сантиметров. β-лучи гораздо меньше
поглощаются веществом. Они способны пройти через слой алюминия толщиной в
несколько миллиметров. Наибольшей проникающей способностью обладают γ-лучи, способные проходить через слой свинца толщиной
5–10 см.

Проникающая способность говорит, прежде
всего, о различной скорости распространения данных излучений в веществе.

А теперь поглядим с другой стороны.

Для начала надо определиться, что такое
частица и что такое эм. Излучение.

Вся разница в том, что частица это
материальное тело(тело имеющее массу), имеющее способность вращаться,
обладающая каким не каким магнитным полем(магнитным моментом), то есть имеет
способность реагировать своим движением на воздействии внешнего магнитного
поля. Частица обладает свойством инерционности. Таким образом, вещественная
частица, находящаяся между полюсами магнита должна в зависимости от расстояния
и своей собственной ориентации притягиваться к тому или иному полюсу. (Частица
вещества может быть и молекулой и атомом и предполагаемой элементарной
частицей).

Электромагнитное излучение этими
свойствами не обладает. При прохождении потока излучения между полюсами магнита
оно отклоняется в плоскости перпендикулярной направлению поля. Либо его сила и
скорость такова, что слабым магнитным полем не отклоняется заметно вообще. Это
и продемонстрировал опыт Резерфорда.

А это и означает, что носителем
электрического поля является излучение, которое ныне по квантовой теории
переносит квант электромагнитного поля – фотон.

Противоречие уже и в том, что и
предполагаемые частицы и гамма-излучение ведут себя по отношению к магнитному
полю одинаково. Не притягиваются.

А вот отклонение в разные стороны еще
раз говорит мы наблюдаем излучение аналогичное свету. Как это похоже на
расщепление спектральных линий. Эффект Зеемана.

О спонтанности.

Спонтанность деления атомного ядра
странная с точки зрения закона сохранения энергии штука.  Для того чтобы процесс распада начался в
относительно замкнутой системе, в данном случае в атоме, необходим внешний
источник энергии, должно быть какое-либо излучение для вывода ядра из состояния
стабильности: либо это должно быть столкновение, либо внутренне излучение. Ну,
никто тебя не трогает, с чего бы разваливаться. Таким образом, о спонтанности
или случайности и речи быть не может, что-то заставляет атом извне либо
размножаться, либо увеличивать атомный вес. Причинность и следствие + закон
сохранения энергии. Иначе надо предположить, что ядра кем-то созданные имеют
некий конструкционный запас прочности. В них с 
избытком, за счет конструкции, энергии и когда одна из деталек ломается, спонтанно конечно, шарик разваливается.

 Всюду утверждается спонтанность и в тоже время
альфа распад и соответственно деление у 
урана 235, и урана 238  вызвано
нейтронами. Неоднозначность порождает недоверие.

Откуда берется энергия – раз.

 Откуда берутся электроны для заполнения
оболочек ядер Гелия? Можно подумать, что электроны просто из воздуха, где их немеряно. Или из стекла, которое их теряет и присоединятся
к ядрам.

Почему как из пушки все летит
наружу,  а не остается хотя бы большая
часть всех этих компонент внутри контейнера с распадающимся веществом – это
два. Особенно это касается гелия. По опыту можно истолковать, что все ядра
гелия вылетают только с поверхности образца, 
а что творится внутри образца, никто и не задумался. Не внушает доверия
и странно большая скорость истечения гелия, даже большая чем скорость истечения
электронов. Энергия и проникающая способность альфа частиц меньше? Да. А  магнитом отклоняется больше электрон. Если
это частица, то почему все в комплексе излучение отклоняется не к полюсам
магнита, а в перпендикулярной полю 
плоскости.

Почему только потом ядра гелия
приобретают электроны?

Даже если не учитывать, что большая
часть излучения просто обязана остаться в контейнере с образцом, поскольку он
излучает во все стороны; не учитывать, что ядро якобы излученного гелия просто
обязано подхватить якобы электроны хотя бы от B- потока; даже если
предположить, что все излучение целиком отражается от материала контейнера; все
равно приходится для удовлетворения закону сохранения придумывать, как
оставшееся после таких допущений  Aльфа – ядра спокойно вылетают из образца только с его
поверхности, летят обязательно в пространство не рассеиваясь, попадают все в
магнитное поле, да еще имеют скорость большую скорости электрона имея к тому же
и невероятно большую по сравнению с ним массу. Прикидочный  расчет показывает, что сила отдачи у образца
должна быть такова, что вполне можно использовать его в качестве реактивного
двигателя.

Для этого современная
квантово-механическая теория напрочь забывает об электромагнитном
взаимодействии всех трех типов излучений в едином потоке. Заряды частиц разные
по знаку по теории.  То есть сами частицы
по закону Кулона должны притягиваться, а не отталкиваться.

О неодновременности
единичных событий – выход альфа частицы и электрона  можно не говорить, поскольку времена при
достаточно большой массе радиоактивного образца 
ничтожно малы и поток тех и других достаточно плотен.

И еще одно замечание: отсутствие во сей
литературе описания опытов с излучением в присутствии электрического поля.
Наводит на некоторые мысли.

И во всех своих теориях распада Классика
не учла, не ущучила еще один вид излучения:   инфракрасное!!!!! Исключительно все образцы
с радиоактивными элементами греются и имеют температуру, выше чем нормальная –
21 градуса по Цельсию.  Поток этого
излучения никак не регистрируется и не учитывается, но совершенно удачно
используется в реакторах…

Наверняка в данной статье есть
спорные моменты.

Но  можно с уверенность сказать, одно только
различие в поведении атомов и предполагаемых частиц в магнитном поле говорит о
том, что частицами вещества данный поток не является.

А значит это излучение света.

Следовательно рассматривая все
опыты в которых  якобы обнаружена та или
иная «элементарная частица», которая не притягивается полюсами магнита, в
действительности даже отдельной частицей считаться не может, а является
электромагнитным   излучением.

Следует отметить, что и опыты, в которых
якобы открыты протон и нейтрон могут быть истолкованы иначе при более
тщательном их рассмотрении

Фатьянов А.В.    Спб.  24.10.2009   Fatyalink@mai.ru

В
начало на лист изменений