Ток или поток? Магнитные цепи и их основные характеристики
Время на прочтение
6 мин
Количество просмотров 13K
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это… а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим.
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции – а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм».
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель – рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову – провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи – ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
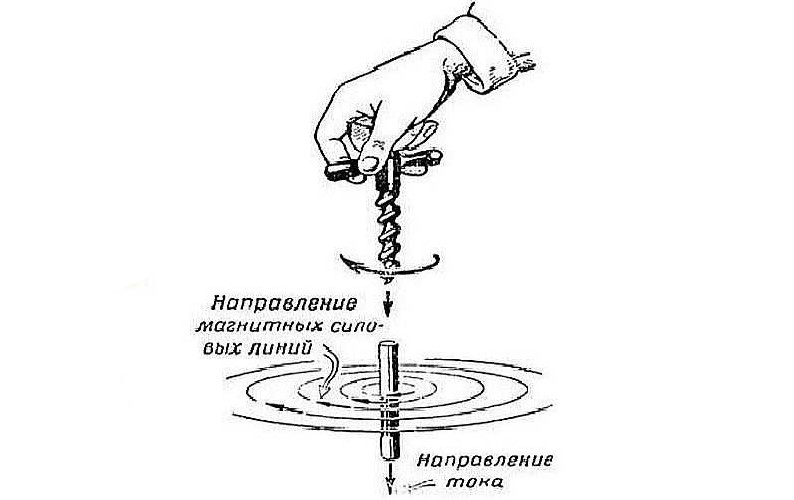
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
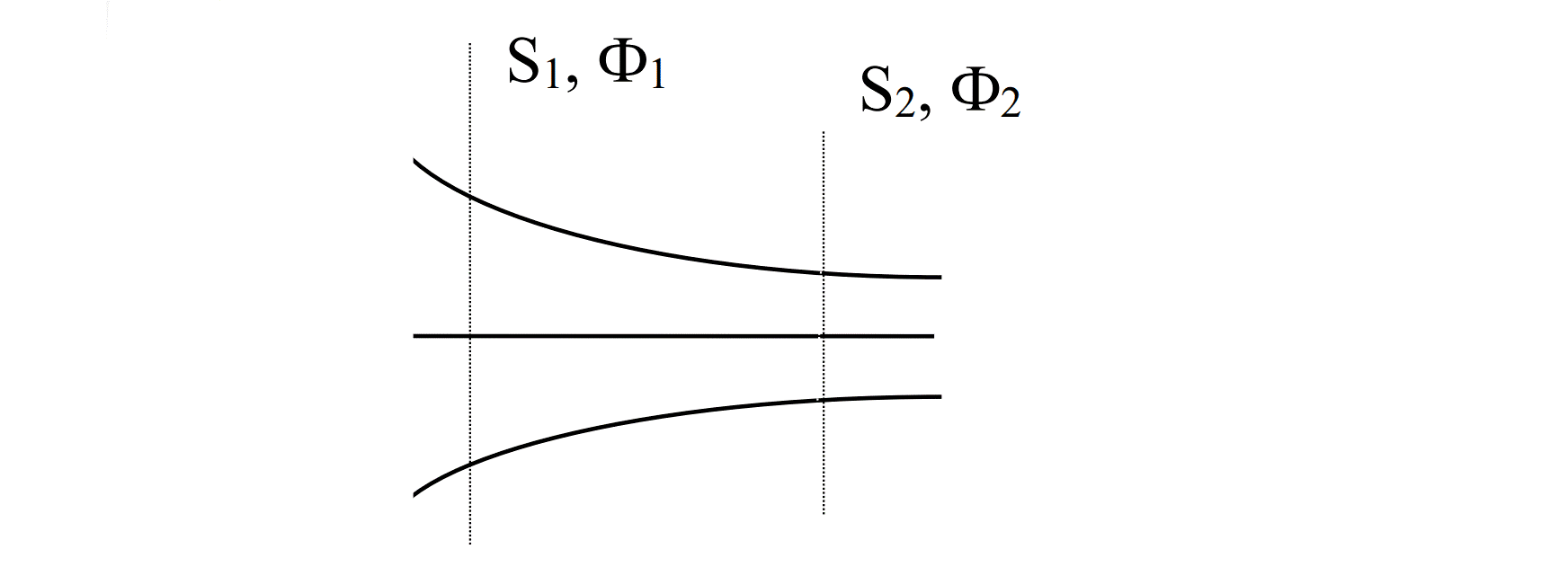
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю… Мне одному это что-то напоминает?
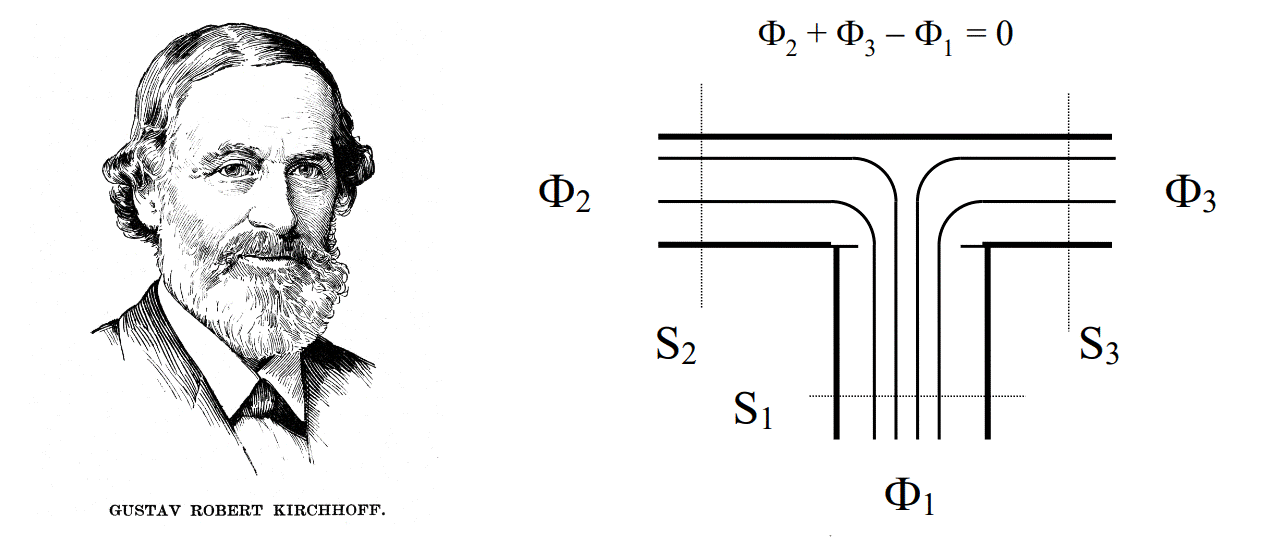
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае – магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи – силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
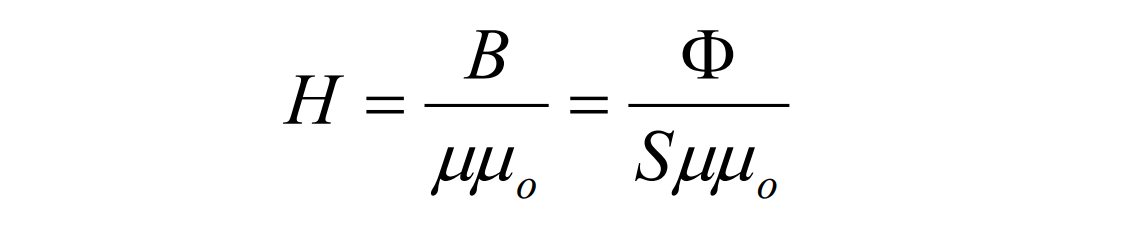
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
-
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
-
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
-
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
-
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь – нет. А по ссылке – да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора – подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны…
Магнитный поток катушки индуктивности L с током I.
Ф — магнитный поток, Вб (Вебер)
L — индуктивность катушки, Гн (Генри)
I — сила тока, А (Ампер)

Катушка индуктивности состоит из витков изолированного проводника. Обычно это витки медного провода, покрытого краской или любой не проводящей оболочкой. Основная особенность катушки в том, что при пропускании электрического тока, она становится электромагнитом. То есть начинает создавать магнитное поле. При постоянном токе свойства катушки ничем не примечательны — это кусок провода, который можно заменить перемычкой.
При подключении к катушке переменного напряжения начинаются удивительные вещи. Ток меняется, а значит меняется сила магнитного поля, которое создает катушка. Меняется магнитная индукция создаваемая витками и следовательно меняется магнитный поток. А согласно закону электромагнитной индукции — изменение магнитного потока приводит к появлению ЭДС.
Проще говоря, переменный ток превращает катушку в электрогенератор. Причем генерируемый ток направлен противоположно внешнему току. Но стоит отметить, что так можно говорить только с математической точки зрения, с точки зрения формул. На практике, изменение тока в катушке похоже на удар рукой по водной глади: чем медленнее движется рука, тем меньше сопротивление со стороны воды, но чем быстрее движется рука, тем большее сопротивление она испытывает при ударе об жидкость. Это явление в физике называется самоиндукцией. Индуктивность катушки называют также коэффициентом самоиндукции.
Что такое индуктивность, как она зависит от числа витков и других параметров — лучше всего разбирать на практике.
В этом видео, на практических примерах показаны все основные свойства катушки индуктивности.
В обычной жизни люди практически не встречаются с измерением индуктивностей и магнитных потоков, поэтому эти термины запоминаются не очень хорошо.
Простой способ усвоить эти термины — это разобраться с принципом работы металлоискателей и металлодетекторов. Стойки металлодетекторов можно наблюдать на вокзалах и в торговых центрах. Если вы поймете как они работают, станет понятна важность таких терминов как индуктивность и магнитный поток.
Задача 42.
При силе тока 10 А, в катушке возникает магнитный поток 50 мВб. Чему равна индуктивность катушки.
Показать ответ
Электромагнитная индукция

Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):


Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):

При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.47%) 98 votes
В этой статье мы увидим, как найти магнитный поток через одиночный контур и проводник с током с числом витков.
Магнитный поток обозначается как произведение магнитного поля, в котором находится материал, и площади, через которую проходит магнитный поток, и определяется соотношением
Как найти плотность магнитного потока?
Наблюдения и советы этой статьи мы подготовили на основании опыта команды магнитный поток Плотность определяется как общее количество линий магнитного потока, пронизывающих единицу площади поверхности материала.
Магнитный поток можно рассчитать, найдя общий поток через проводящий материал и площадь материала, через которую магнитный поток проникает через поверхность.
Магнитный поток через поверхность равен

Следовательно плотность магнитного потока становится магнитным потоком через единицу площади поверхности.

Плотность магнитного потока представляет собой отношение магнитного потока к площади поперечного сечения, через которое проходят силовые линии.
Как найти размер магнитного потока?
Размерность — это математический способ выражения единиц измерения измеряемой величины в простой фигуре.
Размерность магнитного потока можно определить по формуле зная размерность магнитного поля и площадь через которые проходят силовые линии магнитного поля.
Магнитное поле определяется как сила, действующая на заряженную частицу в присутствии магнитного поля скоростью и магнитным потоком через частицу, и, соответственно, размерность магнитного поля основана на размерностях этих величин.
Мы можем математически представить единицу магнитного поля, записав все величины в размерном формате. Сила, действующая на заряды из-за комбинации электрического и магнитного полей, равна
F=qVB
Итак, магнитное поле, в котором находится материал, равно
F=qVB
Теперь нам нужно найти, как мы можем представить эти термины в форме математического измерения.
Мы знаем, что сила определяется как ускорение объекта, когда к нему приложена внешняя сила, в зависимости от массы объекта, поэтому согласно второму закону движения Ньютона мы можем написать F = ma
Единицей ускорения является метр на квадрат времени, поэтому мы можем записать размерность ускорения как M0L1T-2 а единицей массы является кг только соответственно мы можем записать размерность массы как M0L1T-2 что равно М1
Следовательно, размерность магнитная сила is
Ф=М*(М0L1T-2)
Ф = М1L1T-2
Точно так же размерность скорости равна M0L1T-2 так как единица скорости м/с, а заряда М0L1T-2 как I=dQ/dt
Теперь, используя это измерение, мы можем найти размеры магнитного поля как
Б=Ф/кV
Б=М1L1T-2
Магнитный поток является произведением магнитного поля и площади материала, поэтому
Ø=BACosΘ
Θ — безразмерная величина, поэтому ею можно пренебречь и рассматривать размерности остаточных величин.
Ø=[М1L0I-1T-2]*[М0L2T0]
Ø=М1L2-1T-2
Это размер магнитного потока, представленный математически.
Как найти магнитный поток через контур?
Основываясь на направлении магнитного потока, мы можем найти чистое магнитное поле через материал.
Магнитное поле, образованное колеблющимися зарядами в материале, можно рассчитать по всей площади контура и, таким образом, найти магнитный поток через эту площадь.
Рассмотрим круглую петлю радиуса «R» и ток I, протекающий через эту круглую петлю. Пусть начало круга будет «О». Заряд помещен в точку «P», которая находится на расстоянии «x» от начала координат на плоскости оси x. Между линией, соединяющей частицу с началом координат, и контуром с током образуется угол θ.

Пусть dl — малый элемент круглой петли, по которой течет ток I. Магнитное поле через малый элемент dl на круглой петле от заряда, помещенного в точку P, равно

Где мк0/4π – константа пропорциональности, равная 10-7Тм/А
дБ=мк0/4π*IdlrSinθ/r3
дБ=мк0/4π*IdlrSinθ/r2
Направление dB перпендикулярно dl и r, и перпендикулярное магнитное поле компенсируется.
дБ=мк0/4π*холост./об2
Здесь, р2=R2+x2 следовательно, мы можем написать то же уравнение, что и
дБ=мк0/4π*холост./R2+x2
Чистое магнитное поле обусловлено x-компонентой магнитного поля, то есть
дБх=дБКосθ
Поскольку,
Cosθ=R/√x2+R2
Подставляя рассчитанные значения в приведенное выше уравнение, мы получаем

дБх=мк0/4π*IdlR/(R2+x2)3/2
Это уравнение для магнитного поля через небольшой элемент dl на круглом контуре. Теперь найдем магнитное поле на всем контуре.
Bx=∫дБx= μ0/4π∫IdlR/(R2+x2)3/2
Bx= μ0/4π*lR/(R2+x2)3/2∫дл
Bx= μ0/4π*lR/(R2+x2)3/2L
Длина — это полная длина окружности круглой петли, L = 2πR.
Вставка этого в приведенное выше уравнение
Bx= μ0/4π*lR/(R2+x2)3/2*2πr
Отсюда получаем,
Bx= μ0IR2/2((R2+x2)3/2
Если поле находится в центре петли, то x=0 и уравнение примет вид
B0= μ0я/2р
Это магнитное поле через контур, тогда магнитный поток равен
ф=ВА
φ=μ0I/2R*πR2
φ=μ0πIR/2
Это магнитный поток через круговой контур с током, если поле находится в центре контура.
Как найти магнитный поток из магнитного поля?
Линии магнитного потока показывают величину магнитного поля, проникающего через материал.
Линии магнитного поля, падающие на поверхность поперечного сечения материала, образующие определенный угол θ с нормалью к поверхности, дают магнитный поток через эту область.
Предположим, вы поместили проводящий материал площадью A в магнитное поле B так, что линия магнитного поля составляет угол θ с нормальной плоскостью поверхности материала, как показано на рисунке ниже.

Магнитный поток через этот материал будет скалярным произведением линий магнитного поля и площади материала, через которую проходят эти линии.
φ=ВА
φ=BACosθ
Таким образом, мы можем найти магнитный поток через материал от магнитного поля.
Как найти магнитный поток через соленоид?
Чтобы узнать магнитный поток через соленоид, мы должны будем вычислить напряженность магнитного поля через каждую катушку соленоида.
Мы можем определить магнитное поле соленоида, применив закон Био-Савара, который дает связь между током и магнитным полем. Рассчитав магнитное поле, мы можем рассчитать поток через площадь материала.
Рассмотрим цилиндрический соленоид длины ‘2l’ и радиуса ‘a’. Пусть «О» будет точкой в центре соленоида, которая делит соленоид на две половины. Пусть небольшой заряд присутствует в точке P на расстоянии «r» от центральной точки «O». Рассмотрим небольшой сегмент соленоида длиной «dx» на расстоянии «x» от центрального сегмента соленоида. Направление магнитного поля показано на рисунке ниже.

Магнитный поток через этот небольшой сегмент «dx» составляет дБ. Пусть соленоид состоит из n витков на единицу длины соленоида и, следовательно, магнитное поле через этот элемент dx равно

Интегрируя это уравнение, мы получим магнитное поле, создаваемое во всем соленоиде.

В осевом поле r>>a и r>>l тогда
[(прием)2+a2]3/2≅ г3
Следовательно, мы можем записать приведенное выше уравнение как

Магнитный момент m=NIA
Где N — число витков проводника с током вокруг соленоида, I — ток, а A — площадь соленоида.
Здесь количество витков по длине соленоида равно
N=n*2l=2nl
Магнитное поле входит с одной поверхности соленоида и выходит с другого конца.
Площадь, через которую проходит магнитный поток, равна A=πa2
Следовательно, магнитный момент равен
m=n*2l*I*πa2
Поэтому уравнение для магнитного поля мы можем записать в терминах магнитного момента как
В=мк0/4π*2м/р3
Теперь магнитный поток через соленоид равен
ɸ=БА
ɸ=μ0/4π*2м/р3* πа2
ɸ=μ0ma2/ 2r3
Это магнитный поток через соленоид.
Как рассчитать магнитную потокосцепление?
Связь магнитного потока наблюдается в трансформаторе и генераторах, где объединяются магнитные потоки разных контуров.
Связанный магнитный поток дает большое количество магнитного потока через материал. Если магнитный поток через один виток провода равен ɸ =БА тогда катушка, состоящая из n витков, будет давать чистый магнитный поток ɸ =nBA и член λ=nɸ называется утечкой магнитного потока.
Как рассчитать плотность магнитного потока катушки?
Плотность магнитного потока представляет собой полный магнитный поток, проходящий через материал на единицу его площади, и определяется соотношением B=ɸ/A
Плотность магнитного потока можно рассчитать, найдя полный магнитный поток, проникающий через единицу площади материала, находящегося в области магнитного поля.
Какова плотность магнитного потока через квадратный лист длиной 11.3 см, помещенный в область магнитного поля, если магнитный поток через лист равен 1 Вб?
Данный: л = 11.3 см = 0.113 м
ɸ=1Вб
Площадь квадратного листа, через который проходят силовые линии магнитного поля, равна
А=я2= 0.1132= 0.013 м2
У нас есть,
B= ɸ/A
= 76.92Т
B=1T.м2/ 0.013m2= 76.92Т
Следовательно магнитный поток плотность через квадратный лист составляет 76.92 Тл.
Часто задаваемые вопросы
Каков магнитный поток через прямоугольную поверхность длиной 5 см и шириной 2.8 см, помещенную в однородное магнитное поле силой 0.5 Тл, если магнитное поле образует угол 600 с нормалью поверхности?
Данный: л = 5 см = 0.05 м
б = 2.8 см = 0.028 м
В = 0.5 т
Θ = 600
Площадь прямоугольной поверхности равна
А=л*б
=0.05*0.028=0.0014 м2
У нас есть
ɸ=BACosθ
=0.5T* 0.0014 м2
=0.5Т*0.0014м2* 1/2
= 3.5 * 10-4Tm2
Магнитный поток через прямоугольный лист = 3.5*10-4Tm2
Чему равен магнитный поток через круглую петлю с током радиусом 7 см, если сила тока в проводнике равна 2 мА?
Данный: г = 7 см = 0.07 м
I=2 мА
Формула для расчета магнитного потока через круглую петлю имеет вид
ɸ=μ0πIr/2
Вставка заданных значений в это уравнение
ɸ=(4π*10-7Тм/А*π*2*10-3А*0.07м)/2
=4π*π*0.07*10-10Tm2
= 2.76 * 10-10Tm2
Следовательно, магнитный поток через круговой контур с током равен =2.76*10-10Tm2
Поток вектора магнитной индукции
Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:
Φ = B S cos α = B n S = B → S → с углом между n → и B → , обозначаемым α , n → является нормалью к площадке S .
Формула магнитного потока
Φ равняется количеству линий магнитной индукции, пересекающих площадку S , как показано на рисунке 1 . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.
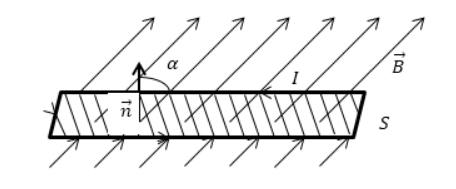
В чем измеряется магнитный поток
В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки d S , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока d Φ производится через эту поверхность. Запись примет вид:
d Φ = B d S cos α = B → d S → .
Нахождение полного потока через поверхность S :
Φ = ∫ S B d S cos α = ∫ S B → d S → .
Основной единицей измерения магнитного потока в системе СИ считаются веберы ( В б ) . 1 В б = 1 Т л 1 м 2 .
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δ A , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции d Φ :
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
A = I Φ 2 – Φ 1 с Φ 1 , обозначаемым потоком через контур в начале перемещения, Φ 2 является потоком через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:
Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током I , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I ‘ . Сторона рамки равна a . Она располагается в одной плоскости с проводом, как показано на рисунке 2 . Значение расстояния от ближайшей стороны рамки до проводника равняется b . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
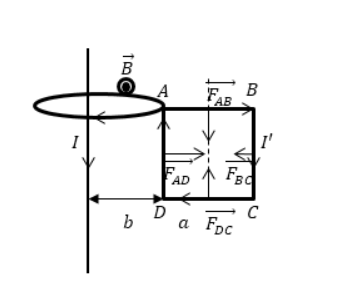
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
A = I ‘ Φ 2 – Φ 1 ( 1 . 1 ) , где I ‘ принимают за силу тока в рамке, Φ 1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b . Φ 2 = 0 . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы ( 1 . 1 ) изменится:
A = – I ‘ Φ 1 ( 1 . 2 ) .
Перейдем к нормали n → и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n → и вектором B → равняется π . Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:
d Φ = – B d S = – B · a · d x = – μ 0 2 π I l d x x ( 1 . 3 ) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:
B = μ 0 2 π x I l ( 1 . 4 ) .
Отсюда следует, что для нахождения всего потока из ( 1 . 3 ) потребуется:
Φ 1 = ∫ S – μ 0 2 π I l d x x = – μ 0 2 π I l ∫ b b + a d x x = – μ 0 2 π I l · ln b + a b ( 1 . 5 ) .
Произведем подстановку формулы ( 1 . 5 ) в ( 1 . 2 ) . Искомая работа равняется:
A = I ‘ μ 0 2 π I l · ln b + a b .
Ответ: A = μ 0 2 π I I ‘ l · ln b + a b .
Найти силу, действующую на рамку, из предыдущего примера.
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние d x . Это говорит о совершении силой работы, равной:
δ A = F d x ( 2 . 1 ) .
Элементарная работа δ A может быть выражена как:
δ A = I ‘ d Φ ( 2 . 2 ) .
Произведем то же с силой, применяя формулы ( 2 . 1 ) , ( 2 . 2 ) . Получаем:
F d x = I ‘ d Φ → F = I ‘ d Φ d x ( 2 . 3 ) .
Используем выражение, которое было получено в примере 1 :
d Φ = – μ 0 2 π I l d x x → d Φ d x = – μ 0 2 π I l x ( 2 . 4 ) .
Произведем подстановку d Φ d x в ( 2 . 3 ) . Имеем:
F = I ‘ μ 0 2 π I l x ( 2 . 5 ) .
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:
F A B → + F D C → = 0 ( 2 . 6 ) , то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
F → = F A D → + F B C → ( 2 . 6 ) .
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
F = F A D – F B C ( 2 . 7 ) .
Произведем поиск силы F A D , действующей на сторону A D , применив формулу ( 2 . 5 ) , где x = b :
F A D = I ‘ м 0 2 π I l b ( 2 . 8 ) .
Значение F B C будет:
F B C = I ‘ μ 0 2 π I l b + a ( 2 . 9 ) .
Для нахождения искомой силы:
F = I ‘ μ 0 2 π I l b – I ‘ μ 0 2 π I l b + a = I I ‘ μ 0 l 2 π 1 b – 1 b + a .
Ответ: F = I I ‘ μ 0 l 2 π 1 b – 1 b + a . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.
Поток вектора магнитной индукции (магнитный поток)
Вы будете перенаправлены на Автор24
Определение
Потоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную:
где $alpha $ угол между $overrightarrow$ и $overrightarrow$, $overrightarrow$ — нормаль к площадке S.
Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току.
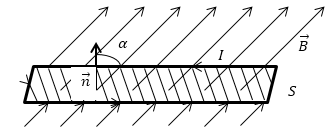
В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как:
Тогда полный поток через поверхность S находится как:
Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac<1Тл><1м^2>$.
Связь магнитного потока и работы сил магнитного поля
Элементарную работу ($delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ):
[delta A=IdФ left(4right).]
В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна:
где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Суммарный магнитный поток через замкнутую поверхность S равен нулю:
Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского – Гаусса в электростатике (в вакууме):
Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов».
Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I’$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
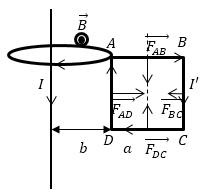
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас.
При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода.
В качестве основы для решения задачи используем формулу связи потока и работы:
$I’$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как:
Выберем направление нормали ($overrightarrow$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow$ и вектором $overrightarrow$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид:
где индукция магнитного поля бесконечно длинного проводника с током силы I равна:
Следовательно, весь поток из (1.3) найдем как:
Подставим формулу (1.5) в выражение (1.2) найдем искомую работу:
Электромагнитная индукция и магнитный поток
теория по физике 🧲 магнетизм
Английский физик и химик Майкл Фарадей считал, что если электрический ток может намагнитить кусок железа, то магнит тоже каким-то образом должен вызывать появление электрического тока. И он оказался прав. В 1831 году он открыл явление электромагнитной индукции.
Электромагнитная индукция — явление, заключающееся в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитной поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.
Опыты Фарадея
Сначала Фарадей открыл электромагнитную индукцию в неподвижных друг относительно друга проводниках пи замыкании и размыкании цепи. Он собрал установку, состоящую из источника тока, реостата, гальванометра, ключа и двух катушек. Одну катушку он соединил с реостатом, ключом и подключил к источнику питания. Вторую он подключил к гальванометру и устанавливал ее на тот же сердечник, что и первую. Всякий раз, как он замыкал или размыкал цепь, стрелка гальванометра отклонялась от нулевого значения шкалы.
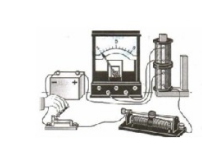
Затем электромагнитная индукция была обнаружена при сближении и удалении катушек в замкнутой цепи. Если ученый перемещал одну катушку относительно второй, стрелка гальванометра также отклонялась.
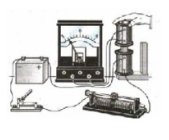
Потом явление электромагнитной индукции было обнаружено при изменении силы тока в подключенной к источнику питания катушке с помощью реостата. Если сила тока уменьшалась или увеличивалась, стрелка гальванометра отклонялась от начального положения. Но она вставала на нулевое значение, если прекращать перемещение ползунка реостата (делать силу тока постоянной).
Ученый понимал, что магнит представляет собой совокупность маленьких токов, циркулирующих в молекулах. Поэтому он поставил следующий опыт.
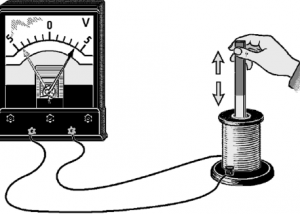
Фарадей собрал установку, состоящую из катушки и подключенного к ней гальванометра. Затем он взял полосовой магнит и ввел его внутрь катушки. В этот момент стрелка амперметра отклонилась от нулевого значения. Если же ученый останавливал движение магнита внутри катушки, стрелка прибора возвращалась в исходное положение. При извлечении магнита из катушки стрелка амперметра отклонялась в противоположную сторону.
Все эти опыты позволили Фарадею уловить то общее, от чего зависит появление индукционного тока в катушках. В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть изменение числа линий магнитной индукции, пронизывающих поверхность неподвижного проводящего контура вследствие изменения силы тока в соседней катушке, и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве.
Магнитный поток
Вектор магнитной индукции → B характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значения вектора → B не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром. Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль → n к плоскости проводника составляет угол α с направлением вектора магнитной индукции → B (см. рисунок).
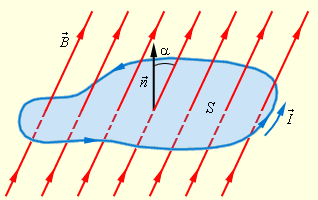
Магнитным потоком, или потоком магнитной индукции через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции → B на площадь S и косинус угла α между векторами → B и → n . Обозначается магнитный поток как Φ .
Произведение B cos . α = B n представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:
Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.
Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции.
Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м 2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?
Выразим модуль вектора магнитной индукции:
Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90 о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:
0 , 2 0 , 5 cos . ( 9 0 ° − 30 ° ) . . = 0 , 2 0 , 5 · 0 , 5 . . = 0 , 8 ( Т л )
Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции которого перпендикулярны её плоскости. Если площадь рамки увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза, то магнитный поток через рамку
а) увеличится в 9 раз
в) уменьшится в 3 раза
г) уменьшится в 9 раз
Алгоритм решения
Решение
Магнитный поток, пронизывающий площадь, ограниченную рамкой, определяется формулой:
По условию задачи площадь рамки увеличивают в 3 раза, а индукцию магнитного поля уменьшают во столько же раз. Следовательно:
Φ 1 = B 1 S 1 cos . α = 3 S · B 3 . . cos . α = B S cos . α = Φ
Следовательно, магнитный поток не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м 2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?
[spoiler title=”источники:”]
http://spravochnick.ru/fizika/postoyannoe_magnitnoe_pole/potok_vektora_magnitnoy_indukcii_magnitnyy_potok_/
[/spoiler]
