Условие задачи:
Найти максимальный магнитный поток через прямоугольную рамку, вращающуюся в однородном магнитном поле с частотой 10 об/с, если амплитуда индуцируемой в рамке ЭДС 3 В.
Задача №8.3.4 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu=10) об/с, (rm E_{imax}=3) В, (Phi_{max}-?)
Решение задачи:
 Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока (то есть первой производной функции изменения потока от времени):
Согласно закону Фарадея для электромагнитной индукции, ЭДС индукции, возникающая в контуре при изменении магнитного потока, пересекающего этот контур, равна по модулю скорости изменения магнитного потока (то есть первой производной функции изменения потока от времени):
[{rm E_i} = – Phi ^prime left( t right);;;;(1)]
Магнитный поток через некоторую площадку, помещённую в однородном магнитном поле, можно определить по такой формуле:
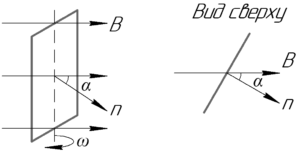
[Phi = BScos alpha ;;;;(2)]
В этой формуле (B) – индукция магнитного поля, (S) – площадь поверхности, через которую определяется магнитный поток, (alpha) – угол между нормалью к площадке и вектором магнитной индукции.
Учитывая, что произведение индукции магнитного поля (B) на площадь поверхности (S) дают максимальный магнитный поток (Phi_{max}), то формулу (2) можно записать в следующем виде:
[Phi = {Phi _{max }}cos alpha ;;;;(3)]
Прямоугольная рамка вращается в магнитном поле, то есть угол (alpha) меняется со временем. Чтобы формула (3) стала выглядеть как функция изменения магнитного потока от времени, нужно представить угол (alpha) в следующем виде:
[alpha = omega t + {alpha _0}]
Здесь (alpha_0) – некоторый начальный угол (также называют начальной фазой), а (omega) – угловая скорость вращения рамки, которую можно определить через известную частоту (nu) по формуле:
[omega = 2pi nu ]
Учитывая всё написанное, формула (3) примет вид:
[Phi = {Phi _{max }}cos left( {2pi nu t + {alpha _0}} right)]
Это выражение подставим в формулу (1):
[{rm E_i} = – {left( {{Phi _{max }}cos left( {2pi nu t + {alpha _0}} right)} right)^prime }]
Теперь нужно взять производную, тогда мы получим:
[{rm E_i} = {Phi _{max }} cdot 2pi nu cdot sin left( {2pi nu t + {alpha _0}} right)]
Очевидно, что ЭДС индукции достигнет своего максимального значения, когда синус будет равен единице, поэтому:
[{{rm E}_{imax}} = {Phi _{max }} cdot 2pi nu ]
Откуда искомый максимальный магнитный поток (Phi_{max}) равен:
[{Phi _{max }} = frac{{{{rm E}_{imax} }}}{{2pi nu }}]
Задача решена в общем виде, посчитаем численный ответ (об/с и Гц – это одно и то же):
[{Phi _{max }} = frac{3}{{2 cdot 3,14 cdot 10}} = 0,0478;Вб = 47,8;мВб]
Ответ: 47,8 мВб.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
8.3.3 Определить силу тока, протекающего по плоскому контуру площадью 5 см2, находящемуся
8.3.5 Определить индуктивность катушки, в которой возникает поток 0,12 Вб при силе тока
8.3.6 Полоску площадью 200 см2, расположенную под углом 60 к направлению однородного
Поток вектора магнитной индукции
Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:
Φ=BScos α=BnS=B→S→ с углом между n→ и B→, обозначаемым α, n→ является нормалью к площадке S.
Формула магнитного потока
Φ равняется количеству линий магнитной индукции, пересекающих площадку S, как показано на рисунке 1. Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S. Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.
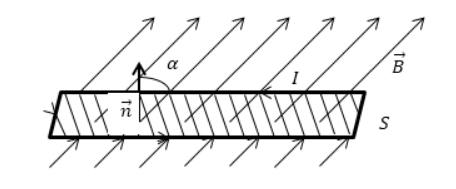
Рисунок 1
В чем измеряется магнитный поток
В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки dS, рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока dΦ производится через эту поверхность. Запись примет вид:
dΦ=BdScos α=B→dS→.
Нахождение полного потока через поверхность S:
Φ=∫SBdScos α=∫SB→dS→.
Основной единицей измерения магнитного потока в системе СИ считаются веберы (Вб). 1 Вб=1 Тл1 м2.
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δA, совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции dΦ:
δA=IdΦ.
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
A=IΦ2-Φ1 с Φ1, обозначаемым потоком через контур в начале перемещения, Φ2 является потоком через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:
∮B→dS→=0.
Выражение ∮B→dS→=0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
∮E→dS→=qε0.
Запись ∮B→dS→=0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
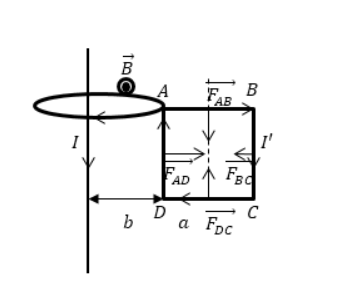
Рисунок 2
Решение
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=0. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:
A=-I’Φ1 (1.2).
Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:
dΦ=-BdS=-B·a·dx=-μ02πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:
B=μ02πxIl (1.4).
Отсюда следует, что для нахождения всего потока из (1.3) потребуется:
Φ1=∫S-μ02πIldxx=-μ02πIl∫bb+adxx=-μ02πIl·lnb+ab (1.5).
Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:
A=I’μ02πIl·lnb+ab.
Ответ: A=μ02πII’l·lnb+ab.
Найти силу, действующую на рамку, из предыдущего примера.
Решение
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:
δA=Fdx (2.1).
Элементарная работа δA может быть выражена как:
δA=I’dΦ (2.2).
Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:
Fdx=I’dΦ→F=I’dΦdx (2.3).
Используем выражение, которое было получено в примере 1:
dΦ=-μ02πIldxx→dΦdx=-μ02πIlx (2.4).
Произведем подстановку dΦdx в (2.3). Имеем:
F=I’μ02πIlx (2.5).
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:
FAB→+FDC→=0 (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
F→=FAD→+FBC→ (2.6).
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
F=FAD-FBC (2.7).
Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:
FAD=I’м02πIlb (2.8).
Значение FBC будет:
FBC=I’μ02πIlb+a (2.9).
Для нахождения искомой силы:
F=I’μ02πIlb-I’μ02πIlb+a=II’μ0l2π1b-1b+a.
Ответ: F=II’μ0l2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.
![]()
Поток вектора магнитной индукции через площадь рамки
Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м 2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля? (Ответ дать в теслах.)
Поток вектора магнитной индукции через поверхность площадью S вычисляется по формуле где — угол между вектором и нормалью к плоскости рамки. В условии задачи дан угол между плоскостью рамки и вектором индукции, следовательно, угол α = 90° − 30°=60°. Откуда
cos 30 =√3/2 , в итоге у вас неверный ответ
В формуле , — угол между вектором магнитной индукции и нормалью к плоскости рамки.
Данное задание решено Вами неверно, поскольку cos30=(sqrt(3))/2, а не 1/2, как Вы полагаете.
Поток вектора магнитной индукции
Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:
Φ = B S cos α = B n S = B → S → с углом между n → и B → , обозначаемым α , n → является нормалью к площадке S .
Формула магнитного потока
Φ равняется количеству линий магнитной индукции, пересекающих площадку S , как показано на рисунке 1 . Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S . Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

В чем измеряется магнитный поток
В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки d S , рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока d Φ производится через эту поверхность. Запись примет вид:
d Φ = B d S cos α = B → d S → .
Нахождение полного потока через поверхность S :
Φ = ∫ S B d S cos α = ∫ S B → d S → .
Основной единицей измерения магнитного потока в системе СИ считаются веберы ( В б ) . 1 В б = 1 Т л 1 м 2 .
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δ A , совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции d Φ :
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
A = I Φ 2 – Φ 1 с Φ 1 , обозначаемым потоком через контур в начале перемещения, Φ 2 является потоком через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:
Выражение ∮ B → d S → = 0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
Запись ∮ B → d S → = 0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током I , недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I ‘ . Сторона рамки равна a . Она располагается в одной плоскости с проводом, как показано на рисунке 2 . Значение расстояния от ближайшей стороны рамки до проводника равняется b . Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
A = I ‘ Φ 2 – Φ 1 ( 1 . 1 ) , где I ‘ принимают за силу тока в рамке, Φ 1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b . Φ 2 = 0 . Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы ( 1 . 1 ) изменится:
A = – I ‘ Φ 1 ( 1 . 2 ) .
Перейдем к нормали n → и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n → и вектором B → равняется π . Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:
d Φ = – B d S = – B · a · d x = – μ 0 2 π I l d x x ( 1 . 3 ) , значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:
B = μ 0 2 π x I l ( 1 . 4 ) .
Отсюда следует, что для нахождения всего потока из ( 1 . 3 ) потребуется:
Φ 1 = ∫ S – μ 0 2 π I l d x x = – μ 0 2 π I l ∫ b b + a d x x = – μ 0 2 π I l · ln b + a b ( 1 . 5 ) .
Произведем подстановку формулы ( 1 . 5 ) в ( 1 . 2 ) . Искомая работа равняется:
A = I ‘ μ 0 2 π I l · ln b + a b .
Ответ: A = μ 0 2 π I I ‘ l · ln b + a b .
Найти силу, действующую на рамку, из предыдущего примера.
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние d x . Это говорит о совершении силой работы, равной:
δ A = F d x ( 2 . 1 ) .
Элементарная работа δ A может быть выражена как:
δ A = I ‘ d Φ ( 2 . 2 ) .
Произведем то же с силой, применяя формулы ( 2 . 1 ) , ( 2 . 2 ) . Получаем:
F d x = I ‘ d Φ → F = I ‘ d Φ d x ( 2 . 3 ) .
Используем выражение, которое было получено в примере 1 :
d Φ = – μ 0 2 π I l d x x → d Φ d x = – μ 0 2 π I l x ( 2 . 4 ) .
Произведем подстановку d Φ d x в ( 2 . 3 ) . Имеем:
F = I ‘ μ 0 2 π I l x ( 2 . 5 ) .
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны A B и D C равные по модулю и противоположные по направлению. Выражение принимает вид:
F A B → + F D C → = 0 ( 2 . 6 ) , то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
F → = F A D → + F B C → ( 2 . 6 ) .
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
F = F A D – F B C ( 2 . 7 ) .
Произведем поиск силы F A D , действующей на сторону A D , применив формулу ( 2 . 5 ) , где x = b :
F A D = I ‘ м 0 2 π I l b ( 2 . 8 ) .
Значение F B C будет:
F B C = I ‘ μ 0 2 π I l b + a ( 2 . 9 ) .
Для нахождения искомой силы:
F = I ‘ μ 0 2 π I l b – I ‘ μ 0 2 π I l b + a = I I ‘ μ 0 l 2 π 1 b – 1 b + a .
Ответ: F = I I ‘ μ 0 l 2 π 1 b – 1 b + a . Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.
Электромагнитная индукция и магнитный поток
теория по физике 🧲 магнетизм
Английский физик и химик Майкл Фарадей считал, что если электрический ток может намагнитить кусок железа, то магнит тоже каким-то образом должен вызывать появление электрического тока. И он оказался прав. В 1831 году он открыл явление электромагнитной индукции.
Электромагнитная индукция — явление, заключающееся в возникновении электрического тока в проводящем контуре, который либо покоится в переменном во времени магнитной поле, либо движется в постоянном магнитном поле таким образом, что число линий магнитной индукции, пронизывающих контур, меняется.
Опыты Фарадея
Сначала Фарадей открыл электромагнитную индукцию в неподвижных друг относительно друга проводниках пи замыкании и размыкании цепи. Он собрал установку, состоящую из источника тока, реостата, гальванометра, ключа и двух катушек. Одну катушку он соединил с реостатом, ключом и подключил к источнику питания. Вторую он подключил к гальванометру и устанавливал ее на тот же сердечник, что и первую. Всякий раз, как он замыкал или размыкал цепь, стрелка гальванометра отклонялась от нулевого значения шкалы.
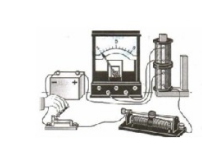
Затем электромагнитная индукция была обнаружена при сближении и удалении катушек в замкнутой цепи. Если ученый перемещал одну катушку относительно второй, стрелка гальванометра также отклонялась.
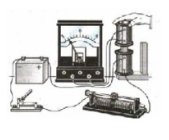
Потом явление электромагнитной индукции было обнаружено при изменении силы тока в подключенной к источнику питания катушке с помощью реостата. Если сила тока уменьшалась или увеличивалась, стрелка гальванометра отклонялась от начального положения. Но она вставала на нулевое значение, если прекращать перемещение ползунка реостата (делать силу тока постоянной).
Ученый понимал, что магнит представляет собой совокупность маленьких токов, циркулирующих в молекулах. Поэтому он поставил следующий опыт.
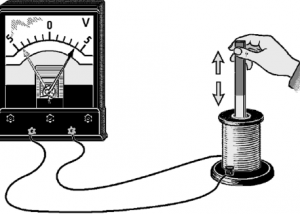
Фарадей собрал установку, состоящую из катушки и подключенного к ней гальванометра. Затем он взял полосовой магнит и ввел его внутрь катушки. В этот момент стрелка амперметра отклонилась от нулевого значения. Если же ученый останавливал движение магнита внутри катушки, стрелка прибора возвращалась в исходное положение. При извлечении магнита из катушки стрелка амперметра отклонялась в противоположную сторону.
Все эти опыты позволили Фарадею уловить то общее, от чего зависит появление индукционного тока в катушках. В замкнутом проводящем контуре возникает ток при изменении числа линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром. При этом причина изменения числа линий магнитной индукции совершенно безразлична. Это может быть изменение числа линий магнитной индукции, пронизывающих поверхность неподвижного проводящего контура вследствие изменения силы тока в соседней катушке, и изменение числа линий индукции вследствие движения контура в неоднородном магнитном поле, густота линий которого меняется в пространстве.
Магнитный поток
Вектор магнитной индукции → B характеризует магнитное поле в каждой точке пространства. Можно ввести еще одну величину, зависящую от значения вектора → B не в одной точке, а во всех точках поверхности, ограниченной плоским замкнутым контуром. Для этого рассмотрим плоский замкнутый проводник (контур) с площадью поверхности S, помещенный в однородное магнитное поле. Нормаль → n к плоскости проводника составляет угол α с направлением вектора магнитной индукции → B (см. рисунок).
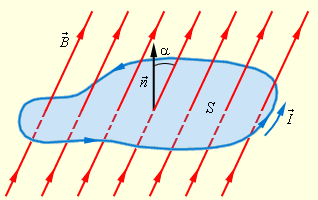
Магнитным потоком, или потоком магнитной индукции через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции → B на площадь S и косинус угла α между векторами → B и → n . Обозначается магнитный поток как Φ .
Произведение B cos . α = B n представляет собой проекцию вектора магнитной индукции на нормаль к плоскости контура. Поэтому:
Магнитный поток можно представить как величину, пропорциональную числу линий магнитной индукции, пронизывающих поверхность площадью S.
Единица измерения магнитного потока — вебер (Вб). Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции.
Пример №1. Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м 2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?
Выразим модуль вектора магнитной индукции:
Так как нам дан угол между поверхностью рамки и вектором магнитной индукции, угол между вектором магнитной индукцией и нормалью будет равен разности 90 о и угла поверхностью рамки и вектором магнитной индукции. Отсюда:
0 , 2 0 , 5 cos . ( 9 0 ° − 30 ° ) . . = 0 , 2 0 , 5 · 0 , 5 . . = 0 , 8 ( Т л )
Плоская рамка помещена в однородное магнитное поле, линии магнитной индукции которого перпендикулярны её плоскости. Если площадь рамки увеличить в 3 раза, а индукцию магнитного поля уменьшить в 3 раза, то магнитный поток через рамку
а) увеличится в 9 раз
в) уменьшится в 3 раза
г) уменьшится в 9 раз
Алгоритм решения
Решение
Магнитный поток, пронизывающий площадь, ограниченную рамкой, определяется формулой:
По условию задачи площадь рамки увеличивают в 3 раза, а индукцию магнитного поля уменьшают во столько же раз. Следовательно:
Φ 1 = B 1 S 1 cos . α = 3 S · B 3 . . cos . α = B S cos . α = Φ
Следовательно, магнитный поток не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Линии индукции однородного магнитного поля пронизывают рамку площадью 0,5 м 2 под углом 30° к её поверхности, создавая магнитный поток, равный 0,2 Вб. Чему равен модуль вектора индукции магнитного поля?
[spoiler title=”источники:”]
http://zaochnik.com/spravochnik/fizika/magnitnoe-pole/potok-vektora-magnitnoj-induktsii/
[/spoiler]
Задача: магнитный поток через квадратную проволочную рамку со стороной 5 см, плоскость которой перпендикулярна линиям индукции однородного магнитного поля, равен 0,1 мВб. Каков модуль вектора магнитной индукции поля?
Решение:
Формула магнитного потока: ΔФ = BScosα, где B – вектор магнитной индукции, S – площадь поверхности, находящейся в магнитном поле, α – угол между нормалью и вектором магнитной индукции.
ΔФ = 0.1 мВб = 0.0001 Вб
Сторона рамки L = 5 см = 0.05 м²
S = = 0.05*0.05 = 0.0025
В данной задаче cosα = 1 => B = ΔФ/S = = 0.04 Тл
Ответ: B = 0.04 Тл
Или вот такое объяснение решения:
Магнитный поток равен:
Ф=BScosa
B-вектор магнитной индукции
S-площадь рамки (площадь квадрата)
S=5²=25 см²= 0.0025 м²
Так как плоскость рамки перпендикулярна линиям магнитной индукции, значит угол равен 0 градусов (угол между нормалью плоскости рамки и вектором магнитной индукции)
cos0=1, значит
Ф=ВS
B=Ф/S=0,1 мВб / 0.0025 м²= 0.0001 Вб/ 0.0025 м²=0.04 Тл= 40 мТл
Ответ: 0.04 Тл или 40 мТл

* 5 * 5 * 5 * 5 * 5 *
Удачи тебе на экзаменах! У тебя всё получится – мы в тебя верим!
Поделись этой информацией с помощью кнопок ниже (облегчи учёбу другим ученикам, и будет тебе плюс в карму!)
Магнитный поток


3.9
Средняя оценка: 3.9
Всего получено оценок: 123.
3.9
Средняя оценка: 3.9
Всего получено оценок: 123.
Для количественного описания явления электромагнитной индукции необходимо введение понятия магнитного потока. Рассмотрим эту тему подробнее.
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):

Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Понятие магнитного потока
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
$$Ф=BScosalpha$$
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
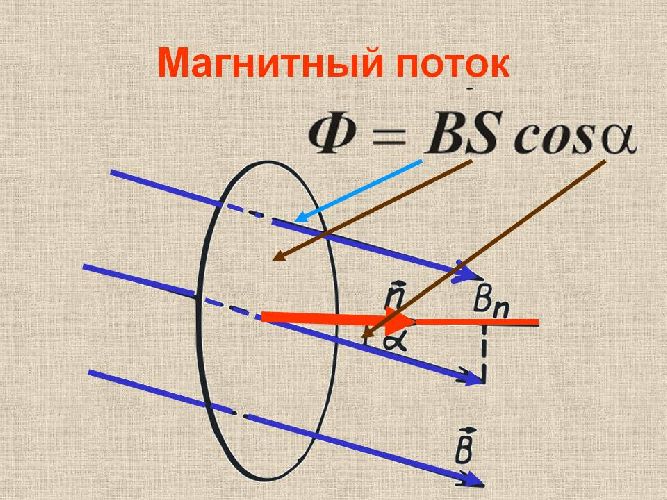
Из приведенной формулы магнитного потока можно вывести определение его единицы – вебер(Вб):
$$1Вб=1Тл×1м^2×cosalpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.

Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.

Что мы узнали?
Для описания явления электромагнитной индукции в проводящем контуре необходимо учесть индукцию магнитного поля, «охват» поля контуром и ориентацию контура. Все эти факторы объединяются в понятии «магнитный поток». Изменение магнитного потока приводит к возникновению ЭДС в контуре. Постоянный магнитный поток ЭДС не вызывает.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 123.
А какая ваша оценка?
