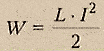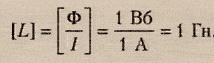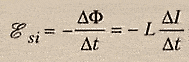| Магнитный поток | |
|---|---|
 |
|
| Размерность | ML2T−2I−1 |
| Единицы измерения | |
| СИ | Вб |
| СГС | Мкс |
| Примечания | |
| Скалярная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тный пото́к — поток вектора магнитной индукции 
через некоторую поверхность. Для бесконечно малого участка равен произведению модуля 
на площадь участка 
и косинус угла 
между и нормалью 
к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам. Стандартное обозначение — .
Важнейшая физическая формула, в которую входит магнитный поток, — выражение для закона электромагнитной индукции Фарадея.
Определение магнитного потока[править | править код]
Разбиение поверхности на малые участки 
Изменение вектора нормали к поверхности
Магнитным потоком через бесконечно малый элемент поверхности называется произведение
,
где — угол между вектором магнитной индукции и единичным вектором нормали к участку поверхности, а векторный элемент dS площади поверхности S определяется как
- .
Магнитным потоком через поверхность конечной площади называется интеграл от 
по поверхности:
- .
Направление вектора в общем случае непостоянно (см. рис.), магнитное поле также может изменяться вдоль поверхности. Точка в произведениях означает скалярное умножение векторов. Интеграл понимается как предел суммы по малым участкам при стремлении их размеров к нулю. Поверхность может быть незамкнутой (как на рис.) или замкнутой.
В случае однородного поля и плоской поверхности магнитный поток рассчитывается как 
.
Единицы измерения магнитного потока[править | править код]
В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с =
кг·м²·с-2·А-1), в системе СГС — максвелл (Мкс, 1 Вб = 108 Мкс).
Приборы для измерения потока[править | править код]
Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.
Некоторые свойства магнитного потока[править | править код]
В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции через любую замкнутую поверхность 
равен нулю:
- .
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
В соответствии с теоремой Стокса, магнитный поток через поверхность, «натянутую» на некий контур 
, можно выразить через циркуляцию векторного потенциала 
магнитного поля по этому контуру:
- ,
поскольку имеет место связь 
. Этот поток не зависит от конфигурации натянутой поверхности.
Переменный во времени магнитный поток[править | править код]
По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила
в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции и/или геометрии контура.
Квантование магнитного потока[править | править код]
При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:
- ,
где 
— постоянная Планка, 
— элементарный заряд.
Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):
- Вб (в СИ);
- Гаусс·см2 (в СГС), — скорость света.
Экспериментально квантование магнитного потока было обнаружено в 1961 году.
См. также[править | править код]
- Уравнения Максвелла
- Электродвигатель постоянного тока
- Потокосцепление
- Индуктивность
Магнитный поток
Содержание:
-
Что такое магнитный поток
- В чем измеряется, обозначение и размерность
- От чего зависит величина основного магнитного потока
-
Чему равен магнитный поток, как найти
- Скорость изменения магнитного потока через контур
- Какой формулой определяется величина магнитного потока
- Связь магнитного потока и работы сил магнитного поля
Что такое магнитный поток
Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.
Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд (triangle Q). Этот заряд прямо пропорционален количеству( triangle Ф) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля.
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий (triangle Ф), пересекаемых контуром за время (triangle t). Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.
В чем измеряется, обозначение и размерность
Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.
Размерность магнитного потока — (В times с = кг times м^{2} times с^{-2} times А^{-1}.)
От чего зависит величина основного магнитного потока
Его можно изменить следующими способами:
- изменив площадь контура;
- изменив угол его наклона;
- изменив магнитное напряжение.
Чему равен магнитный поток, как найти
Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла (varphi) между направлением индукции В и нормали к данной поверхности.
Нормаль — перпендикуляр к плоскости контура.
Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.
Обозначение суммарного потока — буква ( psi). Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.
Скорость изменения магнитного потока через контур
Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:
(;underset С{oint;};(overrightarrow{Е;}times;doverrightarrow l) = – frac{1}{c}frac{d}{dt}int underset S{int;};(overrightarrow{B} times doverrightarrow{S}).)
Интеграл в левой части уравнения — циркуляция вектора (overrightarrow{Е;}) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С.
Интеграл — целое, определяемое как сумма его бесконечно малых частей.
Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:
(epsilon_{i} = – frac{triangleФ}{triangle t}.)
Какой формулой определяется величина магнитного потока
Математически величину Ф описывают двумя формулами:
(Ф;=;sum_{triangle S};;Btriangle S = B times S times cosvarphi. )
Связь магнитного потока и работы сил магнитного поля
Герман Гельмгольц первым связал закон Фарадея и закон сохранения энергии. Возьмем проводник с током I, находящийся внутри однородного магнитного поля, которое перпендикулярно плоскости контура, и перемещающийся в нем. Под влиянием силы Ампера F проводник перемещается на отрезок dx. Сила F производит работу dA = IdФ.
Работу источника тока можно измерить, сложив работу на джоулеву теплоту и работу по перемещению проводника внутри поля:
(epsilon Idt = I^{2}Rdt + IdФ.)
(I = frac{epsilon – frac{dФ}{dt}}{R}.)
Насколько полезной была для вас статья?
Рейтинг: 4.40 (Голосов: 5)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Вероятно, термин «поток» ассоциируется у вас с потоком воды. Если бы вы хотели описать этот поток количественно, то имели бы в виду определенное количество воды, протекающей через поперечное сечение в определенной точке. Такой поток может нести большое или малое количество воды в зависимости от скорости воды и площади этого поперечного сечения.
Магнитный поток — это физическая величина, тесно связанная с явлением электромагнитной индукции. Это сложная величина, довольно абстрактная. Но, как вы правильно догадались, его название берет свое начало в гидродинамике. Здесь, однако, нет потока материи через поверхность, есть только векторы магнитной индукции B, «пронзающие» поверхность и иногда «скользящие» по ней.
Представьте себе однородное магнитное поле, описываемое вектором магнитной индукции B. Мы помещаем плоскую поверхность с полем S в это поле совершенно произвольным образом, то есть под любым углом по отношению к вектору B (рис. 1). Теперь определим вектор B, перпендикулярный плоскости поверхности. Пусть длина этого вектора равна величине поверхности.
Потоком вектора магнитной индукции ФB через поверхность S называется скалярное произведение векторов B и S.
Итак можно дать следующее определение термину «магнитный поток»:
Магнитный поток — это поток вектора магнитной индукции B через некоторую поверхность. Для бесконечно малого участка равен произведению модуля | B | на площадь участка dS и косинус угла α между B и нормалью n к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам.
Википедия
Зависимости магнитного потока
Используя формулу, можно увидеть, что магнитный поток зависит от трех переменных: магнитного поля B, площади S и угла α.
Магнитный поток линейно зависит от B и S. Например, если увеличить площадь S, но оставить магнитное поле B и угол α прежними, то магнитный поток будет больше. Поэтому большая площадь означает большой поток, а маленькая площадь — маленький магнитный поток.
Если, с другой стороны, увеличить магнитное поле B, то магнитный поток также увеличится. Сильное магнитное поле приводит к большому потоку, слабое поле — к малому магнитному потоку.
В целом, чем больше магнитное поле B или площадь S, тем больше магнитный поток.
Ситуация с углом α немного сложнее. Представьте, что ваша поверхность перпендикулярна магнитному полю, тогда ваш угол α = 0° . Здесь у вас самый большой магнитный поток. Если теперь шаг за шагом увеличивать угол, магнитный поток уменьшается. Когда вы достигаете α = 90°, магнитный поток равен нулю, потому что магнитное поле параллельно поверхности. После этого он снова начинает увеличиваться.
Единица измерения и обозначение магнитного потока
Магнитное поле B имеет единицу Тесла (T), а площадь — единицу квадратный метр м2 .
Поток является скалярной величиной и его единицей измерения является вебер (Вб): 1 Вб = 1 Т * м2 , то есть [Ф] = Т * м2 . Обозначается магнитный поток как Ф (символ формулы — греческая фи).
Примеры
Приведенные ниже примеры дадут вам лучшее понимание того, что представляет собой новая концепция и аналогия с потоком воды.
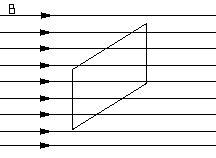
- В случае, показанном на рис. 2, поток магнитного поля с магнитной индукцией B через поверхность S составляет: ФB = B * S и при этом его значение максимально, так как:
2. А в каком случае при ненулевой магнитной индукции ФB = 0 ?
Определение магнитного потока показывает, что это тот случай, когда:
потому что cos 90° = 0.
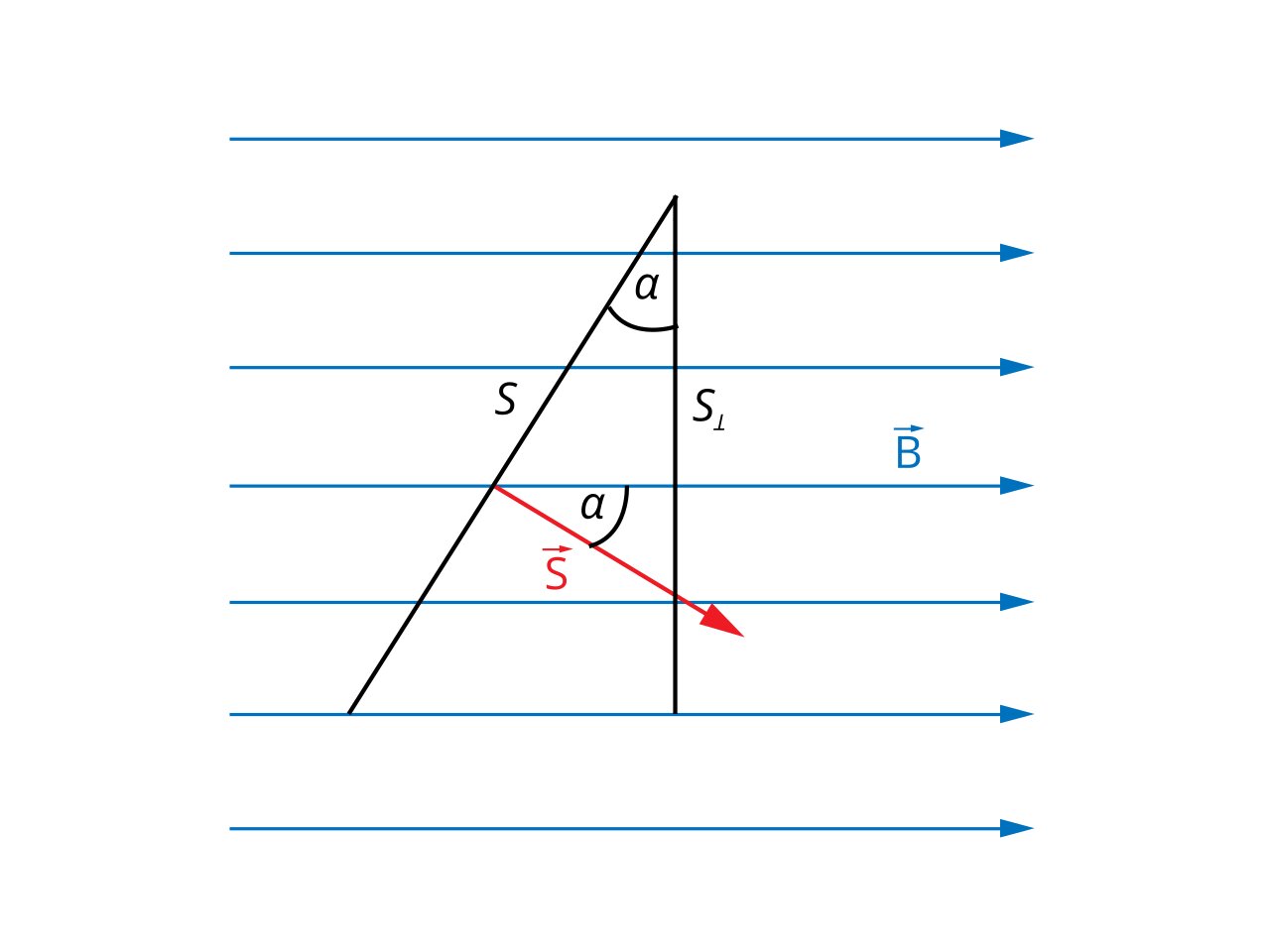
На рис. 3 мы видим, как в этой ситуации располагается плоская поверхность относительно векторов магнитной индукции.
Обратите внимание, что ФB можно представить как произведение В и S⟂, где S⟂ = S * cos α. Аналогично, вы всегда можете рассчитать величину потока магнитного поля, умножив составляющую магнитной индукции, перпендикулярную поверхности, на величину площади поверхности (см. рис. 4а. и 4б.).
Как можно рассчитать поток магнитного поля, если поле неоднородно и/или поверхность искривлена? Мы делим поверхность, через которую мы должны вычислить поток, на такие маленькие участки, что можно считать, что они плоские и поле однородное. Все это для того, чтобы можно было применить определение потока. Поэтому мы вычисляем небольшие «потоки» и суммируем их. Описанная процедура называется вычислением поверхностного интеграла, который записывается в виде:
Вычислять такие интегралы совсем не обязательно, но полезно понимать смысл такой процедуры.
Магнитный поток
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
Для количественного описания явления электромагнитной индукции необходимо введение понятия магнитного потока. Рассмотрим эту тему подробнее.
Проводящая рамка в магнитном поле
Явление электромагнитной индукции состоит в том, что при изменении поля, пронизывающего проводящую рамку или катушку, в ней возникает электродвижущая сила (ЭДС):
Энергия используемого в этом опыте магнитного поля характеризуется магнитной индукцией. Однако, при попытке описать наблюдаемое явление выяснилось, что одной этой величины мало.
Если выписать в таблицу значения ЭДС, наводимые магнитным полем, имеющим одну и ту же плотность магнитных линий, в разных условиях, то окажется, что ЭДС, возникающая в квадратной рамке, имеет гораздо большее значение, чем ЭДС в длинной узкой рамке (при одном периметре).
А наибольшая ЭДС возникает в круглом витке.
Причиной этого оказался разный «охват поля» рамкой. Площадь длинной узкой рамки невелика, она «охватывает» малое «количество поля», и ЭДС в ней также мала. У квадратной рамки площадь при одинаковом периметре больше, а у круглого витка – она наибольшая, в результате рамка «охватывает» большее «количество поля», и ЭДС в такой рамке тоже получается больше.
Не менее важной оказалась ориентация рамки по отношению к направлению магнитного поля. Наибольшая ЭДС возникает, если проводящая рамка перпендикулярна линиям магнитной индукции. Если плоскость рамки параллельна этим линиям – то независимо от ее площади и силы магнитного поля ЭДС в рамке не возникнет.
Понятие магнитного потока
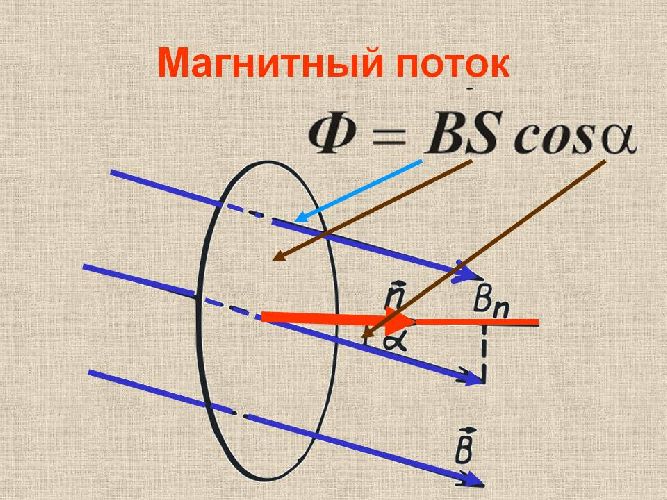
Таким образом, для описания явления электромагнитной индукции было введено понятие «магнитный поток», характеризующее «охват поля» рамкой. В этом понятии объединяются все величины, от которых зависит наведенная в рамке ЭДС – индукция поля, площадь и ориентация рамки. Для обозначения используется большая греческая буква Ф (фи):
$$Ф=BScosalpha$$
Таким образом, магнитный поток – это величина, равная произведению индукции магнитного поля, площади проводящего контура, и косинуса угла между нормалью к контуру и направлением линий индукции.
Из приведенной формулы магнитного потока можно вывести определение его единицы – вебер(Вб):
$$1Вб=1Тл×1м^2×cosalpha$$,
то есть, магнитный поток 1 Вебер – это магнитный поток, проходящий через рамку площадью 1 квадратный метр, которая ориентирована перпендикулярно линиям однородного магнитного поля с индукцией 1Тесла.
Для понимания термина «магнитный поток» можно представить аналогию с обычным водяным потоком. Водяной поток, как правило, зависит от напора воды (аналог индукции) и площади сечения трубы (аналог площади рамки), а поскольку вода, в отличие от магнитного поля, всегда заключена внутрь трубы, то водяной поток всегда ориентирован поперек сечения трубы, и значение косинуса в формуле всегда равно единице.
Что мы узнали?
Для описания явления электромагнитной индукции в проводящем контуре необходимо учесть индукцию магнитного поля, «охват» поля контуром и ориентацию контура. Все эти факторы объединяются в понятии «магнитный поток». Изменение магнитного потока приводит к возникновению ЭДС в контуре. Постоянный магнитный поток ЭДС не вызывает.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 124.
А какая ваша оценка?
Магнитный поток
Автор:
Субботин Б.П.
На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.
Определение
магнитного потока:
Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.
Формула
магнитного потока:
Ф
= BS cos α
здесь
α – угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.
Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.
Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 108 мкс.
Соответственно 1 мкс = 10-8 вб.
Магнитный
поток является скалярной величиной.
ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА
Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? – выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)
4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность
Основные
формулы
· Закон
электромагнитной индукции (закон
Фарадея):
,
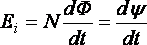
(39)
где 
– эдс индукции;
–
полный магнитный поток (потокосцепление).
· Магнитный
поток, создаваемый током в контуре,
,
(40)
где 
–
индуктивность контура;
–
сила тока.
· Закон
Фарадея применительно к самоиндукции
.
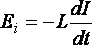
(41)
· Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,
,
(42)
где 
–
индукция магнитного поля;
–
площадь рамки;
–
угловая скорость вращения.
· Индуктивность
соленоида
,
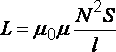
(43)
где 
–
магнитная постоянная;
–
магнитная проницаемость вещества;
–
число витков соленоида;
–
площадь сечения витка;
–
длина соленоида.
· Сила
тока при размыкании цепи
,
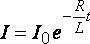
(44)
где 
–
установившаяся в цепи сила тока;
–
индуктивность контура,
–
сопротивление контура;
–
время размыкания.
· Сила
тока при замыкании цепи
.
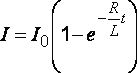
(45)
· Время
релаксации
.
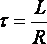
(46)
Примеры
решения задач
Пример
1.
Магнитное
поле изменяется по закону 
,
где
=
15 мТл,
. В
магнитное поле помещен круговой
проводящий виток радиусом 
= 20
см под углом
к
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени
=
5 с.
Решение
По
закону электромагнитной индукции возникающая в
витке эдс индукции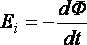 
,
где
–
магнитный поток, сцепленный в витке.
,
где 
–
площадь витка,
;
– угол
между направлением вектора магнитной
индукции
и
нормалью к контуру:
.
.
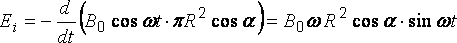
Подставим
числовые значения: 
=
15 мТл,
,
= 20
см = = 0,2 м,
.
Вычисления
дают 
.
|
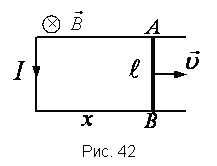
Пример В Решение При |
|
=
= 0,2
=
По
закону Фарадея 
,
где
,
тогда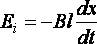
,
но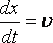
,
поэтому
.
Так, 
.
Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.
САМОИНДУКЦИЯ
Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции.
Это
явление называется самоиндукцией.Самоиндукция –
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
Проявление
явления самоиндукции
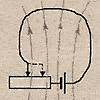
Замыкание
цепи
При
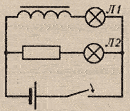
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.
Размыкание
цепи
При
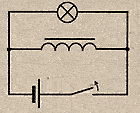
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От
чего зависит ЭДС самоиндукции?
Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.
Индуктивность –
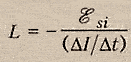
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:
где
Ф – магнитный поток через контур, I – сила
тока в контуре.
Единицы
измерения индуктивности в
системе СИ:
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(
возможен сердечник).
ЭДС
САМОИНДУКЦИИ
ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.
Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Рм). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.
Магнитный
момент единицы объема вещества
характеризует его намагниченность
– I,
определяется по формуле:
I= Рм /V,
(2.4)
где V –
объем вещества.
Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.
Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью – cо , величина
безразмерная.
Если
какое-либо тело поместить в магнитное
поле с индукцией В0,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В‘,
которое взаимодействует с намагничивающим
полем.
В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:
В
= В0 +
В‘(знак
вектора опущен), (2.5)
где В‘ –индукция
собственного магнитного поля
намагнитившегося вещества.
Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
– cо ,
справедливо выражение:В‘ = cо В0 (2.6)
Разделим
на m0 выражение
(2.6):
В‘/
mо= cо В0 /m0
Получим: Н‘ = cо Н0 , (2.7)
но Н‘ определяет
намагниченность вещества I,
т.е. Н‘ = I,
тогда из (2.7):
I
= cо Н0.
(2.8)
Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН0,
то внутри него индукция определяется
выражением:
В=В0 +
В‘ =
m0Н0 +m0Н‘ =
m0 (Н0 +
I) (2.9)
Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
