В этой статье мы увидим, как найти магнитный поток через одиночный контур и проводник с током с числом витков.
Магнитный поток обозначается как произведение магнитного поля, в котором находится материал, и площади, через которую проходит магнитный поток, и определяется соотношением
Как найти плотность магнитного потока?
Наблюдения и советы этой статьи мы подготовили на основании опыта команды магнитный поток Плотность определяется как общее количество линий магнитного потока, пронизывающих единицу площади поверхности материала.
Магнитный поток можно рассчитать, найдя общий поток через проводящий материал и площадь материала, через которую магнитный поток проникает через поверхность.
Магнитный поток через поверхность равен

Следовательно плотность магнитного потока становится магнитным потоком через единицу площади поверхности.

Плотность магнитного потока представляет собой отношение магнитного потока к площади поперечного сечения, через которое проходят силовые линии.
Как найти размер магнитного потока?
Размерность — это математический способ выражения единиц измерения измеряемой величины в простой фигуре.
Размерность магнитного потока можно определить по формуле зная размерность магнитного поля и площадь через которые проходят силовые линии магнитного поля.
Магнитное поле определяется как сила, действующая на заряженную частицу в присутствии магнитного поля скоростью и магнитным потоком через частицу, и, соответственно, размерность магнитного поля основана на размерностях этих величин.
Мы можем математически представить единицу магнитного поля, записав все величины в размерном формате. Сила, действующая на заряды из-за комбинации электрического и магнитного полей, равна
F=qVB
Итак, магнитное поле, в котором находится материал, равно
F=qVB
Теперь нам нужно найти, как мы можем представить эти термины в форме математического измерения.
Мы знаем, что сила определяется как ускорение объекта, когда к нему приложена внешняя сила, в зависимости от массы объекта, поэтому согласно второму закону движения Ньютона мы можем написать F = ma
Единицей ускорения является метр на квадрат времени, поэтому мы можем записать размерность ускорения как M0L1T-2 а единицей массы является кг только соответственно мы можем записать размерность массы как M0L1T-2 что равно М1
Следовательно, размерность магнитная сила is
Ф=М*(М0L1T-2)
Ф = М1L1T-2
Точно так же размерность скорости равна M0L1T-2 так как единица скорости м/с, а заряда М0L1T-2 как I=dQ/dt
Теперь, используя это измерение, мы можем найти размеры магнитного поля как
Б=Ф/кV
Б=М1L1T-2
Магнитный поток является произведением магнитного поля и площади материала, поэтому
Ø=BACosΘ
Θ — безразмерная величина, поэтому ею можно пренебречь и рассматривать размерности остаточных величин.
Ø=[М1L0I-1T-2]*[М0L2T0]
Ø=М1L2-1T-2
Это размер магнитного потока, представленный математически.
Как найти магнитный поток через контур?
Основываясь на направлении магнитного потока, мы можем найти чистое магнитное поле через материал.
Магнитное поле, образованное колеблющимися зарядами в материале, можно рассчитать по всей площади контура и, таким образом, найти магнитный поток через эту площадь.
Рассмотрим круглую петлю радиуса «R» и ток I, протекающий через эту круглую петлю. Пусть начало круга будет «О». Заряд помещен в точку «P», которая находится на расстоянии «x» от начала координат на плоскости оси x. Между линией, соединяющей частицу с началом координат, и контуром с током образуется угол θ.

Пусть dl — малый элемент круглой петли, по которой течет ток I. Магнитное поле через малый элемент dl на круглой петле от заряда, помещенного в точку P, равно

Где мк0/4π – константа пропорциональности, равная 10-7Тм/А
дБ=мк0/4π*IdlrSinθ/r3
дБ=мк0/4π*IdlrSinθ/r2
Направление dB перпендикулярно dl и r, и перпендикулярное магнитное поле компенсируется.
дБ=мк0/4π*холост./об2
Здесь, р2=R2+x2 следовательно, мы можем написать то же уравнение, что и
дБ=мк0/4π*холост./R2+x2
Чистое магнитное поле обусловлено x-компонентой магнитного поля, то есть
дБх=дБКосθ
Поскольку,
Cosθ=R/√x2+R2
Подставляя рассчитанные значения в приведенное выше уравнение, мы получаем

дБх=мк0/4π*IdlR/(R2+x2)3/2
Это уравнение для магнитного поля через небольшой элемент dl на круглом контуре. Теперь найдем магнитное поле на всем контуре.
Bx=∫дБx= μ0/4π∫IdlR/(R2+x2)3/2
Bx= μ0/4π*lR/(R2+x2)3/2∫дл
Bx= μ0/4π*lR/(R2+x2)3/2L
Длина — это полная длина окружности круглой петли, L = 2πR.
Вставка этого в приведенное выше уравнение
Bx= μ0/4π*lR/(R2+x2)3/2*2πr
Отсюда получаем,
Bx= μ0IR2/2((R2+x2)3/2
Если поле находится в центре петли, то x=0 и уравнение примет вид
B0= μ0я/2р
Это магнитное поле через контур, тогда магнитный поток равен
ф=ВА
φ=μ0I/2R*πR2
φ=μ0πIR/2
Это магнитный поток через круговой контур с током, если поле находится в центре контура.
Как найти магнитный поток из магнитного поля?
Линии магнитного потока показывают величину магнитного поля, проникающего через материал.
Линии магнитного поля, падающие на поверхность поперечного сечения материала, образующие определенный угол θ с нормалью к поверхности, дают магнитный поток через эту область.
Предположим, вы поместили проводящий материал площадью A в магнитное поле B так, что линия магнитного поля составляет угол θ с нормальной плоскостью поверхности материала, как показано на рисунке ниже.

Магнитный поток через этот материал будет скалярным произведением линий магнитного поля и площади материала, через которую проходят эти линии.
φ=ВА
φ=BACosθ
Таким образом, мы можем найти магнитный поток через материал от магнитного поля.
Как найти магнитный поток через соленоид?
Чтобы узнать магнитный поток через соленоид, мы должны будем вычислить напряженность магнитного поля через каждую катушку соленоида.
Мы можем определить магнитное поле соленоида, применив закон Био-Савара, который дает связь между током и магнитным полем. Рассчитав магнитное поле, мы можем рассчитать поток через площадь материала.
Рассмотрим цилиндрический соленоид длины ‘2l’ и радиуса ‘a’. Пусть «О» будет точкой в центре соленоида, которая делит соленоид на две половины. Пусть небольшой заряд присутствует в точке P на расстоянии «r» от центральной точки «O». Рассмотрим небольшой сегмент соленоида длиной «dx» на расстоянии «x» от центрального сегмента соленоида. Направление магнитного поля показано на рисунке ниже.

Магнитный поток через этот небольшой сегмент «dx» составляет дБ. Пусть соленоид состоит из n витков на единицу длины соленоида и, следовательно, магнитное поле через этот элемент dx равно

Интегрируя это уравнение, мы получим магнитное поле, создаваемое во всем соленоиде.

В осевом поле r>>a и r>>l тогда
[(прием)2+a2]3/2≅ г3
Следовательно, мы можем записать приведенное выше уравнение как

Магнитный момент m=NIA
Где N — число витков проводника с током вокруг соленоида, I — ток, а A — площадь соленоида.
Здесь количество витков по длине соленоида равно
N=n*2l=2nl
Магнитное поле входит с одной поверхности соленоида и выходит с другого конца.
Площадь, через которую проходит магнитный поток, равна A=πa2
Следовательно, магнитный момент равен
m=n*2l*I*πa2
Поэтому уравнение для магнитного поля мы можем записать в терминах магнитного момента как
В=мк0/4π*2м/р3
Теперь магнитный поток через соленоид равен
ɸ=БА
ɸ=μ0/4π*2м/р3* πа2
ɸ=μ0ma2/ 2r3
Это магнитный поток через соленоид.
Как рассчитать магнитную потокосцепление?
Связь магнитного потока наблюдается в трансформаторе и генераторах, где объединяются магнитные потоки разных контуров.
Связанный магнитный поток дает большое количество магнитного потока через материал. Если магнитный поток через один виток провода равен ɸ =БА тогда катушка, состоящая из n витков, будет давать чистый магнитный поток ɸ =nBA и член λ=nɸ называется утечкой магнитного потока.
Как рассчитать плотность магнитного потока катушки?
Плотность магнитного потока представляет собой полный магнитный поток, проходящий через материал на единицу его площади, и определяется соотношением B=ɸ/A
Плотность магнитного потока можно рассчитать, найдя полный магнитный поток, проникающий через единицу площади материала, находящегося в области магнитного поля.
Какова плотность магнитного потока через квадратный лист длиной 11.3 см, помещенный в область магнитного поля, если магнитный поток через лист равен 1 Вб?
Данный: л = 11.3 см = 0.113 м
ɸ=1Вб
Площадь квадратного листа, через который проходят силовые линии магнитного поля, равна
А=я2= 0.1132= 0.013 м2
У нас есть,
B= ɸ/A
= 76.92Т
B=1T.м2/ 0.013m2= 76.92Т
Следовательно магнитный поток плотность через квадратный лист составляет 76.92 Тл.
Часто задаваемые вопросы
Каков магнитный поток через прямоугольную поверхность длиной 5 см и шириной 2.8 см, помещенную в однородное магнитное поле силой 0.5 Тл, если магнитное поле образует угол 600 с нормалью поверхности?
Данный: л = 5 см = 0.05 м
б = 2.8 см = 0.028 м
В = 0.5 т
Θ = 600
Площадь прямоугольной поверхности равна
А=л*б
=0.05*0.028=0.0014 м2
У нас есть
ɸ=BACosθ
=0.5T* 0.0014 м2
=0.5Т*0.0014м2* 1/2
= 3.5 * 10-4Tm2
Магнитный поток через прямоугольный лист = 3.5*10-4Tm2
Чему равен магнитный поток через круглую петлю с током радиусом 7 см, если сила тока в проводнике равна 2 мА?
Данный: г = 7 см = 0.07 м
I=2 мА
Формула для расчета магнитного потока через круглую петлю имеет вид
ɸ=μ0πIr/2
Вставка заданных значений в это уравнение
ɸ=(4π*10-7Тм/А*π*2*10-3А*0.07м)/2
=4π*π*0.07*10-10Tm2
= 2.76 * 10-10Tm2
Следовательно, магнитный поток через круговой контур с током равен =2.76*10-10Tm2
Всем доброго времени суток. В прошлой статье я начал рассказывать о магнитном поле в веществе и затронул вопросы напряженности магнитного поля, магнитной проницаемости и восприимчивости, а также рассказал о намагничивании и гистерезисе в ферромагнетиках. Однако магнитное поле зависит не только от свойств веществ, но и от их формы. Об этом я и расскажу в статье.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Что такое магнитная цепь?
Магнитной цепью называется, соединение магнетиков, по которым замыкается магнитный поток. То есть сердечник, на который намотан любой дроссель, трансформатор, катушка индуктивности и т.д. является магнитной цепью. Более того если веществом такого сердечника является воздух (то есть катушки индуктивности не имеющие каркаса), то и он является магнитной цепью. Очень часто магнитную цепь называют магнитопроводом, что по сути так и есть, сердечник проводит магнитное поле, также как и проводник проводит электрический ток. Более того на магнитные цепи распространяются законы электрического тока: закон Ома, правила Кирхгофа и так далее, но об этом ниже.
Магнитные цепи бывают однородные и неоднородные. Однородными называют магнитные цепи, которые на протяжении всей своей длины изготовлены из одного материала (то есть имеет одинаковую магнитную проницаемость) и одинаковое поперечное сечение. Если хотя бы одно из этих условий не выполняется, то такая магнитная цепь называется неоднородной.
Также различают разветвлённые и неразветвлённые магнитные цепи. То есть не разветвлённые цепи состоят из одного контура, а разветвлённые, соответственно, состоят из нескольких контуров, по которым замыкается магнитный поток. Разветвлённые цепи могут быть симметричные и несимметричные. У симметричных цепей магнитный поток каждого контура одинаков.
Параметры магнитных цепей
Как я уже говорил многие законы для электрических цепей подходят и для магнитных. Для обобщения этих законов необходимо ввести некоторые параметры, характеризующие магнитные цепи. Представим неоднородную и неразветвлённую магнитную цепь
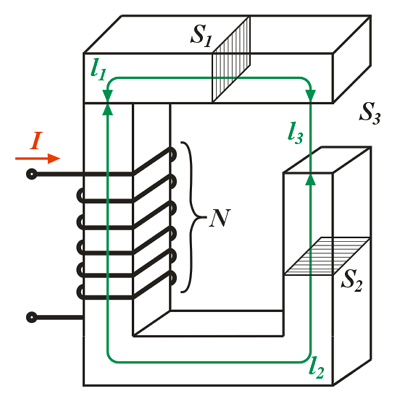
Неоднородная и неразветвлённая магнитная цепь.
Данная цепь состоит из трёх участков длиной l1, l2, l3, имеющих поперечное сечение S1, S2, S3, причем магнитное поле создается током I, протекающим по соленоиду, содержащему N витков. Так как линии магнитного поля в основном замыкаются через магнитопровод, то магнитный поток Φ, можно считать одинаковым на всём протяжении магнитной цепи и определяется следующим выражением
![]()
где В – магнитная индукция,
S – площадь поперечного сечения, которую пронизывает магнитный поток.
Таким образом, магнитный поток является аналогом силы тока в электрических цепях.
Согласно закона полного тока и циркуляции вектора магнитной индукции составим уравнение
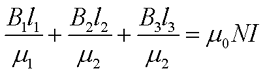
где В1, В2, В3 – соответственно магнитная индукция на участках l1, l2, l3 магнитной цепи;
μ0 – магнитная постоянная, μ0 = 4π*10-7 Гн/м;
μ1, μ2, μ3 – соответственно относительная магнитная проницаемость участков l1, l2, l3 сердечника;
N – количество витков провода;
I – ток, протекающий по проводу.
При использовании ферромагнетиков определение относительной магнитной проницаемость составляет некоторые трудности, поэтому вместо магнитной индукции в данном законе используют напряженность магнитного поля, следовательно для данной магнитной цепи закон полного тока можно представить следующим образом
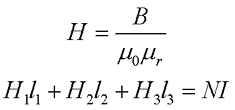
Выражая магнитную индукцию через магнитный поток, получим следующее выражение
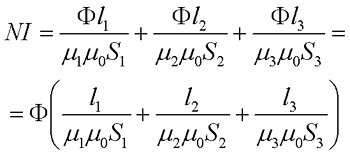
где S1, S2, S3 – соответственно, площадь поперечного сечения участков l1, l2, l3 магнитной цепи.
Таким образом, проводя аналогию с электрической цепью, получим следующие параметры магнитной цепи
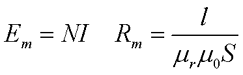
где Em – магнитодвижущая сила,
Rm – магнитное сопротивление цепи.
Следовательно, вышеописанное выражение можно представить следующим выражением
![]()
где Rm1, Rm1, Rm1 – соответственно магнитные сопротивления участков l1, l2, l3 магнитной цепи.
Законы магнитной цепи
Как я писал выше многие законы электрических цепей подходят и для магнитных цепей. Например, закон Ома для магнитной цепи звучит следующим образом: магнитный поток Φ прямо пропорционален магнитодвижущей силе Em и обратно пропорционален полному сопротивлению магнитной цепи Rm. И выражается он следующей формулой, называемой также формулой Гопкинсона
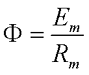
Кроме закона Ома для магнитных цепей действуют правила Кирхгофа. Так первый закон Киргхофа для магнитных цепей звучит следующим образом: алгебраическая сумма магнитных потоков ∑Φ в узле магнитной цепи равна нулю. Для пояснения данного правила изобразим разветвлённую магнитную цепь
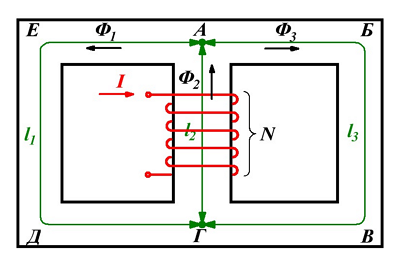
Разветвлённая магнитная цепь.
Данная магнитная цепь состоит из двух контуров АБВГ и АГДЕ. Ветвь АГ создает магнитный поток Φ2, который в точке А делится на два потока Φ1 и Φ3. Таким образом, в точке А алгебраическая сумма магнитных потоков равна нулю
![]()
Аналогично второй закон Кирхгофа для магнитной цепи звучит следующим образом: в контуре магнитной цепи алгебраическая сумма магнитодвижущижся сил ∑Еm равна алгебраической сумме магнитных напряжений на отдельных участках.
Магнитное напряжение на участке цепи определяется произведение магнитного потока Φ на магнитное сопротивление участка Rm, следовательно, второй закон Кирхгофа будет иметь вид
![]()
тогда для магнитной цепи изображённой выше второе правило Кирхгофа будет иметь вид
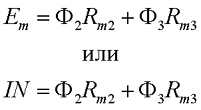
Использую данные соотношения достаточно просто рассчитать необходимые геометрические размеры магнитопроводов для различных магнитных систем, например, трансформаторы, дроссели, катушки индуктивности и так далее, чем мы и займёмся ниже.
Расчёт магнитных цепей
Теория без практического приложения мало интересна радиолюбителям, поэтому приступим к практическому применению теории магнитных цепей. Практический расчёты магнитный цепей сводится к определению магнитодвижущей силы Em (или как вариант определению количества витков провода N при некотором токе I), которая создает заданную магнитную индукцию B (или магнитный поток Φ). Для данных расчётов необходимо знать геометрические размеры магнитной цепи и магнитную проницаемость материала.
Для начала рассчитаем неразветвлённую магнитную цепь, пример которой дан на рисунке ниже
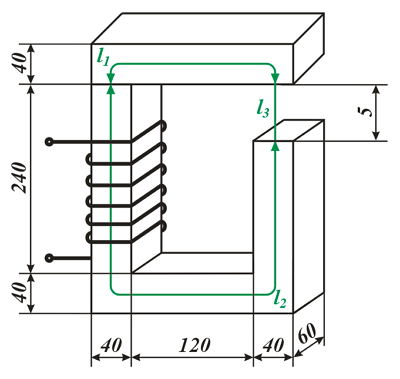
Расчёт неразветвлённой магнитной цепи (магнитопровода).
Данная магнитная цепь состоит из трех частей l1, l2, l3 выполненных из различных материалов. Где участок l1 – литая сталь, l2 – электротехническая сталь, l3 – воздушный разрыв.
Необходимо рассчитать число витков N обмотки для создания магнитного потока Φ = 3,6 * 10-3 Вб, если сила тока протекающего по обмоткам составляет I = 2 A.
Так как магнитная цепь у нас неоднородная, то для начала необходимо рассчитать среднюю длину магнитных силовых линий l1, l2, l3, которая проходит по центру магнитной цепи, а также сечение магнитной цепи S.
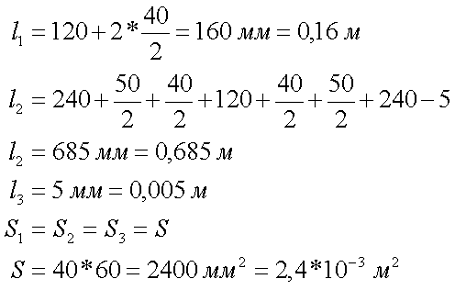
Далее рассчитываем магнитную индукцию заданных участков l1, l2, l3
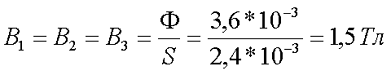
Найдём значение напряженности магнитного поля. Так как часть магнитопровода представлена ферромагнетиками, то магнитную индукцию для них находим с помощью графической зависимости магнитной индукции от напряженности магнитного поля
Зависимость индукции от напряженности магнитного поля электротехнической и листовой стали.
Так l1 – литая сталь, то при В1 = 1,5 Тл, напряженность магнитного поля Н1 ≈ 7 А/см = 700 А/м;
l2 – электротехническая сталь, про В2 = 1,5 Тл, напряженность магнитного поля Н2 ≈ 30 А/см = 3000 А/м;
l3 – воздушный разрыв, напряженность магнитного поля определяется как
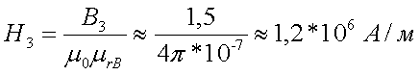
где μ0 = 4π*10-7 – магнитная постоянная,
μrB – относительная магнитная проницаемость воздуха, μrB ≈ 1.
Теперь используя закон полного тока, в котором магнитную индукцию выразим через напряженность магнитного поля, можно рассчитать количество витков провода N
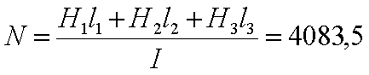
В итоге получаем количество витков N = 4083,5.
Кроме неразветвленных магнитных цепей часто встречаются разветвлённые магнитные цепи, пример которой представлен на рисунке ниже
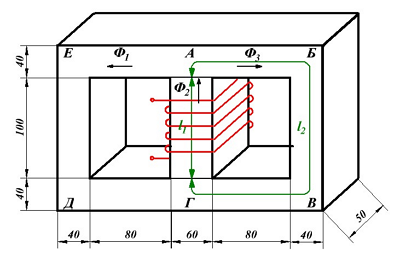
Расчёт разветвлённой магнитной цепи (магнитопровода).
В качестве примера рассчитаем количество витков провода N, который намотан на центральном стержне, при котором в крайних стержнях создается магнитная индукция B2 = 1,2 Тл. При этом сила тока, протекающая по виткам провода I = 1 А, а материал магнитопровода – электротехническая сталь.
Первоначально разобьем контур АБВГА на два участка l1 и l2, для который вычислим длину и поперечное сечение
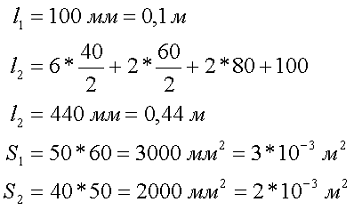
Затем вычислим, какой магнитный поток необходимо создать в правом стержне
![]()
Согласно первому закону Кирхгофа для магнитных цепей магнитный поток центрального стержня Φ1 будет равен сумме потоков из крайних стержней. Ввиду того, что данная разветвлённая магнитная цепь является симметричной, то
![]()
Тогда магнитная индукция в центральном стержне составит
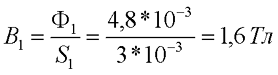
Теперь определим напряженность магнитного поля по графику зависимости от магнитной индукции:
при В1 = 1,6 Тл, напряженность составит Н1 = 44 А/см = 4400 А/м;
при В2 = 1,2 Тл, напряженность составит Н1 = 10 А/см = 1000 А/м;
В итоге можно рассчитать количество витков провода, необходимых по условию задачи
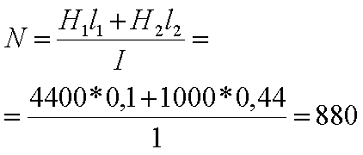
На сегодня всё, в следующей статье я расскажу о таком явлении как электромагнитная индукция и самоиндукция, а также важнейшем параметре электромагнитных элементов – индуктивности.
- Подробности
- Обновлено 03.07.2018 17:37
- Просмотров: 1894

Задачи по физике – это просто!
Не забываем, что решать задачи надо всегда в системе СИ!
А теперь к задачам!
Элементарные задачи из курса школьной физики на вычисление ЭДС индукции.
Задача 1
За время 5 мс в соленоиде, содержащем 500 витков провода, магнитный поток равномерно убывает от 7 мВб до 3 мВб.
Найдите ЭДС индукции в соленоиде.

Задача 2
Какой магнитный поток пронизывает каждый виток катушки, имеющей 1000 витков, если при равномерном исчезновении магнитного поля в течение 0,1 с в катушке индуцируется ЭДС равная 10 В ?

Задача 3
Виток проводника площадью 2 см2 расположен перпендикулярно вектору магнитной индукции.
Чему равна ЭДС индукции в витке, если за время 0,05 секунд магнитная индукция равномерно убывает с 0,5 Тл до 0,1 Тл?

Задача 4
В однородном
магнитном поле перпендикулярно к направлению вектора индукции , модуль которого 0,1 Тл, движется провод длиной 2 метра со скоростью 5 м/с, перпендикулярной проводнику.
Какая ЭДС индуцируется в этом проводнике?

Задача 5
Перпендикулярно вектору магнитной индукции перемещается проводник длиной 1,8 метра со скоростью 6 м/c. ЭДС индукции равна 1,44 В.
Найти магнитную индукцию магнитного поля.

Задача 6
Самолет имеет размах крыльев 15 метров. Горизонтальная скорость полета равна720 км/час.
Определить разность потенциалов, возникающих между концами крыльев. Вертикальная составляющая магнитной индукции (перпендикулярно поверхности Земли) равна 50 мкТл.

Задача 7
Магнитный поток через контур проводника сопротивлением 0,03 Ом за 2 секунды изменился на 0,012 Вб.
Найдите силу тока в проводнике если изменение потока происходило равномерно.

Задача 8
В однородном магнитном поле находится плоский виток площадью 10 см2, расположенный перпендикулярно вектору магнитной индукции.
Какой ток течет по витку, если поле будет убывать с постоянной скоростью 0,5 Тл/с?

Задача 9
Сопротивление замкнутого контура равно 0,5 Ом. При перемещении кольца в магнитном поле магнитный поток через кольцо изменился на 5×10-3 Вб.
Какой за это время прошел заряд через поперечное сечение проводника?

Содержание:
Магнитные цепи:
В конструкцию многих электротехнических устройств (электрических машин, трансформаторов, электрических аппаратов, измерительных приборов и т. д.) входят магнитные цепи.
Магнитной цепью называется часть электротехнического устройства, содержащая ферромагнитные тела, в которой при наличии намагничивающей силы возникает магнитный поток и вдоль которой замыкаются линии магнитной индукции. Источниками намагничивающей силы могут быть катушки с токами, постоянные магниты.
В конструктивном отношении магнитные цепи выполняют неразветвленными и разветвленными; применение того или иного вида цепи определяется в основном назначением электромагнитного устройства.
Расчет неразветвленной однородной магнитной цепи
В неразветвленной магнитной цепи (рис. 9.1, 9.2) магнитный поток во всех участках один и тот же.
При расчете и конструировании магнитной цепи электромагнитного устройства решаются вопросы, связанные с выбором размеров, формы, материалов. Эти вопросы изучают в специальных курсах.
Здесь рассмотрим расчет для существующей или сконструированной магнитной цепи, размеры и материалы которой, а также расположение обмоток с токами известны. При этом решают задачи двух типов.
Прямая задача:
По заданному магнитному потоку в цепи требуется определить намагничивающую силу, необходимую для создания этого потока.
Рассмотрим решение этой задачи для неразветвленной однородной магнитной цепи (см. рис. 9.1) без учета потоков рассеяния.
1. По заданному магнитному потоку и известной площади S поперечного сечения сердечника находят магнитную индукцию:
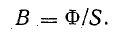
2. Определяют напряженность магнитного поля Н в сердечнике. Зависимость В(Н) — характеристика намагничивания — для стали нелинейная, а магнитная проницаемость 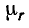
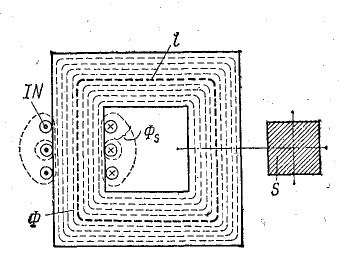
Рис. 9.1. Неразветвленная однородная магнитная цепь
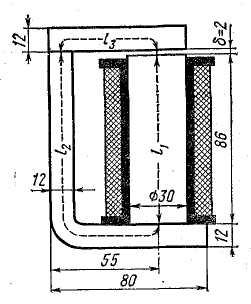
Рис. 9.2. Неразветвленная неоднородная магнитная цепь
Обычно напряженность магнитного поля определяют по кривой намагничивания данного сорта стали (см. рис. 8.30 и приложение 4).
3. Находят намагничивающую силу по закону полного тока [см. формулу (8.41)]:
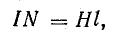
где l — длина магнитопровода, подсчитанная по средней линии без учета закруглений, причем условно принимается, что эта средняя линия во всех точках совпадает с линией магнитной индукции.
Обратная задача:
По заданной намагничивающей силе требуется найти магнитный поток в магнитопроводе.
1. Определяют напряженность магнитного поля в сердечнике:
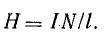
2. По кривой намагничивания данного сорта стали находят магнитную индукцию В.
3. Определяют магнитный поток:
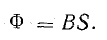
Для конкретных величин В и Н, определенных в ходе решения задачи, можно подсчитать статическую магнитную проницаемость данного сорта стали по формуле (8.37):
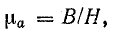
тогда магнитная индукция
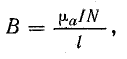
магнитный поток
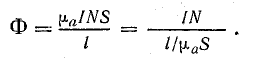
Обозначив знаменатель этого выражения через Rм:
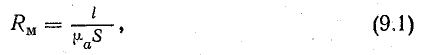
получим
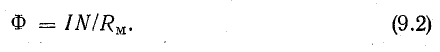
Магнитное сопротивление
Выражение (9.2) по форме напоминает закон Ома для электрической цепи: на месте тока стоит магнитный поток, на месте э. д. с. — намагничивающая сила (ее называют еще магнитодвижущей силой — м. д. с.). Величину Rм называют магнитным сопротивлением. Выражение магнитного сопротивления сердечника по форме аналогично выражению для определения сопротивления проводника электрическому току. Нужно отметить, что формулы для электрической и магнитной цепей похожи только написанием. Никакого физического подобия явлений в электрической и магнитной цепях не существует.
Расчет магнитных цепей обычно проводят без определения магнитного сопротивления. Это понятие используют в некоторых случаях при качественном рассмотрении явлений в магнитных цепях. Пользуясь им, найдем, как должна измениться намагничивающая сила катушки, если в стальном сердечнике (см. рис. 9.1) сделать хотя бы незначительный воздушный зазор, а магнитный поток при этом должен остаться таким же.
Предположим, что в стальном сердечнике длиной l = 100 мм имеется воздушный зазор δ = 1 мм.
Магнитное сопротивление сердечника
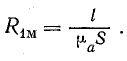
Магнитное сопротивление сердечника с воздушным зазором равно сумме сопротивлений двух участков.
Сопротивление стальной части магнитной цепи при той же магнитной индукции останется практически без изменения, так как уменьшение длины ее очень незначительно (≈ 1 %).
Сопротивление воздушного зазора
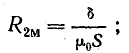
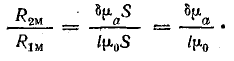
Предположим, что относительная магнитная проницаемость стали 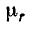 = 1000, тогда
= 1000, тогда
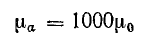
и
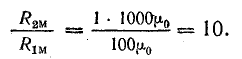
Магнитное сопротивление воздушного зазора оказывается в 10 раз больше сопротивления стального сердечника.
Отсюда следует, что для обеспечения того же магнитного потока при наличии воздушного зазора в 1 мм нужно иметь намагничивающую силу примерно в 10 раз большую, чем при его отсутствии. Эта разница оказывается во много раз большей для сердечников из специальных сплавов, для которых величина 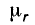 достигает сотен тысяч.
достигает сотен тысяч.
Поэтому во всех случаях, когда по условиям работы электромагнитного устройства без воздушного зазора обойтись нельзя, следует по возможности его сокращать.
Задача 9.1.
В сердечнике кольцевой формы из электротехнической стали нужно получить магнитный поток Ф = 2 • 10-3 Вб. Определить: 1) ток в обмотке, имеющей N = 100 витков; 2) магнитную проницаемость стали при заданном потоке в сердечнике; 3) индуктивность катушки.
Размеры сердечника заданы в миллиметрах на рис. 9.3.
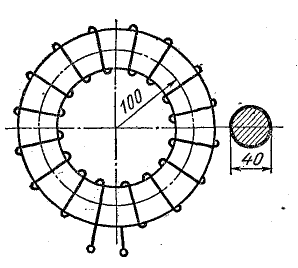
Рис. 9.3. К задаче 9.1
Решение. Площадь сечения сердечника
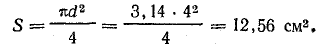
Считая магнитную индукцию по сечению сердечника постоянной, найдем ее величину по заданному потоку:
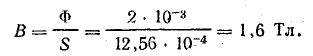
По кривой намагничивания (см.рис. 8.30) определим напряженность магнитного поля: H = 50 А/см = 5000 А/м.
Намагничивающая сила, необходимая для создания заданного потока,
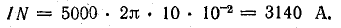
Ток в обмотке
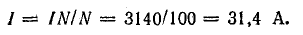
Магнитная проницаемость стали при найденных величинах В и H
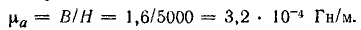
Относительная магнитная проницаемость
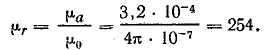
Индуктивность катушки
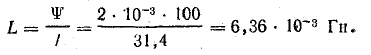
Задача 9.3.
Определить магнитный поток и магнитное сопротивление сердечника (рис. 9.4), размеры которого заданы в миллиметрах, если в катушке с числом витков N = 200 ток I = 6 А. Сердечник изготовлен из электротехнической стали 1511, причем 10% его сечения занимает изоляция между листами.
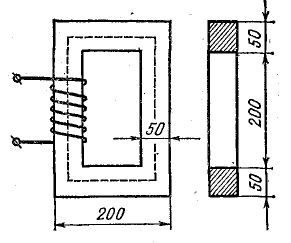
Рис. 9.4. К задаче 9.3
Решение. Намагничивающая сила и напряженность поля
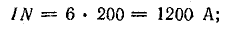
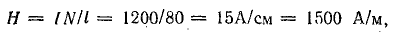
где I — длина замкнутого сердечника по средней линии; согласно размерам, указанным на чертеже, l = 80 см = 0,8 м.
Магнитная индукция по характеристике намагничивания электротехнической стали 1511 В = 1,42 Тл.
Полная площадь сечения сердечника
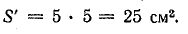
Активная площадь
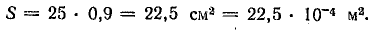
Магнитный поток
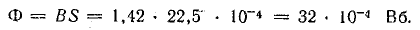
Магнитная проницаемость при заданной величине намагничивающей силы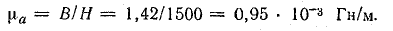
Магнитное сопротивление
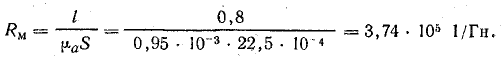
Расчет неразветвленной неоднородной магнитной цепи
Неоднородная магнитная цепь состоит из нескольких участков, отличающихся в общем случае длиной, поперечным сечением и материалом. Чаще всего встречаются магнитные цепи, у которых кроме участков из ферромагнитных материалов имеются воздушные зазоры.
Прямая задача:
При решении прямой задачи размеры и материалы каждого участка цепи известны, а магнитный поток задан; определяют намагничивающую силу. Порядок решения прямой задачи такой же, как и для однородной цепи, но магнитную индукцию и напряженность поля определяют для каждого участка; при этом потоки рассеяния в расчет не принимают.
Магнитная индукция k-го участка
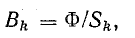
где Sk — площадь поперечного сечения k-го участка.
По магнитной индукции определяют напряженность поля: для участков из ферромагнитных материалов — по кривым намагничивания; для воздушных зазоров и других участков из неферромагнитных материалов — по формуле 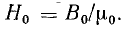
Далее составляют уравнение согласно закону полного тока:

где Нk — напряженность магнитного поля k-го участка (принимают ее одинаковой во всех точках этого участка); lk — длина k-то участка, взятая по средней линии; Нklk — магнитное напряжение к-то участка (далее магнитное напряжение будем обозначать Um); 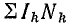 — алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
— алгебраическая сумма намагничивающих сил всех обмоток, входящих в рассматриваемую цепь.
Намагничивающую силу считают положительной в левой части уравнения (9.3), если ее направление, определенное по правилу буравчика, совпадает с направлением обхода магнитного контура. Магнитное напряжение в правой части уравнения считают положительным, если направление магнитного потока совпадает с направлением обхода контура.
Для магнитной цепи (см. рис. 9.2) развернутое уравнение (9.3) имеет вид
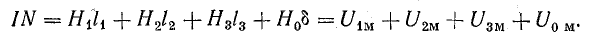
Обратная задача:
Обратную задачу — определение магнитного потока по заданным намагничивающим силам — нельзя решить так же просто, как для однородной цепи, так как нельзя сразу установить распределение магнитного напряжения между участками.
Нельзя воспользоваться формулой (9.2), так как магнитное сопротивление участка из ферромагнитного материала зависит от величины 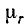 , которая определяется не известной еще магнитной индукцией.
, которая определяется не известной еще магнитной индукцией.
Задачу можно решить методом последовательных приближений.
При наличии в цепи воздушного зазора первое значение магнитного потока можно взять, считая магнитное сопротивление воздушного зазора равным сопротивлению всей магнитной цепи.
Основанием для такого выбора является то, что даже малый воздушный зазор имеет магнитное сопротивление, значительно большее, чем вся остальная часть цепи, выполненная из ферромагнитных материалов.
Пренебрегая в первом приближении магнитным сопротивлением ферромагнитной части цепи, получим поток
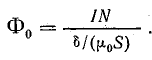
Определить магнитный поток можно, построив кривую намагничивания цепи в целом. Для этого нужно задаться произвольно несколькими величинами магнитного потока и определить соответствующие им величины намагничивающей силы.
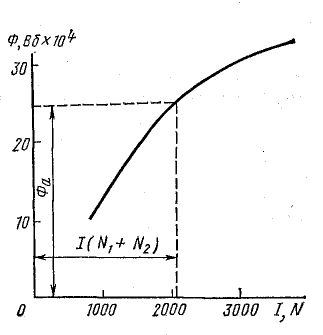
Рис. 9.5. Кривая намагничивания магнитной цепи
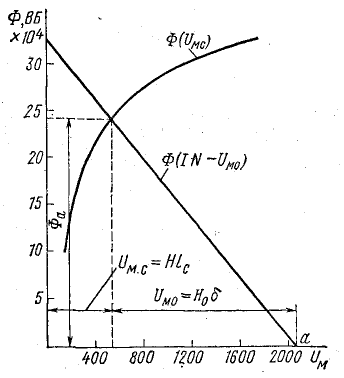
Рис. 9.6. К расчету неразветвленной неоднородной магнитной цепи (обратная задача)
По результатам расчета строится кривая намагничивания цепи (рис. 9.5). По кривой находят магнитный поток, соответствующий заданной намагничивающей силе.
Возможен и другой путь графо-аналитического решения обратной задачи (рис. 9.6). По взятым произвольно нескольким величинам магнитного потока находят величины 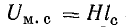 (для стальной части цепи) и
(для стальной части цепи) и 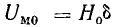 (для воздушного зазора). Затем из начала координат строят кривую
(для воздушного зазора). Затем из начала координат строят кривую 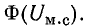
На оси абсцисс находят точку a, соответствующую заданной намагничивающей силе IN, из которой влево проводят прямую Ф(IN — Uм0).
В точке пересечения этих графиков по оси ординат находят искомый поток, а по оси абсцисс — величины Uм.с = Нlс и Uм0 = Н0δ.
Задача 9.5.
Магнитная цепь электромагнитного реле клапанного типа, изготовленная из стали, имеет поток Ф = 1,2 • 10-3 Вб. Определить число витков катушки реле, необходимое для возбуждения созданного магнитного потока при токе в катушке 0,2 А. Ярмо и якорь реле прямоугольного сечения 7,5 x 1,2 см, сердечник круглого сечения диаметром 3 см. Другие размеры показаны на рис. 9.2.
Решение. Магнитная цепь реле делится на однородные участки:
а) сердечник круглого сечения
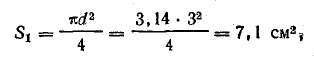
длина l1 = 8,6 см;
б) ярмо прямоугольного сечения
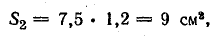
длина l2 = 14,9 см (см. рис. 9.2);
в) якорь прямоугольного сечения
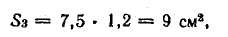
длина l3 = 6,1 см;
г) воздушный зазор, сечение которого принимаем равным сечению сердечника, пренебрегая некоторым увеличением его за счет выпучивания линий магнитной индукции:
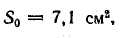
длина δ = 0,2 см.
Магнитная индукция в участках цепи:
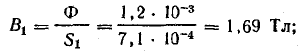
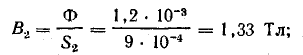
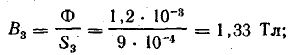
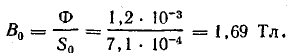
Напряженность магнитного поля в стальных участках определена по кривой намагничивания литой стали, которая принята такой же и для кованой стали: Н1 = 57 А/см; Н2 = 18 А/см; Нз = 18 А /см.
В воздушном зазоре
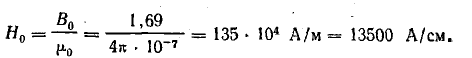
Составляем уравнение по закону полного тока:
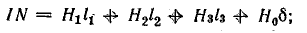
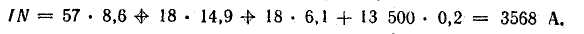
Число витков обмотки
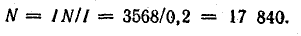
Задача 9.7.
Две катушки N1 = 2000 и N2 = 600 витков насажены на стержни сердечника из электротехнической стали 1211. Размеры магнитной цепи показаны на рис. 9.7. Определить магнитный поток при токе в катушках I = 0,8 А и при соединении концов катушек по схеме: К1 соединен с К2 напряжение приложено к зажимам Н1 и Н2.
Решение. Магнитная цепь рис. 9.7 имеет шесть участков, размеры которых найдены из чертежа:
а) воздушный зазор — δ01 = 0,09 см, S01 = 5 • 4,5 = 22,5 см2;
б) стержень А — l1 = 20 см, S1 = 22,5 см2;
в) ярмо Б — l2 = 25 см, S2 = 22,5 см2;
г) стержень В — lз = 20 см, S3 = 22,5 см2;
д) воздушный зазор — δ02 = 0,09 см, S02 = 22,5 см2;
е) якорь Д — l0 = 25 см, S6 = 22,5 см2.
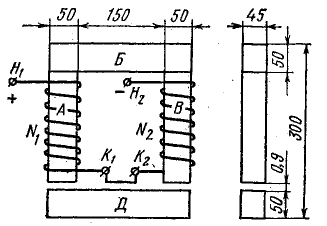
Рис. 9.7. К задаче 9.7
Задаемся несколькими величинами магнитного потока, причем наибольший возможный поток найдем в предположении, что магнитное сопротивление создают только воздушные зазоры [см. формулы (9.1), (9.2)]:
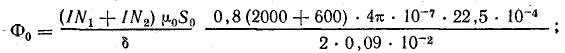
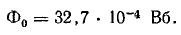
При определении потока учтено, что катушки включены согласно, поэтому их намагничивающие силы сложены.
Для полученного потока найдем намагничивающую силу с учетом стальной части магнитной цепи. Последовательность решения та же, что и при решении задачи 9.5. Результаты расчета для Ф0 и других величин потока сведены в табл. 9.1.
Таблица 9.1
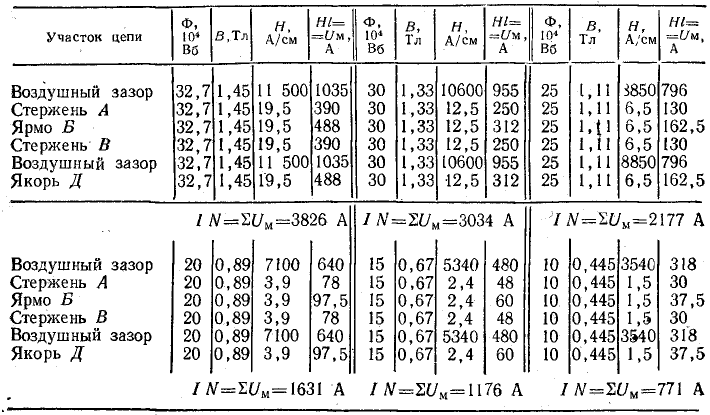
Зависимость Ф(IN) построена на рис. 9.5.
По этой кривой определяем искомый поток, соответствующий намагничивающей силе:
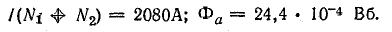
Для графо-аналитического способа определения потока по типу рис. 9.6 из табл. 9.1 выпишем величины Ф и Нlc в табл. 9.2.
Таблица 9.2

Зависимости Ф(Um.c) и Ф(IN — Um0) показаны на рис. 9.6, причем прямая Ф(IN — Um0) построена по двум точкам. При IN — Um0 = 0
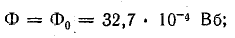
при Ф = 0
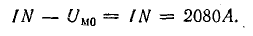
В точке пересечения графиков определяем искомый магнитный поток, а также величины Hlc = Um.c и H0δ = Um0, соответствующие этому потоку:
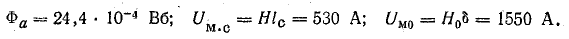
Расчет разветвленной магнитной цепи
В разветвленной магнитной цепи магнитные потоки в общем случае различны в разных ветвях (рис. 9.8).
Разветвленные магнитные цепи делятся на симметричные и несимметричные.
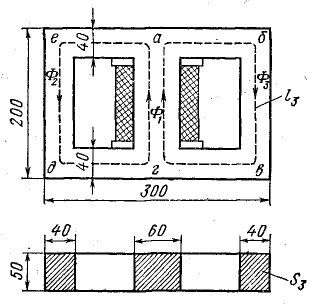
Рис. 9.8. Разветвленная симметричная магнитная цепь
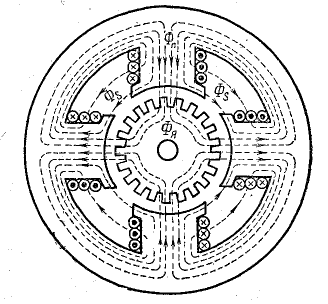
Рис. 9.9. Магнитная цепь четырехполюсной электрической машины
Симметричную магнитную цепь мысленно можно разделить на неразветвленные цепи таким образом, что во всех участках выделенной цепи магнитный поток будет один и тот же. Кроме того, предполагается симметричное расположение намагничивающих сил (рис. 9.8, 9.9).
Если указанные условия симметрии не соблюдаются, то магнитная цепь относится к несимметричным (рис. 9.10).
Узловые и контурные уравнения магнитной цепи
Симметричная магнитная цепь (см. рис. 9.8) состоит из двух одинаковых контуров. Средний стержень вместе с катушкой (источником намагничивающей силы) входит в оба контура.
Место соединения среднего стержня с ярмом является узлом магнитной цепи, в котором магнитный поток Ф1, делится на два равных потока, если магнитное сопротивление обоих контуров одинаково:
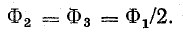
Расчет разветвленной симметричной цепи из-за равенств потоков симметричных контуров сводится к расчету одного контура, который выполняют в том же порядке, что и расчет неразветвленной цепи.
В аналогичной несимметричной магнитной цепи поток в узле делится на неравные части, но для любого узла пригодно уравнение
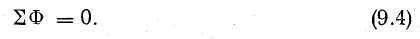
Для схемы рис. 9.8 это уравнение в развернутом виде записывают так:
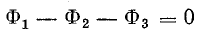 или
или 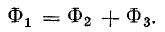
При составлении такого уравнения учитывают направления потоков: направленные к узлу и направленные от узла потоки берутся с разными знаками.
Для каждого контура магнитной цепи можно также составить уравнение по закону полного тока.
Предположим, что все участки магнитной цепи выполнены из материалов с постоянными значениями магнитной проницаемости. Каждый участок и вся цепь имеют линейную зависимость магнитного потока от магнитного напряжения Ф(Uм).
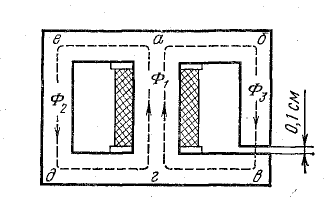
Рис. 9.10. Разветвленная несимметричная магнитная цепь
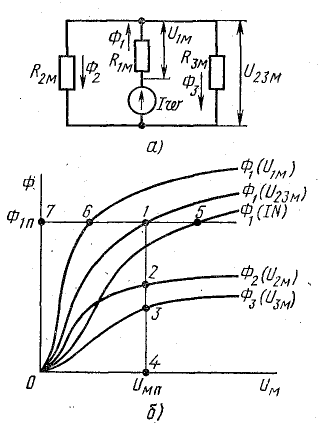
Рис. 9.11. К расчету разветвленной магнитной цепи графическим методом
Определив для каждого участка магнитное сопротивление Rм, магнитную цепь можно представить соответствующей схемой замещения, в которую войдут постоянные магнитные сопротивления участков и намагничивающие силы.
На рис. 9.11, а показана схема замещения магнитной цепи (см. рис. 9.8). Пренебрегая потоками рассеяния, расчет магнитной цепи можно выполнить аналогично расчету электрической цепи, решая систему линейных уравнений, составленных для узлов (см. формулу (9.4)] и контуров [см. формулу (9.3)].
Графический расчет разветвленной цепи
Элементы схем замещения магнитных цепей, осуществляемых на практике (кроме элементов, соответствующих воздушным зазорам), имеют нелинейные характеристики Ф(Uм), так как магнитная проницаемость ферромагнитных материалов зависит от напряженности поля. Нелинейными являются и магнитные цепи в целом.
Аналогия с электрической цепью указывает на возможность графического расчета нелинейной магнитной цепи в порядке. Первый этап расчета состоит в построении характеристик Ф(Uм) для каждого участка цепи в общей системе координат. Для этого используются характеристики намагничивания материалов, из которых изготовлена магнитная цепь. Например, чтобы построить характеристику Ф3(U3м), нужно ряд величин напряженности поля Н3, взятых из характеристики намагничивания материала третьего участка магнитной цепи, умножить на длину этого участка (H3l3 = U3м), а соответствующие им величины магнитной индукции умножить на площадь S3 этого участка (В3S3 = Ф3).
По полученным значениям U3м и Ф3 строят график Ф3(U3м) (рис. 9.11, б). Магнитные сопротивления R2м и R3м соединены параллельно. Поэтому магнитные напряжения второго и третьего участков одинаковы: U2м = U3м = U2.3м.
Сумма магнитных потоков этих участков равна магнитному потоку первого участка (сопротивление R1м): Ф1 = Ф2 + Ф3.
Складывая магнитные потоки Ф2 и Ф3 для ряда значений магнитного напряжения, получим кривую Ф1 (U2.3м).
На рис. 9.11, б это показано для одного значения Uм.п.Отрезки 4-3 и 4-2 в масштабе магнитных потоков выражают потоки Ф3 и Ф2. Сумма этих отрезков, равная отрезку 4-1, выражает магнитный поток Ф1П. Магнитное сопротивление R1м и сопротивление, эквивалентное R2м и R3м, соединены последовательно. Поэтому намагничивающая сила всей цепи IN равна сумме магнитных напряжений U1м и U2.3м: IN = U1м + U2.3м. Магнитные же потоки участков цепи с сопротивлениями R1м и R2.3м одинаковы.
Складывая магнитные напряжения U1м и U2.3м для ряда значений магнитного потока, получим кривую Ф1(IN). На рис. 9.11, б это показано для одного значения Ф1п. Отрезки 7-6 и 7-1 в масштабе магнитных напряжений выражают магнитные напряжения U1м и U2.3м. Сумма этих отрезков дает отрезок 7-5, выражающий намагничивающую силу IN.
Выполнив указанные построения, нетрудно решить различные задачи расчета магнитной цепи.
Задача 6.9.
Катушка, имеющая 500 витков, расположена на среднем стержне магнитопровода, изготовленного из стали 1511 (см. рис. 9.8). Определить ток в катушке, если в крайнем стержне поток Ф2 = Ф3 = 2 • 10-3Вб. Рассеяние потока не учитывается.
Решение. В данной симметричной цепи можно наметить два одинаковых в магнитном отношении контура: а-б-в-г-а и а-е-д-г-а. В каждом из них по два участка:
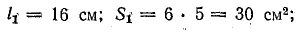
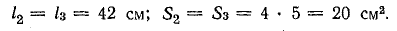
Рассматривая один из контуров, решим задачу в порядке, принятом для неразветвленной цепи:
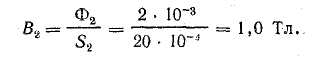
Магнитный поток в среднем стержне в два раза больше, чем в крайних:
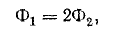
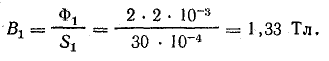
По кривым намагничивания стали 1511 находим:
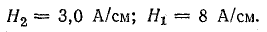
По закону полного тока,
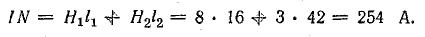
Ток в катушке
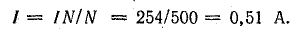
Задача 9.10.
В крайнем стержне магнитопровода, взятого по условию задачи 9.9, имеется воздушный зазор δ = 0,1 см. Определить, как нужно изменить ток в катушке, чтобы сохранить прежнюю величину потока в этом стержне (см. рис. 9.10).
Решение. При наличии воздушного зазора в одном крайнем стержне магнитная цепь становится несимметричной.
В контуре а-е-д-г-а сохранились те же участки; в контуре а-б-в-г-а: l1 = 16 см; l3 = 41,9 см; δ = 0,1 см; S1 = 30 см2;
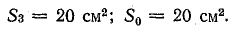
Магнитная индукция в воздушном зазоре и крайнем стержне 6-в
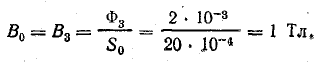
Напряженность поля
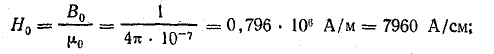
по кривой намагничивания стали 1511 Н3 = 3 А/см.
В магнитной цепи можно наметить третий контур (а-б-в-г-д-е-а). Для этого контура, по закону полного тока,
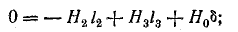
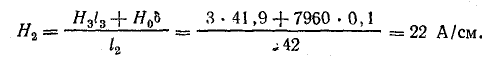
Магнитная индукция на участке l2 по кривой намагничивания В2 = 1,48 Тл. Магнитный поток на участке l2
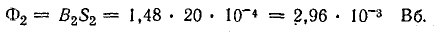
Магнитный поток в среднем стержне (участок l1) определим на основании первого закона Кирхгофа для узла а:
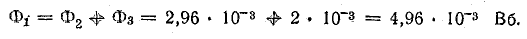
Магнитная индукция на этом участке
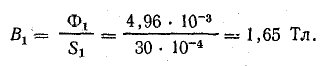
Напряженность поля Н1 = 69,5 А/см.
Для одного из контуров, включающего средний стержень, например а-б-в-г-а, по закону полного тока,
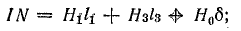
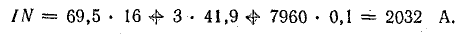
Ток в катушке
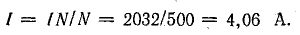
Вывод. Для того чтобы сохранить в крайнем стержне такой же магнитный поток при наличии воздушного зазора δ = 0,1 см, требуется увеличить ток в катушке почти в восемь раз по сравнению с тем случаем, когда зазор отсутствует.
Постоянные магниты
В измерительных приборах, электрической аппаратуре и других устройствах в качестве источников намагничивающей силы широко применяют постоянные магниты.
На рис. 9.12 схематично изображены магнитные системы магнито-электрического измерительного прибора (а) и поляризованного реле (б).
Эти системы, как и большинство им подобных, имеют несколько участков: 1) из магнитно-твердого материала— постоянного магнита 1; 2) из магнитно-мягкого материала 2, служащего магнитопроводом, и воздушного зазора 3, форма и размеры которого определяются конструкцией и назначением устройства.
При расчете магнитной цепи с постоянным магнитом требуется определить магнитный поток и индукцию в воздушном зазоре или по заданному потоку найти оптимальные размеры постоянного магнита (наименьшие объем и габариты).
Характеристики размагничивания постоянных магнитов
Величины остаточной магнитной индукции Вг и коэрцитивной силы Hс характеризуют материал постоянного магнита: чем они больше, тем выше его качество. Как известно, на петле гистерезиса Вг соответствует Н = 0, а при В = 0 Н = Нс.
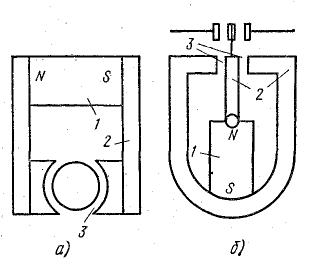
Рис. 9.12. Магнитные цепи с постоянными магнитами
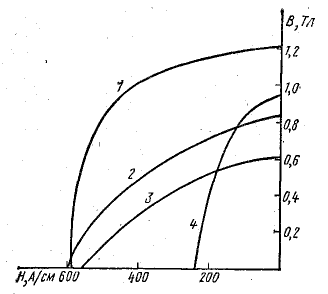
Рис. 9.13. Характеристики размагничивания постоянных магнитов:
1 — АНКО-4; 2 — АНКО-2; З-АН-2; 4 — сталь с 30% СО
Промежуточные магнитные состояния определяются частью петли магнитного гистерезиса, лежащей во второй четверти, — характеристикой размагничивания (рис. 9.12). Эта характеристика используется при расчете постоянных магнитов.
Согласно закону полного тока, сумма магнитных напряжений участков магнитной цепи (рис. 9.12) равна нулю, так как внешняя намагничивающая сила (ампер-витки) отсутствует:
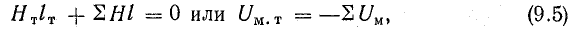
где Uм.т — магнитное напряжение постоянного магнита; 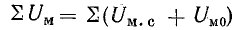 — сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
— сумма магнитных напряжений всех участков магнитной цепи, включая воздушные зазоры, но без постоянного магнита.
Левая и правая части равенства (9.5) связаны с магнитной индукцией и потоком определенными зависимостями: Фт(Uм.т) — кривая размагничивания постоянного магнита (по форме повторяет кривую размагничивания материала, из которого выполнен постоянный магнит); Фм(Uм.с) — кривая намагничивания части конструкции устройства, изготовленной из магнитно-мягкого материала; Ф0(Uм0) — прямая, проходящая через начало координат и повторяющая в других масштабах зависимость 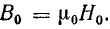
Определение магнитного потока в магнитной цепи с постоянным магнитом
Пренебрегая потоком рассеяния 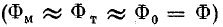 и магнитным напряжением в участках из магнитно-мягкого материала (
и магнитным напряжением в участках из магнитно-мягкого материала (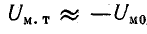 ), можно построить в общей системе координат зависимости
), можно построить в общей системе координат зависимости 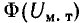 и
и 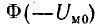 .
.
В этом случае искомый магнитный поток Ф0 определяется точкой их пересечения (рис. 9.14).
Магнитная индукция в воздушном зазоре
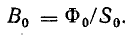
Из равенства (9.5) следует, что напряженности поля в воздушном зазоре и магните направлены в противоположные стороны.
При отсутствии воздушного зазора (постоянный магнит замкнут) остаточная индукция имеет величину Вг, а при наличии зазора будет меньше Вг (рис. 9.14). Воздушный зазор создает эффект размагничивания магнита.
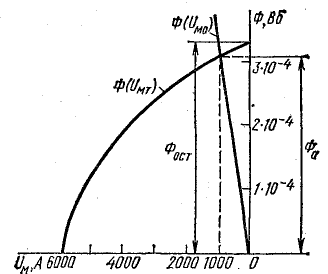
Рис. 9.14. К расчету магнитной цепи с постоянным магнитом
Задача 9.12.
Определить магнитный поток и индукцию в воздушном зазоре постоянного магнита (см. рис. 9.12, а), если магнит, изготовленный из сплава АНКО-2, имеет длину lт = 10 см; SТ = 4 см2. Полюса и цилиндрический сердечник изготовлены из магнитно-мягкой стали, имеют общую длину lм = 15 см; воздушный зазор между полюсом и сердечником δ = 0,2 см с каждой стороны и площадь S = 10 см2. Характеристика размагничивания сплава АНКО-2 представлена на рис. 9.13.
Решение. Построим зависимость магнитного потока в магните от магнитного напряжения Ф(Uм.т).
Для этого, согласно кривой 2 на рис. 9.13, берем величины В и Н, подсчитываем Ф и Uм.т и результаты подсчета сводим в табл. 9.3.
Для тех же величин магнитного потока определим Uм0 = Н0δ для воздушного зазора. Величинами Hсlс для участков из стали пренебрегаем из-за их незначительной величины.
Т а б л и ц а 9.3

Для потока Ф = 3,28 • 10-4 Вб
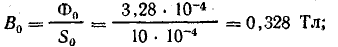
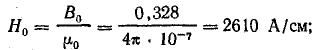
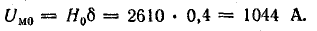
Результаты подсчетов сводим в табл. 9.4.
Таблица 9.4
Зависимости Ф(Uм.т) и Ф(Uм0) построены на рис. 9.14. В точке пересечения этих графиков находим магнитный поток:
Магнитная индукция в воздушном зазоре
- Энергия магнитного поля
- Синусоидальные Э.Д.С. и ток
- Электрические цепи с взаимной индуктивностью
- Резонанс в электрических цепях
- Электромеханические аналогии
- Индуктивно связанные электрические цепи
- Фильтры и топологические методы анализа линейных электрических цепей
- Электрическое поле и его расчёт
Циркуляция вектора магнитной индукции
В вдоль замкнутого контура
![]()
где
Bi
— проекция
вектора магнитной индукции на направление
элементарного перемещения dl
вдоль контура L.
Циркуляция вектора напряженности Н
вдоль замкнутого контура
![]() ,
,
Закон полного тока (для магнитного
поля в вакууме)
![]()
где 0
— магнитная постоянная;
![]()
— алгебраическая сумма токов,
охватываемых контуром; п — число
токов.
Закон полного тока (для произвольной
среды)
![]()
Магнитный
поток Ф через плоский контур площадью
S:
а) в случае однородного поля
Ф=BS cos
; или Ф = BnS,
где — угол между
вектором нормали n к
плоскости контура и вектором магнитной
индукции В; Вn
— проекция вектора В на нормаль
n (Bn=B
cos );
б) в случае неоднородного поля
![]()
где интегрирование ведется во всей
поверхности S.
Потокосцепление,
т.е. полный магнитный поток, сцепленный
со всеми витками соленоида или тороида,
![]()
где Ф — магнитный поток через один
виток; N — число витков соленоида
или тороида.
Магнитное поле тороида, сердечник
которого составлен из двух частей,
изготовленных из веществ с различными
магнитными проницаемостями:
а) магнитная индукция на осевой линии
тороида
![]()
где I — сила тока в
обмотке тороида; N — число ее
витков; l1 и l2 -
длины первой и второй частей сердечника
тороида; 1 и
2
—магнитные проницаемости веществ
первой и второй частей сердечника
тороида; 0
—магнитная постоянная
б) напряженность магнитного поля на
осевой линии тороида в первой и второй
частях сердечника
H1=B
/(1
2);
H1=B
/(2
0
);
в) магнитный поток в сердечнике тороида
![]()
или по аналогии с законом Ома (формула
Гопкинсона)
Фm=Fm/Rm,
где Fm
— магнитодвижущая сила; Rm
— полное магнитное сопротивление
цепи;
г) магнитное
сопротивление участка цепи
Rm=l/(μμ0S).
• Магнитная проницаемость μ,
ферромагнетика связана с магнитной
индукцией В поля в нем и напряженностью
Н намагничивающего поля соотношением
μ=B/(μ0H).
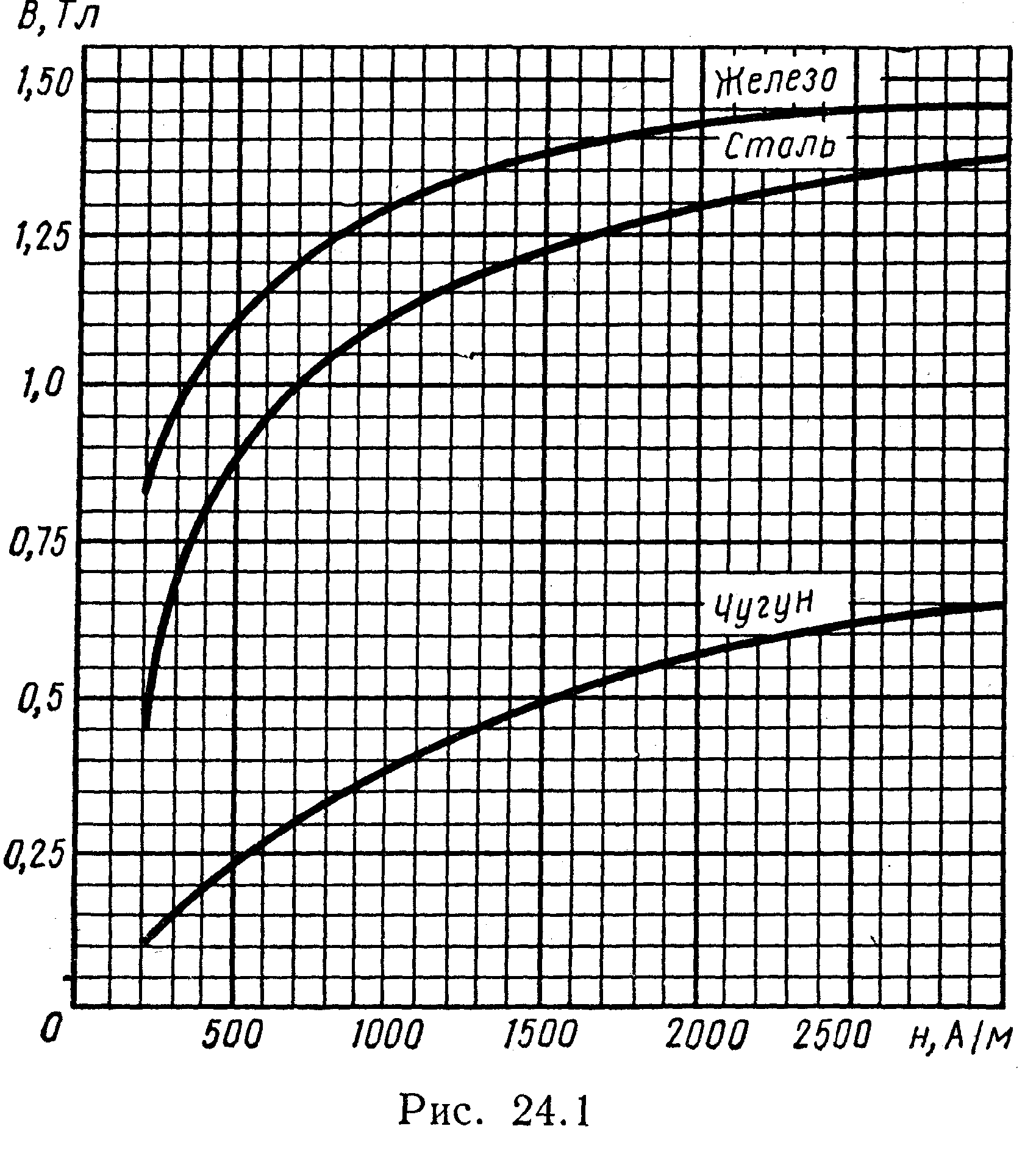
• Связь между магнитной индукцией В
поля в ферромагнетике и напряженностью
Н намагничивающего поля выражается
графически (рис. 24.1).
Примеры решения задач
Пример 1. В одной плоскости с бесконечно
длинным прямым проводом, по которому
течет ток I=50 А,
расположена прямоугольная рамка
так, что две большие стороны ее длиной
l=65 см параллельны
проводу, а расстояние от провода до
ближайшей из этих сторон равно ее ширине.
Каков магнитный поток Ф, пронизывающий
рамку?
Р ешение.
ешение.
Магнитный поток Ф через поверхность
площадью S определяется
выражением
![]()
В нашем случае вектор магнитной индукции
В перпендикулярен плоскости рамки.
Поэтому для всех точек рамки Вn=В.
Магнитная индукция В, создаваемая
бесконечно длинным прямым проводником
с током, определяется формулой
![]() ,
,
где x— расстояние
от провода до точки, в которой определяется
В.
Для вычисления магнитного потока
заметим, что так как В зависит от х
и элементарный поток Ф будет также
зависеть от х, то
dф=B(x)dS.
Разобьем площадь рамки на узкие
элементарные площадки длиной l,
шириной dx и площадью
dS=ldx
(рис. 24.2). В пределах этой площадки
магнитную индукцию можно считать
постоянной, так как все части площадки
равноудалены (на расстояние х) от
провода. С учетом сделанных замечаний
элементарный магнитный поток можно
записать в виде
dФ=![]()
Проинтегрировав полученное выражение
в пределах от x1=a
до х2=2а, найдем
![]() |2.
|2.
Подставив пределы, получим
![]()
Убедимся в том, что правая часть
полученного равенства дает единицу
магнитного потока (Вб): [0]
[I] [l]=
Гн/м 1 А 1
м=1 Вб. Произведя вычисления по формуле
(1), найдем Ф=4,5 мкВб.
Пример 2. Определить индукцию В
и напряженность Н магнитного
поля на оси тороида без сердечника, по
обмотке которого, содержащей N=200
витков, идет ток I=5 А. Внешний диаметр
d1 тороида
равен 30 см, внутренний d2=
20 см.
Решение. Для определения напряженности
магнитного поля внутри тороида вычислим
циркуляцию вектора Н вдоль линии
магнитной индукции поля:
![]()
Из условия симметрии следует, что линии
магнитной индукции тороида представляют
собой окружности и что во всех точках
этой линии напряженности одинаковы.
Поэтому в выражении циркуляции
напряженность Н можно вынести за
знак интеграла, а интегрирование
проводить в пределах от нуля до 2 r,
где r — радиус
окружности, совпадающей с линией
индукции, вдоль которой вычисляется
циркуляция, т. e.
![]()
(1)
С другой стороны, в соответствии с
законом полного тока циркуляция
вектора напряженности магнитного поля
равна сумме токов, охватываемых
контуром, вдоль которого вычисляется
циркуляция:
![]()
(2)
Приравняв
правые части равенств (1) и (2), получим
![]()
(2)
Линия, проходящая вдоль тороида,
охватывает число токов, равное числу
витков тороида. Сила тока во всех витках
одинакова. Поэтому формула (3) примет
вид 2rH=-NI,
откуда
![]()
(4)
Для средней линии тороида
r=1/2(R1R2)=1/4(d1+d2).
Подставив это выражение r в формулу
(4), найдем
![]()
(5)
Магнитная индукция В0 в
вакууме связана с напряженностью поля
соотношением B0=0H.
Следовательно,
![]()
(6)
Подставив значения величин в выражения
(5) и (6), получим:
H=1,37 кА/м, B0=1,6
мТл.
Пример. 3. Чугунное кольцо имеет
воздушный зазор длиной lо=5 мм. Длина
l средней линии кольца равна 1 м.
Сколько витков N содержит обмотка
на кольце, если при силе тока I=4 А
индукция В магнитного поля в воздушном
зазоре равна 0,5 Тл? Рассеянием магнитного
потока в воздушном зазоре можно
пренебречь. Явление гистерезиса не
учитывать.
Решение. Пренебрегая рассеянием
магнитного потока, мы можем принять,
что индукция поля в воздушном зазоре
равна индукции поля в чугуне. На
основании закона полного тока запишем
IN=Hl+H0I0.
По графику (см. рис. 24.1) находим, что при
В=0,5 Тл напряженность Н
магнитного поля в чугуне равна 1,2 кА/м.
Так как для воздуха =1,
то напряженность поля в воздушном
зазоре
H0=B0=0,4
MA/м.
Искомое число витков
N=(Hl+H0
lo)/I==800.
