Как найти магнитный поток по графику

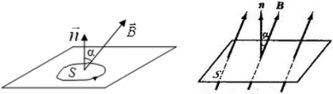
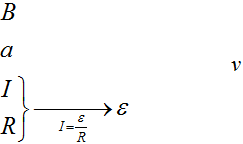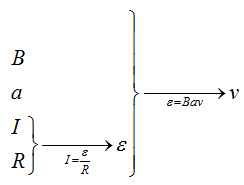Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

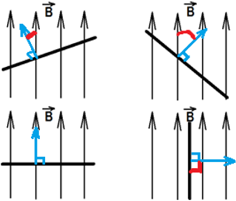
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

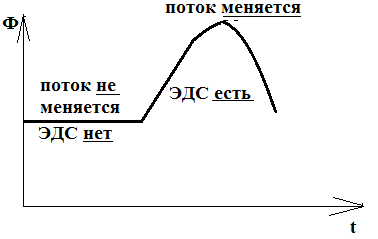
Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

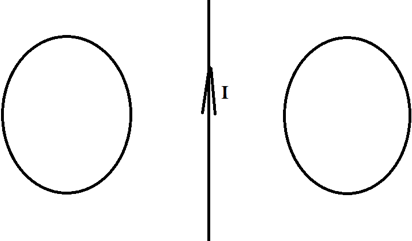
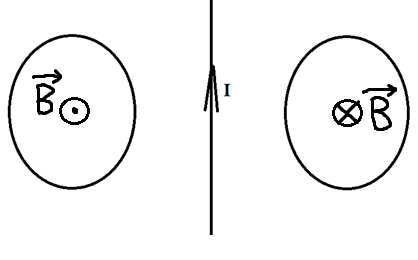
Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

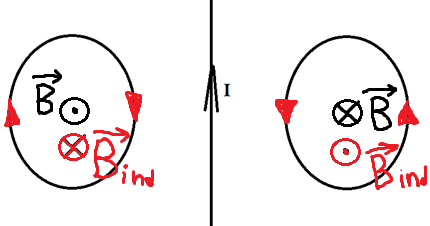
Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

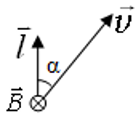
Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

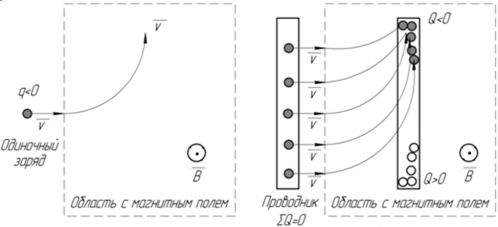
На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

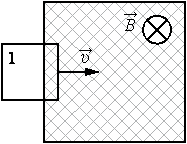
Задача 3

В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

 Циркуляция вектора магнитной индукции
В вдоль замкну­того контура

где
B_i
— проекция
вектора магнитной индукции на направление
элементарного перемещения dl
вдоль контура L.
Циркуляция век­тора напряженности Н
вдоль замкнутого контура

,

 Закон полного тока (для магнитного
поля в вакууме)

где ₀
— магнитная постоянная;

— алгебраическая сумма токов,
охватываемых контуром; п — число
токов.

Закон полного тока (для произвольной
среды)

 Магнитный
поток Ф через плоский контур площадью
S:

а) в случае однородного поля

Ф=BS cos
; или Ф = B_nS,

где  — угол между
вектором нормали n к
плоскости контура и век­тором магнитной
индукции В; В_n
— проекция вектора В на нормаль
n (B_n=B
cos );

б) в случае неоднородного поля

где интегрирование ведется во всей
поверхности S.

 Потокосцепление,
т.е. полный магнитный поток, сцепленный
со всеми витками соленоида или тороида,

где Ф — магнитный поток через один
виток; N — число витков со­леноида
или тороида.


Магнитное поле тороида, сердечник
которого составлен из двух частей,
изготовлен­ных из веществ с раз­личными
магнитными проницаемостями:

а) магнитная индук­ция на осевой линии
тороида

где I — сила тока в
об­мотке тороида; N — чис­ло ее
витков; l₁ и l₂ -­
длины первой и второй частей сердечника
торо­ида; ₁ и
₂
—магнитные проницаемости ве­ществ
первой и второй частей сердечника
торо­ида; ₀
—магнитная постоянная

б) напряженность магнитного поля на
осе­вой линии тороида в первой и второй
частях сердечника

H₁=B
/(₁
₂);
H₁=B
/(₂
₀
);

в) магнитный поток в сердечнике тороида

или по аналогии с законом Ома (формула
Гопкинсона)

Ф_m=F_m/R_m,

где F_m
— магнитодвижущая сила; R_m
— полное магнитное сопро­тивление
цепи;

г) магнитное
сопротивление участка цепи

R_m=l/(μμ₀S).

• Магнитная проницаемость μ,
ферромагнетика связана с маг­нитной
индукцией В поля в нем и напряженностью
Н намагничи­вающего поля соотношением

μ=B/(μ₀H).

• Связь между магнитной индукцией В
поля в ферромагнетике и напряженностью
Н намагничивающего поля выражается
графи­чески (рис. 24.1).

Примеры решения задач

Пример 1. В одной плоскости с бесконечно
длинным прямым проводом, по которому
течет ток I=50 А,
расположена прямоуголь­ная рамка
так, что две большие стороны ее длиной
l=65 см парал­лельны
проводу, а расстояние от провода до
ближайшей из этих сторон равно ее ширине.
Каков магнитный поток Ф, пронизываю­щий
рамку?

Решение.
Магнитный поток Ф через поверхность
площадью S определяется
выражением

В нашем случае вектор магнитной индукции
В перпендикулярен плоскости рамки.
Поэтому для всех точек рамки В_n=В.
Магнитная индукция В, создаваемая
бесконечно длинным прямым проводником
с током, определяется формулой

,

где x— расстояние
от провода до точки, в которой определяется
В.

Для вычисления магнитного потока
заметим, что так как В зависит от х
и элементарный поток Ф будет также
за­висеть от х, то

dф=B(x)dS.

Разобьем площадь рамки на узкие
элементарные площадки длиной l,
шири­ной dx и площадью
dS=ldx
(рис. 24.2). В пределах этой площадки
магнитную индукцию можно считать
постоянной, так как все части площад­ки
равноудалены (на расстояние х) от
провода. С учетом сделанных замечаний
элементарный магнитный поток можно
записать в виде

dФ=

Проинтегрировав полученное выражение
в пределах от x₁=a
до х₂=2а, найдем

|_^2.

Подставив пределы, получим

Убедимся в том, что правая часть
полученного равенства дает единицу
магнитного потока (Вб): [₀]
[I] [l]=
Гн/м 1 А 1
м=1 Вб. Произведя вычисления по формуле
(1), найдем Ф=4,5 мкВб.

Пример 2. Определить индукцию В
и напряженность Н магнит­ного
поля на оси тороида без сердечника, по
обмотке которого, со­держащей N=200
витков, идет ток I=5 А. Внешний диаметр
d₁ тороида
равен 30 см, внутренний d₂=
20 см.

Решение. Для определения напряженности
магнитного поля внутри тороида вычислим
циркуляцию вектора Н вдоль линии
маг­нитной индукции поля:

Из условия симметрии следует, что линии
магнитной индукции тороида представляют
собой окружности и что во всех точках
этой линии напряженности одинаковы.
Поэтому в выражении циркуля­ции
напряженность Н можно вынести за
знак интеграла, а интегри­рование
проводить в пределах от нуля до 2 r,
где r — радиус
ок­ружности, совпадающей с линией
индукции, вдоль которой вычис­ляется
циркуляция, т. e.

(1)

С другой стороны, в соответствии с
законом полного тока цир­куляция
вектора напряженности магнитного поля
равна сумме то­ков, охватываемых
контуром, вдоль которого вычисляется
цирку­ляция:

(2)

Приравняв
правые части равенств (1) и (2), получим

(2)

Линия, проходящая вдоль тороида,
охватывает число токов, равное числу
витков тороида. Сила тока во всех витках
одинакова. Поэтому формула (3) примет
вид 2rH=-NI,
откуда

(4)

Для средней линии тороида
r=1/2(R₁R₂)=1/4(d₁+d₂).
Подставив это выражение r в формулу
(4), найдем

(5)

Магнитная индукция В₀ в
вакууме связана с напряженностью поля
соотношением B₀=₀H.
Следовательно,

(6)

Подставив значения величин в выражения
(5) и (6), получим:

H=1,37 кА/м, B₀=1,6
мТл.

Пример. 3. Чугунное кольцо имеет
воздушный зазор длиной lо=5 мм. Длина
l средней линии кольца равна 1 м.
Сколько витков N содержит обмотка
на кольце, если при силе тока I=4 А
индукция В магнитного поля в воздушном
зазоре равна 0,5 Тл? Рассеянием маг­нитного
потока в воздушном зазоре можно
пренебречь. Явление гистерезиса не
учитывать.

Решение. Пренебрегая рассеянием
магнитного потока, мы можем принять,
что индукция поля в воздушном зазоре
равна ин­дукции поля в чугуне. На
основании закона полного тока запишем

IN=Hl+H₀I₀.

По графику (см. рис. 24.1) находим, что при
В=0,5 Тл напря­женность Н
магнитного поля в чугуне равна 1,2 кА/м.
Так как для воздуха =1,
то напряженность поля в воздушном
зазоре

H₀=B₀=0,4
MA/м.

Искомое число витков

N=(Hl+H₀
l_o)/I==800.

Поскольку магнитный поток — это мера магнитного поля, проходящего сквозь поверхность определённой площади, его можно измерить магнитометром, точно так же, как и индукцию магнитного поля. Например, представьте, что небольшой щуп магнитометра перемещается (без вращения) по поверхности площадью 0, comma, 5, space, м, squared неподалёку от большого плоского магнетика. Магнитометр показывает во всех точках этой поверхности постоянное значение индукции 5, space, м, Т, л. Тогда магнитный поток, проходящий сквозь эту поверхность, будет равен left parenthesis, 5, dot, 10, start superscript, minus, 3, end superscript, space, Т, л, right parenthesis, dot, left parenthesis, 0, comma, 5, space, м, squared, right parenthesis, equals, 0, comma, 0025, space, В, б. Если же магнитная индукция в разных точках поверхности различается, тогда сначала необходимо найти её среднее значение.

С магнитным потоком тесно связан ещё один термин, с которым вы можете столкнуться, — плотность магнитного потока. Она измеряется в В, б, slash, м, squared. Поскольку мы делим магнитный поток на площадь, плотность магнитного потока можно было бы измерять сразу в тесла. Однако в действительности термин «плотность магнитного потока» часто используется как синоним величины магнитной индукции.

На рисунке 2 показана схема неоднородного магнитного поля неподалёку от большого плоского магнетика. Зелёной линией обозначен замкнутый провод. Чему равен магнитный поток, проходящий сквозь ограниченную им поверхность?