Как найти магнитный поток проводника

Магнитный поток
Размерность	ML2T−2I−1
Единицы измерения
СИ	Вб
СГС	Мкс
Примечания
Скалярная величина

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тный пото́к — поток вектора магнитной индукции через некоторую поверхность. Для бесконечно малого участка равен произведению модуля на площадь участка и косинус угла между и нормалью к плоскости участка. Для поверхности конечных размеров находится как сумма (интеграл) по её малым фрагментам. Стандартное обозначение — .

Важнейшая физическая формула, в которую входит магнитный поток, — выражение для закона электромагнитной индукции Фарадея.

Определение магнитного потока[править | править код]

Магнитным потоком через бесконечно малый элемент поверхности называется произведение

,

где — угол между вектором магнитной индукции и единичным вектором нормали к участку поверхности, а векторный элемент dS площади поверхности S определяется как

.

Магнитным потоком через поверхность конечной площади называется интеграл от по поверхности:

.

Направление вектора в общем случае непостоянно (см. рис.), магнитное поле также может изменяться вдоль поверхности. Точка в произведениях означает скалярное умножение векторов. Интеграл понимается как предел суммы по малым участкам при стремлении их размеров к нулю. Поверхность может быть незамкнутой (как на рис.) или замкнутой.

В случае однородного поля и плоской поверхности магнитный поток рассчитывается как .

Единицы измерения магнитного потока[править | править код]

В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с =
кг·м²·с^-2·А^-1), в системе СГС — максвелл (Мкс, 1 Вб = 10⁸ Мкс).

Приборы для измерения потока[править | править код]

Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.

Некоторые свойства магнитного потока[править | править код]

В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции  через любую замкнутую поверхность  равен нулю:

.

Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.

В соответствии с теоремой Стокса, магнитный поток через поверхность, «натянутую» на некий контур , можно выразить через циркуляцию векторного потенциала  магнитного поля по этому контуру:

,

поскольку имеет место связь . Этот поток не зависит от конфигурации натянутой поверхности.

Переменный во времени магнитный поток[править | править код]

По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила

в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции и/или геометрии контура.

Квантование магнитного потока[править | править код]

При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:

,

где  — постоянная Планка,  — элементарный заряд.

Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):

Вб (в СИ);

Гаусс·см² (в СГС),  — скорость света.

Экспериментально квантование магнитного потока было обнаружено в 1961 году.

См. также[править | править код]

• Уравнения Максвелла
• Электродвигатель постоянного тока
• Потокосцепление
• Индуктивность

Магнитный поток, проходящий через площадь S равен:

Ф = BScosα;

где:

Ф ― величина магнитного потока [Вб],

S ― площадь контура [м2],

B ― индукция магнитного поля [Тл],

α ― угол между нормалью $overrightarrow{n}$ к площади контура и вектором индукции магнитного поля $overrightarrow{B}$.

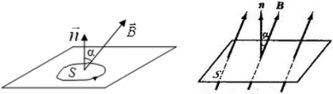
Если вектор индукции магнитного поля $overrightarrow{B}$ перпендикулярен площади контура, то магнитный поток равен:

Ф = BScos90° = BS;

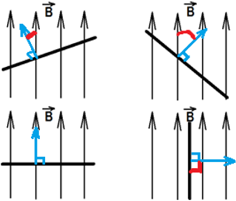
Максимальное значение потока будет тогда, когда косинус будет максимальным (cosα = 1), то есть угол между вектором $overrightarrow{B}$ и вектором нормали к пластинке равен 0°, чему соответствует картинка 3. Наименьшее же значение потока будет тогда, когда косинус будет равен нулю (cosα = 0), то есть угол между нормалью к пластинке и вектором индукции равен 90°, чему соответствует картинка 4.

Электромагнитная индукция ― явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через контур. Если контур разомкнут, то на его концах наблюдается разносность потенциалов, равная ЭДС индукции.

ЭДС электромагнитной индукции возникает только тогда, когда изменяется магнитный поток.

Закон Фарадея об электромагнитной индукции и гласит, что индуцируемая ЭДС прямо пропорциональна скорости изменения магнитного потока:

$varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

где:

$varepsilon_i $ ― ЭДС электромагнитной индукции [B],

$frac{Delta text{Ф}}{Delta t}$ ― скорость изменения магнитного потока [Вб/с],

∆Ф ― изменение магнитного потока [Вб],

∆t ― время, за которое происходит это изменение [c].

Кроме того, ЭДС индукции равна производной магнитного потока по времени:

$varepsilon_i = -text{Ф}_t’$

где:

• ― ЭДС электромагнитной индукции [B],
• ― производная магнитного потока по времени [Вб/с].

Задача 1

Замкнутый контур площадью S из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. В контуре возникают колебания тока с амплитудой iм = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos (bt), где a = 6 · 10-3Тл, b = 3500 c-1. Электрическое сопротивление контура R = 1,2 Ом. Чему равна площадь контура?

Решение:

Обратите внимание на величины, данные в условии. Они здесь совсем не такие, к которым вы привыкли, потому что не дано значение магнитного поля, а дана зависимость магнитного поля от времени. Посмотрим, как это скажется на решении задачи.

Поскольку магнитное поле, а вместе с ним и поток меняются, то будет возникать ЭДС индукции, именно это ЭДС и вызовет электрический ток, поэтому запишем закон электромагнитной индукции.

По закону электромагнитной индукции $varepsilon_i = -frac{Delta text{Ф}}{Delta t}$

ЭДС — это изменение магнитного потока за время. Ничего в определении ЭДС не сказано про это самое время. Дело в том, что изменение какой-то величины за небольшой промежуток времени называется производной по времени. То есть наше ЭДС, которое является изменением магнитного потока за небольшой промежуток времени, это просто производная магнитного потока по времени $varepsilon_i = -text{Ф}_t’$

И это очень важный момент, без которого мы не сможем решить такого рода задачу.

Теперь посчитаем ЭДС индукции.

Напишем, чему равен магнитный поток Ф = BS = acos (bt) · S.

ЭДС индукции — это производная магнитного потока по времени. Теперь придётся вспомнить немного математики. Множители “a” и “S” перед косинусом не зависят от времени, поэтому производная их не трогает, а вот у косинуса в скобках стоит зависимость от времени, поэтому именно от косинуса производную и нужно взять.

Обратите внимание на полученную формулу магнитного потока. В ней стоит просто множитель aS перед сложной функцией косинуса

$text{Ф} underset{text{множитель}}{underbrace{aS}} ;; cdot ;; underset{text{сложная функция}}{underbrace{cos(bt)}}$.

Взяв производную от этой функции, получаем Ф´ = –abS · sin (bt). А теперь, раз мы знаем производную магнитного потока, значит, знаем и ЭДС индукции, потому что $varepsilon_i = -text{Ф}_t’$

Подставив сюда значение производной, получим $varepsilon_i = -text{Ф}_t’$ = abS · sin (bt).

Мы получили значение ЭДС. Кроме этого, мы знаем сопротивление и максимальную силу тока, поэтому запишем закон Ома.

По закону Ома $I = frac{varepsilon}{R}$ , подставив сюда значение ЭДС, получаем $I = frac{abScdot sin(bt)}{R}$.

Мы получили зависимость силы тока от времени.

Из-за синуса, который стоит в этой формуле, ток постоянно меняет свое значение, то он становится больше, то меньше, поскольку синус меняет своё значение от -1 до 1.

В условии дано максимальное значение силы тока, которое протекает по контуру. Когда эта величина будет максимальной? В тот момент, когда синус будет максимальным, то есть равный единице. Поэтому запишем sin (bt) = 1.

Максимальное значение тока будет в тот момент, когда будет максимальным значение ЭДС индукции, то есть когда, $I_{max} = frac{abS}{R}$.

Отсюда можно легко выразить площадь контура $S = frac{I_{max}R}{ab}$, подставив сюда все значения, получим $S = frac{I_{max}R}{ab} = frac{35cdot 10^{-3} Acdot 1,2text{Ом}}{6cdot 10^{-3}text{Тл} cdot 35000c^{-1}} = 0,002text{м}^2$

Ответ: 0,002

Как видно из формулы магнитного потока Ф = BScosα, изменение магнитного потока может быть вызвано разными факторами:

• увеличением или уменьшением модуля индукции магнитного поля (т. е. величины $frac{Delta B}{Delta t}$);
• изменением направления вектора магнитного поля (т. е. изменением угла α);
• деформацией контура, причем такой деформацией, при которой изменяется площадь контура (т. е. изменением величины $frac{Delta S}{Delta t}$ );
• изменением нескольких из этих величин одновременно.

Таким образом, изменение модуля или направление вектора магнитной индукции или площади контура неизбежно приводят к тому, что в контуре возникает электродвижущая сила.

Если нарисовать график зависимости магнитного потока, то он может выглядеть либо так: тогда поток не будет менятьсяи ЭДС не возникает.

Либо так, тогда будет меняться поток и возникать ЭДС:

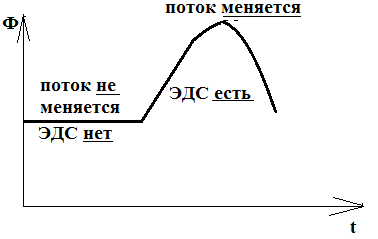
Знак «минус» перед скоростью изменения магнитного потока в формуле отражает правило Ленца: индуцированный ток всегда направлен так, чтобы магнитное поле, которое он создает, препятствовало изменению магнитного потока.

Если магнитный поток, проходящий через площадь контура, уменьшается, то магнитное поле индуцированных токов будет стремиться его увеличить.

Если поток увеличивается ― магнитное поле индуцированных токов будет стремиться его уменьшить.

Задача 2

Два проводящих кольца расположены относительно проводника с током в одной плоскости, как это показано на рисунке. В каком направлении будет индуцироваться ток в этих кольцах, если начать двигать их в направлении проводника?

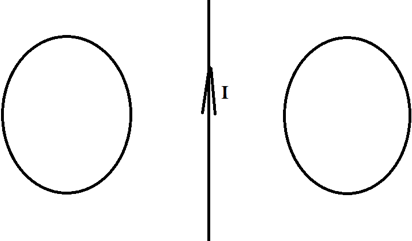
Решение:

Первым делом необходимо понять, как вообще может возникать индуцированный ток, если даже магнитного поля нет?

Его направление мы можем определить по правилу правого винта. Отметим это на рисунке.

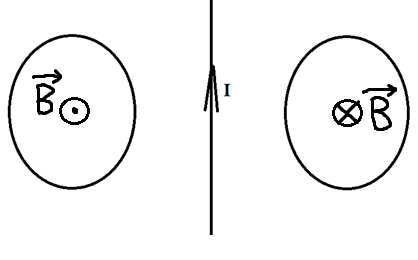
Теперь эти два проводника начинают двигать. Разве от этого меняется поток? Ведь площадь остаётся та же самая, угол между нормалью и вектором тоже не меняется. Однако, чем ближе к проводнику с током, тем сильней поле, а чем дальше от него, тем слабее! Поэтому, когда мы двигаем кольца к проводнику, мы увеличиваем поток, ведь ближе поле сильнее. Значит, будет появляться ток, а его направление можно определить по правилу Ленца. Что нам говорит правило Ленца?

Раз поток увеличивается, то по правилу Ленца ток будет индуцироваться так, чтобы уменьшить поток, то есть магнитное поле в левом кольце будет направлено от нас, а в правом ─ на нас. А значит, по правилу правого винта мы можем определить, что ток будет течь по часовой стрелке слева и против часовой стрелки справа.

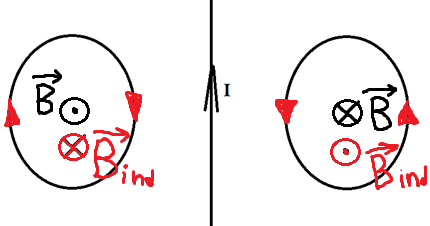
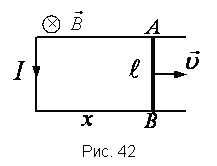
Движение проводников

Если к концам проводника, движущегося в магнитном поле, подключить вольтметр, то прибор покажет наличие разности потенциалов на концах проводника. Таким образом, когда проводник перемещается в области с магнитным полем, в нем возникает электромагнитная движущая сила (ЭДС).

Согласно закону Лоренца, в проводнике, движущемся в магнитном поле, создается ЭДС $|varepsilon_i| = Blvsinalpha$;

где:

$varepsilon_i$― ЭДС электромагнитной индукции [B],

B ― индукция магнитного поля [Тл],

l ― длина проводника [м],

v ― скорость движения проводника [м/с],

α ― угол между направлением вектора скорости $overrightarrow{v}$ и длиной проводника $overrightarrow{l}$ , если вектор индукции магнитного поля $overrightarrow{B}$перпендикулярен проводнику и вектору скорости его движения: $overrightarrow{B} perp overrightarrow{v}, overrightarrow{B} perp overrightarrow{l}$

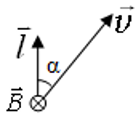
Используя силу Лоренца, можно получить это определение ЭДС. Сила Лоренца ― это проявленное действие магнитного поля на заряженную частицу.

В проводнике присутствует большое количество свободных зарядов (именно это отличает проводники от диэлектриков), и на каждый из зарядов действует сила Лоренца, перемещая их по проводнику так, что в одной его части скапливается отрицательный заряд, а в другой, соответственно, положительный. Это распределение зарядов и является физической основой для возникновения электродвижущей силы.

На рисунке показано как сила Лоренца, действующая на каждый из зарядов проводника, создаёт ЭДС в проводнике. Если одиночный отрицательный заряд попадает в магнитное поле, направленное от нас, то, согласно правилу левой руки, направление его движения изменяется так, как показано на рисунке. Если в область с таким же магнитным полем входит проводник, суммарный заряд которого равен нулю, но внутри которого находятся электроны, способные свободно перемещаться в проводнике, то электроны стекаются в один конец проводника. Так как электроны переместились в один конец проводника, то этот конец приобретает отрицательный заряд, а противоположный ему ― положительный. Таким образом, в проводнике возникает разность потенциалов и электродвижущая сила.

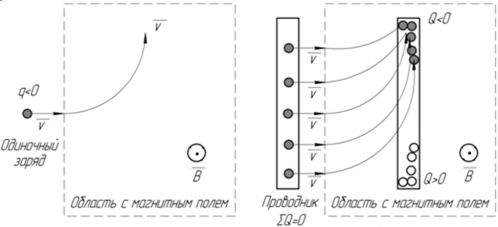
В некоторых случаях удобно решать задачи, используя определение ЭДС через закон Лоренца (обычно это задачи о движении прямолинейного проводника в поле), в других ― через закон Фарадея.

В проводнике, движущемся в магнитном поле, образуется разность потенциалов U = lvBsinα;

где:

U — разность потенциалов [В],

l — длина проводника [м],

v — скорость движения проводника $big[ frac{text{м}}{c} big]$

B — индукция магнитного поля [Тл],

α — угол между направлением скорости и длиной проводника.

В случае, если есть какой-то замкнутый контур, то ЭДС в нем возникает только тогда, когда меняется магнитный потокчерез этот контур. В случае же тонкого стержня, для которого нельзя применить понятия магнитного потока, потому что у него просто нет площади, ЭДС возникает при движении в постоянном магнитном поле.

В случае, если в задаче дана проводящая рамка или контур, для определения ЭДС (напряжения) используем формулу $varepsilon_i = – frac{Delta text{Ф}}{Delta t}$

В случае, если в задачи дан проводник, движущейся в поле, для определения ЭДС (напряжения) используем формулу $varepsilon$ =U= lvBsinα.

Задача 3

В заштрихованной области на рисунке действует однородное магнитное поле, перпендикулярное плоскости рисунка с индукцией В = 0,1 Тл. Квадратную проволочную рамку, сопротивление которой 10 Ом и длина стороны 10 см, перемещают в этом поле в плоскости рисунка поступательно равномерно с некоторой скоростью υ. При попадании рамки в магнитное поле в положении 1 в ней возникает индукционный ток, равный 1 мА. Какова скорость движения рамки?

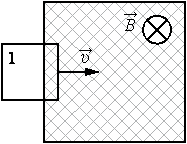
Решение:

Составим цепочку.

Зная силу тока и сопротивление, что можно найти? Мы сможем найти напряжение, то есть ЭДС, а ЭДС, уже можно легко связать со скоростью движения рамки.

Составим цепочку. Мы знаем магнитное поле (В), длину стороны (a), сопротивление (R) и силу тока (I), а найти нужно скорость(v).

Зная ток и сопротивление, что сразу можно найти? Напряжение, то есть ЭДС, которое мы сможем найти по закону Ома.

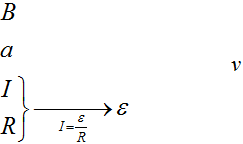
А связать ЭДС с индукцией поля, стороной рамки и скоростью движения очень легко, воспользовавшись той формулой, которую мы получили в прошлой задаче.

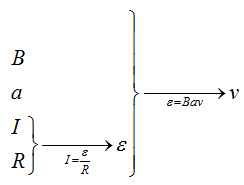
Пройдёмся вдоль этой цепочки.

Запишем закон Ома $I = frac{varepsilon}{R}$, подставив сюда формулу для ЭДС, которую мы получили в прошлой задаче, отбросив знак «минус» получим $I = frac{varepsilon}{R} = frac{Bav}{R}$отсюда выразим скорость, и, подставив все величины, получим $v = frac{IR}{Ba} = frac{1cdot 10^{-3} Acdot 10text{Ом}}{0,1 text{Тл} cdot 0,1 text{м}} = 1 frac{text{м}}{c}$

Ответ: 1

Поток вектора магнитной индукции

Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:

Φ=BScos α=BnS=B→S→ с углом между n→ и B→, обозначаемым α, n→ является нормалью к площадке S.

Формула магнитного потока

Φ равняется количеству линий магнитной индукции, пересекающих площадку S, как показано на рисунке 1. Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S. Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.

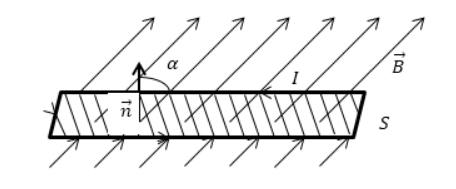
Рисунок 1

В чем измеряется магнитный поток

В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки dS, рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока dΦ производится через эту поверхность. Запись примет вид:

dΦ=BdScos α=B→dS→.

Нахождение полного потока через поверхность S:

Φ=∫SBdScos α=∫SB→dS→.

Основной единицей измерения магнитного потока в системе СИ считаются веберы (Вб). 1 Вб=1 Тл1 м2.

Связь магнитного потока и работы сил магнитного поля

Элементарная работа δA, совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции dΦ:

δA=IdΦ.

Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:

A=IΦ2-Φ1 с Φ1, обозначаемым потоком через контур в начале перемещения, Φ2 является  потоком через контур в конце перемещения.

Теорема Гаусса для магнитного поля

Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:

∮B→dS→=0.

Выражение ∮B→dS→=0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:

∮E→dS→=qε0.

Запись ∮B→dS→=0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.

Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.

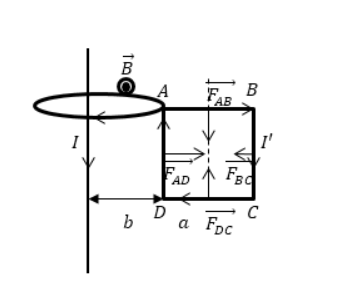
Рисунок 2

Решение

Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.

Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.

За основу возьмем формулу магнитного потока и работы, которая их связывает:

A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=0. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:

A=-I’Φ1 (1.2).

Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:

dΦ=-BdS=-B·a·dx=-μ02πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:

B=μ02πxIl (1.4).

Отсюда следует, что для нахождения всего потока из (1.3) потребуется:

Φ1=∫S-μ02πIldxx=-μ02πIl∫bb+adxx=-μ02πIl·lnb+ab (1.5).

Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:

A=I’μ02πIl·lnb+ab.

Ответ: A=μ02πII’l·lnb+ab.

Найти силу, действующую на рамку, из предыдущего примера.

Решение

Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:

δA=Fdx (2.1).

Элементарная работа δA может быть выражена как:

δA=I’dΦ (2.2).

Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:

Fdx=I’dΦ→F=I’dΦdx (2.3).

Используем выражение, которое было получено в примере 1:

dΦ=-μ02πIldxx→dΦdx=-μ02πIlx (2.4).

Произведем подстановку dΦdx в (2.3). Имеем:

F=I’μ02πIlx (2.5).

Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:

FAB→+FDC→=0 (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:

F→=FAD→+FBC→ (2.6).

Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:

F=FAD-FBC (2.7).

Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:

FAD=I’м02πIlb (2.8).

Значение FBC будет:

FBC=I’μ02πIlb+a (2.9).

Для нахождения искомой силы:

F=I’μ02πIlb-I’μ02πIlb+a=II’μ0l2π1b-1b+a.

Ответ: F=II’μ0l2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.

Магнитный поток

Автор:
Субботин Б.П.

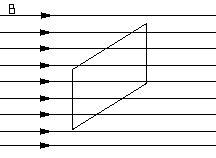
На
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.

Определение
магнитного потока:

Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.

Формула
магнитного потока:

Ф
= BS cos α

здесь
α – угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.

Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.

А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.

Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 10⁸ мкс.
Соответственно 1 мкс = 10^-8 вб.

Магнитный
поток является скалярной величиной.

ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА

Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.

Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.

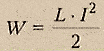
Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? – выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)

4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность

Основные
формулы

·            Закон
электромагнитной индукции (закон
Фарадея):

,
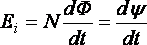                                       (39)

где – эдс индукции;–
полный магнитный поток (потокосцепление).

·            Магнитный
поток, создаваемый током в контуре,

,   
                                           (40)

где  –
индуктивность контура;–
сила тока.

·            Закон
Фарадея применительно к самоиндукции

.                              
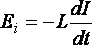             (41)

·            Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,

,                                 
       (42)

где –
индукция магнитного поля;–
площадь рамки;–
угловая скорость вращения.

·            Индуктивность
соленоида

, 
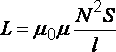                                           (43)

где –
магнитная постоянная;–
магнитная проницаемость вещества;–
число витков соленоида;–
площадь сечения витка;–
длина соленоида.

·            Сила
тока при размыкании цепи

 ,   
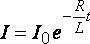                                        (44)

где –
установившаяся в цепи сила тока;–
индуктивность контура,–
сопротивление контура;–
время размыкания.

·            Сила
тока при замыкании цепи

.
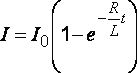                                        (45)

·            Время
релаксации

.   
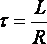                                              (46)

Примеры
решения задач

Пример
1.

Магнитное
поле изменяется по закону ,
где=
15 мТл,. В
магнитное поле помещен круговой
проводящий виток радиусом = 20
см под угломк
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени=
5 с.

Решение

По
закону электромагнитной индукции возникающая в
витке эдс индукции ,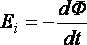
где–
 магнитный поток, сцепленный в витке.

,

где –
площадь витка,;– угол
между направлением вектора магнитной
индукциии
нормалью к контуру:.

.

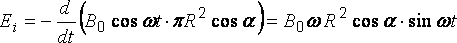Подставим
числовые значения: =
15 мТл,,= 20
см =   = 0,2 м,.

Вычисления
дают .

Пример 2 В однородном магнитном поле с индукцией = 0,2 Тл расположена прямоугольная рамка, подвижная сторона которой длиной= 0,2 м перемещается со скоростью= 25 м/с перпендикулярно линиям индукции поля (рис. 42). Определить эдс индукции, возникающую в контуре. Решение При движении проводника АВ в магнитном поле площадь рамки увеличивается, следовательно, возрастает магнитный поток сквозь рамку и возникает эдс индукции.

По
закону Фарадея ,
 где,
тогда,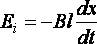
но,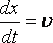
поэтому.

Так, .

Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.

САМОИНДУКЦИЯ

Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.

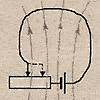
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции. 

Это
явление называется самоиндукцией.Самоиндукция –
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции

Проявление
явления самоиндукции

Замыкание
цепи

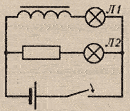При
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.

Размыкание
цепи

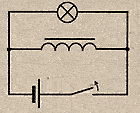При
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.

Вывод

в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ

От
чего зависит ЭДС самоиндукции? 

Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника 
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.

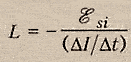Индуктивность –
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:

где
Ф – магнитный поток через контур, I – сила
тока в контуре.

Единицы
измерения индуктивности в
системе СИ:

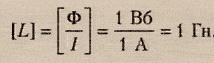
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды 
(
возможен сердечник).

ЭДС
САМОИНДУКЦИИ

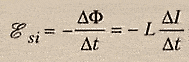
ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.

Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Р_м). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.

Магнитный
момент единицы объема вещества
характеризует его намагниченность
– I,
определяется по формуле:

I= Р_м /V,
(2.4)

где V –
объем вещества.

Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.

Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью – c_о , величина
безразмерная.

Если
какое-либо тело поместить в магнитное
поле с индукцией В₀,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В^‘,
которое взаимодействует с намагничивающим
полем.

В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:

В
= В₀ +
В^‘(знак
вектора опущен), (2.5)

где В^‘ –индукция
собственного магнитного поля
намагнитившегося вещества.

Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
– c_о ,
справедливо выражение:В^‘ = c_о В₀ (2.6)

Разделим
на m₀ выражение
(2.6):

В^‘/
m_о= c_о В₀ /m₀

Получим: Н^‘ = c_о Н₀ , (2.7)

но Н^‘ определяет
намагниченность вещества I,
т.е. Н^‘ = I,
тогда из (2.7):

I
= c_о Н₀.
(2.8)

Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН₀,
то внутри него индукция определяется
выражением:

В=В₀ +
В^‘ =
m₀Н₀ +m₀Н^‘ =
m₀ (Н₀ +
I) (2.9)

Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Магнитный поток

Содержание:

• Что такое магнитный поток 
  • В чем измеряется, обозначение и размерность
• От чего зависит величина основного магнитного потока
• Чему равен магнитный поток, как найти
  • Скорость изменения магнитного потока через контур
• Какой формулой определяется величина магнитного потока
• Связь магнитного потока и работы сил магнитного поля

Что такое магнитный поток 

Магнитный поток — величина, характеризующая число магнитных силовых линий поля, проходящих через замкнутый контур.

Майкл Фарадей опытным путем пришел к выводу, что при любом соприкосновении проводника и магнитных линий по проводнику проходит заряд (triangle Q). Этот заряд прямо пропорционален количеству( triangle Ф) пересеченных линий и обратно пропорционален сопротивлению R контура. Пересечение линий вызывается или движением проводника, или изменением поля. 
Позже, представляя замкнутый контур, в котором действует ЭДС индукции, Джеймс Клерк Максвелл подсчитывал количество силовых линий (triangle Ф), пересекаемых контуром за время (triangle t). Ф он при этом отождествлял с магнитным потоком сквозь всю поверхность.

В чем измеряется, обозначение и размерность

Единица измерения — вебер, сокращенно Вб. Он обозначается буквой Ф. 

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Размерность — выражение, демонстрирующее связь физической величины с другими величинами данной системы, разложение ее на сомножители из других величин.

Размерность магнитного потока — (В times с = кг times м^{2} times с^{-2} times А^{-1}.)

От чего зависит величина основного магнитного потока

Его можно изменить следующими способами:

• изменив площадь контура;
• изменив угол его наклона;
• изменив магнитное напряжение.

Чему равен магнитный поток, как найти

Магнитный поток в случае однородного магнитного поля равен произведению модуля индукции В этого поля, площади S плоской поверхности, через которую вычисляется поток, и косинуса угла (varphi) между направлением индукции В и нормали к данной поверхности.

Нормаль — перпендикуляр к плоскости контура.

Также поток можно вычислить через индуктивность, которая пропорциональна отношению полного, или суммарного потока к силе тока.

Обозначение суммарного потока — буква ( psi). Он равен сумме потоков, проходящих через всю поверхность. И в простом случае, где рассматриваются одинаковые потоки, проходящие через одинаковые витки катушки, и в случаях, когда поверхность имеет очень сложную форму, эта пропорциональность сохраняется.

Скорость изменения магнитного потока через контур

Закон электромагнитной индукции Фарадея в интегральном виде выглядит следующим образом:

(;underset С{oint;};(overrightarrow{Е;}times;doverrightarrow l) = – frac{1}{c}frac{d}{dt}int underset S{int;};(overrightarrow{B} times doverrightarrow{S}).)

Интеграл в левой части уравнения — циркуляция вектора (overrightarrow{Е;}) по замкнутому контуру С, это отражает знак интеграла, записанный с кругом. В правой части — скорость изменения потока Ф, который вычисляется как интеграл по поверхности S, «натянутой» на С. 

Интеграл — целое, определяемое как сумма его бесконечно малых частей.

Если считать изменение потока в замкнутом контуре равномерным, то закон Фарадея примет следующий вид:

(epsilon_{i} = – frac{triangleФ}{triangle t}.)

Какой формулой определяется величина магнитного потока

Математически величину Ф описывают двумя формулами:

(Ф;=;sum_{triangle S};;Btriangle S = B times S times cosvarphi. )

Связь магнитного потока и работы сил магнитного поля

Герман Гельмгольц первым связал закон Фарадея и закон сохранения энергии. Возьмем проводник с током I, находящийся внутри однородного магнитного поля, которое перпендикулярно плоскости контура, и перемещающийся в нем. Под влиянием силы Ампера F проводник перемещается на отрезок dx. Сила F производит работу dA = IdФ.

Работу источника тока можно измерить, сложив работу на джоулеву теплоту и работу по перемещению проводника внутри поля:

(epsilon Idt = I^{2}Rdt + IdФ.)

(I = frac{epsilon – frac{dФ}{dt}}{R}.)

Текст с ошибкой:

Расскажите, что не так