Магнитный поток
Автор:
Субботин Б.П.
На
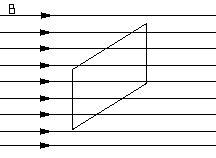
картинке показано однородное магнитное
поле. Однородное означает одинаковое
во всех точках в данном объеме. В поле
помещена поверхность с площадью S. Линии
поля пересекают поверхность.
Определение
магнитного потока:
Магнитным
потоком Ф через поверхность S называют
количество линий вектора магнитной
индукции B, проходящих через поверхность
S.
Формула
магнитного потока:
Ф
= BS cos α
здесь
α – угол между направлением вектора
магнитной индукции B и нормалью к
поверхности S.
Из
формулы магнитного потока видно, что
максимальным магнитный поток будет при
cos α = 1, а это случится, когда вектор B
параллелен нормали к поверхности S.
Минимальным магнитный поток будет при
cos α = 0, это будет, когда вектор B
перпендикулярен нормали к поверхности
S, ведь в этом случае линии вектора B
будут скользить по поверхности S, не
пересекая её.
А
по определению магнитного потока
учитываются только те линии вектора
магнитной индукции, которые пересекают
данную поверхность.
Измеряется
магнитный поток в веберах (вольт-секундах):
1 вб = 1 в * с. Кроме того, для измерения
магнитного потока применяют максвелл:
1 вб = 108 мкс.
Соответственно 1 мкс = 10-8 вб.
Магнитный
поток является скалярной величиной.
ЭНЕРГИЯ
МАГНИТНОГО ПОЛЯ ТОКА
Вокруг
проводника с током существует магнитное
поле, которое обладает энергией.
Откуда
она берется? Источник тока, включенный
в эл.цепь, обладает запасом энергии.
В
момент замыкания эл.цепи источник тока
расходует часть своей энергии на
преодоление действия возникающей ЭДС
самоиндукции. Эта часть энергии,
называемая собственной энергией тока,
и идет на образование магнитного
поля.
Энергия магнитного поля
равна собственной
энергии тока.
Собственная
энергия тока численно равна работе,
которую должен совершить источник тока
для преодоления ЭДС самоиндукции, чтобы
создать ток в цепи.
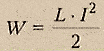
Энергия
магнитного поля, созданного током, прямо
пропорциональна квадрату силы тока.
Куда
пропадает энергия магнитного поля после
прекращения тока? – выделяется ( при
размыкании цепи с достаточно большой
силой тока возможно возникновение искры
или дуги)
4.1. Закон электромагнитной индукции. Самоиндукция. Индуктивность
Основные
формулы
· Закон
электромагнитной индукции (закон
Фарадея):
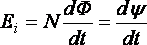 ,
,
(39)
где ![]() – эдс индукции;
– эдс индукции;![]() –
–
полный магнитный поток (потокосцепление).
· Магнитный
поток, создаваемый током в контуре,
![]() ,
,
(40)
где ![]() –
–
индуктивность контура;![]() –
–
сила тока.
· Закон
Фарадея применительно к самоиндукции
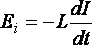 .
.
(41)
· Эдс индукции, возникающая при
вращении рамки с током в магнитном поле,
![]() ,
,
(42)
где ![]() –
–
индукция магнитного поля;![]() –
–
площадь рамки;![]() –
–
угловая скорость вращения.
· Индуктивность
соленоида
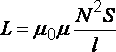 ,
,
(43)
где ![]() –
–
магнитная постоянная;![]() –
–
магнитная проницаемость вещества;![]() –
–
число витков соленоида;![]() –
–
площадь сечения витка;![]() –
–
длина соленоида.
· Сила
тока при размыкании цепи
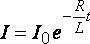 ,
,
(44)
где ![]() –
–
установившаяся в цепи сила тока;![]() –
–
индуктивность контура,![]() –
–
сопротивление контура;![]() –
–
время размыкания.
· Сила
тока при замыкании цепи
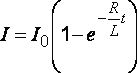 .
.
(45)
· Время
релаксации
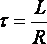 .
.
(46)
Примеры
решения задач
Пример
1.
Магнитное
поле изменяется по закону ![]() ,
,
где![]() =
=
15 мТл,![]() . В
. В
магнитное поле помещен круговой
проводящий виток радиусом ![]() = 20
= 20
см под углом![]() к
к
направлению поля (в начальный момент
времени). Найти эдс индукции, возникающую в
витке в момент времени![]() =
=
5 с.
Решение
По
закону электромагнитной индукции возникающая в
витке эдс индукции 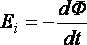 ,
,
где![]() –
–
магнитный поток, сцепленный в витке.
![]() ,
,
где ![]() –
–
площадь витка,![]() ;
;![]() – угол
– угол
между направлением вектора магнитной
индукции![]() и
и
нормалью к контуру:![]() .
.
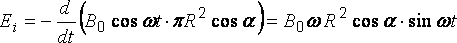 .
.
Подставим
числовые значения: ![]() =
=
15 мТл,![]() ,
,![]() = 20
= 20
см = = 0,2 м,![]() .
.
Вычисления
дают ![]() .
.
|
Пример В Решение При |
|
По
закону Фарадея ![]() ,
,
где![]() ,
,
тогда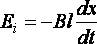 ,
,
но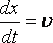 ,
,
поэтому![]() .
.
Так, ![]() .
.
Знак
«–» показывает, что эдс индукции
и индукционный ток направлены против
часовой стрелки.
САМОИНДУКЦИЯ
Каждый
проводник, по которому протекает эл.ток,
находится в собственном магнитном поле.
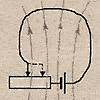
При
изменении силы тока в проводнике меняется
м.поле, т.е. изменяется магнитный поток,
создаваемый этим током. Изменение
магнитного потока ведет в возникновению
вихревого эл.поля и в цепи появляется
ЭДС индукции.
![]() Это
Это
явление называется самоиндукцией.Самоиндукция –
явление возникновения ЭДС индукции в
эл.цепи в результате изменения силы
тока.
Возникающая при этом ЭДС
называется ЭДС
самоиндукции
Проявление
явления самоиндукции
Замыкание
цепи
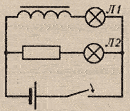 При
При
замыкании в эл.цепи нарастает ток, что
вызывает в катушке увеличение магнитного
потока, возникает вихревое эл.поле,
направленное против тока, т.е. в катушке
возникает ЭДС самоиндукции, препятствующая
нарастанию тока в цепи ( вихревое поле
тормозит электроны).
В результатеЛ1
загорается позже, чем
Л2.
Размыкание
цепи
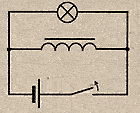 При
При
размыкании эл.цепи ток убывает, возникает
уменьшение м.потока в катушке, возникает
вихревое эл.поле, направленное как ток
( стремящееся сохранить прежнюю силу
тока) , т.е. в катушке возникает ЭДС
самоиндукции, поддерживающая ток в
цепи.
В результате Л при выключении ярко
вспыхивает.
Вывод
в
электротехнике явление самоиндукции
проявляется при замыкании цепи (эл.ток
нарастает постепенно) и при размыкании
цепи (эл.ток пропадает не сразу).

ИНДУКТИВНОСТЬ
От
чего зависит ЭДС самоиндукции?
Эл.ток
создает собственное магнитное поле .
Магнитный поток через контур пропорционален
индукции магнитного поля (Ф ~ B), индукция
пропорциональна силе тока в проводнике
(B
~ I), следовательно магнитный поток
пропорционален силе тока (Ф ~ I).
ЭДС
самоиндукции зависит от скорости
изменения силы тока в эл.цепи, от свойств
проводника
(размеров и формы) и от
относительной магнитной проницаемости
среды, в которой находится
проводник.
Физическая величина,
показывающая зависимость ЭДС самоиндукции
от размеров и формы проводника и от
среды, в которой находится проводник,
называется коэффициентом самоиндукции
или индуктивностью.
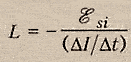 Индуктивность –
Индуктивность –
физ. величина, численно равная ЭДС
самоиндукции, возникающей в контуре
при изменении силы тока на 1Ампер за 1
секунду.
Также индуктивность можно
рассчитать по формуле:
![]() где
где
Ф – магнитный поток через контур, I – сила
тока в контуре.
Единицы
измерения индуктивности в
системе СИ:
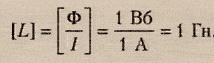
Индуктивность
катушки зависит от:
числа витков,
размеров и формы катушки и от относительной
магнитной проницаемости среды
(
возможен сердечник).
ЭДС
САМОИНДУКЦИИ
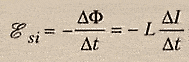
ЭДС
самоиндукции препятствует нарастанию
силы тока при включении цепи и убыванию
силы тока при размыкании цепи.
Для
характеристики намагниченности вещества
в магнитном поле используетсямагнитный
момент (Рм). Он
численно равен механическому моменту,
испытываемому веществом в магнитном
поле с индукцией в 1 Тл.
Магнитный
момент единицы объема вещества
характеризует его намагниченность
– I,
определяется по формуле:
I= Рм /V,
(2.4)
где V –
объем вещества.
Намагниченность
в системе СИ измеряется, как и напряженность,
в А/м,
величина векторная.
Магнитные
свойства веществ характеризуются объемной
магнитной восприимчивостью – cо , величина
безразмерная.
Если
какое-либо тело поместить в магнитное
поле с индукцией В0,
то происходит его намагничивание.
Вследствие этого тело создает свое
собственное магнитное поле с индукцией В‘,
которое взаимодействует с намагничивающим
полем.
В
этом случае вектор индукции в среде (В)будет
слагаться из векторов:
В
= В0 +
В‘(знак
вектора опущен), (2.5)
где В‘ –индукция
собственного магнитного поля
намагнитившегося вещества.
Индукция
собственного поля определяется магнитными
свойствами вещества, которые характеризуются
объемной магнитной восприимчивостью
– cо ,
справедливо выражение:В‘ = cо В0 (2.6)
Разделим
на m0 выражение
(2.6):
В‘/
mо= cо В0 /m0
Получим: Н‘ = cо Н0 , (2.7)
но Н‘ определяет
намагниченность вещества I,
т.е. Н‘ = I,
тогда из (2.7):
I
= cо Н0.
(2.8)
Таким
образом, если вещество находится во
внешнем магнитном поле с напряженностьюН0,
то внутри него индукция определяется
выражением:
В=В0 +
В‘ =
m0Н0 +m0Н‘ =
m0 (Н0 +
I) (2.9)
Последнее
выражение строго справедливо, когда
сердечник (вещество) находится полностью
во внешнем однородном магнитном поле
(замкнутый тор, бесконечно длинный
соленоид и т.д.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Электромагнитная индукция

Содержание
- Явление электромагнитной индукции
- Магнитный поток
- Закон электромагнитной индукции Фарадея
- Правило Ленца
- Самоиндукция
- Индуктивность
- Энергия магнитного поля
- Основные формулы раздела «Электромагнитная индукция»
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
Опыты Фарадея
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.
Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ), площади поверхности ( S ), пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):


Обозначение – ( Phi ), единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ):

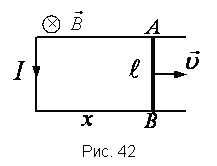
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec{B} ) ЭДС электромагнитной индукции равна:

где ( alpha ) – угол между векторами ( vec{B} ) и ( vec{v} ).
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_{is} ), возникающая в катушке с индуктивностью ( L ), по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec{B} ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ), создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитная индукция
3.2 (63.33%) 96 votes
| Магнитный поток | |
|---|---|
 |
|
| Размерность | ML2T−2I−1 |
| Единицы измерения | |
| СИ | Вб |
| СГС | Мкс |
| Примечания | |
| Скалярная величина |
| Классическая электродинамика |
|---|
 |
| Электричество · Магнетизм |
|
Электростатика Закон Кулона |
|
Магнитостатика Закон Био — Савара — Лапласа |
|
Электродинамика Векторный потенциал |
|
Электрическая цепь Закон Ома |
|
Ковариантная формулировка Тензор электромагнитного поля |
| См. также: Портал:Физика |
Магни́тный пото́к — поток вектора магнитной индукции 






Важнейшая физическая формула, в которую входит магнитный поток, — выражение для закона электромагнитной индукции Фарадея.
Определение магнитного потока[править | править код]

Разбиение поверхности на малые участки

Изменение вектора нормали к поверхности
Магнитным потоком через бесконечно малый элемент поверхности 
,
где 


.
Магнитным потоком через поверхность конечной площади называется интеграл от 
.
Направление вектора 
В случае однородного поля и плоской поверхности магнитный поток рассчитывается как 
Единицы измерения магнитного потока[править | править код]
В СИ единицей магнитного потока является вебер (Вб, размерность — Вб = В·с =
кг·м²·с-2·А-1), в системе СГС — максвелл (Мкс, 1 Вб = 108 Мкс).
Приборы для измерения потока[править | править код]
Прибор для измерения магнитных потоков называется флюксметром (от лат. fluxus — «течение» и греч. metron — мера) или веберметром.
Некоторые свойства магнитного потока[править | править код]
В соответствии с теоремой Гаусса для магнитной индукции, поток вектора магнитной индукции 

.
Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.
В соответствии с теоремой Стокса, магнитный поток 


,
поскольку имеет место связь 
Переменный во времени магнитный поток[править | править код]
По закону электромагнитной индукции Фарадея, если магнитный поток через некоторую поверхность изменяется со временем, то создаётся электродвижущая сила
в контуре, на который натянута данная поверхность. Если вдоль такого контура «проложен» электрический провод, то в нём возникнет индукционный ток. Изменение потока со временем может быть вызвано изменением вектора магнитной индукции 
Квантование магнитного потока[править | править код]
При рассмотрении ряда квантовых явлений, таких как эффект Ааронова — Бома или квантовый эффект Холла, используется квант магнитного потока:
,
где 

Опыты с неодносвязным сверхпроводником (например, со сверхпроводящим кольцом) показывают, что магнитный поток через кольцо всегда кратен половине кванта магнитного потока, откуда следует, что носители тока в сверхпроводнике являются парами связанных элементарных зарядов. Это прямое подтверждение теории БКШ, согласно которой сверхпроводимость обусловлена электронными парами (куперовскими парами):
Вб (в СИ);
Гаусс·см2 (в СГС),
— скорость света.
Экспериментально квантование магнитного потока было обнаружено в 1961 году.
См. также[править | править код]
- Уравнения Максвелла
- Электродвигатель постоянного тока
- Потокосцепление
- Индуктивность
В этой статье мы увидим, как найти магнитный поток через одиночный контур и проводник с током с числом витков.
Магнитный поток обозначается как произведение магнитного поля, в котором находится материал, и площади, через которую проходит магнитный поток, и определяется соотношением
Как найти плотность магнитного потока?
Наблюдения и советы этой статьи мы подготовили на основании опыта команды магнитный поток Плотность определяется как общее количество линий магнитного потока, пронизывающих единицу площади поверхности материала.
Магнитный поток можно рассчитать, найдя общий поток через проводящий материал и площадь материала, через которую магнитный поток проникает через поверхность.
Магнитный поток через поверхность равен

Следовательно плотность магнитного потока становится магнитным потоком через единицу площади поверхности.

Плотность магнитного потока представляет собой отношение магнитного потока к площади поперечного сечения, через которое проходят силовые линии.
Как найти размер магнитного потока?
Размерность — это математический способ выражения единиц измерения измеряемой величины в простой фигуре.
Размерность магнитного потока можно определить по формуле зная размерность магнитного поля и площадь через которые проходят силовые линии магнитного поля.
Магнитное поле определяется как сила, действующая на заряженную частицу в присутствии магнитного поля скоростью и магнитным потоком через частицу, и, соответственно, размерность магнитного поля основана на размерностях этих величин.
Мы можем математически представить единицу магнитного поля, записав все величины в размерном формате. Сила, действующая на заряды из-за комбинации электрического и магнитного полей, равна
F=qVB
Итак, магнитное поле, в котором находится материал, равно
F=qVB
Теперь нам нужно найти, как мы можем представить эти термины в форме математического измерения.
Мы знаем, что сила определяется как ускорение объекта, когда к нему приложена внешняя сила, в зависимости от массы объекта, поэтому согласно второму закону движения Ньютона мы можем написать F = ma
Единицей ускорения является метр на квадрат времени, поэтому мы можем записать размерность ускорения как M0L1T-2 а единицей массы является кг только соответственно мы можем записать размерность массы как M0L1T-2 что равно М1
Следовательно, размерность магнитная сила is
Ф=М*(М0L1T-2)
Ф = М1L1T-2
Точно так же размерность скорости равна M0L1T-2 так как единица скорости м/с, а заряда М0L1T-2 как I=dQ/dt
Теперь, используя это измерение, мы можем найти размеры магнитного поля как
Б=Ф/кV
Б=М1L1T-2
Магнитный поток является произведением магнитного поля и площади материала, поэтому
Ø=BACosΘ
Θ — безразмерная величина, поэтому ею можно пренебречь и рассматривать размерности остаточных величин.
Ø=[М1L0I-1T-2]*[М0L2T0]
Ø=М1L2-1T-2
Это размер магнитного потока, представленный математически.
Как найти магнитный поток через контур?
Основываясь на направлении магнитного потока, мы можем найти чистое магнитное поле через материал.
Магнитное поле, образованное колеблющимися зарядами в материале, можно рассчитать по всей площади контура и, таким образом, найти магнитный поток через эту площадь.
Рассмотрим круглую петлю радиуса «R» и ток I, протекающий через эту круглую петлю. Пусть начало круга будет «О». Заряд помещен в точку «P», которая находится на расстоянии «x» от начала координат на плоскости оси x. Между линией, соединяющей частицу с началом координат, и контуром с током образуется угол θ.

Пусть dl — малый элемент круглой петли, по которой течет ток I. Магнитное поле через малый элемент dl на круглой петле от заряда, помещенного в точку P, равно

Где мк0/4π – константа пропорциональности, равная 10-7Тм/А
дБ=мк0/4π*IdlrSinθ/r3
дБ=мк0/4π*IdlrSinθ/r2
Направление dB перпендикулярно dl и r, и перпендикулярное магнитное поле компенсируется.
дБ=мк0/4π*холост./об2
Здесь, р2=R2+x2 следовательно, мы можем написать то же уравнение, что и
дБ=мк0/4π*холост./R2+x2
Чистое магнитное поле обусловлено x-компонентой магнитного поля, то есть
дБх=дБКосθ
Поскольку,
Cosθ=R/√x2+R2
Подставляя рассчитанные значения в приведенное выше уравнение, мы получаем

дБх=мк0/4π*IdlR/(R2+x2)3/2
Это уравнение для магнитного поля через небольшой элемент dl на круглом контуре. Теперь найдем магнитное поле на всем контуре.
Bx=∫дБx= μ0/4π∫IdlR/(R2+x2)3/2
Bx= μ0/4π*lR/(R2+x2)3/2∫дл
Bx= μ0/4π*lR/(R2+x2)3/2L
Длина — это полная длина окружности круглой петли, L = 2πR.
Вставка этого в приведенное выше уравнение
Bx= μ0/4π*lR/(R2+x2)3/2*2πr
Отсюда получаем,
Bx= μ0IR2/2((R2+x2)3/2
Если поле находится в центре петли, то x=0 и уравнение примет вид
B0= μ0я/2р
Это магнитное поле через контур, тогда магнитный поток равен
ф=ВА
φ=μ0I/2R*πR2
φ=μ0πIR/2
Это магнитный поток через круговой контур с током, если поле находится в центре контура.
Как найти магнитный поток из магнитного поля?
Линии магнитного потока показывают величину магнитного поля, проникающего через материал.
Линии магнитного поля, падающие на поверхность поперечного сечения материала, образующие определенный угол θ с нормалью к поверхности, дают магнитный поток через эту область.
Предположим, вы поместили проводящий материал площадью A в магнитное поле B так, что линия магнитного поля составляет угол θ с нормальной плоскостью поверхности материала, как показано на рисунке ниже.

Магнитный поток через этот материал будет скалярным произведением линий магнитного поля и площади материала, через которую проходят эти линии.
φ=ВА
φ=BACosθ
Таким образом, мы можем найти магнитный поток через материал от магнитного поля.
Как найти магнитный поток через соленоид?
Чтобы узнать магнитный поток через соленоид, мы должны будем вычислить напряженность магнитного поля через каждую катушку соленоида.
Мы можем определить магнитное поле соленоида, применив закон Био-Савара, который дает связь между током и магнитным полем. Рассчитав магнитное поле, мы можем рассчитать поток через площадь материала.
Рассмотрим цилиндрический соленоид длины ‘2l’ и радиуса ‘a’. Пусть «О» будет точкой в центре соленоида, которая делит соленоид на две половины. Пусть небольшой заряд присутствует в точке P на расстоянии «r» от центральной точки «O». Рассмотрим небольшой сегмент соленоида длиной «dx» на расстоянии «x» от центрального сегмента соленоида. Направление магнитного поля показано на рисунке ниже.

Магнитный поток через этот небольшой сегмент «dx» составляет дБ. Пусть соленоид состоит из n витков на единицу длины соленоида и, следовательно, магнитное поле через этот элемент dx равно

Интегрируя это уравнение, мы получим магнитное поле, создаваемое во всем соленоиде.

В осевом поле r>>a и r>>l тогда
[(прием)2+a2]3/2≅ г3
Следовательно, мы можем записать приведенное выше уравнение как

Магнитный момент m=NIA
Где N — число витков проводника с током вокруг соленоида, I — ток, а A — площадь соленоида.
Здесь количество витков по длине соленоида равно
N=n*2l=2nl
Магнитное поле входит с одной поверхности соленоида и выходит с другого конца.
Площадь, через которую проходит магнитный поток, равна A=πa2
Следовательно, магнитный момент равен
m=n*2l*I*πa2
Поэтому уравнение для магнитного поля мы можем записать в терминах магнитного момента как
В=мк0/4π*2м/р3
Теперь магнитный поток через соленоид равен
ɸ=БА
ɸ=μ0/4π*2м/р3* πа2
ɸ=μ0ma2/ 2r3
Это магнитный поток через соленоид.
Как рассчитать магнитную потокосцепление?
Связь магнитного потока наблюдается в трансформаторе и генераторах, где объединяются магнитные потоки разных контуров.
Связанный магнитный поток дает большое количество магнитного потока через материал. Если магнитный поток через один виток провода равен ɸ =БА тогда катушка, состоящая из n витков, будет давать чистый магнитный поток ɸ =nBA и член λ=nɸ называется утечкой магнитного потока.
Как рассчитать плотность магнитного потока катушки?
Плотность магнитного потока представляет собой полный магнитный поток, проходящий через материал на единицу его площади, и определяется соотношением B=ɸ/A
Плотность магнитного потока можно рассчитать, найдя полный магнитный поток, проникающий через единицу площади материала, находящегося в области магнитного поля.
Какова плотность магнитного потока через квадратный лист длиной 11.3 см, помещенный в область магнитного поля, если магнитный поток через лист равен 1 Вб?
Данный: л = 11.3 см = 0.113 м
ɸ=1Вб
Площадь квадратного листа, через который проходят силовые линии магнитного поля, равна
А=я2= 0.1132= 0.013 м2
У нас есть,
B= ɸ/A
= 76.92Т
B=1T.м2/ 0.013m2= 76.92Т
Следовательно магнитный поток плотность через квадратный лист составляет 76.92 Тл.
Часто задаваемые вопросы
Каков магнитный поток через прямоугольную поверхность длиной 5 см и шириной 2.8 см, помещенную в однородное магнитное поле силой 0.5 Тл, если магнитное поле образует угол 600 с нормалью поверхности?
Данный: л = 5 см = 0.05 м
б = 2.8 см = 0.028 м
В = 0.5 т
Θ = 600
Площадь прямоугольной поверхности равна
А=л*б
=0.05*0.028=0.0014 м2
У нас есть
ɸ=BACosθ
=0.5T* 0.0014 м2
=0.5Т*0.0014м2* 1/2
= 3.5 * 10-4Tm2
Магнитный поток через прямоугольный лист = 3.5*10-4Tm2
Чему равен магнитный поток через круглую петлю с током радиусом 7 см, если сила тока в проводнике равна 2 мА?
Данный: г = 7 см = 0.07 м
I=2 мА
Формула для расчета магнитного потока через круглую петлю имеет вид
ɸ=μ0πIr/2
Вставка заданных значений в это уравнение
ɸ=(4π*10-7Тм/А*π*2*10-3А*0.07м)/2
=4π*π*0.07*10-10Tm2
= 2.76 * 10-10Tm2
Следовательно, магнитный поток через круговой контур с током равен =2.76*10-10Tm2
Поток вектора магнитной индукции
Магнитный поток Φ через площадку S (поток вектора магнитной индукции) – это скалярная величина:
Φ=BScos α=BnS=B→S→ с углом между n→ и B→, обозначаемым α, n→ является нормалью к площадке S.
Формула магнитного потока
Φ равняется количеству линий магнитной индукции, пересекающих площадку S, как показано на рисунке 1. Поток магнитной индукции по формуле принимает положительные и отрицательные значения. Его знак зависит от выбора положительного направления нормали к площадке S. Зачастую положительное направление нормали связано с направлением обхода контура током. За такое направление берут поступательное перемещение правого винта во время его вращения по току.
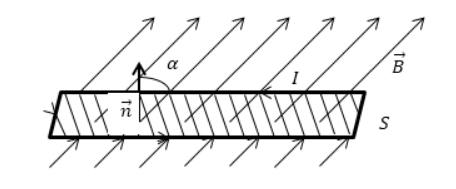
Рисунок 1
В чем измеряется магнитный поток
В случае неоднородности магнитного поля S не будет плоской, а плоскость может быть разбита на элементарные площадки dS, рассматриваемые в качестве плоских, поле которых также считается однородным. Определение магнитного потока dΦ производится через эту поверхность. Запись примет вид:
dΦ=BdScos α=B→dS→.
Нахождение полного потока через поверхность S:
Φ=∫SBdScos α=∫SB→dS→.
Основной единицей измерения магнитного потока в системе СИ считаются веберы (Вб). 1 Вб=1 Тл1 м2.
Связь магнитного потока и работы сил магнитного поля
Элементарная работа δA, совершаемая силами магнитного поля, выражается через элементарное изменение потока вектора магнитной индукции dΦ:
δA=IdΦ.
Если проводник с током совершает конечное перемещение, сила тока постоянна, то работа сил поля равняется:
A=IΦ2-Φ1 с Φ1, обозначаемым потоком через контур в начале перемещения, Φ2 является потоком через контур в конце перемещения.
Теорема Гаусса для магнитного поля
Значение суммарного магнитного потока через замкнутую поверхность S равняется нулю:
∮B→dS→=0.
Выражение ∮B→dS→=0 является справедливым для любых магнитных полей. Данное уравнение считается аналогом теоремы Остроградского-Гаусса в электростатике в вакууме:
∮E→dS→=qε0.
Запись ∮B→dS→=0 говорит о том, что источник магнитного поля – это не магнитные заряды, а электрические токи.
Дан бесконечно длинный прямой проводник с током I, недалеко от которого имеется квадратная рамка. По ней проходит ток с силой I’. Сторона рамки равна a. Она располагается в одной плоскости с проводом, как показано на рисунке 2. Значение расстояния от ближайшей стороны рамки до проводника равняется b. Найти работу магнитной силы при удалении рамки из поля. Считать токи постоянными.
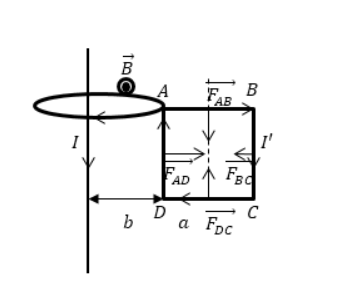
Рисунок 2
Решение
Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направляется на нас.
Следует учитывать нахождение рамки с током в неоднородном поле, что означает убывание магнитной индукции при удалении от провода.
За основу возьмем формулу магнитного потока и работы, которая их связывает:
A=I’Φ2-Φ1 (1.1), где I’ принимают за силу тока в рамке, Φ1 – за поток через квадратную рамку при расстоянии от ее стороны к проводу равняющимся b. Φ2=0. Это объясняется тем, что конечное положение рамки вне магнитного поля, как дано по условию. Отсюда следует, запись формулы (1.1) изменится:
A=-I’Φ1 (1.2).
Перейдем к нормали n→ и выберем ее направление к квадратному контуру относительно нас, используя правило правого винта. Отсюда следует, что для всех элементов поверхности, ограниченной при помощи контура квадратной рамки, угол между нормалью n→ и вектором B→ равняется π. Запись формулы потока через поверхность рамки на расстоянии х от провода примет вид:
dΦ=-BdS=-B·a·dx=-μ02πIldxx (1.3), значение индукции магнитного поля бесконечно длинного проводника с током силы I будет:
B=μ02πxIl (1.4).
Отсюда следует, что для нахождения всего потока из (1.3) потребуется:
Φ1=∫S-μ02πIldxx=-μ02πIl∫bb+adxx=-μ02πIl·lnb+ab (1.5).
Произведем подстановку формулы (1.5) в (1.2). Искомая работа равняется:
A=I’μ02πIl·lnb+ab.
Ответ: A=μ02πII’l·lnb+ab.
Найти силу, действующую на рамку, из предыдущего примера.
Решение
Для нахождения искомой силы, действующей на квадратную рамку с током в поле длинного провода, предположим, что под воздействием магнитной силы рамка смещается на незначительное расстояние dx. Это говорит о совершении силой работы, равной:
δA=Fdx (2.1).
Элементарная работа δA может быть выражена как:
δA=I’dΦ (2.2).
Произведем то же с силой, применяя формулы (2.1), (2.2). Получаем:
Fdx=I’dΦ→F=I’dΦdx (2.3).
Используем выражение, которое было получено в примере 1:
dΦ=-μ02πIldxx→dΦdx=-μ02πIlx (2.4).
Произведем подстановку dΦdx в (2.3). Имеем:
F=I’μ02πIlx (2.5).
Каждый элемент контура квадратной рамки находится под воздействием сил (силы Ампера). Отсюда следует, что на рамку действует 4 силы, причем на стороны AB и DC равные по модулю и противоположные по направлению. Выражение принимает вид:
FAB→+FDC→=0 (2.6), то есть их сумма равняется нулю. Тогда значение результирующей силы, приложенной к контуру, запишется:
F→=FAD→+FBC→ (2.6).
Используя правило левой руки, получаем направление этих сил вдоль одной прямой в противоположные стороны:
F=FAD-FBC (2.7).
Произведем поиск силы FAD, действующей на сторону AD, применив формулу (2.5), где x=b:
FAD=I’м02πIlb (2.8).
Значение FBC будет:
FBC=I’μ02πIlb+a (2.9).
Для нахождения искомой силы:
F=I’μ02πIlb-I’μ02πIlb+a=II’μ0l2π1b-1b+a.
Ответ: F=II’μ0l2π1b-1b+a. Магнитные силы выталкивают рамку с током до тех пор, пока она находится в первоначальной ориентации относительно поля провода.
![]()