Как найти максимально возможную скорость

Как найти максимальную скорость

Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Запишите уравнение зависимости скорости от времени.

Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.

Из полученных значений t выберите точки максимума функции. Точка максимума — это минус.

Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.

Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.

Движение тела, брошенного под углом к горизонту

H = m g l 1 m g . . + m v 2 2 m g . . = l 1 + v 2 2 g . .

h − l 1 = v 2 sin 2 . β 2 g . . = v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

l 1 = h − v 2 sin 2 . ( 90 − 2 α ) o 2 g . .

H = l 1 + v 2 2 g . . = h − ( g t ) 2 sin 2 . ( 90 − 2 α ) o 2 g . . + ( g t ) 2 2 g . .

H = h − g t 2 sin 2 . ( 90 − 2 α ) 2 . . + g t 2 2 . . = h − g t 2 2 . . ( sin 2 . ( 90 − 2 α ) o − 1 )

H = 1 , 4 − 10 · 0 , 4 2 2 . . ( sin 2 . ( 90 − 6 0 ) o − 1 )

H = 1 , 4 − 5 · 0 , 16 ( sin 2 . 3 0 o − 1 )

H = 1 , 4 − 0 , 8 ( ( 1 2 . . ) 2 − 1 ) = 1 , 4 − 0 , 8 ( 1 4 . . − 1 )

H = 1 , 4 + 0 , 6 = 2 ( м )

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF17980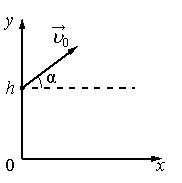

В момент t=0 мячик бросают с начальной скоростью v₀ под углом α к горизонту с балкона высотой h (см. рисунок).

Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).

К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.

1. Установить вид механического движения, исходя из условий задачи.
2. Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
3. Определить, как зависят эти величины от времени.
4. Установить соответствие между графиками и величинами.

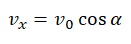
pазбирался: Алиса Никитина | обсудить разбор | оценить

Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?

Для каждой величины определите соответствующий характер изменения:

1. увеличивается
2. уменьшается
3. не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Как найти предельную скорость

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).

Количество просмотров этой статьи: 34 610.

Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.

Как найти максимальную скорость

Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Инструкция

Запишите уравнение зависимости скорости от времени.

Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.

Из полученных значений t выберите точки максимума функции. Точка максимума – это минус.

Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.

Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.

Видео по теме

Полезный совет

Функцию зависимости скорости от времени можно получить, дифференцируя функцию пройденного пути, либо интегрируя функцию ускорения. Во втором случае понадобятся еще начальные условия.

Источники:

• как находится максимальная скорость

Если вам дали уравнение для скорости, чтобы найти ее максимум (и, возможно, время, когда этот максимум наступил), навыки исчисления работают в вашу пользу. Однако, если ваша математика останавливается на алгебре, используйте калькулятор, чтобы найти ответ. Проблемы со скоростью включают в себя все, что движется, от бейсбола до ракеты.

Использование исчисления

1. Возьмите производную уравнения

Возьмем производную уравнения скорости по времени. Эта производная является уравнением для ускорения. Например, если уравнение для скорости v = 3sin (t), где t – время, уравнение для ускорения a = 3cos (t).

2. Решите уравнение для времени

Установите уравнение ускорения равным нулю и решите за время. Может существовать более одного решения, и это нормально. Помните, что ускорение – это наклон уравнения скорости, а производная – это наклон исходной линии. Когда наклон равен нулю, линия горизонтальна. Это происходит в экстремуме, то есть в максимуме или минимуме. В этом примере a = 3cos (t) = 0, когда t = pi ÷ 2 и t = (3pi) ÷ 2.

3. Тестовые решения

Протестируйте каждое решение, чтобы определить, является ли оно максимальным или минимальным. Выберите точку слева от экстремума, а другую точку справа. Если ускорение отрицательно слева и положительно справа, точка является минимальной скоростью. Если ускорение положительно влево и отрицательно вправо, точка является максимальной скоростью. В этом примере a = 3cos (t) является положительным как раз перед t = pi ÷ 2 и отрицательным сразу после, так что это максимум; однако (3pi) ÷ 2 является минимумом, потому что a = 3cos (t) является отрицательным непосредственно перед (3pi) ÷ 2 и положительным сразу после.

Если вы найдете более одного максимума, просто подключите время к исходному уравнению скорости, чтобы сравнить скорости в этих экстремумах. Какая бы ни была скорость, это абсолютный максимум.

Использование калькулятора

1. Введите уравнение скорости

Нажмите кнопку «Y =» и введите уравнение скорости.

2. Функция графика

График функции. Посмотрите на график, чтобы оценить, где находится максимум.

3. Угадай позицию максимума

Нажмите «2-й», «Calc», «Макс.» Используйте кнопки со стрелками для перемещения по графику слева от максимума и нажмите ввод. Стрелка справа от максимума и снова нажмите «Enter». Стрелка между этими точками и введите ваше лучшее предположение о позиции максимума.

4. Записать значения

Запишите время (значение x) и скорость (значение y) более точного решения максимума в калькуляторе.

Если исходное уравнение скорости включает синус или косинус, следите за временем, которое калькулятор сообщает, используя много десятичных знаков. Ваш реальный ответ на время может быть связан с пи. Разделите десятичное время на пи. Если частное близко к дроби, это, вероятно, та дробь, округленная калькулятором до десятичной дроби. Вернитесь к графику, нажмите «Trace» и введите точную дробь – включая кнопку «пи» на вашем калькуляторе. Если вы получите тот же максимум, который изначально нашел калькулятор, тогда этот максимум действительно будет получен при дробном кратном пи.

Максимальную скорость
V_amax
, развивающую проектируемым автомобилем
на горизонтальной дороге, определим
как по тяговой характеристике, так и по
динамической. Допускается небольшое
несовпадение максимальных скоростей,
определенным по двум разным характеристикам;
большое несовпадение (более 4%) говорит
о погрешности в ходе проведения тягового
расчета.

Используя данные
таблицы 15, на графике тяговой характеристики
(пункт 1.7.1) строим кривую, соответствующую
суммарной силе сопротивления движения
автомобиля (сила сопротивления дороги
F_ψ
плюс сила сопротивления воздуха F_B);
точка пересечения данной кривой (F_ψ
+ F_B)
и кривой, соответствующей полной окружной
силе F_K0
на высшей передаче, позволяет определить
максимальную скорость V_a
max на дороге без
уклона: опустив линию на горизонтальную
ось (I = 0), по которой
отложена скорость V_a
автомобиля. Если кривые F_ψ
+ F_B и
F_K0
на высшей передаче не пересеклись, то
V_amax
соответствует максимальной скорости
по кривой F_K0
на высшей передаче (данная V_amax
называется максимальной кинематической
скоростью, определяемой передаточными
числами трансмиссии и максимальной
частотой вращения коленчатого вала
двигателя); запас окружной силы F_K0
в данном случае (кривые F_ψ
+ F_B и
F_K0
не пересеклись) может быть использован
для достижения V_amax
при движении автомобиля на подъеме.

Аналогично определяется
V_amax
по динамической характеристике: используя
данные таблицы 15 на графике динамической
характеристики (пункт 1.7.2) строится для
высшей передачи кривая ψ = f_V
(i=0) – безразмерного
фактора сопротивления движению
автомобиля. Точка пересечения кривой
ψ и кривой динамического фактора D
(движущего фактора) определяет V_amax,
если кривее не пересеклись, то V_amax
(кинематическая) соответствует максимуму
скорости по кривой D на
высшей передаче.

Максимально возможные
скорости движения автомобиля, определенные
по тяговой и динамической характеристикам,
должны быть равны между собой, и
соответствовать той максимальной
скорости V_a
max, которая была
определена в техническом задании на
проектирование (см. пункт 1.2). Результаты
расчетов заносим в таблицу 16.

Таблица 16 – Максимальная
скорость V_аmax
автомобиля

Условия определения	Vаmax , км/ч	Погрешность
Тяговая характеристика	92	0%
Динамическая характеристика	92	0%
Мощносной баланс	92	0%

При движении автомобиля
на подъем (уклон дороги i)
максимальную скорость, по динамической
характеристике, в данных дорожных
условиях определяют следующим образом:
величину уклона i складывают
с коэффициентом сопротивления качению
колес f_V
и ищут точку пересечения кривой i+f_V
с кривой D – полученная
точка позволяет определить: какую
максимальную скорость развивает
проектируемый автомобиль и на какой
передаче в КПП.

Определяется максимальная
скорость автомобиля при преодолении
уклона в 5% и максимального уклона по
таблице 15. Найденные значения скоростей
не должны быть меньше значений, приведенных
в таблице 17.

Таблица 17 – Максимальные
скорости автомобилей

Максимальная скорость, км/ч	Грузовые автомобили
полноприводные	неполноприводные	автопоезда
На горизонтальной дороге, i = 0	80	90	80
На подъеме в 5%, i = 0,05	40	45	25
На максимальном подъеме i max	5	12	8

Максимальная скорость
при преодолении уклона в 5%

V_аmax
= 40км/ч

Максимальная скорость
при преодолении максимального уклона

V_аmax
=7 км/ч

что соответствует
рекомендациям.

1.8
Путь и время разгона автомобиля

Считаем, что разгон
начинается с минимальной устойчивой
скорости

V_amin
(соответствующей n_emin
– минимальной устойчивой частоте
вращения коленчатого вала ДВС) на
передаче, используемой для трогания
автомобиля с места. Разгон осуществляется
при полной подаче топлива т.е. двигатель
работает по ВСХ (имеем наибольшую
интенсивность разгона).

Ускорение, как известно,
можно определить по формуле:

а_x

(45)

где dV_a
– приращение скорости за промежуток
времени dt.

Тогда

dt

(46)

откуда время разгона

t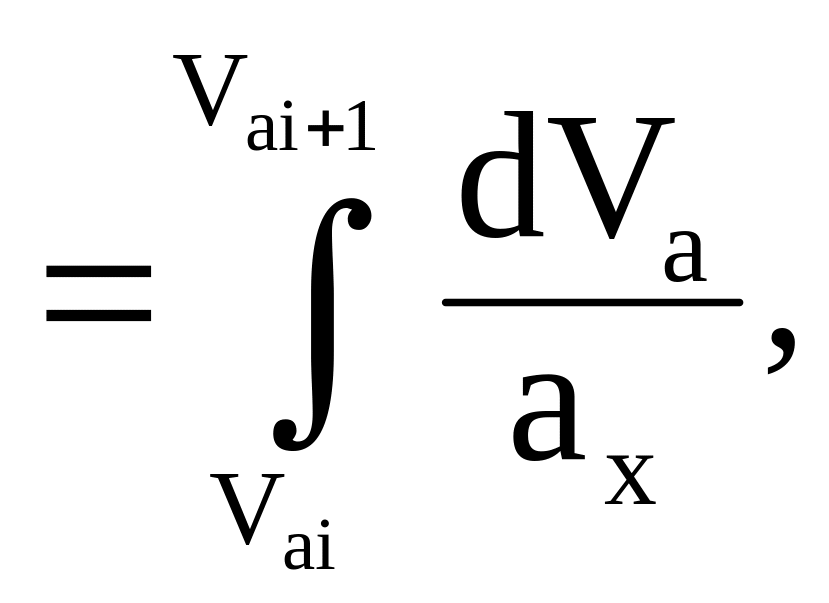

(47)

Считаем, что в небольшом
интервале скоростей ΔV_ai=V_ai+1-V_ai
движение является равноускоренным
со средним ускорением а_mi
, тогда время движения в данном
интервале, между двумя точками, определим
по формуле:

(48)

где ∆V_ai
– изменение скорости между двумя
точками, м/с;

Дальнейшие результаты
расчётов сведены в таблицу 18.

а_mi
– среднее ускорение между двумя точками

(49)

Дальнейшие результаты
расчётов сведены в таблицу

Путь, проходимый за
время движения между двумя точками:

∆S=V_mi·∆t_i
(50)

где V_mi
– средняя скорость в рассматриваемом
интервале

(51)

Дальнейшие результаты
расчётов сведены в таблицу 18.

Потери скорости за
время переключения ∆V_n
определим по формуле:

,
м/с (52)

где t_n=1c
– время переключения передач

δ_i+1
– коэффициент учёта вращающихся масс

Путь, проходимый
автомобилем, за время переключения tn
c К-ой на К+1 передачу:

∆S_n=(V_кmax–
0,5∆V_nк-(к+1))·t_n,
м (53)

где V_кmax
– скорость, соответствующая моменту
переключения

Таблица 18 – Разгон
автомобиля

Разгон автомобиля на
первой передаче

Пара- метр	Раз-мер- ность	№ точки
1	2	3	4	5	6	7	8
Va	км/ч	3,0	3,86	4,71	5,57	6,43	7,28	8,14	9
Va	м/с	0,83	1,07	1,31	1,55	1,79	2,02	2,26	2,5
∆Vi	м/с	–	0,24	0,24	0,24	0,24	0,23	0,24	0,24
ax	м/с2	0,748	0,816	0,869	0,899	0,908	0,899	0,866	0,818
ami	м/с2	–	0,872	0,843	0,884	0,904	0,904	0,883	0,842
∆ti	с	–	0,31	0,29	0,27	0,27	0,25	0,27	0,29
t	с	–	0,31	0,6	0,87	1,14	1,39	1,66	1,95
Vmi	м/с	–	0,95	1,19	1,43	1,67	1,91	2,14	2,38
∆Si	м	–	0,3	0,35	0,39	0,45	0,48	0,58	0,69
S	м	–	0,3	0,65	1,04	1,49	1,97	2,55	3,24

Разгон автомобиля на
второй передаче

Параметр	Размерность	№ точки
9	10	11	12	13	14
Va	км/ч	8,68	9,67	11,15	12,64	14,13	15,61
Va	м/с	2,41	2,69	3,1	3,51	3,93	4,34
∆Vi	м/с	(0,09)	0,28	0,41	0,41	0,42	0,41
ax	м/с2	0,895	0,923	0,936	0,925	0,892	0,836
ami	м/с2	–	0,91	0,93	0,93	0,91	0,87
∆ti	с	(1,5)	0,31	0,44	0,44	0,46	0,47
t	с	3,45	3,76	4,2	4,64	5,1	5,57
Vmi	м/с	–	2,55	2,9	3,31	3,72	4,14
∆Si	м	3,68	0,79	1,28	1,46	1,71	1,95
S	м	6,92	7,71	8,99	10,45	12,16	14,11

Разгон автомобиля на
третьей передаче

Параметр	Размерность	№ точки
15	16	17	18	19
Va	км/ч	15,23	16,26	18,43	20,6	22,76
Va	м/с	4,23	4,52	5,12	5,72	6,32
∆Vi	м/с	(0,11)	0,29	0,6	0,6	0,6
ax	м/с2	0,785	0,796	0,788	0,759	0,71
ami	м/с2	–	0,791	0,792	0,77	0,735
∆ti	с	(1,5)	0,37	0,76	0,78	0,82
t	с	7,07	0,44	8,2	8,98	9,8
Vmi	м/с	–	4,38	4,82	5,42	6,02
∆Si	м	(6,43)	1,62	3,66	4,23	4,94
S	м	20,54	22,16	25,82	30,05	34,99

Разгон автомобиля на
четвёртой передаче

Параметр	Размерность	№ точки
20	21	22	23	24
Va	км/ч	22,31	22,42	25,41	28,4	31,39
Va	м/с	6,193	6,23	7,06	7,89	8,72
∆Vi	м/с	(0,123)	0,037	0,83	0,83	0,83
ax	м/с2	0,63	0,634	0,618	0,593	0,552
ami	м/с2	–	0,632	0,626	0,606	0,573
∆ti	с	(1,5)	0,06	1,33	1,37	1,45
t	с	11,3	11,36	12,69	14,06	15,51
Vmi	м/с	–	6,21	6,65	7,48	8,31
∆Si	м	(9,39)	0,37	8,85	10,25	12,05
S	м	44,38	44,75	53,6	63,85	75,9

Разгон автомобиля на
пятой передаче

Параметр	Размерность	№ точки
25	26	27	28
Va	км/ч	30,91	34,24	38,27	42,3
Va	м/с	8,586	9,51	10,63	11,75
∆Vi	м/с	(0,134)	0,924	1,12	1,12
ax	м/с2	0,465	0,47	0,443	0,408
ami	м/с2	–	0,47	0,46	0,43
∆ti	с	(1,5)	1,97	2,43	2,6
t	с	17,01	18,98	21,41	24,01
Vmi	м/с	–	9,05	10,07	11,19
∆Si	м	(12,98)	17,83	24,47	29,09
S	м	88,88	106,71	131,18	160,27

Разгон автомобиля на
шестой передаче

Параметр	Размерность	№ точки
29	30	31	32
Va	км/ч	41,79	45,12	50,43	55,72
Va	м/с	11,61	12,53	14,01	15,48
∆Vi	м/с	(0,142)	0,92	1,48	1,47
ax	м/с2	0,34	0,333	0,313	0,285
ami	м/с2	–	0,336	0,323	0,299
∆ti	с	(1,5)	2,74	4,58	4,92
t	с	25,51	28,25	32,83	37,75
Vmi	м/с	–	12,07	13,27	14,75
∆Si	м	(17,52)	33,07	60,78	72,57
S	м	177,79	210,86	271,64	344,21

Разгон автомобиля на
седьмой передаче

Параметр	Размерность	№ точки
33	34	35	36
Va	км/ч	55,18	58,17	65,01	71,86
Va	м/с	15,33	16,16	18,06	19,96
∆Vi	м/с	(0,151)	0,83	1,9	1,9
ax	м/с2	0,225	0,225	0,204	0,174
ami	м/с2	–	0,225	0,215	0,189
∆ti	с	(1,5)	3,69	8,84	10,05
t	с	39,25	42,94	51,78	61,83
Vmi	м/с	–	15,75	17,11	19,01
∆Si	м	(23,11)	58,12	151,25	191,05
S	м	367,32	425,44	576,69	767,74

Разгон автомобиля на
восьмой передаче

Параметр	Размерность	№ точки
37	38	39	40
Va	км/ч	71,26	74,28	83,02	92
Va	м/с	19,795	20,63	23,06	25,56
∆Vi	м/с	(0,165)	0,84	2,43	2,5
ax	м/с2	0,125	0,12	0,097	0,064
ami	м/с2	–	0,123	0,109	0,081
∆ti	с	(1,5)	6,83	22,29	30,86
t	с	63,33	70,16	92,45	123,31
Vmi	м/с	–	20,21	21,85	24,31
∆Si	м	29,82	138,03	487,04	750,21
S	м	797,56	935,59	1422,63	2172,84

По данным таблицы 18
строим графики пути и времени разгона
автомобиля, по которым определяем:

1) время разгона до
скорости 60 км/ч

t₆₀=45с

2) путь проходимый АТС
до достижения V_amax
– Sv

Sv=2172,84м

3) время разгона с места
на пути 1000м – t₁₀₀₀

t₁₀₀₀=72c

1.9
Мощностной баланс

Расчет мощностного
баланса, проведем на высшей передаче.

Уравнение мощностного
баланса имеет вид:

N_K=N_B+
N_+
N_ia
(54)

где N_К
– мощность, подведенная к ведущим
колесам:

N_K
= N_е 
_Т, кВт
(55)

где Ne –
эффективная мощность двигателя (таб.2),
кВт;

η_Т – КПД
трансмиссии;

Nк=73,34,38·0,82=60,14
кВт

Дальнейшие результаты
расчётов сведены в таблицу 19

N_
– мощность, затрачиваемая на преодоление
сопротивления дороги;

N_ψ=F_ψ·Va,
кВт (56)

где F_ψ
– сила сопротивления дороги (таблица
15), Н;

Va –
скорость автомобиля (таблица 15),м/с;

N_ψ=2900·8,5=24650Вт=24,65кВт

Дальнейшие результаты
расчётов сведены в таблицу 19

N_В
– мощность, затрачиваемая на преодоление
сопротивления воздуха:

N_В =
F_B
 V_a,
кВт (57)

где F_B
– сила сопротивления воздуха (таблица
15),Н;

N_В=51,8·5,047=261Вт=0,261кВт

Дальнейшие результаты
расчётов сведены в таблицу 12

N_ia
– мощность, которая может быть затрачена
на разгон автомобиля.

Таблица 19 – Мощносной
баланс автомобиля на высшей передаче

ne, об/мин	Va, км/ч	Va, м/с	Ne, кВт	NК, кВт	NВ, кВт	NК – NВ, кВт	N, кВт
700	30,59	8,5	73,34	60,14	1,95	58,19	24,65
900	39,32	10,92	102,57	84,11	4,13	79,98	32,54
1100	48,06	13,35	133,01	109,07	7,53	101,54	40,72
1300	56,8	15,78	162,73	133,44	12,43	121,01	49,71
1500	65,54	18,21	190,05	155,84	19,1	136,74	59,36
1700	74,28	20,63	212,82	174,51	27,79	146,72	69,52
1900	83,02	23,06	229,83	188,46	38,81	149,65	80,94
2100	92	25,56	239,66	196,52	52,91	143,61	94,06

По данным таблицы 19
строим график мощностного баланса
автомобиля на высшей передаче и определяем
V_аmax
– точка пересечения кривых N_ψ
и N_к-N_в

V_аmax=92
км/ч

1.10
Топливная экономичность

Построим топливную
характеристику установившегося движения
– зависимость путевого расхода топлива
Q_s от скорости
движения V_а и
определим эксплуатационный расход
топлива проектируемого автомобиля,
(все расчёты будем вести на высшей
передаче).

Путевой расход будет
определяться по зависимости:

,
л/100 км (58)

где g_eN
– средний удельный эффективный расход
топлива при максимальной мощности
двигателя, г/кВтч;

g_eN
= (1,05 … 1,1) g_emin
(59)

где g_emin
– минимальный удельный расход топлива,
г/кВтч;

g_emin
= 180 … 240 г/кВтч;

g_eN
=1,05·180=189 г/кВтч

K_И
– коэффициент использования мощности
двигателя;

K_И =
1, 2 + 0,14 · U – 1.8 · U²
+ 1,46 · U³
(60)

(61)

Дальнейшие результаты
расчётов сведены в таблицу 20

K_И =
1,2 + 0,14 · 0,442 – 1,8 · 0,442 ² + 1,46 · 0,442 ³=
1,036

Дальнейшие результаты
расчётов сведены в таблицу 20

K_Е
– коэффициент использования частоты
вращения коленчатого вала двигателя;

K_Е
= 1,25 – 0,99 · Е + 0,98 · Е² – 0,24 · Е³
(62)

(63)

где n_e,
V_a –
текущая соответственно частота вращения
коленчатого вала и скорость АТС;

n_N,
V_aN –
соответственно частота вращения
коленчатого вала и скорость автомобиля
при максимальной мощности двигателя;

Дальнейшие результаты
расчётов сведены в таблицу 20

K_Е
= 1,25 – 0,99·0,333 + 0,98·0,333² –
0,24·0,333³=1,018

Дальнейшие результаты
расчётов сведены в таблицу 20

N_
и N_В – см. таблицу
19

_T
– плотность топлива, кг/м³ : для
дизельного топлива;

_T=835
кг/м³

V_a,
км/ч – см. таблицу 15

л/100 км

Дальнейшие результаты
расчётов заносим в таблицу 20 и строим
топливную характеристику автомобиля,
по которой определяем:

1) расход топлива при
скорости 80км/ч и 60км/ч

расход топлива при
скорости 80км/ч равен 35,5 л/100 км

расход топлива при
скорости 60км/ч равен 30,2 л/100 км

2) эксплуатационный
расход (э.р.) топлива

э.р. = 1,1·Q_P
(64)

где Q_P
– путевой расход при расчетной скорости
V_P

;
(65)

км/ч;

Q_P=32,4
л/100 км;

э.р. = 1,1·32,4=35,64 л/100 км;

3) контрольный расход
топлива Q_к –
минимальный расход по топливной
характеристике

Q_к=28
л/100 км

Таблица 20 – Топливная
экономичность автомобиля на высшей
передаче

Va, км/ч	NК, кВт	N + NВ, кВт	U	E	KИ	KЕ	QS , л/100кмч
30,59	60,14	26,6	0,442	0,333	1,036	1,018	25,32
39,32	84,11	36,67	0,436	0,427	1,04	0,987	26,43
48,06	109,07	48,25	0,442	0,522	1,036	0,966	27,74
56,8	133,44	62,14	0,466	0,617	1,022	0,956	29,5
65,54	155,84	78,46	0,504	0,712	1,001	0,955	31,59
74,28	174,51	97,31	0,558	0,807	0,972	0,963	33,85
83,02	188,46	119,75	0,635	0,902	0,937	0,978	36,48
92	196,52	146,97	0,748	1	0,909	1	40,08

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Была ли эта статья полезной?