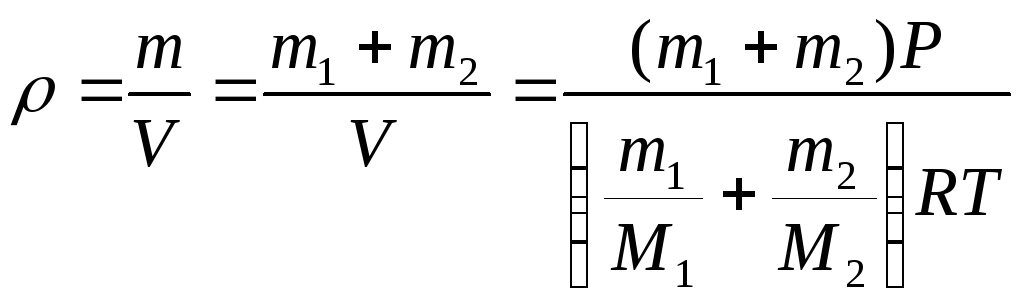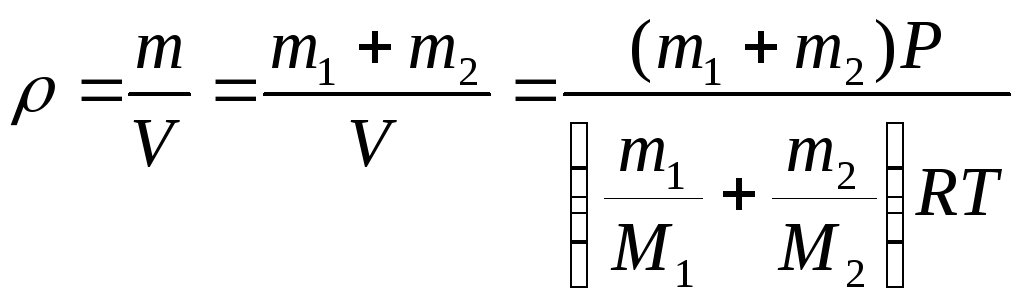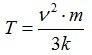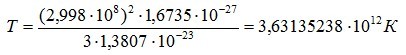Как найти максимально возможную температуру

2018-04-16   

Найти максимально возможную температуру идеального газа в каждом из нижеследующих процессов:

а) $p = p_{0} – alpha V^{2}$; б) $p = p_{0} e^{ – beta V}$,

где $p_{0}, alpha$ и $beta$ — положительные постоянные, $V$ — объем одного моля газа.

Решение:

(a) $p = p_{0} – alpha V^{2} = p_{0} – alpha left ( frac{RT}{p} right )^{2}$ (так как, $V = RT/p$ для одного моля газа)

Таким образом, $T = frac{1}{R sqrt{ alpha} } p sqrt{p_{0} – p } = frac{1}{R sqrt{ alpha } } sqrt{ p_{0}p^{2} – p^{3} }$ (1)

Для $T_{max}, frac{d(p_{0}p^{2} – p^{3} ) }{dp}$ должно быть равным нулю

что дает, $p = frac{2}{3} p_{0}$ (2)

Следовательно, $T_{max} = frac{1}{R sqrt{ alpha} } frac{2}{3} p_{0} sqrt{p_{0} – frac{2}{3}p_{0} } = frac{2}{3} left ( frac{p_{0} }{R} right ) sqrt{ frac{p_{0} }{3 alpha} }$

(б) $p = p_{0} e^{ – beta V} = p_{0}e^{ – beta RT/p }$

$frac{ beta RT}{p} = ln frac{p_{0} }{p}$, $T = frac{p}{ beta R} ln frac{p_{0} }{p}$ (1)

Для $T_{max}$ условие равно $frac{dT}{dp} = 0$, что дает

$p = frac{p_{0} }{e}$

Следовательно, используя это значение $p$ в уравнении (1), получаем

$T_{max} = frac{p_{0} }{e beta R}$

Если вы изымете всю энергию из чего-нибудь, вы достигнете абсолютного ноля, самой низкой температуры во Вселенной (ну или почти абсолютного ноля, чем больше, тем лучше). Но какова самая высокая температура? «Ничто не пропадает. Все трансформируется», — говорил Майкл Энде. Думаю, очень многие задавались вопросом касательно самой высокой возможной температуры и не находили ответа. Если есть абсолютный ноль, должен быть и абсолютный… что?

Возьмем классический эксперимент: капнем пищевым красителем в воду с разной температурой. Что мы увидим? Чем выше температура воды, тем быстрее пищевой краситель распределяется по всему объему воды.

Почему так происходит? Потому что температура молекул непосредственно связана с кинетическим движением — и скоростью — участвующих частиц. Это значит, что в воде погорячее отдельные молекулы воды движутся с большей скоростью, и это значит, что частицы пищевого красителя быстрее будут транспортироваться в горячей воде, нежели в холодной.

Если бы вы остановили все это движение — довели все до идеального состояния отдыха (даже преодолели законы квантовой физики ради этого) — тогда вы достигли бы абсолютного ноля: самой холодной возможной термодинамической температуры.

Но как насчет движения в другую сторону? Если вы будете нагреваться систему частиц, очевидно, они будут двигаться все быстрее и быстрее. Но есть ли предел тому, как сильно вы сможете их нагреть, нет ли какой-нибудь катастрофы, которая помешает вам нагревать их после определенного предела?

При температуре в тысячи градусов тепло, которое вы передаете молекулам, начнет разрушать сами связи, которые удерживают молекулы вместе, и если вы будете продолжать увеличивать температуру, электроны начнут отделяться от самих атомов. Вы получите ионизированную плазму, состоящую из электронов и атомных ядер, в которой не будет нейтральных атомов вовсе.

Это еще в рамках разумного: у нас имеются отдельные частицы — электроны и положительные ионы — которые будут прыгать при высоких температурах, подчиняясь привычным законам физики. Вы можете повышать температуру и ждать продолжения.

При дальнейшем повышении температуры отдельные сущности, которые известны вам под «частицами», начинают разбиваться. Примерно при 8 миллиардах градусов (8 x 10^9), вы начнете спонтанно производить пары материи-антиматерии — электроны и позитроны — из сырой энергии столкновений частиц.

При 20 миллиардах градусов атомные ядра начнут спонтанно разрываться на отдельные протоны и нейтроны.

При 2 триллионах градусов протоны и нейтроны перестанут существовать, и появятся фундаментальные частицы, их составляющие — кварки и глюоны, их связи при таких высоких энергиях уже не выдерживают.

Примерно при 2 квадриллионах градусов вы начнете производить все известные частицы и античастицы в огромных количествах. Но и это не является верхним пределом. В этих пределах происходит много интересного. Видите ли, это та энергия, при которой вы можете произвести бозон Хиггса, а значит и та энергия, при которой вы можете восстановить одну из фундаментальных симметрий во Вселенной: симметрию, которая дает частице массу покоя.

Другими словами, как только вы нагреете систему до этого энергетического предела, вы обнаружите, что все ваши частицы теперь безмассовые и летают со скоростью света. То, что было для вас смесью материи, антиматерии и радиации, станет чистой радиацией (будет вести себя как она), оставаясь при этом материей, антиматерией или ни тем ни другим.

И это еще не конец. Вы можете нагревать систему до еще более высоких температур, и хотя быстрее двигаться в ней все не будет, оно будет преисполняться энергией, подобно тому как являются формой света радиоволны, микроволны, видимый свет и рентгеновские лучи (и все движутся со скоростью света), даже если обладают совершенно разной энергией.

Возможно, рождаются пока неизвестные нам частицы или проявляются новые законы (или симметрии) природы. Вы могли бы подумать, что достаточно просто нагревать и нагревать все до бесконечных энергией, чтобы это узнать, но не тут-то было. Есть три причины, почему это невозможно.

1. Во всей наблюдаемой Вселенной имеется только конечное количество энергии. Возьмите все, что существует в нашем пространстве-времени: всю материю, антиматерию, радиацию, нейтрино, темную материю, даже энергию, присущую самому космосу. Существует порядка 10^80 частиц обычной материи, порядка 10^89 нейтрино и антинейтрино, чуть больше фотонов, плюс вся энергия темной материи и темной энергии, распространенные в радиусе 46 миллиардов световых лет наблюдаемой Вселенной, центр которой находится в нашей позиции.

Но даже если бы вы превратили все это в чистую энергию (с помощью E = mc^2), и даже если бы вы использовали всю эту энергию для нагрева своей системы, вы не получили бы бесконечное количество энергии. Если заключить все это в единую систему, вы получите гигантское количество энергии, равное примерно температуре в 10^103 градуса, но и это еще не бесконечность. Получается, верхний предел остается. Но прежде чем вы до него доберетесь, у вас будет еще одно препятствие.

1. Если вы заключите слишком большое количество энергии в любом ограниченном регионе пространства, вы создадите черную дыру. Обычно вы думаете о черных дырах как об огромных, массивных, плотных объектах, способных проглотить орды планет: не заморачиваясь, небрежно, легко.

Дело в том, что если вы придадите отдельной квантовой частице достаточно энергии — даже если она будет безмассовой частицей, движущейся со скоростью света — она превратится в черную дыру. Есть масштаб, на котором просто иметь что-то с определенным количеством энергии, будет означать, что частицы не будут взаимодействовать как обычно, и если вы получите частицы с такой энергией, эквивалентной 22 микрограммам по формуле E = mc^2, вы сможете набрать энергию в 10^19 ГэВ, прежде чем ваша система откажется становиться горячее. У вас начнут появляться черные дыры, которые будут моментально распадаться до состояния низкоэнергетической термальной радиации. Получается, этот энергетический предел — планковский предел — является верхним для Вселенной и соответствует температуре в 10^32 кельвина.

Это намного ниже предыдущего предела, поскольку не только сама Вселенная конечна, но и черные дыры выступают сдерживающим фактором. Впрочем, это не все: есть ограничение и пуще.

1. При определенной высокой температуре вы высвободите потенциал, который привел нашу Вселенную к космической инфляции, расширению. Еще во времена Большого Взрыва Вселенная пребывала в состоянии экспоненциального расширения, когда пространство раскладывалось, как космический воздушный шар, только в геометрической прогрессии. Все частицы, античастицы и излучение быстро разделялись с другими квантовыми частицами материи и энергии, и когда инфляция завершилась, настал Большой Взрыв.

Если вам удастся достичь температур, необходимых для возвращения состояния инфляции, вы нажмете кнопку перезапуска Вселенной и вызовете инфляцию, затем Большой Взрыв и так далее, все по новой. Если до вас пока не дошло, учтите: если вы доберетесь до этой температуры и вызовете нужный эффект, вы никак не выживете. Теоретически это может возникнуть при температурах порядка 10^28 – 10^29 кельвинов, это пока только теория.

Получается, вы можете легко набрать очень высокие температуры. Хотя физические явления, к которым вы привыкли, будут отличаться в деталях, вы по-прежнему сможете набирать температуры выше и выше, но только до точки, после которой все, что вам дорого, будет уничтожено. Но не бойтесь Большого адронного коллайдера. Даже на самом мощном ускорителе частиц на Земле мы достигаем энергий, которые в 100 миллиардов раз ниже, чем необходимые для вселенского апокалипсиса.

План решения задач на газовые законы

1. Если
   в задаче рассматривается одно состояние
   газа и требуется найти какой-либо
   параметр этого состояния, нужно
   воспользоваться уравнением Менделеева
   – Клапейрона.

2. Если
   значения давления и объема явно не
   заданы, их нужно выразить через заданные
   величины, подставить в записанное
   уравнение и, решив его, найти неизвестный
   параметр.

3. В
   том случае, когда в задаче рассматриваются
   два различных состояния газа, нужно
   установить, изменяется ли масса газа
   при переходе из одного состояния в
   другое. Если масса остается постоянной,
   можно применить уравнение Клапейрона.
   Если же при постоянной массе в данном
   процессе не изменяется какой-либо из
   параметров ( р,V или Т), применяются
   уравнение соответствующего закона
   (Гей-Люссака, Шарля или Бойля-Мариотта).

4. Если
   в двух состояниях масса газа разная,
   то для каждого состояния записывают
   уравнение Менделеева-Клапейрона. Затем
   систему уравнений решают относительно
   искомой величины.

Примеры решения задач

Пример 3.1. Определите
число молекул воды в бутылке вместимостью
0,33л. Молярная масса воды М=18∙10^-3
кг/моль, плотность воды ρ=1г/см³.

Дано:
V=0,33л=0,33∙10^-3
м³;
М=18∙10^-3
кг/моль; ρ=1г/см³=
1∙10³
кг/м³;

Найти:
N.

Решение:
Масса
воды, занимающей объём V,

m=ρV,
(1)

где
ρ – плотность воды.

Масса
молекулы

,
(2)

где
М – молярная масса; N_A=6,02∙
10²³моль^-1
–
постоянная Авогадро.

Число
молекул в бутылке

(3)

Подставляя
в выражение (3) формулы (1) и (2), получим
искомое число молекул:

.

Ответ:
N=1,1∙10²⁵.

Пример 3.1. Узкая
цилиндрическая трубка, закрытая с одного
конца, содержит воздух, отделённый от
наружного воздуха столбиком ртути.
Когда трубка обращена закрытым концом
кверху, воздух внутри неё занимает длину
ℓ, когда же трубка обращена кверху
открытым концом, то воздух внутри неё
занимает длину ℓ’ < ℓ. Длина ртутного
столбика h мм. Определить атмосферное
давление.

Дано:
ℓ; ℓ’ < ℓ; h.

Найти:
Р.

Решение:
В данном процессе
изменяются давление и объём воздуха, а
температура остаётся постоянной.
Следовательно, если начальные параметры
воздуха обозначить Р₁
и V₁,
а конечные как Р₂
и V₂ получаем
следующее соотношение:

Р₁V₁
= Р₂V₂

Когда
трубка обращена закрытым концом кверху,
воздух в ней находится под давлением
Р₁=
Р_атм
– h ( здесь и далее измеряем в мм.рт. ст.).
Если же трубку перевернуть, давление
воздуха в ней будет равно Р₂
= Р_атм
+ h .

Учитывая,
что V₁ =
Sℓ₁,
V₂ =
Sℓ₂,
где S – площадь сечения трубки, получаем:

(Р_атм
– h) Sℓ =
(Р_атм
+ h) Sℓ’,

Отсюда
находим атмосферное давление

Ответ.

Пример
3.2. В сосуде находится
смесь m = 7 г азота и m = 11г углекислого
газа при температуре Т = 290 К и давлении
Р = 1 атм. Найти плотность этой смеси,
считая газа идеальными.

Дано:
m₁=7
г=7∙10^-3кг;
m₂=11
г=11∙10^-3кг;
Т=290К; Р=1атм=10⁵Па.

Найти:
ρ.

Решение:
Давление газов в сосуде
известно. Если через Р₁
обозначить давление
азота, если бы углекислого газа не было,
а через Р₂ давление
углекислого газа, если бы не было азота
(так называемые парциальными давления),
то давление смеси газов Р будет согласно
закону Дальтона Р =
Р₁ +
Р₂.
Учитывая, что температура каждого газа
Т запишем для азота и кислорода уравнение
Менделеева-Клапейрона:

Складывая
эти выражения, получаем:

Отсюда
находим объём, занимаемый смесью газов

Плотность
смеси газов вычисляется по формуле

Ответ:

Пример
3.3. Кислород массой
m=10г
находится под давлением 200кПа при
температуре 280К. В результате изобарного
расширения газ занял объём 9л. Определите:
1) объём газа V₁
до расширения; 2) температуру газа T₂
после расширения; 3) плотность газа ρ₂
после расширения.

Дано:
M=32∙10^-3кг/моль;
m=10г=10∙10^-3кг;
р=200кПа=2∙10⁵Па=const;
Т₁=280К;
V₂=9г=9∙10^-3м³.

Найти:
1) V₁;
2) Т₂;
3) ρ₂.

Решение:
Объём газа до расширения найдём, согласно
уравнению Клапейрона-Менделеева,

,

откуда

Записав уравнение Клапейрона-Менделеева
для конечного состояния газа:

,

найдём искомую температуру

Плотность газа после расширения газа

.

Ответ:
1) V₁=3,64
л; 2) Т₂=693
К; 3) ρ₂=1,11
кг/м³.

Пример 3.3. В
цилиндре с площадью основания 100 см²
находится воздух. Поршень расположен
на высоте 50 см от дна цилиндра. На поршень
кладут груз массой 50 кг, при этом он
опускается на 10 см. Найти температуру
воздуха после опускания поршня, если
до его опускания давление было равно
101 кПа, а температура 12С.

Дано: S=100см²=1∙10^-2м²;h₁=50см=0,5
м;m=50кг; Δh=10см=0,1
мt;P₁=101∙10³Па; Т₁=12С=285
К.

Найти:
Т₂.

Решение:

Рассмотрим два состояния воздуха под
поршнем: до опускания поршня и после
его опускания. До опускания поршня
состояние воздуха характеризуется
параметрами Р₁,
V₁,
T₁,
после опускания поршня – параметрами
Р₂,
V₂,
T₂,
где V₁=Sh₁,
Р₂=Р₀+Р,

,
V₂=Sh₂,
или, поскольку h₂=h₁–
Δh,

V₂=S(h₁–
Δh).

Применим
к этим двум состояниям формулу Клапейрона:

,

откуда

(1)

Подставим
в формулу (1) выражения для Р₁,
V₁,
Р₂
и V₂:

;

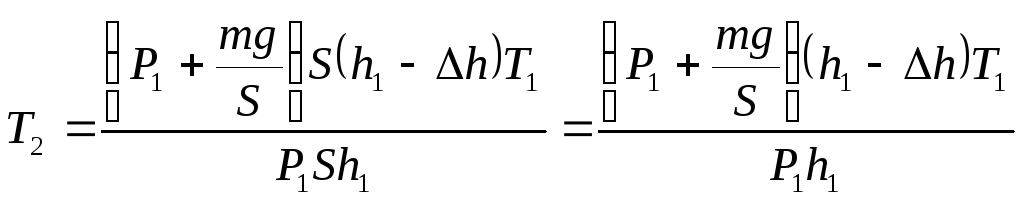
Ответ:
Т₂=338К

Пример 3.3. Имеются
два сосуда с газом: один вместимостью
3 л, другой 4 л. В первом сосуде газ
находится под давлением 202 кПа, а во
втором 101 кПа. Под каким давлением будет
находиться газ, если эти cосуды соединить
между собой? Считать, что температура
в сосудах одинакова и постоянна.

Дано: V₁=3л=3∙10^–3м³;V₂=4л=4∙10^–3м³;Р₁=202кПа=202∙10³Па; Р₂=101кПа=101∙10³Па.

Найти:
Р.

Решение:

По закону Дальтона,

Р
= Р₃
+ Р₄ (1)

Так
как процесс изотермический, то парциальное
давление газа в каждом сосуде можно
найти по закону Бойля-Мариотта:

Р₁V₁
=
Р₃V,
Р₂V₂
=
Р₄V,

где
V=V₁+V₂.
Тогда парциальное давление газа в каждом
из сосудов после их соединения

,

, (2)

Подставляем
выражения (2) в (1):

Ответ:
Р=141 Па

Пример 3.3. В
баллоне содержатся сжатый газ при
температуре t₁
= 27С
и давлении p₁
= 4 МПа. Каково будет давление, если из
баллона выпустить

Δm
= 0,4m
массы газа, а температуру понизить до
t₂
= 17С?

Дано: Т₁=27С
=300 К;Р₁=4МПа=4∙10⁶
Па;Δm
= 0,4m;
Т₂=17С
=290 К Найти:
Р.

Решение: Рассмотрим
два состояния газа: до разрежения и
после, когда осталось1-n массы m газа.
Параметры каждого из этих состояний
связаны уравнением Менделеева-Клапейрона:

,

где
Р₁,
Т₁,
Р₂,
Т₂
– соответственно давление и температура
газа до и после выпуска; m – масса газа;
М – молярная масса; V – объем.

Разделив
почленно первое равенство на второе,
получим:

,

oткуда

(1)

Ответ:
Р₂
= 2,310⁶
Па = 2,3 МПа.

Пример
3.3. Найти максимально
возможную температуру идеального газа
в процессе P = P₀
– αV²,
где P₀,
α – положительные постоянные.

Дано:
P = P₀
– αV²;
P₀, α
– const

Найти:
T_max.

Решение:
Для нахождения максимальной температуры
необходимо получить явную зависимость
последней от параметров и исследовать
эту зависимость на экстремум. Так как
газ является идеальным, выразим давление
из уравнения Менделеева-Клапейрона и
подставим его в уравнение процесса

Отсюда
выражаем температуру

Условие экстремума
,
которое сводится к выражению.

Решая
данное уравнение, получаем значение
объёма, при котором температура принимает
экстремальное значение
.
Исследуя знак второй производной, приходим к выводу, что при данном
значении объёма температура газа будет
идеальной. Подставляя выражение для
объёма в выражение для температуры при
данном процессе, получаем:

Ответ:

Пример
3.3. В сосуде
вместимостью V=5л
находится кислород массой m=15г.
определите: 1) концентрацию молекул
кислорода в сосуде; 2) число N
молекул газа в сосуде.

Дано:
V=5л=5∙10^-3м³;
M=32∙10^-3кг/моль;
m=15г=1,5∙10^-2кг.

Найти:
1) n; 2) N.

Решение:
Записав
уравнение Клапейрона-Менделеева

(1)

И
уравнение состояния идеального газа

Р=nkT
(2)

И
поделив (1) на (2), найдём искомую концентрацию
молекул кислорода в сосуде

.

Концентрация
молекул

,

Откуда
искомое число молекул газа в сосуде

N=nV.

Ответ:
1)
n=5,64∙10²⁵
м^-3;
2) N=2,82∙10²³.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Горячий вопрос: можно ли достичь самой высокой температуры во Вселенной и какая она

Человечество всегда стремится ставить рекорды. Но удастся ли нам когда-нибудь нагреть на Земле вещество до самой высокой температуры во Вселенной?

«Существует ли теоретическая максимальная температура вещества? Но такого понятия я не встречал нигде»

(Вопрос и ответ с форума)

В своей книге А. Азимов приводит интересное сравнение температуры звезд с температурой в Нью-Йорке: «При взрыве водородной бомбы развивается температура примерно 100 миллионов градусов. И все-таки природа превысила эту рекордную температуру: центральные области некоторых очень горячих звезд (Солнце лишь среднетеплая звезда), как свидетельствуют оценки, могут достигать температур до 2 миллиардов градусов. Два миллиарда градусов – температура значительная (даже по сравнению с температурой самого жаркого дня в Нью-Йорке). Но вот вопрос: до каких пределов она может расти? Есть ли потолок? Иными словами, как горячо самое горячее?» [1, с. 159. ]

Максимально возможная температура вещества в природе, какова она? В предыдущей статье: «Постоянная гравитации – величина переменная» я показал предельную температуру, которая равна 4,392365·10¹²К. Корректно ли данное число? Сопоставим значение максимальной температуры с температурами, найденными другими способами. Максимальную температуру можно найти через средне кинетическую энергию молекул газа.

E_k=3/2 kT/m

Температура – это механическая величина, которая выражает среднюю кинетическую энергию, или – температура есть статистическая величина, отражающая меру средней кинетической энергии молекул газа.

Для расчета возьмем протон самой легкой молекулы водорода с массой (m) и попробуем разогнать его с помощью тепловой энергии до скорости света, поднимая температуру до максимально возможной. В расчете не будем учитывать релятивистские эффекты при приближении к скорости света. Сейчас важно сделать оценку (прикидку), порядка, полученной температуры.

Е_к=½ m v²=3/2 kT

Откуда следует, что

Где m – масса протона,

k – постоянная Больцмана,

Т – температура. Здесь температура обозначена символом T, как в источниках. В настоящее время температура обозначается греческой буквой Θ (Тета).

Вместо квадратичной скорости подставим скорость света, тогда максимальная температура будет равна:

Как видим, полученное значение имеет тот же порядок, да и число близко к значению максимальной температуры.

А. Азимов пришел к аналогичному результату (3,6·10¹² К), но он засомневался в правильности результата, т.к. поверил Эйнштейну, у которого масса в пределе приближения к скорости света может возрастать до бесконечности[1]. Подводя итог Азимов заключает: «Ни в ньютоновской, ни в эйнштейновской Вселенной нет предела увеличению температуры. Здесь нет наивысшей высоты самого высокого».

[1] В настоящее время эта концепция опровергнута, растет энергия, но не масса.

Вот такие беспредельно подобные выводы находятся на вооружении и современной физики. Я не разделяю их, т.к. считаю, что в природе все конечно – все имеет начало и имеет конец. В данном случае температура всегда конечна.

Решение обратной задачи приводит нас к результату, что масса протона близка к расчетной. Эквивалентная масса частицы, которой соответствует максимальная температура T_max , немного превышает массу протона водорода (m_p=1,6735·10^-27 кг).

m=3 kT/ v²

m=3∙1,3807∙10^-23∙4,392365·10¹² /(2,998∙10⁸)²=2,02∙10^-27 кг

На сегодня экспериментально не зафиксировано ни одного физического процесса связанного с массой, движущейся со скоростью света. Поэтому, достичь максимальной температуры невозможно т.к. разогнать до скорости света даже легкий протон водорода нереально. Для этого потребовалась бы температура, близкая к максимальной, где ее взять?

Несмотря на то, что расчет был проверочным, он явно показал, что найденная ранее максимальная температура (4,392365·10¹²К) вполне корректна и может быть использована в физических расчетах.

Еще один подход к максимальной температуре можно сделать через максимальную частоту излучения, читаем следующую статью.

Азимов А., Вид с высоты, Мир, М., 1965, (пер. с англ. Жуков Д., с. 159-170)

Назад  Вперед