Принцип поиска максимального или
минимального элемента массива заключается
в следующем: в дополнительную переменную
заносится значение первого элемента
массива, которое принимается за максимум
(минимум); затем организовывается перебор
оставшихся элементов массива, каждый
из которых сравнивается с максимумом
(минимумом); если текущий элемент массива
оказывается больше (меньше), чем принятый
за максимум (минимум), то этот элемент
становится максимальным (минимальным).
Таким образом, после завершения перебора
элементов массива в дополнительной
переменной окажется максимальное
(минимальное) значение среди элементов
массива. Фрагмент блок-схемы алгоритма,
реализующий описанный метод приведен
на рисунке 5.2.1.
В блоке 1 дополнительным переменным maxиmin, в которых
будут храниться максимальное и минимальное
значения соответственно, присваивается
значение 1-го элемента массива. Кроме
этого введены еще две переменныеimaxиimin, которые будут
использоваться для хранения номеров
максимального и минимального элементов
массива. С помощью блока модификации
(блок 2) организовывается цикл по перебору
элементов массива Х (перебор начинается
со 2-го элемента, так как 1-й элемент уже
обработан в блоке 1). Если текущий элемент
массиваXiбольше значения, которое хранится в
переменнойmax(блок 3), то за максимум принимается
значение этого элемента:max=Xi,
и запоминается его номер:imax=i(блок 4). Если текущий элемент массива
не больше максимума, то проверяется, не
меньше ли он минимума (блок 5). В случае
если текущий элементXiокажется меньше минимального значения,
которое хранится в переменнойmin,
то за минимум принимается значение
этого элемента:min=Xi,
и запоминается его номер:imin=i(блок 6). После выхода из цикла будут
выведены значения максимального и
минимального элементов, а также их
номера в массиве (блок 7).
П
выше алгоритм имеет один недостаток –
в нем используется две лишние переменныеmaxиmin.
Зная индекс элемента массива всегда
можно получить его значение, поэтому
нет необходимости хранить максимальное
и минимальное значения в отдельных
переменных. Оптимальный алгоритм
приведен на рис. 5.2.2.
В блоке 1 дополнительным переменным
imaxиimin,
используемых для хранения номеров
максимального и минимального элемента,
присваивается значение 1. Таким образом,
за максимум и минимум принимается 1-й
элемент массива, само же значение этого
элемента нигде дополнительно не
сохраняется. Оставшиеся элементы массива
также перебираются, начиная со второго
(блок 2). При этом каждый элемент массиваXi
сравнивается с
элементами, имеющими номер равныйimax(блок 3) иimin(блок
6), т.е. с элементами принятыми за максимум
(минимум). Если результат проверки
условий является истиной, то в переменныхimaxиiminсохраняются индексы новых максимального
(блок 4) и минимального (блок 6) элементов.
После выхода из цикла будут выведены
значения максимального и минимального
элементов, а также их номера в массиве
(блок 7).
Если в массиве имеется несколько
элементов равных по значению максимальному
(минимальному) элементу, то алгоритмы,
приведенные на рис 5.2.1 и 5.2.2, определят
позицию только первого такого элемента.
Например, чтобы найти количество
элементов массива равных максимальному
и позицию последнего такого элемента,
можно воспользоваться алгоритмом,
приведенным на рис. 5.2.3.
В начале алгоритма за максимум принимается
1-й элемент массива и вводится переменная
kдля подсчета
количества элементов равных максимальному
(блок 1). Затем организовывается цикл по
перебору оставшихся элементов массива
(блок 2). На каждом шаге цикла выполняется
следующая последовательность действий.
Вначале текущий элемент массива Xiсравнивается с максимальным (блок 3).
Если он оказывается больше элемента,
принятого за максимальный, то запоминается
номер этого элемента и переменнойkприсваивается 1 (блок 4). Это означает,
что встретился первый «новый» максимальный
элемент.
Если текущий элемент не больше максимума,
значит, он может быть равным или меньше
максимального элемента. Поэтому в блоке
5 текущий элемент массива Xi
проверяется на равенство
максимальному. Если он оказывается
равным максимуму, то опять запоминается
номер текущего элемента и значение
переменнойkувеличивается на 1 (блок 6). Это означает,
что встретился следующий элемент равный
максимальному элементу. В итоге после
выхода из цикла в переменнойimaxбудет храниться индекс последнего по
счету элемента равного максимальному,
а в переменнойkколичество элементов, равных максимуму.
Если же из блока 6 убрать операциюimax=i,
то в переменнойimax,
как и в предыдущих примерах будет
сохранен номер первого по счету элемента
равного максимальному.
В некоторых задачах невозможно вначале
принять за максимум (минимум) первый
элемент массива. Например, если элементы
массива ещё не определены (не введены
или не вычислены), или если необходимо
найти максимум (минимум) только среди
положительных, четных по значению и
т.д. элементов. Во втором случае неизвестно
когда в массиве встретится первый такой
элемент. В таких ситуациях можно
использовать способ, реализованный в
алгоритме из примера 5.2.
Пример 5.2.В массиве Х [N]
найти минимальный положительный элемент.
М
Х может содержать как положительные,
так и отрицательные элементы. Поэтому
неизвестно какой элемент массива или
произвольное значение можно принять
за начальный минимум. Решение поставленной
задачи можно разбить на два этапа: поиск
положительных элементов в массиве с
определением первого такого элемента
и поиск среди положительных элементов
минимального по значению. Блок-схема
алгоритма приведена на рис. 5.2.4.
В нашем примере нумерация элементов
массива начинается с единицы, поэтому
в качестве начального значения для
переменной iminпринимается 0 (блок 1), т.е. значение
которое не могут принимать индексы
элементов массива Х. Таким образом
показывается, что при обработке массива
еще не встречался положительный элемент,
который можно принять за начальное
значение для минимума. Затем организовывается
цикл по перебору всех элементов массива
(блок 2). На каждом шаге цикла выполняется
следующая последовательность действий.
В блоке 3 проверяется, не является ли
текущий элемент массива Xiположительным. Если он отрицательный
или равен нулю, то такой элемент
пропускается и над ним не выполняется
никаких действий. ЕслиXi> 0, то в блоке 4 проверяется, не является
ли этот элемент первым встретившимся
положительным элементом массива
(признаком чего служит значениеiminравное 0). В этом случае в блоке 5 переменнойiminбудет присвоено
текущее значениеi.
Таким образом, за начальное значение
для минимума будет принято значение
первого по счету положительного элемента
массива Х. Эта ситуация может возникнуть
только один раз, и при дальнейшей работе
цикла блок 5 больше выполняться не будет.
Остальные положительные элементы
массива в блоке 6 будут сравниваться с
элементом массива, принятым в текущий
момент за минимум. Если такой элемент
окажется меньше минимального, то в блоке
7 в переменнойiminбудет сохранен его номерi.
После выхода из цикла проверяется, не
равно ли значение iminнулю (блок 8), так как сразу же выводить
значение минимального элемента массиваXimin
и его номерimin(блок 9) нельзя. Это объясняется тем что,
если в массиве Х не будет положительных
элементов, то значение переменнойiminостанется равным нулю, а обращение к
несуществующему элементу массиваХ0не допустимо.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- Авторы
- Научный руководитель
- Файлы
- Литература
Прусаков И.В.
1
1 г. Новочеркасск, Гуманитарно-технический колледж ФГБОУ ВО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»
Растеряев Н.В. (Новочеркасск, ФГБОУ ВО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»)
1. Логинов В.И., Шемагина Л.Н. Основы алгоритмизации : учеб.-метод. пособие для студ. оч. заоч. обуч. техн. специальностей. – Н. Новгород : Изд-во ФГОУ ВПО «ВГАВТ», 2010. – 81 с.
2. Михалкович С.С., Логинов В.И., Шемагина Л.Н. Основы программирования : учеб.-метод. пособие для студ. 1 курса. – Ростов н/Д. : Изд-во ЮФУ, 2007. – 40 с.
Основу современной инженерной деятельности составляет умение ставить задачи, разрабатывать алгоритмы и получать решения, производить анализ полученных данных и делать выводы. Поэтому в своей профессиональной деятельности инженер должен уметь грамотно применять персональный компьютер, современное программное обеспечение для решения научных и инженерных задач.
Типичной задачей при обработке больших массивов данных является задача поиска максимума или минимума. Например, в списке успеваемости учеников класса найти самого прилежного. Иначе говоря, требуется выбрать наибольшее значение среднего балла и указать фамилию ученика. Или, в массиве среднесуточных температур окружающего воздуха за некоторый период наблюдений определить минимальное значение и указать дату самого холодного дня.
Цель работы: разработка программы нахождения максимального и минимального элемента в среде программирования Паскаль-ABC.
Задачи:
1) ознакомиться с алгоритмами поиска в массивах и методами их программной реализации;
2) освоить приемы программирования в интегрированной среде Паскаль-ABC;
3) разработать алгоритм и блок-схему нахождения максимального и минимального элемента в массиве;
4) создать программу нахождения максимального и минимального элемента в массиве и протестировать ее.
Объект исследования: алгоритмы поиска в массивах.
Предмет исследования: Паскаль-программа нахождения максимального и минимального элемента массива в среде Паскаль-ABC.
Алгоритмы поиска информации
Очень часто в реальной жизни нам приходится сталкиваться с задачей поиска информации в объеме данных. Например, поиск фамилии ученика в журнале, поиск нужного слова в словаре. Существует множество алгоритмов поиска, но из всего многообразия алгоритмов рассмотрим два основных и наиболее часто используемых на практике.
В алгоритмах поиска существует два возможных окончания работы: поиск может оказаться удачным – заданный элемент найден в массиве и определено его месторасположение, либо проведенный поиск может оказаться неудачным – необходимого элемента в данном объеме информации нет.
Несмотря на то, что целью поиска является значение элемента, алгоритм поиска в случае удачного окончания выдает так же и местоположение искомого элемента, например его номер в массиве, так как по номеру элемента можно однозначно восстановить и его значение.
Для оценки алгоритмов мы будем использовать такую характеристику, как сложность.
Пусть, например, человек ищет на полке книжку с определенным названием. Книги на полке стоят вразнобой, то есть не по алфавиту. Как будет действовать человек? Он будет сравнивать по порядку название каждой книги на полке с тем названием, которое ему нужно найти. В итоге он или найдет нужную ему книгу, или, просмотрев все книги на полке, не обнаружит нужной книги. Этот пример передает суть алгоритма последовательного поиска в неупорядоченном массиве. Приведем его формальную запись.
Имеется одномерный массив a[1 … n], требуется найти элемент массива, равный P:
Алгоритм последовательного поиска в неупорядоченном массиве
Установить i = 1.
Если ai = P, алгоритм завершил работу успешно.
Увеличить i на 1.
Если i – n, то перейти к шагу 2. В противном случае алгоритм завершил работу безуспешно.
Оценим сложность алгоритма последовательного поиска. Естественно оценивать сложность по числу сравнений с искомым элементом. В худшем случае искомый элемент окажется на последнем месте или не будет найден, и тогда необходимо будет проделать n сравнений, то есть сложность алгоритма будет равна n. Такой поиск также называют линейным, так как он решает задачу поиска с линейной скоростью по количеству сравнений.
Усложним задачу. Пусть нам требуется найти минимальный элемент в неупорядоченном массиве. Оказывается, что и эта задача имеет линейную сложность, и для поиска минимального (максимального) элемента в неупорядоченном массиве требуется n – 1 сравнение. Запишем алгоритм поиска максимального элемента в текстовой (вербальной) форме.
Алгоритм поиска максимального элемента в неупорядоченном массиве
Установить счетчик равным 1 (i = 1).
Положим значение текущего максимума равным первому исследуемому элементу (max = a1).
Если исследованы еще не все элементы (i < n), то перейти к шагу 5, иначе алгоритм окончен (максимальный элемент равен max).
Перейти к следующему элементу (увеличить i на единицу).
Если рассматриваемый элемент больше, чем текущий максимум (ai > max), то значение ai присвоить max.
Перейти к шагу 4.
Последовательный поиск не является самым эффективным алгоритмом поиска. Например, человеку нужно найти в русско-английском словаре перевод слова на английский язык. Если он будет искать его с помощью алгоритма последовательного поиска (просматривая все слова подряд), то он потратит очень много времени. На самом же деле интуитивно человек действует совсем по-другому.
Поиск слова в словаре наиболее приближен к алгоритму бинарного (двоичного) поиска, который также называют логарифмическим поиском, или методом деления пополам (дихотомией). Этот алгоритм достаточно эффективен, но использовать его можно только в случае, когда данные упорядочены. В этом алгоритме мы используем сравнение искомого элемента с серединным элементом и с помощью результата этого сравнения устанавливаем, в какой части данных находится искомый элемент.
Заметим, что даже если данные упорядочены, то использовать алгоритм бинарного поиска мы можем не всегда. Это касается тех случаев, когда мы не имеем доступа к любому элементу массива. Например, если данные поступают к нам последовательно.
Алгоритмы поиска максимального или минимального элемента массива
Алгоритмизация – это общая последовательность действий, которые необходимо выполнить для построения алгоритма решения задачи, в том числе – выделение конкретных шагов алгоритмического процесса, определение вида формальной записи для каждого шага и установление определенного порядка выполнения каждого шага [1]
Разработка алгоритма решения задачи – это разбиение задачи на последовательно выполняемые этапы, причем результаты выполнения предыдущих этапов могут использоваться при выполнении последующих. При этом должны быть четко указаны как содержание каждого этапа, так и порядок выполнения этапов. Отдельный этап алгоритма представляет собой либо другую, более простую задачу, алгоритм решения которой известен (разработан заранее), либо должен быть достаточно простым и понятным без пояснений.
Пусть поставлена следующая задача: по известным данным среднесуточных температур и дат найти максимальную или минимальную температуру и соответствующую ей дату.
Принцип поиска максимального или минимального элемента массива заключается в следующем. Первое, что необходимо сделать – создать массивы данных и дат. При этом сначала вводится параметр n – число элементов создаваемых массивов. Для ввода элементов массива используется цикл с параметром. Вводятся числовое значение и дата в формате ДД.ММ.ГГ.
Для определения того, будем находить максимальный или минимальный элемент, целочисленной переменной flag будем присваивать значения 1 или 0.
В дополнительную переменную заносится значение первого элемента массиваDan[ ], которое принимается за максимум (минимум); затем организовывается перебор оставшихся элементов массива, каждый из которых сравнивается с максимумом (минимумом); если текущий элемент массива оказывается больше (меньше), чем принятый за максимум (минимум), то этот элемент становится максимальным (минимальным). Таким образом, после завершения перебора элементов массива в дополнительной переменной окажется максимальное (минимальное) значение среди элементов массива.
Кроме этого введены еще две переменные imax и imin, которые будут использоваться для хранения номеров максимального и минимального элементов массива. После выхода из цикла будут найдены значения максимального или минимального элементов массива Dan[ ], а также их номера, по которым будут найдены соответствующие даты в массиве Tim[ ].
Представим разработанный выше алгоритм в виде блок-схемы.
Блок-схемой называется наглядное графическое изображение алгоритма, когда отдельные его этапы изображаются при помощи различных геометрических фигур – блоков, а связи между этапами (последовательность выполнения этапов) указываются при помощи стрелок. Типичные действия алгоритма изображаются геометрическими фигурами согласно ГОСТ 19.701-90.
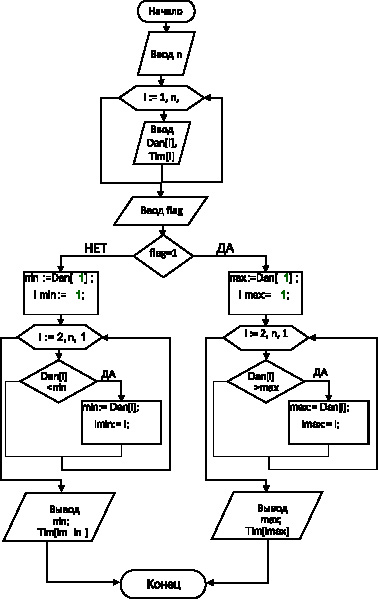
Блок-схема алгоритма представлена на рис. 1.
Рис. 1. Блок-схема алгоритма нахождения максимального и минимального элемента
Интегрированная среда программирования Паскаль-ABC. Разработка и тестирование программы
На рис. 2 представлен скриншот разработанной программы в интегрированной среде программирования Паскаль-АВС.
Рис. 2. Скриншот программы
Система программирования Паскаль-ABC представляет собой диалект стандартного языка Паскаль. Система создавалась на факультете математики, механики и компьютерных наук ЮФУ как учебная среда программирования (автор – кандидат физико-математических наук, доцент кафедры алгебры и дискретной математики С.С. Михалкович) [2]. По мнению разработчиков этой системы, первоначальное обучение программированию должно проходить в достаточно простых и дружественных средах, в то же время эти среды должны быть близки к стандартным и иметь богатые и современные библиотеки подпрограмм.
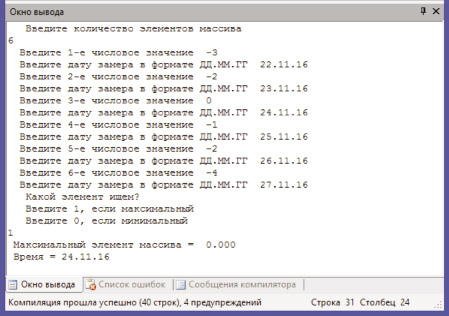
На рис. 3 представлен скриншот результатов нахождения максимального значения температуры и соответствующей ей дате.
Рис. 3. Скриншот результатов нахождения максимального элемента
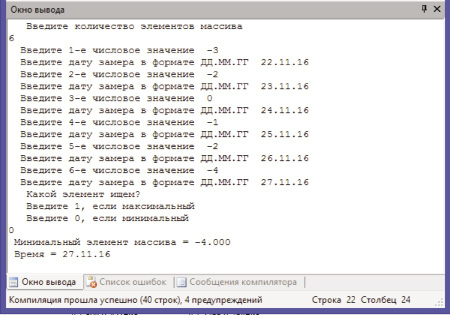
Рис. 4. Скриншот результатов нахождения минимального элемента массива
На рис. 4 представлен скриншот результатов нахождения минимального значения температуры в массиве и соответствующей ей дате.
Выводы
В результате выполнения моей научно-исследовательской работы достигнута цель исследования – разработана программа нахождения максимального и минимального элемента в среде программирования Паскаль-ABC. Программа протестирована по двум ветвям вычислительного процесса: нахождение максимального и нахождение минимального элемента. При этом я ознакомился с алгоритмами поиска информации в больших объемах данных. Освоил некоторые приемы программирования в интегрированной среде Паскаль-ABC. Разработал блок-схему и программу нахождения максимального и минимального элемента одномерного массива. Надеюсь, что полученные знания и навыки помогут мне успешно сдать экзамен по дисциплине информатика.
Библиографическая ссылка
Прусаков И.В. НАХОЖДЕНИЕ МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЭЛЕМЕНТА В МАССИВЕ // Международный школьный научный вестник. – 2017. – № 2.
;
URL: https://school-herald.ru/ru/article/view?id=181 (дата обращения: 21.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
5.4.4 Поиск максимального элемента в массиве и его номера
Дан массив X, состоящий из n элементов. Найти максимальный элемент массива и номер, под которым он хранится в массиве.
Алгоритм решения задачи следующий. Пусть в переменной с именем Max хранится значение максимального элемента массива, а в переменной с именем Nmax – его номер. Предположим, что нулевой элемент массива является максимальным, и запишем его в переменную Max, а в Nmax — его номер (то есть ноль). Затем все элементы, начиная с первого, сравниваем в цикле с максимальным. Если текущий элемент массива оказывается больше максимального, то записываем его в переменную Max, а в переменную Nmax – текущее значение индекса i. Процесс определения максимального элемента в массиве приведён в табл. 5.3 и изображён при помощи блок-схемы на рис. 5.8. Соответствующий фрагмент программы имеет вид:
for (Max=X [ 0 ], Nmax= i =0; i<n; i++)
if (Max<X [ i ] )
{
Max=X [ i ];
Nmax= i;
}
cout<<" Max = "<<Max<<" n ";
cout<<" Nmax = "<<Nmax<<" n ";
| Номера элементов | 0 | 1 | 2 | 3 | 4 | 5 |
| Исходный массив | 4 | 7 | 3 | 8 | 9 | 2 |
Значение переменной 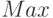
|
4 | 7 | 7 | 8 | 9 | 9 |
Значение переменной 
|
1 | 2 | 2 | 4 | 5 | 5 |
Рис.
5.8.
Поиск максимального элемента и его номера в массиве
При поиске максимального элемента и его номера, можно найти только номер максимального элемента, а потом по номеру извлечь значение максимального элемента из массива.
Текст программы поиска номера максимального элемента:
#include <iostream>
using namespace std;
int main ( )
{
float *X;
int i,N, nom;
cout<<"Введите размер массива "; cin>>N; //Ввод размерности динамического массива
X=new float [N ]; //Выделение памяти для хранения динамического массива X.
cout<<"Введите элементы массива X n "; //Ввод динамического массива X.
for ( i =0; i<N; i++)
cin>>X [ i ];
//В переменной nom будем хранить номер максимального элемента.
nom=0; //Предположим, что максимальным элементом является элемент с номером 0.
for ( i =1; i<N; i++)
//Если очередной элемент больше X[nom], значит nom не является номером максимального
//элемента, элемент с номером i больше элемента X[nom], поэтому переписываем
//число i в переменную nom.
if (X [ i ]>X [ nom ] ) nom= i;
cout << "Максимальный элемент= "<<X [ nom]<<", его номер= " << nom << endl;
return 0;
}
Совет. Алгоритм поиска минимального элемента в массиве будет отличаться от приведённого выше лишь тем, что в условном блоке и, соответственно, в конструкции if текста программы знак поменяется с “<” на “>”.
Рассмотрим несколько задач.
Задача 5.3. Найти минимальное простое число в целочисленном массиве x[N].
Эта задача относится к классу задач поиска минимума (максимума) среди элементов, удовлетворяющих условию. Подобные задачи рассматривались в задачах на обработку последовательности чисел. Здесь поступим аналогично. Блок-схема приведена на рис. 5.9.
Необходимо первое простое число объявить минимумом, а все последующие простые элементы массива сравнивать с минимумом. Будем в цикле последовательно проверять, является ли элемент массива простым числом (функция prostoe). Если X[i] является простым числом, то количество простых чисел (k) увеличиваем на 1 (k++), далее, проверяем, если k равен 1 (if (k==1)), то этот элемент объявляем минимальным (min=x[i]; nom=i;), иначе сравниваем его с минимальным (if (x[i]<min) {min=x[i];nom=i;}).
Текст программы:
#include <iostream>
using namespace std;
bool prostoe ( int N)
{ int i; bool pr;
if (N<2) pr=false;
else
for ( pr=true, i =2; i<=N/ 2; i++)
if (N%i ==0)
{
pr=false;
break;
}
return pr;
}
int main ( int argc, char **argv )
{
int i, k, n, nom, min, *x;
cout<<" n = "; cin>>n; //Ввод количества элементов в массиве.
x=new int [ n ]; //Выделяем память для динамического массива x.
cout<<"Введите элементы массива X "; //Ввод элементов массива.
for ( i =0; i<n; i++)
cin>>x [ i ];
//С помощью цикла по переменной i, перебираем все элементы в массиве x,
//k — количество простых чисел в массиве.
for ( i=k=0; i<n; i++)
//Проверяем, является ли очередной элемент массива простым числом.
if ( prostoe ( x [ i ] ) ) //Если x[i] — простое число.
{
k++; //Увеличиваем счётчик количества простых чисел в массиве.
//Если текущий элемент является первым простым числом в массиве,
// объявляем его минимумом, а его номер сохраняем в перемнной nom.
if ( k==1) {min=x [ i ]; nom= i; }
else
//Все последующие простые числа в массиве сравниваем с минимальным простым числом.
//Если текущее число меньше min, перезаписываем его в переменную min,
//а его номер — в переменную nom.
if ( x [ i ]<min ) {min=x [ i ]; nom= i; }
}
//Если в массиве были простые числа, выводим значение и номер минимального простого числа.
if ( k>0)
cout<<" min = "<<min<<" tnom = "<<nom<<endl;
//Иначе выводим сообщение о том, что в массиве нет простых чисел.
else cout<<"Нет простых чисел в массиве"<<endl;
return 0;
}
Рис.
5.9.
Блок-схема решения задачи 5.3
Аналогичным образом можно написать программу любой задачи поиска минимума (максимума) среди элементов, удовлетворяющих какому-либо условию (минимум среди положительных элементов, среди чётных и т.д.).
Задача 5.4. Найти 
Перед решением этой довольно сложной задачи рассмотрим более простую задачу.
Найти два наименьших элемента в массиве. Фактически надо найти номера (nmin1, nmin2) двух наименьших элементов массива. На первом этапе надо найти номер минимального (nmin1) элемента массива. На втором этапе надо искать номер минимального элемента, при условии, что он не равен nmin1. Вторая часть очень похожа на предыдущую задачу (минимум среди элементов, удовлетворяющих условию, в этом случае условие имеет вид i!=nmin1).
Решение задачи с комментариями:
#include <iostream>
using namespace std;
int main ( int argc, char **argv )
{
int kvo, i, n, nmin1, nmin2;
double *X;
cout<<" n = "; cin>>n;
X=new double [ n ];
cout<<"Введите элементы массива X n ";
for ( i =0; i<n; i++)
cin>>X [ i ];
//Стандартный алгоритм поиска номера первого минимального элемента (nmin1).
for ( nmin1=0, i =1; i<n; i++)
if (X [ i ]<X [ nmin1 ] ) nmin1= i;
//Второй этап — поиск номера минимального элемента среди элементов, номер
//которых не совпадает nmin1. kvo — количество таких элементов.
for ( kvo= i =0; i<n; i++)
if ( i !=nmin1 ) //Если номер текущего элемента не совпадает с nmin1,
{
kvo++; //увеличиваем количество таких элементов на 1.
//Номер первого элемента, индекс которого не равен nmin1,
//объявляем номером второго минимального элемента.
if ( kvo==1) nmin2= i;
else
//очередной элемент, индекс которого не равен nmin1, сравниваем с минимальным,
//если он меньше, номер перезаписываем в переменную nmin2.
if (X [ i ]<X [ nmin2 ] ) nmin2= i;
}
//Вывод двух минимальных элементов и их индексов.
cout<<" nmin1 = "<<nmin1<<" tmin1 = "<<X [ nmin1]<< endl;
cout<<" nmin2 = "<<nmin2<<" tmin2 = "<<X [ nmin2]<< endl;
return 0;
}
По образу и подобию этой задачи можно написать задачу поиска трёх минимальных элементов в массиве. Первые два этапа (поиск номеров двух минимальных элементов в массиве) будут полным повторением кода, приведённого выше. На третьем этапе нужен цикл, в котором будем искать номер минимального элемента, при условии, что его номер не равен nmin1 и nmin2. Авторы настоятельно рекомендуют читателям самостоятельно написать подобную программу. Аналогично можно написать программу поиска четырёх минимальных элементов. Однако при этом усложняется и увеличивается код программы. К тому же, рассмотренный приём не позволит решить задачу в общем случае (найти k минимумов).
Для поиска 







#include <iostream>
using namespace std;
int main ( int argc, char **argv )
{
int p, j, i, n, *nmin, k, kvo, nmin_temp;
bool pr;
double *x;
cout<<" n = "; cin>>n;
x=new double [ n ];
cout<<"Введите элементы массива Хn ";
for ( i =0; i<n; i++)
cin>>x [ i ];
cout<<"Введите количество минимумовn "; cin>>k;
nmin=new int [ k ];
for ( j =0; j<k; j++) //Цикл по переменной j для поиска номера j + 1 минимального элемента
{
kvo=0;
for ( i =0; i<n; i++) //Перебираем все элементы массива.
{
//Цикл по переменной p проверяет, содержится ли номер i в массиве nmin.
pr=false;
for ( p=0;p<j; p++)
if ( i==nmin [ p ] ) pr=true;
if ( ! pr ) //Если не содержится, то количество элементов увеличить на 1.
{
kvo++;
//Если kvo=1, то найден первый элемент, который не содержится в массиве
//nmin, его номер объявляем номером минимального элемента массива
if ( kvo==1) nmin_temp= i;
else
//Если kvo>1, сравниваем текущий элемент x[i] с минимальным.
if ( x [ i ]<x [ nmin_temp ] ) nmin_temp= i;
}
}
nmin [ j ]=nmin_temp; //Номер очередного минимального элемента записываем в массив.
}
for ( j =0; j<k; j++) //Вывод номеров и значений k минимальных элементов массива.
cout<<" nmin1 = "<<nmin [ j ]<<" tmin1 = "<<x [ nmin [ j ]]<< endl;
return 0;
}
Проверку, содержится ли число i в массиве nmin, можно оформить в виде функции, тогда программа может быть записана следующим образом:
#include <iostream>
using namespace std;
//Функция проверяет, содержится ли число i в массиве x из n элементов.
//Функция возвращает true, если содержится, и false, если не содержится.
bool proverka ( int i, int *x, int n )
{
bool pr;
int p;
pr=false;
for ( p=0;p<n; p++)
if ( i==x [ p ] ) pr=true;
return pr;
}
int main ( int argc, char **argv )
{
int j, i, n, *nmin, k, kvo, nmin_temp;
double *x;
cout<<" n = "; cin>>n;
x=new double [ n ];
cout<<"Введите элементы массива Хn ";
for ( i =0; i<n; i++)
cin>>x [ i ];
cout<<"Введите количество минимумовn "; cin>>k;
nmin=new int [ k ];
for ( j =0; j<k; j++) //Цикл по переменной j для поиска номера j + 1 минимального элемента
{
kvo=0;
for ( i =0; i<n; i++) //Перебираем все элементы массива.
{
//Вызов функции proverka, определяем, содержится ли число i в массиве nmin из j элементов
if ( ! proverka ( i, nmin, j ) )
{
kvo++;
if ( kvo==1) nmin_temp= i;
else
if ( x [ i ]<x [ nmin_temp ] ) nmin_temp= i;
}
}
nmin [ j ]=nmin_temp;
}
for ( j =0; j<k; j++) //Вывод номеров и значений k минимальных элементов массива.
cout<<" nmin1 = "<<nmin [ j ]<<" tmin1 = "<<x [ nmin [ j ]]<< endl;
return 0;
}
Авторы настоятельно рекомендуют читателю разобрать все версии решения задачи 5.4.
Задача 5.5. Поменять местами максимальный и минимальный элементы в массиве X.
Алгоритм решения задачи можно разбить на следующие этапы.
- Ввод массива.
- Поиск номеров максимального (nmax) и минимального (nmin) элементов массива.
- Обмен элементов местами. Не получится записать “в лоб” (X[nmax]=X [nmin]; X[nmin]=X[nmax];). При таком присваивании мы сразу же теряем максимальный элемент. Поэтому нам понадобится временная (буферная) переменная temp. Обмен элементов местами должен быть таким: temp=X[nmax]; X[nmax]=X[nmin]; X[nmin]=temp;
Далее приведён текст программы с комментариями.
#include <iostream>
using namespace std;
int main ( int argc, char **argv )
{
int i,N, nmax, nmin;
float temp;
cout<<" N = "; cin>>N;
float X [N ];
cout<<"Введите элементы массива Хn ";
for ( i =0; i<N; i++)
cin>>X [ i ];
//Поиск номеров максимального и минимального элементов массива.
for (nmax=nmin=0, i =1; i<N; i++)
{
if (X [ i ]<X [ nmin ] ) nmin= i;
if (X [ i ]>X [ nmax ] ) nmax= i;
}
//Обмен максимального и минимального элементов местами.
temp=X [ nmax ]; X [ nmax]=X [ nmin ]; X [ nmin ]=temp;
cout<<"Преобразованный массив Хn "; //Вывод преобразованного массива.
for ( i =0; i<N; i++)
cout<<X [ i ]<<" ";
cout<<endl;
return 0;
}
Задача 5.6. Найти среднее геометрическое среди простых чисел, расположенных между максимальным и минимальным элементами массива.
Среднее геометрическое 

![SG=sqrt[{k}]{P}, P](https://intuit.ru/sites/default/files/tex_cache/fef0d3b185eddc391aacdc22a5d1174b.png)

Алгоритм решения задачи состоит из следующих этапов:
- Ввод массива.
- Поиск номеров максимального (nmax) и минимального (nmin) элементов массива.
- В цикле перебираем все элементы массива, расположенные между максимальным и минимальным элементами. Если текущий элемент является простым числом, то необходимо увеличить количество простых чисел на 1, и умножить
на значение элемента массива.
- Вычислить
.
При решении этой задачи следует учитывать, что неизвестно, какой элемент расположен раньше — максимальный или минимальный.
Текст программы с комментариями приведён ниже.
#include <iostream>
#include <math.h>
using namespace std;
bool prostoe ( int N)
{
int i;
bool pr;
if (N<2) pr=false;
else
for ( pr=true, i =2; i<=N/ 2; i++)
if (N%i ==0)
{
pr=false;
break;
}
return pr;
}
int main ( int argc, char **argv )
{
int i, k, n, nmax, nmin, p, *x;
cout<<" n = "; cin>>n; //Ввод количества элементов в массиве.
x=new int [ n ]; //Выделяем память для динамического массива x.
cout<<"Введите элементы массива X"; //Ввод элементов массива.
for ( i =0; i<n; i++)
cin>>x [ i ];
//Поиск номеров максимального и минимального элементов в массиве.
for (nmax=nmin= i =0; i<n; i++)
{
if ( x [ i ]<x [ nmin ] ) nmin= i;
if ( x [ i ]>x [ nmax ] ) nmax= i;
}
if ( nmin<nmax )
for ( p=1,k=0, i=nmin+1; i<nmax; i++)
//Обратите особое внимание на использование в следующей строке фигурной скобки
//(составного оператора). В цикле всего один оператор!!! При этом, при отсутствии
//составного оператора, программа начинает считать с ошибками!!!
{
//Проверяем, является ли очередной элемент массива простым числом.
if ( prostoe ( x [ i ] ) ) //Если x[i] — простое число.
{
//Домножаем y[i] на p, а также увеличиваем счётчик количества простых чисел в массиве.
k++;p*=x [ i ];
}
}
else
for ( p=1,k=0, i=nmax+1; i<nmin; i++)
//Проверяем, является ли очередной элемент массива простым числом.
if ( prostoe ( x [ i ] ) ) //Если x[i] — простое число.
{//Домножаем y[i] на p, а также увеличиваем счётчик количества простых чисел в массиве.
k++;p*=x [ i ];
}
//Если в массиве были простые числа, выводим среднее геометрическое этих чисел на экран
if ( k>0)
cout<<" SG "<<pow ( p, 1./ k )<<endl;
//Иначе выводим сообщение о том, что в массиве нет простых чисел.
else cout<<"Нет простых чисел в массиве"<<endl;
return 0;
}
На чтение 10 мин Просмотров 4 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023
Содержание
- Максимальный элемент массива в Pascal
- Блок-схема максимальный элемент массива
- Программа максимальный элемент массива Pascal
- Нахождение максимального и минимального
- Уроки 55 — 57 Поиск наибольшего и наименьшего элементов массива (§ 20. Поиск наибольшего и наименьшего элементов массива) Составление программы на Паскале поиска минимального и максимального элементов
- Содержание урока
- § 20. Поиск наибольшего и наименьшего элементов массива Поиск максимума и минимума в электронной таблице
- Поиск максимума и минимума в электронной таблице
- Блок-схемы алгоритмов поиска максимума и минимума в массиве
Максимальный элемент массива в Pascal
Часто встречаются задачи, где необходимо найти максимальный элемент в массиве. Рассмотрим общий алгоритм решения такой задачи.
Первое, что придётся сделать – создать массив. Как нам уже известно, нужно использовать цикл с параметром. Также удобнее будет создать массив случайным образом, если в условии задачи не оговорён способ задания массива.
Алгоритм нахождения максимального элемента массива выполняется следующим образом.
Сначала указываем, что первый элемент массива считается максимальным, иначе говоря – Max = A[i].
Потом начинаем процесс сравнивания последующих элементов массива с максимальным элементом в массиве.
Тут возможно два случая :
- Если максимальный элемент больше следующего, то ничего не меняем.
- Если максимальный элемент меньше следующего, то он становиться максимальным.
После этого выводим на экран максимальный элемент.
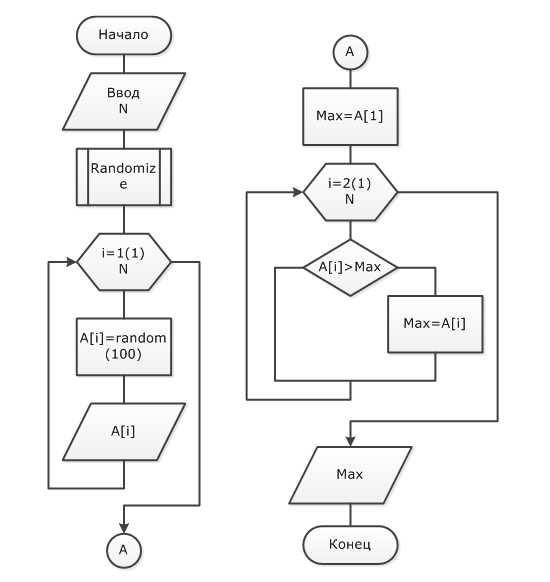
Блок-схема максимальный элемент массива
Программа максимальный элемент массива Pascal
Ниже представлен текст программы на языке Pascal, как найти максимальный элемент массива. Как было указанно в алгоритме выше, сначала создается сам массив (в моем случает любые целые числа от 0 до 100 включительно).
Источник
Нахождение максимального и минимального



Элементов массива
Принцип поиска максимального или минимального элемента массива заключается в следующем: в дополнительную переменную заносится значение первого элемента массива, которое принимается за максимум (минимум); затем организовывается перебор оставшихся элементов массива, каждый из которых сравнивается с максимумом (минимумом); если текущий элемент массива оказывается больше (меньше), чем принятый за максимум (минимум), то этот элемент становится максимальным (минимальным). Таким образом, после завершения перебора элементов массива в дополнительной переменной окажется максимальное (минимальное) значение среди элементов массива. Фрагмент блок-схемы алгоритма, реализующий описанный метод приведен на рисунке 5.2.1.
В блоке 1 дополнительным переменным max и min, в которых будут храниться максимальное и минимальное значения соответственно, присваивается значение 1-го элемента массива. Кроме этого введены еще две переменные imax и imin, которые будут использоваться для хранения номеров максимального и минимального элементов массива. С помощью блока модификации (блок 2) организовывается цикл по перебору элементов массива Х (перебор начинается со 2-го элемента, так как 1-й элемент уже обработан в блоке 1). Если текущий элемент массива Xi больше значения, которое хранится в переменной max (блок 3), то за максимум принимается значение этого элемента: max=Xi, и запоминается его номер: imax=i (блок 4). Если текущий элемент массива не больше максимума, то проверяется, не меньше ли он минимума (блок 5). В случае если текущий элемент Xi окажется меньше минимального значения, которое хранится в переменной min, то за минимум принимается значение этого элемента: min=Xi, и запоминается его номер: imin=i (блок 6). После выхода из цикла будут выведены значения максимального и минимального элементов, а также их номера в массиве (блок 7).
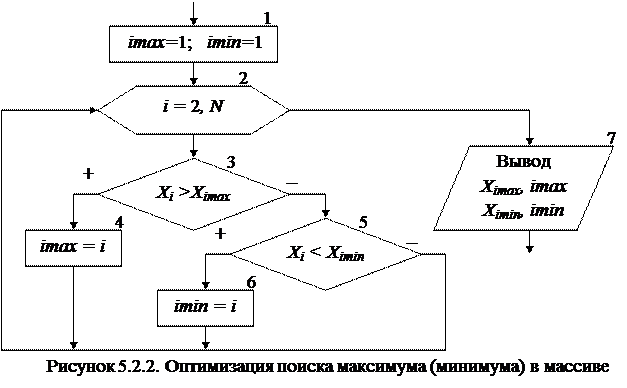
В блоке 1 дополнительным переменным imax и imin, используемых для хранения номеров максимального и минимального элемента, присваивается значение 1. Таким образом, за максимум и минимум принимается 1-й элемент массива, само же значение этого элемента нигде дополнительно не сохраняется. Оставшиеся элементы массива также перебираются, начиная со второго (блок 2). При этом каждый элемент массива Xi сравнивается с элементами, имеющими номер равный imax (блок 3) и imin (блок 6), т.е. с элементами принятыми за максимум (минимум). Если результат проверки условий является истиной, то в переменных imax и imin сохраняются индексы новых максимального (блок 4) и минимального (блок 6) элементов. После выхода из цикла будут выведены значения максимального и минимального элементов, а также их номера в массиве (блок 7).
Если в массиве имеется несколько элементов равных по значению максимальному (минимальному) элементу, то алгоритмы, приведенные на рис 5.2.1 и 5.2.2, определят позицию только первого такого элемента. Например, чтобы найти количество элементов массива равных максимальному и позицию последнего такого элемента, можно воспользоваться алгоритмом, приведенным на рис. 5.2.3.
В начале алгоритма за максимум принимается 1-й элемент массива и вводится переменная k для подсчета количества элементов равных максимальному (блок 1). Затем организовывается цикл по перебору оставшихся элементов массива (блок 2). На каждом шаге цикла выполняется следующая последовательность действий.
Вначале текущий элемент массива Xi сравнивается с максимальным (блок 3). Если он оказывается больше элемента, принятого за максимальный, то запоминается номер этого элемента и переменной k присваивается 1 (блок 4). Это означает, что встретился первый «новый» максимальный элемент.
Если текущий элемент не больше максимума, значит, он может быть равным или меньше максимального элемента. Поэтому в блоке 5 текущий элемент массива Xi проверяется на равенство максимальному. Если он оказывается равным максимуму, то опять запоминается номер текущего элемента и значение переменной k увеличивается на 1 (блок 6). Это означает, что встретился следующий элемент равный максимальному элементу. В итоге после выхода из цикла в переменной imax будет храниться индекс последнего по счету элемента равного максимальному, а в переменной k количество элементов, равных максимуму. Если же из блока 6 убрать операцию imax=i, то в переменной imax, как и в предыдущих примерах будет сохранен номер первого по счету элемента равного максимальному.
В некоторых задачах невозможно вначале принять за максимум (минимум) первый элемент массива. Например, если элементы массива ещё не определены (не введены или не вычислены), или если необходимо найти максимум (минимум) только среди положительных, четных по значению и т.д. элементов. Во втором случае неизвестно когда в массиве встретится первый такой элемент. В таких ситуациях можно использовать способ, реализованный в алгоритме из примера 5.2.
Пример 5.2. В массиве Х [N] найти минимальный положительный элемент.
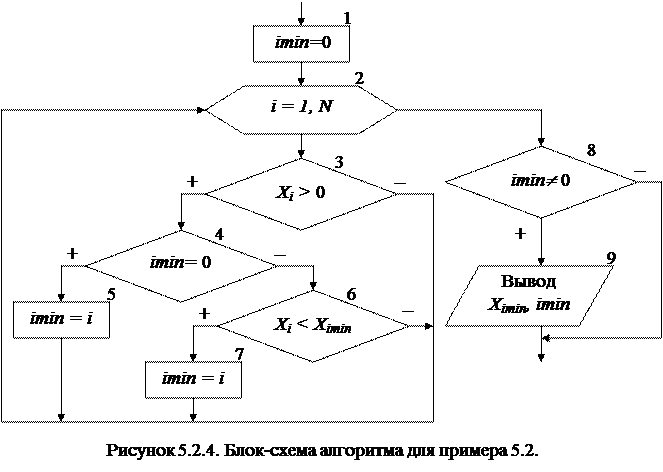
В нашем примере нумерация элементов массива начинается с единицы, поэтому в качестве начального значения для переменной imin принимается 0 (блок 1), т.е. значение которое не могут принимать индексы элементов массива Х. Таким образом показывается, что при обработке массива еще не встречался положительный элемент, который можно принять за начальное значение для минимума. Затем организовывается цикл по перебору всех элементов массива (блок 2). На каждом шаге цикла выполняется следующая последовательность действий.
В блоке 3 проверяется, не является ли текущий элемент массива Xi положительным. Если он отрицательный или равен нулю, то такой элемент пропускается и над ним не выполняется никаких действий. Если Xi > 0, то в блоке 4 проверяется, не является ли этот элемент первым встретившимся положительным элементом массива (признаком чего служит значение imin равное 0). В этом случае в блоке 5 переменной imin будет присвоено текущее значение i. Таким образом, за начальное значение для минимума будет принято значение первого по счету положительного элемента массива Х. Эта ситуация может возникнуть только один раз, и при дальнейшей работе цикла блок 5 больше выполняться не будет. Остальные положительные элементы массива в блоке 6 будут сравниваться с элементом массива, принятым в текущий момент за минимум. Если такой элемент окажется меньше минимального, то в блоке 7 в переменной imin будет сохранен его номер i.
После выхода из цикла проверяется, не равно ли значение imin нулю (блок 8), так как сразу же выводить значение минимального элемента массива Ximin и его номер imin (блок 9) нельзя. Это объясняется тем что, если в массиве Х не будет положительных элементов, то значение переменной imin останется равным нулю, а обращение к несуществующему элементу массива Х0 не допустимо.
Источник
Уроки 55 — 57
Поиск наибольшего и наименьшего элементов массива
(§ 20. Поиск наибольшего и наименьшего элементов массива)
Составление программы на Паскале
поиска минимального и максимального элементов
Содержание урока
§ 20. Поиск наибольшего и наименьшего элементов массива. Поиск максимума и минимума в электронной таблице
§ 20. Поиск наибольшего и наименьшего элементов массива
Поиск максимума и минимума в электронной таблице
 |
 |
|
|
|
 |
 |
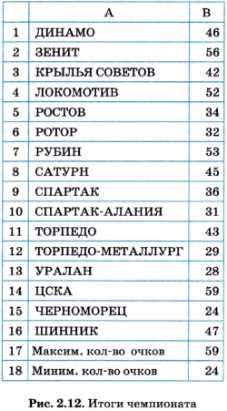
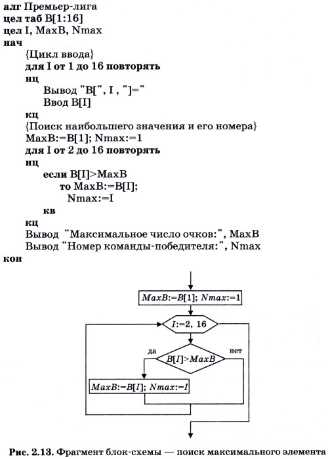
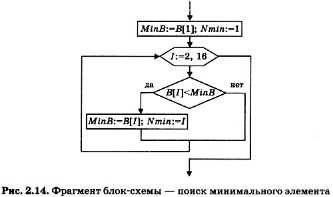
Поиск максимума и минимума в электронной таблице Одной из типовых задач обработки массивов является поиск наибольшего или наименьшего значения среди значений его элементов. Построим алгоритм решения этой задачи и составим программу на Паскале. Для примера возьмем итоговые данные чемпионата России по футболу в премьер-лиге за 2003 год. На рисунке 2.12 показана электронная таблица с итогами чемпионата. В столбце А расположены названия команд, в столбце В — количество очков, набранных каждой командой. Команды перечислены в алфавитном порядке. Победителем является команда, набравшая наибольшее количество очков. Команда, набравшая очков меньше всех других, в следующем сезоне покидает премьер-лигу. Для определения максимального значения в электронной таблице существует функция МАКС(), а для нахождения минимального значения — функция МИН( ). В ячейке B17 записана формула МАКС(В1:В16), а в ячейке В18 — формула МИН(В1:В16). Результаты вы видите в таблице. Отсюда делаем вывод: чемпионом России стала команда ЦСКА, а на последнем месте — «Черноморец». Блок-схемы алгоритмов поиска максимума и минимума в массивеРазберемся, как же программируется определение максимального и минимального значений в числовом массиве. Начнем с поиска максимума. Опишем алгоритм на Алгоритмическом языке. Пусть в целочисленный массив B[1:16] заносятся очки команд в том порядке, в каком они расположены в таблице на рис. 2.12. Максимальное количество очков получим в переменной МахВ. Кроме того, найдем еще и номер команды, занявшей первое место. Для этого будем использовать переменную Nmax. Рассмотрим алгоритм решения задачи. Алгоритм будет составлен исходя из упрощающего предположения о том, что максимальное количество баллов набрала только одна команда. Именно ее номер и будет выведен в качестве результата. Более общий вариант предлагается для рассмотрения в задании к данному параграфу. Ниже приведен полный алгоритм на Алгоритмическом языке, а на рис. 2.13 — фрагмент блок-схемы, относящийся только к выбору максимального элемента (без ввода и вывода). Идея алгоритма состоит в следующем. В переменную МахВ заносится значение первого элемента массива, в переменную Nmax — единица, т. е. номер первого элемента. Затем в цикле последовательно с МахВ сравниваются все остальные элементы массива В. Если очередной элемент оказывается больше текущего значения МахВ, то его значение заносится в МахВ, а его номер — в Nmax. Когда закончится цикл, в МахВ останется наибольшее число из всего массива, а в Nmax — его номер. Теперь нетрудно догадаться, как искать минимальное значение в массиве и его номер. Если для этого использовать в программе переменные MinB и Nmin и в условии ветвления заменить знак отношения «больше» на «меньше», то получим нужный алгоритм. Его фрагмент показан блок-схемой на рис. 2.14. Если в алгоритме нужно одновременно искать максимальное и минимальное значения, то соответствующие ветвления можно объединить в одном цикле. Именно так сделано в приведенной ниже программе на Паскале. Следующая страница Источник Adblock |
Часто встречаются задачи, где необходимо найти максимальный элемент в массиве. Рассмотрим общий алгоритм решения такой задачи.
Первое, что придётся сделать – создать массив. Как нам уже известно, нужно использовать цикл с параметром. Также удобнее будет создать массив случайным образом, если в условии задачи не оговорён способ задания массива.
Алгоритм нахождения максимального элемента массива выполняется следующим образом.
Сначала указываем, что первый элемент массива считается максимальным, иначе говоря – Max = A[i].
Потом начинаем процесс сравнивания последующих элементов массива с максимальным элементом в массиве.
Тут возможно два случая :
- Если максимальный элемент больше следующего, то ничего не меняем.
- Если максимальный элемент меньше следующего, то он становиться максимальным.
После этого выводим на экран максимальный элемент.
Блок-схема максимальный элемент массива
Программа максимальный элемент массива Pascal
Ниже представлен текст программы на языке Pascal, как найти максимальный элемент массива. Как было указанно в алгоритме выше, сначала создается сам массив (в моем случает любые целые числа от 0 до 100 включительно).
Program Max_element_massiva ;
Var i, n, max : integer ;
A : array [1..100] of integer;
Begin
Writeln('Введите количество элементов массива') ;
Readln(N) ;
Randomize;
For i := 1 to N do
begin
A[i] := Random(100);
Write(A[i]);
end;
Max := A[1];
For i := 2 to N do
if A[i]>Max then Max := A[i];
Writeln('Максимальный Элемент массива = ',Max) ;
Readln ;
End.





 на значение элемента массива.
на значение элемента массива.![SG=sqrt[{k}]{P}](https://intuit.ru/sites/default/files/tex_cache/f82988a0c52a19e1239efbcb41a1e2a5.png) .
.







 § 20. Поиск наибольшего и наименьшего элементов массива. Программа на Паскале поиска максимума и минимума в массиве
§ 20. Поиск наибольшего и наименьшего элементов массива. Программа на Паскале поиска максимума и минимума в массиве