Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Given undirected weighted graph G, the task is to find the Maximum Spanning Tree of the Graph using Prim’s Algorithm
Prims algorithm is a Greedy algorithm which can be used to find the Minimum Spanning Tree (MST) as well as the Maximum Spanning Tree of a Graph.
Examples:
Input: graph[V][V] = {{0, 2, 0, 6, 0}, {2, 0, 3, 8, 5}, {0, 3, 0, 0, 7}, {6, 8, 0, 0, 9}, {0, 5, 7, 9, 0}}
Output:
The total weight of the Maximum Spanning tree is 30.
Edges Weight
3 – 1 8
4 – 2 7
0 – 3 6
3 – 4 9
Explanation:
Choosing other edges won’t result in maximum spanning tree.
Maximum Spanning Tree:
Given an undirected weighted graph, a maximum spanning tree is a spanning tree having maximum weight. It can be easily computed using Prim’s algorithm. The goal here is to find the spanning tree with the maximum weight out of all possible spanning trees.
Prim’s Algorithm:
Prim’s algorithm is a greedy algorithm, which works on the idea that a spanning tree must have all its vertices connected. The algorithm works by building the tree one vertex at a time, from an arbitrary starting vertex, and adding the most expensive possible connection from the tree to another vertex, which will give us the Maximum Spanning Tree (MST).
Follow the steps below to solve the problem:
- Initialize a visited array of boolean datatype, to keep track of vertices visited so far. Initialize all the values with false.
- Initialize an array weights[], representing the maximum weight to connect that vertex. Initialize all the values with some minimum value.
- Initialize an array parent[], to keep track of the maximum spanning tree.
- Assign some large value, as the weight of the first vertex and parent as -1, so that it is picked first and has no parent.
- From all the unvisited vertices, pick a vertex v having a maximum weight and mark it as visited.
- Update the weights of all the unvisited adjacent vertices of v. To update the weights, iterate through all the unvisited neighbors of v. For every adjacent vertex x, if the weight of the edge between v and x is greater than the previous value of v, update the value of v with that weight.
Below is the implementation of the above algorithm:
C++
#include <bits/stdc++.h>
using namespace std;
#define V 5
int findMaxVertex(bool visited[], int weights[])
{
int index = -1;
int maxW = INT_MIN;
for (int i = 0; i < V; i++) {
if (visited[i] == false
&& weights[i] > maxW) {
maxW = weights[i];
index = i;
}
}
return index;
}
void printMaximumSpanningTree(int graph[V][V],
int parent[])
{
int MST = 0;
for (int i = 1; i < V; i++) {
MST += graph[i][parent[i]];
}
cout << "Weight of the maximum Spanning-tree "
<< MST << 'n'
<< 'n';
cout << "Edges tWeightn";
for (int i = 1; i < V; i++) {
cout << parent[i] << " - " << i << " t"
<< graph[i][parent[i]] << " n";
}
}
void maximumSpanningTree(int graph[V][V])
{
bool visited[V];
int weights[V];
int parent[V];
for (int i = 0; i < V; i++) {
visited[i] = false;
weights[i] = INT_MIN;
}
weights[0] = INT_MAX;
parent[0] = -1;
for (int i = 0; i < V - 1; i++) {
int maxVertexIndex
= findMaxVertex(visited, weights);
visited[maxVertexIndex] = true;
for (int j = 0; j < V; j++) {
if (graph[j][maxVertexIndex] != 0
&& visited[j] == false) {
if (graph[j][maxVertexIndex] > weights[j]) {
weights[j] = graph[j][maxVertexIndex];
parent[j] = maxVertexIndex;
}
}
}
}
printMaximumSpanningTree(graph, parent);
}
int main()
{
int graph[V][V] = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
maximumSpanningTree(graph);
return 0;
}
Java
import java.io.*;
class GFG
{
public static int V = 5;
static int findMaxVertex(boolean visited[],
int weights[])
{
int index = -1;
int maxW = Integer.MIN_VALUE;
for (int i = 0; i < V; i++)
{
if (visited[i] == false && weights[i] > maxW)
{
maxW = weights[i];
index = i;
}
}
return index;
}
static void printMaximumSpanningTree(int graph[][],
int parent[])
{
int MST = 0;
for (int i = 1; i < V; i++)
{
MST += graph[i][parent[i]];
}
System.out.println("Weight of the maximum Spanning-tree "
+ MST);
System.out.println();
System.out.println("Edges tWeight");
for (int i = 1; i < V; i++)
{
System.out.println(parent[i] + " - " + i + " t"
+ graph[i][parent[i]]);
}
}
static void maximumSpanningTree(int[][] graph)
{
boolean[] visited = new boolean[V];
int[] weights = new int[V];
int[] parent = new int[V];
for (int i = 0; i < V; i++) {
visited[i] = false;
weights[i] = Integer.MIN_VALUE;
}
weights[0] = Integer.MAX_VALUE;
parent[0] = -1;
for (int i = 0; i < V - 1; i++) {
int maxVertexIndex
= findMaxVertex(visited, weights);
visited[maxVertexIndex] = true;
for (int j = 0; j < V; j++) {
if (graph[j][maxVertexIndex] != 0
&& visited[j] == false) {
if (graph[j][maxVertexIndex]
> weights[j]) {
weights[j]
= graph[j][maxVertexIndex];
parent[j] = maxVertexIndex;
}
}
}
}
printMaximumSpanningTree(graph, parent);
}
public static void main(String[] args)
{
int[][] graph = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
maximumSpanningTree(graph);
}
}
Python3
import sys
V = 5;
def findMaxVertex(visited, weights):
index = -1;
maxW = -sys.maxsize;
for i in range(V):
if (visited[i] == False and weights[i] > maxW):
maxW = weights[i];
index = i;
return index;
def printMaximumSpanningTree(graph, parent):
MST = 0;
for i in range(1, V):
MST += graph[i][parent[i]];
print("Weight of the maximum Spanning-tree ", MST);
print();
print("Edges tWeight");
for i in range(1, V):
print(parent[i] , " - " , i , " t" , graph[i][parent[i]]);
def maximumSpanningTree(graph):
visited = [True]*V;
weights = [0]*V;
parent = [0]*V;
for i in range(V):
visited[i] = False;
weights[i] = -sys.maxsize;
weights[0] = sys.maxsize;
parent[0] = -1;
for i in range(V - 1):
maxVertexIndex = findMaxVertex(visited, weights);
visited[maxVertexIndex] = True;
for j in range(V):
if (graph[j][maxVertexIndex] != 0 and visited[j] == False):
if (graph[j][maxVertexIndex] > weights[j]):
weights[j] = graph[j][maxVertexIndex];
parent[j] = maxVertexIndex;
printMaximumSpanningTree(graph, parent);
if __name__ == '__main__':
graph = [[0, 2, 0, 6, 0], [2, 0, 3, 8, 5], [0, 3, 0, 0, 7], [6, 8, 0, 0, 9],
[0, 5, 7, 9, 0]];
maximumSpanningTree(graph);
C#
using System;
class GFG
{
public static int V = 5;
static int findMaxVertex(bool[] visited,
int[] weights)
{
int index = -1;
int maxW = int.MinValue;
for (int i = 0; i < V; i++)
{
if (visited[i] == false && weights[i] > maxW)
{
maxW = weights[i];
index = i;
}
}
return index;
}
static void printMaximumSpanningTree(int[, ] graph,
int[] parent)
{
int MST = 0;
for (int i = 1; i < V; i++)
{
MST += graph[i, parent[i]];
}
Console.WriteLine(
"Weight of the maximum Spanning-tree " + MST);
Console.WriteLine();
Console.WriteLine("Edges tWeight");
for (int i = 1; i < V; i++) {
Console.WriteLine(parent[i] + " - " + i + " t"
+ graph[i, parent[i]]);
}
}
static void maximumSpanningTree(int[, ] graph)
{
bool[] visited = new bool[V];
int[] weights = new int[V];
int[] parent = new int[V];
for (int i = 0; i < V; i++) {
visited[i] = false;
weights[i] = int.MinValue;
}
weights[0] = int.MaxValue;
parent[0] = -1;
for (int i = 0; i < V - 1; i++) {
int maxVertexIndex
= findMaxVertex(visited, weights);
visited[maxVertexIndex] = true;
for (int j = 0; j < V; j++) {
if (graph[j, maxVertexIndex] != 0
&& visited[j] == false) {
if (graph[j, maxVertexIndex]
> weights[j]) {
weights[j]
= graph[j, maxVertexIndex];
parent[j] = maxVertexIndex;
}
}
}
}
printMaximumSpanningTree(graph, parent);
}
static public void Main()
{
int[, ] graph = { { 0, 2, 0, 6, 0 },
{ 2, 0, 3, 8, 5 },
{ 0, 3, 0, 0, 7 },
{ 6, 8, 0, 0, 9 },
{ 0, 5, 7, 9, 0 } };
maximumSpanningTree(graph);
}
}
Javascript
<script>
var V = 5;
function findMaxVertex(visited, weights)
{
var index = -1;
var maxW = -1000000000;
for (var i = 0; i < V; i++) {
if (visited[i] == false
&& weights[i] > maxW) {
maxW = weights[i];
index = i;
}
}
return index;
}
function printMaximumSpanningTree(graph, parent)
{
var MST = 0;
for (var i = 1; i < V; i++) {
MST += graph[i][parent[i]];
}
document.write( "Weight of the maximum Spanning-tree "
+ MST + '<br>'
+ '<br>');
document.write( "Edges tWeight<br>");
for (var i = 1; i < V; i++) {
document.write( parent[i] + " - " + i + " "
+ graph[i][parent[i]] + " <br>");
}
}
function maximumSpanningTree(graph)
{
var visited = Array(V).fill(false);
var weights = Array(V).fill(-1000000000);
var parent = Array(V).fill(0);
weights[0] = 1000000000;
parent[0] = -1;
for (var i = 0; i < V - 1; i++) {
var maxVertexIndex
= findMaxVertex(visited, weights);
visited[maxVertexIndex] = true;
for (var j = 0; j < V; j++) {
if (graph[j][maxVertexIndex] != 0
&& visited[j] == false) {
if (graph[j][maxVertexIndex] > weights[j]) {
weights[j] = graph[j][maxVertexIndex];
parent[j] = maxVertexIndex;
}
}
}
}
printMaximumSpanningTree(graph, parent);
}
var graph = [ [ 0, 2, 0, 6, 0 ],
[ 2, 0, 3, 8, 5 ],
[ 0, 3, 0, 0, 7 ],
[ 6, 8, 0, 0, 9 ],
[ 0, 5, 7, 9, 0 ] ];
maximumSpanningTree(graph);
</script>
Output:
Weight of the maximum Spanning-tree 30 Edges Weight 3 - 1 8 4 - 2 7 0 - 3 6 3 - 4 9
Time Complexity: O(V2) where V is the number of nodes in the graph.
Auxiliary Space: O(V2)
Last Updated :
10 Nov, 2021
Like Article
Save Article
Привет, Вы узнаете про алгоритм прима онлайн, Разберем основные ее виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое
алгоритм прима онлайн, минимальное остовное дерево, алгоритм прима, prim algorithm, остовное дерево, максимальное остовное дерево , настоятельно рекомендую прочитать все из категории Классические алгоритмы онлайн.
минимальное
остовное дерево (
алгоритм прима , Prim Algorithm) онлайн калькулятор
.
Алгоритм Прима принимает квадратную матрицу (представляющую собой граф с взвешенными дугами) и находит дуги, которые образуют минимального остов . .
Онлайн алгоритм Прима (prima)
Открыть на весь экран
Описание
1. введите размерность матрицы
2. заполните матрицу инцидентности для вашего графа
3. нажмите “запустить Prim”
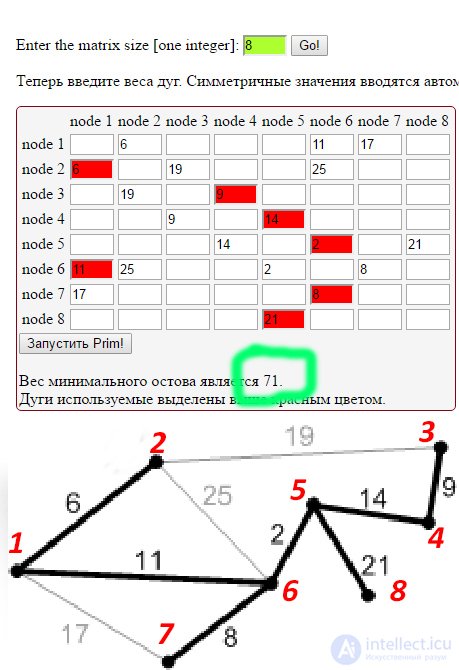
4. выделите на вашем графе нужные дуги входящие в остновное дерево, проверьте общий вес
пример расчета и преобразования графа в матрицу на картинке ниже
Задача построения минимального остовного дерева встречается в различных областях. Интересным ее применением является проблема построения смешанного остовного дерева (Dana Richards and Jeffrey S. Salowe. Mixed spanning trees in theory and practice. International Journal Of Computational Geometry & Applications. Vol. 9, No. 3 (1999), 277-292): построить для графа дерево со свойствами минимального остовного дерева и дерева кратчайших путей. Другой важной задачей является быстрое обновление минимального остовного дерева при изменении графа. В статьеSajal K. Das, Paolo Ferragina “An Erew Pram algorithm for updating minimum spanning trees” показано, как для графа с n вершинами и m ребрами выполнить обновление одного ребра за учетное время O(logn).
Проблема построения минимального остовного дерева достаточно разносторонняя, и продолжает исследоваться и сегодня. В настоящей статье представлены только базовые алгоритмы. Ознакомиться с более продвинутыми алгоритмами можно по статьям из списка используемой литературы.
Построение минимального остовного дерева
Алгоритм Крускала
Алгоритм Крускала объединяет вершины графа в несколько связных компонент, каждая из которых является деревом. На каждом шаге из всех ребер, соединяющих вершины из различных компонент связности, выбирается ребро с наименьшим весом. Необходимо проверить, что оно является безопасным. Безопасность ребра гарантируется ранее доказанной теоремой о безопасных ребрах. Так как ребро является самым легким из всех ребер, выходящих из данной компоненты, оно будет безопасным.
Остается понять, как реализовать выбор безопасного ребра на каждом шаге. Для этого в алгоритме Крускала все ребра графа G перебираются по возрастанию веса. Для очередного ребра проверяется, не лежат ли концы ребра в разных компонентах связности, и если это так, ребро добавляется, и компоненты объединяются.
Удобно использовать для хранения компонент структуры данных для непересекающихся множеств, как, например, списки или, что лучше, лес непересекающихся множеств со сжатием путей и объединением по рангу (один из самых быстрых известных методов). Элементами множеств являются вершины графа, каждое множество содержит вершины одной связной компоненты. Для работы с множествами используются следующие процедуры:
| Make-Set(v) | Создание множества из набора вершин |
| Find-Set(v) | Возвращает множество, содержащее данную вершину |
| Union(u,v) | Объединяет множества, содержащие данные вершины |
Общая схема алгоритма выглядит так:
MST-KRUSKAL(G,w)
1: A ← 0
2: foreach (для каждой) вершины v ∈ V[G]
3: do Make-Set(v)
4: упорядочить ребра по весам
5: for (u,v) ∈ E (в порядке возрастания веса)
6: do if Find-Set(u) ≠ Find-Set(v) then
7: A ← A ∪ {(u,v)}
8: Union(u,v)
9: return A
На рисунках К1-К8 представлена работа алгоритма.
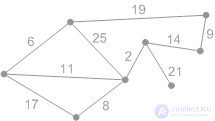
Рис. К1. Начальная фаза. Минимальный покрывающий лес пуст. |
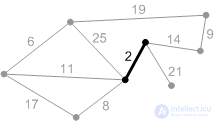
Рис. К2. Перебираем ребра в порядке возрастания веса: первое ребро с весом 2. Добавляем его к А. |
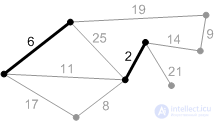
Рис. К3. Следующее безопасное ребро с весом 6. Добавляем его. |

Рис. К4. |
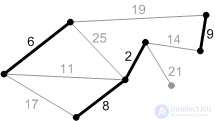
Рис. К5. |
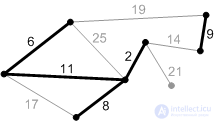
Рис. К6. |
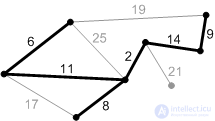
Рис . Об этом говорит сайт https://intellect.icu . К7. |
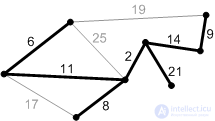
Рис. К8. Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено. |
Подсчитаем время работы алгоритма. Будем считать, что для хранения непересекающихся множеств используется метод с объединением по рангу и сжатием путей ( , 21.3), т.к. это самый быстрый способ из известных на сегодняшний день. Инициализация занимает время O(V), упорядочение ребер в строке 4 – O(ElogE). Далее производится O(E) операций, в совокупности занимающих время O(Eα’(E,V)), где α’ – функция, обратная к функции Аккермана (см. , 21.4). Поскольку α’(E,V) = o(logE), общее время работы алгоритма Крускала составляет O(ElogE) (основное время уходит на сортировку).
Алгоритм Прима
Как и алгоритм Крускала, алгоритм Прима следует общей схеме алгоритма построения минимального остовного дерева: на каждом шаге мы добавляем к строящемуся остову безопасное ребро. Алгоритм Прима относится к группе алгоритмов наращивания минимального остова: на каждом шаге существует не более одной нетривиальной (не состоящей из одной вершины) компоненты связности, и каждый к ней добавляется ребро наименьшего веса, соединяющее вершины компоненты с остальными вершинами. По теореме такое ребро является безопасным.
При реализации надо уметь на каждом шаге быстро выбирать безопасное ребро. Для этого удобно воспользоваться очередью с приоритетами (кучей). Алгоритм получает на вход граф G и его корень r – вершина, на которой будет наращиваться минимальный остов. Все вершины G, еще не попавшие в дерево, хранятся в очереди с приоритетом Ω. Приоритет вершины v определяется значением key[v], которое равно минимальному весу ребер, соединяющих v с вершинами минимального остова. Поле p[v] для вершин дерева указывает на родителя, а для вершин из очереди, указывает на ноду дерева, в которою ведет ребро с весом key[v] (одно из таких ребер, если их несколько).
Тогда алгоритм Прима выглядит следующим образом:
MST-PRIM(G,w, r)
1: Ω ← V[G]
2: foreach (для каждой) вершины u ∈ Ω
3: do key[u] ← ∞
4: key[r] ← 0
5: p[r] = NIL
6: while (пока) Ω ≠ 0
7: do u ← EXTRACT-MIN(Ω)
8: foreach (для каждой) вершины v ∈ Adj(u)
9: do if v ∈ Ω и w(u,v) < key[v] then
10: p[v] ← u
11: key[v] ← w(u,v)
На рисунках П1-П8 показана схема работы алгоритма Прима с корнем r.
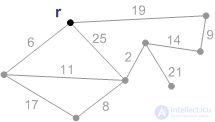
Рис. П1. Начальная фаза. Минимальный покрывающий лес состоит из корня и пустого множества ребер. |
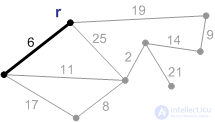
Рис. П2. Ребро с весом 6 является минимальным ребром, соединяющим корень с остальными вершинами. Добавляем его к минимальному остову. |
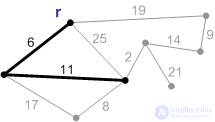
Рис. П3. Следующее безопасное ребро с весом 11. Добавляем его. |
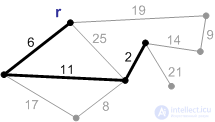
Рис. П4. |
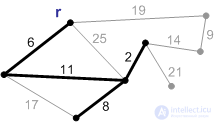
Рис. П5. |
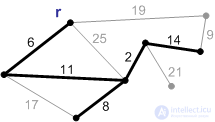
Рис. П6. |
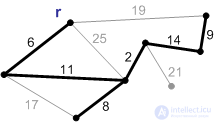
Рис. П7. |
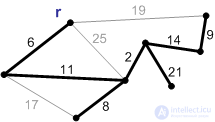
Рис. П8. Ребра с весом 17, 19 и 25 – не безопасные. Их концы лежат в одной компоненте связности. Ребро с весом 21 – безопасное, поэтому добавляем его. Минимальное остовное дерево построено. |
Время работы алгоритма Прима зависит от того, как реализована очередь с приоритетами Ω. Если использовать двоичную кучу, инициализацию в строках 1-4 можно выполнить за время O(V). Далее цикл выполняется |V| раз, и каждая операция EXTRACT-MIN занимает время O(VlogV). Цикл for в строках 8-11 выполняется в общей сложности O(E), поскольку сумма степеней вершин графа равна 2|E|. Проверку принадлежности в строке 9 можно выполнить за время O(1), если хранить состояние очереди еще и как битовый вектор размера |V|. Присваивание в строке 11 подразумевает выполнение операции уменьшения ключа (DECREASE-KEY), которая для двоичной кучи может быть выполнена за время O(logV). Таким образом всего получаем O(VlogV+ElogV)=O(ElogV).
Лучшую оценку можно получить, если использовать фибоначчиевы кучи. С помощью фибоначчиевых куч можно выполнить операцию EXTRACT-MIN за учетное время O(logV), а операциюDECREASE-KEY – за учетное время O(1). В этом случае суммарное время работы алгоритма Прима составит O(E+VlogV).
Хотя оба алгоритма работают за (O(M log N)), существуют константные различия в скорости их работы. На разреженных графах (количество ребер примерно равно количеству вершин) быстрее работает алгоритм Крускала, а на насыщенных (количество ребер примерно равно квадрату количеству вершин) – алгоритм Прима (при использовании матрицы смежности).
На практике чаще используется алгоритм Крускала.
максимальное остовное дерево
противоположность алгоритму Крускала для минимального остовного дерева – является нахождение максимального остовного дерева.
Один из методов вычисления максимального веса остовного дерева сети G – благодаря Крускалу-можно резюмировать следующим образом.
- Отсортируйте ребра G в порядке убывания по весу. Пусть t-множество ребер, образующих остовное дерево максимального веса. Установите T = ∅.
- Добавьте первое ребро к т.
- Добавьте следующее ребро к T тогда и только тогда, когда оно не образует цикл в T. Если оставшихся ребер нет, выйдите и сообщите, что G отключен.
- Если T имеет n-1 ребер (где n-число вершин в G), остановитесь и выведите T . В противном случае перейдите к шагу 3.
“Максимальное связующее дерево – это связующее дерево взвешенного графа, имеющего максимальный вес. Он может быть вычислен путем отрицания весов для каждого ребра и применения алгоритма Крускала (Pemmaraju and Skiena, 2003, p. 336).”
Если вы инвертируете вес на каждом ребре и минимизируете его, получите ли вы максимальное связующее дерево? Если это сработает, вы можете использовать тот же алгоритм. Конечно, нулевой вес будет проблемой.
алгоритм улучшения:
- сначала постройте произвольное дерево (используя BFS или DFS)
- затем выберите ребро вне дерева, добавьте к дереву, оно образует цикл, сбросьте наименьший вес ребра в цикле.
- продолжайте делать это до тех пор, пока не будут рассмотрены все ребра rest
Таким образом, мы получим максимальное связующее дерево.
Это дерево удовлетворяет любому ребру вне дерева, если оно добавлено, то образует цикл, а ребро вне <=-любые веса ребер в цикле
На самом деле это необходимое и достаточное условие для того, чтобы связующее дерево было максимальным связующим деревом.
ПФ.
Необходимо: очевидно, что это необходимо, или мы могли бы поменять ребро местами, чтобы сделать дерево с большей суммой Весов ребер.
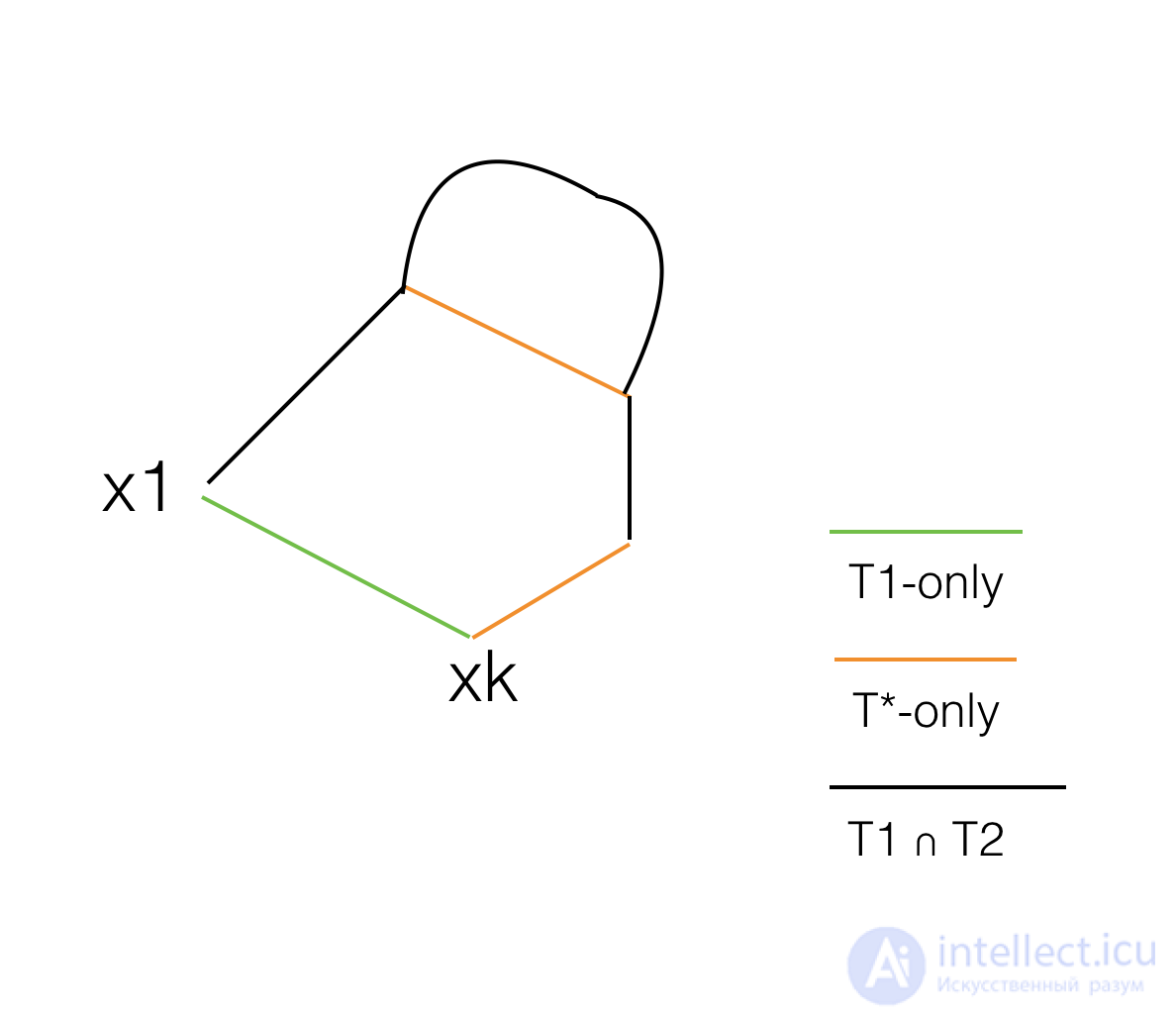
Достаточно: предположим, что дерево T1 удовлетворяет этому условию, а T2-максимальное связующее дерево.
Тогда для ребер T1 ∪ T2 существуют только ребра T1, только ребра T2, только ребра T1 ∩ T2, если мы добавим к T2 только ребро T1(x1, xk), мы знаем, что оно образует цикл, и мы утверждаем, что в этом цикле должно существовать одно только ребро T2, которое имеет те же веса ребер, что и (x1, xk). Затем мы можем обменять эти ребра, чтобы получить дерево с еще одним ребром, общим с T2, и иметь ту же сумму весов ребер, повторяя это, мы получим T2. таким образом, T1 также является максимальным остовным деревом.
Докажите это утверждение:
предположим, что это не так, в цикле мы должны иметь только ребро T2, так как T1-это дерево. Если ни одно из T2-только ребер не имеет значения, равного значению (x1, xk), то каждое из T2-только ребер делает петлю с деревом T1, тогда T1 имеет петлю, приводящую к противоречию.
Этот алгоритм взят у UTD профессора R. Примечания цхандрасекаран по. Вы можете обратиться сюда: Single Commodity Multi-terminal Flows.
есть другой подход для нахождения максимального остовного дерева (MST) в графе G=(V, E)
Мы можем применить какой-то алгоритм Прима для нахождения MST. Для этого я должен определить свойство Cut для максимального взвешенного ребра.
Свойство Cut: допустим, в любой точке у нас есть множество S, которое содержит вершины, находящиеся в MST( пока предположим, что оно вычисляется каким-то образом ). Теперь рассмотрим множество S/V ( вершины не в MST ):
Утверждение: ребро от S до S/V, имеющее максимальный вес, всегда будет находиться в каждом MST.
Доказательство: предположим,что в точке, когда мы добавляем вершины в наше множество S, максимальное взвешенное ребро от S до S/V равно e=(u, v), где u находится в S, а v-в S/V.. Добавьте ребро e к MST. Это создаст цикл в исходном MST. Пересеките цикл и найдите вершины u’ в S и v’ в S/V такие, что u’ – последняя вершина в S, после которой мы входим в S / V, а v’ – первая вершина в S/V на пути в цикле от u до v.
Удалите ребро e’=(u’, v’), и результирующий граф все еще связан, но вес e больше, чем e’ [ так как e является максимальным взвешенным ребром от S до S/V в этой точке], так что это приводит к MST, который имеет сумму весов больше, чем исходный MST. Так что это противоречие. Это означает, что ребро e должно быть в каждом MST.
Алгоритм поиска MST:
Start from S={s} //s is the start vertex while S does not contain all vertices do { for each vertex s in S add a vertex v from S/V such that weight of edge e=(s,v) is maximum } end while
Реализация: мы можем реализовать с помощью Max Heap / Priority Queue, где ключ – это максимальный вес ребра от вершины в S до вершины в S/V, а значение-сама вершина. Добавление вершины в S равно Extract_Max из кучи, и при каждом Extract_Max изменяется ключ вершин, соседних с только что добавленной вершиной.
Таким образом, требуется m операций Change_Key и n операций Extract_Max.
Extract_Min и Change_Key как можно реализовать за o(зарегистрируйте N). n – число вершин.
Таким образом, это занимает O(m log n) времени. m – это число ребер в графе.
См. также
- Алгоритм Краскала
- Алгоритм Дейкстры
- Минимальное остовное дерево
- Алгоритмы на графах
- Задачи, решаемые жадным алгоритмом
- Остовное дерево
- Алгоритмы поиска на графах
- алгоритм прима ,
- кратчайший путь , алгоритмы поиска кратчайшего пути , поиск пути ,
К сожалению, в одной статье не просто дать все знания про алгоритм прима онлайн. Но я – старался.
Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое алгоритм прима онлайн, минимальное остовное дерево, алгоритм прима, prim algorithm, остовное дерево, максимальное остовное дерево
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Классические алгоритмы онлайн
В планарных графах возможно построить остовное дерево за , что заметно быстрее, чем алгоритмы, используемые для поиска остовного дерева в общем случае.
Рассмотрим более общую задачу — построение остовного дерева минимального (максимального) веса в планарном графе, которая также может быть решена за .
Содержание
- 1 Остовное дерево минимального (максимального) веса в планарном графе
- 2 Формальное описание алгоритма
- 3 Корректность и время работы
- 4 Примечания
- 5 Источники информации
Остовное дерево минимального (максимального) веса в планарном графе
Пусть есть граф , где – множество вершин, – множество рёбер. Для произвольной вершины графа обозначим как множество рёбер графа , инцидентных . Для любого подмножества рёбер граф будем называть остовным лесом графа , когда граф ацикличен. Остовный лес является остовным деревом, когда он связен. Вес ребра обозначим как . Вес подмножества рёбер обозначим как , он является суммой весов рёбер, входящих в . Максимальный остовный лес называется остовным лесом минимального (максимального) веса, когда вес минимален (максимален).
Для решения этой задачи, помимо исходного планарного графа , потребуется его двойственный граф , который можно легко построить геометрически по укладке на плоскости[1].
Если данный граф связен, задача эквивалентна обычной задаче поиска минимального (максимального) по весу остовного дерева. Известно, что подмножество рёбер – максимальный остовный лес тогда и только тогда, когда – максимальный остовный лес . Таким образом, задача поиска минимального по весу остовного леса графа – по сути то же самое, что задача поиска максимального по весу остовного леса .
Формальное описание алгоритма
Итак, имеется планарный граф , его двойственный граф и веса рёбер , на выходе нужно получить остовный лес минимального веса графа и остовный лес максимального веса графа .
Шаг 0: Запись графов. ; .
Шаг 1: Если графы и пусты одновременно, выведем и .
Шаг 2: Выберем вершину в графе или :
Если – изолированная вершина, удалим её и вернёмся к шагу 1;
Если – вершина и в есть петля, перейдём к шагу 3;
Если v – вершина и в нет петель, перейдём к шагу 4;
Если – вершина и в есть петля, перейдём к шагу 5;
Если – вершина и в нет петель, перейдём к шагу 6;
Шаг 3: Пусть – петля , инцидентная .
; ; .
Вернёмся к шагу 1.
Шаг 4: Найдём ребро , достигающее минимального веса среди рёбер из .
; ; . ( обозначает операцию стягивания ребра)
Вернёмся к шагу 1.
Шаг 5: Пусть – петля , инцидентная .
; ; .
Вернёмся к шагу 1.
Шаг 6: Найдём ребро , достигающее максимального веса среди рёбер из .
; ; .
Вернёмся к шагу 1.
Корректность и время работы
Легко убедиться в том, что на протяжении всех итераций приведённого алгоритма является двойственным графом графа , из чего следует корректность этого алгоритма.
На каждой итерации алгоритма происходит удаление ребра или вершины, из этого следует, что количество итераций алгоритма не превосходит .
Далее опишем, как добиться того, чтобы каждая итерация осуществлялась за . Для каждой вершины графа обозначим степень этой вершины (петли считаются дважды). Из формулы Эйлера следует, что в или , где – планарный граф, а – двойственный к нему, существует вершина, степень которой меньше четырёх.
На шаге 2 будем выбирать именно такую вершину. Сначала покажем, что каждая интеграция алгоритма выполняется за , предполагая, что нужная вершина на шаге 2 всегда выбирается за константное время, реализацию обсудим позже.
Итак, оба графа хранятся в виде списков смежности. Тогда, очевидно, шаги 1 и 2 выполняются за . Поскольку при такой реализации рёбра удаляются за константное время, шаги 3 и 5 выполняются за . Рассмотрим шаг 4. Поскольку степень вершины не больше четырёх, поиск ребра минимального веса займёт константное время. Стягивание ребра происходит за . Для шага 6 рассуждения аналогичны.
Вернёмся к выбору вершины на шаге 2. Для этого создадим хэш-таблицу, содержащую все вершины степени меньше четырёх. Это позволяет выбрать нужную вершину за , но хэш-таблицу также нужно обновлять. При удалении ребра из графа степени вершин, инцидентных ему, уменьшаются на 1 (или на 2 в случае петли), степени же остальных вершин не меняются. Теперь рассмотрим случай стягивания ребра. Удаляются концы стягиваемого ребра, а получающаяся в результате этого вершина должна быть добавлена в хэш-таблицу, если её степень меньше четырёх. Таким образом, на каждой итерации алгоритма из хэш-таблицы может быть удалено максимум две вершины, а добавлено – максимум четыре, значит, хэш-таблица обновляется за константное время.
Создание хэш-таблицы должно происходить вместе с шагом 0 и осуществляется за .
Примечания
- ↑ E.L. Lawler, Combinatorial Optimization: Networks and Matroids (Holt, Rinehart and Winston, New York, 1976)
Источники информации
Sciencedirect — The minimum spanning tree problem on a planar graph
Хотя этот поток слишком стар, у меня есть другой подход для поиска максимального остовного дерева (MST) в графе G = (V, E)
Мы можем применить какой-то алгоритм Прима для поиска MST. Для этого я должен определить свойство Cut для максимально взвешенного края.
Свойство Cut: скажем, в любой точке у нас есть множество S, которое содержит вершины, которые находятся в MST (пока предположим, что оно каким-то образом вычислено). Теперь рассмотрим множество S / V (вершины не в MST):
Утверждение: ребро от S до S / V, имеющее максимальный вес, всегда будет в каждом MST.
Доказательство: предположим, что в момент, когда мы добавляем вершины к нашему множеству S, максимальное взвешенное ребро от S до S / V равно e = (u, v), где u находится в S, а v находится в S / V. Теперь рассмотрим MST, который не содержит e. Добавьте ребро e к MST. Это создаст цикл в исходном MST. Пройдите цикл и найдите вершины u ‘в S и v’ в S / V, такие, что u ‘является последней вершиной в S, после чего мы входим в S / V, а v’ – первая вершина в S / V на пути в цикл от u до v.
Удалите ребро e ‘= (u’, v ‘), и результирующий граф все еще будет связан, но вес e больше, чем e’ [поскольку e – это максимальное взвешенное ребро от S до S / V в этой точке], так что это приводит к MST, сумма весов которого превышает исходную MST. Это противоречие. Это означает, что ребро e должно быть в каждом MST.
Алгоритм поиска MST:
Начать с S = {s} // s - начальная вершина, в то время как S не содержит всех вершин do {для каждой вершины s в S добавить вершину v из S / V так, чтобы вес ребра e = (s, v) был максимум} конец пока
Реализация: мы можем реализовать с использованием Max Heap / Priority Queue, где ключ – это максимальный вес ребра от вершины в S до вершины в S / V, а значение – это сама вершина. Добавление вершины в S равно Extract_Max из кучи, и при каждом изменении Extract_Max ключ вершин, смежных с только что добавленной вершиной.
Таким образом, требуется m операций Change_Key и n операций Extract_Max.
Extract_Min и Change_Key могут быть реализованы за O (log n). n – количество вершин.
Итак, это занимает время O (m log n). m – количество ребер в графе.
Дерево
– это граф без циклов.
Понятие дерева
широко используется во многих областях
математики и информатики. Например, как
инструмент при вычислениях, как удобный
способ хранения данных, способ сортировки
или поиска данных.
Достаточно
развитое генеалогическое дерево образует
дерево.
Типичное
частичное организационное дерево для
университета.
Если
дерево имеет хотя бы одно ребро, оно
имеет две вершины со степенью 1. Вершины
со степенью 1 называются листьями.
Другие вершины называются внутренними
вершинами.
Предположим, что
дерево представляет физический объект,
подвижный в вершинах, и подвесим дерево
за одну из его вершин:
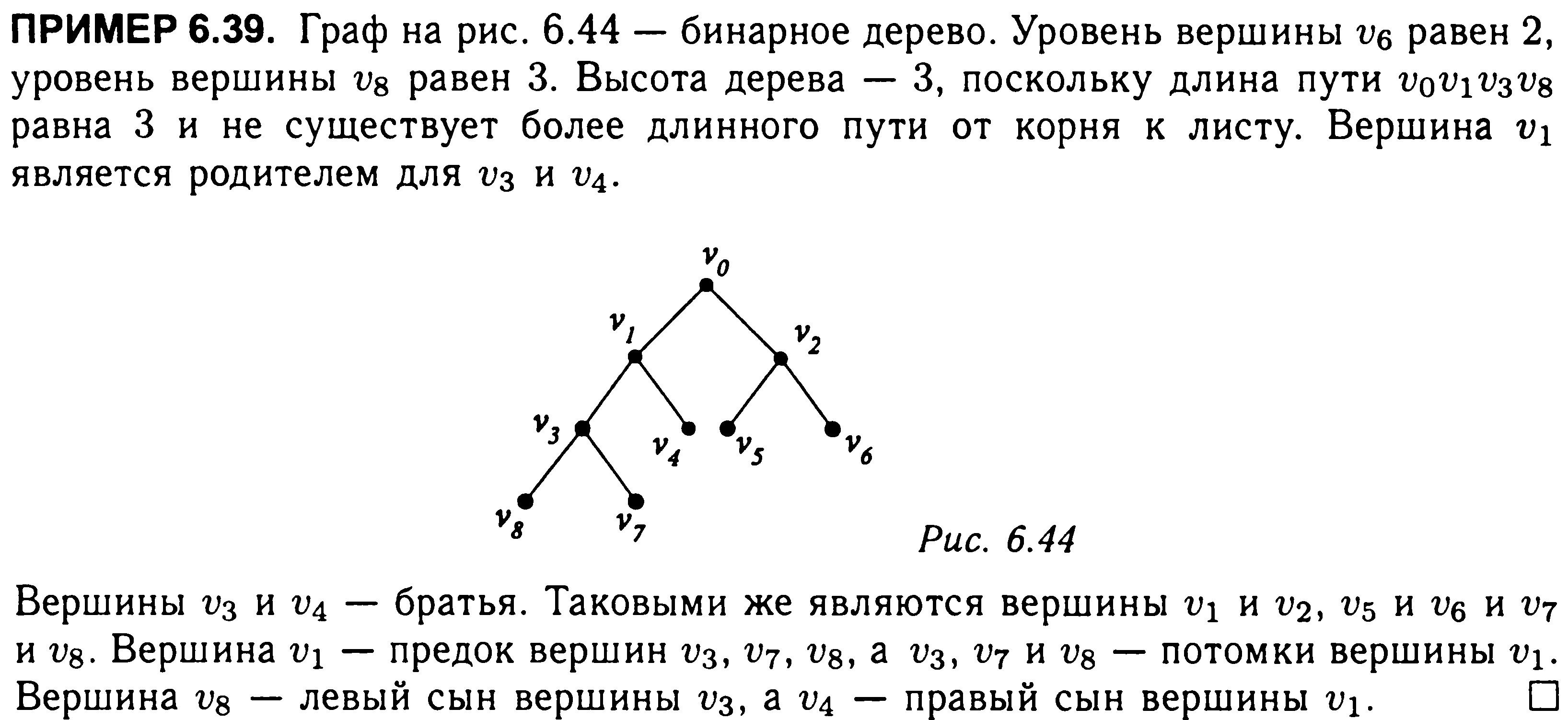
Если
подвесить за вершину V3
или V4
Вершина
в верхней части называется корнем
дерева, если корень определен, то дерево
называется корневым.
При необходимости корневое дерево Т
можно заменить на ориентированное
корневое дерево Т’,
порожденное корневым деревом Т.
Если корень выбран,
уровень
вершины V
определяется длиной единственного пути
из корня в вершину V.
Высотой
дерева называется длина самого длинного
пути от корня дерева до листа.
Если рассматривается
корневое
ориентированное дерево Т’,
порожденное данным корневым деревом
Т, тогда вершина u
называется родителем
вершины v;
a v
называется сыном вершины u,
если существует ориентированное ребро
из u
в v.
Если u
— родитель v
и v1,
тогда v и
v1
называются братьями.
Если существует
ориентированный путь из вершины u
в вершину v,
тогда u
называется предком
вершины v,
a v
называется потомком
вершины u.
Если наибольшая
из степеней выхода для вершин дерева
равна m,
тогда дерево называется m
– арным
деревом.
В частном случае,
когда m
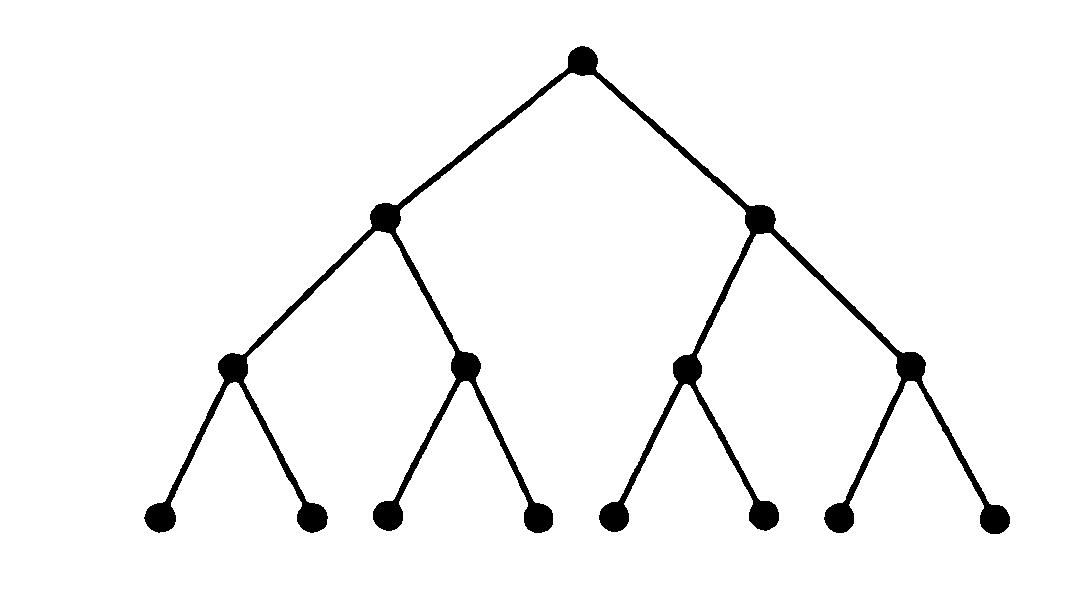
= 2, дерево называется бинарным
деревом.
В каждом бинарном
дереве каждый сын родителя обозначается
либо как левый сын, либо как правый сын
(но не то и другое одновременно).
Связный
граф G(V,E),
не имеющий циклов, называется деревом.
ТЕОРЕМА (основные свойства
деревьев):
Пусть граф G(V,E)
имеет n
вершин. Тогда следующие утверждения
эквивалентны:
-
G
является деревом; -
G
не содержит циклов и имеет n-1
рёбер; -
G
связен и имеет n-1
рёбер; -
G
связен, но удаление ”
ребра нарушает связность; -
”
две вершины графа G
соединены ровно одним путём; -
G
не имеет циклов, но добавление ”
ребра порождает ровно один цикл.
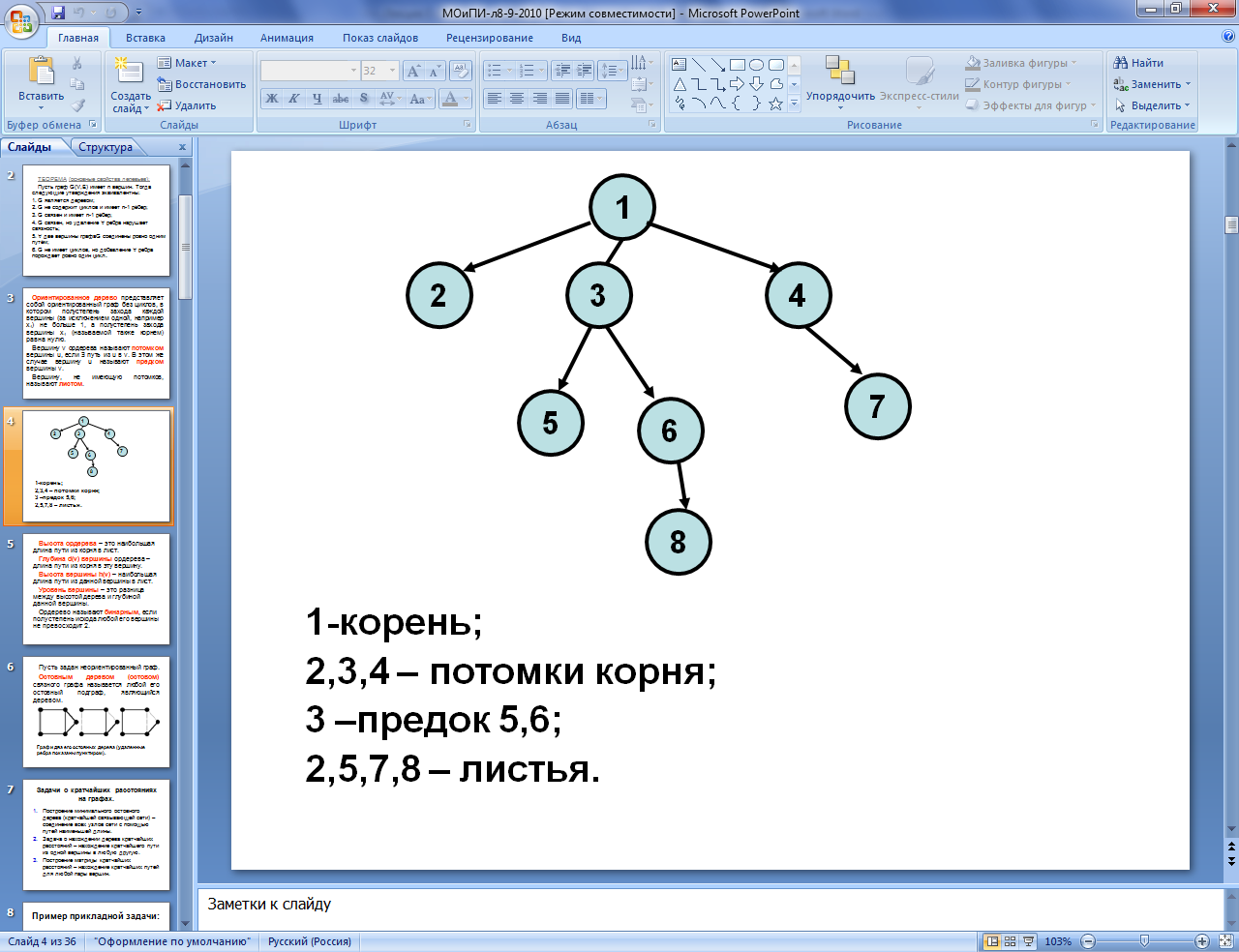
Ориентированное
дерево
представляет собой ориентированный
граф без циклов, в котором полустепень
захода каждой вершины (за исключением
одной, например v1)
не больше 1, а полустепень захода вершины
v1
(называемой также корнем)
равна нулю.
Вершину v
ордерева называют потомком
вершины u,
если $
путь из u
в v.
В этом же случае вершину u
называют предком
вершины v.
Вершину, не имеющую
потомков, называют листом.
Высота ордерева
– это наибольшая длина пути из корня
в лист.
Уровень вершины
ордерева – длина пути из корня в эту
вершину.
Ордерево называют
бинарным,
если полустепень исхода любой его
вершины не превосходит 2.
Пусть задан
неориентированный граф.
Остовным деревом
(остовом)
связного графа называется любой его
остовный подграф, являющийся деревом.
Граф и два его
остовных дерева (удаленные ребра
показаны пунктиром).
Задачи о кратчайших
расстояниях на графах.
-
Построение
минимального остовного дерева
(кратчайшей связывающей сети) –
соединение всех узлов сети с помощью
путей наименьшей длины. -
Задача
о нахождении дерева кратчайших
расстояний – нахождение кратчайшего
пути из одной вершины в любую другую. -
Построение
матрицы кратчайших расстояний –
нахождение кратчайших путей для любой
пары вершин.
Необходимо
проложить линии коммуникаций (дороги,
линии связи, электропередач и т.п.) между
n
заданными “точечными” объектами,
при условии:
во-первых,
известны “расстояния” между каждой
парой объектов (это может быть
геометрическое расстояние или стоимость
прокладки коммуникаций между ними),
во-вторых,
объекты могут быть связаны как
непосредственно, так и с участием
произвольного количества промежуточных
объектов.
При допущении,
что разветвления возможны только в
этих же n
объектах, задача сводится к нахождению
кратчайшего остовного дерева (SST –
shortest spanning tree, или MST – minimal spanning tree) во
взвешенном графе, вершины которого
соответствуют заданным объектам, а
веса ребер равны “расстояниям”
между ними.
Определение.
Вес
остовного
дерева взвешенного графа G
равен сумме весов, приписанных ребрам
остовного дерева. Будем обозначать
(T).
Минимальным
остовным деревом
(МОД) называется такое остовное дерево
графа G,
что вес T
меньше или равен весу любого другого
остовного дерева графа G.
Вес минимального остовного дерева
будем обозначать min(T).
Задача 1:
найти кратчайшее остовное дерево
(минимальный покрывающий остов)
взвешенного графа.
Пусть дан
неориентированный связный граф со
взвешенными ребрами. Вес ребра (xi,xj)
обозначим cij.
Из всех остовов графа необходимо найти
один, у которого сумма весов на ребрах
наименьшая.
Стоимость остовного
дерева вычисляется как сумма стоимостей
всех рёбер, входящих в это дерево.
Построение остова
графа G,
имеющего наименьший вес, имеет широкое
применение при решении некоторого
класса задач прикладного характера.
Например:
Пусть, например,
G=(V,
E,
)
служит моделью железнодорожной сети,
соединяющей пункты v1,
v2,
…, vnV,
а (vi,
vj)
– расстояние между пунктами vi
и vj.
Требуется проложить
сеть телеграфных линий вдоль
железнодорожной сети так, чтобы все
пункты v1,
v2,
…, vn
были связаны между собой телеграфной
сетью, протяженность которой была бы
наименьшей.
Рассмотрим два
способа построения минимального
остовного дерева взвешенного графа:
алгоритм Крускала и алгоритм Прима.
Алгоритм
Крускала:
1) Выбрать в графе
G
ребро e
минимального веса, не принадлежащее
множеству E
и такое, что его добавление в E
не создает цикл в дереве T.
2) Добавить это
ребро во множество ребер E.
3) Продолжить,
пока имеются ребра, обладающие указанными
свойствами.
Пример.
Для данного взвешенного графа найти
минимальное корневое остовное дерево,
используя алгоритм Крускала. Определить
высоту построенного дерева.
Алгоритм
Крускала.
Выбираем
ребро с минимальным весом. Это ребро,
(,
)
с весом, равным 4.
Пусть
вершина
будет корнем дерева. Далее выбираем
ребра, инцидентные вершинам
,
и имеющие минимальный вес.
Это
ребро (,
)
с весом 5. Затем к вершине
присоединяем ребро (,
)
с весом 7.
Далее,
добавляем ребро (,
)
с весом 7 и ребро (,
)
с весом 6.
Минимальный
вес построенного дерева равен:
min(T)=4+5+7+7+6=29.