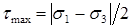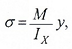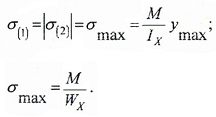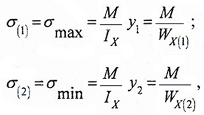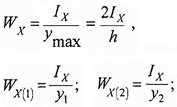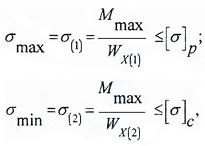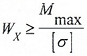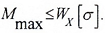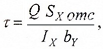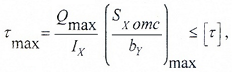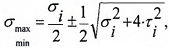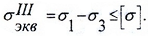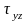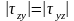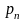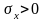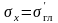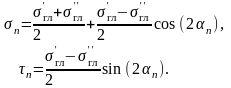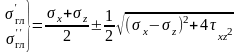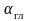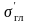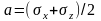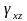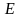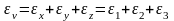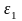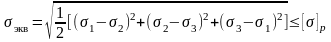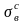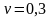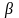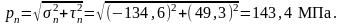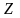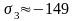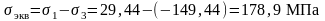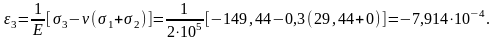Наибольшее касательные напряжение в точке тела
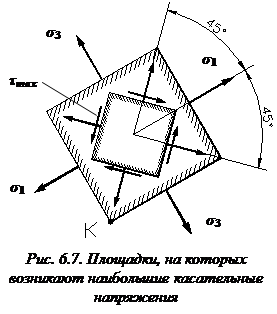
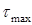
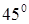
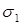
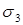
По закону парности касательных напряжений, такие же касательные напряжения возникают на площадках, перпендикулярных к этой наклонной площадке.
В общем случае нагружения (при объемном напряженном состоянии) на площадках, на которых возникают максимальные касательные напряжения, возникают и нормальные напряжения. Последние равны половине суммы главных напряжений 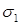
Если на площадках, где возникают наибольшие касательные напряжения, нормальные напряжения отсутствуют, то это площадки чистого сдвига.
Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки
Расчет напряжений
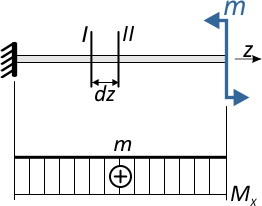
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.
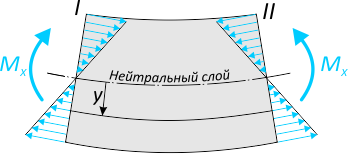
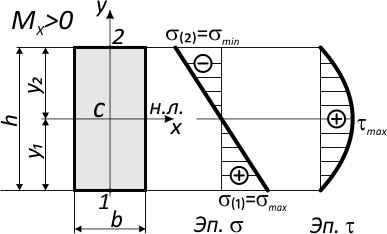
Закон распределения нормальных напряжений по высоте сечения выражается формулой:
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2:
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.
Для несимметричного сечения
напряжения определяются отдельно для нижней точки 1 и верхней точки 2:
где:
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.
В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[σ], [σ]р, [σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]с>[σ]р.
В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности
- Подбор сечений
- Определение максимально допустимой нагрузки
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Другие видео
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax:
где [τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Другие видео
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >
В прошлой части мы выяснили, какие нормальные напряжения будут возникать при изгибе. Однако это не все воздействия, которые есть в сечении. Также необходимо учесть и касательные напряжения. Последние обычно возникают либо если сечение скручивают, либо если в нем возникают поперечные силы. О скручивании будет написано в других частях, а сегодня мы обсудим влияние поперечной силы на изгибающийся стержень. Для вычисления изменения поперечной силы и момента нам потребуется теорема Журавского, а для нахождения касательных напряжений формула Журавского
Какие силы действуют в изгибаемом стержне
В случае если на конструкцию давит сила или по ней распределена нагрузка, в ней возникают поперечные силы. Как мы уже говорили, момент – это произведение силы на плечо. И вполне естественно, что действующие в конструкциях поперечные силы будут приводить и к возникновению момента.
Для того, чтобы выяснить, как именно этот момент возникает, проведем мысленный эксперимент:
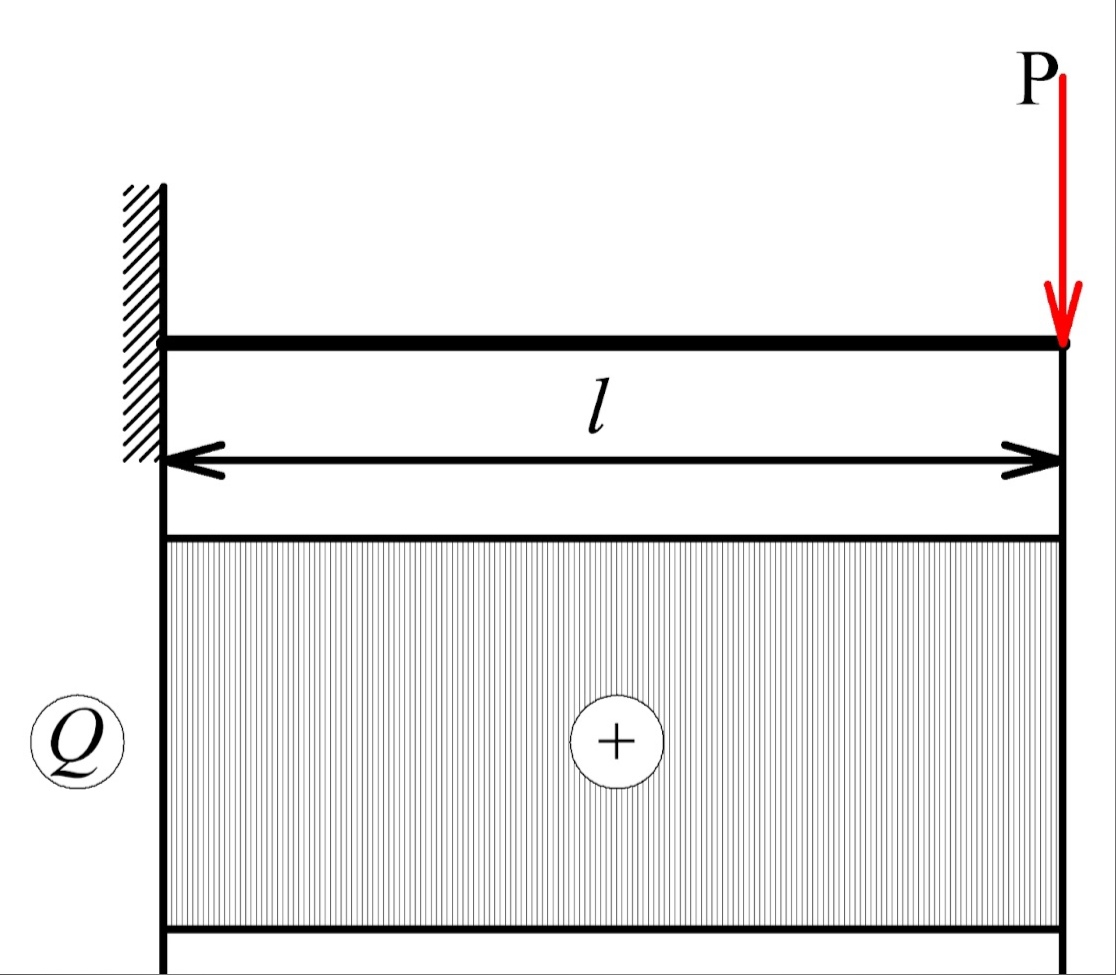
Жестко (чтобы не менял угол наклона в месте закрепления, противодействовал моменту) закрепим некоторый стержень на стене и надавим на его конец:
Теперь разделим стержень на бесконечное количество пластинок с практически нулевой шириной dx:
Сила P будет пытаться сдвинуть самую крайнюю пластинку вниз. В компенсацию этой силе в стержне возникает поперечная сила сопротивления материала Qy, направленная в противоположную приложенной сторону по плоскости сечения. По закону Ньютона, где действие, там противодействие. И по этому закону в компенсацию поперечной силы сопротивления возникает ей противоположная сила, которая будет воздействовать на следующую пластинку:
В итоге получаем достаточно прозаичную формулу распределения поперечной силы:
Qy=P
Не менее прозаично будет выглядеть и эпюра продольных сил:
Численно она будет равна приложенной к концу стержня силе. При этом, так как между центрами пластинок будет некоторое расстояние dx, на следующий элемент будет передаваться момент равный произведению силы на dx:
Итого, на первой пластинке, так как сила будет приложена к ее центру, момента m1 не будет. Момент m2 на второй пластинке будет равен произведению силы на расстояние между центрами пластинок:
m2=P*dx=P*dx
Момент третьей пластинки будет складываться из момента, который перейдет со второй пластинки и момента возникающего под действием силы:
m3=m2+P*dx=2*P*dx
В конечном счете, каждый раз, когда мы будем смещаться в сторону от места приложения силы на одну пластинку, будет меняться лишь множитель. Общая формула для момента m n-ной пластинки будет выглядеть так:
mn=n*P*dx
Ну если мы умножаем количество пластинок n на их ширину dx, то получаем расстояние от места приложения силы c. В итоге, эпюра момента под действием силы P будет выглядеть вот так:
Впрочем, помимо сил нам может попасться и распределенная нагрузка. Как в таком случае будет изменяться момент?
Рассуждения нашим будут абсолютно аналогичны. Разделим стержень на много тоненьких пластинок.
На каждую пластинку ширины dx будет действовать небольшая сила q и поперечная сила от соседней пластинки:
Сила взаимодействия между пластинками в таком случае будет накапливаться.
Найти ее можно просто перемножив расстояние от начала действия распределенной нагрузки до интересующей нас точки на величину распределенной нагрузки:
Qy=q*n*dx=q*l
Теперь разберемся с моментом. На первой пластинке момента не будет, по допущению, что сила q действует по ее середине.
На вторую пластинку же по касательной будет действовать сила q. Так как между центрами пластинок есть расстояние dx, в ней возникнет момент равный произведению q на dx:
m2=q*dx.
На третью пластинку будет действовать по касательной уже вдвое большая сила. Как следствие, для этой пластинки момент увеличится уже на 2q*dx:
dm2-3=2q*dx
Суммарный момент третьей пластинки будет складываться из момента передавшегося со второй пластинки и момента возникающего под действием нагрузки:
m3=m2+2q*dx=(2+1)dx*q
Если мы будем продолжать данную операцию и дальше, то получим общую формулу для момента m n-ной пластинки:
mn=(n+…+2+1)dx*q
Многочлен Sn=(n+…+2+1)dx- это сумма арифметической прогрессии. Ее находят как полусумму первого и последнего элемента умноженную на количество элементов:
S_n=frac{a_1+a_n}{2}cdot n
Примечание: желающие могут взглянуть на вывод этой формулы в числах (в общем виде вывод практически аналогичен, но на числах он нагляднее), с сайта umath.ru[7]:

По легенде эту формулу вывел Карл Гаусс, когда школьный учитель математики решил подшутить над учениками, заставив посчитать сумму чисел от 1 до 100.
Подставляем нашу последовательность x1=ndx+…+2dx+dx и получаем:
xn=ndx+…+2dx+dx=(dx+ndx)*ndx/2=(n+n2)dx2/2
Так как число пластинок мы сделали ну очень большим (практически бесконечным), по сравнению с n2 обычное n будет пренебрежительно мало. Например, если мы разделим стержень на 1000 пластинок, n2 от n2+n будет отличаться на одну тысячную.
В итоге, получившуюся формулу можно представить как простейшее n2/2.
Подставляем все в исходную формулу:
mn=(n+…+2+1)*q*dx=n2*dx2*q/2=ql2/2
А эпюра момента под равномерно-распределенной нагрузкой будет выглядеть как полупарабола:
Теорема Журавского
Обобщает и упрощает расчет интегрирование. А метод нахождения поперечных сил и моментов известен как теорема Журавского. Для того, чтобы найти момент в определенной точке, необходимо взять интеграл от поперечной силы по длине:
Поперечная сила не всегда постоянна на всем протяжении участка, как это, например, бывает при распределенной нагрузке. Чтобы найти поперечную силу, если балка находится под воздействием распределенной нагрузки, необходимо последнюю проинтегрировать:
Ну а для нахождения момента при распределенной нагрузке, нужно эту нагрузку дважды проинтегрировать:
M_z=int_{0}^{x}int_{0}^{x}q_y dx
Если обобщить, то для нахождения момента в сечении надо дважды проинтегрировать распределенную нагрузку, сложить это с интегралом силы по расстоянию до опоры и с моментами, которые мы приложили к этом сечении.
Теорема Журавского в дифференциальной форме выглядит так:
q=frac{dQ_y}{dx}=frac{d^2M_z}{dx^2}
Теорема Журавского позволяет вычислять попереченые силы и моменты. Отрезок балки под воздействием сложной системы сил:
Изображение расчета балки взято из онлайн-калькулятора.
Подробнее почитать о построении эпюр можно в соответствующей статье.
Выражены формулы взаимосвязи распределенной нагрузки, поперечных напряжений и моментов были Дмитрием Ивановичем Журавским и обобщаются как теорема Журавского.
Формула Журавского
В процессе проектирования железнодорожных мостов деревянные балки часто давали скол. На тот момент не было теоретического аппарата для выяснения точных значений касательных напряжений в сечении. Их либо не учитывали, либо, по аналогии с нормальными напряжениями при растяжении/сжатии, считали равномерно-распределенными по всему сечению (т.е. τ=Qy/F).
Однако реальность упорно не хотела следовать расчетам: конструкции разрушались, хотя не должны были.
При этом нормальных напряжений явно было недостаточно для скола. Журавский данную проблему решил за счет добавления в уравнение касательных напряжений и нашёл закон их распределения по сечению. Попробуем и сами вывести закон распределения касательных напряжений (более известный как формула Журавского).
У нас есть балка произвольного сечения под нагрузкой:

В этом стержне, под действием распределенной нагрузки изменяются момент и нормальные напряжения:

Если мы отсечем верхнюю или нижнюю часть стержня (так, чтобы линия среза была параллельна нейтральной линии), на данном участке возникнет нескомпенсированная продольная сила:

Журавский предположил, что ключом к ответу на вопрос, как именно распределяются по сечению касательные напряжения, может стать решение проблемы этой нескомпенсированной силы.
Разберемся в том, как касательные напряжения вообще могут распространяться в материале.
Для этого вырежем из какой-то не разрушившейся конструкции куб с пренебрежительно малыми сторонами. Затем приложим к одной из его граней силу по касательной. Для того, чтобы куб уравновесить, необходимо приложить к поверхности этой грани касательную силу, но в другом направлении:

От касательных сил возникнет момент. А так как мы вырезаем куб из целой, не разрушенной конструкции, все силы и моменты должны быть скомпенсированы. Поэтому на соседних гранях возникнут такие же касательные напряжения с противоположным моментом:

Иными словами, если конструкция сохраняет свою форму, каждое касательное напряжение по оси x на одной из сторон куба будет уравновешено точно таким же, но в обратном направлении на противоположной стороне куба. А получившийся момент будет скомпенсирован касательными напряжениями по оси y.
Так как касательные напряжения по y приведут к возникновению точно таких же касательных напряжений по x, разумно предположить, что приращение нормальных напряжений можно скомпенсировать касательными напряжениями.
Возвращаемся к нашему стержню. Мы вырезали некоторую его часть и хотим компенсировать избыток продольной силы, за счет касательных напряжений приложенных к поверхности горизонтального сечения:

Для того, чтобы система оставалась неподвижной, необходимо, чтобы продольные и касательные силы в сумме давали ноль:
-N+(N+dN)-τ*b(y)=0
dN-τ*b(y)=0
dN=τ*b(y)
Остается дело за малым: выяснить чему будет равно изменение продольной силы на отсеченной нами части. Для этого нам нужно просуммировать все напряжения в ней возникающие:
dN=∑dσ=∫dσdF
Подставляем формулу из прошлой части для нахождения нормальных напряжений при изгибе и изменения момента под действием поперечной силы из этой:
dσ=ydMz/Jz, dMz=Qy
Примечание: дальше мы будем использовать такие понятия как момент инерции I и статический момент S. Если вы хотите поподробнее узнать про то, откуда появились данные величины, каков их физический смысл и как их находить, то вы можете это сделать прочитав наши статьи:
- Статический момент
- Момент инерции
- Момент сопротивления изгибу
В итоге избыток продольной силы будет равен:
dN=frac{Q_ycdot dx}{I_z} int y dF
Fотс.∫ydF — это статический момент инерции отсеченной фигуры Sотс. Таким образом формулу можно записать чуть элегантнее:
dN=frac{Q_ycdot S_{отс.}cdot dx}{I_z}
Как мы уже говорили, чтобы тело находилось в равновесии необходимо, чтобы избыточная продольная сила компенсировалась касательной:
dN-τcdot bcdot dx=dx(frac{Q_ycdot S_{отс.}}{I_z}-τcdot b)=0;
Или:
τcdot b=frac{Q_ycdot S_{отс.}}{I_z}
Теперь мы можем сказать, по какому закону будут распределяться касательные напряжения при изгибе:
τ=frac{Q_ycdot S_{отс.}}{I_zcdot b}
Вычисление касательных напряжений по формуле Журавского
Разберем распределение касательных нагрузок на простейшем примере. На прямоугольном брусе.
Нам нужно выяснить, какие касательные напряжения будут в каждой точке сечения. Величина Qy нам задана. Ширина b тоже. Момент инерции Iz мы тоже для всего сечения мы тоже знаем:
I_z=frac{bcdot h^3}{12}
Остаётся найти момент отсеченной части. В данном случае мы отсекаем все, что снизу:

Статический момент (посмотреть как вычисляется можно по ссылке) равен произведению площади на центр масс:
Sотс=F*l
Где l расстояние до центра масс (в данном случае до середины) отсеченной фигуры, а F площадь, которую можно найти перемножив высоту отсекаемого прямоугольника (h/2-y) на его ширину b. Расстояние до центра масс же можно найти сложив верхнюю (h/2) и нижнюю (y) границу и поделив это выражение на два (потому-что нам интересно найти середину):
I_z=frac{frac{h}{2}+y}{2}
S_{отс.}=Fcdot l=frac{b(frac{h}{2}+y)(frac{h}{2}-y)}{2}
Получаем напряжение в середине:
τ=frac{Q_ycdot S_{отс.}}{bcdot I_z}=frac{12cdot Q_y cdot bcdot(frac{h^2}{4}-y^2)}{2cdot b^3cdot h^3}=frac{6cdot Q_y cdot (frac{h^2}{4}-y^2)}{b^2cdot h^3}
Теперь остается только подставить в уравнение получившуюся для этого сечения поперечную силу Qy и можно посчитать, какие касательные напряжения будут возникать на каждом расстоянии y от нейтральной линии.
Так как в уравнении меняться будет только y, выражение можно представить в виде:
τ=C-B*y^2
Где B и C константы, а при y=h/2 τ=0.
Ну и, очевидно, что когда y=0 (т.е. посередине сечения), напряжение максимально.

Т.е. изменяться касательные напряжения будут по параболе, где максимум будет на средней линии, а ноль на верхней и нижней грани сечения.

Если сечение не прямоугольное, ширину b надо будет представить как некую функцию b(y).
τ=frac{Q_y cdot S_{отс.}(y)}{b(y)cdot I_z}
Форма эпюры напряжений могут меняться, но характер будет будет остаться прежним: по мере движения к центру напряжения будут расти.

Ещё в прошлой части мы вывели закон распределения нормальных напряжений при изгибе: напряжения изменяются по линейному закону от своего минимального (максимальное сжатие) до максимального (максимальное растяжение) значения.

А сейчас мы выяснили, как распределяются по сечению касательные напряжения. Если стержень имеет одинаковую ширину на всей высоте сечения, то напряжения меняются по параболе. Но в прошлой части мы также говорили, что для экономии материала гораздо целесообразнее использовать сечения сложной формы (для нахождения моментов инерции гуглить “сортамент, прокатные профили”).
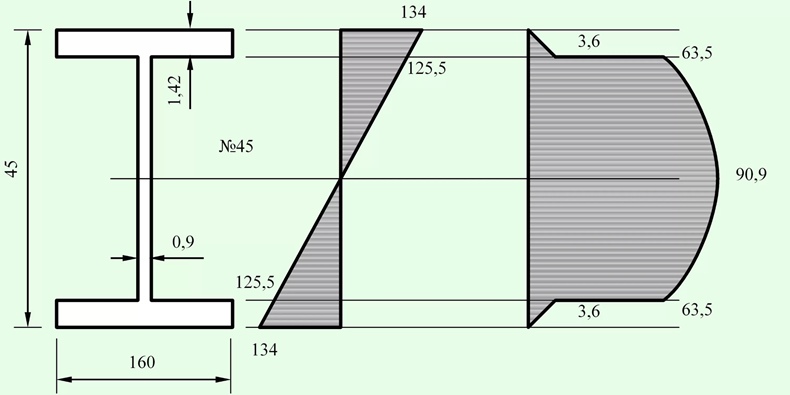
Например двутавр, у которого максимальная ширина по краям, где нормальные напряжения максимальны. Как мы уже выяснили, касательные напряжения сильно зависят от ширины сечения. Есть точки, где ширина уменьшается и происходит увеличение касательных напряжений, но нормальные напряжения все ещё велики. Их следует проверить, точно ли они выдержат нагрузки. И необходим математический аппарат для предсказания прочности, учитывающий эти два вида нагрузок.
И на него нет однозначного, исчерпывающего ответа. Но есть ответы практические, каждый справедливый для своих границ применимости. И эти ответы называются теориями прочности. И о них мы расскажем в будущем.
В рамках темы изгиба наибольшую применимость имеет теория «Наибольших касательных напряжений» (Третья теория прочности). Чаще всего её используют для металлов или материалов, плохо сопротивляющихся сдвигу.
Для того, чтобы понять, выдержит ли материал, в рамках теории наибольших касательных напряжений, нормальные и касательные напряжения приводят к эквивалентным напряжениям, которые должны быть меньше предельных напряжений при растяжении/сжатии по определенной формуле. Ее вывод мы сейчас производить не будем, предлагаем просто поверить на слово, что эквивалентные напряжения должны быть меньше опасных и рассчитываются так:
σэкв.=√(σ2+4τ2)<[σ]
Возвращаемся к двутавру. Какие у него будут самые опасные точки, которые надо проверить? Такие, где возникают максимальные напряжения и где высокие и нормальные и касательные напряжения:
Из прошлой части мы знаем, что наибольшие нормальные напряжения находятся на самых удаленных от нейтральной линии участках сечения. Так как там отсутствуют касательные напряжения, достаточно чтобы нормальные напряжения были меньше опасных:
134МПа<[σ]
Максимальные касательные напряжения возникают в середине сечения. Так как нормальные напряжения будут равны нулю, формула σэкв.=√(σ2+4τ2) превращается в простейшее σэкв.=√(4τ2)=σэкв.=2τ
Подставляем значение и оказывается, что материал должен выдерживать аж 182 МПа:
2τ=91*2=182МПа<[σ]
Если данный материал такие напряжения выдерживать не способен, придется выбирать другой прокатный профиль (например, с большей шириной промежуточной полки). Ну а если способен, надо рассчитать третью точку. Она будет находиться на месте, где промежуточная узкая полка переходит в широкую. Подставляем в формулу значения нормальных и касательных напряжений:
σэкв.=√(σ2+4τ2)=√(1342+4*642)=√(19.000+4*4.100)=√35400=188,2 МПа<[σ]
Если допускаемые напряжения меньше, значит сечение подходит. Если нет, значит придется искать сечение с лучшей способностью сопротивления касательным и нормальным напряжениям. Например, следующий номер двутавра.
Для того, чтобы выяснить, выдержит ли деталь нагрузку, необходимо проверять эквивалентные напряжения (с чем поможет формула Журавского и третья теория прочности) в максимумах моментов и поперечных сил (с чем поможет теорема Журавского), а также на местах, где совпадают большие моменты и поперечные силы:
Вот мы и разобрались с ещё одним источником опасности для прочности конструкции: с касательными напряжениями от поперечных сил. Главный инструмент в поиске поперечных сил, моментов — теорема Журавского. А найти касательные напряжения поможет формула Журавского.
Теперь в теме изгиба нам остаётся только научиться считать, как будет деформироваться балка под действием момента.
Информация о произведении
Автор: К.А.Овчинников
Редактор, факт-чекер: Д.А. Сабуров, Марк Ершов
Иллюстратор: Михаил Корнев [I]
Информация о произведении:
Условия использования: свободное некоммерческое использование при условии указания людей участвовавших в его создании и ссылку на первоисточник (статьи на действующем сайте интернет-журнала «Стройка Века»).
Для коммерческого использования — обращаться на почту:
buildxxvek@gmail.com
Источники
- Лекции по сопротивлению материалов в СПбПУ им. Петра Великого
- Горшков А. Г., Трошин В. Н., Шалашилин В. И. Сопротивление материалов. – Физматлит, 2002. – С. 548-548.
- iSopromat Формула Журавского // https://youtu.be/4rsFdn5fSrU
- Kirsanov2011 Формула Журавского // https://youtu.be/AZE70B9m2lA
- Основные теории прочности // http://sopromat.in.ua/handbook/teorii-prochnosti
- Гипотезы прочности // http://k-a-t.ru/tex_mex/5-sochetanie_defor2/index.shtml
- https://umath.ru/theory/posledovatelnosti/arifmeticheskaya-progressiya/
5 683
Рекомендуемая
литература
Александров А. В.,
Потапов В. Д., Державин Б. П. Сопротивление
материалов. М.: Высш. шк., 1995. Гл. 13
(§
13.6).
Гастев В. А. Краткий
курс сопротивления материалов. М.:
Физматгиз, 1977. Гл. 3 (§
10, 11), гл. 4 (§
14, 15, 20).
Дарков А. В., Шпиро
Г. С. Сопротивление материалов. М.: Высш.
шк., 1989. Гл. 3 (§
3.1–3.5, 3.7), гл. 8 (§
8.1, 8.2).
Основные понятия и формулы
Напряженное состояние в точке
тела. Пусть в нагруженном
теле выбрана точка
.
Под напряженным состоянием в
этой точке понимают совокупность
напряжений на всех площадках, проведенных
через нее. Задают напряженное состояние
три вектора напряжений на трех взаимно
перпендикулярных площадках. Эти три
взаимно перпендикулярные площадки
можно выбрать произвольно. Векторы
напряжений на всех других площадках
можно вычислить по указанным трем
векторам напряжений.
Когда говорят о точке
тела, подразумевают малую ее окрестность,
в которой напряженное состояние
практически постоянно. В этой окрестности
напряжения на параллельных площадках
одинаковы, поэтому, говоря о напряженном
состоянии в точке, параллельные площадки
не различают. Важна только ориентация
площадки, которую принято задавать
перпендикулярным к ней вектором единичной
длины – вектором внешней нормали
.
Вводится прямоугольная система координат
и три площадки, перпендикулярные ее
осям x, y,
z, которые образуют
элементарный параллелепипед (элемент).
Векторы напряжений на
этих трех площадках обозначаются
соответственно
,
,
.
Они задаются своими проекциями на оси
координат. Проекции, перпендикулярные
площадкам, называются нормальными
напряжениями
,
,
.
Индекс в обозначении указывает направление
нормали
к площадке. Проекции, лежащие в плоскости
площадок, называются касательными
напряжениями
,
,
,
,
,
.
Первый индекс здесь определяет площадку,
на которой действует напряжение, второй
индекс указывает ось, в направлении
которой напряжение действует.
Правило знаков для нормального
напряжения: нормальное напряжение
положительно, если направление напряжения
совпадает с направлением внешней
нормали
(направлено от площадки, растягивающее).
Следствием условий равновесия элемента
тела является закон парности касательных
напряжений:
;
;
.
При этом касательные напряжения
,
направлены либо навстречу друг другу,
либо в противоположные стороны.
С учетом закона парности касательных
напряжений для задания напряженного
состояния в точке нужно указать шесть
параметров: три нормальных напряжения
,
,
и три касательных напряжения
,
,
.
Графически напряженное состояние в
точке
изображается системой напряжений,
действующих на гранях элементарного
параллелепипеда, вырезанного из тела
в окрестности точки
.
Ребра этого параллелепипеда параллельны
осям координат и имеют длину
,
,
.
Каково бы ни было напряженное состояние
в точке, всегда можно найти три взаимно
перпендикулярные площадки, на которых
действуют только нормальные напряжения,
а касательные напряжения равны нулю.
Эти площадки называются
главными, действующие на них
нормальные напряжения – главными
напряжениями. Три главные площадки,
являясь взаимно перпендикулярными,
образуют элементарный параллелепипед.
Главные напряжения принято обозначать
,
,
с соблюдением условия
.
Главные напряжения обладают свойством
экстремальности: одно из них самое
большое среди нормальных напряжений
на площадках с произвольной нормалью
,
другое – наименьшее. В принятых
обозначениях
,
.
Пусть
– модуль полного напряжения на
произвольной наклонной площадке с
нормалью
.
Свойство экстремальности означает
также следующее:
.
Главными направлениями напряженного
состояния называют направления нормалей
к главным площадкам. Эти направления
обозначают цифрами 1, 2, 3. Главные площадки
обозначают соответственно 1, 2, 3.
Напряженное состояние, при котором ни
одно из трех главных напряжений не равно
нулю, называется объемным. Если
одно из главных напряжений равно нулю,
то напряженное состояние называется
плоским. Наконец, линейным
именуется напряженное состояние, при
котором отлично от нуля только одно
главное напряжение. Далее рассматривается
плоское напряженное состояние, которое
часто реализуется в конструкциях.
Пусть главная площадка с нулевым главным
напряжением (а следовательно, вообще
ненапряженная) расположена перпендикулярно
оси y. Тогда при плоском
напряженном состоянии отличны от нуля
напряжения
,
,
,
(рис. 2.1; здесь ради простоты напряжения
на левой и нижней гранях элементарного
параллелепипеда не показаны; ненапряженная
площадка совпадает с плоскостью чертежа).
Аналитическое исследование плоского
напряженного состояния. Когда
говорят об исследовании напряженного
состояния, понимают вычисление по
заданным на взаимно перпендикулярных
площадках напряжениям напряжений на
площадках произвольной ориентации,
определение главных площадок и главных
напряжений, площадок, по которым действуют
экстремальные касательные напряжения.
При исследовании плоского напряженного
состояния удобно пользоваться следующим
правилом знаков для касательного
напряжения: касательное напряжение
положительно, если в плоскости чертежа
оно обходит площадку по часовой стрелке.

Рис. 2.2. Напряжения
на произвольной
наклонной площадке

Рис. 2.1. Плоское
напряженное
состояние в точке
тела
Пусть на двух взаимно перпендикулярных
площадках заданы напряжения
,
,
,
.
На рис. 2.1, 2.2 нормальные напряжения
,
(растягивающие), касательное напряжение
(обходит площадку по часовой стрелке),
касательное напряжение
(обходит площадку против часовой
стрелки). При указанном правиле знаков
для
закон парности касательных напряжений
принимает вид
.
(2.1)
Если рассматривать только площадки,
перпендикулярные незагруженной площадке,
то положение площадки определяет угол
между нормалью к ней и осью x
(см .рис. 2.2). Угол
отсчитывается от оси x к
нормали
и считается положительным, если
отсчет происходит против часовой
стрелки.
Нормальное напряжение
и касательное напряжение
на этой площадке определяются по формулам
;
(2.2а)
.
(2.2б)
Примечание. В правой части формул
(2.2а) и (2.2б) на первом месте стоит нормальное
напряжение на той площадке, от нормали
к которой отсчитан угол
.
Касательное напряжение берется с этой
же площадки.
Формулы (2.2а) и (2.2б) показывают, что
плоское напряженное состояние в точке
определяется тремя параметрами –
напряжениями
,
,
:
зная эти три параметра, можно вычислить
напряжения по любой площадке.
Пусть
– нормальное напряжение на площадке,
перпендикулярной площадке с нормалью
n. Из выражения (2.2а)
следует, что
,
(2.3)
то
есть сумма нормальных напряжений на
двух взаимно перпендикулярных площадках
не изменяется при совместном повороте
этих площадок (является инвариантом
напряженного состояния).
Формулы (2.2а) и (2.2б) упрощаются, когда
заданные площадки являются главными
(то есть на них отсутствуют касательные
напряжения). Пусть в этом случае главные
напряжения обозначены
,
,
тогда
(2.4)
Если исходные площадки не являются
главными, то главные напряжения могут
быть вычислены по формуле
.
(2.5)
Согласно (2.3)
.
(2.6)
Положение
главных площадок определяет угол
,
который находится из уравнения
.
(2.7)
Формуле
(2.7) отвечает множество углов
,
отличающихся друг от друга на величину,
кратную 90. Разные
главные площадки соответствуют только
двум из этих углов, которые обозначают
,
.
Для определения площадки, на которой
действует бульшее
из напряжений
,
,
можно установить, исследуя при
знак второй производной функции
,
заданной выражением (2.2а). Эта производная
.
(2.8)
Если
при
,
то на этой площадке действует меньшее
из напряжений
,
,
если
,
– то бульшее
(случай равенства нулю не встречается).
Для главных напряжений, как уже было
сказано, используется специальное
обозначение:
,
,
(
).
В рассматриваемом случае плоского
напряженного состояния
– максимальное, а
– минимальное (с учетом знака) из трех
напряжений
,
,
0.
Касательное напряжение, максимальное
среди касательных напряжений на всех
вообще площадках в рассматриваемой
точке,
.
(2.9)
Такое
напряжение действует на площадке,
перпендикулярной площадке 2 и повернутой
относительно площадки 1 на угол 45.
На площадке с
действует нормальное напряжение
.
Площадка
2 может совпадать с плоскостью чертежа,
но может и совпадать с одной из площадок,
по которым действуют
,
.
Соответственно рассматриваемая площадка
с
может
быть перпендикулярна плоскости чертежа,
но может быть и повернута из плоскости
чертежа.
Касательное напряжение, максимальное
по модулю среди напряжений на площадках,
перпендикулярных плоскости чертежа,
.
(2.10)
Величина
в общем случае не равна
.
Соответствующая ей площадка перпендикулярна
плоскости чертежа и наклонена к площадкам
,
на угол 45 . На этой
же площадке действует нормальное
напряжение
.
(2.11)
Графическое исследование плоского
напряженного состояния. Формулы
(2.2а) и (2.2б) можно представить в графической
форме. Как известно из аналитической
геометрии, в декартовой системе координат
параметрическое уравнение окружности
радиуса
с координатами центра
,
имеет вид
;
.
(2.12)
Если в формулах (2.12) обозначить
,
,
,
,
,
то формулы примут вид (2.2а) и (2.2б). Значит,
напряжения
,
на площадке с нормалью
,
заданной углом
,
являются координатами точки окружности
радиуса
,
центр которой лежит на горизонтальной
оси и имеет координату
.
Построенную таким образом окружность
обычно называют “кругом Мора”.
Деформированное состояние в точке.
Деформированное состояние в
точке нагруженного тела есть совокупность
линейных относительных деформаций
отрезков, проведенных через эту точку,
и изменений углов между отрезками
(угловых деформаций). Деформированное
состояние в точке задано, если для любых
двух направлений могут быть вычислены
линейные и угловые деформации.
Деформированное состояние в точке
определяют шесть параметров: линейные
относительные деформации
,
,
по трем взаимно перпендикулярным
направлениям
,
,
и изменения прямых углов между этими
направлениями
,
,
.
Всегда можно провести через точку три
взаимно перпендикулярные прямые, углы
между которыми не изменятся вследствие
деформации. Оси координат, совпадающие
с этими прямыми, называются главными
осями деформированного состояния в
точке.
Связь между напряжениями и деформациями.
Для изотропного материала (свойства
материала одинаковы во всех направлениях)
при не слишком большом уровне напряжений
связь напряжений и деформаций описывает
обобщенный закон Гука:
(2.13)
Здесь
,
,
– упругие характеристики материала;
– модуль Юнга (модуль упругости);
– коэффициент Пуассона (
);
– модуль сдвига, для которого имеет
место соотношение
.
Для
изотропного материала главные оси
деформированного состояния и главные
оси напряженного состояния совпадают,
поэтому линейные деформации вдоль
главных осей напряженного состояния
определяются соотношениями (2.13):
,
,
(2.14)
.
Соответствующие
угловые деформации равны нулю.
Относительная
объемная деформация в точке (отношение
абсолютного изменения объема элементарного
параллелепипеда к первоначальному
объему) не зависит от выбора системы
координат:
.
(2.15)
Оценка прочности. Прочность материала
в точке проверяется по соответствующей
материалу теории прочности. Из большого
числа ныне существующих теорий прочности
при выполнении студенческих задач
используются перечисляемые ниже.
Под исчерпанием прочности подразумевается
переход материала в предельное состояние
– разрушение для хрупкого материала и
развитие пластической деформации для
пластичного материала. Расчет должен
обеспечивать некоторый нормативный
запас прочности, что проще всего
достигается введением коэффициента
запаса прочности, понижающего разрешаемый
уровень напряжений.5
Для всех применяемых при выполнении
расчетно-проектировочной работы теорий
прочности условие прочности можно
записать в едином виде
,
(2.16)
где
– допускаемое напряжение. Величина
представляет собой предельный уровень
напряжения и определяется из эксперимента.
Для хрупких материалов она совпадает
с пределом прочности при осевом
растяжении, для пластичных материалов
– с пределом текучести при осевом
растяжении. n –
нормируемый коэффициент запаса прочности.
– комбинация главных напряжений
,
,
(эквивалентное напряжение).
Согласно
первой теории прочности, справедливой
для хрупких материалов, разрушение
происходит от отрыва при достижении
максимальным напряжением
(оно должно быть положительным, т. е.
растягивающим) предельного значения.
Плоскость отрыва (опасное сечение)
перпендикулярна направлению главного
напряжения
.
Условие прочности имеет вид
.
(2.17)
Вторая
теория прочности также применяется к
хрупким материалам. Согласно этой теории
разрушение происходит от отрыва при
достижении максимальной деформацией
(она должна быть положительной) предельного
значения. Деформации вплоть до момента
разрушения считаются малыми и вычисляются
по закону Гука. Плоскость отрыва (опасное
сечение) перпендикулярна направлению
действия главного напряжения
.
Условие прочности приводится к виду
.
(2.18)
Третья
теория прочности определяет уровень
напряжений, при котором в пластичном
материале возникают заметные остаточные
деформации. Согласно третьей теории
прочности переход материала в предельное
состояние происходит от сдвига при
достижении максимальным касательным
напряжением
предельного значения. Плоскость
пластического сдвига (опасное
сечение) совпадает с плоскостью
действия напряжения
.
Данной теории соответствует условие
прочности
.
(2.19)
Согласно
четвертой теории прочности пластическое
деформирование возникает от сдвига при
достижении энергией изменения формы
предельного значения. Условием прочности
служит соотношение
.
(2.20)
Сама
эта теория прочности непосредственно
не определяет положения опасных площадок.
Последние (на основании иной трактовки
теории) можно считать равнонаклоненными
к главным осям (октаэдрические площадки).
Условие прочности, соответствующее
теории прочности Мора (пятой теории
прочности), относящейся к хрупким
материалам, имеет вид
.
(2.21)
Здесь
,
– пределы прочности при растяжении и
при сжатии. Эта теория учитывает
взаимодействие нормального и касательного
напряжений на площадке с
,
которая, следовательно, должна считаться
плоскостью зарождения начальной
микротрещины. (Согласно опыту плоскость
развивающейся далее макротрещины
перпендикулярна первому главному
направлению.)
Среди
первой, второй и пятой теорий лучше
количественно согласуется с опытом при
плоском напряженном состоянии последняя
теория. Третья и четвертая теории обе
имеют достаточную пригодность для
использования в инженерных расчетах.
Примеры решения
задач
2.1.
ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО
СОСТОЯНИЯ
ПО ЗАДАННЫМ НАПРЯЖЕНИЯМ
НА
ПРОИЗВОЛЬНЫХ ПЛОЩАДКАХ.
ПРОВЕРКА
ПРОЧНОСТИ (ЗАДАЧА № 7)
Условие
задачи

Рис. 2.3. Заданное
напряженное
состояние
в условии задачи
№ 7
Элемент, выделенный из тела, находится
в плоском напряженном состоянии
(рис. 2.3). По граням элемента заданы
нормальные и касательные напряжения,
значения которых приведены на рисунке.
Материал элемента – сталь с такими
характеристиками: предел текучести
МПа;
модуль Юнга
МПа;
коэффициент Пуассона
;
модуль сдвига
МПа;
нормируемый коэффициент запаса прочности
.
Требуется:
-
найти нормальное, касательное и полное
напряжения на наклонной площадке,
заданной углом
105 (см. рис. 2.3);
-
определить величины главных напряжений
и положение главных площадок; -
найти наибольшее касательное напряжение
и положение площадки, по которой оно
действует; -
оценить прочность материала в точке и
показать вероятное направление плоскости
сдвига или отрыва (опасной площадки); -
найти величины относительных продольных
деформаций в исходной системе координат
и по главным направлениям; вычислить
относительную объемную деформацию.
Примечание. Пп. 1–3 следует выполнить
двумя способами: аналитическим и
графическим.

Рис. 2.4. Определение
напряжений на
заданной
наклонной площадке
Решение
Изобразим элемент в виде плоского
рисунка, на котором должна быть указана
система координат (см. рис. 2.4). Введенная
система координат позволяет присвоить
напряжениям обозначения:
МПа,
МПа,
МПа.
На рисунке следует показать также
наклонную площадку, указать штриховкой
ее внутреннюю сторону, задать внешнюю
нормаль к площадке.
Аналитический способ исследования
напряженного состояния
Определение напряжений на наклонной
площадке. Напряжения, действующие
на наклонной площадке (см. рис. 2.4),
находим по формулам (2.2а) и (2.2б). В этих
формулах положение площадки задает
угол
между нормалью
к площадке и осью
.
Этот угол нельзя путать с углом
,
указанным на рис. 2.3.
Можно отсчитывать угол
не от оси
,
а от оси z, но тогда в
формулах (2.2а) и (2.2б) напряжения
,
надо поменять местами и напряжение
заменить напряжением
.
Надо выбирать более удобный способ.
Используем угол
между
и осью
,
отсчитывая его от оси
к нормали
:
( см. рис. 2.4). Значение угла положительное,
так как угол отсчитывается против
часовой стрелки.
Согласно (2.2а) и (2.2б)
,

Получившееся нормальное напряжение
отрицательно, значит, оно направлено к
площадке (сжимающее). Касательное
напряжение
положительно, это значит, что оно обходит
площадку по часовой стрелке.
Используем теперь угол
между нормалью
и осью
,
отсчитывая его от z к
:
.
Формулы (2.2а) и (2.2б) записываем в измененном
виде:



Рис. 2.5. Напряжения
на наклонной
площадке
Абсолютная величина полного
напряжения (или просто полное напряжение)
Вычисленные
напряжения показаны на рис. 2.5.
Определение главных напряжений и
главных направлений. Согласно
(2.5) главные напряжения

.
После вычисления главные напряжения
следует пронумеровать согласно убыванию.
Чтобы не путать напряжения до и после
нумерации, специально используются для
этих напряжений разные обозначения.
Главные напряжения, пронумерованные
согласно их величине,
,
,
.
Найдем положение главных площадок.
Сказанное о способах вычисления
напряжений по наклонной площадке
относится и к способам вычисления
положения главных площадок. Здесь мы
вычислим углы
,
,
определяющие положения главных площадок,
одним способом: будем отсчитывать эти
углы от направления оси
.
Углы являются решениями уравнения
(2.7):
,
то
есть


Рис. 2.6. Определение
положения главных
площадок

Рис. 2.7. Площадка
с максимальным
касательным
напряжением
Получены два значения
угла, которые отвечают площадкам с
напряжениями
,
(рис. 2.6). Выясним, какому из этих
напряжений соответствует угол
.
Для этого определим по формуле (2.8) знак
второй производной
при
:
.
Знак отрицательный, следовательно, по
этой площадке действует бульшее
из найденных главных напряжений
– напряжение
.
Теперь можно в соответствии с нумерацией
главных напряжений пронумеровать и
углы:
,
.
Определение максимального
касательного напряжения.
Касательное напряжение, максимальное
среди касательных напряжений на
площадках, перпендикулярных плоскости
(рис. 2.7), определяется формулой (2.10):
МПа.
В рассматриваемом примере главные
напряжения
,
,
поэтому касательное напряжение
является максимальным среди касательных
напряжений для всей совокупности
площадок, проходящих через заданную
точку:
.
Нормальные
напряжения на той же площадке даются
формулой (2.11):
МПа.
Графический способ исследования
напряженного состояния
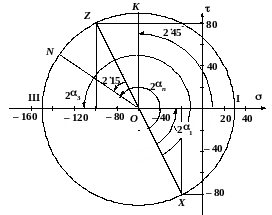
Рис. 2.8. Круг Мора,
изображающий заданное
плоское напряженное
состояние
Круг напряжений Мора
является средством вычисления. При
выполнении задачи его необходимо
построить в крупном масштабе на
миллиметровке, используя заточенный
карандаш. Чем точнее выполнены построения,
тем точнее будет получен результат.
Строим круг напряжений Мора
(рис. 2.8). Изображаем систему координат
с одинаковым масштабом по вертикальной
и горизонтальной осям. Отмечаем на
координатной плоскости
две точки X,
,
соответствующие заданным площадкам с
нормалями
.
Координатами точек
,
являются нормальные и касательные
напряжения на заданных площадках.
Соединяем точки отрезком, который
представляет собой диаметр круга Мора.
Точка О пересечения диаметра с осью
– центр круга. Проводим окружность.
Точкам
I, III
пересечения круга с горизонтальной
осью соответствуют главные площадки
1, 3. Горизонтальные
координаты этих точек (измеренные в
масштабе) являются главными напряжениями:
МПа,
МПа.
Углы
,
,
определяют положения главных площадок.
Отмеченные на рисунке углы дают удвоенные
значения
,
.
По рисунку сразу видно, какому главному
напряжению соответствует каждое значение
угла. Графически найденные значения:
,
.
Графический способ дает возможность
проверить аналитическое решение, поэтому
в расчетной работе следует рядом с
кругом напряжений на отдельном рисунке
показать положения главных площадок и
напряжения на них.
Площадке, по которой действует максимальное
касательное напряжение, соответствует
точка
круга. Координаты точки
дают значения
МПа,
МПа.
Найдем
с помощью круга напряжений напряжения
на наклонной площадке. Построим на круге
точку
,
соответствующую наклонной площадке.
Для этого отложим от радиуса OX
(соответствующего оси x)
против часовой стрелки угол
,
либо от радиуса ОZ
(соответствующего оси z)
в том же направлении угол 215.
Координаты точки
дают напряжения на наклонной площадке:
,
.
Полное
представление о напряженном состоянии
дают три круга напряжений. Точки каждого
круга соответствуют площадкам, которые
перпендикулярны одной из главных
площадок. Круги строятся по главным
напряжениям. Обычно изображение
напряженного состояния в виде трех
кругов Мора используется в качестве
иллюстрации, а не в качестве способа
вычисления, поэтому данный рисунок
можно выполнить в меньшем масштабе и
не обязательно на миллиметровке. Все
три круга напряжений для рассматриваемого
напряженного состояния показаны на
рис. 2.9. Построенный на рис. 2.8 круг
напряжений соответствует площадкам,
перпендикулярным плоскости чертежа
(перпендикулярным второй главной
площадке). Из рис. 2.9 видно, что
максимальное касательное напряжение
определяется по бульшему
кругу.

Рис. 2.9. Круги
Мора,
изображающие
объемное
напряженное
состояние
Проверка прочности. Главные
напряжения
,
,
уже известны (вычислены выше).
Начать решение вопроса нужно с выбора
соответствующей материалу теории
прочности. По условию задачи материал
– сталь (пластичный материал), поэтому
используем третью и четвертую теории
прочности.
Согласно
третьей теории прочности эквивалентное
напряжение
.
Сравнение
с пределом текучести
показывает, что материал работает
упруго. Действительно,
.
Но
условие прочности не выполнено:
.
Это
означает, что не обеспечен нормативный
коэффициент запаса прочности. Конструкцию,
имеющую точку с такими напряжениями,
эксплуатировать запрещается. Действительный
(фактический) коэффициент запаса

меньше
нормативного
.
Согласно
четвертой теории прочности
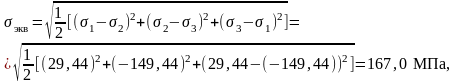
МПа.
Условие
прочности не выполнено и согласно
четвертой теории. Однако фактический
коэффициент запаса оказывается другим:
.
Положения опасных площадок согласно
третьей и четвертой теориям приведены
на рис. 2.10, 2.11. По площадке, показанной
жирной линией на рис. 2.10, действует
максимальное касательное напряжение.
Эта площадка перпендикулярна к площадке
2 и наклонена под углом в
45° к площадкам
1 и 3. Площадка, показанная
жирной линией на рис. 2.11, соответствует
четвертой теории прочности. Она равно
наклонена ко всем трем главным площадкам.

Рис. 2.11. Опасная
площадка
по четвертой
теории прочности
Специально обратим внимание
на способ изображения опасных площадок:
эти площадки показаны с привязкой к
исходному элементу. Так необходимо
сделать и при оформлении задачи.
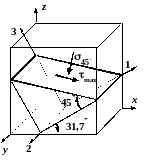
Рис. 2.10. Опасная
площадка
по третьей теории
прочности
Положение исходного
элемента по отношению к конструкции,
из которой вырезан элемент, известно.
Примененный способ изображения опасных
площадок позволяет указать эти площадки
непосредственно на конструкции.
Определение деформаций в точке.
Следует начать с выяснения, работает
ли материал в упругой области. Вычисленное
выше эквивалентное напряжение оказалось
меньше предела текучести. Это означает,
что уровень напряжений соответствует
упругой стадии деформирования и можно
использовать обобщенный закон Гука.
Если
уровень напряжений соответствует
неупругой стадии деформирования, то
закон Гука определяет только упругую
часть полных деформаций. В задаче при
этой ситуации нужно вычислить только
упругую составляющую деформации, отметив
это примечанием в тексте.
Линейные деформации в направлении осей

,
,
.
Угловая
деформация
.
Знак
минус означает, что угол (
)
уменьшается. Две другие угловые деформации
отсутствуют:
,
так как равны нулю соответствующие
касательные напряжения.
Линейные
деформации вдоль главных направлений
1, 2, 3

Относительная
объемная деформация
.

Рис. 2.13. Деформации
элемента по главным
направлениям 1,
3

Рис. 2.12. Деформации
элемента по
заданным направлениям х,
z
Рис. 2.12, 2.13 разъясняют результаты
вычислений. Условно исходные длины
ребер элемента считаются равными
единице. При этом линейные относительные
деформации в направлении этих ребер
равны абсолютным изменениям длин. В
исходном недеформированном состоянии
грани элемента параллельны координатным
плоскостям системы координат
.
В результате деформации тела элемент
перемещается как жесткое целое и
деформируется. На рис. 2.12 жирной
линией изображен деформированный
элемент. Недеформированный элемент
показан штриховой линией. Перемещение
элемента как жесткого целого не
изображено. Этот элемент получает
угловые и линейные деформации.
Деформированный
элемент, грани которого в исходном
недеформированном состоянии были
параллельны главным площадкам, показан
на рис. 2.13. Этот элемент получает
только линейные деформации.
2.2.
ИССЛЕДОВАНИЕ ПЛОСКОГО НАПРЯЖЕННОГО
СОСТОЯНИЯ ПО
ЗАДАННЫМ НАПРЯЖЕНИЯМ
НА
ГЛАВНЫХ ПЛОЩАДКАХ.
ПРОВЕРКА
ПРОЧНОСТИ (ЗАДАЧА № 8)
Условие
задачи
На гранях элементарного параллелепипеда
заданы главные напряжения (рис. 2.14).
Материал элемента – чугун c
характеристиками
МПа,
МПа,
МПа,
.
Нормативный коэффициент запаса прочности
.

Рис. 2.14.
Заданное
напряженное
состояние
в условии задачи
№ 8
Требуется:
-
найти нормальное
,
касательноеи полное
напряжения на наклонной площадке,
заданной угломи изображенной на рис. 2.14;
Макеты страниц
Разложим вектор напряжения 




Рис. 2.13.
Эта операция продемонстрирована на рис. 2.13, где оси координат выбраны по главным осям тензора напряжений и главные напряжения упорядочены так, что 


а из (2.33) получается величина нормальной компоненты

Подставляя (2.48) и (2.49) в формулу (2.47), вычислим квадрат величины касательного напряжения как функцию направляющих косинусов 

Максимальное и минимальное значения 

где скаляр 




которые вместе с условием 


Вот одно из решений системы (2.52) и соответствующее ему касательное напряжение, найденное по формуле (2.50):

Величины касательного напряжения в (2.53), очевидно, являются минимальными. Кроме того, так как (2.53) указывает на то, что эти величины обращаются в нуль на главных площадках, то направления, полученные в (2.53), совпадают с главными осями тензора напряжений.
Другие решения системы (2.52) имеют вид:

Формулы (2.546) дают максимальное значение касательного напряжения, равное полуразности наибольшего и наименьшего главных напряжений. Таким образом, из (2.546) следует, что максимальная компонента касательного напряжения действует в плоскости, которая делит пополам прямой угол между направлениями максимального и минимального главных напряжений.