Как найти математическое ожидание?
Математическое ожидание случайной величины $X$ (обозначается $M(X)$ или реже $E(X)$) характеризует среднее значение случайной величины (дискретной или непрерывной). Мат. ожидание – это первый начальный момент заданной СВ.
Математическое ожидание относят к так называемым характеристикам положения распределения (к которым также принадлежат мода и медиана). Эта характеристика описывает некое усредненное положение случайной величины на числовой оси. Скажем, если матожидание случайной величины – срока службы лампы, равно 100 часов, то считается, что значения срока службы сосредоточены (с обеих сторон) от этого значения (с тем или иным разбросом, о котором уже говорит дисперсия).
Нужна помощь? Решаем теорию вероятностей на отлично
Спасибо за ваши закладки и рекомендации
Формула среднего случайной величины
Математическое ожидание дискретной случайной величины Х вычисляется как сумма произведений значений $x_i$ , которые принимает СВ Х, на соответствующие вероятности $p_i$:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Для непрерывной случайной величины (заданной плотностью вероятностей $f(x)$), формула вычисления математического ожидания Х выглядит следующим образом:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Пример нахождения математического ожидания
Рассмотрим простые примеры, показывающие как найти M(X) по формулам, введеным выше.
Пример 1. Вычислить математическое ожидание дискретной случайной величины Х, заданной рядом:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$
Используем формулу для м.о. дискретной случайной величины:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i}.
$$
Получаем:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Вот в этом примере 2 описано также нахождение дисперсии Х.
Пример 2. Найти математическое ожидание для величины Х, распределенной непрерывно с плотностью $f(x)=12(x^2-x^3)$ при $x in(0,1)$ и $f(x)=0$ в остальных точках.
Используем для нахождения мат. ожидания формулу:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx.
$$
Подставляем из условия плотность вероятности и вычисляем значение интеграла:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{1} 12(x^2-x^3) cdot x dx = int_{0}^{1} 12(x^3-x^4) dx = \
=left.(3x^4-frac{12}{5}x^5) right|_0^1=3-frac{12}{5} = frac{3}{5}=0.6.
$$
Другие задачи с решениями по ТВ
Подробно решим ваши задачи по теории вероятностей
Вычисление математического ожидания онлайн
Как найти математическое ожидание онлайн для произвольной дискретной случайной величины? Используйте калькулятор ниже.
- Введите число значений случайной величины К.
- Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
- Нажмите на кнопку “Вычислить”.
- Калькулятор покажет вычисленное математическое ожидание $M(X)$.
Видео. Полезные ссылки
Видеоролики: что такое среднее (математическое ожидание)
Если вам нужно более подробное объяснение того, что такое мат.ожидание, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).
Лучшее спасибо – порекомендовать эту страницу
Полезные ссылки
А теперь узнайте о том, как находить дисперсию или проверьте онлайн-калькулятор для вычисления математического ожидания, дисперсии и среднего квадратического отклонения дискретной случайной величины.
Что еще может пригодиться? Например, для изучения основ теории вероятностей – онлайн учебник по терверу. Для закрепления материала – еще примеры решений по теории вероятностей.
А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте
его в существующую тему, а создайте новую в корневом разделе “Помогите решить/разобраться (М)”.
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву
, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения
и указать конкретные затруднения.
Обязательно просмотрите тему
Правила данного раздела, иначе Ваша тема может быть удалена
или перемещена в Карантин, а Вы так и не узнаете, почему.
|
|
Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Здравствуйте, в ходе решения более крупной задачи возникла необходимость вычислить математические ожидания максимума независимых случайных величин, т.е. Заранее спасибо,
|
|
|
|
|
Хорхе |
Re: Математическое ожидание максимума независимых с.в.
|
||
14/02/07 |
Довольно легко вывести формулу для функции распределения максимума независимых, если есть функция распределения одной величины. Для Пуассона и для биномиального ничего хорошего, чувствую, не выйдет, а для остальных математическое ожидание должно легко считаться.
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Очень прошу вас помочь советом или ссылкой, где это можно узнать. Е.С.Венцель, Л.А.Овчаров “Теория вероятностей и её инженерные приложения” 2000г.
|
|
|
|
|
marishka82 |
Re: Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Спасибо, мальчики, за ответы. Т.е. все таки необходимо в явном виде найти функцию распределения максимума? Какими-то косвенными способами найти математическое ожидание не получится?
|
|
|
|
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Т.е. все таки необходимо в явном виде найти функцию распределения максимума? А в чём проблема, если функция распределения случайной величины вам известна?
|
|
|
|
|
–mS– |
Re: Математическое ожидание максимума независимых с.в.
|
||
23/11/06 |
Какими-то косвенными способами найти математическое ожидание не получится? Нет, не получится. А в чём проблема, если функция распределения случайной величины вам известна? Думаю, никто не будет против, если Вы покажете здесь отсутствие проблем при нахождении, например, математического ожидания максимума
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
Думаю, никто не будет против, если Вы покажете здесь отсутствие проблем при нахождении, например, математического ожидания максимума Укажите параметр распределения и значение
|
|
|
|
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
|
||
|
|
|||
|
Александрович |
Re: Математическое ожидание максимума независимых с.в.
|
|
21/01/09 |
|
|
|
|
|
Хорхе |
Re: Математическое ожидание максимума независимых с.в.
|
||
14/02/07 |
(Оффтоп) – Штурман, приборы! Расскажите же нам, как Вы это нашли.
|
||
|
|
|||
|
marishka82 |
Re: Математическое ожидание максимума независимых с.в.
|
|
22/12/06 |
Хорхе писал(а): Расскажите же нам, как Вы это нашли. Возможно воспользовались одним из замечательных продуктов WolframResearch? Но меня к сожалению мало интересуют числовые значения математических ожиданий, мне нужно найти аналитическое выражение для нескольких классов распределений. Александрович, а что в той книжке, которую вы рекомендовали есть? Там объясняется как найти функцию распределия max{X1,…,Xn}?
|
|
|
|
|
–mS– |
Re: Математическое ожидание максимума независимых с.в.
|
||
23/11/06 |
А в чём проблема искать функцию распределения максимума? Если величины независимы и имеют одно и то же распределение с функцией распределения Да и всё равно не 5,6.
|
||
|
|
|||
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
Проблема в том, что функция невыразима. А численно-то и я умею.
|
||
|
|
|||
|
PAV |
Re: Математическое ожидание максимума независимых с.в.
|
||
29/07/05 |
marishka82 фамильярный тон на форуме не поощряется. По сути вопроса: Вам может помочь книга В.Б. Невзорова “Рекорды. Математическая теория”. Там написано и то, как считать распределения порядковых статистик (частным случаем которых является максимум), и приведены явные формулы для моментов. Однако красивых формул для них может не оказаться. В частности, в соответствующей главе утверждается, что для случая нормального распределения моменты представляются через элементарные функции только для моментах для различных порядковых статистик. В частном случае первого момента и максимума, возможно, дело обстоит чуть лучше. В качестве примера в книге приведено явное значение математического ожидания максимума из пяти величин, имеющих стандартное нормальное распределение:
|
||
|
|
|||
|
ИСН |
Re: Математическое ожидание максимума независимых с.в.
|
||
18/05/06 |
представляются через элементарные функции только для Ушёл думать, как такое вообще может быть.
|
||
|
|
|||
Модераторы: Модераторы Математики, Супермодераторы
Математическое ожидание — это ожидаемый результат от какого-то действия.
Например, можно рассчитать ожидаемую стоимость инвестиции в определённый момент в будущем. Рассчитывая математическое ожидание перед тем, как инвестировать, можно выбрать наилучший сценарий который, по мнению инвестора, даст наилучший результат.
Случайная величина может быть двух типов:
- Дискретной: число возможных значений X — это числимое конечное или бесконечное множество точек; пример: количество дефектных устройств в производстве фабрики.
- Непрерывной: X может принимать любое значение в заданном диапазоне; пример: концентрация углекислого газа в воде.
Математическое ожидание дискретной случайной величины рассчитывается этой формулой:

Где:
М — математическое ожидание,
X — случайная величина,
p — вероятность появления случайной величины.
Математическое ожидание дискретной случайной величины рассчитывается:
1. Сначала нужно умножить каждое из возможных результатов на свою вероятность (например: вероятность, что выпадет “1” — 1/6, “2” — 1/3, значит умножаем 1 на 1/6, 2 на 1/3, и т.д.),
2. Затем суммируем все эти значения (1 × 1/6 + 2 × 1/3 и т.д.).
Для непрерывной случайной величины используется эта формула:

Где:
М — математическое ожидание
f (x) — функция (которая будет предоставлена в условии задачи)
x — случайная величина
dx — элемент интегрирования
В этом случае рассчитывается интеграл в заданном интервале.
Примеры вычисления математического ожидания
Кратко:
- если в задаче даётся таблица с данными, то перемножаем каждое событие на его вероятность и потом всё складываем;
- если в задаче дают функцию с заданным интервалом, то вычисляем интеграл с этим интервалом.
Пример 1
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | −1 | 1 | 2 | 3 | 4 |
| pi | 0,1 | 0,2 | 0,3 | 0,1 | 0,3 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = −1×0,1+ 1×0,2 + 2×0,3 + 3×0,1 + 4×0,3 = −0,1 + 0,2 + 0,6 + 0,3 + 1,2 = 2,2
Пример 2
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = 2x, при x∈(0,1) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:


Пример 3
Вычислить математическое ожидание дискретной случайной величины Х со следующими данными:
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,3 | 0,3 | 0,1 | 0,1 | 0,2 |
Используется формула для дискретной случайной величины:

M(X) = ∑ xi×pi = 1×0,3 + 2×0,3 + 3×0,1 + 4×0,1 + 5×0,2 = 0,3 + 0,6 + 0,3 + 0,4 + 1 = 2,6
Пример 4
Найти математическое ожидание для величины Х, распределённой непрерывно с плотностью f(x) = (1/10).(3x²+1), при x∈(0,2) и f(x) = 0 в остальных точках.
Используется формула для непрерывной случайной величины:



Узнайте больше про Интегралы.
Основные свойства математического ожидания
- Математическое ожидание постоянной равно самой постоянной: М(c)=c.
- Математическое ожидание сложения/вычитания двух случайных величин равно сумме/вычитанию их математических ожиданий: пусть X и Y — две случайные величины, значит М (X ± Y) = М (X) ± М (Y).
- Если умножить случайную величину X на c, её среднее значение также умножается на эту константу (c): М (cX) = cМ (X).
- Если добавить или вычесть c из случайной величины X, то произойдёт та же операция (сложение или вычитание константы) с её средним значением: М (X ± c) = М (X) ± c.
- Если X и Y — две независимые случайные величины, значит: М(XY)=М(X)×М(Y).
Узнайте больше про Теорию вероятностей.
Критерий максимального математического ожидания выигрыша
Критерий
максимального математического ожидания
выигрыша применяется в тех случаях,
когда ЛПР известны вероятности состояний
окружающей среды. Платёжная матрица
дополняется столбцом, каждый элемент
которого представляет собой значение
математического ожидания выигрыша при
выборе соответствующей стратегии ЛПР:
![]()
где
pj
–вероятность j-го
состояния окружающей среды.
Оптимальной
по данному критерию
считается та стратегия ЛПР, при выборе
которой значение математического
ожидания выигрыша максимально:
W
= max
Wi
Применение
критерия максимального математического
ожидания выигрыша, таким образом,
оправдано, если ситуация, в которой
принимается решение, следующая:
1. ЛПР известны
вероятности всех состояний окружающей
среды;
2.
Минимизация риска проигрыша представляется
ЛПР менее существенным фактором принятия
решения, чем максимизация среднего
выигрыша.
Необходимость
иметь информацию о вероятностях состояний
окружающей среды ограничивает область
применения данного критерия.
Критерий недостаточного основания Лапласа
Данный
критерий используется при наличии
неполной информации о вероятностях
состояний окружающей среды в задаче
принятия решения. Вероятности состояний
окружающей среды принимаются равными
и по каждой стратегии ЛПР в платёжной
матрице определяется, таким образом,
среднее значение выигрыша:

Оптимальной по
данному критерию считается та стратегия
ЛПР, при выборе которой значение среднего
выигрыша максимально:
W
= max
Wi
Использование
данного критерия оправдано в следующей
ситуации:
1.
ЛПР не имеет информации, либо имеет
неполную информацию о вероятностях
состояний окружающей среды;
2.
Вероятности состояний окружающей среды
близки по своим значениям;
3.
Минимизация риска проигрыша представляется
ЛПР менее существенным фактором принятия
решения, чем максимизация среднего
выигрыша.
Максиминный критерий Вальда
Правило выбора
решения в соответствии с максиминным
критерием (ММ-критерием) можно
интерпретировать следующим образом:
Платёжная
матрица дополняется столбцом, каждый
элемент которого представляет собой
минимальное значение выигрыша в
соответствующей стратегии ЛПР:
Wi
= minj
aij
(4)
Оптимальной по
данному критерию считается та стратегия
ЛПР, при выборе которой минимальное
значение выигрыша максимально:
W
= max
Wi
Выбранная
таким образом стратегия полностью
исключает риск. Это означает, что
принимающий решение не может столкнуться
с худшим результатом, чем тот, на который
он ориентируется. Это свойство позволяет
считать ММ-критерий одним из фундаментальных.
Применение
ММ-критерия оправдано, если ситуация,
в которой принимается решение следующая:
1.
О возможности появления состояний
окружающей среды ничего не известно;
2. Решение реализуется
только один раз;
3. Необходимо
исключить какой бы то ни было риск.
Критерий минимаксного риска Сэвиджа
Величина
(amax
j
– aij
), где amax
j
– максимальный
элемент j
– го столбца, может быть интерпретирована
как дополнительный выигрыш, получаемый
в условиях состояния окружающей среды
Sj
при выборе ЛПР наиболее выгодной
стратегии, по сравнению с выигрышем,
получаемым ЛПР при выборе в тех же
условиях любой другой стратегии. Эта
же разность может быть интерпретирована
как величина возможного проигрыша при
выборе ЛПР i
– й стратегии по сравнению с наиболее
выгодной стратегией. На основе данной
интерпретации разности выигрышей
производится определение наиболее
выгодной стратегии по критерию
минимаксного риска.
Для
определения оптимальной стратегии по
данному критерию на основе платёжной
матрицы рассчитывается матрица рисков,
каждый коэффициент которой (rij)
определяется по формуле:
rij
= amax
j
– aij
(5)
Матрица
рисков дополняется столбцом, содержащим
максимальные значения коэффициентов
rij
по каждой из стратегий ЛПР:
Ri
= maxj
rij
Оптимальной
по данному критерию считается та
стратегия, в которой значение Ri
минимально:
W
= min
Ri
Ситуация,
в которой оправдано применение критерия
Сэвиджа, аналогична ситуации ММ-критерия,
однако наиболее существенным в данном
случае является учёт степени воздействия
фактора риска на величину выигрыша.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Поможем решить контрольную, написать реферат, курсовую и диплом от 800р
Узнать стоимость
Математическое ожидание дискретной случайной величины
Содержание:
- Свойства математического ожидания
Для понимания, что собой представляет матожидание от случайной величины,
являющейся дискретной, достаточно представить себе ряд значений, которые
принимает эта величина, в виде $ X_1, X_2 … X_n$. Любому из параметров
— исход случающийся с некоторой вероятностью. Значит каждому из них
соответствует определённое значение вероятности, поэтому для сучайной
величины, являющейся дискретной, вторая часть закона распределения —это
ряд $ P_1, P_2 … P_n$. Целиком же закон распределния представляет собой
таблицу, где в одной строке значения принимемые величиной, а в другой
вероятности им сосответствующие.
Определение 1
Чтобы произвести расчёт матожидания для случайной величины, являющейся
дискретной, следует произвести суммирование результатов, получаемых за
счёт умножения каждого значения величины на ту вероятность, которая ей
соответствует.
$M(X)= X_1cdot P_1 + X_2cdot P_2 + … + X_ncdot P_n$
Пример 1
Регулярно в театре проводятся спектакли, в зависимости от места
расположения билеты имеют разную стоимость. Всего тысяча мест, а их
стоимость определяется следующим образом:
• 50 рублей — 300 мест;
• 75 рублей — 200 мест;
• 100 рублей — 200 мест;
• 200 рублей — 150 мест;
• 400 рублей — 100 мест;
• 600 рублей — 50 мест;
Какова средняя стоимость одного театрального билета?
Решение
Средняя стоимость одного билета позволяет оценивать общую доходность, а
также помогает рассчитать необходимые стоимости зрительных мест для
получения равной выручки для разных залов. Вычислим среднюю цену для
одного билета, как среднее арифметическое от всех цен на все места.
$ frac {50 cdot 300 + 75 cdot 200 + 100 cdot 200 + 200 cdot 150 + 400
cdot 100 + 600 cdot 50}{1000} = 150 $
Среднее арифметическое получается 150 рублей. Именно такова средняя
выручка с одного места в зрительном зале. Следует отметить, что для
матожидания, математическое вычисление проводится фактически точно так же.
Указанное выше выражение можно представить в другом виде:
$ frac { 50 cdot 300}{1000} + frac { 75 cdot 200}{1000} + frac
{ 100 cdot 200}{1000} + frac { 200 cdot 150}{1000} + frac
{ 400 cdot 100}{1000} + frac { 600 cdot 50 }{1000}= 50 cdot
frac { 300}{1000} + 75 cdot frac { 200}{1000} + 100 cdot frac {
200}{1000} + 200 cdot frac { 150}{1000} + 400 cdot frac {
100}{1000} + 600 cdot frac { 50 }{1000} $
Если рассматривать вопрос в рамках теории вероятности, то представим себе
ситуацию, где театральные билеты положили в чёрный ящик и наудачу
вытягивают один из них. Тогда элементы $frac { 300}{1000}$, $ frac
{ 200}{1000}$, $ frac { 200}{1000}$, $ frac { 150}{1000}$, $ frac {
100}{1000}$, $ frac { 50 }{1000} $ соответствуют вероятности, получить
тот или иной билет. Таким образом, математическое ожидание для случайной
величины, являющейся дискретной, имеет смысл такого значения, которое
удастся получить с наибольшей вероятностью, а оно вычисляется как среднее
арифметическое.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример 2
На ферме осваивают новый вид растений. Рыночная цена при продаже одного
килограмма готового продукта, произведённого из растения составит 300
рублей. Из этой суммы фермер получает 150 рублей, 100 рублей отходит
посреднику, который продаёт готовый товар, а 50 рублей составляют зарплата
сотрудников. При этом, так как продукция новая, то остаётся неизвестным,
сколько килограмм удастся сбыть за ограниченное время, месяц. Только лишь
отдел маркетинга магазина даёт прогноз, что с некоторой вероятностью будет
реализовано определённое количество килограмм продукции:
• 500 килограмм будет реализовано с вероятностью 0,2,
затраты на изготовление, не считая зарплаты сотрудников, составят 100 000;
• 1000 килограмм будет реализовано с вероятностью 0,4,
затраты 150000;
• 2000 килограмм будет реализовано с вероятностью 0,25,
затраты 200000;
• 3000 килограмм будет реализовано с вероятностью 0,10,
затраты 250000;
• 4000 килограмм будет реализовано с вероятностью 0,05,
затраты 300000;
Требуется рассчитать какой доход получит фермер.
Решение
В соответствии с исходными данными «прибыль» —это
случайное значение, так как у неё имеется зависимость от количества
проданных изделий, которое само по себе является случайной величиной.
Вычислим сколько же в итоге составит прибыль и математическое ожидание:
• 500 килограмм, доход $500 cdot 150 – 100
000=-25000$ с вероятностью 0,2;
• 1000 килограмм, доход $1000 cdot 150 – 150
000=0$ с вероятностью 0,4;
• 2000 килограмм, доход $2000 cdot 150 – 200
000=100 000$ с вероятностью 0,25;
• 3000 килограмм доход $3000 cdot 150 – 250
000=200 000$ с вероятностью 0,10;
• 4000 килограмм, доход $4000 cdot 150 – 300
000=300 000$ с вероятностью 0,05;
По полученным значениям мы в состоянии определить математическое ожидание.
Для этого используем формулу, указанную в определении:
$M(X)= -25000cdot 0,2 + 0 cdot 0,4 + 100 000 cdot 0,25 + 200 000 cdot
0,10 + 300 000 cdot 0,05 = 55 000$
Результатом наших вычислений стало то, что матожидание, характеризующее
средневероятный доход в долгосрочной перспективе, составляет сумму в 55
000 рублей.
Свойства математического ожидания
Свойство 1
Рассчитывая матожидание от константы (постоянной величины) получаем в
значении ту же постоянную величину.
$М(C)=C$
Свойство 2
При вычислении матожидания от умножения постоянной величины на случайную,
такую постоянную, согласно первому свойству, допустимо вынести за знак
матожидания.
$М(CX)=Cdot М(X)$
Свойство 3
Когда складывают две или более случайных величин, то матожидание от их
суммы можно вычислить, также как и сумму матожиданий данных величин,
рассчитываемых по отдельности. Аналогичным образом данное свойство
применимо к случаю вычитания.
$М(Xpm Y)=М(X) pm М(Y)$
Свойство 4
Для произведения двух случайных величин являющихся независимыми,
матожидание может быть рассчитано как два умноженных друг на друга
матожидания, взятых от каждой из рассматриваемых случайных величин.
$М(Xcdot Y)=М(X) cdot М(Y)$
Свойство 5
В случае, сложения постоянной и случайной величин математическое ожидание
допустимо представить в том виде, когда слагаемыми выступают постоянная
величина (матожидание от которой, согласно первому правилу равно ей самой)
и матожидания велчиины, являющейся случайной. Таким же образом может
производиться расчёт для
$М(Xpm С)=М(X) pm С $
Пример 3
При игре в дартс в одном из городов Ирландии придумали соревнование, на
котором необходимо кидать дротики в три мишени, расположенные на разном
расстоянии друг от игрока. При этом вероятность набрать максимальное
количество очков на первой мишени (событие $X_1$) составляет $P_1=0,4$, на
второй мишени (событие $X_2$) $P_2=0,3$, из третьей мишени (событие $X_2$)
$P_3=0,6$. Требуется рассчитать матожидание события X, при котором на всех
мишенях будут набраны максимальные очки.
Решение
Событие заключающееся в том, что игрок набирает максимальное количество
очков на мишени является случайной величиной, которая может принимать
исключительно два значения 1, если данное количество набрано и 0, если не
набрано. Поэтому математические ожидания от выполнения событий $X_1, X_2,
X_3$ составят величины равные вероятностям данных событий. То есть
$M(X_1)=P_1=0,4$;
$M(X_2)=P_2=0,3$;
$M(X_3)=P_3=0,6$;
Событие состоящее в том, что на всех трёх мишенях набраны максимальные
очки, тоже является случайной величиной и представляет собой сумму событий
$X_1, X_2, X_3$:
$ X=X_1+ X_2+ X_3$
Значит можно записать:
$ M(X)=M(X_1+ X_2+ X_3)$
Согласно третьему свойству матожидания выражение примет вид:
$ M(X)=M(X_1+ X_2+ X_3)=M(X_1)+M( X_2)+ M(X_3)= 0,4+0,3+0,6=1,3$
Таким образом, математическое ожидание события X составляет 1,3.
Не получается написать работу самому?
Доверь это кандидату наук!

 независимых случайных величин с распределением Пуассона (даже одним и тем же). Функция распределения, полагаю, известна.
независимых случайных величин с распределением Пуассона (даже одним и тем же). Функция распределения, полагаю, известна.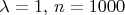
 , то
, то 
 . Правда, здесь речь идет, видимо, о
. Правда, здесь речь идет, видимо, о 
