Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

А ‑ расчетная схема; б ‑ эпюра продольных сил; в ‑ эпюра напряжений; г ‑ эпюра продольных перемещений
Решение.
1. Построение
эпюры N.
На
брус действуют три силы, следовательно,
продольная сила по его длине
будет изменяться. Разбиваем брус на
участки, в пределах которых продольная
сила будет постоянной. В данном случае
границами участков являются сечения,
в которых приложены силы. Обозначим
сечения буквами А,
В, С, D, начиная
со свободного конца, в данном случае
правого.
Для
определения продольной силы на каждом
участке рассматриваем произвольное
поперечное сечение, сила в котором
определяется по правилу, приведенному
ранее. Чтобы не определять предварительно
реакцию в заделке D,
начинаем расчеты со свободного конца
бруса А.
Участок
АВ,
сечение 1-1.
Справа от сечения действует растягивающая
сила P1
(рис. 15, а).
В соответствии с упомянутым ранее
правилом, получаем
NAB=+P1=40
кН.
Участок
ВС,
сечение 2-2.
Справа от него расположены две силы,
направленные в разные стороны. С
учетом правила знаков, получим
NBС=+P1-P2=40-90=-50
кН.
Участок
СD,
сечение 3-3: аналогично получаем
NСD=+P1-P2-P3=40-90-110=-160
кН.
По
найденным значениям N
в выбранном масштабе строим эпюру,
учитывая, что в пределах каждого
участка продольная сила постоянна
(рис.15,б)
Положительные
значения N
откладываем вверх от оси эпюры,
отрицательные – вниз.
2.
Построение эпюры напряжений σ.
Вычисляем напряжения
в поперечном сечении для каждого участка
бруса:
![]()
![]()
![]()
При
вычислении нормальных напряжений
значения продольных сил N
берутся по эпюре с учетом их знаков.
Знак плюс соответствует растяжению,
минус – сжатию. Эпюра напряжений показана
на рис. 15, в.
3. Построение
эпюры продольных перемещений.
Для построения
эпюры перемещений вычисляем абсолютные
удлинения отдельных участков бруса,
используя закон Гука:
![]()
![]()
![]()
Определяем
перемещения сечений, начиная с неподвижного
закрепленного конца. Сечение
D
расположено в заделке, оно не может
смещаться и его перемещение
равно нулю:
∆D=0.
Сечение
С
переместится в результате изменения
длины участка CD.
Перемещение сечения
С определяется
по формуле
∆C=∆lCD=-6,7∙10-4
м.
При
отрицательной (сжимающей) силе точка С
сместится влево.
Перемещение
сечения В
является
результатом изменения длин DC
и CB.
Складывая их удлинения, получаем
∆B=∆lCD+∆lBC
=-6,7∙10-4
-2,1∙10-4
= -8,8∙10-4
м.
Рассуждая
аналогично, вычисляем перемещение
сечения А:
∆A=∆lCD+∆lBC+∆lAB
=-6,7∙10-4
-2,1∙10-4
+0,57∙10-4=
-8,23∙10-4
м.
В
выбранном масштабе откладываем от
исходной оси значения вычисленных
перемещений. Соединив полученные точки
прямыми линиями, строим
эпюру перемещений (рис.15,
г).
4. Проверка
прочности бруса.
Условие прочности
записывается в следующем виде:
σmax≤[σ].
Максимальное
напряжение σmax
находим по эпюре напряжений, выбирая
максимальное по абсолютной величине:
σmax=267
Мпа.
Это
напряжение действует на участке DC,
все сечения которого являются опасным.
Допускаемое
напряжение вычисляем по формуле:
![]()
Сравнивая
σmax
и [σ],
видим, что условие прочности не
выполняется, так как максимальное
напряжение превышает допускаемое.
Пример
4
Подобрать
из условий прочности и жесткости размеры
прямоугольного поперечного сечения
чугунного стержня (см. рис. 16, а).
Дано:
F=40
кН; l=0,4
м; [σp]=350
Мпа; [σс]=800
Мпа; Е=1,2∙105
МПа; [∆l]=l/200;
h/b=2,
где h
– высота, b
– ширина поперечного сечения.
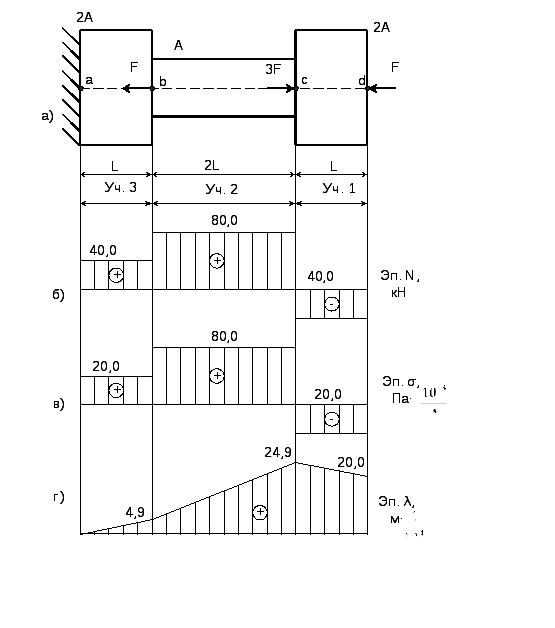
Рис.16
Решение.
1.
Построение эпюры внутренних усилий N
Стержень разделен
на 3 участка в зависимости от изменения
внешней нагрузки и площади поперечного
сечения. Применяя метод сечений,
определяем продольную силу на каждом
участке.
На
участке 1: N1=-F=-40
кН.
На
участке 2: N2=-F+3F=2F=80
кН.
На
участке 3: N3=-F+3F-2F=F=40
кН.
Эпюра
N
приведена
на рис. 16, б.
2.
Построение
эпюры нормальных напряжений
Найдем напряжения
на участках стержня.
На
участке 1: ![]()
На
участке 2: ![]()
На
участке 3: ![]()
Эпюра
σ
приведена на рис. 16, в.
3. Нахождение
площади поперечного сечения из условия
прочности
Наибольшие
растягивающие напряжения возникают на
участке 2, наибольшие сжимающие напряжения
– на участке 1. Для вычисления площади
поперечного сечения используем условия
прочности σmax.p≤[σp]
и σmax.с≤[σс].
Напряжения на
участке 1 равны
![]()
Тогда
![]()
Следовательно,
![]()
Напряжения на
участке 2 равны
![]()
По
условию прочности ![]()
Отсюда:
![]()
Напряжения на
участке 3 равны
![]()
Тогда
![]()
Следовательно,
![]()
Необходимую площадь
сечения следует принять из условия
прочности при растяжении:
![]()
При
заданном соотношении h/b=2
площадь поперечного сечения можно
записать, как A=h∙b=2b2.
Размеры
поперечного сечения будут равны:

![]()
4. Нахождение
площади поперечного сечения из условия
жесткости
При
расчете на жесткость следует учитывать,
что перемещение в точке d
будет равно
сумме деформаций всех участков стержня.
Величину абсолютной деформации для
каждого участка найдем по формуле
![]() или
или
![]()
На
участке 1: ![]()
На
участке 2: ![]()
На
участке 3: ![]()
Абсолютная
деформация всего стержня:
![]()
Из
условия жесткости ∆l≤[∆l],
![]()
найдем
![]() ,
,
откуда
![]()
Размеры поперечного
сечения будут равны:

![]()
Сопоставляя
результаты расчета на прочность и
жесткость, принимаем большее значение
площади поперечного сечения A=2,65
см2.
5.
Построение эпюры перемещений 𝜆
Для
определения перемещения любого сечения
стержня строят
эпюру
перемещений![]() 𝜆.
𝜆.
За начало
отсчета принимаем сечение в заделке,
так как перемещение этого сечения равно
нулю. При построении эпюры последовательно
определяем перемещения характерных
сечений стержня, которые равны
алгебраической сумме изменений длин
всех участков от начала отсчета до
рассматриваемого сечения.
Сечение
а: ![]()
Сечение
b:
![]()
Сечение
с: ![]()
Сечение
d:
![]()
Эпюра
перемещений λ
представлена на рис.16, г.
Пример
5
Для
ступенчатого бруса (рис. 17, а)
при Е=2∙105
Мпа, σТ=
240 МПа, требуется определить:
1. Внутренние
продольные силы по его длине и построить
эпюру продольных сил.
2. Нормальные
напряжения в поперечных сечениях и
построить эпюру нормальных напряжений.
3. Запас прочности
для опасного сечения.
4. Перемещения
сечений и построить эпюру перемещений.
Дано:
F1
= 30кН; F2
= 20кН; F3
= 60 кН; l1
= 0,5м; l2
= 1,5м; l3
= 1м; l4
= 1м; l5
= l6
= 1м; d1
= 4см; d2
= 2см.

Рис.17
Решение.
1. Определение
продольных сил в характерных сечениях
бруса, и построение эпюры продольных
сил.
Изображаем
расчетную схему (рис. 17,а)
и определяем реакцию опоры в заделке,
которую направляем с внешней стороны
заделки влево. Если в результате
определения реакции RВ
окажется отрицательной, то это указывает
на то, что ее направление противоположно.
Ступенчатый брус под действием сил F1,
F2,
F3
и реакции RВ
находятся в равновесии, поэтому для
определения RВ
достаточно составить одно уравнение
проекций всех сил на ось х,
совпадающую с осью бруса.
ΣFix=-F1-F2+F3-RB=0
Откуда
RB=-F1-F2+F3=-30-20+60=10
кН
Разграничим брус
на участки. Границами участков являются
сечения, в которых приложены внешние
силы, а для напряжений также и места
изменения размеров поперечного сечения
(рис. 17,а)
Пользуясь методом
сечений, определяем для каждого участка
величину и знак продольной силы. Проведем
сечение 1–1 и рассмотрим равновесие
правой отсеченной части бруса (рис.
17,б). Внутренние силы в каждом сечении
условно направляем в сторону отброшенной
части. Если внутренняя продольная сила
положительна на участке, имеет место
деформация растяжения; отрицательна –
сжатие.
Рассматривая
правую отсеченную часть, находим
ΣFix=-N1-RB=0;
N1=-RB=-10
кН (сжатие)
Значение продольной
силы в пределах первого участка не
зависит от того, какую из отсеченных
частей мы рассматривали. Целесообразнее
всегда рассматривать ту часть бруса, к
которой приложено меньше сил. Проведя
сечения в пределах второго, третьего и
четвертого участков, аналогично найдем:
для сечения 2–2
(рис. 17,в)
ΣFix=-N2+F3-RB=0;
N2=F3-RB=60-10=50
кН (растяжение).
для сечения 3–3,
рассматриваем левую часть бруса (рис.
17,г)
ΣFix=-F1-N3=0;
N3=F1=30
кН (растяжение).
для
сечения 4–4 (рис. 17,д)
ΣFix=N4=0;
N4=0
эта часть бруса не испытывает деформации.
После
определения внутренних продольных сил
в характерных сечениях, строят график
их распределения по длине бруса. График,
показывающий, как изменяются продольные
силы (N)
при переходе от одного сечения к другому,
т.е. график, изображающий закон изменения
N
вдоль оси бруса, называется эпюрой
продольных сил.
Эпюра продольной
силы строится в следующей последовательности.
В разграниченном на участки брусе
провести через точки приложения внешних
сил линии, перпендикулярные его оси. На
некотором расстоянии от оси бруса
провести линию параллельную его оси:
на перпендикуляре к этой линии отложить
в выбранном масштабе отрезок,
соответствующий продольной силе для
каждого участка: положительные вверх
от оси эпюры, отрицательные – вниз.
Через концы отрезков провести линии,
параллельные оси. Ось эпюры проводят
тонкой линией, а саму эпюру очерчивают
толстыми линиями, эпюру штрихуют тонкими
линиями, перпендикулярными ее оси. В
масштабе каждая линия равна продольной
силе в соответствующем сечении бруса.
На эпюре указывают знаки плюс и минус
и в характерных ее точках, где изменяется
сила, проставляют ее значение. В сечениях,
в которых приложены сосредоточенные
силы, на эпюре имеются скачки – резкое
изменение продольной силы “Скачок”
продольной силы равен внешней силе,
приложенной в данном сечении, что
является проверкой правильности
построенной эпюры. На (рис. 18,б) построена
эпюра продольных сил для заданного
ступенчатого бруса.
2. Определение
нормальных напряжений в поперечных
сечениях бруса и построение эпюры
нормальных напряжений.
Нормальные
напряжения на каждом участке определяем
по формуле σ=N/A,
подставляя в ее значение сил (в Н)
и площадей (в мм2).
Площади поперечных сечений бруса
определяем по формуле A=πd2/4
Тогда
![]()
![]()
![]()
Нормальные
напряжения на участках I–VI
равны соответственно:
I.
![]()
т.к.
N4
= 0
II.
![]()
III.
![]()
VI.
![]()
V.
![]()
VI.
![]()
В
пределах каждого участка напряжение
одинаково, так как одинаковы во всех
сечениях значения продольной силы и
площади поперечного сечения. Эпюра σ
очерчена прямыми, параллельными ее оси.
Построение по вычисленным значениям
эпюры представлена на (рис. 18,в).
3. Определение
запаса прочности для опасного сечения.
Из
эпюры нормальных напряжений, построенной
по длине бруса видно, что наибольшее
напряжение возникает в пределах
четвертого участка σmax=159,2
Н/мм2,
следовательно, запас прочности
![]()
4. Определение
перемещений сечений и построение эпюры
перемещений.
Для построения
эпюры перемещений достаточно определить
перемещения крайних сечений каждого
участка. Перемещение сечения определим
как алгебраическую сумму деформаций
участков стержня, расположенных между
этим сечением и заделкой, т.е. неподвижным
сечением.
Абсолютные
перемещения сечений вычислим по формулам:
![]()
![]()
![]()
![]()
![]()
![]()
Эпюра
продольных перемещений представлена
на (рис. 18,г). В случае проверки жесткости
следует сравнить полученное максимальное
значение ∆l
= 1,55 мм
с допускаемым [∆l]
для данного бруса.

Рис.18
Пример
6
Для ступенчатого
бруса (рис.19) требуется:
1.
Построить эпюру продольных сил
![]()
2. Определить
нормальные напряжения
![]() в поперечных сечениях и построить эпюру
в поперечных сечениях и построить эпюру![]()
3. Построить эпюру
перемещений
![]() поперечных сечений.
поперечных сечений.
Дано:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
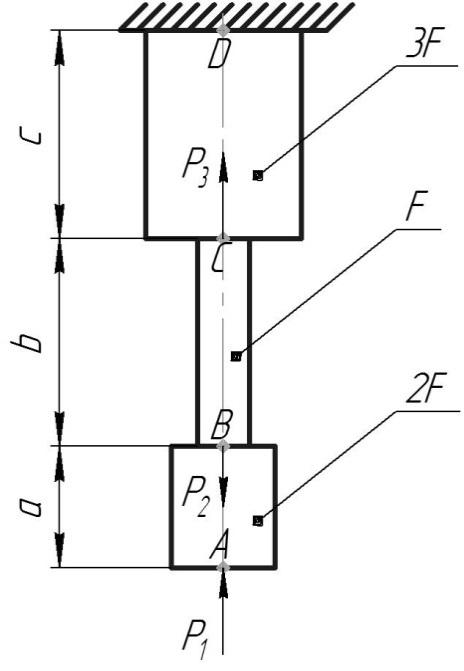
Рис.19
Решение.
1. Определим
нормальные усилия
Участок AB:
![]()
Участок BC:
![]()
Участок CD:
![]()
Эпюра продольных
сил
![]() показана на рис.20.
показана на рис.20.
2. Определим
нормальные напряжения
Участок
AB:
![]()
Участок
BC:
![]()
Участок
CD:
![]()
Эпюра
нормальных напряжений σ
показана на рис.20.
3. Определим
перемещения поперечных сечений
![]()
![]()
![]()
![]()
Эпюра перемещений
δ показана на
рис.20.
|
Эпюра |
Эпюра |
Эпюра |
|
|
|
|
Рис.20
Пример
7
Для ступенчатого
стального стержня (рис.21) требуется:
1.
Построить эпюры продольных сил N
и нормальных
напряжений σ.
2.
Определить продольную деформацию
стержня ∆l.
Дано:
Е
= 2∙105
МПа; А1
= 120 мм2;
А2
= 80 мм2;
А3
= 80 мм2;
а1
= 0,1 м; а2
= 0,2 м; а3
= 0,2 м; F1
= 12 кН; F2
= 18 кН; F3
= -12 кН.
Решение.
1.
Построение эпюр N
и σ
Применяем метод
сечений.
Участок 1.

ΣХ
= 0 →
-N1
+ F1
= 0; N1
= F1
= 12 кН;
![]()
Участок 2.

ΣХ
= 0 →
-N2
+ F2
+ F1
= 0;
N2
= F2
+ F1
= 18 + 12 = 30 кН;
![]()
Участок 3

ΣХ
= 0 →
– N3
– F3
+ F2
+ F1
= 0;
N3
= – F3
+ F2
+ F1=
-12 + 18 + 12 = 18 кН;
![]()
2. Расчетная схема
с истинным направлением внешней нагрузки
и расчетными эпюрами.
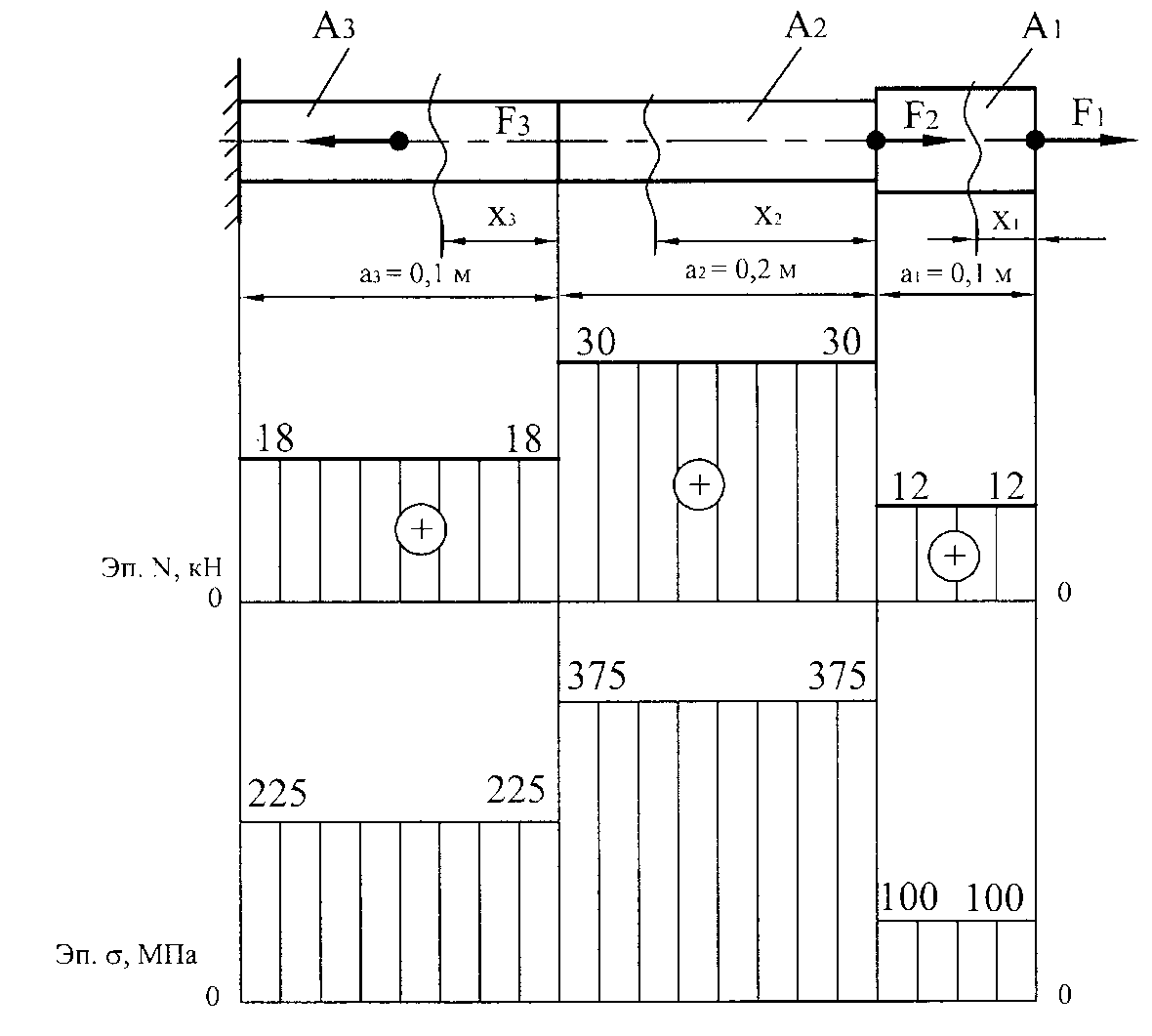
Рис.21
3. Определение
продольной деформации стержня
![]()
![]()
![]()
Пример
8
Для
бруса, жестко заделанного обоими концами
и нагруженного вдоль оси силами F1
и F2
приложенными в его промежуточных
сечениях (рис. 22,а),
требуется
1) Построить эпюры
продольных сил,
2) Построить эпюры
нормальных напряжений
3) Построить эпюры
перемещений поперечных сечений
4) Проверить
прочность бруса.
Дано:
если материал – сталь ст.3, F = 80 кН, σт
= 240 МПа, А = 4 см2,
а = 1 м, требуемый коэффициент запаса [n]
= 1,4, Е
= 2∙105
МПа.

Рис.22
Решение.
1.
Статическая сторона задачи.
Поскольку
силы F1
и F2
действуют вдоль оси стержня на его
концах, под действием сил F1
и F2
в заделках
могут возникнуть только горизонтальные
опорные реакции RА
и RВ.
В данном случае имеем систему сил,
направленных по одной прямой (рис. 22,а),
для которой статика дает лишь одно
уравнение равновесия.
ΣFix
= -RА
+ F1
+ F2
– RВ
= 0; RА +
RВ
= F1
+ F2
= 3F (1)
Неизвестных
реактивных сил две RА
и RВ,
следовательно, система один раз статически
неопределима, т.е. необходимо составить
одно дополнительное уравнение перемещений.
2.
Геометрическая сторона задачи.
Для
раскрытия статической неопределимости,
т.е. составления уравнения перемещений,
отбросим одну из заделок, например
правую (рис. 22,б).
Получаем статически определимый брус,
заделанный одним концом. Такой брус
называют основной системой. Действие
отброшенной опоры заменяем реакцией
RВ
= Х.
В результате имеем статически определимый
брус, нагруженный кроме заданных сил
F1
и F2
неизвестной реактивной силой RВ
= Х. Этот
статически определимый брус нагружен
так же как заданный статически
неопределимый, т.е. эквивалентен ему.
Эквивалентность этих двух брусьев
позволяет утверждать, что второй брус
деформируется так же, как первый, т.е.
перемещение ∆В
– сечения
В
равно нулю, так как фактически (в заданном
брусе) оно жестко заделано: ∆В
= 0.
На
основе принципа независимости действия
сил (результатом действия на тело системы
сил не зависит от последовательности
их приложения и равен сумме результатов
действия каждой силы в отдельности)
перемещение сечения В
представим как алгебраическую сумму
перемещений от сил F1,
F2
и Х,
т.е. уравнение совместности деформаций
примет вид:
∆B=∆BF1+∆BF2+∆BX=0
(2)
В
обозначениях перемещений первая буква
индекса указывает о перемещении какого
сечения идет речь; вторая – причину,
вызывающую это перемещение (силы F1,
F2
и Х).
3.
Физическая сторона задачи.
На
основании закона Гука выражаем перемещения
сечения В,
через
действующие силы F1,
F2
и неизвестную реакцию Х.
На
(рис. 22, в, г,
д), показаны
схемы нагружения бруса каждой из сил в
отдельности и перемещения сечения В
от этих сил.
Пользуясь этими
схемами, определяем перемещения:
![]() равно
равно
удлинению участка АС;
![]() равно
равно
удлинению участков АД
и
ДЕ;
![]() равно
равно
сумме укорочений участков АД,
ДК, КВ.
4. Синтез.
Подставим
значения ![]() ,
,
![]() ,
,
![]()
в уравнение
(2), имеем
![]()
Откуда
![]()
Следовательно:
![]()
Подставляя
RВ
в уравнение (1), получим:
RА
+ 66,7 =3∙80
= 240
отсюда
RА
=240–66,7=173,3 кН, RА
= 173,3 кН, таким образом, статическая
неопределимость раскрыта – имеем
статически определимый брус, заделанный
одним концом, нагруженный известными
силами F1,
F2
и Х = 66,7 кН.
Эпюру продольных
сил строим как для статически определимого
бруса. На основании метода сечений
внутренние продольные силы в характерных
участках равны:
NАС
= RА
= 173,3 кН;
NСЕ
= RА
– 2F = 173,3 – 80∙2
= 13,3 кН;
NЕВ
= -RА
= – 66,7 кН.
Эпюра
продольных сил представлена на (рис.
22, е).
Значения нормальных напряжений в
характерных сечениях определяем по
формуле
![]()
Для
участка АС
![]()
для
участка СД
![]()
для
участка ДЕ
![]()
для
участка ЕК
![]()
для
участка КВ
![]()
В
пределах каждого из участников напряжения
постоянны, т.е. эпюра “σ”
– прямая, параллельная оси бруса (рис.22,
ж).
При
расчете на прочность интерес представляют
те сечения, в которых возникают наибольшие
напряжения. В рассмотренном примере
они не совпадают с теми сечениями, в
которых продольные силы максимальны,
наибольшее напряжение возникает на
участке ЕК,
где σмах
= – 166,8 МПа.
Из условия задачи
следует, что предельное напряжение для
бруса
σпред
= σт
= 240 МПа, поэтому допускаемое напряжение
![]()
Отсюда
следует, что расчетное напряжение σ
= 166,8 МПа < 171,4 МПа, т.е. условие прочности
выполняется. Разница между расчетным
напряжением и допускаемым составляет:
![]()
Перегрузка
или недогрузка допускается в пределах
±5%.
При
построении эпюры перемещений достаточно
определить перемещения сечений
совпадающих с границами участков, так
как между указанными сечениями эпюра
∆l
имеет
линейный характер. Начинаем строить
эпюру перемещений от левого защемленного
конца бруса, в котором ∆А
= 0; так как оно неподвижно.
![]()
![]()
![]()
![]()
![]()
Итак,
на правом конце бруса в сечении В,
ордината эпюры ∆l
равна
нулю, так как в заданном брусе это сечение
жестко защемлено, по вычисленным
значениям построена эпюра ∆l
(рис.22, з).
Пример
9
Для
составного ступенчатого бруса, состоящего
из меди и стали и нагруженного
сосредоточенной силой F
(рис. 23,а),
определить внутренние продольные силы
и построить их эпюры, если известны
модули упругости материала: для стали
Ec,
для меди EM.
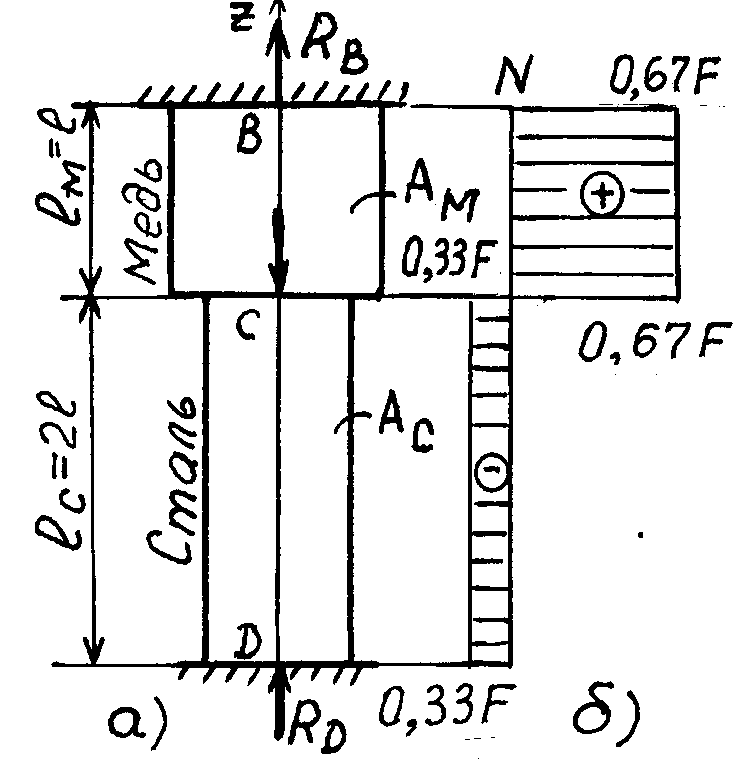
Рис.23
Решение.
1.
Составляют уравнение статического
равновесия:
ΣZ=0;RB-F+RD=0.
(1)
Задача
один раз статически неопределима,
поскольку обе реакции могут быть
определены только из одного уравнения.
2.
Условие совместности перемещений должно
выразить тот факт, что общая длина бруса
не меняется, т.е. перемещения, например,
сечения
![]() (2)
(2)
Используя
закон Гука σ=Eε,
с учетом того факта, что перемещения
какого-либо поперечного сечения бруса
численно равны удлинению или
укорочению его участков, расположенных
между заделкойBи
«перемещающимся» сечениемD,
преобразуют уравнение (2) к виду:
![]()
Отсюда
RD=0,33F.
(4)
Подставив
(4) в (1), определяют
RB=F-RD=F-0,33F=0,67F.
(5)
Тогда,
применив метод сечений, согласно
выражению Ni=ΣFi,
получают:
NDC=-RD;NBC=RB.
Приняв
для наглядности решения
lM=l;
lc=2l;
AM=4AC;
EC=2EM.
с учетом
(4) получают NDC=-RD=
-0,33F,
a с
учетом (5) получают NBC=RB=0,67F.
Эпюра
продольных сил N показана
на рис. 16, б.
Расчет
на прочность после этого выполняют
согласно условию прочности ![]()
Пример
10
Брус
ступенчато-переменного сечения, расчетная
схема которого показана на рисунке 24,
находится в условиях центрального
(осевого) растяжения-сжатия под действием
заданной нагрузки.
Требуется:
1) Раскрыть статическую
неопределимость;
2) Построить эпюры
нормальных сил и нормальных напряжений
(в буквенном выражении величин);
3) Подобрать сечение
бруса по условию прочности;
4) Построить эпюру
продольных перемещений поперечных
сечений.
Влиянием собственного
веса бруса пренебречь, опорные устройства
считать абсолютно жесткими.
Дано:
![]()
материал – чугун,
допускаемые напряжения (расчетные
сопротивления):![]()
Принять:для
чугуна![]()
![]()
Параметр Fподлежит определению из условий
прочности, а параметрP при
выполнении п.3 задания, принять:![]()
Примечание:
1) В расчетной схеме
между нижним торцом бруса и опорой до
нагружения бруса имеется зазор
![]() .
.
Коэффициент![]() принять соответственно равным 1.
принять соответственно равным 1.
2) При отсутствии
на расчетной схеме одной из сил P1илиP2соответствующий
коэффициент (α1или α2) считать
равным нулю
3) При выполнении
п.3 задания следует пользоваться методом
допускаемых напряжений

Рис.24
Решение:
1) В результате
нагружения бруса, в его заделках возникают
реакции
![]() направленные вдоль оси (рис.25). Определяем
направленные вдоль оси (рис.25). Определяем
реакцию в заделке. Предварительно
направляем ее вверх.

Рис.25
Составляем уравнение
равновесия:
![]()
Это уравнение
является единственным и содержит две
неизвестные силы. Следовательно, система
один раз статически неопределима.
Раскрываем
статическую неопределимость:
![]()
Выразим удлинения
через силы:
![]()
![]()
![]()
![]()
![]()
![]()
Подставим в
уравнение равновесия:
![]()
![]()
![]()
![]()
Таким образом,
статическая неопределимость раскрыта.
![]()
2) Разобьем брус
на 3 участка (рис.26), начиная от его
свободного конца; границами участков
служат сечения, где приложены внешние
силы, а также места изменения размеров
поперечного сечения.

Рис.26
Произведем
произвольное сечение 1 – 1 на участке
I, и, отбросив верхнюю
часть бруса, рассмотрим условия равновесия
оставленной нижней части, изображенной
отдельно (рис.27,б).
На оставленную
часть действует сила RB
искомое усилие![]() .
.
Проектируя на осьZсилы,
действующие остальную часть, получаем![]() .
.
Отсюда
![]() .
.
Проведем произвольное
сечение 2 – 2 на участке II,
и, отбросив верхнюю часть бруса, рассмотрим
условия равновесия оставленной нижней
части, изображенной отдельно (рис.27,в).
![]() .
.
![]() .
.
Проведем произвольное
сечение 3 – 3 на участке III,
и, отбросив верхнюю часть бруса, рассмотрим
условия равновесия оставленной нижней
части, изображенной отдельно (рис.27,г).
![]() .
.
![]() .
.
Построим график
(эпюру), показывающий, как меняется N
по длине бруса (рис.27,д).
Эпюру нормальных
напряжений получим, разделив значения
Nна соответствующие
площади поперечных сечений бруса, т.е.![]()
Для Iучастка:
![]()
Для IIучастка:
![]()
Для IIIучастка:
![]()
Построим эпюру
нормальных напряжений (рис.27, е).
3) Расчет прочности
выполняется с использованием условий
прочности. Условие прочности конструкции
записывается в виде:
![]()
![]()
где
![]() – наибольшие расчетные растягивающие
– наибольшие расчетные растягивающие
и сжимающие напряжения в конструкции;
![]() –допускаемые
–допускаемые
напряжения при растяжении и сжатии
соответственно.
Подбор сечения
бруса в данном случае осуществляется
по условию прочности третьего участка,
т.к. на этом участке возникают наибольшие
растягивающие напряжения:
![]()
откуда
![]()
Принимаем
![]()
По найденному
значению параметра F определяем
площади сечений участков бруса:
![]()
![]()
Подбор сечений
чугунного бруса по условию прочности
на сжатие производить не будем, т.к.
наибольшее значения сжимающих напряжений
![]() меньше растягивающих
меньше растягивающих![]() , а
, а![]()
4) Построим эпюру
продольных перемещений поперечных
сечений. Она строится суммированием
упругих удлинений участков, начиная с
неподвижного конца.
Определим изменение
длин участков бруса по формуле:
![]()
Для III
участка–
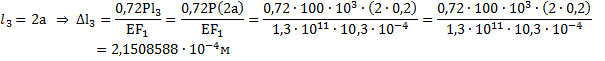
Для II
участка–![]()

Для I
участка–

По условию в
расчетной схеме между нижним торцом
бруса и опорой до нагружения бруса
(участок I) имеется зазор![]() .
.
Коэффициент![]() по условию равен 1, тогда зазор будет
по условию равен 1, тогда зазор будет
равен![]() .
.
Находим осевые
перемещения сечений бруса по границам
участком:
![]()
![]()
![]()
![]()
![]()
![]()
Построим эпюру
продольных перемещений поперечных
сечений (рис.27, ж).

Рис.27
Пример
11
Для статически
неопределимого стержня (рис.28) требуется
построить эпюры продольных сил и
нормальных напряжений.
Дано: l1= 1 м;l2= 0,8 м;F2= 15 см2= 15·10-4м2;F2/F1=
2,1;P=190 кН = 190·103Н;
∆t= 30K; δ
= 0,006 см = 6·10-5м;E=
1·105МПа =1·1011Па; α= 17·10-6K.
iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки
Расчет напряжений
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx 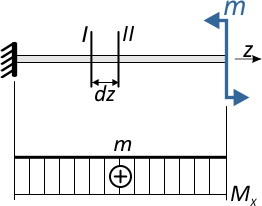
представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения. 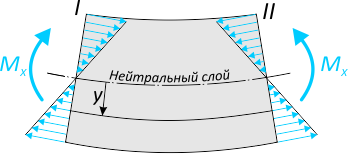
Закон распределения нормальных напряжений по высоте сечения выражается формулой: 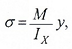
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2: 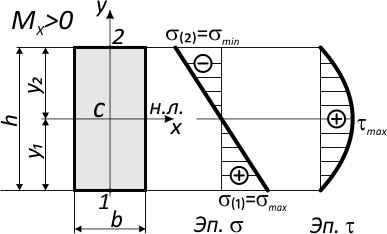
Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку. 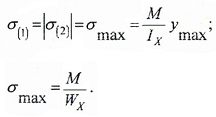
Для несимметричного сечения 
напряжения определяются отдельно для нижней точки 1 и верхней точки 2: 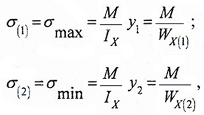
где: 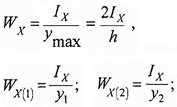
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке. 
В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения. 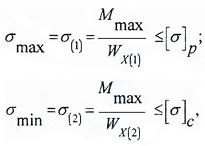
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[ σ], [ σ]р, [ σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]с>[ σ]р. 
В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности

- Подбор сечений
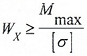
- Определение максимально допустимой нагрузки
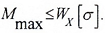
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского 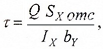
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax: 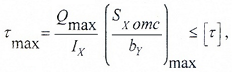
где [ τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: 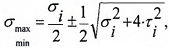
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений: 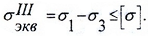
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Источник
Основы сопромата. Определение касательных напряжений.
Расчет разного рода балок, особенно постоянного прямоугольного сечения, на прочность при действии касательных напряжений очень редко является определяющим в отличие от приведенных выше расчетов. Тем не менее знать, что такое — касательные напряжения — и как они влияют на работу конструкции, пусть даже очень упрощенно, но все-таки надо
Ранее мы для простоты и наглядности рассматривали обычную деревянную линейку в качестве балки, что позволило с известными допущениями вывести основные уравнения и формулы для расчета несущей способности балки. Благодаря этим уравнениям мы построили эпюры поперечных сил «Q» и эпюры изгибающих моментов «М».
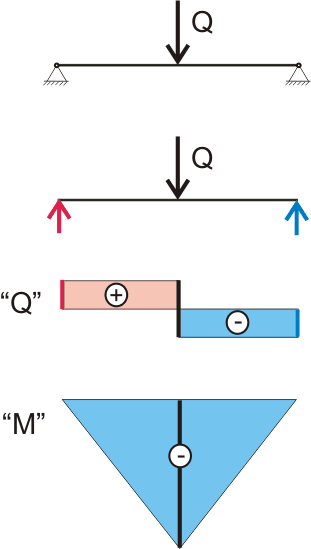
Рисунок 149.2.1. Эпюры поперечных сил и изгибающих моментов, действующих в поперечных сечениях балки при сосредоточенной нагрузке.
Что в итоге позволило достаточно просто и наглядно определить значение максимального изгибающего момента и соответственно значение максимальных нормальных растягивающих и сжимающих напряжений, возникающих в наиболее нагруженном поперечном сечении балки.
Дальше, зная расчетное сопротивление материала балки (значения расчетных сопротивлений проводятся в соответствующих СНиПах), можно достаточно легко определить момент сопротивления поперечного сечения, а затем и другие параметры балки, высоту и ширину, если балка прямоугольного сечения, диаметр, если балка круглого сечения, номер по сортаменту, если балка из металлического горячекатаного профиля.
Такой расчет на прочность является расчетом по первой группе предельных состояний и позволяет определить максимально допустимую нагрузку, которую может выдержать рассчитываемая конструкция. Превышение максимально допустимой нагрузки приведет к разрушению конструкции. Как именно будет разрушаться конструкция, нас в данном случае не интересует, так как данный сайт посвящен не вопросам теоретических и практических исследований предельных состояний материалов, а всего лишь некоторым методам расчетов наиболее распространенных строительных конструкций.
Как правило инженерные расчеты конструкций, которые будут использоваться сотнями тонн и десятками кубометров, выполняются так, чтобы получить максимально загруженную конструкцию. Поэтому такие расчеты достаточно сложные и разного рода коэффициентов, учитывающих срок службы конструкции, характер нагрузок, цикличность, динамичность нагрузок, неоднородность используемого материала и т.д. — десятки. Это логично так как при валовом производстве каждый процент в итоге дает ощутимую экономию. В частном строительстве, выполняемом один раз, прочность конструкции, пусть даже с двукратным запасом намного важнее возможной экономии материалов и потому расчеты для частного малоэтажного строительства можно максимально упростить, используя всего лишь один поправочный коэффициент γ = 1.6÷2, если на этот коэффициент будут умножаться значения напряжений, или γ = 0.5÷0.7, если на этот коэффициент будет умножаться значение расчетного сопротивления. Однако этим даже такие простые расчеты не ограничиваются.
Любая балка, имеющая длину значительно больше, чем высоту поперечного сечения, представляющая собой стержень, под действием нагрузок будет деформироваться. Результатами деформации являются смещение центральной оси балки по оси у относительно оси х, проще говоря прогиб, а также поворот поперечных сечений балки относительно плоскости поперечного сечения. И эти самые прогибы и углы поворота вне зависимости от того, какие опоры у балки и какие на нее действуют нагрузки, также можно определить. Для определения максимального угла поворота и максимального прогиба также строятся соответствующие эпюры, позволяющие определить, какое поперечное сечение сместится в результате прогиба больше всего и какое будет наклонено больше всего.
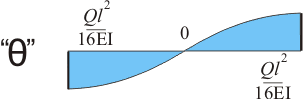
Рисунок 174.5.6. Эпюра углов поворота при действии сосредоточенной нагрузки посредине балки
Эпюра прогибов здесь не приводится, но как ни странно, это самая простая эпюра, показывающая положение оси, проходящей через поперечные сечения балки в результате деформации и эту эпюру воочию можно наблюдать на любой достаточно прогнувшейся балке или любой другой конструкции. Зная модуль упругости материала балки и момент инерции поперечного сечения определить максимальный прогиб также не очень сложно. Максимально упростить решение этих задач позволяют расчетные схемы для балок, к которым в зависимости от характера опор и вида нагружения даны соответствующие формулы.
Такой расчет деформаций является расчетом по предельным состояниям второй группы и достаточно наглядно показывает, на какую величину прогнется балка. Это бывает важно не только в связи с технологическими ограничениями, например для подкрановых балок, но также и из эстетических соображений. Например, когда потолок, а точнее перекрытие, хотя и достаточно прочное, заметно прогнется, то приятного в этом мало. Максимально допустимые величины прогибов для различных строительных конструкций приводятся в СНиП 2.01.07-85 «Нагрузки и воздействия» (в его актуализированной редакции). Впрочем при расчетах для себя никто не запрещает использовать еще меньшие значения прогиба.
Тут у читателя может возникнуть вполне резонный вопрос, а зачем понадобилось строить эпюру касательных напряжений «Q», если ни в каких расчетах эта эпюра не участвует. Что ж, пришло время ответить на этот вопрос.
Дело в том, что расчет разного рода балок, особенно постоянного прямоугольного сечения, лежащих горизонтально, на прочность при действии касательных напряжений очень редко является определяющим в отличие от приведенных выше расчетов. Тем не менее знать, что такое — касательные напряжения — и как они влияют на работу конструкции, пусть даже очень упрощенно, но все-таки надо.
Как следует из определения, касательные напряжения действуют в плоскости поперечного сечения, как бы касаются поперечного сечения потому и названы касательными. Определить значение касательных напряжений на первый взгляд просто: достаточно разделить значение поперечной силы (для этого нам и нужна эпюра «Q»), на площадь поперечного сечения (в рассматриваемом нами примере поперечные силы действовали только вдоль оси у и далее этого нам вполне хватит, усложнить любой расчет мы успеем всегда):
т = Q/F = Q/(bh) (270.1)
В итоге мы можем построить эпюру касательных напряжений «τ«(в дополнение к нормальным напряжениям «σ») следующего вида:

Рисунок 270.1. Предварительная эпюра касательных напряжений «τ«
Однако такая эпюра касательных напряжений была бы справедлива для некоего абстрактного материала, обладающего линейной упругостью вдоль оси у, и абсолютно жесткого вдоль оси z, в результате чего в поперечном сечении такого материала не происходит перераспределения напряжений и есть только один вид деформации относительно оси у. В действительности же любое тело, обладающее изотропными свойствами, под действием нагрузок пытается сохранить свой объем, а значит и рассматриваемое нами сечение пытается сохранить свою площадь. Наглядный пример, когда вы садитесь на мяч, высота его под действием вашего веса уменьшается, но увеличивается ширина. Причем процесс этот носит не линейный характер. Если вырезать из теста кубик или параллелепипед, а затем надавить на него, то боковые грани станут выпуклыми, подобный процесс происходит и при лабораторных испытаниях на сжатие образцов металла или других материалов.
Кроме всего прочего это означает еще и то, что касательные напряжения, действующие вдоль оси у, вызывают появление касательных напряжений вдоль оси z и эпюра касательных напряжений вдоль оси z будет более наглядно показывать изменение касательных напряжений по отношению к высоте балки. При этом форма эпюры будет напоминать боковую грань сплюснутого кубика из теста, а площадь эпюры конечно же не изменится. Т.е. значения эпюры касательных напряжений в самом низу и в самом верху поперечного сечения будут равны нулю, а максимальное значение (при прямоугольном сечении) будет посредине высоты сечения и явно больше Q/F. Исходя из условия равенства площадей эпюр максимальное значение эпюры касательных напряжений не может быть более 2Q/F, да и то только в том случае, если эпюра будет представлять собой два треугольника и в этом случае максимальное значение и есть высота треугольников. Однако как мы уже выяснили эпюра по своему виду больше напоминает часть круга или параболу, т.е. значение максимального касательного напряжения будет составлять около 1.5Q/F:

Рисунок 270.2. Более точная эпюра касательных напряжений.
Серой линией показана предварительно принятая нами эпюра касательных напряжений, но теперь касательные напряжения направлены вдоль оси z.
Математически изменение касательных напряжений в зависимости от высоты сечения можно выразить через изменение статического момента отсеченной части сечения с учетом изменения ширины сечения, так как далеко не всегда балки имеют прямоугольную форму сечения. В итоге формула для определения касательных напряжений (вывод формулы здесь не приводится) имеет следующий вид:
т = QySz отс /bIz (270.2) — формула проф. Д. И. Журавского
где Qy — значение поперечной силы в рассматриваемом поперечном сечении, определяется по эпюре «Q»
Sz отс — статический момент отсеченной части сечения на рассматриваемой высоте относительно оси z. Определяется как площадь отсеченной части, умноженная на расстояние между центром тяжести всего сечения и центром тяжести отсеченной части сечения. Например, в самом низу поперечного сечения, т.е. при высоте h=0, площадь отсеченной части сечения будет также равна 0, а значит и касательные напряжения, действующие по ширине b поперечного сечения, также будут равны нулю. Для сечения, проходящего через центр тяжести поперечного сечения, т.е. при высоте отсеченной части сечения, равной h/2, статический момент будет составлять (bh/2)(h/4) = bh 2 /8. При высоте отсеченного сечения, равной высоте поперечного сечения статический момент будет равен нулю, так как центр тяжести отсеченной части сечения в этом случае будет совпадать с центром тяжести сечения.
b — ширина поперечного сечения на рассматриваемой высоте поперечного сечения. Для балок прямоугольного сечения ширина сечения величина постоянная, однако бывают балки круглого, таврового, двутаврового и любого другого сечения. Более того, определение касательных напряжений чаще всего и используется при расчете балок не прямоугольного сечения, так как при переходе сечения из полок в стенку появляется значительный скачок касательных напряжений в связи с изменением ширины сечения, причем переход из полок в стенку обычно происходит на такой высоте, где нормальные напряжения достаточно велики и это учитывается соответствующим расчетом.
Iz — момент инерции поперечного сечения относительно оси z. В данном случае единственная более менее постоянная величина. Для прямоугольного поперечного сечения момент инерции составляет bh 3 /12.
Таким образом, согласно формулы (270.2) максимальное значение касательных напряжений для прямоугольного сечения составит:
т = 12Qbh 2 /(8b 2 h 3 ) = 1.5Q/F (270.3)
Такой же результат дала нам и геометрия.
И еще. Для материалов, обладающих ярко выраженными анизотропными свойствами, например, для древесины проверка на прочность по касательным напряжениям необходима. Дело в том, что прочность древесины сжатию вдоль волокон и прочность древесины сжатию поперек волокон — абсолютно разные вещи. Поэтому проверка выполняется для поперечных сечений, в которых касательные напряжения максимальны, как правило это сечения на опорах балки (при равномерно распределенной нагрузке). В этом случае полученное значение касательных напряжений сравнивается со значением расчетного сопротивления древесины сжатию или смятию поперек волокон — Rc90.
Впрочем, существует и другой подход к вопросу определения касательных напряжений: под действием нагрузок балка деформируется, при этом максимальные нормальные сжимающие и растягивающие напряжения возникают в самом низу и в самом верху поперечного сечения балки, что можно видеть по эпюре «σ» на рис.270.1.
При этом между волокнами такого неоднородного материала, как древесина, как впрочем и между слоями любого другого материала возникают касательные напряжения, направленные теперь по оси х, т.е. по той же оси, что и нормальные сжимающие и касательные напряжения, возникающие в результате действия изгибающего момента.
Происходит это от того, что каждый рассматриваемый слой испытывает разные по значению нормальные нагрузки и в результате все того же перераспределения напряжений и возникают касательные напряжения. Эти касательные напряжения как бы пытаются расколоть балку на отдельные слои, каждый из которых будет работать как отдельная балка.
Разница же несущей способности между отдельно взятыми слоями и цельной балкой очевидна. Например, если взять пачку бумаги хоть в 500 листов, то согнуть такую пачку — пара пустяков, а если склеить все листы, т.е. слои балки между собой, то мы получим цельную балку и вот ее уже согнуть будет намного труднее. Но между склеенными листами и будут возникать те самые, условно говоря, нормальные касательные напряжения. Впрочем, значение нормальных касательных напряжений определяется таким же образом и в расчетах участвует все та же поперечная сила, определяемая по эпюре «Q». Вот только рассматривается не отсеченная, а скалываемая часть сечения, соответственно статический момент может обозначаться — Sz ск . В этом случае полученное значение касательных напряжений сравнивается со значением расчетного сопротивления древесины сколу вдоль волокон — Rcк.
Правда, значения Rс90 и Rcк для древесины имеют одинаковое значение, но тем не менее касательные напряжения от действия поперечных сил и от деформаций в результате прогиба принято различать (так как рассматриваются две перрпендикулярные друг другу главные площадки напряжений), да и направление действия касательных напряжений важно при определении общего напряжения в исследуемой точке тела.
Впрочем, все это не более чем общие понятия о касательных напряжениях. В реальных материалах процесс перераспределения напряжений намного более сложный, все потому, что даже металл отнести к изотропным материалам можно достаточно условно. Впрочем эти вопросы рассматривает отдельная научная дисциплина — теория упругости. При расчете строительных конструкций, представляющих собой стержни — балки или пластины — плиты размером на помещение, вполне можно пользоваться формулой (270.2), выведенной на основе общих положений линейной теории упругости. При расчете массивных тел следует использовать методы нелинейной теории упругости.
Доступ к полной версии этой статьи и всех остальных статей на данном сайте стоит всего 30 рублей. После успешного завершения перевода откроется страница с благодарностью, адресом электронной почты и продолжением статьи. Если вы хотите задать вопрос по расчету конструкций, пожалуйста, воспользуйтесь этим адресом. Зараннее большое спасибо.)). Если страница не открылась, то скорее всего вы осуществили перевод с другого Яндекс-кошелька, но в любом случае волноваться не надо. Главное, при оформлении перевода точно указать свой e-mail и я обязательно с вами свяжусь. К тому же вы всегда можете добавить свой комментарий. Больше подробностей в статье «Записаться на прием к доктору»
Для терминалов номер Яндекс Кошелька 410012390761783
Номер карты Ymoney 4048 4150 0452 9638 SERGEI GUTOV
Для Украины — номер гривневой карты (Приватбанк) 5168 7422 4128 9630
Примечание: Возможно ваш вопрос, особенно если он касается расчета конструкций, так и не появится в общем списке или останется без ответа, даже если вы задатите его 20 раз подряд. Почему, достаточно подробно объясняется в статье «Записаться на прием к доктору» (ссылка в шапке сайта).
Источник
Важнейшим критерием оценки прочности балок при изгибе являются напряжения.
Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки
Расчет напряжений
Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент Mx

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.

Закон распределения нормальных напряжений по высоте сечения выражается формулой:
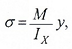
где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
Ix — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.
Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.
По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.
Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.
Например, для симметричного относительно нейтральной оси сечения, где y1=y2=h/2:

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.
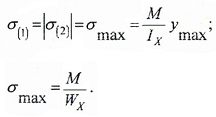
Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2:
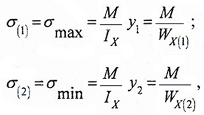
где:
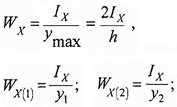
WX — осевой момент сопротивления симметричного сечения;
WX(1) и WX(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.
Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.
Условия прочности при изгибе
Прочность по нормальным напряжениям
Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.
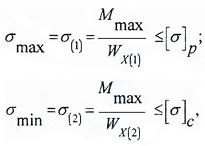
Здесь:
Mmax — максимальное значение изгибающего момента, определяемого по эпюре Mx;
[σ], [σ]р, [σ]с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).
Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [σ]с>[σ]р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.
При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:
- Проверка прочности

- Подбор сечений
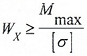
- Определение максимально допустимой нагрузки
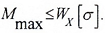
Прочность по касательным напряжениям
В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.
Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского
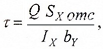
где
Sx отс — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
by — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.
Другие видео
Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Qmax:
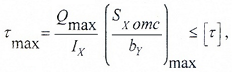
где [τ] – допустимое значение касательных напряжений для материала балки.
Полная проверка прочности
Полную проверку прочности балки производят в следующей последовательности:
- По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
- По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
- По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда Mmax и Qmax действуют в одном и том же сечении балки).
При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид:
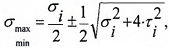
так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.
Другие видео
Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:
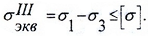
Деформации при изгибе >
Угловые и линейные перемещения в балках >
Примеры решения задач >
Лекции по сопромату >
Максимальные напряжения при кручении
Из формулы для определения напряжений и эпюры распределения касательных напряжений при кручении видно, что максимальные напряжения возникают на поверхности.
Определим максимальное напряжение, учитывая, что 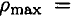
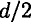 , где
, где 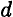 — диаметр бруса круглого сечения.
— диаметр бруса круглого сечения.
Для круглого сечения полярный момент инерции рассчитывается по формуле (см. лекцию 25).
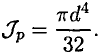
Максимальное напряжение возникает на поверхности, поэтому имеем
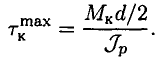
Обычно 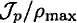 обозначают
обозначают 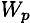 и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения
и называют моментом сопротивления при кручении, или полярным моментом сопротивления сечения
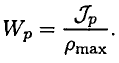
Таким образом, для расчета максимального напряжения на поверхности круглого бруса получаем формулу
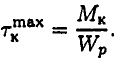
Для круглого сечения
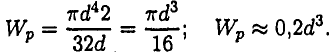
Для кольцевого сечения
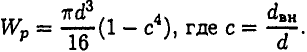
Условие прочности при кручении
Разрушение бруса при кручении происходит с поверхности, при расчете на прочность используют условие прочности
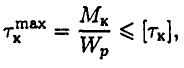
где 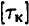 — допускаемое напряжение кручения.
— допускаемое напряжение кручения.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:




