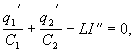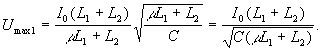Как найти максимальное напряжение на конденсаторе контура

Условие задачи:

Максимальное напряжение в колебательном контуре, состоящем из катушки с индуктивностью 5 мкГн и конденсатора емкостью 13330 пФ, равно 1,2 В. Сопротивление ничтожно мало. Определить действующее значение тока в контуре.

Задача №9.10.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(L=5) мкГн, (C=13330) пФ, (U_m=1,2) В, (I_д-?)

Решение задачи:

Известно, что согласно закону сохранения энергии при колебаниях максимальная энергия электрического поля конденсатора равна максимальной энергии магнитного поля тока катушки, поэтому справедливо записать следующее равенство:

[frac{{CU_m^2}}{2} = frac{{LI_m^2}}{2}]

Откуда максимальное (амплитудное) значение силы тока (I_m) равно:

[{I_m} = {U_m}sqrt {frac{C}{L}};;;;(1)]

Действующее значение силы тока (I_д) связано с максимальным значением силы тока (I_m) по формуле:

[{I_д} = frac{{{I_m}}}{{sqrt 2 }};;;;(2)]

Подставим выражение (1) в формулу (2):

[{I_д} = {U_m}sqrt {frac{C}{{2L}}} ]

Задача решена в общем виде, теперь посчитаем численный ответ:

[{I_д} = 1,2 cdot sqrt {frac{{13330 cdot {{10}^{ – 12}}}}{{2 cdot 5 cdot {{10}^{ – 6}}}}} = 0,044;А]

Ответ: 0,044 А.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

9.10.6 Вольтметр, включенный в цепь переменного тока, показывает 220 В. На какое
9.10.8 При включении конденсатора на синусоидальное напряжение 220 В с частотой 50 Гц
9.10.9 Определить емкость конденсатора фильтра выпрямителя, если частота тока 50 Гц

0 Пользователей и 1 Гость просматривают эту тему.

---

---

В курсе средней школы задачи по физике, при
решении которых требуется явное применение
дифференциального и интегрального исчисления
встречаются нечасто и в большинстве своем
вызывают значительные затруднения у
выпускников. Конечно, формулировки многих из
этих задач требуют ответы на вопросы, которые
можно легче получить не из явного решения
описывающих протекающие в них явления
дифференциальных уравнений, а привлекая
известные в физике законы сохранения.

Однако, сравнительный анализ различных
способов решения заданий, а также умение
использовать изученный в курсе алгебры и начал
анализа математический аппарат, безусловно
пригодятся выпускникам средней школы для
продолжения образования в стенах высшей.

Кроме того, весьма важно установление четкой
связи в умах учеников между различными ветвями
познания окружающего мира, их
взаимодополняющего влияния на точность и
четкость воссоздаваемой картины реальности. Я
полагаю, что задумываться об этом человек должен
как можно раньше, для того чтобы в будущей
деятельности плодотворно заниматься творческой
исследовательской работой.

Для начала рассмотрим задачу №1,
предлагавшуюся на вступительных экзаменах в
МФТИ , так как её результаты можно будет
использовать при решении последующих задач.

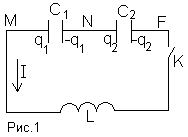
Задача 1. В цепи, изображенной на рис.1 , при
разомкнутом ключе К заряд на конденсаторе с
емкостью С₂ (С₂=С₁/3) равен q₂,
а  конденсатор с емкостью С₁ не заряжен.
Через какое время после замыкания ключа заряд на
конденсаторе С₁ будет иметь максимальное
значение? Чему будет равен этот заряд? Омическими
потерями в катушке с индуктивностью L пренебречь.

Как показывает опыт работы, простая замена
преподавателем схемы из двух последовательно
соединенных конденсаторов С₁ и С₂
эквивалентным конденсатором хотя бы для
расчетов частоты колебаний контура может
совершенно запутать учеников, если они
предварительно сами не придут к осознанию
равносильности такой замены для ответа на
некоторые вопросы задачи. Попробуем составить
дифференциальное уравнение для описания
колебательных явлений в контуре. Хочется
отметить, что то, что близкому к радиотехнике
человеку кажется очевидным, вызывает кучу
вопросов у учеников, и преподаватель не должен
оставлять у них ощущения, что какие-то члены в
уравнении или, допустим, их знаки появляются
из-за случайных догадок, и подробно
последовательно остановиться на всех этапах
решения.

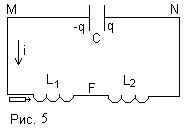
Обозначим буквами М, N, F соответствующие точки
схемы. Изначально на левой пластине конденсатора
С₂ был заряд q₂₀, на правой – (-q₂₀).По
закону сохранения заряда сумма зарядов на левой
пластине конденсатора С₂ правой пластине
конденсатора С₁ остается постоянной, так
как заряды в эту часть схемы извне не поступают q₁+q₂=q₂₀.

j _M-j _N=q₁/C₁; (1) j _N-j _F=q₂/C₂
(2). Выберем направление тока в цепи против
часовой стрелки, при этом заряд q₂ должен
уменьшаться.

Падение напряжения на катушке индуктивности IR=j
_M-j _F+e _{сам. инд}. По закону
электромагнитной индукции e _cам.инд=Так как активное
сопротивление катушки индуктивности равно 0, то j _M-j
_FСкладывая
уравнения (1) и (2),получим j _M-j _F=q₁/C₁+q₂/C₂.
Подставляя данное соотношение в (3), мы получим
уравнение (4), справедливое для любого момента
времени:

q₁/C₁+q₂/C₂–
Продифференцируем это уравнение по времени,
получим:

учитывая, что мы приходим к
дифференциальному уравнению
которое является уравнением гармонических
колебаний.

Общее решение этого уравнения I(t) = I_max sin(w
t+j ), где w ²=.

Инерционной частью в данной модели являются
заряды на конденсаторах q₁ и q₂,
которые не могут измениться мгновенно из-за
наличия индуктивности в цепи.

В момент замыкания ключа j _M=j _N, так
как конденсатор C₁ не заряжен.

j _M-j _F=j _N-j _F=q₂₀/C₂.
Скорость изменения тока в начальный момент
времени конечна и равна q₂₀/(C₂L)(см.(3)),
его значение в этот момент времени также равно 0,
откуда в общем уравнении гармонических
колебаний находим первую const: j =0,
тогда I(t)=I_max sinw t.

w t; так как
q₂(0)=q₂₀, то const=, а зависимость величин
зарядов конденсаторов от времени имеет вид:

В
моменты времени, когда ток в цепи максимален, Поскольку
активное сопротивление цепи равно 0, энергия
электромагнитного поля в процессе колебаний
сохраняется, т.е. в любой момент времени
справедливо соотношение

а
при максимальном значении тока из этого
соотношения получаем: отсюда

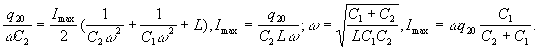
Данный результат можно получить и иначе. Найдем
равновесное распределение зарядов на
конденсаторах, которое отвечает отсутствию
протекания тока в цепи. При этом конденсаторы С₁
и С₂ оказываются включенными параллельно
друг другу.

U₁=U₂=q_1p/C₁=q_2p/C₂.Сумма
же зарядов на конденсаторах равна q₂₀. Из
этих условий получаем, чтоВокруг этих положений и
осуществляются колебания зарядов на
конденсаторах с течением времени, амплитуда же
колебаний соответствует величине I_max/w , что
позволяет определить I_max.

В нашем конкретном случае 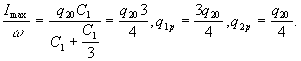Максимальная величина
заряда q₁ будет равняться 3q₂₀/2, а
достигаться она будет в моменты времени t=T/2+n? T,
где Т – период колебаний, а n=0,1,2… На рис.2
приведены зависимости от времени величины
зарядов на конденсаторах и тока, протекающего в
цепи.

Подробный анализ данной задачи позволяет
подойти к решению более сложного задания,
предложенного на вступительных экзаменах в МФТИ.

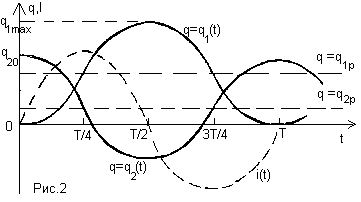
Задача 2. В схеме, предложенной на рисунке,
сначала замыкают ключ К₁ и после того, как
конденсатор емкостью С₂ полностью
зарядится от батареи с ЭДС E , ключ К₁ раз-

мыкают и замыкают ключ К₂. После замыкания
ключа К₂ в схеме происходят свободные
незатухающие колебания. Когда напряжение на
конденсаторе емкостью С₁ достигает
максимального значения, в него быстро (за время,
малое по сравнению с периодом колебаний)
вставляют диэлектрическую пластину, что
приводит к увеличению его емкости в e раз.

1)Чему равен начальный ток в цепи после
замыкания ключа К₂?

2)Определить максимальный ток в цепи после
вставки пластины.

После замыкания ключа К₁ конденсатор С₂
заряжается до напряжения U= E , на его пластинах
скапливаются заряды q₂₀ и -q₂₀, q₂₀=UC₂.
После размыкания ключа К₁ источник ЭДС не
играет роли в дальнейших процессах и
промежуточный этап после замыкания ключа К₂
описывается найденными в задаче №1
соотношениями. Из зависимости зарядов q₁ и q₂
от времени следует, что а

За
время, малое по сравнению с периодом колебаний, в
процессе внесения в конденсатор C₁ диэлектрической
пластины заряды на пластинах конденсаторов не
могут измениться, т.к. до начала процесса ток в
цепи равнялся 0,а максимальную скорость его
изменения можно оценить из уравнения (3).

Она конечна, следовательно, сразу после внесения
диэлектрической пластины ток в цепи по-прежнему
будет равняться 0.

Колебания зарядов на конденсаторах после
внесения диэлектрической пластины будут
осуществляться около новых равновесных
положений, определяемых условиями: Отсюда
находим равновесные распределения зарядов: В
момент времени, когда система проходит это
равновесное положение, ток в цепи достигает
своего максимального значения. Найдем величину
этого тока из закона сохранения энергии
электромагнитного поля в контуре в процессе
колебаний после помещения в него
диэлектрической пластины.

Данное уравнение относительно I_max является
квадратным, одно из его решений I_max=0
соответствует тривиальному случаю отсутствия
колебаний в контуре, а после упрощений можно
найти и его второе, интересующее нас решение:

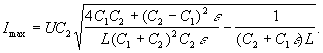
Следующие схемы предлагались на экзамене в
МФТИ в качестве наиболее сложных задач.

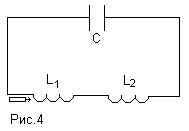
Задача №3. В колебательном контуре,
состоящем из двух последовательно соединенных
катушек с индуктивностью L₁ и L₂ и
конденсатора с емкостью С, происходят свободные
незатухающие колебания, при которых амплитуда
колебаний тока равна I₀. Когда сила тока в
катушке L₁ максимальна, в неё быстро ( за
время, малое по сравнению с периодом колебаний)
вставляют сердечник, что приводит к увеличению
её индуктивности в m раз.

1)Определить максимальное напряжение на
конденсаторе до вставки сердечника.

2)Определить максимальное напряжение на
конденсаторе после вставки сердечника.

Составим дифференциальное уравнение
колебаний, описывающее поведение данной цепи.
Все её элементы соединены последовательно, пусть
ток , протекающий в цепи, будет i(t), выберем его
направление так, как показано на рис.5. Пусть
заряд на правой пластине конденсатора q, тогда j _N-j
_M=q(t)/C; (1).

Падение напряжения на катушке L₁ равно 0,
так как её активное сопротивление равно 0

( колебания в контуре по условию задачи
незатухающие.)

Складывая уравнения (2) и (3) и учитывая (1), получаем
уравнение (4), справедливое для любого момента
времени до вставки сердечника. (4)
Продифференцируем его по времени: Данное
дифференциальное уравнение показывает, что
колебания в контуре происходят по
гармоническому закону, а квадрат частоты
собственных колебаний равен .
Максимальное напряжение на конденсаторе
соответствует максимальному заряду на нем;
учитывая, что в точках экстремума
дифференцируемой функции q(t) её производная
обращается в 0, получаем, что ток в этот момент в
цепи равен 0.

По закону сохранения электромагнитной энергии
в контуре:

,
где U_max– максимальное напряжение на
конденсаторе до вставки сердечника.
Рассмотрим процесс введения в катушку L₁
сердечника. В это время конденсатор полностью
разряжен, j _M=j _N.

j _M-j _F+e _{инд 1}=0, j _F-j _N+e _инд
2=0, тогда e _{инд 1}+e _{инд 2}=0, т.е. поскольку
вставка сердечника происходит быстро и
конденсатор всё это время остается незаряженным.
Получаем равенство, вытекающее из сохранения
магнитного потока в системе: (L₁+L₂) I_max
нач=(m L₁+L₂)I_{max кон}.
Следовательно, к моменту окончания вставки
сердечника I_{max кон}= Тогда для максимального
напряжения на конденсаторе после вставки
сердечника имеем:

Для школьников.

В предыдущих статьях говорилось о механических колебаниях (механических колебательных системах).

Например, о колебательной системе, состоящей из груза, подвешенного на пружине (пружинном маятнике).

При оттягивании груза от положения устойчивого равновесия (сообщении системе начальной энергии) и предоставлении далее системы самой себе, получали возникновение в ней свободных механических колебаний.

Подобно механическим, существуют электрические колебательные системы, в которых могут возникать свободные электрические колебания.

Такой системой является колебательный контур, представляющий собой электрическая цепь, состоящую из конденсатора и катушки индуктивности.

Если активное сопротивление R такой цепи пренебрежимо мало, то в колебательном контуре могут возникнуть свободные (собственные) незатухающие электрические колебания.

Для этого колебательный контур надо вывести из состояния равновесия, сообщив, например, конденсатору порцию энергии путём присоединения его на некоторое время к источнику постоянного тока.

При этом конденсатор заряжается до некоторого напряжения (между его обкладками появляется электрическое поле).

После отключения конденсатора от источника, замыкания его на катушку и предоставления колебательного контура самому себе, в нём возникают свободные (собственные) электрические колебания.

Рассмотрим этот процесс, сопроводив его рисунком.

Итак, в начальный момент времени конденсатор зарядили, сообщив ему электрическое поле с энергией

Одна обкладка конденсатора получила положительный заряд, другая – такой же отрицательный заряд.

Далее, под действием сил электрического поля, возникшего в проводе катушки, свободные электроны начинают переходить с отрицательно заряженной обкладки конденсатора на положительную.

В проводе возникает и растёт электрический ток, что сопровождается появлением вблизи катушки увеличивающегося магнитного поля.

При этом энергия электрического поля конденсатора уменьшается.

В катушке появляется эдс самоиндукции (индукционный ток), направленные так, чтобы препятствовать увеличению тока разряда конденсатора (или уменьшению напряжения между обкладками конденсатора).

(В электротехнике для краткости говорят, что напряжение катушки направлено навстречу напряжению конденсатора, то есть напряжение на катушке и напряжение на конденсаторе имеют разные знаки. Это противодействие приводит к тому, что ток разряда конденсатора возрастает не мгновенно, а происходит во времени).

Если рассматривать этот процесс с энергетической точки зрения то энергия конденсатора уменьшается, а энергия движущихся электронов растёт (ток растёт).

Когда конденсатор полностью разрядится в момент времени Т/4 вся энергия поля конденсатора окажется переданной электронам. Ток в катушке достигает максимального значения и энергия магнитного поля тоже достигает максимального значения:

В этот момент времени Т/4 энергия электрического поля конденсатора перешла в энергию магнитного поля катушки, что согласуется с законом сохранения энергии, так как активное сопротивление катушки считаем равным нулю.

Электрические свойства колебательного контура, в котором могут возникать свободные электрические (электромагнитные) колебания, определяются ёмкостью С конденсатора и индуктивностью L катушки.

На рисунке показаны пять состояний колебательного контура (через промежуток времени, равный четвёртой части периода), а под рисунками даны графики зависимости заряда конденсатора и тока в катушке от времени.

Хотя в момент времени Т/4 электрическое поле в конденсаторе исчезло, но электроны не могут мгновенно остановиться, они по инерции продолжают двигаться в том же направлении, но с уменьшающейся скоростью.

В результате ток в катушке уменьшается, уменьшается магнитный поток и уменьшается энергия магнитного поля. Возникает эдс самоиндукции. Теперь индукционный ток, по правилу Ленца, препятствует уменьшению тока в катушке. Это уменьшение идёт постепенно, но в прежнем направлении.

В результате обкладки конденсатора снова заряжаются, но противоположным знаком. Энергия магнитного поля уменьшается, а энергия электрического поля растёт.

Конденсатор заряжается до тех пор, пока вся энергия магнитного поля не израсходуется на поддержание тока, то есть пока ток в катушке не прекратится.

В момент времени Т/2 конденсатор имеет напряжение, равное напряжению в начале процесса, но противоположное по знаку.

Далее описанный процесс повторяется в обратном направлении и в момент времени 3Т/4 заряд конденсатора становится равным нулю, а ток в катушке достигает максимального значения.

В момент времени равный Т конденсатор оказывается заряженным так же, как и в начальный момент времени.

Завершился полный цикл изменения напряжения и тока в колебательном контуре или завершилось одно колебание электрического и магнитного полей. Далее процесс колебаний повторяется.

Таким образом, в контуре возникает переменный ток и происходят колебания энергии – превращение энергии электрического поля в энергию магнитного поля и обратно.

Рассмотренные электромагнитные колебания происходят только благодаря первоначальному заряду конденсатора, то есть эти колебания происходят без воздействия внешней силы и поэтому называются собственными колебаниями контура.

Таким образом, для получения переменного тока в колебательном контуре достаточно сообщить ему некоторый запас энергии.

Сопоставление графиков для заряда и тока колебательного контура показывает, что колебания заряда и тока в контуре смещены относительно друг друга по фазе:

Задача

Конденсатору колебательного контура был сообщён заряд 10 -4 Кл, и в контуре начались свободные затухающие колебания. Зная, что ёмкость конденсатора равна 0,01 мкФ, найти количество теплоты, которое выделится к моменту, когда колебания полностью прекратятся.

Решение

Зарядив конденсатор, сообщили колебательному контуру начальную энергию. Контур обладает сопротивлением R, поэтому электромагнитные колебания в нём будут затухающими.

Когда вся энергия, сообщённая контуру, перейдёт в тепло, колебания прекратятся. Тогда

Ответ: Q = 0,5 Дж

Задача

В контуре с индуктивностью и ёмкостью С совершаются свободные незатухающие колебания. Зная максимальное напряжение на конденсаторе, найти максимальный ток в этом контуре.

Решение

Согласно условию задачи, активным сопротивлением контура пренебрегаем.

При незатухающих колебаниях полная энергия колебательного контура остаётся постоянной. Её можно выразить через максимальную энергию электрического поля конденсатора и через максимальную энергию магнитного поля катушки:

отсюда

Задача

Колебательный контур состоит из катушки индуктивностью 0,2 Гн и конденсатора ёмкостью 10 -5 Ф. Конденсатор зарядили до напряжения 2 В, и он начал разряжаться. Каким будет ток в контуре в момент, когда энергия контура окажется распределённой поровну между электрическим и магнитным полями?

Решение

Энергия контура равна первоначальной энергии, сообщённой конденсатору:

W = 2 10 -5 Дж

Так как энергия распределилась поровну между электрическим и магнитным полями, то в рассматриваемый момент времени имеем

тогда искомый ток найдём по формуле

Ответ: ток равен 0,01 А.

https://yandex.ru/video/preview/?filmId=424804333889897260&parent-reqid=1640175761709976-5654111253126596084-sas6-5248-baf-sas-l7-balancer-8080-BAL-5262&path=wizard&text=%D1%81%D0%B2%D0%BE%D0%B1%D0%BE%D0%B4%D0%BD%D1%8B%D0%B5+%D1%8D%D0%BB%D0%B5%D0%BA%D1%82%D1%80%D0%BE%D0%BC%D0%B0%D0%B3%D0%BD%D0%B8%D1%82%D0%BD%D1%8B%D0%B5+%D0%BA%D0%BE%D0%BB%D0%B5%D0%B1%D0%B0%D0%BD%D0%B8%D1%8F+%D0%B4%D0%B5%D0%BC%D0%BE%D0%BD%D1%81%D1%82%D1%80%D0%B0%D1%86%D0%B8%D1%8F+%D0%BF%D0%BE+%D1%84%D0%B8%D0%B7%D0%B8%D0%BA%D0%B5&wiz_type=vital

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Незатухающие колебания. Автоколебания.

Следующая запись: Вынужденные электромагнитные колебания. Электрический резонанс.

Ссылки на занятия до электростатики даны в Занятии 1 .

Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .

Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58.

Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .