|
Найти максимальное отклонение между графиками |
||||||||
Ответить |
||||||||
Ответить |
||||||||
Ответить |
MathCAD: intercept, slope и линейная регрессия
Интерполяция данных одной формулой всегда актуальна, особенно если речь об “эконометрике” и подобных любимых экономистами заморочках, активно использующих классический регрессионный анализ на уровне построения уравнения прямой 🙂
Между тем, в MathCAD по заданным векторам значений X и Y как раз и можно непосредственно найти коэффициенты регрессионной прямой y=a+b*x функциями intercept (“отрезок, отсекаемый с оси”) и slope (“наклон”).
Просто у них принято изучать intercept equation of a line x/a + y/b = 1, уравнение прямой в отрезках, отсекаемых на координатных осях.
Вообще говоря, эти функции не предполагают, что данные отсортированы по возрастанию значений X, не предполагает этого и встроенный инструмент построения графиков, но без сортировки на больших размерностях пакет может тормозить, так что отсортируем пару векторов (X, Y) очевидным кодом
M:=csort(augment(X,Y),0) (X Y):=(M<0> M<1>)
Вместе с вводом начальных данных эта часть расчёта будет выглядеть так:

Определение данных и сортировка по возрастанию значений X
Непосредственный поиск коэффициентов регрессионной прямой функциями intercept и slope будет следующим шагом:

Линейная аппроксимация через функции “отсечка” и “наклон”, непосредственно возвращающие коэффициенты регрессионной прямой (то же, что МНК первого порядка)
Конечно, вы понимаете, что тот же результат будет и при использовании алгоритма МНК 1 порядка.
Вот таким красивым кодом найдём номер точки с максимальным отклонением от прямой, которую потом покажем на графике отдельным рядом. В эконометрике максимальное отклонение называется безумным словом нотна:

Найдём номер точки с максимальным отклонением от прямой
Строго говоря, код выше работает только если искомый номер элемента – единственный. В общем случае (максимальных расстояний несколько) следует пользоваться примерно таким решением. Оно не программистски красивое, зато надёжное.
Наконец, построим график. Заметим, что не следует путать прямую регрессии, она же прямая МНК 1 порядка, с кусочно-линейной интерполяцией, которую мы могли бы выполнить просто строкой кода
linterp(X,Y,X)
Добавил её четвёртым рядом данных на график.

Построение графика с отметкой отдельной категорией самой дальней точки
![]() Скачать этот пример в архиве .zip с документом MathCAD 15 (22 Кб)
Скачать этот пример в архиве .zip с документом MathCAD 15 (22 Кб)
16.09.2015, 15:38 [18094 просмотра]
В 63 выпуске журнала ForTrader.org мы исследуем торговую стратегию «Максимальное отклонение от средней», которая использует в своем арсенале только, как видно из названия, скользящую среднюю и историю котировок.
Итак, как уже было сказано, для работы по стратегии нам понадобится скользящая средняя и цены закрытия свечей (см. рис. 1).

Рис. 1. Шаблон торговой стратегии «Максимальное отклонение от средней».
Идея предложенной для рассмотрения торговой стратегии основана на понятии цикличности рынка – мы знаем, что цена не может расти или падать вечно (хотя долгосрочные тренды конечно никто не отменял), всегда наступает переломный момент, особенно если мы говорим о волатильных парах и невысоких таймфреймах. В рамках исследования мы как раз и попытаемся «поймать» разворотные моменты, то есть точки цены, когда разворот произойдет вероятнее всего.

Если говорить точнее, то мы будем брать исторические данные за определенный период времени, например, за месяц, и смотреть, на сколько пунктов максимально отклонялась цена от скользящей средней. Полученную цифру нужно будет запомнить, и при повторном отклонении на то же количество пунктов, мы будем входить в сделку.
В исследовании предлагаю испробовать два варианта:
1. С помощью тестера MetaTrader 5 мы будем подбирать наиболее оптимальное отклонение для сделок на продажу и на покупку.
2. Займемся подбором оптимального значения отклонения средней на основе временного диапазона, заданного заранее. Например, будем искать нужный нам параметр за последние 100 баров, при этом поиском количества баров будет заниматься тестер стратегий.
На рисунке 1 вы можете наглядно увидеть те места на графике, где цена максимально отклоняется от средней после чего незамедлительно меняет свое направление. В ближайших нескольких номерах журнала мы попытаемся доработать стратегию на основе этой идеи, пока же попробуем в действии первоначальный вариант.

Рис. 2. Индикатор «Отклонение от средней» в действии.
Для удобства анализа был написан торговый индикатор MaDEv, с помощью которого можно быстро определить размер максимальных отклонений цены от средней (см. рис. 2). В качестве сигнальных линий были выбраны первые максимальные отклонения от средней линии. Обратите внимания, во всех полученных нами сигналах разворот происходил либо на том же баре, либо даже чуть позднее появления сигнала.
Правила входа и выхода из сделки:
Итак, давайте попробуем сформулировать основные правила на вход и выход по торговой стратегии.
Длинная позиция (см. рис. 3):

Рис. 3. Сигнал на покупку по торговой стратегии.
Все довольно просто: мы ожидаем, когда цена максимально сильно отклонится от скользящей средней вниз после пересечения. Как только индикатор MaDEv пересекает сигнальную линию, на закрытии свечи мы открываем покупку. Из позиции выходим, как только цена касается скользящей средней.
Короткая позиция (см. рис. 4):

Рис. 4. Сигнал на продажу по торговой стратегии.
Ситуация аналогична: ожидаем, когда цена максимально сильно отклонится от скользящей средней вверх после пересечения. Как только индикатор MaDEv пересекает сигнальную линию сверху, на закрытии свечи мы открываем продажу. Из позиции выходим, как только цена касается скользящей средней.
Тестирование торговой стратегии
С точки зрения программирования стратегия оказалась достаточно простой. Реализовав ее правила и задав максимальное отклонение в 30 пунктов, пробуем идею на ценовых графиках. Наиболее волатильной валютной парой считается EURUSD, таймфрейм выбираем небольшой – M15, тестировать будем, начиная с 2009 года (см. рис. 5).

Рис. 5. Тестирование торговой стратегии на EURUSD. Скачать отчет
Как видим, потенциал к нашей идее есть. График баланса похож на кардиограмму, а это значит, что есть моменты рынка, когда стратегия работает хорошо, и те, в которые все не так удачно. Как всегда, обратимся к оптимизации для поиска хороших параметров, позволяющих сгладить шероховатости.
Оптимизация торговой стратегии
Оптимизацию будем проводить на той же паре EURUSD, на 15-тиминутном графике. Ищем удачные параметры отклонения в период с 2009.01.01 по 2010.01.01. Кроме того, в качестве форвард-теста посмотрим, как параметры будут работать на участке вне оптимизации до 2010.09.10 (см. рис. 6).

Рис. 6. Оптимизация торгового эксперта на паре EURUSD с использованием форвард-теста.
Скачать отчет
Не знаю как вам, но мне картинка на рисунке 6 очень по душе. Отрицательных периодов мы не наблюдаем, хотя период «в нуле» также довольно продолжителен. Судая по тому, что основной заработок происходит в начале года, когда рынки нестабильны, делаем вывод, что наиболее актуальны для данного эксперта моменты, когда рынок находится в максимальной волатильности. Будет от чего отталкиваться в следующих выпусках…
Подведем итоги
Как мы видим, идея, предложенная нами для рассмотрения, имеет право на существование. Хотя статистика работы и не выглядит очень впечатляющей, сделаем скидку на то, что мы не пытались усовершенствовать саму стратегию путем добавления дополнительных параметров и индикаторов. Возможно, нам может неплохо помочь Фибоначчи и его уровни.
Пока же основной нашей задачей является поиск метода, который позволит адаптироваться советнику к конкретному рынку – волатильный он или нет. Поэтому в следующем номере мы продолжим наше исследование.
Описание параметров полученного советника
– InpStopLoss – размер СтопЛосса;
– InpTakeProfit – размер ТейкПрофита;
– InpLots – объем совершаемых сделок;
– InpMaDevPeriod – период индикатора скользящей средней;
– Maxdevbuy, maxdevsell – размер максимальных отклонений от средней в пунктах для покупки и продажи соответственно.
Продолжение: Часть II
Скачать эксперта | Скачать Индикатор | Обсудить на форуме
Находим максимальное
отклонение аппроксимированной кривой
разгона от натуральной кривой разгона
с запаздыванием
![]() .
.
В программе
Razgon.exe
рассчитываем ординаты аппроксимирующей
кривой разгона (приложение Б). По данным
таблицы 4 строим экспериментальную
кривую разгона объекта с запаздыванием
и аппроксимированную кривую разгона
(приложение В). Находим, что максимальное
отклонение Y'(t)
от Y(t)
наблюдается в точке
t = 12
c;
Y'(t)
= 2,45
Y(t)
= 2,93

Следовательно,
точность аппроксимации не меньше
допустимой (![]() ),
),
и найденная модель объекта достаточно
точно описывает его динамику.
Находим постоянную
времени объекта. Для этого из точки t
= 6 c
(соответствует времени запаздывания)
к участку максимальной скорости
нарастания температуры проводим
касательную до момента пересечения её
с линией
![]() (T
(T
= 35 °С). Временной участок, заключенный
между точкой пересечения касательной
с
![]() и
и![]() ,
,
равен постоянной времени объекта:
Т =48 – 6 = 42 с.
Результаты исследований объекта.
-
Объект с запаздыванием
является инерционным, статическим
(определяется
по виду кривой разгона). -
Описывается
дифференциальным уравнением второго
порядка:
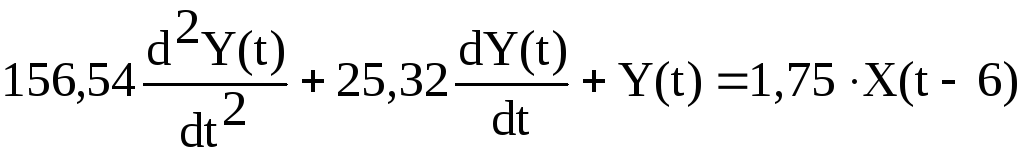 ,
,
с точностью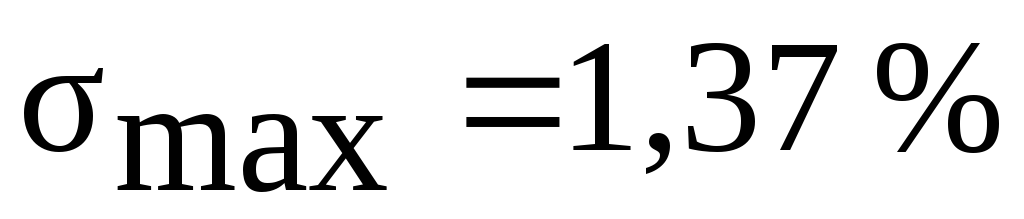
-
Имеет следующие
характеристики:
Коэффициент
передачи
![]()
Постоянная времени
Т = 42 с
2. Определение оптимальных настроечных параметров регулятора на заданный по “m” запас устойчивости системы (заданную степень затухания переходного процесса).
-
Теоретические предпосылки
Запас устойчивости
системы может быть охарактеризована
величиной степени затухания “Ψ”,
которая связана со степенью колебательности
системы”m”
зависимостью:
![]()
расчет на заданную
степень затухания (заданный запас
устойчивости m)
проводят по расширенным частотным
характеристикам – АФХ регулятора
и объекта.
Структурная схема САР.
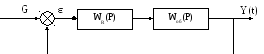
P = (j – m)·ω
Используя критерий
Найквиста, согласно которому система
будет находиться на границе устойчивости,
если АФХ разомкнутой системы пройдет
через критическую точку с координатами
(1; j0)
и с учетом заданного запаса устойчивости
m:
А
(1)
ФХ разомкнутой системы:
Wраз.(m
; jω)
= -1
WR.(m
; jω)
·Wоб.(m
; jω)
= 1
(в регуляторе
происходит перемена знака сигнала).
Представим АФХ
регулятора и объекта в показательной
форме, тогда:
![]()
(2)
Равенство (2) при
условии выполнения равенств:
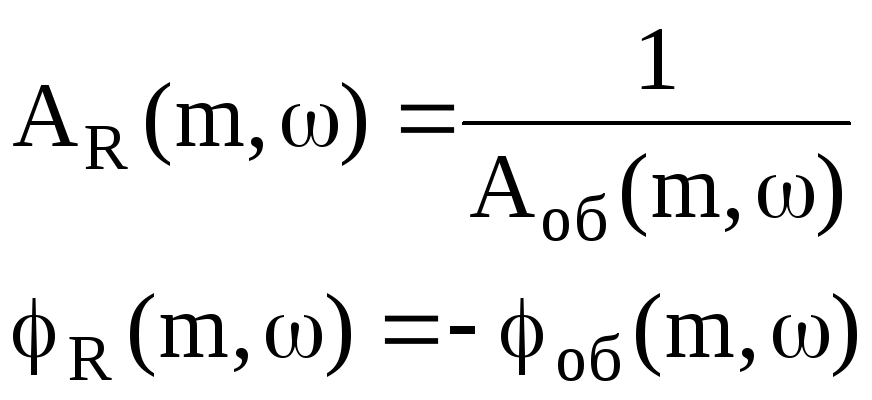
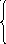
(3)
Настроечные
параметры регулятора, определяемые
системой, будут оптимальными с точки
зрения обеспечения заданной степени
затухания m,
и следовательно, заданного запаса
устойчивости САР.
Расчет предусматривает
два этапа:
На первом этапе
определяется
значение параметров регулятора, при
которых система будет обладать заданным
запасом устойчивости.
На втором этапе
из совокупности
значений параметров, удовлетворяющих
первому требованию, выбираются такие,
при которых обеспечивается минимум
интегрального критерия качества.
Таким образом, для
определения настроечных параметров
регулятора необходимо:
-
Определить
расширенные частотные характеристики
объекта исходя из его передаточной
функции (раздел I)
– Аоб(m,ω)
и φоб(m,ω). -
Определить
оптимальные настройки регулятора.
Соседние файлы в папке курсовик по ТАУготоваый
- #
22.02.2014915.46 Кб441.XLS
- #
- #
- #
22.02.201436.35 Кб46МУ к КП ТАУ.xls
- #
- #
- #
Определить максимальное отклонение от средней премии.
Построить график отклонений премии от среднего значения.
Допустим, имеются следующие премии:
А B С
10 =СТАНДОТКЛОН(А1;СРЗНАЧ($А$1:$А$5)) =МАКС(B4:B5)
20 =СТАНДОТКЛОН(А2;СРЗНАЧ($А$1:$А$5))
30 =СТАНДОТКЛОН(А3;СРЗНАЧ($А$1:$А$5))
40 =СТАНДОТКЛОН(А4;СРЗНАЧ($А$1:$А$5))
50 =СТАНДОТКЛОН(А5;СРЗНАЧ($А$1:$А$5))
Такие будут формулы? Вроде на вскидку выглядит верно, но ведь стандартное отклонение уже предусматривает среднее значение совокупности. Голова кругом 



