import java.awt.*;
import java.util.*;
import java.util.Map.Entry;
public class Main {
static int orientation(Point p,
Point q,
Point r)
{
int x = area(p, q, r);
if (x > 0) {
return 1;
}
if (x < 0) {
return -1;
}
return 0;
}
static int area(Point p, Point q, Point r)
{
return ((p.y - q.y) * (q.x - r.x)
- (q.y - r.y) * (p.x - q.x));
}
static int absArea(Point p,
Point q, Point r)
{
return Math.abs(area(p, q, r));
}
static int dist(Point p1, Point p2)
{
return ((p1.x - p2.x) * (p1.x - p2.x)
+ (p1.y - p2.y) * (p1.y - p2.y));
}
static ArrayList<Point>
convexHull(Point points[])
{
int n = points.length;
Point min = new Point(Integer.MAX_VALUE,
Integer.MAX_VALUE);
int ind = -1;
for (int i = 0; i < n; i++) {
if (min.y > points[i].y) {
min.y = points[i].y;
min.x = points[i].x;
ind = i;
}
else if (min.y == points[i].y
&& min.x > points[i].x) {
min.x = points[i].x;
ind = i;
}
}
points[ind] = points[0];
points[0] = min;
Arrays.sort(points, 1, n,
new Comparator<Point>() {
@Override
public int compare(Point o1,
Point o2)
{
int o = orientation(min, o1, o2);
if (o == 0) {
return dist(o1, min)
- dist(o2, min);
}
if (o == 1) {
return 1;
}
return -1;
}
});
Stack<Point> st = new Stack<>();
st.push(points[0]);
int k;
for (k = 1; k < n - 1; k++) {
if (orientation(points[0],
points[k],
points[k + 1])
!= 0)
break;
}
st.push(points[k]);
for (int i = k + 1; i < n; i++) {
Point top = st.pop();
while (orientation(st.peek(),
top,
points[i])
>= 0) {
top = st.pop();
}
st.push(top);
st.push(points[i]);
}
ArrayList<Point> hull
= new ArrayList<>();
for (int i = 0; i < st.size(); i++) {
hull.add(st.get(i));
}
return hull;
}
static double
rotatingCaliper(Point points[])
{
ArrayList<Point> convexHull
= convexHull(points);
int n = convexHull.size();
Point hull[] = new Point[n];
n = 0;
while (n < convexHull.size()) {
hull[n] = convexHull.get(n++);
}
if (n == 1)
return 0;
if (n == 2)
return Math.sqrt(dist(hull[0], hull[1]));
int k = 1;
while (absArea(hull[n - 1],
hull[0],
hull[(k + 1) % n])
> absArea(hull[n - 1],
hull[0],
hull[k])) {
k++;
}
double res = 0;
for (int i = 0, j = k;
i <= k && j < n; i++) {
res = Math.max(res,
Math.sqrt((double)dist(hull[i],
hull[j])));
while (j < n
&& absArea(hull[i],
hull[(i + 1) % n],
hull[(j + 1) % n])
> absArea(hull[i],
hull[(i + 1) % n],
hull[j])) {
res = Math.max(
res,
Math.sqrt(dist(hull[i],
hull[(j + 1) % n])));
j++;
}
}
return res;
}
public static void main(String[] args)
{
int n = 5;
Point p[] = new Point[n];
p[0] = new Point(4, 0);
p[1] = new Point(0, 2);
p[2] = new Point(-1, -7);
p[3] = new Point(1, 10);
p[4] = new Point(2, -3);
System.out.println(rotatingCaliper(p));
}
}
Срочноо!!! Помогите пожалуйста
Антонина
Знаток
(299),
на голосовании
1 год назад
1)На рисунке дан график зависимости проекции υx скорости тела, движущегося вдоль одной прямой, от времени t. Найдите путь, пройденный телом с начала движения по 8‑ю минуту. Ответ выразите в метрах. Определите, на какое максимальное расстояние удалялось тело от начальной точки за все время движения. Ответ выразите в метрах.
Голосование за лучший ответ
Алексей Бараев
Гений
(69534)
1 год назад
Хитроумная задачка. По идее надо бы задать по отрезкам функцию движения и интегрировать… Но!
Если внимательно посмотреть на участок с 0 по 6 минуту, можно сообразить, что сначала тело двигалось вперед, а потом назад и вернулось на старт.
А вот уже с 6 минуты по 10 (то есть четыре минуты) двигалось со скоростью 5 м/с
5 м/сек * 4 * 60 = 1200 метров
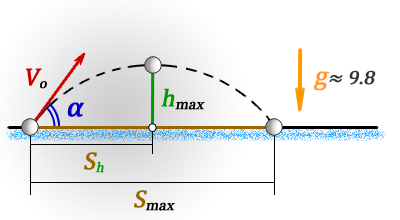
hmax – максимальная высота
Smax – максимальная дальность полета, если бросок и падение на одном уровне
Sh – расстояние пройденное по горизонтали до момента максимального подъема
tmax – время всего полета
th – время за которое тело поднялось на максимальную высоту
Vo – начальная скорость тела
α – угол под которым брошено тело
g ≈ 9,8 м/с2 – ускорение свободного падения
Формула для расчета максимальной высоты достигнутое телом, если даны, начальная скорость Vo и угол α под которым брошено тело. :
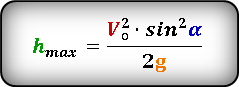
Формула для вычисления максимальной высоты, если известны, максимальное расстояние S max или расстояние по горизонтали при максимальной высоте Sh и угол α под которым брошено тело. :
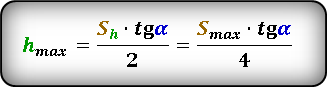
По этой формуле, можно определить максимальную высоту, если известно время th за которое тело поднялось на эту высоту. :
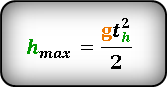
Формула для расчета максимальной дальности полета, если даны, начальная скорость броска Vo и угол α под которым брошено тело. :
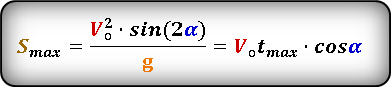
или известны максимальная высота hmax и угол α под которым брошено тело. :
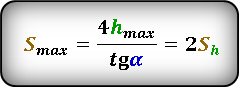
Формула для нахождения расстояния по горизонтали при максимальной высоте, если даны, начальная скорость броска Vo и угол α под которым брошено тело. :
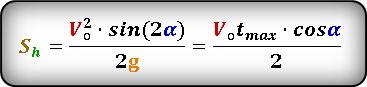
или известны максимальная высота hmax и угол α под которым брошено тело. :
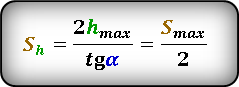
* т. к. траектория движения симметрична относительно линии максимальной высоты, то расстояние Sh ровно в два раза, меньше максимальной дальности броска Smax
Формула для определения времени затраченного на весь полет, если даны, начальная скорость Vo и угол α под которым брошено тело или если известна только максимальная высота hmax :
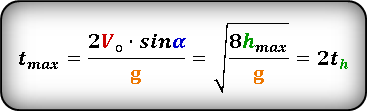
* т. к. траектория движения симметрична относительно линии максимальной высоты, то время максимального подъема th ровно в два раза, меньше максимального времени tmax
Формула для определения времени за которое тело поднялось на максимальную высоту, если даны, начальная скорость Vo и угол α под которым брошено тело или если известна только максимальная высота hmax :
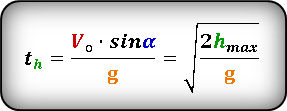
- Подробности
-
Опубликовано: 11 августа 2015
-
Обновлено: 13 августа 2021
Это можно решить с помощью динамической программы. Предположим, что D[i][j] максимальное расстояние, которое вы можете получить от начальной точки до iпромежуточная точка, где последняя точка j, Ваше решение будет D[n][endPoint],
Так как это решить? Первый столбец D[0][...] легко рассчитать. Это будут просто расстояния от соответствующей точки до начальной точки. Другие столбцы немного сложнее. Вам необходимо проверить все записи в предыдущем столбце, где последняя точка находится строго перед текущей точкой. Итак, для расчета входа D[i][j], вы должны рассчитать:
D[i][j] = max_{k < j} (D[i - 1][k] + distance(k, j))
Это значит: повторять все возможное k такой, что k меньше чем j (т.е. точка k находится перед текущей точкой j). Рассчитайте полученное расстояние как сумму расстояний до k (это D[i - 1][k] часть) и расстояние от k в j, Поместите максимум этих значений в D[i][j], Вы также можете отслеживать k если вам нужно восстановить путь в конце (то есть вас интересует не только максимальное расстояние). Обратите внимание, что могут быть ячейки без действительных решений (например, D[1][0] – вы не можете добраться до точки 0 как второй (индекс 1промежуточная точка).
Сделайте это для каждой промежуточной точки в каждом столбце до D[n - 1][...], Последний шаг – сделать этот процесс еще раз для D[n][endPoint]который, строго говоря, не должен быть расположен в D массив (потому что вас интересует только одно значение, а не целый столбец).
Как только вы вычислили это значение, это ваше решение. Если вы хотите найти фактический путь, вы должны вернуться назад, используя сохраненные k значения для каждой ячейки.
В данной статье рассмотрим способы определить расстояние от точки до точки теоретически и на примере конкретных задач. И для начала введем некоторые определения.
Расстояние между точками – это длина отрезка, их соединяющего, в имеющемся масштабе. Задать масштаб необходимо, чтобы иметь для измерения единицу длины. Потому в основном задача нахождения расстояния между точками решается при использовании их координат на координатной прямой, в координатной плоскости или трехмерном пространстве.
Расстояние между точками на координатной прямой
Исходные данные: координатная прямая Ox и лежащая на ней произвольная точка А. Любой точке прямой присуще одно действительное число: пусть для точки А это будет некое число хA, оно же – координата точки А.
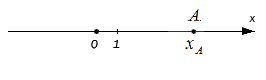
В целом можно говорить о том, что оценка длины некого отрезка происходит в сравнении с отрезком, принятым за единицу длины в заданном масштабе.
Если точке А соответствует целое действительное число, отложив последовательно от точки О до точки по прямой ОА отрезки – единицы длины, мы можем определить длину отрезка OA по итоговому количеству отложенных единичных отрезков.
К примеру, точке А соответствует число 3 – чтобы попасть в нее из точки О, необходимо будет отложить три единичных отрезка. Если точка А имеет координату -4 – единичные отрезки откладываются аналогичным образом, но в другом, отрицательном направлении. Таким образом в первом случае, расстояние ОА равно 3; во втором случае ОА = 4.
Если точка A имеет в качестве координаты рациональное число, то от начала отсчета (точка О) мы откладываем целое число единичных отрезков, а затем его необходимую часть. Но геометрически не всегда возможно произвести измерение. К примеру, затруднительным представляется отложить на координатной прямой дробь 4111.
Вышеуказанным способом отложить на прямой иррациональное число и вовсе невозможно. К примеру, когда координата точки А равна 11 . В таком случае возможно обратиться к абстракции: если заданная координата точки А больше нуля, то OA=xA (число принимается за расстояние); если координата меньше нуля, то OA=-xA . В общем, эти утверждения справедливы для любого действительного числа xA.
Резюмируя: расстояние от начала отсчета до точки, которой соответствует действительное число на координатной прямой, равно:
- 0, если точка совпадает с началом координат;
- xA , если xA>0;
- -xA , если xA<0 .
При этом очевидно, что сама длина отрезка не может быть отрицательной, поэтому, используя знак модуля, запишем расстояние от точки O до точки A с координатой xA: OA=xA
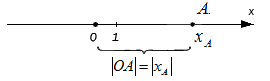
Верным будет утверждение: расстояние от одной точки до другой будет равно модулю разности координат. Т.е. для точек A и B, лежащих на одной координатной прямой при любом их расположении и имеющих соответственно координаты xA и xB : AB=xB-xA.
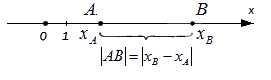
Расстояние между точками на плоскости
Исходные данные: точки A и B, лежащие на плоскости в прямоугольной системе координат Oxy с заданными координатами: A(xA, yA) и B(xB, yB) .
Проведем через точки А и B перпендикуляры к осям координат Ox и Oy и получим в результате точки проекции: Ax, Ay, Bx, By. Исходя из расположения точек А и B далее возможны следующие варианты:
– если точки А и В совпадают, то расстояние между ними равно нулю;
– если точки А и В лежат на прямой, перпендикулярной оси Ox (оси абсцисс), то точки и совпадают, а |АВ| = |АyBy|. Поскольку, расстояние между точками равно модулю разности их координат, то AyBy=yB-yA , а, следовательно AB=AyBy=yB-yA.
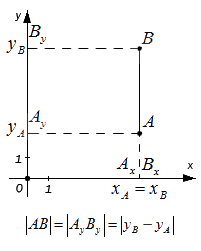
– если точки A и B лежат на прямой, перпендикулярной оси Oy (оси ординат) – по аналогии с предыдущим пунктом: AB=AxBx=xB-xA
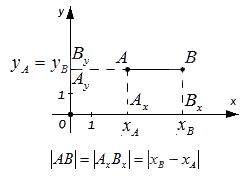
– если точки A и B не лежат на прямой, перпендикулярной одной из координатных осей, найдем расстояние между ними, выведя формулу расчета:
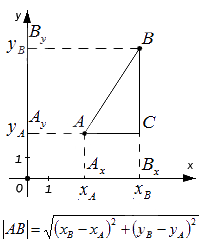
Мы видим, что треугольник АВС является прямоугольным по построению. При этом AC=AxBx и BC=AyBy. Используя теорему Пифагора, составим равенство: AB2=AC2+BC2⇔AB2=AxBx2+AyBy2 , а затем преобразуем его: AB=AxBx2+AyBy2=xB-xA2+yB-yA2=(xB-xA)2+(yB-yA)2
Сформируем вывод из полученного результата: расстояние от точки А до точки В на плоскости определяется расчётом по формуле с использованием координат этих точек
AB=(xB-xA)2+(yB-yA)2
Полученная формула также подтверждает ранее сформированные утверждения для случаев совпадения точек или ситуаций, когда точки лежат на прямых, перпендикулярных осям. Так, для случая совпадения точек A и B будет верно равенство: AB=(xB-xA)2+(yB-yA)2=02+02=0
Для ситуации, когда точки A и B лежат на прямой, перпендикулярной оси абсцисс:
AB=(xB-xA)2+(yB-yA)2=02+(yB-yA)2=yB-yA
Для случая, когда точки A и B лежат на прямой, перпендикулярной оси ординат:
AB=(xB-xA)2+(yB-yA)2=(xB-xA)2+02=xB-xA
Расстояние между точками в пространстве
Исходные данные: прямоугольная система координат Oxyz с лежащими на ней произвольными точками с заданными координатами A(xA, yA, zA) и B(xB, yB, zB) . Необходимо определить расстояние между этими точками.
Рассмотрим общий случай, когда точки A и B не лежат в плоскости, параллельной одной из координатных плоскостей. Проведем через точки A и B плоскости, перпендикулярные координатным осям, и получим соответствующие точки проекций: Ax, Ay, Az, Bx, By, Bz
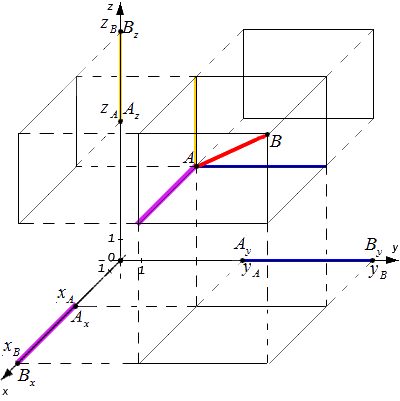
Расстояние между точками A и B являет собой диагональ полученного в результате построения параллелепипеда. Согласно построению измерения этого параллелепипеда: AxBx, AyBy и AzBz
Из курса геометрии известно, что квадрат диагонали параллелепипеда равен сумме квадратов его измерений. Исходя из этого утверждения получим равенство: AB2=AxBx2+AyBy2+AzBz2
Используя полученные ранее выводы, запишем следующее:
AxBx=xB-xA, AyBy=yB-yA, AzBz=zB-zA
Преобразуем выражение:
AB2=AxBx2+AyBy2+AzBz2=xB-xA2+yB-yA2+zB-zA2==(xB-xA)2+(yB-yA)2+zB-zA2
Итоговая формула для определения расстояния между точками в пространстве будет выглядеть следующим образом:
AB=xB-xA2+yB-yA2+(zB-zA)2
Полученная формула действительна также для случаев, когда:
– точки совпадают;
– лежат на одной координатной оси или прямой, параллельной одной из координатных осей.
Примеры решения задач на нахождение расстояния между точками
Исходные данные: задана координатная прямая и точки, лежащие на ней с заданными координатами A(1-2) и B(11+2) . Необходимо найти расстояние от точки начала отсчета O до точки A и между точками A и B.
Решение
- Расстояние от точки начала отсчета до точки равно модулю координаты этой точки, соответственно OA=1-2=2-1
- Расстояние между точками A и B определим как модуль разности координат этих точек: AB=11+2-(1-2)=10+22
Ответ: OA=2-1, AB=10+22
Исходные данные: задана прямоугольная система координат и две точки, лежащие на ней A(1, -1) и B (λ+1, 3) . λ – некоторое действительное число. Необходимо найти все значения этого числа, при которых расстояние АВ будет равно 5.
Решение
Чтобы найти расстояние между точками A и B, необходимо использовать формулу AB=(xB-xA)2+yB-yA2
Подставив реальные значения координат, получим:AB=(λ+1-1)2+(3-(-1))2=λ2+16
А также используем имеющееся условие, что АВ=5 и тогда будет верным равенство:
λ2+16=5λ2+16=25λ=±3
Ответ: АВ = 5, если λ=±3 .
Исходные данные: задано трехмерное пространство в прямоугольной системе координат Oxyz и лежащие в нем точки A (1, 2, 3) и B-7, -2, 4 .
Решение
Для решения задачи используем формулу AB=xB-xA2+yB-yA2+(zB-zA)2
Подставив реальные значения, получим: AB=(-7-1)2+(-2-2)2+(4-3)2=81=9
Ответ: |АВ| = 9
