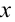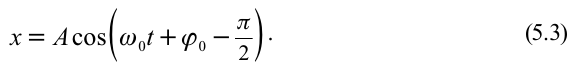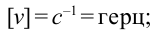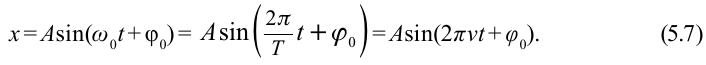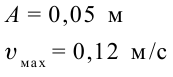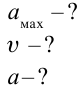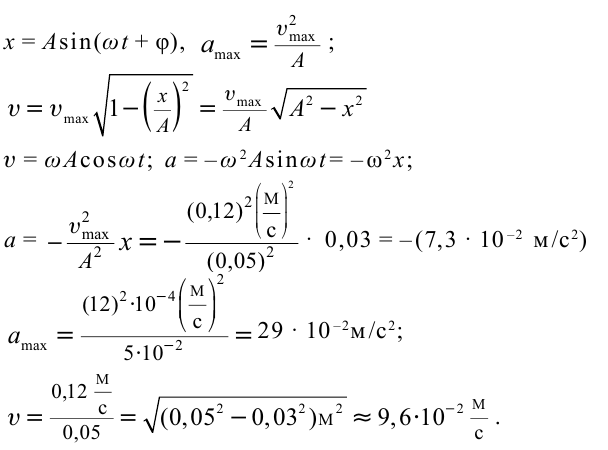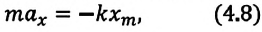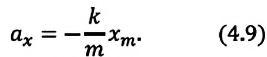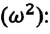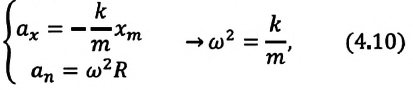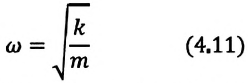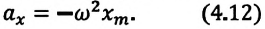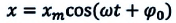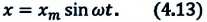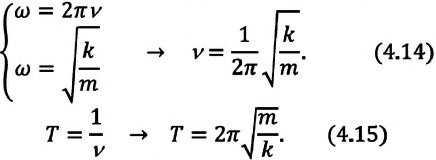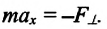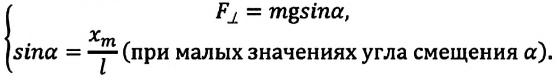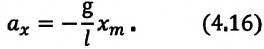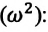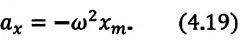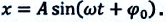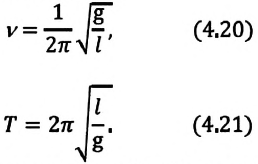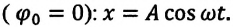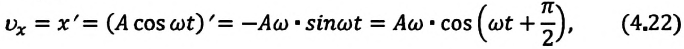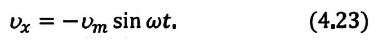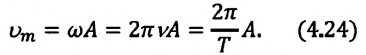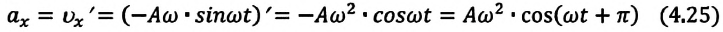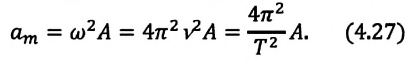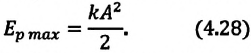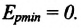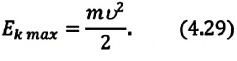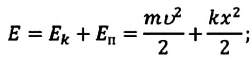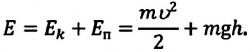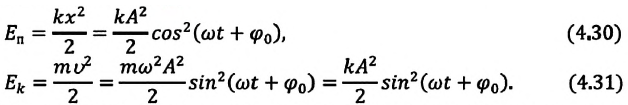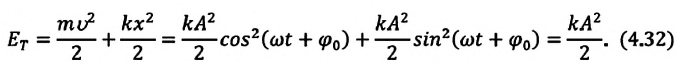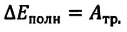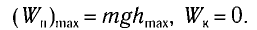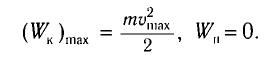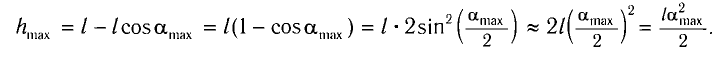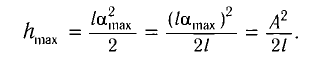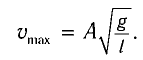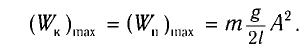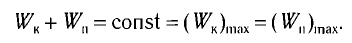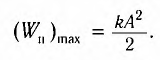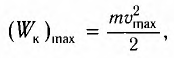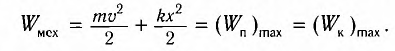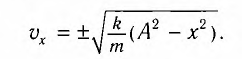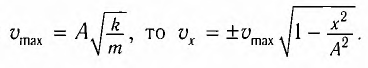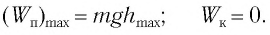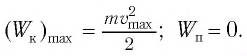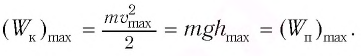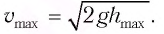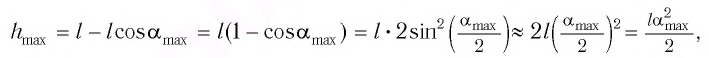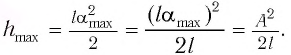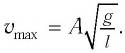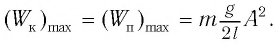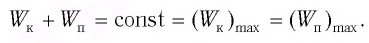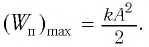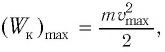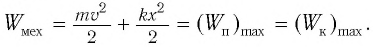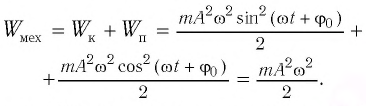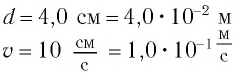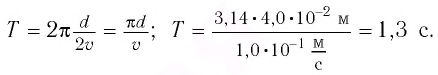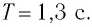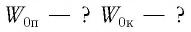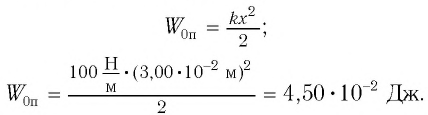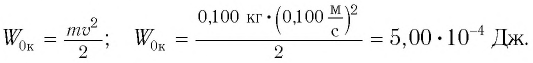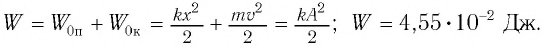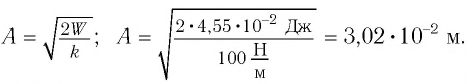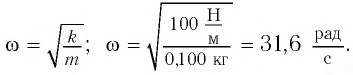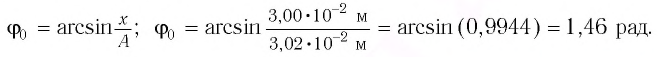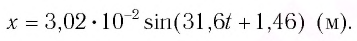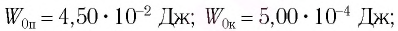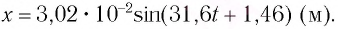Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.94 (Голосов: 35)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Как найти максимальное ускорение?
A = F / M (ускорение = сила / масса) — хороший расчет для ускорения, и обычно это тот, который вы используете для максимального ускорения.
Далее, что такое пример формулы ускорения?
Когда она нажимает на педаль газа, машина ускоряется вперед. Далее, по прошествии 10.0 секунд, она прекращает ускорение и продолжает поддерживать постоянную скорость v = 25.0 м / с. Рассчитайте ускорение автомобиля. … Ускорение свободного падения г = 9.80 м / с 2 .
Кроме того, почему ускорение является максимальным, когда скорость равна нулю?
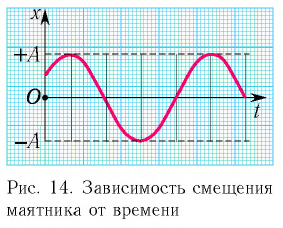
В положении равновесия, скорость максимальна, а ускорение (а) упало до нуля. Простое гармоническое движение характеризуется этим изменяющимся ускорением, которое всегда направлено к положению равновесия и пропорционально смещению от положения равновесия.
Во-вторых, почему ускорение максимальное в крайнем положении? Ускорение равно нулю, потому что в этой точке это среднее положение, что означает, что это положение равновесия. … Скорость там максимальная потому что ускорение меняет направление в этой точке, следовательно, во всех других точках ускорение замедляет объект.
Каковы три формулы ускорения?
Три уравнения: v = u + при. v² = u² + 2ас. с = ут + ½ат²
Какое ускорение выводят по формуле ускорения?
Направление ускорения не обязательно должно совпадать с направлением скорости. Ускорение измеряется в метрах на секунду в квадрате (м / с. 2 ). a = ускорение (м / с 2 ) vf = конечная скорость (м / с)
Каковы две формулы ускорения?
Задайте уравнение для среднего ускорения.
Для этого вам необходимо знать уравнение ускорения: а = Δv / Δt где a — ускорение, Δv — изменение скорости, а Δt — количество времени, которое потребовалось для того, чтобы это изменение произошло. Единица измерения ускорения — метры в секунду в секунду или м / с. 2 .
Означает ли 0 скорость 0 ускорение?
Для того, чтобы получить большая часть скорости не равна нулю, если объект ускоряется. … Однако, если скорость постоянна, ускорение равно нулю (поскольку скорость не меняется со временем). Хотя в определенный момент времени при ускорении можно иметь нулевую скорость.
Когда скорость равна 0 Что такое ускорение?
Ускорение определяется как изменение скорости. Таким образом, ускорение, равное 0, просто означает что не было изменения скорости. Другими словами, он не стал ни быстрее, ни медленнее, ни изменил направление.
Может ли ускорение быть ненулевым при нулевой скорости?
Возможно иметь ненулевое значение ускорения, когда скорость тела равна нулю. … В самой высокой точке скорость мяча становится равной нулю, после чего он начинает падать. В этот момент скорость мяча равна нулю, но его ускорение равно g = 9.8 м / с2.
В какой точке или позиции ускорение является максимальным. Почему?
Когда смещение максимальное, ускорение максимальное, потому что пружина прикладывает максимальное усилие; сила, приложенная пружиной, имеет направление, противоположное перемещению.
Что такое ускорение в крайнем положении?
Крайнее положение можно понять как в простом маятнике, когда боб имеет максимальное смещение относительно своего среднего положения. Поскольку боб находится в самой высокой точке в этом положении, его потенциальная энергия максимальна, а кинетическая энергия минимальна. В крайнем положении, и скорость, и ускорение равны нулю.
Почему ускорение является максимальным в крайнем положении при простом гармоническом движении?
Полный ответ: Ускорение изменение скорости относительно мне. Если скорость простого гармонического движения максимальна, ускорение должно быть равно нулю. … Следовательно, частица будет иметь максимальную скорость в центральном положении и минимальную в крайних положениях.
Что такое формула массы?
Масса тела всегда постоянна. Один из способов вычисления массы: Масса = объем × плотность. Вес — это мера силы тяжести, действующей на массу. Единица измерения массы в системе СИ — «килограмм».
Что такое ВУ в физике?
v = u + at — первое уравнение движения. В этом уравнении v = u + at u есть Начальная скорость. v — конечная скорость. а — ускорение.
Как вам ответить на вопрос об ускорении?
Ключ ответа
- A. Формула ускорения = A = (Vf — V0) / t. …
- A. Формула ускорения = A = (Vf — V0) / t, поэтому A = (120-90) / 5 сек = 6 миль / ч / сек.
- Б. Формула ускорения = A = (Vf — V0) / t. …
- A. Формула для ускорения = A = (Vf — V0) / t, поэтому A = (0 — 12) / 60 сек = -0.2 м / сек.
2
- Б. .
- Б. .
- B.
Что такое положительное ускорение?
Когда объект ускоряется, ускорение происходит в том же направлении, что и скорость.. Таким образом, этот объект имеет положительное ускорение.
Что такое ускорение простыми словами?
Ускорение, скорость, с которой скорость изменяется со временем, с точки зрения скорости и направления. Точка или объект, движущиеся по прямой линии, ускоряются, если они ускоряются или замедляются. … Ускорение определяется как изменение вектора скорости во временном интервале, деленное на временной интервал.
Что такое закон ускорения?
Второй закон движения Ньютона Формально можно сформулировать следующим образом: Ускорение объекта, создаваемое чистой силой, прямо пропорционально величине чистой силы в том же направлении, что и результирующая сила, и обратно пропорционально массе объекта.
Что такое формула ускорения 9 класса?
Формула ускорения. Ускорение = Изменение скорости / времени. Ускорение = (конечная скорость — начальная скорость) / затраченное время. а = (v — u) / t.
Ускорение 0 постоянное?
НЕТ. Потому что нулевое ускорение означает отсутствие изменения ускорения. Это не увеличение или уменьшение ускорения на протяжении всего пути. С другой стороны, постоянное ускорение означает постоянное увеличение или уменьшение ускорения.
Может ли тело иметь ускорение с нулевой скоростью?
Ответ: Да, объект может иметь нулевую скорость и одновременно ускоряться.
Может ли скорость быть постоянной при нулевом ускорении?
Если ускорение объекта постоянное, то он должен двигаться по прямой. …
Равномерное ускорение равно нулю?
Оно однородно для тела, если скорость изменяется на равные величины через равные промежутки времени, и если его скорость изменяется на неравные величины, оно неоднородно. … Например, тело, движущееся по кругу с постоянной скоростью, каждое мгновение меняет свою скорость и, следовательно, его ускорение не равно нулю.
Как узнать, что ускорение равно нулю?
Когда ускорение равно нулю (то есть a = dv / dt = 0), скорость изменения скорости равна нулю. То есть ускорение равно нулю когда скорость объекта постоянна. Графики движения отображают изменения расстояния, скорости и ускорения во времени.
Может ли тело с нулевой скоростью ускоряться?
Ответ: да, объект может иметь нулевую скорость и одновременно ускоряться. … Наблюдая за объектом, вы обнаружите, что он продолжит движение вперед в течение некоторого времени, а затем мгновенно остановится.
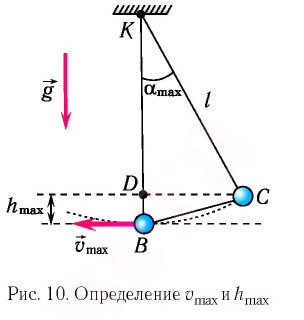
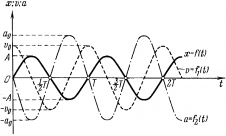
Скорость и ускорение точки, совершающей колебания
Скорость точки, совершающей гармонические колебания
Для того чтобы получить эту зависимость, найдем производную от величины смещения по времени:
Из полученного соотношения видно, что скорость точки, совершающей гармонические колебания, также изменяется по гармоническому закону и опережает по фазе смещение на .
Ускорение точки, совершающей гармонические колебания
Это соотношение получается путем дифференцирования проекции скорости на ось x:
При гармонических колебаниях ускорение точки изменяется по гармоническому закону и опережает по фазе смещение на .
Из последнего соотношения следует, что проекция ускорения на ось x:
Так как , последнее соотношение можно переписать в виде:
Последнее уравнение представляет собой дифференциальное уравнение гармонических колебаний, решением которого является синусоидальная зависимость
Примеры решения задач
| Задание | Поршень в цилиндре двигателя проходит расстояние 66 мм между крайними положениями за |
| Решение | Амплитуда колебаний поршня равна половине расстояния между двумя крайними положениями: |
мм
м
Период колебаний равен удвоенному времени прохождения поршнем расстояния между крайними положениями:
Продифференцировав последнее соотношение, получим закон изменения скорости поршня:
Из этого уравнения определяем максимальную скорость поршня:
м/с
| Задание | Материальная точка массой 10 г колеблется по закону |
| Решение | Уравнение колебаний в общем виде: |
Сопоставив это уравнение с уравнением, данным в условии задачи:
определяем амплитуду колебаний м, циклическую частоту
рад/с и начальную фазу
рад.
Найдем скорость и ускорение материальной точки:
Сила, действующая на точку:
Максимальная сила .
| Задание | На конце пружины подвешен груз. Его оттягивают на 8,0 см от положения равновесия и отпускают. а) На каком расстоянии от положения равновесия его скорость будет равна половине максимальной? б) На каком расстоянии от положения равновесия его ускорение будет равно половине максимального? |
| Решение | Считая, что груз совершает гармонические колебания и начальная фаза колебаний равна нулю, запишем законы изменения со временем смещения груза, его скорости и ускорения: |
а) Найдем фазу колебаний, соответствующую моменту времени, когда скорость груза равна половине его максимальной скорости:
Подставив значение фазы в уравнение для смещения, найдем смещение груза в этот момент времени:
Переведем единицы в систему СИ: амплитуда колебаний см
м.
б) Найдем фазу колебаний, соответствующую моменту времени, когда ускорение груза равно половине его максимального ускорения:
Подставив значение фазы в уравнение для смещения, найдем смещение груза в этот момент времени:
Физика. Ускорение, масса, сила
Ускорение это изменение скорости в единицу времени.
a = V / t
Ускорение в физике это не основная физическая величина, а производная.
Преобразуем: V = S / t тогда : a = S / t 2
именно это дает запись формулы ускорения в основных величинах и единицу измерения ускорения : метры на секунды в квадрате.
Таким образом: ускорение есть там, где есть линейная скорость движения и эта скорость — меняется в числовом значении.
Но у скорости есть еще направление.
И физики не смогли это дело оставить так, чтобы не запутать и сказали: раз скорость векторная величина, пусть будет так, что ускорение возникает и при изменении направления.
Так ускорение появляется при равномерном круговом движении?
Для нас ясность тут очень важна, так как это траектория движения планет.
Как так, спрашиваем мы, скорость движения постоянна, а появилось ускорение?
Это же нонсенс!
Предлагается:1. чтобы исключить двойное толкование, принять ускорение, как только изменение линейной скорости в единицу времени.
Далее”
2.Основным написанием формулы ускорения считать a = S / t 2,
а написание a = V / t — производным. И еще точнее, чтобы убрать квадратную функцию времени (чего не существует) a = S1- S2 / t. Т.е. ускорение это разница (изменение) пройденного пути в единицу времени. И всё!
3. Считать ускорение не физической, а математической величиной, употребимой в узких пределах.
4. Определение “изменение направления” к ускорению не применять. Считать ускорением только изменение величины, а не направления.
Где мы в формулах встречаем ускорение?
Формула силы. По второму закону Ньютона F = m х a означает, что, если к массе m приложить силу F , то тело будет двигаться с скоростью, которая имеет ускорение а. И чтобы вычислить ускорение, нам надо замерить путь и время, так зачем же оно? Только для облегчения записи вычислений.
Ускорение со знаком плюс означает только то, что за одну единицу времени тело будет проходить все более меньший путь.
В случае со свободным падением тела используется понятие ускорение свободного падения тела (без учета сопротивления воздуха) g
И формула пишется F = m х g. Но эта формула справедлива только для случая, когда есть состояние свободного падения. Если тело неподвижно относительно центра Земли, то эта формула не используется, так как приводит к ошибке.
Например. Тело массой m (1 кг.) лежит на весах.
Что показывают весы? Они показывают массу в 1 кг.
А не вес, как силу притяжения ( m х g).
Тело давит на опору весов, с силой притяжения, а по Закону Всемирного тяготения
сила тяжести m х M / R2 ускорения свободного падения не содержит и вес показывают только массу. Таким образом, если задать задачу: арбуз массой m положили на весы и спросили какой вес? А потом перемножить m х g получим неверный результат, потому что весы показывают значение массы, а ускорения g
здесь вообще нет.
Напишите такое уравнение:
m х g = m х M / R2 и получите, после сокращения массы g = M / R2
и эта формула хороша только тем, что объясняет почему ускорение свободного падения не зависит от массы тела , а зависит только от массы Земли и радиуса в квадрате.
Но математически эта формула выглядит как неверная, так как не совпадают единицы измерения.
Наши ученые тут опять отличились. Они ввели гравитационную постоянную и G дали ей единицу измерения м3·с;2·кг;1 (ответ сошелся) а вопрос остался:
Есть от чего сойти с ума : во втором законе ускорение от массы зависит, а при свободном падении — нет!
А происходит это от того, что при увеличении массы силя притяжения растет, а ускорение по второму закону уменьшается и результирующая остается неизменной от массы.
Вообще, вес это еще одна производная от действия гравитации величина, которая в уважающих себя учебниках физики не рассматривается, но очень важна на базаре.
Рассмотрим случай невесомости, когда вес исчезает. Например, парашютист прыгает
с самолета, а парашют дома забыл. (сопротивление воздуха не учитываем, как всегда, зачем ему теперь воздух нужен) Скорость растет соразмерно с величиной 9.8 метров пройденного пути в секунду!
И здесь появляется еще один парадокс: сила гравитации есть, масса есть, ускорение. тоже есть, а давления на опору (как рыночного понятия веса) нет!
А, если есть сопротивление воздуха?
Тогда: F = m х (g — а)
Здесь а это то реальное ускорение, которое возникает и оно меньше ускорения свободного падения. И, если оно равно g — сила давление опору ( или вес ) равен нулю.
После перерыва продолжим.
Вашу статью Николай, прочитали почти 2 сотни людей, но почему-то никто из них не оставил комментарий! Возможно им, как и мне, между прочим, не все понятно. Вот как я рассуждаю. Вот если есть скорость, причем любого тела на поверхности Земли! То это значит, как минимум, что к этому телу приложена какая-то сила!! Так как в отсутствии этой принудительной силы, любое тело, в силу Природой, /Богом/ данной ему сущности! Которая называется инерция, и которая, как это хорошо известно, зависит от количества заключенной в тело материи! Так вот, так или иначе, но любое тело, в силу своей инерции всегда стремиться покоиться относительно поверхности Земли! Причем, это ни какая-то там фантазия, — это данность, о которой нам говорили, которой нас учили еще Древние Греки, если Вы не возражаете!
А теперь будем внимательно не только рассматривать, го и изучать даже СИЛУ, которую мы будем прикладывать к нашему, для простоты скажем, пробному телу! Если эта СИЛА в течение времени изменяет свое значение по постоянному к времени закону, такое движение называется равномерным движением и полностью определяется, во-первых, временем! А во-вторых, постоянным значением величины скорости движения! Все, вопрос закрыт!
Если же сила, в течение времени изменяет свое значение, причем по любому другому от, приведенного выше, Закона! Например, Закона, пропорциональному квадрату времени, или любой другой степени зависимости от времени, тогда появляется ускорение. Таким образом, ускорение — есть не что иное, как изменение скорости, пропорциональное степени зависимости силы от времени, прикладываемой к пробному телу, которое приводит-таки к изменению скорости, пропорциональной конкретной, заметьте, степени зависимости от времени. Другими словами, если сила, например, гравитационного притяжения изменяется пропорционально квадрату времени, тогда такое ускорении можно назвать ускорением свободного падения. А если сила будет прикладываться по, какому-то другому Закону, тогда такое ускорение можно и даже надо называть как то иначе.
В заключение предлагаю Вашему вниманию Рецензию на статью Михаила Близнецова.
Дмитрий Тальковский 14.12.2020 20:38. Глубокоуважаемый Юрий Сопов! Я, в отличие от Исаака Ньютона, не считаю себя чем-то таким, что может вмешиваться в Природу, хотя бы даже просто человеческих мнений! Потому я принимаю высказыванием Исаака Ньютона: «Гипотез не измышляю»! как абсолютную истину, распространяющуюся, в том числе и на самого Ньютона, и конечно, Вас! Если перевести эту, вне всякого сомнения, абсолютную истину: «Гипотез не измышляю» на русский язык, то она будет звучать так, что, мол, писать Законы, прочее и прочее, я имею в виду создавать всякие там красивые теории, можно и нужно даже только после того как у вас на руках будут исключающие двойное толкования измерения.
Например, для преобразований Галилея, это факт, причем объективный, а не высосанный из пальца Галилея, что скорость света есть величина бесконечная! Или в случае написания Законов движения Исааком Ньютоном, объективный факт независимости скорости падения тяжелых и легких тел, что на Земле, что в космосе! Причем, и это очень важно, Ньютон, считавший себя умнее Аристотеля, ошибочно полагал, что тяжелым телом является вовсе не свинцовая пуля, как это есть в действительности, а чугунное ядро!! Цирк на дроте.
В нашем случае, это факт зависимости или независимости скорость распространения света от скорости движения источника света. Все!! До тех пор пока наши только так называемые ученые не положат на стол эти измерения, говорить о теории распространения света не имеет никакой ни возможности, ни ценности!! Так только один прекрасно душный треп!! И ничего более того! Простите за резкость изложения материала.
При этом я не хочу, и не собираюсь даже никого обидеть! Напротив, я хочу, что бы мы все вместе, включая Диму Василькова, Вас, конечно, Виктора Бабинцева и несть числа всем честным ученым и любителям, приверженным отысканию абсолютных истин!! Я хочу, что бы мы все вместе объединились и всегда поддерживали, а не ругались друг с другом.
Что касается: «Тогда вы просто должны представить неопровержимые факты, что свет это не волна, а именно частица»! Я, на уровни рассмотрения отдельных частиц (т.е. весьма детально. ), дал понимание причин преломления лучей и далее объяснил причину восстановления их скорости после прохода через белее плотную среду. Попробуйте это сделать чисто с позиции свет — волна”. Конец цитаты.
Как два пальца, простите! Объяснение, как у Вас и у Ньютона, кстати, тоже простое! Среда, самая плотная среда распространения света, — это, когда есть просто чистое гравитационное поле, у релятивистов это вакуум! Когда в эту среду, гравитационное поле, что на Земле, что в космосе, искусственно вносят постороннее тело, вещество, например, воду, воздух, стекло и так далее, Тогда эта среда распространения света, становится менее плотной, в результате чего скорость распространения света в этой новой среде уменьшается! Спасибо.
“Вот если есть скорость, причем любого тела на поверхности Земли! То это значит, как минимум, что к этому телу приложена какая-то сила!! “
Если тело движется с ускорением, то приложена. Если скорость постоянна то была приложена. А при отсутствии это силы в прошлом и настоящем тело находится в покое (относительно Земли)
Вы строите длинные предложения, смысл которых мне трудно понять. Зачем? Вы же не Лев Толстой.
Глубокоуважаемой Николай Кладов! Спасибо! Конечно, я не Лев Николаевич Толстой, но быть похожим на него, для мен великая честь. Спасибо. Что касается сущности Ваших рассуждений, то как я это конечно понимаю, они не противоречат и моим, в том числе рассуждениям, какими бы пространными они не были. Спасибо
А теперь конкретно, как я понимаю ваши, Николай Кладов, цитирую, слова: «Вот если есть скорость, причем любого тела на поверхности Земли! То это значит, как минимум, что к этому телу приложена какая-то сила»!! Это значит, что это я только так утверждаю.
А теперь как вы именно это понимаете и естественно тогда уточняете, цитирую: «Если тело движется с ускорением, то такая сила приложена». Браво! Все как у Галилея и примкнувшего к нему Ньютона!
Далее Вы продолжаете: «Если скорость постоянная, то была приложена». А при отсутствии этой силы в прошлом и настоящем, тело находится в покое (относительно Земли). Браво!! Все как Аристотеля!!
Выходит, что круг последователей Аристотеля медленно, но уверенно скоро пополнится Николаем Кладовым. Чтобы не сглазить, а главное закрепить успех, продолжим такие вот рассуждения. Рассмотрим мнимую, если угодно виртуальную дискуссию диалектика Аристотеля с релятивистом Галилеем и примкнувшим, вероятно, чтобы его не сожгли на костре инквизиции, Исааком Ньютоном. Так вот диалектик Аристотель, как я уже всем уши прожужжал, различал два вида движения! Впрочем, не стану повторять все, а цитирую: http://proza.ru/2019/10/23/1995. http://proza.ru/2013/01/21/850.%C2%A0. Кратко:
Все дело в том, что физика Галилея – Ньютона принципиально отличие от физики Аристотеля по простой причине. Очевидно Ньютону, строившему физику вместе с Галилеем проще было, не ввязываясь «по мелочам» в войну с Церковью. И потому, пусть в общих чертах только, они могли тогда решить проблему движения в физике. Тогда как, действительно, если исходить из физики Аристотеля, то прикладываемую принудительную СИЛУ, необходимо связывать, но уже не и с изменением скорости движения тел, веществ, а единственно только с самой скоростью движения этих тел, веществ!
Таким образом, в физике Галилея — Ньютона для простого, не ускоренного движения тел, веществ, — сила просто перестала считаться, /являться/ чем-то необходимым. Так как сила у них нужна была для того только, что бы уже изменять скорость движения. А так, если тело движется, то оно должно, /обязано/ двигаться вечно. Живой так сказать вечный двигатель, даже изобретать ничего не надо! Нет, так сказать в этом, никакой такой необходимости. Главная проблема вечного движения тел веществ, — это устранить влияние внешней среды, — воздуха, и естественно, устранить трение! И тогда тела, вещества, согласно Учению Галилея — Ньютона, будут двигаться вечно.
Что касается реальной физики Аристотеля, когда повозка останавливается практически сразу! Или через очень короткий промежуток времени после прекращения на нее внешнего воздействия, то эта физика Аристотеля, очевидно, – осталась не удел.
Именно потому, сложной оказалась проблема для Галилея — Ньютона объяснить, а главное самим понять, почему четверка лошадей не увеличивает скорость движения повозки, например, именно в четыре раза. То есть трудно понять, почему «кажущееся» увеличение силы, например в 4 раза, /4лошади вместо 1 лошади/, не приводят к автоматическому увеличению скорости в 4 раза. То есть сложно понять тогда, а некоторым исследователям и сегодня, что присутствие четырех лошадей, вместо одной! Еще вовсе не обеспечивают автоматически, приложение даже 1 лошадиной силы к повозке до того момента, когда скорость тележки, в силу ее ИНЕРЦИИ, снова упадет до такого ее значения, когда очередная резвая лошадка, сможет снова приложить к ней свою, собственно говоря, силу.
Тем не менее, «трудности в механике Аристотеля», если сравнивать ее с хорошо знакомой нам механикой Ньютона, по словам выдающегося американского философа и историка науки Томаса Куна, как тогда уже считалось, «не были лишены смысла»! Более того, Кун не без основания как следует полагать, считает, что физика Аристотеля «не просто плохая физика Ньютона»! Просто физика Аристотеля, — это совсем другая физика!
Прежде чем найти признаки, по которым физика Аристотеля не просто не совпадает с физикой Ньютона, но и в значительной степени превосходит ее, то есть считается единственно научной физикой, рассмотрим рассуждения Галилея, которые, как мы уже знаем, в значительной степени определили физику Ньютона.
Так вот в отличие от Аристотеля, который со всей определенностью утверждал, что тела, вещества в случае их принудительного движения, могут двигаться, конечно, еще какое-то время по инерции, расходуя эту вновь приобретенную инерционную силу движения. Но только исключительно строго ограниченное время вплоть до своей обязательной и полной остановки в той или другой точке Земли. Галилей утверждал прямо противоположное, а именно, что по инерции тела вещества могут двигаться, сохраняя вновь приобретенную инерцию движения, бесконечно долго. Для этого и надо всего ничего исключить тормозящие действия среды, в том числе и воздуха, а также исключить трение. Теперь же, как представляется самое время уточнить: Кто прав: Аристотель или Галилей?
Так вот пришло время разбираться. И чтобы убедить Кладова и всех еще последователей Галилея и Ньютона, что он идет верным путем, рассмотрим мысленный эксперимент, который конечно при желании и средствах, можно легко даже осуществить. Сначала вспомним, как тело движется в своем свободном падении. Правильно, за 1 секунду тело проходит, как мы это наблюдаем, расстояние 5 м. Скорость изменяется от 0 до 10 м/с. Средняя скорость движения за 1 секунду получается 5 м/с. Что мы наблюдаем: Полет нормальный! Как и кто именно нам организовал этот нормальный полет, об этом чуть позже. А теперь запомним цифры свободного полета за 1 секунду и продублируем такое же движение, но не в свободном полете к центру Земли, а в точно таком же движении, но уже перпендикулярному радиусу Земли и на протяжении уже не 1 секунды, а целого часа, например! А что гулять, так гулять! Причем, раньше, помните, движение было параллельное радиусу, а теперь перпендикулярно радиусу Земли! Вот вся вроде бы разница! Цифры вроде те же, а картина совсем другая и отличается так же, как Небо отличается от Земли. Другими словами, такое движение называется равномерным принудительным движением с постоянной скоростью, которая образуется потому, что к нашему пробному телу через строго определенное время прикладывается строго контролируемая сила! Вот мы, вместе с Аристотелем и Кладовым, в противовес Галилею и Ньютону определили необходимую силу, что бы двигаться со строго заданной постоянно скоростью, причем без всякого ускорения. Другими словами, что бы принудительное движение присутствовало, надо постоянное присутствие принудительной силы. И никакого равномерного движения по инерции! Так как по инерции, и в отсутствие принудительной силы, тело стремится покоиться, или уже покоится.
«Вот если есть скорость, причем любого тела на поверхности Земли! То это значит, как минимум, что к этому телу приложена какая-то сила»!!
это выделено в кавычки так я процитировад ваши слова.
Если Вы хотите знать моей мнение по физ. вопросам, то я изложил их все в одной книге. http://proza.ru/2017/01/15/55
Спасибо, конечно, глубокоуважаемый Николай Кладов! Я тоже, кстати, точно также мог послать вас к моим рассуждениям, например: http://proza.ru/2012/11/21/950. Но я не стану этого это делать, а прошу вас порассуждать над тем, кто прав в споре о решении проблемы движения на нашей Земле в том числе: Исаак Ньютон с Галилеем или Аристотель? Как лично вы считаете? Спасибо. Я имею в виду, согласны ли вы с рассуждением Аристотеля, что есть два вида движения: Естественное!! И Принудительное! Или вы согласны с Исааком Ньютон и Галилеем, что и тяжелые и легкие тела, что на Земле, что в космосе падают с одинаковыми скоростями. Спасибо.
Да я зайду по сслыке. Я не очень разбираюсь в этих спорах между уважаемыми людьми, да и зачем мне их разводить.
Аристотель, как известно, совсем не разбирался в современной физике. Галилей, хотя и проводил полезные опыты на Пизанской башне, не мог понять причины падения тела.
А физика Ньютона, хотя она несовершенна вошла учебники, как классика.
Теперь по теме.
Вот что Вы спрашиваете:
1. “согласны ли вы с рассуждением Аристотеля, что есть два вида движения: Естественное!! И Принудительное! “
Есть два вида движения: Инерционное и под действием силы — внешней или собственной, например двигатель автомобиля реактивной у ракеты..НК
2. “Или вы согласны с Исааком Ньютон и Галилеем, что и тяжелые и легкие тела, что на Земле, что в космосе падают с одинаковыми скоростями.”
Правильно так: ускорение свободного падения не зависит от массы тела. Это значит
время падения и для тяжелых и для легких — одинаково. А скорость тут не рассматривается. НК
Портал Проза.ру предоставляет авторам возможность свободной публикации своих литературных произведений в сети Интернет на основании пользовательского договора. Все авторские права на произведения принадлежат авторам и охраняются законом. Перепечатка произведений возможна только с согласия его автора, к которому вы можете обратиться на его авторской странице. Ответственность за тексты произведений авторы несут самостоятельно на основании правил публикации и законодательства Российской Федерации. Данные пользователей обрабатываются на основании Политики обработки персональных данных. Вы также можете посмотреть более подробную информацию о портале и связаться с администрацией.
Ежедневная аудитория портала Проза.ру – порядка 100 тысяч посетителей, которые в общей сумме просматривают более полумиллиона страниц по данным счетчика посещаемости, который расположен справа от этого текста. В каждой графе указано по две цифры: количество просмотров и количество посетителей.
© Все права принадлежат авторам, 2000-2022. Портал работает под эгидой Российского союза писателей. 18+
Unit Converter
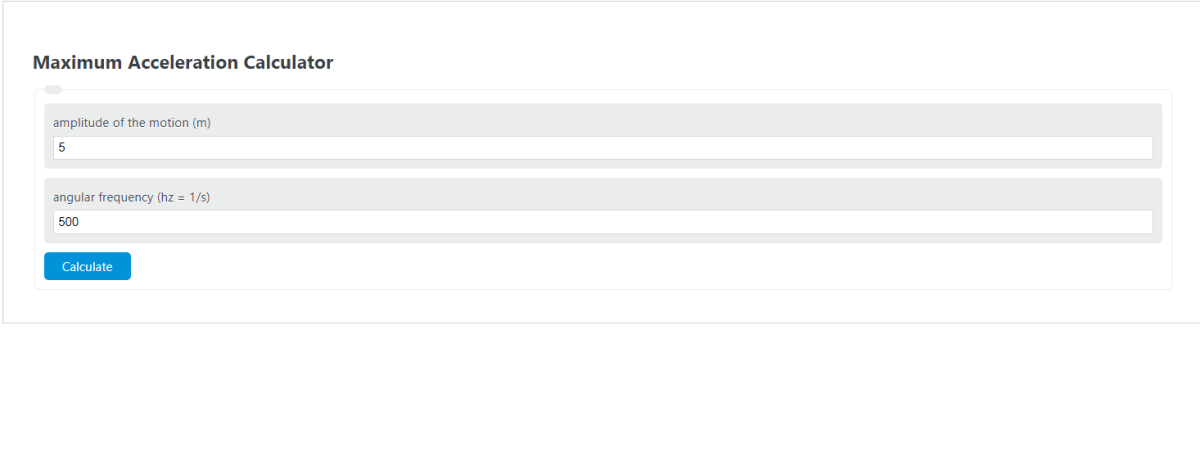
Enter the amplitude of the motion and the angular frequency into the calculator to determine the Maximum Acceleration.
- All Acceleration Calculators
- Angular Acceleration Calculator
- Frequency To Angular Velocity Calculator
- Wave Amplitude Calculator
- Frequency Displacement Acceleration Calculator
- Sine Acceleration Calculator
- Amplitude to Acceleration Calculator
Maximum Acceleration Formula
The following equation is used to calculate the Maximum Acceleration.
- Where Amax is the Maximum Acceleration (m/s^2)
- A is the amplitude of the motion (m)
- f is the angular frequency (hz = 1/s)
To calculate a maximum acceleration, multiply the amplitude of motion by the product of 2 times pi times the frequency raised to the power of 2.
What are the units for Maximum Acceleration?
In the International System of Units, also known as SI units, the units for Maximum Acceleration are m/s^2.
How to Calculate Maximum Acceleration?
Example Problem:
The following example problem outlines the steps and information needed to calculate the Maximum Acceleration.
First, determine the amplitude of the motion. In this example, the amplitude of the motion is calculated or measured to be 5 (m).
Next, determine the angular frequency. For this problem, the angular frequency is determined to be 500 (hz = 1/s).
Finally, calculate the Maximum Acceleration using the formula above:
Amax = A*(2*pi*f)^2
Inserting the values from above and solving the equation with the imputed values gives:
Amax = 5*(2*3.14159*500)^2 = 49,347,938.64 (m/s^2)
|
ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ |
|
|
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают. |
|
|
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0. |
|
|
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени. |
|
|
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе). |
|
|
Скорость и ускорение при гармонических колебаниях. |
|
|
Согласно определению скорости, скорость – это производная от координаты по времени |
|
|
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2. |
|
|
Величина |
|
|
Следовательно, для скорости при гармоническом колебании имеем: |
|
|
Согласно определению ускорения, ускорение – это производная от скорости по времени:
Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе). |
|
|
Величина – максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: |
|
|
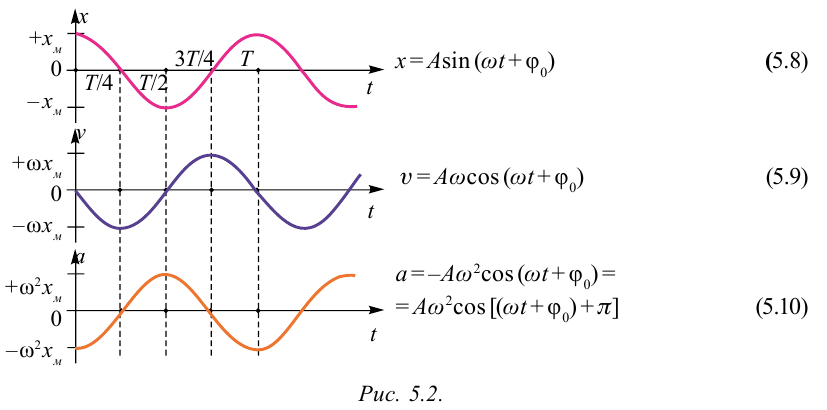
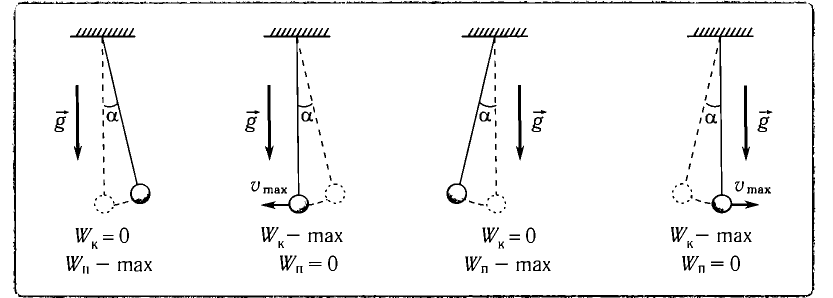
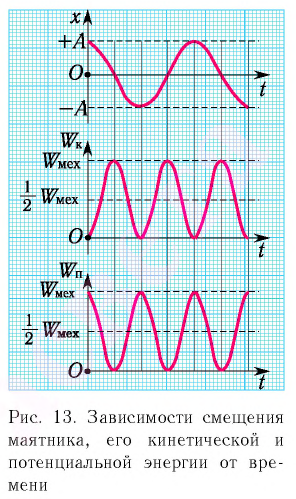
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения). |
|
|
Сравним выражения для смещения и ускорения при гармонических колебаниях:
|
|
|
Можно записать: т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота. |
|
|
Часто бывает удобно записывать уравнения для колебаний в виде: где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: |
|
Содержание:
Гармонические колебания:
Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.
Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (
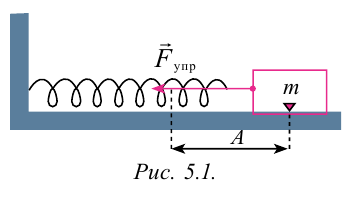
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 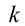
Если груз, который находится в равновесии, потянем вправо на расстояние 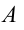
сторону равновесного состояния.
С течением времени смещение груза уменьшается относительно 
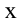
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде (
здесь: 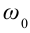
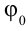
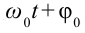
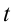
Из математики известно, что 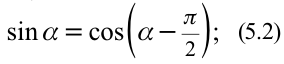
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.
Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.
Основные параметры гармонических колебаний
a) период колебания 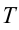

б) частота колебания 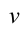
Единица
c) циклическая частота 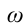
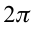
С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:
Пример решения задачи:
Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.
Дано:
Найти:
Формула и решение:
Гармонические колебания пружинного маятника
В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.
Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.
Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:
Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.
Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.
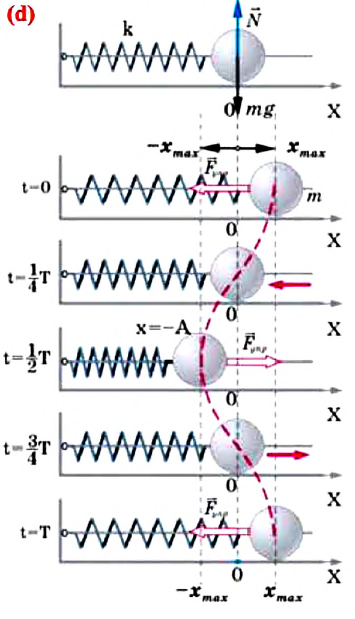
С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения 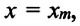
или
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.
Где 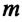
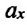
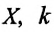
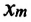
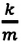
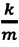
или
Таким образом, уравнение движения пружинного маятника можно записать и так:
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 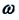
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.
Здесь 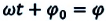
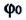
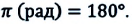
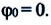

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.
Гармонические колебания математического маятника
До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.
Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.
Математический маятник – это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.
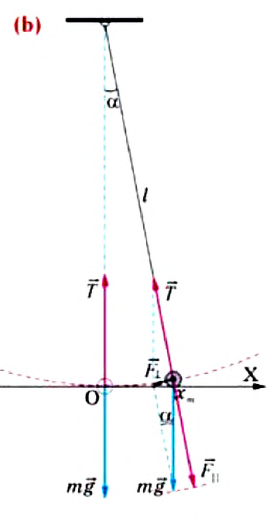
Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).
Сила тяжести 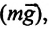
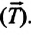
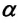
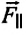
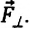
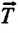
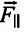
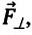
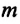
Приняв во внимание, что:
Для уравнения движения математического маятника получим:
Где 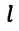
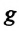
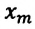
Для данной колебательной системы отношение 

или
Таким образом, уравнение движения математического маятника можно записать и так:
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.
Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.
Скорость и ускорение при гармонических колебаниях
Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.
При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю
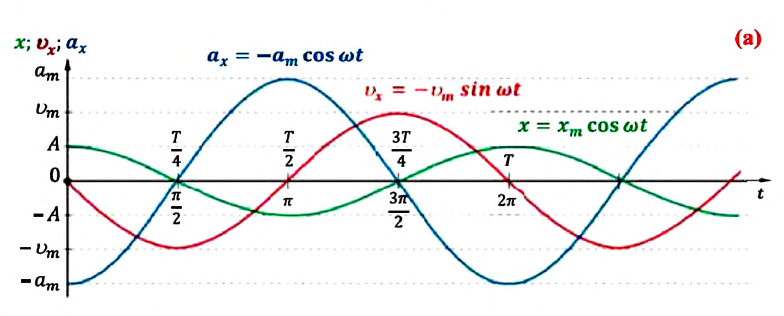
Так как скорость является первой производной смещения (координат) по времени, то:
или
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на 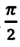
Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:
Так как ускорение является первой производной скорости по времени, то получим:
или
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на 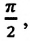
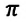
Превращения энергии при гармонических колебаниях
Теоретический материал
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.
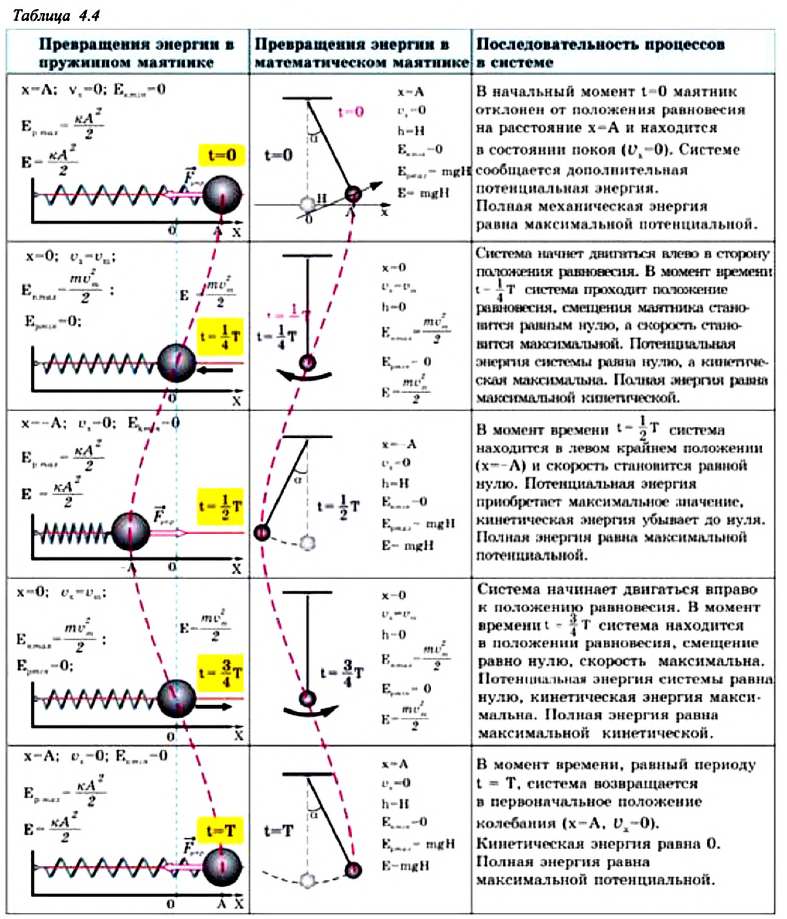
В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 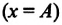
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 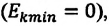
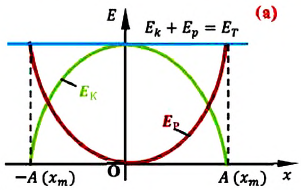
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 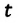
a) для пружинного маятника:
b) для математического маятника:
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.
Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают:
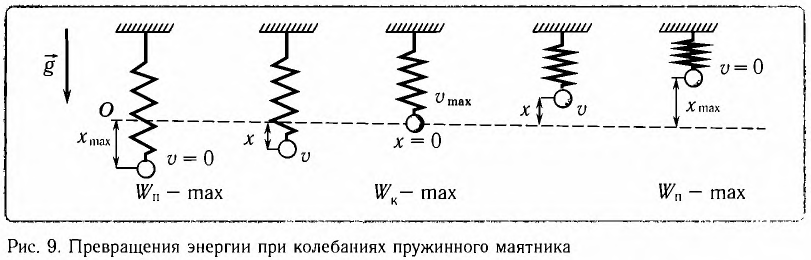
Превращения энергии при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.
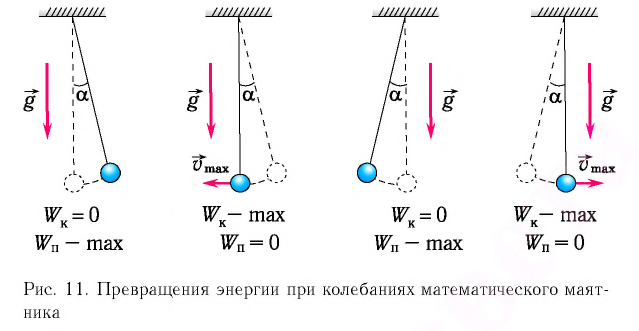
Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
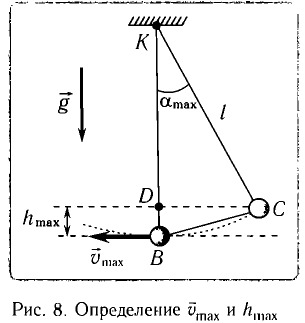
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:
Рис. 7. Превращения энергии при колебаниях математического маятника
Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:
Из закона сохранения механической энергии следует (рис. 8), что
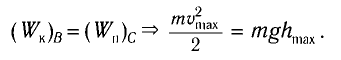
Отсюда найдем модуль максимальной скорости маятника:
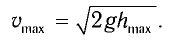
Высоту 
Если колебания малые, то 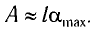
Отсюда
Подставив выражение для 
Подставляя выражения для 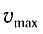

Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.
В любом промежуточном положении
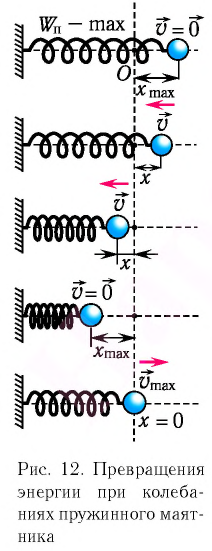
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 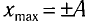
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:
где 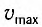
В промежуточных точках полная механическая энергия
Отсюда можно вывести выражение для модуля скорости 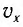
координатой х:
Так как
Энергия при гармонических колебаниях
Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.
Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.
При отклонении маятника на угол 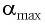
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 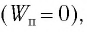
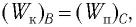
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:
Отсюда найдем модуль максимальной скорости маятника:
Высоту 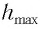
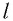
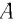
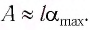
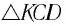
или
Подставив выражение (3) для 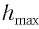
Подставляя выражения (3) для 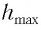
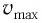
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).
В крайних положениях, когда 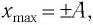
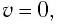
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.
В положении равновесия, когда 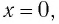
где 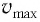
В положениях между крайними точками полная энергия
С учетом выражений для координаты 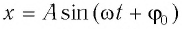
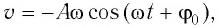
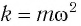
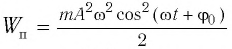
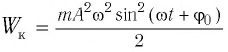
Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:
Таким образом, начальное смещение 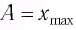
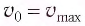
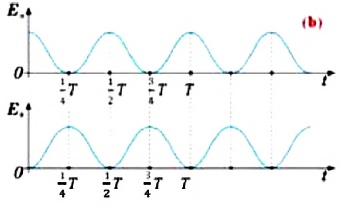
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).
Пример №1
Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 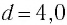
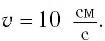
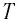
Дано:
Решение
По закону сохранения механической энергии
Отсюда:
Ответ:
Пример №2
Груз массой 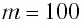
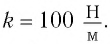
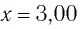
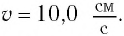
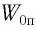
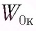
Дано:
Решение Потенциальная энергия груза:
Кинетическая энергия груза:
Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:
Отсюда
Циклическая частота:
В начальный момент времени 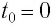
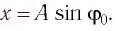
Тогда закон гармонических колебаний имеет вид (рис. 14):
Ответ:
- Вынужденные колебания в физике
- Электромагнитные колебания
- Свободные и вынужденные колебания в физике
- Вынужденные электромагнитные колебания
- Закон Архимеда
- Движение жидкостей
- Уравнение Бернулли
- Механические колебания и волны в физике
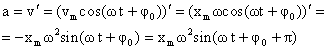 .
.