Как найти ускорение с помощью коэффициента трения – еще одна важная и общепринятая тема, которую необходимо решить. Это фактор, который определенным образом увеличивает ускорение.
Когда тело находится в движении, оно будет продолжать движение до тех пор, пока на него не подействует сила, изменяющая размеры объекта. Таким образом, этот процесс будет продолжаться до тех пор, пока скорость не будет увеличена или уменьшена.
Как только объект изменяет скорость, он либо ускоряется (положительно), либо замедляется (отрицательно), обычно в направлении, противоположном движению. Изменение скорости также известно как скорость с точки зрения физики.
Изменение скорости происходит в другое время, и, следовательно, это будет влиять на ускорение движущегося тела либо положительно, либо отрицательно. Внезапный рывок в системе также влияет на ускорение.
Когда тело находится в движении, на него влияет несколько факторов, и одним из них является ускорение, на которое будет влиять термин, называемый трением. Постепенно мы будем иметь дело с нахождением ускорения с помощью коэффициент трения.
Мы можем продолжать говорить об ускорении по-разному, но когда на ускорение влияет другой фактор, нам нужно сосредоточиться на этом. Трение – это, по сути, фактор, присутствующий между телом и активной поверхностью.
Понимание трения и коэффициента фиксации
Прежде чем мы углубимся в это подробно, необходимы первые знания о трении и коэффициенте трения. Трение по сути, это сила, которая сопротивляется движению при ходьбе, беге и т. д.
Между объектом и поверхностью присутствует небольшой фактор, который называется трением. Эта конкретная сила называется силой трения. Эта сила помогает любому случайному телу в действии двигаться.
Когда поверхность шероховатая, трение больше, а когда поверхность гладкая, трение меньше. Таким образом, когда трение увеличивается, ускорение уменьшается, а когда трение уменьшается, ускорение уменьшается. Это также базовое понимание в знакомых терминах.
Теперь давайте посмотрим, что именно означает коэффициент трения. Этот коэффициент трения представляет собой безразмерный коэффициент, представляющий собой соотношение между нормальной силой и силой трения движущегося тела.
Итак, все мы знаем, что движению тела способствуют несколько различных аспектов. Так или иначе, он будет ускоряться. Во-первых, это изменение скорости, называемое скоростью, которое помогает в подвижности тела.
В некоторых случаях это тоже кажется существенным. Это будет внешняя сила или любая другая сила и чистая сила в целом. Фактор, называемый трением, вносит большой вклад в движение любого объекта или тела. Коэффициент трения будет определять, сколько силы потребуется для такого движения тела.
Поскольку это мера отношения, она будет иметь нулевые размеры, а значение будет варьироваться от минимального 0 до максимального значения 0.5. Также может быть коэффициент трения, который может быть больше единицы.
Как найти ускорение по коэффициенту трения
Требуется знание формулы для определения ускорения. Согласно второму закону Ньютона, ускорение пропорционально силе и косвенно пропорционально массе объекта.
Следовательно, мы получаем его как а = Ф / м. это формула базового ускорения без каких-либо атрибутов. Когда трение действует на тело и его движение, не менее важен тип поверхности.
Таким образом, формула изменяется в соответствии с коэффициентом трения, a = (fn-μ) / m. μ известен как коэффициент трения, и он указывает количество силы, необходимой для дальнейшего движения тела.
Давайте посмотрим, как это сделать, на лучшем примере. Трение весом 10 кг прикладывается к правому трению 7 Н. Допускается ускорение на неровной поверхности. Сила трения имеет значение 0.3 Н. Теперь вычислите ускорение объекта.
а = (20 – 0.3) / 7
а = 19.7 / 7
a = 2.81 мс-2
Вот как найти ускорение с коэффициентом трения. Но где использовать коэффициент трения – это вопрос. Мы тоже с этим разберемся. В вопросе прямо дана постоянная силы трения.
Сила трения и сила нормали не будут указаны явно, но значения могут быть нарисованы с использованием коэффициента трения. По приведенным данным мы должны рассчитать коэффициент трения, чтобы применить его к формуле и найти ускорение.
Задача о том, как найти ускорение по коэффициенту трения
Проблема:
Автомобиль весом 1100 кг с коэффициентом трения μ = 0.95 относительно шин. Теперь определим ускорение. Он движется с силой 880 Н.
Решение:
Нам нужно понять эту проблему, используя диаграмму свободного тела. Теперь давайте погрузимся в движение автомобиля и силы, действующие на него. Поскольку автомобиль находится в движении, на него будет воздействовать как можно больше сил.
Мы знаем, что по умолчанию на тело действует нормальная сила; теперь, когда он находится в движении, действует также сила трения.
Значение, данное для коэффициента трения: μ = 0.95. Здесь нам нужно найти фрикционную и нормальные силы, так как коэффициент значение трения уже задано.
Отметим, что нормальная сила равна силе гравитации. Известно, что сила тяжести составляет 9.8 мс-1. А теперь это значение, умноженное на массу, дает нормальную силу. Fn = 1100 × 9.8 = 10780.
Сила трения – это коэффициент трения, умноженный на нормальную силу. Следовательно ff = 10241. Теперь, когда сила трения найдена, следующим шагом будет определение ускорения. Сила трения также считается чистой силой.
а = ф / м
а = 10241/1100
а = 9.31 мс-2
Часто задаваемые вопросы
Как найти скорость с трением?
Поскольку ускорение можно найти с помощью трения, можно найти и скорость, поскольку это не что иное, как изменение скорости.
Во-первых, нам нужно известна начальная скорость и сила тяжести. Таким образом, скорость с учетом трения находится по формуле: начальная скорость минус коэффициент трения, умноженный на силу тяжести и заданное время. v(t) = v0 – µ g t.
Как найти коэффициент трения?
Коэффициент трения – это фактор, который присутствует между движущимся телом и поверхностью, с которой оно движется.
Формула для коэффициента трения: μ = (сила трения) / (сила в норме). Еще один момент, который следует отметить, заключается в том, что сила трения иногда равна чистой силе, действующей на тело, что упрощает вычисление ускорения. Нормальная сила рассчитывается путем умножения силы тяжести и массу тела.
Какие бывают типы трения?
Статическое и кинетическое трение – это два разных типа, которые подпадают под одну тему трения.
Статическое трение называется трением, когда тело не движется. Из самого слова «статика» очевидно, что ничего не движется. В таких случаях найденное трение называется трением покоя. Когда тело выходит из равновесия, это также происходит из-за трения, которое называется кинетическим трением. Статическое и кинетическое трение различается в зависимости от случая и условий.
Почему статическое трение называется так?
Статическое трение называется так, потому что это сила, противодействующая неподвижному телу.
Когда тело не движется и остается в положении равновесия, трение, действующее на тело, называется трением покоя. Это трение всегда действует в направлении, противоположном силе, действующей вместе с движением тела, даже когда оно не действует.
2017-03-08 
Определите максимальное ускорение, с которым заднеприводный автомобиль с расстоянием между осями $L=1,2 м$, центр тяжести которого расположен на высоте $h=1 м$ от земли посередине между осями, может начать двигаться, если он находится а) на льду, б) на асфальте. Коэффициент трения скольжения колес по льду 0,1; по асфальту 0,7.
Решение:
На автомобиль действуют сила тяжести $M vec{g}$, приложенная к его центру масс, и силы реакции опоры на передние и задние колеса $vec{N}_{1}$ и $vec{N}_{2}$ соответственно (рис.). Кроме того, на задние колеса действует сила трения $vec{F}_{тр}$, являющаяся силой трения покоя и направленная по направлению движения автомобиля (это становится очевидным, если заметить, что нижняя точка колеса неподвижна относительно земли, а действующий на колесо со стороны двигателя момент сил стремится сдвинуть ее против направления движения автомобиля). Именно эта сила трения покоя и движет автомобиль вперед. В то же время на переднее колесо не действуют ни сила трения покоя, ни сила трения скольжения, т.к. оно катится без проскальзывания и не приводится во вращение мотором.
Записав второй закон Ньютона в проекциях на вертикальную и горизонтальную ось и уравнение моментов относительно т.А, являющейся точкой пересечения проведенной через центр тяжести горизонтали и проведенной через ось заднего колеса вертикали (см. рис. 34), получим систему уравнений, описывающую движение автомобиля:
$begin{cases} F_{тр} = Ma_{max} \ N_{1} + N_{2} = Mg \ N_{1} L + F_{тр} h = Mg frac{L}{2} end{cases}$ (1)
Учитывая, что сила трения покоя $F_{тр} leq mu N_{2}$, можно прийти к системе неравенств, ограничивающих значение ускорения:
$begin{cases} a leq mu frac{N_{2}}{M} \ a leq left ( frac{N_{2}}{M} – frac{g}{2} right ) frac{L}{h} end{cases}$ (2)
При нарушении первого условия системы (2) задние колеса начнут проскальзывать, а при нарушении второго условия нарушится третье уравнение системы (1), суммарный момент сил $vec{N}_{1}$ и $vec{F}_{тр}$ превысит момент силы тяжести и автомобиль опрокинется назад.
Поскольку правые части неравенств системы (2) прямо пропорциональны силе $N_{2}$, то максимальное ускорение достигается при ее максимальном значении. Очевидно, что оно равно значению силы тяжести, тогда (2) принимает вид
$begin{cases} a leq mu g \ a leq frac{L}{2h} g end{cases}$. (2)
Непосредственным вычислением несложно убедиться, что при $mu = 0,1$ существенным оказывается первое неравенство, а при $mu = 0,7$ – второе.
Ответ: а)$1 м/с^{2}$, б) $6 м/с^{2}$.
Екатерина Владимировна Мосина
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение тела, возникающее вследствие силы трения
Известно, что сила трения скольжения направлена в сторону, противоположную направлению относительной скорости движения трущихся тел.
Отсюда следует, что ускорение, которое такая сила сообщает движущемуся телу, тоже направлено против относительной скорости. А это значит, что действие силы трения приводит к уменьшению абсолютного значения скорости тела относительно того тела, по которому оно скользит.
Если на тело, которое скользит по неподвижной поверхности, никакие силы, кроме силы трения не действуют, то оно, в конце концов, останавливается. Рассмотри этот часто встречающийся случай.
Представим себе, что перед движущимся поездом неожиданно появилось некоторое препятствие и машинист отключил двигатель и включил тормоз. Начиная с это момента, на поезд действует только сила трения, так как сила тяжести скомпенсирована реакцией рельсов, а сила сопротивления воздуха мала. Через некоторое время $t$ поезд, пройдя расстояние $l$ – тормозной путь, остановится. Найдем время $t$, нужное для остановки, и расстояние $l$, которое поезд пройдет за это время.
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Под действием сила трения $overline{F}_{mp} $поезд будет двигаться с ускорением, равным:
Выберем координатную ось $x$ так, чтобы ее положительное направление совпадало с направлением скорости движения поезда.
Рисунок 1.
Так как сила трения $overline{F}_{mp} $направлена в противоположном направлении, ее проекция на ось х отрицательна. Отрицательна и проекция вектора ускорения на ось $x$. Поэтому если абсолютное значение силы трения равно $left|overline{F}_{mp} right|$, то:
Но ускорение определяется также формулой:
где $v_{0} $- скорость поезда до начала торможения.
Время торможения при движении тела под действием силы трения
Так как нас интересует промежуток времени $t$ от начала торможения до остановки поезда, то конечная скорость $v=0$. Тогда:
«Движение тела под действием силы трения» 👇
Таким образом:
Получим выражения для времени торможения:
Нахождение пути, пройденного телом под действием силы трения
А теперь найдем тормозной путь $l$. Для этого воспользуемся формулой:
Так как $v=0$, то:
Так как $overline{a}=-frac{left|overline{F}_{mp} right|}{m} $, получим:
Из этой формулы видно, что пройденный до остановки путь пропорционален квадрату скорости. Если увеличить скорость вдвое, то потребуется вчетверо больший путь для остановки.
Пример 1
С какой скоростью двигался автомобиль, если после выключения двигателя он прошел до остановки путь равный $80$ м? Коэффициент трения принять равным $0,25$.
Дано: $l=80$м, $mu =0,25$.
Найти: $v$-?
Решение:
Воспользуемся раннее выведенными формулами для нахождения тормозного пути:
$l=frac{mv_{0}^{2} }{2overline{left|F_{mp} right|}} $. (1)
Так как $F_{mp} =mu mg$, подставим в формулу (1) и получим:
$l=frac{mv_{0}^{2} }{2mu mg} $. (2)
Выразив из формулы (2) $v_{0} $найдем величину искомой скорости:
$v_{0} =sqrt{2mu gl} =20$м/с
Ответ: Скорость автомобиля до выключения двигателя $v_{0} =20$ м/с.
Пример 2
Сноубордист массой $80$ кг, имеющий в конце спуска скорость $20$ м/с, останавливается через $40$ с после окончания спуска. Определите силу трения и коэффициент трения.
Дано: $m=80$кг, $v_{0} =20$м/с, $t=40$с.
Найти: $F_{mp} $, $mu $-?
Решение:
Уравнение движения сноубордиста будет иметь вид:
[ma=F_{mp} .]
Используя выражения для нахождения ускорения (конечная скорость $v=0$), получим:
[a=-frac{v_{0} }{t} .]
Тогда:
$F_{mp} =ma=-mfrac{v_{0} }{t} =40H$.
Так как сила трения $overline{F}_{mp} $равна $F_{mp} =mu Bg$, находим коэффициент трения $mu $:
[mu =frac{F_{mp} }{mg} =0,05.]
Ответ: $F_{mp} =40H$, $mu =0,05$.
Пример 3
Сани массой $16$ кг перемещают по горизонтальной плоскости под действием силы $180 H$, направленной под углом $30^circ$ к горизонтали. Коэффициент терния саней о плоскость $0,5$. Определить ускорения, с которым движутся сани.
Дано: $m=16$кг, $F=180 H$, $alpha =30^circ$, $mu =0,5$.
Найти: $a$-?
Решение:
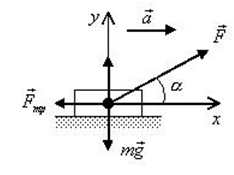
Рисунок 2.
Уравнение движения тела:
[moverline{a}=moverline{g}+overline{N}+overline{F}+overline{F}_{mp} .]
Выберем направление осей $x$ и $y$ и спроецируем на них силы и ускорение:
[begin{array}{l} {ma=Fcos alpha -F_{mp} } \ {0=-Bg+N+Fsin alpha } end{array}]
Поскольку $F_{mp} =mu N$, а из второго уравнения $N=mg-Fsin alpha $, то $F_{mp} =mu (mg-Fsin alpha )$. Тогда из первого уравнения ускорение:
$a=frac{1}{m} [Fcos alpha -mu (mg-Fsin alpha )]approx 7,6м/с^2$
Ответ: $a$=$7,6м/с^2$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Баканина Л.П. Силы трения // Квант. — 1973. — № 9. — С. 68-71.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Сила трения часто вызывает у поступающих в вуз серьезные затруднения, особенно сила трения покоя. Чему равна ее величина? Как она направлена? Попытаемся ответить на эти вопросы, разобрав несколько конкретных примеров. Задачи, рассмотренные в статье, в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт, и многие абитуриенты не смогли с ними справиться.
Прежде всего вспомним некоторые особенности сил сухого трения, возникающего между двумя твердыми телами. При непосредственном взаимодействии (соприкосновении) этих тел возникают силы, действующие на каждое из них. Согласно третьему закону Ньютона эти силы равны по величине и противоположны по направлению. Составляющие этих сил, направленные перпендикулярно соприкасающимся поверхностям, называют силами нормального давления. Составляющие, направленные вдоль поверхности, называют силами трения.
Пусть тело лежит на горизонтальном столе. Будем действовать на него горизонтальной силой, величина которой постепенно увеличивается. До тех пор, пока эта сила меньше определенной величины Fmax, тело будет сохранять состояние покоя потому, что на тело со стороны стола действует сила трения покоя, по величине равная приложенной силе. Направление силы трения противоположно возможному перемещению. Если бы не было трения, тело сразу начало бы скользить. Можно сказать, что тело «пытается» начать скользить, но трение удерживает его на месте. Если же величина воздействия больше Fmax, возникает скольжение. Сила трения скольжения, как известно, не зависит от величины сил, действующих на тело вдоль поверхности:
Fск = μ∙N.
Величина силы нормального давления N не зависит ни от величины касательных взаимодействий, ни от свойств трущихся поверхностей.
Опыт показывает, что обычно Fск несколько меньше Fmax. Однако отличие это невелико, и при решении почти всех задач считают, что Fск = Fmax. Это приближение стало настолько привычным, что его обычно даже и не оговаривают. Точно так же пренебрегают зависимостью силы трения от скорости. На рисунке 1 пунктиром изображена (несколько преувеличено) зависимость силы трения от скорости, наблюдаемая на опыте, а сплошной линией — обычное упрощенное представление этой зависимости.
Рис. 1.
Перейдем теперь к разбору конкретных задач, при решении которых особенности сил трения играют существенную роль.
Задача 1. Поезд, подходя к станции со скоростью υ = 72 км/ч, начинает равномерно тормозить. Каково наименьшее время торможения поезда до полной остановки, безопасное для спящих пассажиров? Коэффициент трения пассажира о полку μ = 0,2.
При торможении поезда скорость движения полки, на которой лежит пассажир, уменьшается, и если бы пассажир сохранил прежнюю скорость, он начал бы скользить по полке вперед, по ходу движения поезда. Однако, как только он начинает или, вернее, как только он «пытается» начать скользить, возникает сила трения. Она сообщает пассажиру тормозящее ускорение. Если это ускорение равно ускорению поезда, скорость пассажира все время равна скорости полки, на которой он лежит, и пассажир не скользит по полке. Максимальное возможное ускорение может сообщить максимальная сила трения покоя, которая, как мы уже говорили, приближенно равна Fcк = μ·N. Согласно второму закону Ньютона
m·amax= μ·N,
где m — масса спящего пассажира, а N — сила его нормального давления на полку. Для горизонтальной полки N = m·g и amax = μ·g. Значит, ускорение поезда, при котором пассажиры не падают с полок, a ≤ μ·g.
Время торможения до полной остановки
Задача 2. Автомобиль, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности в 30° радиуса R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю μ = 0,3.
Единственная внешняя горизонтальная сила, действующая на автомобиль, — это сила трения. Разгон, как мы предполагаем, происходит без проскальзывания, следовательно, мы имеем дело с силой трения покоя. Только эта сила и может сообщить автомобилю необходимое ускорение.
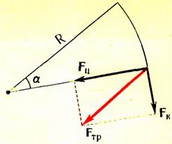
Рис. 2.
Так как движение автомобиля по окружности — это движение с ускорением, сила трения должна быть направлена под углом к скорости (рис.2). При этом составляющая Fk, направленная вдоль скорости, сообщает автомобилю необходимое для разгона ускорение, а составляющая Fn, направленная по радиусу окружности, изменяет направление скорости так, чтобы автомобиль двигался по окружности. Центростремительное ускорение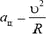 
, следовательно, 
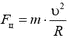. Скорость максимальна в конце разгона, значит, тогда же максимальна и Fц. Так как по условию задачи автомобиль набирает скорость равномерно, сила Fк постоянна.
Как известно, пройденный путь, ускорение и скорость в конце пути связаны соотношением 2aц∙s = υ2. Отсюда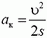 
, а сила 
.
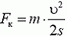Геометрическая сумма сил Fк и Fц не должна превышать максимальной силы трения покоя Fтр = μ∙m∙g. Так как эти силы перпендикулярны друг другу, то в конце разгона
Отсюда
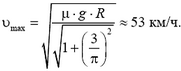
Задача 3. Небольшой кубик массы m покоится на шероховатой плоскости, наклоненной к горизонту под углом α. Коэффициент трения μ = 2·tg α. Определить, с какой минимальной горизонтальной силой F, лежащей в плоскости склона (рис. 3), нужно толкать, кубик, чтобы он начал двигаться.
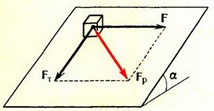
Рис. 3.
При μ > tg α под действием только силы тяжести кубик не будет скользить по наклонной плоскости, так как направленная вдоль наклонной плоскости проекция силы тяжести Fт = m∙g∙sin α меньше максимальной силы трения покоя Fтр = μ∙m∙g∙cos α. Если приложить горизонтальную силу F, то результирующая сила, действующая вдоль наклонной плоскости, будет равна (см. рис. 3).
Если Fp ≥ Fтр, кубик начнет скользить, так как сила трения покоя уже не может его уравновесить. Минимальное значение необходимой для этого силы F можно найти из условия
F2 + (m∙g∙sin α)2 = (μ∙m∙g∙cos α)2.
Отсюда
Задача 4. Хоккейная шайба падает на лед под углом α к вертикали со скоростью υ0. С какой скоростью шайба начнет скользить по льду, если после удара о лед она не подпрыгивает? Коэффициент трения шайбы о лед равен μ.
Изменение количества движения, согласно второму закону Ньютона, равно импульсу действующей силы. По условию задачи вертикальная составляющая вектора количества движения за время удара обращается в нуль. Значит, импульс силы нормального давления на поверхность N·Δt равен
N·Δt = m·υ0·cos α,
где Δt — время удара, а N — средняя сила давления шайбы на лед во время удара.
Так как по условию задачи шайба после удара скользит, сила трения во время удара — это сила трения скольжения Fск = μ·N. Время соударения Δt очень мало, а m·Δυверт — конечная величина, поэтому сила нормального давления при ударе гораздо больше веса шайбы. Среднее значение силы трения во время удара
Импульс силы трения за время удара
Fтр·Δt = μ·N·Δt = μ·m·υ0·cos α.
Изменение горизонтальной составляющей количества движения шайбы за время удара равно
m·υ – m·υ0·sin α = –μ·m·υ0·cos α,
откуда υ = υ0·sin α – μ·υ0·cos α.
Если коэффициент трения μ очень мал, изменение горизонтальной составляющей количества движения шайбы тоже мало, и приближенно можно считать, что для горизонтальной проекции выполняется закон сохранения количества движения.
Следует отметить, что приведенное решение справедливо только тогда, когда μ ≤ tg α. Попробуйте разобраться самостоятельно, что будет происходить в случае, если μ > tg α.
Упражнения
1. Тело опускают без начальной скорости на ленту транспортера, движущуюся со скоростью υ = 3,6 км/ч. Коэффициент трения между телом и лентой μ = 1. Какой путь пройдет тело по ленте?
2. Изучая дорожное происшествие, автоинспектор установил, что след торможения автомобиля, ехавшего по асфальтовой дороге, равен 60 м. С какой скоростью ехал автомобиль, если коэффициент трения колес об асфальт при торможении равен 0,5?
3. Маховик радиуса R = 0,2 м насажен на закрепленную горизонтальную ось радиуса r = 0,02 м. Сила трения между маховиком и осью Fск = 103 Н. Для того чтобы легче было снять маховик с оси, к его ободу прикладывается сила F = 80 Н, создающая вращающий момент относительно оси (рис. 4). С какой минимальной силой N нужно тянуть маховик вдоль оси, чтобы снять его?
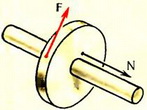
Рис. 4.
4. Две дороги, АВ и CD, направленные под углом 120° друг к другу, выходят на круглую асфальтированную площадь радиуса r = 68 м (рис. 5). С какой максимальной постоянной скоростью может ехать по площади автомобиль, чтобы попасть с одной дороги на другую, если коэффициент трения между асфальтом и шинами автомобиля μ = 0,4?
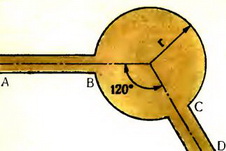
Рис. 5.
Ответы
1. 
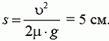
2. υ = 87 км/ч.
3. N = 600 Н.
4. 
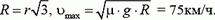
1. Тела в начальном состоянии движутся друг относительно друга
Пусть на гладком столе лежит доска длиной L и массой mд. На краю доски находится небольшой брусок массой mб (рис. 24.1). Коэффициент трения между бруском и доской μ. В начальный момент доска покоится, а бруску толчком сообщают начальную скорость 
0, направленную вдоль доски.
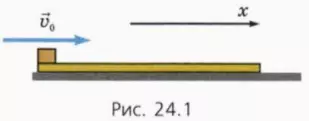
Как будут двигаться тела?
При скольжении бруска по доске на него и на доску действуют противоположно направленные равные по модулю силы трения скольжения 
тр1 и тр2 (рис. 24.2). В результате скорость бруска будет уменьшаться, а скорость доски – увеличиваться.
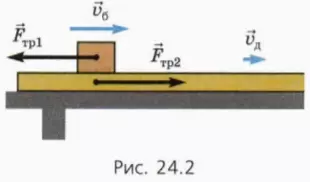
Возможны два варианта дальнейшего развития событий:
1) брусок будет скользить по доске, пока их скорости не станут равными, то есть пока брусок не остановится относительно доски. Начиная с этого момента силы трения перестанут действовать на доску и брусок, и они будут скользить по гладкому столу вместе как единое целое с постоянной конечной скоростью к (рис. 24.3);
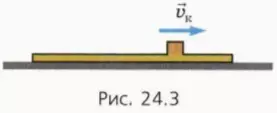
2) скорости бруска и доски не успеют сравняться до того момента, когда брусок дойдёт до противоположного конца доски. В таком случае брусок соскользнёт с доски, после чего они будут двигаться по столу с различными скоростями б и д, причём vб > vд (рис. 24.4).
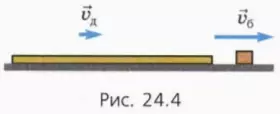
Рассмотрим сначала случай, когда доска с бруском будут двигаться как единое целое (см. рис. 24.3), и выведем условие, при котором этот случай реализуется.
? 1. Как зависят от времени проекции скорости бруска и доски на ось x, показанную на рисунке 24.1?
? 2. Через какой промежуток времени доска и брусок будут двигаться как единое целое?
? 3. Чему будет равна скорость доски с бруском, когда они будут двигаться как единое целое?
Найдём теперь условие того, что брусок будет скользить по доске до тех пор, пока их скорости не сравняются.
Так произойдёт, если путь l, пройденный бруском относительно доски, не превышает длины доски L. Путь l мы найдём, определив ускорение бруска относительно доски.
? 4. Чему равно ускорение бруска относительно доски?
? 5. Чему равен путь l, пройденный бруском относительно доски до того момента. когда их скорости сравнялись?
? 6. При выполнении какого условия доска и брусок будут двигаться как единое целое?
Рассмотрим конкретный пример.
? 7. Небольшой брусок массой 200 г находится на краю доски массой 1 кг, лежащей на гладком столе. Коэффициент трения между доской и бруском 0,5. В начальный момент скорость бруска 2,4 м/с, а доска покоится. Через некоторое время брусок и доска стали двигаться как единое целое.
а) С каким ускорением относительно доски двигался брусок?
б) Сколько времени брусок двигался по доске?
в) Какова минимально возможная длина доски?
г) Чему равна скорость доски с бруском, когда они движутся как единое целое?
Пусть теперь условие того, что доска и брусок станут двигаться как единое целое, не выполнено. Тогда брусок соскользнёт с доски, и скорость каждого тела при дальнейшем скольжении по столу останется такой, какой она была в момент соскальзывания бруска.
Чтобы найти конечные скорости бруска и доски, можно поступить, например, так.
1) Зная длину доски L, начальную скорость бруска v0 и ускорение бруска относительна доски, найдём время tск, в течение которого брусок будет скользить по доске.
2) Зная время tск, найдём скорости бруска и доски в момент соскальзывания бруска с доски. С этими скоростями они и будут скользить далее по столу.
Воспользуйтесь этими советами при выполнении следующего задания.
? 8. Небольшой брусок массой 400 г находится на краю доски длиной 1 м и массой 800 г, лежащей на гладком столе (рис. 24.1). Коэффициент трения между доской и бруском 0,2. В начальный момент скорость бруска 3 м/с, а доска покоится.
а) С каким по модулю ускорением движется брусок относительно доски?
б) Какой должна была бы быть длина доски, чтобы скорость бруска относительно доски стала равной нулю?
в) Сколько времени брусок движется по доске согласно условию задания?
г) Чему равна скорость бруска относительно стола в тот момент, когда брусок соскользнёт с доски?
д) Какой путь пройдёт доска относительно стола до того момента, когда брусок соскользнёт с доски?
2. Тела в начальном состоянии покоятся друг относительно друга
На гладком столе лежат один на другом два бруска (рис. 24.5). Массу нижнего бруска обозначим mн‚ в массу верхнего — mв. Коэффициент трения между брусками μ.
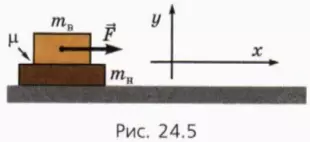
К верхнему бруску прикладывают горизонтально направленную вправо силу .
Самое главное в таких задачах — увидеть две возможности:
1) бруски могут начать двигаться друг относительно друга — тогда между ними будут действовать силы трения скольжения;
2) бруски могут начать двигаться как единое целое — тогда между ними будут действовать силы трения покоя.
Начнём с первой возможности: в таком случае модуль силы трения скольжения, действующей на каждое тело, равен μmвg. Модуль же силы трения покоя заранее неизвестен.
? 9. Объясните, почему в случае, когда верхний брусок скользит по нижнему, их ускорения относительно стола выражаются формулами
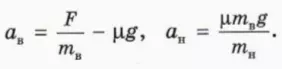
Учтём теперь, что сила приложена к верхнему бруску и что бруски вначале покоились. Если верхний брусок скользит по нижнему, то ускорение верхнего бруска больше, чем ускорение нижнего. Это позволяет получить условие того, что бруски движутся друг относительно друга.
? 10. Объясните, почему бруски будут двигаться друг относительно друга, если
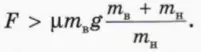
? 11.На столе стоит тележка массой 500 г, а на ней лежит кирпич массой 2,5 кг. Коэффициент трения между кирпичом и тележкой 0,5, трением между тележкой и столом можно пренебречь. С какой горизонтальной силой надо тянуть кирпич, чтобы стащить его с тележки?
Итак, чтобы стащить тяжёлый кирпич со сравнительно лёгкой тележки, надо приложить к нему горизонтальную силу, которая в несколько раз превышает вес кирпича!
? 12. Объясните, почему тела движутся как единое целое, если
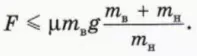
? 13. Объясните, почему, когда бруски движутся как единое целое, их (общее) ускорение а и модуль действующей на каждый брусок силы трения покоя Fтр.пок выражаются формулами
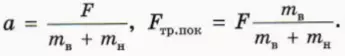
Рассмотрим теперь пример, когда горизонтальная сила приложена к нижнему бруску.
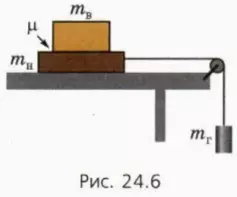
Пусть на гладком горизонтальном столе лежит брусок массой mн, а на нём — брусок массой mв (рис. 24.6). Коэффициент трения между брусками μ. К нижнему бруску привязана лёгкая нерастяжимая нить, переброшеивая через блок, а к нити подвешен груз массой mг. Как будут двигаться тела?
В этой ситуации тоже есть две возможности:
1) бруски могут начать двигаться друг относительно друга;
2) бруски могут начать двигаться как единое целое.
На этот раз проще начать со второй возможности, потому что, когда бруски движутся как единое целое, мы можем рассматривать систему, состоящую только из двух тел — объединённого бруска массой M = mв + mн и груза массой mг.
? 14. С каким ускорением движутся бруски как единое целое?
? 15. С каким максимально возможным ускорением могут двигаться бруски как единое целое?
Подсказка. Ускорение верхнему бруску сообщает сила трения покоя, которая не превышает силу трения скольжения.
? 16. Объясните, почему бруски движутся как единое целое, если выполнено соотношение
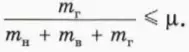
Если это соотношение не выполнено. то бруски будут двигаться порознь. Ускорение верхнему бруску сообщает в таком случае сила трения скольжения, равная по модулю μmвg. Такая же по модулю, но противоположно направленная сила трения скольжения действует на нижний брусок.
? 17. Каковы ускорения брусков, если они движутся друг относительно друга?
? 18. На гладком горизонтальном столе лежит брусок массой mн = 0,5 кг, а на нём — другой брусок массой mв = 0,3 кг (см. рис. 24.6). К нижнему бруску привязана лёгкая нерастяжимая нить, переброшенная через блок, и к нити подвешен груз массой mг = 0,2 кг. В начальный момент бруски покоятся.
а) При каком наименьшем коэффициенте трения μmin между брусками они будут двигаться как единое целое?
б) С каким ускорением (ускорениями) движутся бруски при коэффициенте трения между ними 0,5?
в) С каким ускорением (ускорениями) движутся бруски, если коэффициент трения между ними равен 0,1?
Дополнительные вопросы и задания
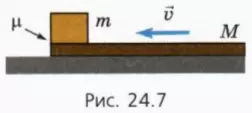
19. На гладком столе лежит доска длиной l и массой M. На одном конце доски находится небольшой брусок массой m (рис. 24.7). Коэффициент трения между бруском и доской μ. В начальный момент тела покоятся. Какую наименьшую скорость надо толчком сообщить доске, чтобы она выскользнула из-под бруска?
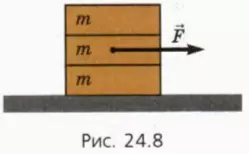
20. На гладком столе лежат один на другом три одинаковых бруска массой m = 100 г каждый (рис. 24.8). Коэффициент трения между брусками μ = 0,2. К среднему бруску приложена горизонтально направленная сила .
а) С каким максимально возможным ускорением может двигаться верхний брусок?
б) С каким максимально возможным ускорением может двигаться нижний брусок?
в) При каких значениях силы F все бруски будут двигаться как единое целое?
