Как найти максимальное значение функции двух переменных

Экстремум функции двух переменных

Назначение сервиса. Онлайн-калькулятор используется для нахождения в онлайн режиме наибольшего и наименьшего значения функции двух переменных (см. пример). Решение оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Оформление Word

Для функции трех переменных можно использовать матрицу Гессе.

Алгоритм исследования функции двух переменных на экстремум

Функция z = f(x,y) имеет максимум в точке M₀(x₀;y₀), если f(x₀;y₀) > f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Функция z = f(x,y) имеет минимум в точке M₀(x₀;y₀), если f(x₀;y₀) < f(x;y) для всех точек (x;y), достаточно близких к точке (x₀;y₀) и отличных от неё. Максимум и минимум функции называются экстремумами функции.

Исследование функции двух переменных на экстремум проводят по следующей схеме.

1. Находят частные производные dz/dx и dz/dy.

2. Решают систему уравнений:

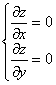
и таким образом находят критические точки функции.

3. Находят частные производные второго порядка:

4. Вычисляют значения этих частных производных второго порядка в каждой из найденных в п.2 критических точках M(x₀;y₀).

5. Делаю вывод о наличии экстремумов:

а) если AC – B² > 0 и A < 0 , то в точке M имеется максимум;

б) если AC – B² > 0 и A > 0 , то в точке M имеется минимум;

в) если AC – B² < 0, то экстремума нет;

г) если AC – B² = 0, то вопрос о наличии экстремума остается открытым;

Пример №1. Найти экстремумы функции f(x,y)=x³+xy²+x²+y² и определить по критерию Сильвестра их тип.

Решение.

1. Найдем первые частные производные.





2. Решим систему уравнений.

3x²+2x+y²=0

2xy+2y=0

Получим:

а) Из первого уравнения выражаем x и подставляем во второе уравнение:

x = -1

y²+1=0

Данная система уравнений не имеет решения.

б) Из первого уравнения выражаем y и подставляем во второе уравнение:





или





или

Откуда x₁ = -2/3; x₂ = 0; x₃ = -2/3; x₄ = 0

Данные значения x подставляем в выражение для y. Получаем: y₁ = 0; y₂ = 0; y₃ = 0; y₄ = 0

Количество критических точек равно 2: M₁(-2/3;0), M₂(0;0)

3. Найдем частные производные второго порядка.







4. Вычислим значение этих частных производных второго порядка в критических точках M(x₀;y₀).

Вычисляем значения для точки M₁(-2/3;0)







AC – B² = -4/3 < 0, то глобального экстремума нет.

Вычисляем значения для точки M₂(0;0)







AC – B² = 4 > 0 и A > 0 , то в точке M₂(0;0) имеется минимум z(0;0) = 0

Вывод: В точке M₂(0;0) имеется минимум z(0;0) = 0

Пример №2. Исследовать функцию на экстремум классическим методом: Z=8x2+2xy-5x+6.

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Наибольшее и наименьшее значения функции двух переменных в замкнутой области.

Пусть функция $z=f(x,y)$ определена и непрерывна в некоторой ограниченной замкнутой области $D$. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.

Алгоритм поиска наибольшего и наименьшего значений функции $z=f(x,y)$ в замкнутой области $D$.

1. Найти критические точки функции $z=f(x,y)$, принадлежащие области $D$. Вычислить значения функции в критических точках.
2. Исследовать поведение функции $z=f(x,y)$ на границе области $D$, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
3. Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.

Что такое критические точки? показатьскрыть

Пример №1

Найти наибольшее и наименьшее значения функции $z=x^2+2xy-y^2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.

Решение

Будем следовать указанному выше алгоритму, но для начала разберёмся с чертежом заданной области, которую обозначим буквой $D$. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая $x=3$ проходит через точку $(3;0)$ параллельно оси ординат (оси Oy). Прямая $y=0$ – это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой $y=x+1$ найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо $x$ парочку произвольных значений. Например, подставляя $x=10$, получим: $y=x+1=10+1=11$. Мы нашли точку $(10;11)$, лежащую на прямой $y=x+1$. Однако лучше отыщем те точки, в которых прямая $y=x+1$ пересекается с линиями $x=3$ и $y=0$. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой $y=x+1$ и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая $y=x+1$ пересекает прямую $x=3$ в точке $(3;4)$, а прямую $y=0$ – в точке $(-1;0)$. Дабы не загромождать ход решения вспомогательными пояснениями, то вопрос о получении этих двух точек вынесу в примечание.

Как были получены точки $(3;4)$ и $(-1;0)$? показатьскрыть

Всё готово для построения чертежа, который будет иметь такой вид:

Вот теперь перейдём к первому шагу алгоритма. Найдём частные производные первого порядка:

$$
frac{partial z}{partial x}=2x+2y-4; frac{partial z}{partial y}=2x-2y.
$$

Заметьте, что найденные производные первого порядка существуют для всех значений $x$ и $y$. Т.е. нету точек, в которых хотя бы одна производная не существует. Попробуем отыскать точки, в которых обе частные производные равны нулю (стационарные точки):

$$
left { begin{aligned}
& 2x+2y-4=0;\
& 2x-2y=0.
end{aligned} right.

;; left { begin{aligned}
& x+y=2;\
& x-y=0.
end{aligned} right.
$$

Мы получили систему линейных алгебраических уравнений. Для решения таких систем можно применить, например, метод Крамера. Однако в данном случае можно поступить попроще. Из второго уравнения имеем: $y=x$. Подставляя $y=x$ в первое уравнение, получим: $x+x=2$, $2x=2$, $x=1$. Так как $x=1$, то $y=x=1$. Итак, $(1;1)$ – единственная стационарная точка функции $z$.

Однако недостаточно просто найти стационарные точки. Нужно выбрать те из них, которые принадлежат области $D$. В нашем случае точка $(1;1)$ принадлежит этой области. Обозначим эту точку как $M_1(1;1)$. Вычислим значение функции в этой точке:

$$z_1=z(M_1)=1^2+2cdot 1cdot 1-1^2-4cdot 1=-2.$$

А почему точка $(1;1)$ принадлежит области $D$? показатьскрыть

Теперь настал черёд исследовать поведение функции на границе области, т.е. переходим ко второму шагу алгоритма. Начнём с прямой $y=0$.

Прямая $y=0$ (ось абсцисс) ограничивает область $D$ при условии $-1 ≤ x ≤ 3$. Подставим $y=0$ в заданную функцию $z(x,y)=x^2+2xy-y^2-4x$. Полученную в результате подстановки функцию одной переменной $x$ обозначим как $f_1(x)$:

$$
f_1(x)=z(x,0)=x^2+2xcdot 0-0^2-4x=x^2-4x.
$$

Теперь для функции $f_1(x)$ нужно найти наибольшее и наименьшее значения на отрезке $-1 ≤ x ≤ 3$. Отыщем производную этой функции и приравняем её к нулю:

$$
f_{1}^{‘}(x)=2x-4;\
2x-4=0; ; x=2.
$$

Значение $x=2$ принадлежит отрезку $-1 ≤ x ≤ 3$, поэтому к списку точек добавим ещё и $M_2(2;0)$. Кроме того, вычислим значения функции $z$ на концах отрезка $-1 ≤ x ≤ 3$, т.е. в точках $M_3(-1;0)$ и $M_4(3;0)$. Кстати, если бы точка $M_2$ не принадлежала рассматриваемому отрезку, то, разумеется, значение функции $z$ в ней вычислять не было бы надобности.

Итак, вычислим значения функции $z$ в точках $M_2$, $M_3$, $M_4$. Можно, конечно, подставлять координаты данных точек в исходное выражение $z=x^2+2xy-y^2-4x$. Например, для точки $M_2$ получим:

$$z_2=z(M_2)=2^2+2cdot 2cdot 0-0^2-4cdot 2=-4.$$

Однако вычисления можно немного упростить. Для этого стоит вспомнить, что на отрезке $M_3M_4$ имеем $z(x,y)=f_1(x)$. Распишу это подробно:

begin{aligned}
& z_2=z(M_2)=z(2,0)=f_1(2)=2^2-4cdot 2=-4;\
& z_3=z(M_3)=z(-1,0)=f_1(-1)=(-1)^2-4cdot (-1)=5;\
& z_4=z(M_4)=z(3,0)=f_1(3)=3^2-4cdot 3=-3.
end{aligned}

Разумеется, что в столь подробных записях обычно нет нужды, и все вычисления в дальнейшем станем записывать покороче:

$$z_2=f_1(2)=2^2-4cdot 2=-4;; z_3=f_1(-1)=(-1)^2-4cdot (-1)=5;; z_4=f_1(3)=3^2-4cdot 3=-3.$$

Теперь обратимся к прямой $x=3$. Эта прямая ограничивает область $D$ при условии $0 ≤ y ≤ 4$. Подставим $x=3$ в заданную функцию $z$. В результате такой подстановки мы получим функцию $f_2(y)$:

$$
f_2(y)=z(3,y)=3^2+2cdot 3cdot y-y^2-4cdot 3=-y^2+6y-3.
$$

Для функции $f_2(y)$ нужно найти наибольшее и наименьшее значения на отрезке $0 ≤ y ≤ 4$. Отыщем производную этой функции и приравняем её к нулю:

$$
f_{2}^{‘}(y)=-2y+6;\
-2y+6=0; ; y=3.
$$

Значение $y=3$ принадлежит отрезку $0 ≤ y ≤ 4$, поэтому к найденным ранее точкам добавим ещё и $M_5(3;3)$. Кроме того, нужно вычислить значение функции $z$ в точках на концах отрезка $0 ≤ y ≤ 4$, т.е. в точках $M_4(3;0)$ и $M_6(3;4)$. В точке $M_4(3;0)$ мы уже вычисляли значение $z$. Вычислим значение функции $z$ в точках $M_5$ и $M_6$. Напомню, что на отрезке $M_4M_6$ имеем $z(x,y)=f_2(y)$, поэтому:

begin{aligned}
& z_5=f_2(3)=-3^2+6cdot 3-3=6;
& z_6=f_2(4)=-4^2+6cdot 4-3=5.
end{aligned}

И, наконец, рассмотрим последнюю границу области $D$, т.е. прямую $y=x+1$. Эта прямая ограничивает область $D$ при условии $-1 ≤ x ≤ 3$. Подставляя $y=x+1$ в функцию $z$, будем иметь:

$$
f_3(x)=z(x,x+1)=x^2+2xcdot (x+1)-(x+1)^2-4x=2x^2-4x-1.
$$

Вновь мы получили функцию одной переменной $x$. И вновь нужно найти наибольшее и наименьшее значения этой функции на отрезке $-1 ≤ x ≤ 3$. Отыщем производную функции $f_{3}(x)$ и приравняем её к нулю:

$$
f_{3}^{‘}(x)=4x-4;\
4x-4=0; ; x=1.
$$

Значение $x=1$ принадлежит отрезку $-1 ≤ x ≤ 3$. Если $x=1$, то $y=x+1=2$. Добавим к списку точек ещё и $M_7(1;2)$ и выясним, чему равно значение функции $z$ в этой точке. Точки на концах отрезка $-1 ≤ x ≤ 3$, т.е. точки $M_3(-1;0)$ и $M_6(3;4)$, были рассмотрены ранее, значение функции в них мы уже находили.

$$z_7=f_3(1)=2cdot 1^2-4cdot 1-1=-3.$$

Второй шаг решения закончен. Мы получили семь значений:

$$z_1=-2;;z_2=-4;;z_3=5;;z_4=-3;;z_5=6;;z_6=5;;z_7=-3.$$

Обратимся к третьему шагу алгоритма. Выбирая наибольшее и наименьшее значения из тех чисел, что были получены в третьем пункте, будем иметь:

$$z_{min}=-4; ; z_{max}=6.$$

Задача решена, осталось лишь записать ответ.

Ответ: $z_{min}=-4; ; z_{max}=6$.

Пример №2

Найти наибольшее и наименьшее значения функции $z=x^2+y^2-12x+16y$ в области $x^2+y^2 ≤ 25$.

Решение

Сначала построим чертёж. Уравнение $x^2+y^2=25$ (это граничная линия заданной области) определяет окружность с центром в начале координат (т.е. в точке $(0;0)$) и радиусом 5. Неравенству $x^2+y^2 ≤ 25$ удовлетворяют все точки внутри и на упомянутой окружности.

Будем действовать по алгоритму. Найдем частные производные и выясним критические точки.

$$
frac{partial z}{partial x}=2x-12; frac{partial z}{partial y}=2y+16.
$$

Точек, в которых найденные частные производные не существуют, нет. Выясним, в каких точках обе частные производные одновременно равны нулю, т.е. найдём стационарные точки.

$$
left { begin{aligned}
& 2x-12=0;\
& 2y+16=0.
end{aligned} right. ;;
left { begin{aligned}
& x=6;\
& y=-8.
end{aligned} right.
$$

Мы получили стационарную точку $(6;-8)$. Однако найденная точка не принадлежит области $D$. Это легко показать, даже не прибегая к помощи рисунка. Проверим, выполняется ли неравенство $x^2+y^2 ≤ 25$, которое определяет нашу область $D$. Если $x=6$, $y=-8$, то $x^2+y^2=36+64=100$, т.е. неравенство $x^2+y^2 ≤ 25$ не выполнено. Вывод: точка $(6;-8)$ не принадлежит области $D$.

Итак, внутри области $D$ нет критических точек. Переходим дальше, ко второму шагу алгоритма. Нам нужно исследовать поведение функции на границе заданной области, т.е. на окружности $x^2+y^2=25$. Можно, конечно, выразить $y$ через $x$, а потом подставить полученное выражение в нашу функцию $z$. Из уравнения окружности получим: $y=sqrt{25-x^2}$ или $y=-sqrt{25-x^2}$. Подставляя, например, $y=sqrt{25-x^2}$ в заданную функцию, будем иметь:

$$
z=x^2+y^2-12x+16y=x^2+25-x^2-12x+16sqrt{25-x^2}=25-12x+16sqrt{25-x^2}; ;; -5≤ x ≤ 5.
$$

Дальнейшее решение будет полностью идентично исследованию поведения функции на границе области в предыдущем примере №1. Однако мне кажется более разумным в этой ситуации применить метод Лагранжа. Нас будет интересовать лишь первая часть этого метода. После применения первой части метода Лагранжа мы получим точки, в которых и исследуем функцию $z$ на предмет минимального и максимального значений.

Составляем функцию Лагранжа:

$$
F=z(x,y)+lambdacdot(x^2+y^2-25)=x^2+y^2-12x+16y+lambdacdot (x^2+y^2-25).
$$

Находим частные производные функции Лагранжа и составляем соответствующую систему уравнений:

$$
F_{x}^{‘}=2x-12+2lambda x; ;; F_{y}^{‘}=2y+16+2lambda y.\
left { begin{aligned}
& 2x-12+2lambda x=0;\
& 2y+16+2lambda y=0;\
& x^2+y^2-25=0.
end{aligned} right.
;; left { begin{aligned}
& x+lambda x=6;\
& y+lambda y=-8;\
& x^2+y^2=25.
end{aligned} right.
$$

Для решения этой системы давайте сразу укажем, что $lambdaneq -1$. Почему $lambdaneq -1$? Попробуем подставить $lambda=-1$ в первое уравнение:

$$
x+(-1)cdot x=6; ; x-x=6; ; 0=6.
$$

Полученное противоречие $0=6$ говорит о том, что значение $lambda=-1$ недопустимо. Вывод: $lambdaneq -1$. Выразим $x$ и $y$ через $lambda$:

begin{aligned}
& x+lambda x=6;; x(1+lambda)=6;; x=frac{6}{1+lambda}. \
& y+lambda y=-8;; y(1+lambda)=-8;; y=frac{-8}{1+lambda}.
end{aligned}

Полагаю, что тут становится очевидным, зачем мы специально оговаривали условие $lambdaneq -1$. Это было сделано, чтобы без помех поместить выражение $1+lambda$ в знаменатели. Т.е., чтобы быть уверенным, что знаменатель $1+lambdaneq 0$.

Подставим полученные выражения для $x$ и $y$ в третье уравнение системы, т.е. в $x^2+y^2=25$:

$$
left(frac{6}{1+lambda} right)^2+left(frac{-8}{1+lambda} right)^2=25;\
frac{36}{(1+lambda)^2}+frac{64}{(1+lambda)^2}=25;\
frac{100}{(1+lambda)^2}=25; ; (1+lambda)^2=4.
$$

Из полученного равенства следует, что $1+lambda=2$ или $1+lambda=-2$. Отсюда имеем два значения параметра $lambda$, а именно: $lambda_1=1$, $lambda_2=-3$. Соответственно, получим и две пары значений $x$ и $y$:

begin{aligned}
& x_1=frac{6}{1+lambda_1}=frac{6}{2}=3; ; y_1=frac{-8}{1+lambda_1}=frac{-8}{2}=-4. \
& x_2=frac{6}{1+lambda_2}=frac{6}{-2}=-3; ; y_2=frac{-8}{1+lambda_2}=frac{-8}{-2}=4.
end{aligned}

Итак, мы получили две точки возможного условного экстремума, т.е. $M_1(3;-4)$ и $M_2(-3;4)$. Найдём значения функции $z$ в точках $M_1$ и $M_2$:

begin{aligned}
& z_1=z(M_1)=3^2+(-4)^2-12cdot 3+16cdot (-4)=-75; \
& z_2=z(M_2)=(-3)^2+4^2-12cdot(-3)+16cdot 4=125.
end{aligned}

На третьем шаге алгоритма следует выбрать наибольшее и наименьшее значения из тех, что мы получили на первом и втором шагах. Но в данном случае выбор невелик 🙂 Имеем:

$$
z_{min}=-75; ; z_{max}=125.
$$

Ответ: $z_{min}=-75; ; z_{max}=125$.

Наибольшее и наименьшее значения функции двух переменных

При нахождении
наибольшего и наименьшего значений
функции нескольких переменных, непрерывной
на некотором замкнутом множестве,
следует помнить, что эти значения
достигаются в точках экстремума или на
границе множества.

Пример
3. Найти
наибольшее и наименьшее значения функции

в области
.

Решение.
Изобразим данную область на координатной
плоскости:

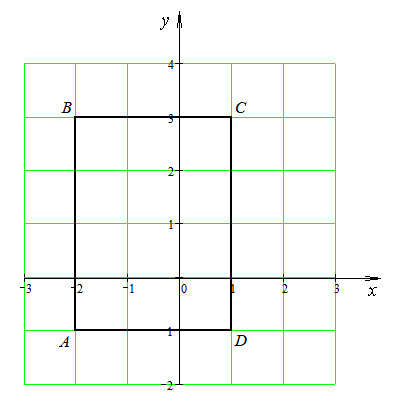
1) Находим критические
точки функции:

–
критическая точка.

значение
функции z
в этой точке вычислять не нужно.

2) Находим значения
функции на границах области:

х
= -2:
–
получили функцию одной переменной.
Находим её производную, приравниваем
её к нулю, чтобы найти критические точки:

.
Находим значение функции z
в точке
.

х
= 1:

.
Находим значение функции z
в точке
.

y
= -1:

точка

значение функции z
в этой точке вычислять не нужно.

y
= 3:

точка

значение функции z
в этой точке вычислять не нужно.

3)
Находим значения функции в угловых
точках:

.

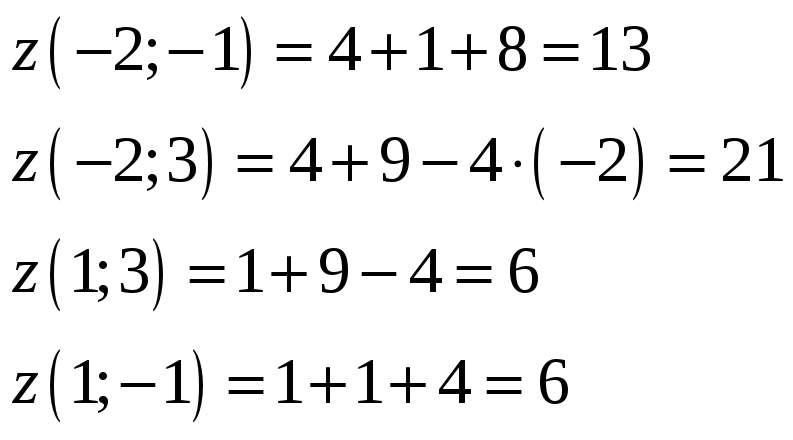
Из найденных
значений 12, -3, 13, 21, 6, выбираем наибольшее
и наименьшее.

Ответ:
М
= 21, m
= -3.

Условный экстремум

Пусть
рассматривается функция
,
аргументы которой удовлетворяют условию
,
называемому уравнением
связи.

Точка

называется точкой условного
максимума
(минимума),
если существует такая окрестность этой
точки, что для всех точек

из этой окрестности, удовлетворяющих
условию
,
выполняется неравенство:

.

Если
выразить у
через х
из уравнения связи

и подставить в функцию
,
то полученная функция

будет являться функцией одной переменной,
для которой можно найти её экстремумы,
они будут являться условными экстремумами
функции
.

Пример
4. Найти точки
максимума и минимума функции

при условии
.

Решение.
Выразим из уравнения связи переменную
у:
.

Находим
экстремумы:

–
точка условного минимума.

В данном примере
уравнение связи являлось линейным,
поэтому его легко можно решить относительно
одной из переменных. Для случаев, когда
уравнение связи имеет более сложный
вид, применяется метод множителей
Лагранжа.

Метод множителей Лагранжа

Рассмотрим
функцию трёх переменных
.
Эта функция называется функцией
Лагранжа, λ
– множителем
Лагранжа.

Теорема.
Если точка

является точкой условного экстремума
функции

при условии
,
то существует значение

такое, что точка

является точкой экстремума функции
.

Таким
образом, для нахождения условного
экстремума функции

при условии

требуется найти решение системы уравнений

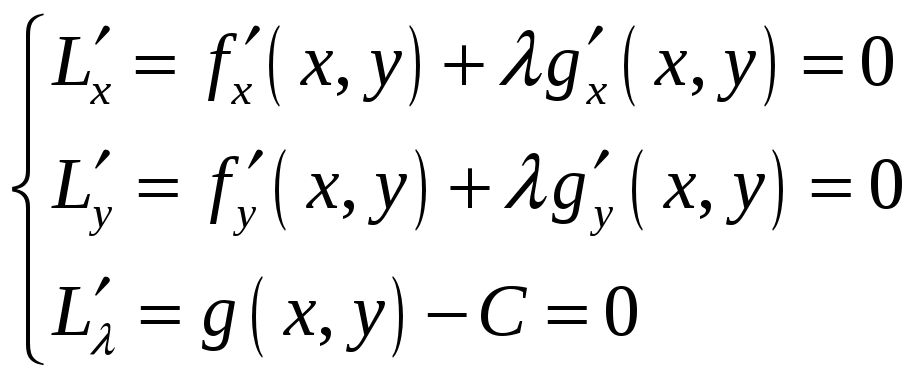
Далее,
для каждой из точек

находят определитель
.

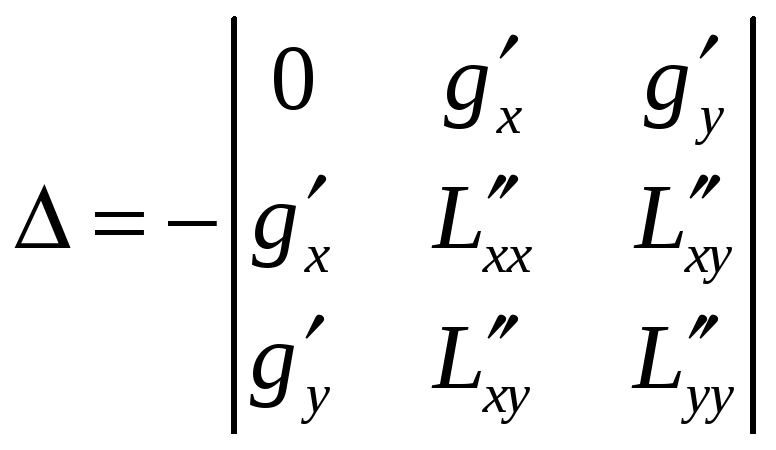Если
,
то точка
является
точкой условного
минимума,
если

– условного
максимума.

Геометрический
смысл условий Лагранжа:
.
В точке условного экстремума градиенты
функций

и

коллинеарны.

Пример
5. Найти
условные экстремумы функции

при
.

Решение.
Запишем функцию Лагранжа:
.

Находим частые
производные функции Лагранжа и решаем
систему уравнений:

.

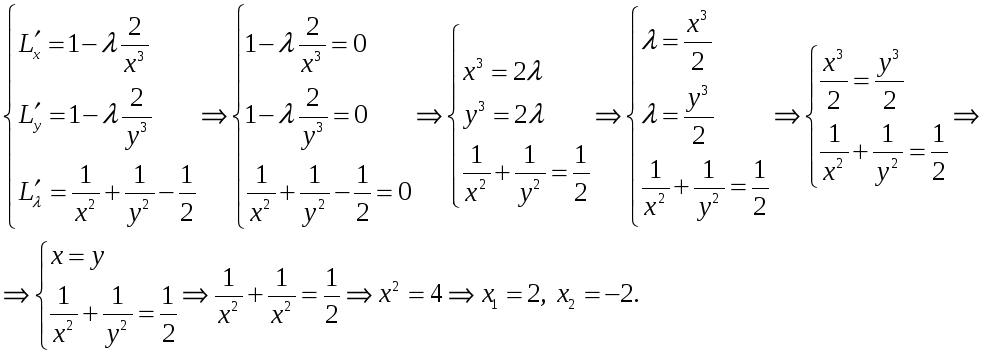
Получили
две точки

и
.
Для каждой из них найдём определитель
Δ.

.

Для
точки
:

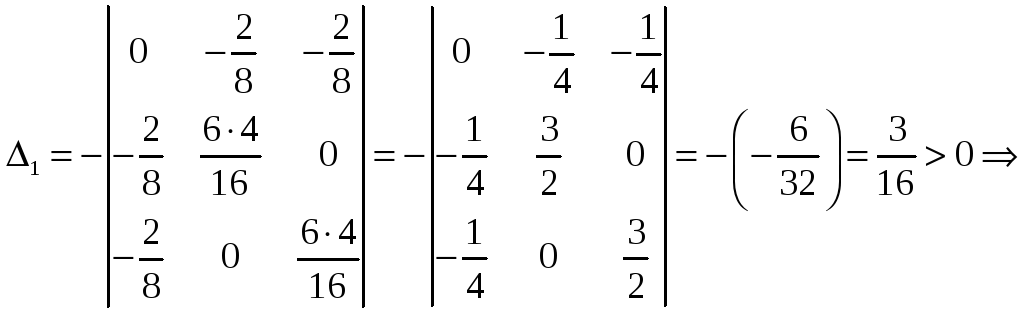в
точке
–

условный
минимум;
.

Для
точки
:

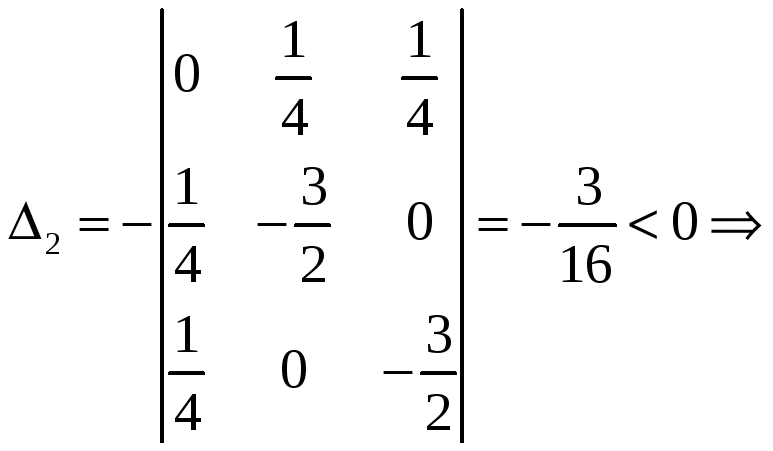в
точке
–
условный максимум;
.

Задания для
самостоятельного решения

Исследовать на
экстремум функции:

1.
2.
3.

4.

5.
6.

7.
8.

9.

10.

11.
12.

Исследовать
функции на условный экстремум:

13.
14.

15.

16.
17.
18.

19.
20.
21.

22.

23.
24.

25.
26.

27.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Экстремум функции двух переменных

Как найти?

Постановка задачи

Найти экстремум функции двух переменных $ z = z(x,y) $

План решения

Экстремумы функции двух переменных возможны в стационарных точках функции. Стационарными точками называются точки $ M(x_1,y_1), M(x_2,y_2)… $, в которых первые частные производные функции равны нулю: $ z(x,y) = 0 $

Для нахождения стационарных точек (подозрительных на экстремум) составляем систему:

$$ begin{cases} z’_x = 0 \ z’_y = 0 end{cases} $$

Решая систему получаем точки $ M(x_1,y_1), M(x_2,y_2)… $, каждую из которых нужно проверить на экстремум.

Проверку осуществляется с помощью подстановки точек в выражение, называемое достаточным условием существования экстремума:

$$ A = z”_{xx} cdot z”_{yy} – (z”_{xy})^2 $$

Если в точке $ M(x_1,y_1) $:

1. $ A>0 $ и $ z”_{xx} > 0 $, то $ M(x_1,y_1) $ точка минимума
2. $ A >0 $ и $ z”_{xx} < 0 $, то $ M(x_1,y_1) $ точка максимума
3. $ A < 0 $, то $ M(x_1,y_1) $ не является точкой экстремума
4. $ A = 0 $, то требуется дополнительное исследование (по определению)

Итак, необходимо выполнить действия:

1. Найти частные производные первого порядка. Приравнять их к нулю и решить систему уравнений. Получить точки $ M(x_1,y_1), M(x_2,y_2),… $
2. Найти частные производные второго порядка в точках $ M(x_1,y_1), M(x_2,y_2),… $
3. Используя достаточное условие существования экстремума делаем вывод о наличии экстремума в точках $ M(x_1,y_1), M(x_2,y_2),… $

Примеры решений

Пример 1

Найти экстремумы функции двух переменных $ z = x^2 -xy +y^2 $

Решение

Находим частные производные первого порядка: $$ z’_x = 2x – y $$ $$ z’_y = -x + 2y $$ Приравниваем полученные выражения к нулю и решаем систему двух уравнений: $$ begin{cases} 2x-y = 0 \ -x + 2y = 0 end{cases} $$ Решив систему получаем стационарную точку (подозрительные на экстремум): $$ M (0,0) $$ Далее вычисляем значения частных производных второго порядка в точке $ M $: $$ z”_{xx} Big |_M = 2 $$ $$ z”_{yy} Big |_M= 2 $$ $$ z”_{xy} Big |_M = -1 $$ Подставляя найденные значения в достаточное условие экстремума функции, проводим исследование знаков: $$ A = Big |_M = z”_{xx} Big |_M cdot z”_{yy} Big |_M – (z”_{xy} Big |_M)^2 = 2 cdot 2 – (-1)^2 = 3 $$ Так как получили $ A > 0 $ и $ z”_{xx} > 0 $, то получается $ M(0,0) $ точка минимума. Наименьшее значение находится в минимуме и равно: $$ z_{min} (0,0) = 0^2 – 0 cdot 0 + 0^2 = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

В точке $ M(0,0) $ находится минимум функции; $ z_{min} = 0 $

Пример 2

Найти экстремумы функции двух переменных $ z = x^3 + y^3 – 15xy $

Решение

Составляем систему уравнений из частных производных первого порядка: $$ begin{cases} z’_x = 3x^2 – 15y = 0 \ z’_y = 3y^2 – 15x =0 end{cases} $$ Получаем стационарные точки $ M_1(0,0) $ и $ M_2(5,5) $, которые необходимо проверить через достаточное условие экстремума. Вычисляем значение частных прозводных второго порядка в точке $ M_1 $: $$ z”_{xx} Big |_{M_1} = 6x Big |_{M_1} = 0 $$ $$ z”_{yy} Big |_{M_1} = 6y Big |_{M_2} = 6y Big |_{M_2} = 0 $$ $$ z”_{xy} Big |_{M_1} = -15 $$ Подставляем данные значения в формулу достаточного условия экстремума: $$ A Big |_{M_1} = 0 cdot 0 – (-15)^2 = -225 $$ Так как $ A < 0 $, то в точке $ M_1(0,0) $ экстремума нет. Получаем значения частных производных 2 порядка в $ M_2 $: $$ z”_{xx} Big |_{M_2} = 6x Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{yy} Big |_{M_2} = 6y Big |_{M_2} = 6 cdot 5 = 30 $$ $$ z”_{xy} Big |_{M_2} = -15 $$ Вычисляем значение выражения достаточного условия экстремума: $$ A = 30 cdot 30 – (-15)^2 = 900 – 225 = 675 $$ Получили $ A > 0 $ и $ z”_{xx} > 0 $, то значит, $ M_2(5,5) $ точка минимума. Наименьшее значение функции $ z = x^3 + y^3 – 15xy $ равно: $$ z_{min} |_{M_2} = 5^3 + 5^3 – 15 cdot 5 cdot 5 = 125 + 125 – 375 = -125 $$

Ответ

В $ M_1 (0,0) $ экстремума нет, в $ M_2(5,5) $ минимум функции $ z_{min}=-125 $

Наибольшее и наименьшее значения функции двух переменных в замкнутой области

Краткая теория

---

Примеры решения задач

---

Задача 1

Найти наибольшее и наименьшее
значение в области

, ограниченной заданными линиями.

Решение

Область

 показана на рисунке:

  

Найдем стационарные точки:

Частные производные:  

Приравняем найденные частные производные к нулю и решим систему
уравнений:

Области

 принадлежит
точка

Исследуем функцию на границах области

:

при

:  

Приравниваем производную к нулю:

Находим значения функции:

При

Приравниваем производную к нулю:

Находим значения функции:

при

Приравниваем производную к нулю:

Находим значения функции:

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Сопоставляя полученные значения, получаем:

---

Задача 2

Найти наименьшее и
наибольшее значения функции

 в
указанной области. Сделать чертеж области.

  в круге

Решение

Область

 показана на рисунке:

Найдем стационарные точки:

Стационарных точек функция
не имеет

Исследуем функцию на
границах области:

при

Приравниваем производную к нулю:

Значение

 в
найденной точке:

Находим значения функции:

при

Приравниваем производную к нулю:

Значение

 в
найденной точке:

Находим значения функции:

Сопоставляя полученные
значения, находим:

 в
точке

 в
точке