Как найти максимально напряжение на обкладках конденсатора, если известны индуктивность, электроемкостьсилатокав катушке
Ученик
(220),
на голосовании
12 лет назад
Голосование за лучший ответ
Валентина Вавилова(Серкова)
Гений
(62183)
12 лет назад
По закону сохранения энергии: мах. энергия катушки = мах. энергии конденсатора.
Wкат=Wкон. Запишем формулы мах. энергии катушки и конденсатора
Wкат=L*Iмах^2 / 2, Wкон=С*Uмах^2 / 2, приравняем, сократим на 2, и выразим
мах. напряжение: L*Iмах^2 / 2=C*Uмах^2 / 2, Uмах= корень квадратный из L*Iмах^2 / C . Можно вынести из под корня Iмах.
Uмах= Iмах*корень кв. из L / C .
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.
Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).
Полярность конденсатора
Полярность: некоторые конденсаторы изготавливаются таким образом, что они могут выдерживать приложенное напряжение только одной полярности, но не другой. Это связано с их конструкцией: диэлектрик представляет собой микроскопически тонкий слой изоляции, нанесенный во время изготовления на одну из пластин с помощью постоянного напряжения. Они называются электролитическими конденсаторами, и их полярность четко обозначена.
Изменение полярности напряжения на электролитическом конденсаторе может привести к разрушению этого сверхтонкого диэлектрического слоя, что приведет к разрушению устройства. Однако толщина этого диэлектрика позволяет получать чрезвычайно высокие значения емкости при относительно небольшом размере корпуса. По той же причине электролитические конденсаторы имеют тенденцию иметь низкое номинальное напряжение по сравнению с другими типами конструкций конденсаторов.
Характеристики конденсаторов
Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.
Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.
Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.
В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.
Вам это будет интересно Формулировка и определение закона Ома
Схемы на все случаи жизни
Под номинальным напряжением конденсатора понимается предельно допустимое напряжение постоянного тока (или сумма напряжений постоянного и переменного токов), при котором конденсатор может работать в течение гарантируемого срока службы при максимально допустимой рабочей температуре.
Номинальное напряжение постоянного тока устанавливается с необходимым запасом по отношению к длительной электрической прочности диэлектрика, исключающим возникновение в течение гарантируемого срока службы сильного старения конденсатора, вызывающего существенное ухудшение его электрических характеристик.
Допускаемые значения амплитуды переменного тока выбираются таким образом, чтобы исключить возможность развития ионизации в конденсаторе и его нагрев сверх допускаемой предельной температуры.
Эти значения обычно приводятся в технических условиях на конденсатор. При эксплуатации конденсаторов на переменном или постоянном с переменной составляющей напряжениях следует придерживаться следующих правил:
• Сумма постоянной составляющей и амплитуды пульсации не должна превышать номинального рабочего напряжения.
• Амплитуда переменного напряжения не должна превышать величины, определяемой формулой: U=400*103*√(Pp/fC), где U — амплитуда переменного напряжения,В; Pp — допустимая реактивная мощность, Вар; С — емкость, пф; f — частота, гц.
• Ток, проходящий через конденсатор, не должен превышать допустимой по ТУ величины. Максимальным значением допустимого переменного напряжения, равным номинальному, обладают керамические низковольтные высокочастотные конденсаторы. Ограничение напряжения для этих конденсаторов обусловливается допустимыми значениями реактивной мощности и тока.
Для слюдяных конденсаторов допустимое значение амплитуды переменного напряжения в процентах от номинального в соответствии с действующими ТУ приведено ниже. Для конденсаторов типов КСО, СГМ: • На номинальные напряжения до 500 В: 100% до 500 гц, 60% от 500 до 10000 гц, 20% более 10000 гц;
• На номинальные напряжения 500 В: 50% до 500 гц, 30% от 500 до 10000 гц, 10% более 10000 гц;
• На номинальные напряжения от 1000 до 3000 в: 30% до 50 гц, 20% от 500 до 10000 гц, 5% более 10000 гц;
• На номинальные напряжения 5000 в и выше: 15% до 500 гц, 20% от 500 до 10000 гц, 3% более 10000 гц.
Срок службы конденсаторов зависит от приложенного напряжения и окружающей температуры. Следовательно, существует принципиальная возможность в зависимости от времени, в течение которого будет эксплуатироваться конденсатор, и окружающей температуры устанавливать допустимые значения рабочих напряжений, значительно отличающиеся от номинальных. Это обстоятельство, расширяющее возможность применения конденсаторов, использовано в некоторых металлобумажных конденсаторах.
Во избежание повреждения конденсатора нельзя допускать, чтобы амплитудное значение переменной составляющей (любой формы, частоты и длительности воздействия) превышало величину приложенного постоянного напряжения, так как при этом на аноде периодически будет создаваться отрицательный потенциал.
Величина допускаемого значения переменной составляющей для электролитических конденсаторов зависит от типа конденсатора и уменьшается пропорционально частоте.
Некоторые типы конденсаторов нежелательно использовать при напряжениях, значительно ниже номинального (особенно ниже 1 в), так как могут возникнуть нарушения в работе схем из-за неустойчивости внутренних контактов между обкладками и выводами, роста потерь и развития окислительных процессов, приводящих к временной или постоянной потери емкости. Примером таких конденсаторов являются конденсаторы типа БМ-1.
При низких напряжениях наиболее надежными являются конденсаторы с припаянными или приваренными, контактами: керамические, стеклоэмалевые, стеклокерамические, бумажные (БМ-2, БМТ-2, К40У-9), металлобумажные (МБГ, МБГТ, МБМ, К42У-2), металлопленочные (МПГ, МПГО, К71П-2Б), фторопластовые (К72П-6).
Для отбраковки конденсаторов с заведомо низкой электрической прочностью, обусловленной грубыми случайными дефектами, заводы-изготовители проверяют конденсаторы испытательным напряжением, значительно превышающим номинальное. Конденсаторы должны выдерживать воздействие испытательного напряжения в течение короткого времени (обычно 10 сек) не пробиваясь.
Обычно испытательное напряжение выбирается, исходя из запаса кратковременной электрической прочности конденсатора.
Для слюдяных конденсаторов испытательное напряжение выбирается обычно в два раза больше номинального, для бумажных на напряжение до 1500 в 3 раза больше, а при 1500 в и выше в 2 раза больше.
Испытательным напряжением на заводах-изготовителях обычно проверяются все выпускаемые конденсаторы (испытание на электрическую прочность), что позволяет отбраковывать образцы с особо грубыми дефектами, но, однако, не обеспечивает безотказность при последующей эксплуатации конденсаторов, выдержавших это испытание. У конденсаторов, истинное пробивное напряжение которых превышало испытательное на сравнительно небольшую величину, воздействие испытательного напряжения может вызвать необратимое изменение в диэлектрике, снижающее запас электрической прочности.
При повторном испытании на электрическую прочность, такие конденсаторы могут выйти из строя. Эксперименты показывают, что если достаточно большую партию конденсаторов неоднократно испытывать одним и тем же испытательным напряжением, то при последующих испытаниях всегда будет иметься некоторое количество пробитых образцов.
Исходя из сказанного, проверки конденсаторов на электрическую прочность следует стремиться уменьшать до предела, например до двух: 1) на заводе-изготовителе конденсаторов и 2) при входном контроле на заводе-потребителе.
Однако при входном контроле рекомендуется проводить испытание конденсаторов всех типов на кратковременную электрическую прочность при испытательном напряжении не выше 1.15*Uном.
Список использованной литературы
- Элементы радиоэлектронной аппаратуры. Электрические конденсаторы постоянной ёмкости. В.Н. Гусев, В.Ф.Смирнов. — М.: Советское радио, 1968.
В чем измеряется напряжение конденсаторов
Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.
Что влияет на напряжение конденсаторов
Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.
Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.
Немного конденсаторов и как они влияют на уровень пульсаций преобразователя
Как-то купил я некоторое количество разных радиокомпонентов в нашем местном магазине. И среди всего прочего там были и электролитические конденсаторы разных типов, которые мне понадобились для небольшой доработки одного из преобразователей и сегодня я расскажу о том, как простая замена конденсатора может сильно изменить характеристики преобразователя, ну или блока питания. Обзор сегодня будет короткий, собственно о конденсаторах вряд ли возможно долго рассказывать, но думаю что все таки и в таком виде он будет полезен. И да, в какой-то степени у меня сегодня «юбилейный», шестисотый обзор на муське.
Плату преобразователя, для которой я их планирую использовать, вы уже видели в одном из моих обзоров, а так как я все таки хочу ее применить по назначению, то решил немного доработать, для чего и были куплены конденсаторы.
Всего было куплено пять видов конденсаторов, двух производителей и с несколькими вариантами рабочего напряжения и емкости. Покупались в харьковском магазине Космодром вместе с кучей другой мелочевки.
Сначала мои любимые конденсаторы фирмы Samwha серии RD, в данном случае это 330мкФ 63 Вольта, стоят примерно по 20 центов, собственно потому что они недорогие и вполне качественные, я их часто и использую.
Следует отметить, что данные конденсаторы не относятся к низкоимпедансным и являются просто высокотемпературным вариантом более привычных SD, но тем не менее очень неплохо работают и в импульсных блоках питания.
Дальше все измеренные параметры будут идти в одном и том же порядке для всех конденсаторов и сюда входит: 1. Фото выштамповки на верхней крышке и форма изолятора 2. Вес, в данном случае двух конденсаторов, т.е. результат надо делить на 2. 3, 4. Габаритные размеры.
Зачем это надо. Конденсаторы очень часто подделывают и чтобы хот как-то иметь представление о виде оригинальных конденсаторов, нужен какой-то образец и в данном случае можно будет сравнивать купленные в других местах с данными фото.
Параметры обоих конденсаторов на частоте 100 Гц и 7.8 кГц.
Тоже Samwha, но уже другой серии, WL. Емкость 1000мкФ, напряжение 35 Вольт. Стоят примерно те же 20 центов — ссылка.
Данные конденсаторы уже относятся к низкоимпедансным, а значит их уже на «законном основании» можно применять в преобразователях и импульсных БП, они уже фигурировали у меня в обзоре доработки светильников.
Форма изолятора, выштамповка и габаритные размеры. Конденсаторы довольно габаритные.
Емкость, ESR.
А вот дальше пойдут конденсаторы фирмы Panasonic и начну с самого компактного из обозреваемых — 470мкФ 35 Вольт. Стоят они конечно уже подороже, примерно по 30-35 центов — ссылка.
Это также низкоимпедансные конденсаторы, о чем и заявлено в даташите.
Выштамповка верхней крышки имеет своеобразную форму, хотя изолятор очень похож Samwha.
Помимо неплохих характеристик отмечу любопытный факт, если посмотреть на фото, то видно что у Samwha маркировка расположена так, что плюс будет справа (если смотреть выводами вниз), а у Panasonic наоборот, плюс получается слева.
Тоже Panasonic, той же серии, на те же 35 Вольт, но уже с емкостью 820мкФ, стоят уже по 80 центов — ссылка.
Выштамповка на крышке такая же как у предыдущих, а вот форма изолятора заметно отличается.
Параметры просто класс, рекомендую однозначно. В даташите параметры приведены для частоты 100кГц, но мой измеритель так не умеет 
И третий Панасоник, выглядит немного по другому, цвет маркировки золотистый и есть логотип «М». Стоят чуть больше одного доллара за штучку — ссылка.
Форма выштамповки и изолятора точно такая же как у предыдущих, отличие только в самой маркировке.
Если сравнивать с Samwha RD, то здесь параметры конечно заметно лучше, но и разница в цене существенная.
Переделка проста и незамысловата, выпаиваем родные конденсаторы, ставим новые. Изначально стоял китайский «Sanyo» 470мкФ 50 Вольт. Из показанных выше пяти типов я выбрал два, на вход Samwha RD 330х63, на выход Panasonic 330х50. Изначально думал поставить на вход 330х50, а на выход пару 470х35 или один 820х35, но решил перестраховаться так как по входу будет около 48-50 Вольт и снижать его не хочется, а по выходу 35 были бы впритык. Samwha WL оказался слишком большим, еле влазил и я не стал его применять. Вообще выбор конденсаторов небольшого диаметра на 50-63 Вольта и емкостью 330мкФ и выше очень мал, хотелось что-то более емкое и желательно качественное с низким ESR, но увы…
Можно было бы конечно этим и ограничится, но мне очень было любопытно, есть ли разница в итоге и если есть, то какая, потому я сначала подключил плату с родными конденсаторами, измерил пульсации на выходе, а потом заменил конденсаторы и провел тот же тест в тех же условиях. Входное напряжение везде около 22 вольт, выходное: 1. 3.3 вольта 8 ампер 2. 6 вольт 8 ампер 3. 15 вольт 3.5 ампера.
Слева до переделки, справа соответственно после, хотя думаю что вы и так догадались «кто есть кто» 
А это измерения родных конденсаторов, самого плохого и самого хорошего, параметры третьего находятся где-то посередине. Если коротко, то примерно как у обычных конденсаторов, например Samwha стандартной серии на 85 градусов, но вот насчет долговечности у меня есть некоторые сомнения, думаю Samwha все таки будет надежнее.
И так, могу сказать что результат есть, причем очень даже наглядный, пульсации снизились примерно в 5-6 раз и это при том, что до переделки по выходу емкость была 940 мкФ, а теперь 660, так что и емкость уменьшили и пульсации снизили, надеюсь что и надежность заметно повысилась.
Если коротко, Panasonic очень понравились, все, Samwha тоже, но с ней я знаком давно и в принципе знал чего ожидать, но если хочется качественно, то лучше все таки Panasonic, в данном случае это была серия FR.
Как всегда буду рад комментариям и вопросам, надеюсь что обзор был полезен.
Как вычислить напряжение и вольтаж
Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.
Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.
Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Как воздействует электрический ток на организм человека
В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Эквивалентная схема конденсатора
Эквивалентная схема: поскольку пластины в конденсаторе имеют некоторое сопротивление, и поскольку ни один диэлектрик не является идеальным изолятором, не существует такой вещи, как «идеальный» конденсатор. В реальной жизни конденсатор имеет как последовательное сопротивление, так и параллельное сопротивление (сопротивление утечки), взаимодействующие с его чисто емкостными характеристиками:
К счастью, относительно легко изготовить конденсаторы с очень маленьким последовательным сопротивлением и очень высоким сопротивлением утечки!
В курсе средней школы задачи по физике, при
решении которых требуется явное применение
дифференциального и интегрального исчисления
встречаются нечасто и в большинстве своем
вызывают значительные затруднения у
выпускников. Конечно, формулировки многих из
этих задач требуют ответы на вопросы, которые
можно легче получить не из явного решения
описывающих протекающие в них явления
дифференциальных уравнений, а привлекая
известные в физике законы сохранения.
Однако, сравнительный анализ различных
способов решения заданий, а также умение
использовать изученный в курсе алгебры и начал
анализа математический аппарат, безусловно
пригодятся выпускникам средней школы для
продолжения образования в стенах высшей.
Кроме того, весьма важно установление четкой
связи в умах учеников между различными ветвями
познания окружающего мира, их
взаимодополняющего влияния на точность и
четкость воссоздаваемой картины реальности. Я
полагаю, что задумываться об этом человек должен
как можно раньше, для того чтобы в будущей
деятельности плодотворно заниматься творческой
исследовательской работой.
Для начала рассмотрим задачу №1,
предлагавшуюся на вступительных экзаменах в
МФТИ , так как её результаты можно будет
использовать при решении последующих задач.
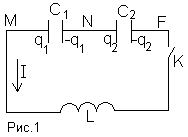
Задача 1. В цепи, изображенной на рис.1 , при
разомкнутом ключе К заряд на конденсаторе с
емкостью С2 (С2=С1/3) равен q2,
а конденсатор с емкостью С1 не заряжен.
Через какое время после замыкания ключа заряд на
конденсаторе С1 будет иметь максимальное
значение? Чему будет равен этот заряд? Омическими
потерями в катушке с индуктивностью L пренебречь.
Как показывает опыт работы, простая замена
преподавателем схемы из двух последовательно
соединенных конденсаторов С1 и С2
эквивалентным конденсатором хотя бы для
расчетов частоты колебаний контура может
совершенно запутать учеников, если они
предварительно сами не придут к осознанию
равносильности такой замены для ответа на
некоторые вопросы задачи. Попробуем составить
дифференциальное уравнение для описания
колебательных явлений в контуре. Хочется
отметить, что то, что близкому к радиотехнике
человеку кажется очевидным, вызывает кучу
вопросов у учеников, и преподаватель не должен
оставлять у них ощущения, что какие-то члены в
уравнении или, допустим, их знаки появляются
из-за случайных догадок, и подробно
последовательно остановиться на всех этапах
решения.
Обозначим буквами М, N, F соответствующие точки
схемы. Изначально на левой пластине конденсатора
С2 был заряд q20, на правой – (-q20).По
закону сохранения заряда сумма зарядов на левой
пластине конденсатора С2 правой пластине
конденсатора С1 остается постоянной, так
как заряды в эту часть схемы извне не поступают q1+q2=q20.
j M-j N=q1/C1; (1) j N-j F=q2/C2
(2). Выберем направление тока в цепи против
часовой стрелки, при этом заряд q2 должен
уменьшаться.
Падение напряжения на катушке индуктивности IR=j
M-j F+e сам. инд. По закону
электромагнитной индукции e cам.инд=
Так как активное
сопротивление катушки индуктивности равно 0, то j M-j
F
Складывая
уравнения (1) и (2),получим j M-j F=q1/C1+q2/C2.
Подставляя данное соотношение в (3), мы получим
уравнение (4), справедливое для любого момента
времени:
q1/C1+q2/C2–
Продифференцируем это уравнение по времени,
получим:
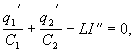
учитывая, что 
мы приходим к
дифференциальному уравнению 
которое является уравнением гармонических
колебаний.
Общее решение этого уравнения I(t) = Imax sin(w
t+j ), где w 2=
.
Инерционной частью в данной модели являются
заряды на конденсаторах q1 и q2,
которые не могут измениться мгновенно из-за
наличия индуктивности в цепи.
В момент замыкания ключа j M=j N, так
как конденсатор C1 не заряжен.
j M-j F=j N-j F=q20/C2.
Скорость изменения тока в начальный момент
времени конечна и равна q20/(C2L)(см.(3)),
его значение в этот момент времени также равно 0,
откуда в общем уравнении гармонических
колебаний находим первую const: j =0,
тогда I(t)=Imax sinw t.
w t; 
так как
q2(0)=q20, то const=
, а зависимость величин
зарядов конденсаторов от времени имеет вид:
В
моменты времени, когда ток в цепи максимален, 
Поскольку
активное сопротивление цепи равно 0, энергия
электромагнитного поля в процессе колебаний
сохраняется, т.е. в любой момент времени
справедливо соотношение
а
при максимальном значении тока из этого
соотношения получаем: 
отсюда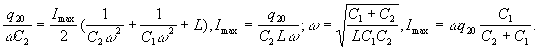 
Данный результат можно получить и иначе. Найдем
равновесное распределение зарядов на
конденсаторах, которое отвечает отсутствию
протекания тока в цепи. При этом конденсаторы С1
и С2 оказываются включенными параллельно
друг другу.
U1=U2=q1p/C1=q2p/C2.Сумма
же зарядов на конденсаторах равна q20. Из
этих условий получаем, что
Вокруг этих положений и
осуществляются колебания зарядов на
конденсаторах с течением времени, амплитуда же
колебаний соответствует величине Imax/w , что
позволяет определить Imax.
В нашем конкретном случае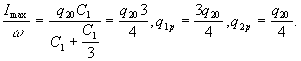 
Максимальная величина
заряда q1 будет равняться 3q20/2, а
достигаться она будет в моменты времени t=T/2+n? T,
где Т – период колебаний, а n=0,1,2… На рис.2
приведены зависимости от времени величины
зарядов на конденсаторах и тока, протекающего в
цепи. 
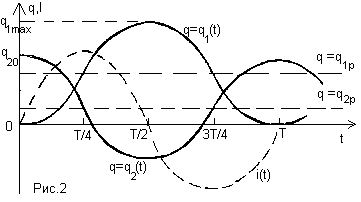
Подробный анализ данной задачи позволяет
подойти к решению более сложного задания,
предложенного на вступительных экзаменах в МФТИ.
Задача 2. В схеме, предложенной на рисунке,
сначала замыкают ключ К1 и после того, как
конденсатор емкостью С2 полностью
зарядится от батареи с ЭДС E , ключ К1 раз-
мыкают и замыкают ключ К2. После замыкания
ключа К2 в схеме происходят свободные
незатухающие колебания. Когда напряжение на
конденсаторе емкостью С1 достигает
максимального значения, в него быстро (за время,
малое по сравнению с периодом колебаний)
вставляют диэлектрическую пластину, что
приводит к увеличению его емкости в e раз.
1)Чему равен начальный ток в цепи после
замыкания ключа К2?
2)Определить максимальный ток в цепи после
вставки пластины.
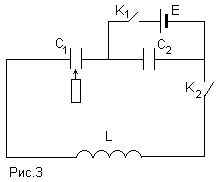
После замыкания ключа К1 конденсатор С2
заряжается до напряжения U= E , на его пластинах
скапливаются заряды q20 и -q20, q20=UC2.
После размыкания ключа К1 источник ЭДС не
играет роли в дальнейших процессах и
промежуточный этап после замыкания ключа К2
описывается найденными в задаче №1
соотношениями. Из зависимости зарядов q1 и q2
от времени следует, что 
а
За
время, малое по сравнению с периодом колебаний, в
процессе внесения в конденсатор C1 диэлектрической
пластины заряды на пластинах конденсаторов не
могут измениться, т.к. до начала процесса ток в
цепи равнялся 0,а максимальную скорость его
изменения можно оценить из уравнения (3).
Она конечна, следовательно, сразу после внесения
диэлектрической пластины ток в цепи по-прежнему
будет равняться 0.
Колебания зарядов на конденсаторах после
внесения диэлектрической пластины будут
осуществляться около новых равновесных
положений, определяемых условиями: 
Отсюда
находим равновесные распределения зарядов: 
В
момент времени, когда система проходит это
равновесное положение, ток в цепи достигает
своего максимального значения. Найдем величину
этого тока из закона сохранения энергии
электромагнитного поля в контуре в процессе
колебаний после помещения в него
диэлектрической пластины.
Данное уравнение относительно Imax является
квадратным, одно из его решений Imax=0
соответствует тривиальному случаю отсутствия
колебаний в контуре, а после упрощений можно
найти и его второе, интересующее нас решение:
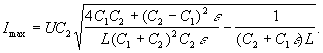
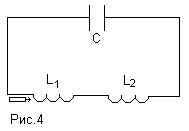
Следующие схемы предлагались на экзамене в
МФТИ в качестве наиболее сложных задач.
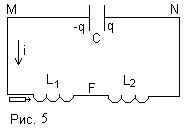
Задача №3. В колебательном контуре,
состоящем из двух последовательно соединенных
катушек с индуктивностью L1 и L2 и
конденсатора с емкостью С, происходят свободные
незатухающие колебания, при которых амплитуда
колебаний тока равна I0. Когда сила тока в
катушке L1 максимальна, в неё быстро ( за
время, малое по сравнению с периодом колебаний)
вставляют сердечник, что приводит к увеличению
её индуктивности в m раз.
1)Определить максимальное напряжение на
конденсаторе до вставки сердечника.
2)Определить максимальное напряжение на
конденсаторе после вставки сердечника.
Составим дифференциальное уравнение
колебаний, описывающее поведение данной цепи.
Все её элементы соединены последовательно, пусть
ток , протекающий в цепи, будет i(t), выберем его
направление так, как показано на рис.5. Пусть
заряд на правой пластине конденсатора q, тогда 
j N-j
M=q(t)/C; (1).
Падение напряжения на катушке L1 равно 0,
так как её активное сопротивление равно 0
( колебания в контуре по условию задачи
незатухающие.)
Складывая уравнения (2) и (3) и учитывая (1), получаем
уравнение (4), справедливое для любого момента
времени до вставки сердечника. 
(4)
Продифференцируем его по времени: 
Данное
дифференциальное уравнение показывает, что
колебания в контуре происходят по
гармоническому закону, а квадрат частоты
собственных колебаний равен 
.
Максимальное напряжение на конденсаторе
соответствует максимальному заряду на нем;
учитывая, что в точках экстремума
дифференцируемой функции q(t) её производная
обращается в 0, получаем, что ток в этот момент в
цепи равен 0.
По закону сохранения электромагнитной энергии
в контуре:
,
где Umax– максимальное напряжение на
конденсаторе до вставки сердечника. 
Рассмотрим процесс введения в катушку L1
сердечника. В это время конденсатор полностью
разряжен, j M=j N.
j M-j F+e инд 1=0, j F-j N+e инд
2=0, тогда e инд 1+e инд 2=0, т.е. 
поскольку
вставка сердечника происходит быстро и
конденсатор всё это время остается незаряженным.
Получаем равенство, вытекающее из сохранения
магнитного потока в системе: (L1+L2) Imax
нач=(m L1+L2)Imax кон.
Следовательно, к моменту окончания вставки
сердечника Imax кон=
Тогда для максимального
напряжения на конденсаторе после вставки
сердечника имеем: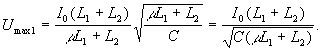 
Что такое конденсатор
Конденсатор – это двухполюсное устройство, имеющее постоянное или переменное емкостное значение и малую проводимость. Это элемент цепи, служащий накопителем энергии, что формирует электрическое поле; пассивный электронный компонент любого подключения. Содержит в себе несколько металлических электродов или обкладок, между которыми находится диэлектрик. Может иметь пакетную, трубчатую, дисковую, литую секционированную и рулонную конструкцию.
Конденсатор имеет в плоскую или цилиндрическую форму. Плоское устройство состоит из относительно далеко расположенных друг от друга пластин, а цилиндрический – из нескольких полых коаксиальных проводящих цилиндров с радиусами r1 и r2 (основное условие – r1 > r2).
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость
. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме
.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации
– смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.
Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
- Воздух – 1.0005
- Бумага – от 2.5 до 3.5
- Стекло – от 3 до 10
- Слюда – от 5 до 7
- Порошки оксидов металлов – от 6 до 20
Характеристики конденсаторов
Главной характеристикой прибора является емкость, то есть, количество энергии, которое он может накопить в виде электронов. Общее число зарядов на пластинах определяет величину емкости конденсатора.
Обратите внимание! Емкость зависит от площади обкладок и диэлектрической проницаемости материала. Чем больше площадь конденсаторных пластин, тем больше заряженных частиц могут поместиться на них и тем выше показатель емкости.
Из важнейших характеристик также можно назвать удельную емкость, плотность, номинальную силу заряда и полярность. Из дополнительных параметров можно указать количество фаз, метод установки конденсатора, рабочую температуру, активный электрический ток переменного или постоянного типа.
В электротехнике существуют также понятия негативных факторов, искажающих рабочие свойства колебательного контура. К ним относятся электрическое сопротивление и эквивалентная последовательная индуктивность. В качестве примера негативного критерия можно привести показатель, показывающий падение заряда после отключения электричества.
Вам это будет интересно Расчет эквивалентного сопротивления
Самовосстановление
Плёночные конденсаторы обладают выдающимися характеристиками по скорости заряда и разряда, что делает их незаменимыми в сетевых фильтрах блоков питания. В сети часто возникают высокоэнергичные импульсы, которые нередко становятся причиной выхода из строя электронных приборов, питающихся от сети. Плёночные конденсаторы могут частично защитить цепи питания, сглаживая такие сетевые помехи. При этом их рабочие свойства меняются незначительно. Данное свойство получило название самовосстановление, так как оно обуславливается способностью самостоятельно избавляться в процессе работы от дефектов (например, пор и примесей в плёнке).
Рассмотрим суть процесса, основываясь на рис. 10. Плёночные конденсаторы имеют металлическое покрытие, нанесённое в вакууме непосредственно на пластиковую плёнку; оно имеет толщину всего лишь 20 .. 50 нм. В результате импульсной перегрузки по напряжению в конденсаторе может случиться локальный пробой диэлектрика. В этот момент происходит дуговой разряд, под действием которого за несколько микросекунд испаряется металлическое покрытие в области пробоя. Металл и диэлектрик выбрасываются за пределы места пробоя, и там образуется непроводящая область. Во время и после этого события конденсатор сохраняет свою функциональность. Из-за уменьшения эффективной площади обкладок после него ёмкость конденсатора в 0,1-1 мкФ уменьшается на очень незначительную величину, не превышающую 100 пФ. С учётом ёмкости конденсатора такие пробои могут быть обнаружены только с помощью прецизионного измерительного оборудования.
- Зазор между диэлектриком и электродом с газообразными парами металла и диэлектрика
- Зона плазмы
- Граничная зона между плазмой и газовыми образованиями
- Канал пробоя диэлектрика
- Зона газообразного диэлектрика
- Зона переместившегося диэлектрика и металлизации
- Зона плазмы
Влагопоглощаемость – характеристика конденсаторов, определяющая, как будет меняться ёмкость конденсатора при изменении влажности рабочей среды. В зависимости от типов конструкции и диэлектрика, а также наличия воздушного зазора между обкладками различные плёночные конденсаторы могут вести себя очень по-разному. Если температура и относительная влажность рабочей среды, указанные производителем, не будут превышать допустимых значений, то процесс изменения ёмкости будет обратимым. В противном случае – нет.
В чем измеряется напряжение конденсаторов
Напряжение отражается на корпусе оборудования и показывает то, при какой силе энергии оно работает. Измеряется напряжение конденсаторов в фарадах. Это единица, названная в честь Майкла Фарадея. Один фарад – это кулон, или заряд, прошедший через проводник за одну секунду при силе тока в один ампер. Как правило, фарады и кулоны не используются для измерения на практике, потому что чаще применяются дробные величины – микро-, нано- и пикофарады.
Напряжение между обкладками
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- Ic — ток конденсатора
- C — Емкость конденсатора
- Vc/t – Изменение напряжения на конденсаторе за отрезок времени
Что влияет на напряжение конденсаторов
Чтобы возник заряд, двухполюсник должен быть подключен к электрической цепи с постоянным током. Для этой цели может быть использован генератор, каждый из которых обладает внутренним сопротивлением. Во время короткого замыкания заряжается прибор, и между его обкладками появляется заряд. Поэтому на вольтаж конденсаторов влияет внутреннее сопротивление. Также, на него оказывают влияние температурные колебания – чем выше нагрев, тем ниже номинальный показатель напряжения.
Важно! На напряжение конденсаторов оказывает большое влияние ток утечки. Вопреки сложившемуся мнению, диэлектрик пропускает небольшое количество электротока, что приводит к потере начального заряда с течением времени, и напряжение в итоге незначительно падает.
Назначение и функции конденсаторов
Конденсатор играет огромную роль как в аналоговой, так и цифровой технике. Они бывают электролитическими и керамическими, и отличаются своими свойствами, но не общей концепцией. Примеры использования:
- Фильтрует высокочастотные помехи;
- Уменьшает и сглаживает пульсации;
- Разделяет сигнал на постоянные и переменные составляющие;
- Накапливает энергию;
- Может использоваться как источник опорного напряжения;
- Создает резонанс с катушкой индуктивности для усиления сигнала.
Примеры использования
В усилителях обычно используются для защиты сабвуферов, фильтрации питания, термостабилизации и разделение постоянной составляющей от переменной. А электролитические в автономных схемах с микроконтроллерами могут долго обеспечивать питание за счет большой емкости.
С2 совместно с резистором R3 выполняет функцию термостабилизации. Когда усилитель работает, транзистор нагревается. Это может внести искажения в сигнал. Поэтому, резистор R3 помогает удержать рабочую точку при нагреве. Но когда транзистор холодный и стабилизации не требуется резистор может уменьшить мощность усилителя. Поэтому, в дело вступает С2. Он проводит через себя усиленный сигнал шунтируя резистор, тем самым, не снижая номинальную мощность схемы. Если его емкость будет ниже расчетной, он начнет вносить фазовые искажения в выходной сигнал.
Чтобы схема качественно работала, обязательно хорошее питание. Когда схема в пиковые значения потребляет больше тока, то это всегда сильная нагрузка на источник питания. С3 фильтрует помехи по питанию и помогает снизить нагрузку. Чем больше емкость — тем лучше звук, но до определенных значений, все зависит от схемы.
А в блоках питания используется тот же принцип, как и в предыдущей схеме по питанию, но здесь емкость нужна гораздо больше. На этой схеме емкость элеткролита может быть как 1000 мкФ, так и 10 000 мкФ.
Еще на диодный мост можно параллельно включить керамические конденсаторы, которые будут шунтировать схему от высокочастотных наводок и шума сети 220 В.
Как вычислить напряжение и вольтаж
Чтобы определить мощность, напряжение и вольтаж двухполюсников, можно использовать мультиметр или специальную формулу для теоретических расчётов. Чтобы проверить мультиметром силу заряда и количество вольт, необходимо вставить щупы в измеряемое оборудование, переключить прибор на режим омметра, нажать на соответствующую клавишу проверки и получить запрашиваемый показатель.
Обратите внимание! Сила заряда при проверке быстро падает, поэтому правильной будет та цифра, которая появилась на индикаторе мультиметра в самом начале измерений.
Номинальное напряжение
Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора
. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).
Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В. Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В. Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.
Формулы измерения напряжения конденсаторов
Численный показатель напряжения равен электродвижущей силе. Также он определяется, как емкость, поделенная на величину заряда, исходя из формулы определения его величины. В соответствии с ещё одним правилом, напряжение равно току утечки, поделенному на изоляционное сопротивление.
Вам это будет интересно Особенности закона Ома для переменного тока
В целом, конденсатор – это устройство для аккумулирования электрического заряда, состоящее из нескольких пластинчатых электродов, которые разделены с помощью диэлектриков. Устройство имеет электрод, измеряемый в фарадах. Один фарад равен одному кулону. На напряжение устройства влияет ток, показатели которого можно вычислить через описанные выше формулы.
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.
Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.
Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.
Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.
Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение
Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.
Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением
Давайте-ка выразим из этой формулы заряд конденсатора:
А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:
Емкость конденсатора у нас является величиной постоянной. Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.
А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:
По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.
Рисунок 1 – Поясняющая картинка
На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.
Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.
Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом
Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную
Или можно записать вот так
Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то 
. Не понятно, откуда взялось это выражение? Погуглите формулы приведения 
. Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с тригонометрическим кругом, на нем все это видно очень наглядно.
Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод – если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения Um и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе
На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).
Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным
Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:
По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом
Здесь мы снова воспользовались интересными сведениями из тригонометрии, что 
. И снова формулы приведения придут вам на помощь, если не понятно, почему получилось именно так.
Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.
Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.
Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.
Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем.
Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.
Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.
Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото 
)
Рисунок 3 – Ищем ток через этот конденсатор
Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.
Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону
Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так
Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока
Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует 
. Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.
Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.
Рисунок 4 – График напряжения в розетке
Рисунок 5 – График тока через конденсатор
Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
