Как найти максимальное значение силы переменного тока

Максимальное, мгновенное и действующее значение переменного тока и напряжения. Фаза и сдвиг фаз. Графическое изображение переменных величин.

Максимальным значением (амплитудой) тока и напряжения называется та наибольшая величина, которой они достигают за один период. Максимальное значение тока и напряжения обозначается: напряжения — Um, тока — Im.

Величину переменной силы тока и напряжения для любого произвольного момента времени называют мгновенным значением этой величины. Обозначают мгновенные значения переменных величин строчными буквами латинского алфавита, например, электрического тока и электрического напряжения i и u соответственно.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Если ток изменяется по закону синуса, т. е.

,

то действующее значение переменного тока, обозначаемое также, как и значение постоянного тока заглавной буквой I латинского алфавита, определится как:

.

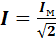
Аналогично для действующих значений синусоидальных напряжений:

.

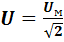
Фаза. Сдвиг фаз.

Пусть на якоре генератора укреплены два одинаковых витка 1 и 2, сдвинутых в пространстве на угол φ. При вращении якоря в витках наводится ЭДС индукции одинаковой частоты ω и амплитуды E_m, так как витки вращаются с одинаковой частотой в одном и том же магнитном поле.

Положение витков задано углами ψ₁ и ψ₂ для произвольного момента времени, которое можно считать t = 0. Мгновенные значения ЭДС как функции времени определяются выражениями:

;

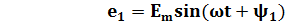
Следовательно, в момент t = 0 значения обеих этих ЭДС отличны от нуля:

;

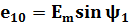
Электрические углы ψ₁ и ψ₂ характеризуют значения ЭДС в начальный момент времени и называются начальными фазами.

Сдвиг фаз — это разность между начальными фазами двух переменных величин, изменяющихся во времени периодически с одинаковой частотой.

Источник

Электрический ток. Закон Ома для цепей постоянного и переменного тока.

Онлайн расчёт электрических величин напряжения, тока и мощности для участка цепи,
полной цепи, цепи с резистивными, ёмкостными и индуктивными элементами.
Теория и практика для начинающих.

Начнём с терминологии.
Электрический ток — это направленное движение заряженных частиц, при котором происходит перенос заряда из одной области электрической цепи в другую.
Силой электрического тока (I) является величина, которая численно равна количеству заряда Δq, протекающего через заданное поперечное сечение проводника S за единицу времени Δt: I = Δq/Δt.
Напряжение электрического тока между точками A и B электрической цепи — физическая величина, значение которой равно работе эффективного электрического поля, совершаемой при переносе единичного пробного заряда из точки A в точку B.
Омическое (активное) сопротивление — это сопротивление цепи постоянному току, вызывающее безвозвратные потери энергии постоянного тока.
Теперь можно переходить к закону Ома.

Закон Ома был установлен экспериментальным путём в 1826 году немецким физиком Георгом Омом и назван в его честь. По большому счёту, Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, определяющих зависимость между электрическими величинами, такими как: напряжение, сопротивление и сила тока исключительно для проводников, обладающих постоянным сопротивлением. При расчёте напряжений и токов в нелинейных цепях, к примеру, таких, которые содержат полупроводниковые или электровакуумные приборы, этот закон в простейшем виде уже использоваться не может.

Тем не менее, закон Ома был и остаётся основным законом электротехники, устанавливающим связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,

где
I – сила тока в проводнике, измеряемая в амперах [А];
U – электрическое напряжение (разность потенциалов), измеря- емая в вольтах [В];
R – электрическое сопротивление проводника, измеряемое в омах [Ом].

Производные от этой формулы приобретают такой же незамысловатый вид: R=U/I и U=R×I.

Зная любые два из трёх приведённых параметров можно произвести и расчёт величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P_(Вт) = U_(В)×I_(А) = I 2 _(А)×R_(Ом) = U 2 _(В)/R_(Ом)

Формулы, описывающие закон Ома, настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта.

Не заслуживают, так не заслуживают. Деревянные счёты Вам в помощь, уважаемые дамы и рыцари!
Считайте, учитывайте размерность, не стирайте из памяти, что:

Единицы измерения напряжения: 1В=1000мВ=1000000мкВ;
Единицы измерения силы тока:1А=1000мА=1000000мкА;
Единицы измерения сопротивления:1Ом=0.001кОм=0.000001МОм;
Единицы измерения мощности:1Вт=1000мВт=100000мкВт.

Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.

ТАБЛИЦА ДЛЯ ПРОВЕРКИ РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.

Вводить в таблицу нужно только два имеющихся у Вас параметра, остальные посчитает таблица.

Все наши расчёты проводились при условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения r_внутр .
Если это условие не соблюдается, то под величиной R следует принять сумму внешнего и внутреннего сопротивлений: R = R_внешн + r_внутр , после чего закон приобретает солидное название — закон Ома для полной цепи:
I=U/(R+r) .

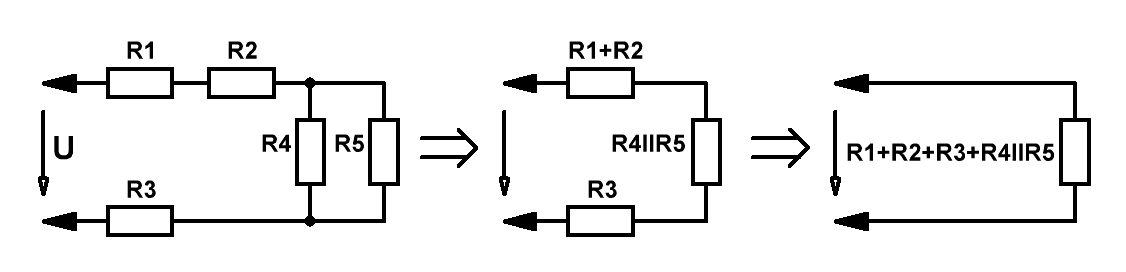
Для многозвенных цепей возникает необходимость преобразования её к эквивалентному виду:

Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/R_ll = 1/R₄+1/R₅ .
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.

Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь в виду для правильной интерпретации закона Ома для переменного тока — под значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.

А что такое действующее значение и как оно связано с амплитудой сигнала переменного тока?
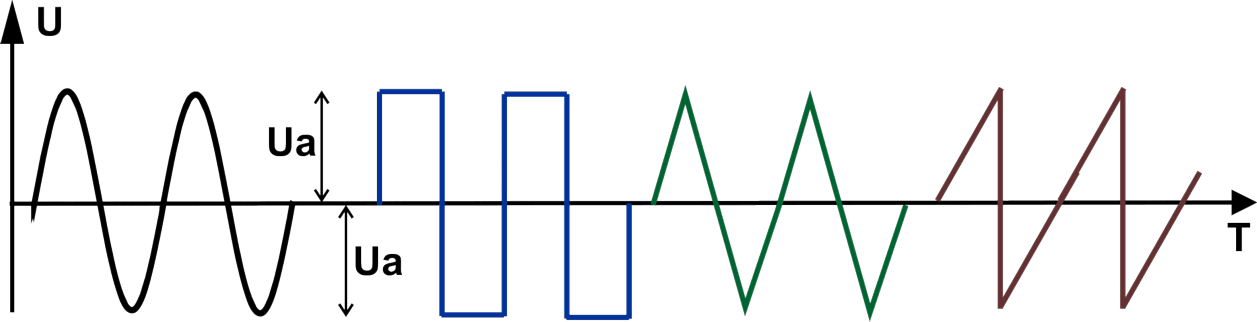
Приведём диаграммы для нескольких различных форм сигнала.

Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал со скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы.
Глядя на рисунок можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда в пределах положительной, или отрицательной (в наших случаях они равны) полуволны.

Рассчитываем действующее значение напряжение интересующей нас формы:

Для синуса U = Uд = Uа/√2;
для треугольника и пилы U = Uд = Uа/√3;
для меандра U = Uд = Uа.

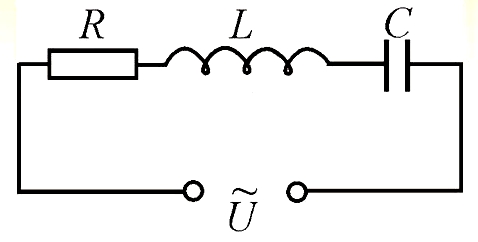
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
В общем случае смотреться это будет так:

А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока не одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись не удаётся, и формула приобретает вид: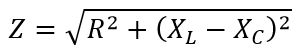
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: X_C = 1/(2πƒС) , X_L = 2πƒL .

Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть не менее одного, при наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !

КАЛЬКУЛЯТОР ДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТИВЛЕНИЯ ЦЕПИ.

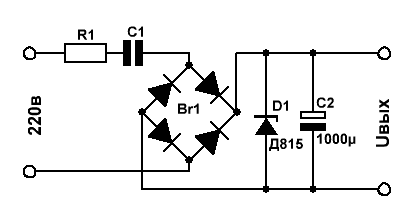
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.

Токозадающими цепями в данной схеме являются элементы R1 и С1.

Допустим, нас интересует выходное напряжение Uвых = 12 вольт при токе нагрузки 100 мА.
Выбираем стабилитрон Д815Д с напряжением стабилизации 12В и максимально допустимым током стабилизации 1,4А.
Зададимся током через стабилитрон с некоторым запасом — 200мА.
С учётом падения напряжения на стабилитроне, напряжение на токозадающей цепи равно 220в — 12в = 208в.
Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200мА: Z = 208в/200мА = 1,04кОм.
Резистор R1 является токоограничивающим и выбирается в пределах 10-100 Ом в зависимости от максимального тока нагрузки.
Зададимся номиналами R1 — 30 Ом, С1 — 1 Мкф, частотой сети f — 50 Гц и подставим всё это хозяйство в таблицу.
Получили полное сопротивление цепи, равное 3,183кОм. Многовато будет — надо увеличивать ёмкость С1.
Поигрались туда-сюда, нашли нужное значение ёмкости — 3,18 Мкф, при котором Z = 1,04кОм.

Всё — закон Ома выполнил свою функцию, расчёт закончен, всем спать полчаса!

Источник

Напряжение цепи переменного тока

Переменное напряжение — это напряжение, которое изменяется с течением времени. Далее будем рассматривать только гармоническое переменное напряжение (изменяется по синусоиде).

Где u = u(t) — мгновенное значение переменного напряжения [В].

U_m — максимальное значение напряжения (амплитудное значение) [В].

f — частота равная числу колебаний в 1 секунду (единица частоты f — герц (Гц) или с -1 )

ω — угловая частота (омега) (единица угловой частоты — рад/с или с -1 )

ω = 2πf = 2π/T

Аргумент синуса, т. е. (ωt + Ψ), называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени t.

U — Действующее значение напряжения [В]:

Рассмотрим параметры напряжения в бытовой электросети.

Все мы знаем, что у нас дома в розетке поступает переменный ток, с напряжением 220 вольт и частотой 50 герц (в идеальных условиях) на самом деле допускается не большая погрешность как в меньшую, так и в большую сторону так, что не удивляйтесь если ваш вольтметр покажет не 220, а например 210 или даже 230 В.).

Большинство приборов измеряет не амплитудное, а действующее значение переменного напряжения, тока, мощности так, что если мы говорим что у нас напряжение сети 220, 380 В и т. д. то имеется виду именно действующие значения.

• Действующее значение напряжения U = 220 В.
• Амплитудное значение напряжения цепи переменного токаU_m = U*√2 = 220 *√2 = 311 В.
• Угловая частота ω = 2πf = 3,14*2*50 = 314рад/с.
• Начальная фаза Ψ = 0град.
• Мгновенное значениеu= 311sin(314t)В.

Источник

ElectronicsBlog

Обучающие статьи по электронике

Переменное напряжение и его параметры

Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

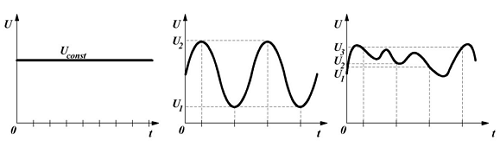
Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

Синусоидальное переменное напряжение.

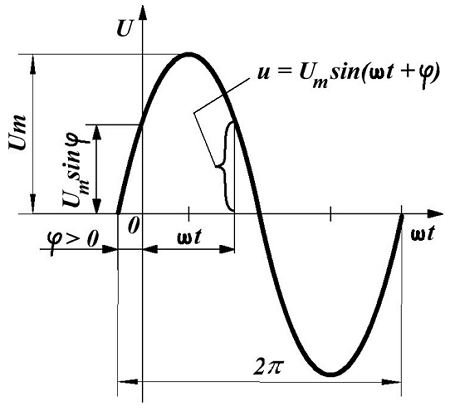
Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда U_m, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда U_m, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному U_m ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

Для переменного напряжения мгновенное значение выделяемой энергии составит

где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t₀ = 0 до t₁ = T составит

Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

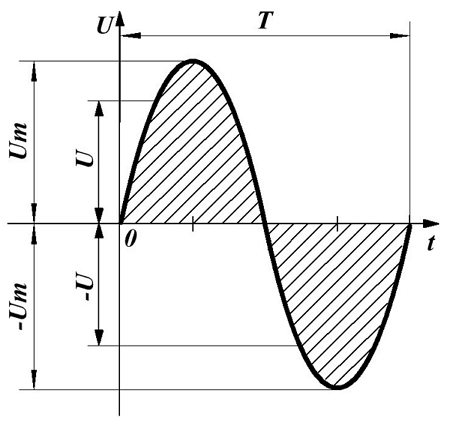
Действующее значение синусоидального напряжения.

Вычислим действующее значение синусоидального напряжения

Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

где Т – период переменного напряжения,

f_u(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией f_u(t) и осью Ox за период Т.

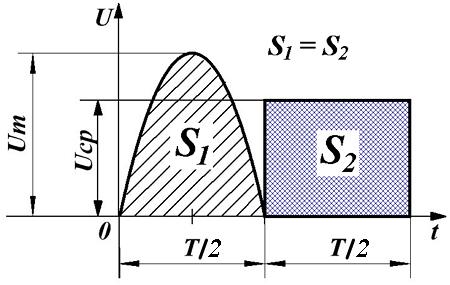
Среднее значение переменного напряжения.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Какие коэффициенты, характеризуют переменное напряжение?

Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:

1. Коэффициент формы переменного напряжения k_ф – показывает как относится действующее значение переменного напряжения U к его среднему значению U_cp.

Так для синусоидального напряжения коэффициент формы составит

2. Коэффициент амплитуды переменного напряжения k_а – показывает как относится амплитудное значение переменного напряжения U_m к его действующему значению U

Так для синусоидального напряжения коэффициент амплитуды составит

На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

Источник

Электродвижущая сила переменного тока

Электродвижущая сила переменного тока

Максимальная сила переменного тока

Действующее (эффективное) значение силы переменного тока

Средняя мощность переменного тока

Действующее (эффективное) значение напряжения переменного тока

Напряжение переменного тока

Максимальная сила переменного тока

Ёмкостное сопротивление

Сила и ёмкостное сопротивление переменного тока

Сила и индуктивное сопротивление переменного тока

Индуктивное сопротивление

Закон Ома для цепи переменного тока

Закон Ома для цепи переменного тока

Сдвиг фаз между током и напряжением переменного тока

Резонанс в цепи переменного тока

Первая формула трансформатора: напряжение

Вторая формула трансформатора: сила тока

Знать максимальный входной ток источника питания полезно при выборе требований к электросети, аварийного выключателя, кабеля питания переменного тока, разъемов и даже изолирующего трансформатора в плавучих блоках. Рассчитать максимальную силу входного тока довольно просто, зная несколько основных параметров и простых математических действий.

Номинальная мощность источника питания высокого напряжения
Для всех источников питания компании Spellman указана номинальная максимальная мощность в ваттах. Это первый нужный нам параметр; получить его можно из техпаспорта изделия. У большей части источников питания компании Spellman максимальная номинальная мощность указана в номере модели. Например, SL30P300/115 — источник питания напряжением 30 кВ с положительной полярностью и максимальной мощностью 300 Вт, работающий от входного напряжения переменного тока 115 В.

КПД источника питания
КПД источника питания — отношение мощности на входе к мощности на выходе. КПД обычно указывается в процентном виде или в виде десятичной дроби меньше 1, например, 80 % или 0,8. Чтобы узнать входную мощность, поделим максимальную выходную мощность на КПД:

300 Вт / 0,8 = 375 Вт

Коэффициент мощности
Коэффициент мощности — отношение реальной мощности к фиксируемой. Обычно он выражается в виде десятичной дроби меньше 1. Реальная мощность указывается в ваттах, а фиксируемая — в вольт-амперах (ВА). У однофазных импульсных источников питания без коррекции коэффициент мощности обычно довольно низок, например, 0,65. Импульсные источники питания без коррекции обладают более высоким коэффициентом мощности, например, 0,85. Блоки питания с активной коррекцией коэффициента мощности могут обладать очень высоким коэффициентом мощности, к примеру, 0,98. В приведенном выше примере используется источник питания без коррекции с питанием от однофазной линии, таким образом:

375 Вт / 0,65 = 577 ВА

Напряжение на входе
Нам необходимо знать входное напряжение переменного тока, для которого предназначен источник питания. В приведенном выше примере оно составляет 115 В. Это номинальное напряжение, в реальности оно указывается с допуском ±10 %. Чтобы предусмотреть наихудший случай с низким напряжением в сети, отнимем 10 %:

115 В – 10 % = 103,5 В

Максимальная сила переменного тока на входе
Взяв 577 ВА и разделив ее на 103,5 В, получаем:

577 ВА / 103,5 В = 5,57 А

Если напряжение на входе однофазное, наш ответ — 5,57 А.

Трехфазное входное напряжение
Источники питания с трехфазным напряжением на входе обладают более высоким коэффициент мощности, чем однофазные. Кроме того, по причине наличия трех фаз, питающих источник, фазовая сила тока будет меньшей. Чтобы узнать силу тока одной фазы, поделим рассчитанную нами силу тока на входе на √3 (1,73).

Рассчитаем данные для следующего примера: STR10N6/208. Из технического паспорта STR узнаем, что максимальная мощность — 6000 Вт, КПД 90 %, а коэффициент мощности 0,85. И хотя STR в силу своей конструкции будет работать с напряжением до 180 В переменного тока, в данном примере его питание будет поступать от трехфазной сети 208 В. Максимальную силу входного тока на одну фазу получаем следующим образом:

КПД источника питания:
6000 Вт / 0,9 = 6666 Вт

Коэффициент мощности:
6666 Вт / 0,85 = 7843 ВА

Напряжение на входе:
208 В – 10 % = 187 В

Максимальная сила переменного тока на входе:
7843 ВА / 187 В = 41,94 А (если бы сеть была однофазной)

Пересчет для трех фаз на входе:
41,94 А / √3 (1,73) = 24,21 А на фазу

Таким образом, у нас есть два уравнения, одно для однофазного и одно для трехфазного напряжения на входе:

Уравнение для максимальной силы однофазного входного тока
Входной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)

Уравнение для максимальной силы трехфазного входного тока
Входной ток = максимальная мощность/(КПД)(коэффициент мощности)(максимальное входное напряжение)(√3)

Данные расчеты входного тока предусматривают наихудший случай, исходя из того, что источник питания работает на максимальной мощности с низким напряжением в линии, а также с учетом КПД и коэффициента мощности.

Прописные истины для новичков.

Как рассчитать шунт для амперметра?
Почему, я намотал вторичную обмотку на 12 вольт, а блок питания у меня выдаёт 16 вольт?.
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.

Закон Ома.

Основным законом, которым руководствуются радиолюбители – является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm,  1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
I = U/R, где R – электрическое сопротивление проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать  U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Вывод: поскольку электрическая мощность «P» в одинаковой степени зависит от тока «I» и от напряжения «U», то, следовательно, одну и ту же электрическую мощность можно получить либо при большом токе и малом напряжении, или же, наоборот, при большом напряжении и малом токе.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.

Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля – Ленца. Звучит так;

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.

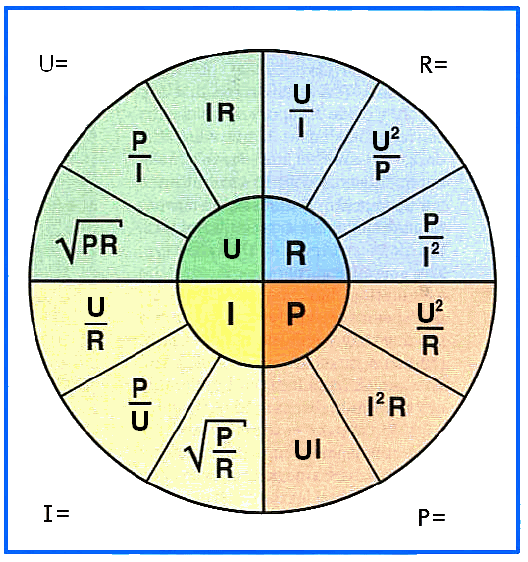
Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами – варианты решений в зависимости от известных величин.

Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье – треугольник Ома.
Выглядит она следующим образом:

В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:

,

• — ЭДС цепи,
• I — сила тока в цепи,
• R — сопротивление всех элементов цепи,
• r — внутреннее сопротивление источника питания.

Закон Ома для полной цепи звучит так – Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.

Электрические измерения.

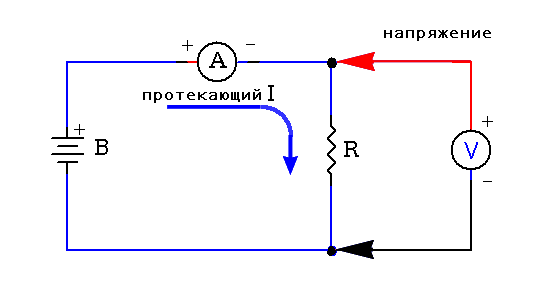
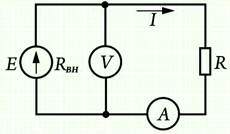
Нарисуем простейшую электрическую цепь, состоящую из батареи “В” и нагрузки “R”, и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.

Постоянный и переменный ток.

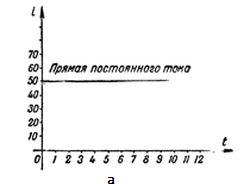
Кратко напомню – постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
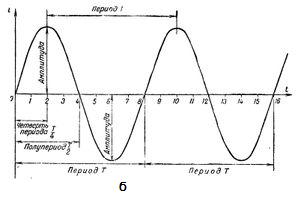
Переменный ток (AC) – это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.

На рисунке выше, на графиках изображены диаграммы постоянного (а), и переменного (б) тока.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.

Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).

В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными “цешками” или бытовыми “цифровиками”, так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт – это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.
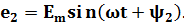
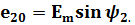
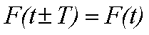
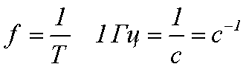
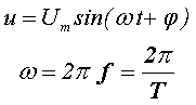
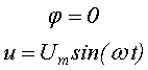
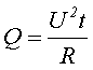
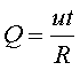
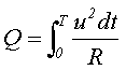
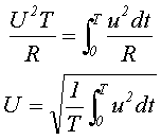
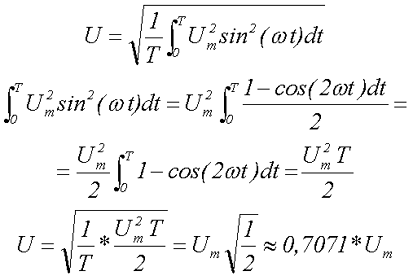
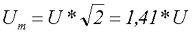
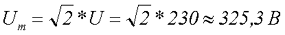
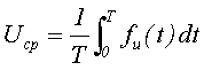
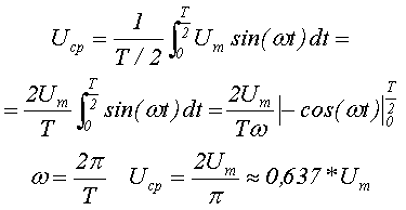
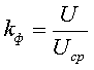
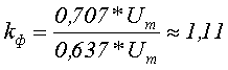
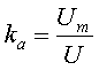
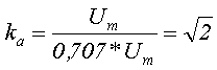
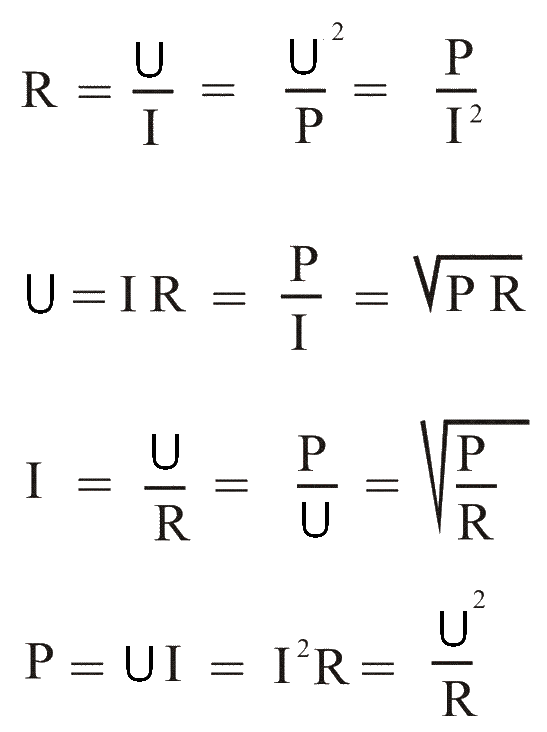
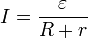