Как найти максимальное значение скорости по графику

Как найти максимальное значение скорости по графику

На чтение 4 мин Просмотров 3к. Опубликовано 25.11.2021

Содержание

  1. Ответ или решение 2
  2. Скорость движения рассчитывается по формуле
  3. Найдем уравнение скорости
  4. Ответ
  5. Уравнение скорости
  6. График скорости
  7. Некоторые частные случаи
  8. Заключение

Ответ или решение 2

Скорость движения рассчитывается по формуле

  • Скорость движения равна производной формулы пути;
  • чтобы найти максимальную скорость, нужно найти производную скорости;
  • затем нужно определить точки максимума;
  • подставить их в уравнение скорости.

Нам дано уравнение пути s = -10t 3 + 15t 2 + 2t

Найдем уравнение скорости

S` = — 10 * 3t 2 + 15 * 2t + 2 = — 30t 2 + 30t + 2

v = — 30t 2 + 30t + 2

Найдем точки максимума этой функции

Для этого найдем производную этой функции.

v`= — 30 * 2t + 30 = — 60t + 30

Приравняем ее к нулю.

Переносим 30 в правую часть, меняя знак.

Делим все уравнение на (- 30).

Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.

Берем любую точку, например, 0.

— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)

Берем например, точку 1.

— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)

Значит, t = 1/2 — это точка максимума.

Подставим это значение в уравнение скорости.

v = — 30t 2 + 30t + 2

v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.

Ответ: максимальная скорость движения равна 9,5.

Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

  • Попроси больше объяснений
  • Следить
  • Отметить нарушение

Vazgen1312 05.07.2019

Ответ

Ответ:

Объяснение:

Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)

1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²

S = 0 + 15*1/2 = 7,5 м

2. S = V*t = 15*3 = 45 м

3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Уравнение скорости

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой

В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.

2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой

Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.

3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны

Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.

Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.

График скорости

График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения

Проанализируем различные графики.

Первый. Уравнение проекции скорости:

Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:

График начинается в точке

Где

Рис. 5. График функции

Это уравнение прямой, что подтверждается графиками, рассмотренными нами.

Некоторые частные случаи

Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, , равняется нулю, проекция ускорения больше нуля.

Запись этого уравнения . А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения

Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси.

Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси . При этом модуль скорости постоянно возрастает, тело ускоряется.

График зависимости ускорения от времени

Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени

Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.

Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.

Рис. 8. Изменение скорости

Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.

Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.

Заключение

На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.

  1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
  2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
  3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Интернет-портал «class-fizika.narod.ru» (Источник)
  2. Интернет-портал «youtube.com» (Источник)
  3. Интернет-портал «fizmat.by» (Источник)
  4. Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)

1. Что такое равноускоренное движение?

2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при ?

«>

Источник

Как найти предельную скорость

wikiHow работает по принципу вики, а это значит, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали, в том числе анонимно, 11 человек(а).

Количество просмотров этой статьи: 34 506.

Вы никогда не задумывались, почему при падении парашютисты в конечном итоге достигают предельной максимальной скорости, хотя сила тяжести в вакууме заставляет тело постоянно ускоряться? Падающее тело достигает предельной скорости, когда есть некая сдерживающая сила, такая, как сопротивление воздуха. Сила тяжести действует на тело с постоянной величиной, но сила сопротивления воздуха увеличивается с увеличением скорости падения тела. Если свободное падение длится достаточно долго, то скорость падения тела достигнет такой величины, при которой сила сопротивления станет равна силе тяжести, и эти силы будут компенсировать друг друга; в результате этого тело будет продолжать падение с постоянной скоростью, пока не коснется земли. Такая скорость называется предельной скоростью.

Как определить максимальную и минимальную скорости движущихся объектов — манекены — Бизнес — 2022

Одним из наиболее практических применений дифференциации является поиск максимальных или минимальных значений функции реального мира, например максимальной и минимальной скоростей движущегося объекта.

Вы можете представить v elocity как более техническую версию скорость .

Вот пример. Йо-йо движется прямо вверх и вниз. Его высота над землей, как функция времени, задается функцией H ( t ) = t 3 — 6 t 2 + 5 t + 30, где t находится в секундах и H ( t ) находится в дюймов. При t = 0 yo-yo составляет 30 дюймов над землей, а через 4 секунды он находится на высоте 18 дюймов, как показано на этом рисунке.

Высота yo-yo, от 0 до 4 секунд.

Чтобы определить общее расстояние, пройденное yo-yo, вам нужно добавить расстояния, пройденные на каждой ноге поездки yo-yo: вверх нога, нога и вторая нога.

Во-первых, йо-йо поднимается с высоты от 30 дюймов до 31 дюймов (где первая точка поворота). Это расстояние около 1,1 дюйма. Затем он опускается примерно с 31. 1 до 16. 9 (высота второй точки поворота). Это расстояние 31. 1 минус 16. 9, или около 14. 2 дюйма. Наконец, yo-yo снова поднимается с 16 дюймов до конечной высоты 18 дюймов. Это еще 1 дюйм. Добавьте эти три расстояния, чтобы получить общее пройденное расстояние:

Примечание: Сравните этот ответ с общим объемом перемещения — 12, который вы получаете от вычитания конечной высоты yo-yo, 18 дюймов, от ее начальная высота 30 дюймов. Смещение отрицательно, потому что движение сети вниз. И положительная величина смещения (а именно 12) меньше расстояния, пройденного 16. 4, потому что при смещении верхние ноги рейса yo-yo отменяют часть расстояния вниз. Посмотрите математику:

Средняя скорость yo-yo определяется общим пройденным пройденным расстоянием, деленным на прошедшее время. Таким образом,

Скажем, вы определяете, что максимальная скорость yo-yo составляет 5 дюймов в секунду, а ее минимальная скорость составляет -7 дюймов в секунду. Скорость -7 — это скорость 7, так что это максимальная скорость yo-yo. Его минимальная скорость равна нулю в двух оборотных точках.

Хорошим способом анализа максимальной и минимальной скорости является рассмотрение функции скорости и ее графика. (Или, если вы являетесь обжором для наказания, ознакомьтесь со следующим mumbo jumbo.) Скорость равна абсолютному значению скорости.

Velocity, V ( t ), является производной от позиции (высота, в этой задаче). Таким образом:

Итак, для задачи yo-yo, функция скорости,

Посмотрите на график S ( t ) на следующем рисунке.

Функция скорости yo-yo S ( t )

Глядя на этот график , легко видеть, что максимальная скорость yo-yo происходит при t = 2

и что минимальная скорость равна нулю на двух x -перехватах.

Минимальная и максимальная скорость: Для непрерывной функции скорость минимальная скорость равна нулю всякий раз, когда максимальная и минимальная скорости имеют противоположные знаки или когда один из них нуль. Когда максимальная и минимальная скорости являются как положительными, так и отрицательными, скорость минимум меньше абсолютных значений максимальной и минимальной скоростей. Во всех случаях максимальная скорость представляет собой больше абсолютных значений максимальной и минимальной скоростей. Это глоток или что?

Как найти максимальную скорость по графику

Чтобы узнать знак производной, рисуем координатную прямую, отмечаем точку 1/2 и определяем знаки производной подбором.

Берем любую точку, например, 0.

— 60 * 0 + 30 = 30 (производная положительна, функция возрастает)

Берем например, точку 1.

— 60 * 1 + 30 = — 30 (производная отрицательна, функция убывает)

Значит, t = 1/2 — это точка максимума.

Подставим это значение в уравнение скорости.

v = — 30t 2 + 30t + 2

v = — 30(1/2) 2 + 30 * 1/2 + 2 = — 7,5 + 15 + 2 = 9,5.

Ответ: максимальная скорость движения равна 9,5.

Из уравнения S = — 10t^3 + 15t^2 + 2t сначала найдем производную пути по времени(это будет уравнение скорости точки): S'(t) = V(t) = — 30t^2 + 30t + 2. Графиком функции данного уравнения является парабола и как видим около t^2(то есть коэффициент а) стоит отрицательное число, значит ветки параболы направлены вниз и максимальное значение t достигается на вершине параболы, найдем ее: tmax = — b / 2a = 30 / 30 * 2 = 0,5. Подставим в уравнение скорости и найдем Vmax получим Vmax = — 30 * 0,5^2 + 30 * 0,5 + 2 = 9,5.

  • Попроси больше объяснений
  • Следить
  • Отметить нарушение

Ответ

Ответ:

Объяснение:

Находим L. Разделим путь на три отрезка(как на графике)(с 0 по 1 секунду, потом с 1 до 4 секунды и с 4 по 5 секунду)

1. S = Vot(начальная скорость умноженная на время) + at²/2 ; a(ускорение) = ΔV/Δt = 15 м/с²

S = 0 + 15*1/2 = 7,5 м

2. S = V*t = 15*3 = 45 м

3. S = Vot + at²/2 ; a = ΔV/Δt = — 15 м/с² (тело тормозит)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

То есть ускорение – это величина, которая определяется изменением скорости за время, в течение которого это изменение произошло.

Еще раз о том, что такое равноускоренное движение

Автомобиль за каждую секунду увеличивает свою скорость на . Движется ли автомобиль равноускоренно?

На первый взгляд, кажется, да, ведь за равные промежутки времени скорость увеличивается на равные величины. Давайте рассмотрим подробнее движение на протяжении 1 с. Возможен такой случай, что первые 0,5 с автомобиль двигался равномерно и увеличил свою скорость на Часто равноускоренным называют такое движение, при котором тело двигается с постоянным ускорением . Самым простым примером равноускоренного движения является свободное падение тела (тело падает под действием силы тяжести).

Уравнение скорости

Воспользовавшись уравнением, определяющим ускорение , удобно записать формулу для вычисления мгновенной скорости любого промежутка и для любого момента времени:

Уравнение скорости в проекциях имеет вид:

Это уравнение дает возможность определить скорость в любой момент движения тела. При работе с законом изменения скорости от времени необходимо учитывать направление скорости по отношению к выбранной СО.

К вопросу о направлении скорости и ускорения

В равномерном движении направление скорости и перемещения всегда совпадают. В случае равноускоренного движения направление скорости не всегда совпадает с направлением ускорения и не всегда направление ускорения указывает направление движения тела.

Рассмотрим наиболее типичные примеры направления скорости и ускорения.

1. Скорость и ускорение направлены в одну сторону вдоль одной прямой (рис. 1).

Рис. 1. Скорость и ускорение направлены в одну сторону вдоль одной прямой

В данном случае тело разгоняется. Примерами такого движения могут быть свободное падение, начало движения и разгон автобуса, старт и разгон ракеты.

2. Скорость и ускорение направлены в разные стороны вдоль одной прямой (рис. 2).

Рис. 2. Скорость и ускорение направлены в разные стороны вдоль одной прямой

Такое движение иногда называют равнозамедленным. В таком случае говорят, что тело тормозит. В конечном итоге оно либо остановится, либо начнет двигаться в противоположном направлении. Пример такого движения – камень, подброшенный вертикально вверх.

3. Скорость и ускорение взаимно перпендикулярны (рис. 3).

Рис. 3. Скорость и ускорение взаимно перпендикулярны

Примерами такого движения является движение Земли вокруг Солнца и движение Луны вокруг Земли. В этом случаи траекторией движения будет окружность.

Таким образом, направление ускорения не всегда совпадает с направлением скорости, но всегда совпадает с направлением изменения скорости.

График скорости

График скорости (проекции скорости) представляет собой закон изменения скорости (проекции скорости) от времени для равноускоренного прямолинейного движения, представленный графически.

Рис. 4. Графики зависимости проекции скорости от времени для равноускоренного прямолинейного движения

Проанализируем различные графики.

Первый. Уравнение проекции скорости:

Второй – это зависимость при отрицательном значении проекции ускорения, когда движение замедленно, то есть скорость по модулю сначала уменьшается. В этом случае уравнение выглядит так:

График начинается в точке

Где

Рис. 5. График функции

Это уравнение прямой, что подтверждается графиками, рассмотренными нами.

Некоторые частные случаи

Чтобы окончательно разобраться с графиком скорости, рассмотрим частные случаи. На первом графике зависимость скорости от времени связана с тем, что начальная скорость, , равняется нулю, проекция ускорения больше нуля.

Запись этого уравнения . А сам вид графика достаточно простой (график 1).

Рис. 6. Различные случаи равноускоренного движения

Еще два случая равноускоренного движения представлены на следующих двух графиках. Второй случай – это ситуация, когда сначала тело двигалось с отрицательной проекцией ускорения, а затем начало разгоняться в положительном направлении оси.

Третий случай – это ситуация, когда проекция ускорения меньше нуля и тело непрерывно движется в направлении, противоположном положительному направлению оси . При этом модуль скорости постоянно возрастает, тело ускоряется.

График зависимости ускорения от времени

Равноускоренное движение – это движение, при котором ускорение тела не меняется.

Рис. 7. График зависимости проекций ускорения от времени

Если какая-либо зависимость является постоянной, то на графике она изображается прямой, параллельной оси абсцисс. Прямые I и II – прямые движения для двух разных тел. Обратите внимание, что прямая I лежит выше прямой абсцисс (проекция ускорения положительна), а прямая II – ниже (проекция ускорения отрицательна). Если бы движение было равномерным, то проекция ускорения совпала бы с осью абсцисс.

Рассмотрим рис. 8. Площадь фигуры, ограниченной осями, графиком и перпендикуляром к оси абсцисс, равна:

Произведение ускорения и времени –это изменение скорости за данное время.

Рис. 8. Изменение скорости

Площадь фигуры, ограниченной осями, зависимостью и перпендикуляром к оси абсцисс, численно равна изменению скорости тела.

Мы использовали слово «численно», поскольку единицы измерения площади и изменения скорости не совпадают.

Заключение

На данном уроке мы познакомились с уравнением скорости и научились графически изображать данное уравнение.

  1. Кикоин И.К., Кикоин А.К. Физика: Учебник для 9 класса средней школы. – М.: «Просвещение».
  2. Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений/А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
  3. Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Интернет-портал «class-fizika.narod.ru» (Источник)
  2. Интернет-портал «youtube.com» (Источник)
  3. Интернет-портал «fizmat.by» (Источник)
  4. Интернет-портал «sverh-zadacha.ucoz.ru» (Источник)

1. Что такое равноускоренное движение?

2. Охарактеризуйте движение тела и определите пройденный путь тела по графику за 2 с от начала движения:

3. На каком из графиков изображена зависимость проекции скорости тела от времени при равноускоренном движении при ?

Источник

Как найти максимальную скорость

Задачи физики и математики часто требуют найти максимальную скорость объекта на протяжении всего пути. Данный вид задач относится к разделу кинематики. Рассмотрим алгоритм нахождения максимальной скорости.

Как найти максимальную скорость

Инструкция

Запишите уравнение зависимости скорости от времени.

Найдите производную правой части уравнения и приравняйте её к нулю. Найдите момент времени t, в который производная равна нулю. Если функция периодическая, достаточно рассмотреть какой-либо один период.

Из полученных значений t выберите точки максимума функции. Точка максимума – это минус.

Посчитайте значение функции скорости в точках максимума. Выберите наибольшее.

Если задан конкретный промежуток времени, сравните значения функции скорости на граничных точках и в точках максимума. Выберите наибольшее из них.

Видео по теме

Полезный совет

Функцию зависимости скорости от времени можно получить, дифференцируя функцию пройденного пути, либо интегрируя функцию ускорения. Во втором случае понадобятся еще начальные условия.

Источники:

  • как находится максимальная скорость

Источник

Максимальную скорость
Vamax
, развивающую проектируемым автомобилем
на горизонтальной дороге, определим
как по тяговой характеристике, так и по
динамической. Допускается небольшое
несовпадение максимальных скоростей,
определенным по двум разным характеристикам;
большое несовпадение (более 4%) говорит
о погрешности в ходе проведения тягового
расчета.

Используя данные
таблицы 15, на графике тяговой характеристики
(пункт 1.7.1) строим кривую, соответствующую
суммарной силе сопротивления движения
автомобиля (сила сопротивления дороги
Fψ
плюс сила сопротивления воздуха FB);
точка пересечения данной кривой (Fψ
+ FB)
и кривой, соответствующей полной окружной
силе FK0
на высшей передаче, позволяет определить
максимальную скорость Va
max на дороге без
уклона: опустив линию на горизонтальную
ось (I = 0), по которой
отложена скорость Va
 автомобиля. Если кривые Fψ
+ FB и
FK0
на высшей передаче не пересеклись, то
Vamax
соответствует максимальной скорости
по кривой FK0
на высшей передаче (данная Vamax
называется максимальной кинематической
скоростью, определяемой передаточными
числами трансмиссии и максимальной
частотой вращения коленчатого вала
двигателя); запас окружной силы FK0
в данном случае (кривые Fψ
+ FB и
FK0
не пересеклись) может быть использован
для достижения Vamax
при движении автомобиля на подъеме.

Аналогично определяется
Vamax
по динамической характеристике: используя
данные таблицы 15 на графике динамической
характеристики (пункт 1.7.2) строится для
высшей передачи кривая ψ = fV
(i=0) – безразмерного
фактора сопротивления движению
автомобиля. Точка пересечения кривой
ψ и кривой динамического фактора D
(движущего фактора) определяет Vamax,
если кривее не пересеклись, то Vamax
(кинематическая) соответствует максимуму
скорости по кривой D на
высшей передаче.

Максимально возможные
скорости движения автомобиля, определенные
по тяговой и динамической характеристикам,
должны быть равны между собой, и
соответствовать той максимальной
скорости Va
max, которая была
определена в техническом задании на
проектирование (см. пункт 1.2). Результаты
расчетов заносим в таблицу 16.

Таблица 16 – Максимальная
скорость Vаmax
автомобиля

Условия определения

Vаmax
, км/ч

Погрешность

Тяговая характеристика

92

0%

Динамическая
характеристика

92

0%

Мощносной баланс

92

0%

При движении автомобиля
на подъем (уклон дороги i)
максимальную скорость, по динамической
характеристике, в данных дорожных
условиях определяют следующим образом:
величину уклона i складывают
с коэффициентом сопротивления качению
колес fV
и ищут точку пересечения кривой i+fV
с кривой D – полученная
точка позволяет определить: какую
максимальную скорость развивает
проектируемый автомобиль и на какой
передаче в КПП.

Определяется максимальная
скорость автомобиля при преодолении
уклона в 5% и максимального уклона по
таблице 15. Найденные значения скоростей
не должны быть меньше значений, приведенных
в таблице 17.

Таблица 17 – Максимальные
скорости автомобилей

Максимальная скорость,
км/ч

Грузовые автомобили

полноприводные

неполноприводные

автопоезда

На горизонтальной
дороге, i = 0

80

90

80

На подъеме в 5%,

i
= 0,05

40

45

25

На максимальном
подъеме i max

5

12

8

Максимальная скорость
при преодолении уклона в 5%

Vаmax
= 40км/ч

Максимальная скорость
при преодолении максимального уклона

Vаmax
=7 км/ч

что соответствует
рекомендациям.

1.8
Путь и время разгона автомобиля

Считаем, что разгон
начинается с минимальной устойчивой
скорости

Vamin
(соответствующей nemin
– минимальной устойчивой частоте
вращения коленчатого вала ДВС) на
передаче, используемой для трогания
автомобиля с места. Разгон осуществляется
при полной подаче топлива т.е. двигатель
работает по ВСХ (имеем наибольшую
интенсивность разгона).

Ускорение, как известно,
можно определить по формуле:

аx

(45)

где dVa
– приращение скорости за промежуток
времени dt.

Тогда

dt

(46)

откуда время разгона

t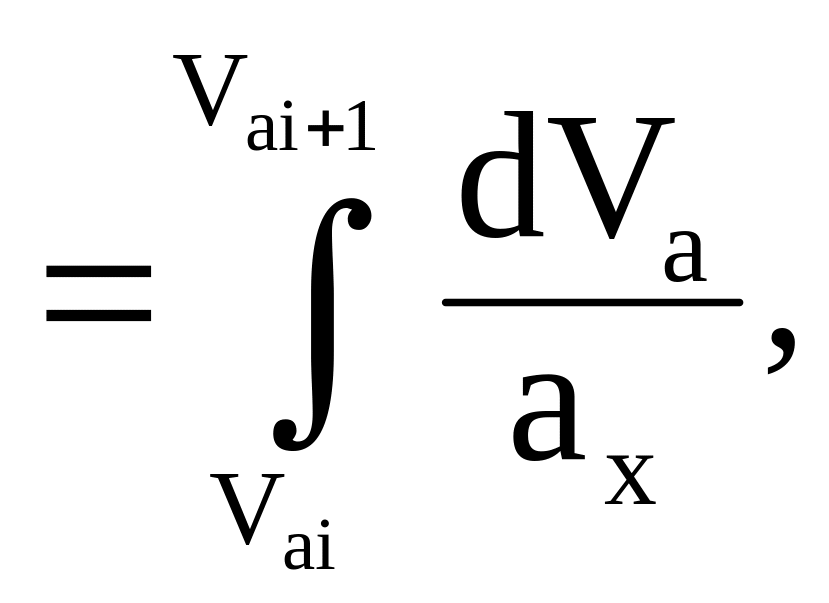

(47)

Считаем, что в небольшом
интервале скоростей ΔVai=Vai+1-Vai
движение является равноускоренным
со средним ускорением аmi
, тогда время движения в данном
интервале, между двумя точками, определим
по формуле:

(48)

где ∆Vai
– изменение скорости между двумя
точками, м/с;

Дальнейшие результаты
расчётов сведены в таблицу 18.

аmi
– среднее ускорение между двумя точками

(49)

Дальнейшие результаты
расчётов сведены в таблицу

Путь, проходимый за
время движения между двумя точками:

∆S=Vmi·∆ti
 (50)

где Vmi
– средняя скорость в рассматриваемом
интервале

(51)

Дальнейшие результаты
расчётов сведены в таблицу 18.

Потери скорости за
время переключения ∆Vn
определим по формуле:


,
м/с (52)

где tn=1c
– время переключения передач

δi+1
– коэффициент учёта вращающихся масс

Путь, проходимый
автомобилем, за время переключения tn
c К-ой на К+1 передачу:

∆Sn=(Vкmax–
0,5∆Vnк-(к+1))·tn,
м (53)

где Vкmax
– скорость, соответствующая моменту
переключения

Таблица 18 – Разгон
автомобиля

Разгон автомобиля на
первой передаче

Пара-

метр

Раз-мер-

ность

№ точки

1

2

3

4

5

6

7

8

Va

км/ч

3,0

3,86

4,71

5,57

6,43

7,28

8,14

9

Va

м/с

0,83

1,07

1,31

1,55

1,79

2,02

2,26

2,5

∆Vi

м/с

–

0,24

0,24

0,24

0,24

0,23

0,24

0,24

ax

м/с2

0,748

0,816

0,869

0,899

0,908

0,899

0,866

0,818

ami

м/с2

–

0,872

0,843

0,884

0,904

0,904

0,883

0,842

∆ti

с

–

0,31

0,29

0,27

0,27

0,25

0,27

0,29

t

с

–

0,31

0,6

0,87

1,14

1,39

1,66

1,95

Vmi

м/с

–

0,95

1,19

1,43

1,67

1,91

2,14

2,38

∆Si

м

–

0,3

0,35

0,39

0,45

0,48

0,58

0,69

S

м

–

0,3

0,65

1,04

1,49

1,97

2,55

3,24

Разгон автомобиля на
второй передаче

Параметр

Размерность

№ точки

9

10

11

12

13

14

Va

км/ч

8,68

9,67

11,15

12,64

14,13

15,61

Va

м/с

2,41

2,69

3,1

3,51

3,93

4,34

∆Vi

м/с

(0,09)

0,28

0,41

0,41

0,42

0,41

ax

м/с2

0,895

0,923

0,936

0,925

0,892

0,836

ami

м/с2

–

0,91

0,93

0,93

0,91

0,87

∆ti

с

(1,5)

0,31

0,44

0,44

0,46

0,47

t

с

3,45

3,76

4,2

4,64

5,1

5,57

Vmi

м/с

–

2,55

2,9

3,31

3,72

4,14

∆Si

м

3,68

0,79

1,28

1,46

1,71

1,95

S

м

6,92

7,71

8,99

10,45

12,16

14,11

Разгон автомобиля на
третьей передаче

Параметр

Размерность

№ точки

15

16

17

18

19

Va

км/ч

15,23

16,26

18,43

20,6

22,76

Va

м/с

4,23

4,52

5,12

5,72

6,32

∆Vi

м/с

(0,11)

0,29

0,6

0,6

0,6

ax

м/с2

0,785

0,796

0,788

0,759

0,71

ami

м/с2

–

0,791

0,792

0,77

0,735

∆ti

с

(1,5)

0,37

0,76

0,78

0,82

t

с

7,07

0,44

8,2

8,98

9,8

Vmi

м/с

–

4,38

4,82

5,42

6,02

∆Si

м

(6,43)

1,62

3,66

4,23

4,94

S

м

20,54

22,16

25,82

30,05

34,99

Разгон автомобиля на
четвёртой передаче

Параметр

Размерность

№ точки

20

21

22

23

24

Va

км/ч

22,31

22,42

25,41

28,4

31,39

Va

м/с

6,193

6,23

7,06

7,89

8,72

∆Vi

м/с

(0,123)

0,037

0,83

0,83

0,83

ax

м/с2

0,63

0,634

0,618

0,593

0,552

ami

м/с2

–

0,632

0,626

0,606

0,573

∆ti

с

(1,5)

0,06

1,33

1,37

1,45

t

с

11,3

11,36

12,69

14,06

15,51

Vmi

м/с

–

6,21

6,65

7,48

8,31

∆Si

м

(9,39)

0,37

8,85

10,25

12,05

S

м

44,38

44,75

53,6

63,85

75,9

Разгон автомобиля на
пятой передаче

Параметр

Размерность

№ точки

25

26

27

28

Va

км/ч

30,91

34,24

38,27

42,3

Va

м/с

8,586

9,51

10,63

11,75

∆Vi

м/с

(0,134)

0,924

1,12

1,12

ax

м/с2

0,465

0,47

0,443

0,408

ami

м/с2

–

0,47

0,46

0,43

∆ti

с

(1,5)

1,97

2,43

2,6

t

с

17,01

18,98

21,41

24,01

Vmi

м/с

–

9,05

10,07

11,19

∆Si

м

(12,98)

17,83

24,47

29,09

S

м

88,88

106,71

131,18

160,27

Разгон автомобиля на
шестой передаче

Параметр

Размерность

№ точки

29

30

31

32

Va

км/ч

41,79

45,12

50,43

55,72

Va

м/с

11,61

12,53

14,01

15,48

∆Vi

м/с

(0,142)

0,92

1,48

1,47

ax

м/с2

0,34

0,333

0,313

0,285

ami

м/с2

–

0,336

0,323

0,299

∆ti

с

(1,5)

2,74

4,58

4,92

t

с

25,51

28,25

32,83

37,75

Vmi

м/с

–

12,07

13,27

14,75

∆Si

м

(17,52)

33,07

60,78

72,57

S

м

177,79

210,86

271,64

344,21

Разгон автомобиля на
седьмой передаче

Параметр

Размерность

№ точки

33

34

35

36

Va

км/ч

55,18

58,17

65,01

71,86

Va

м/с

15,33

16,16

18,06

19,96

∆Vi

м/с

(0,151)

0,83

1,9

1,9

ax

м/с2

0,225

0,225

0,204

0,174

ami

м/с2

–

0,225

0,215

0,189

∆ti

с

(1,5)

3,69

8,84

10,05

t

с

39,25

42,94

51,78

61,83

Vmi

м/с

–

15,75

17,11

19,01

∆Si

м

(23,11)

58,12

151,25

191,05

S

м

367,32

425,44

576,69

767,74

Разгон автомобиля на
восьмой передаче

Параметр

Размерность

№ точки

37

38

39

40

Va

км/ч

71,26

74,28

83,02

92

Va

м/с

19,795

20,63

23,06

25,56

∆Vi

м/с

(0,165)

0,84

2,43

2,5

ax

м/с2

0,125

0,12

0,097

0,064

ami

м/с2

–

0,123

0,109

0,081

∆ti

с

(1,5)

6,83

22,29

30,86

t

с

63,33

70,16

92,45

123,31

Vmi

м/с

–

20,21

21,85

24,31

∆Si

м

29,82

138,03

487,04

750,21

S

м

797,56

935,59

1422,63

2172,84

По данным таблицы 18
строим графики пути и времени разгона
автомобиля, по которым определяем:

1) время разгона до
скорости 60 км/ч

t60=45с

2) путь проходимый АТС
до достижения Vamax
– Sv

Sv=2172,84м

3) время разгона с места
на пути 1000м – t1000

t1000=72c

1.9
Мощностной баланс

Расчет мощностного
баланса, проведем на высшей передаче.

Уравнение мощностного
баланса имеет вид:

NK=NB+
N+
Nia
(54)

где NК
– мощность, подведенная к ведущим
колесам:

NK
= Nе
Т, кВт
(55)

где Ne –
эффективная мощность двигателя (таб.2),
кВт;

ηТ – КПД
трансмиссии;

Nк=73,34,38·0,82=60,14
кВт

Дальнейшие результаты
расчётов сведены в таблицу 19

N
– мощность, затрачиваемая на преодоление
сопротивления дороги;

Nψ=Fψ·Va,
кВт (56)

где Fψ
– сила сопротивления дороги (таблица
15), Н;

Va –
скорость автомобиля (таблица 15),м/с;

Nψ=2900·8,5=24650Вт=24,65кВт

Дальнейшие результаты
расчётов сведены в таблицу 19

NВ
– мощность, затрачиваемая на преодоление
сопротивления воздуха:

NВ =
FB
 Va,
кВт (57)

где FB
– сила сопротивления воздуха (таблица
15),Н;

NВ=51,8·5,047=261Вт=0,261кВт

Дальнейшие результаты
расчётов сведены в таблицу 12

Nia
– мощность, которая может быть затрачена
на разгон автомобиля.

Таблица 19 – Мощносной
баланс автомобиля на высшей передаче

ne,

об/мин

Va,

км/ч

Va,

м/с

Ne,

кВт

NК,

кВт

NВ,

кВт

NК
– NВ,

кВт

N,

кВт

700

30,59

8,5

73,34

60,14

1,95

58,19

24,65

900

39,32

10,92

102,57

84,11

4,13

79,98

32,54

1100

48,06

13,35

133,01

109,07

7,53

101,54

40,72

1300

56,8

15,78

162,73

133,44

12,43

121,01

49,71

1500

65,54

18,21

190,05

155,84

19,1

136,74

59,36

1700

74,28

20,63

212,82

174,51

27,79

146,72

69,52

1900

83,02

23,06

229,83

188,46

38,81

149,65

80,94

2100

92

25,56

239,66

196,52

52,91

143,61

94,06

По данным таблицы 19
строим график мощностного баланса
автомобиля на высшей передаче и определяем
Vаmax
– точка пересечения кривых Nψ
и Nк-Nв

Vаmax=92
км/ч

1.10
Топливная экономичность

Построим топливную
характеристику установившегося движения
– зависимость путевого расхода топлива
Qs от скорости
движения Vа и
определим эксплуатационный расход
топлива проектируемого автомобиля,
(все расчёты будем вести на высшей
передаче).

Путевой расход будет
определяться по зависимости:


,
л/100 км (58)

где geN
– средний удельный эффективный расход
топлива при максимальной мощности
двигателя, г/кВтч;

geN
= (1,05 … 1,1) gemin
 (59)

где gemin
– минимальный удельный расход топлива,
г/кВтч;

gemin
= 180 … 240 г/кВтч;

geN
=1,05·180=189 г/кВтч

KИ
– коэффициент использования мощности
двигателя;

KИ =
1, 2 + 0,14 · U – 1.8 · U2
+ 1,46 · U3
(60)

(61)

Дальнейшие результаты
расчётов сведены в таблицу 20

KИ =
1,2 + 0,14 · 0,442 – 1,8 · 0,442 2 + 1,46 · 0,442 3=
1,036

Дальнейшие результаты
расчётов сведены в таблицу 20

KЕ
– коэффициент использования частоты
вращения коленчатого вала двигателя;

KЕ
= 1,25 – 0,99 · Е + 0,98 · Е2 – 0,24 · Е3
(62)

(63)

где ne,
Va –
текущая соответственно частота вращения
коленчатого вала и скорость АТС;

nN,
VaN –
соответственно частота вращения
коленчатого вала и скорость автомобиля
при максимальной мощности двигателя;

Дальнейшие результаты
расчётов сведены в таблицу 20

KЕ
= 1,25 – 0,99·0,333 + 0,98·0,3332 –
0,24·0,3333=1,018

Дальнейшие результаты
расчётов сведены в таблицу 20

N
и NВ – см. таблицу
19

T
– плотность топлива, кг/м3 : для
дизельного топлива;

T=835
кг/м3

Va,
км/ч – см. таблицу 15

л/100 км

Дальнейшие результаты
расчётов заносим в таблицу 20 и строим
топливную характеристику автомобиля,
по которой определяем:

1) расход топлива при
скорости 80км/ч и 60км/ч

расход топлива при
скорости 80км/ч равен 35,5 л/100 км

расход топлива при
скорости 60км/ч равен 30,2 л/100 км

2) эксплуатационный
расход (э.р.) топлива

э.р. = 1,1·QP
 (64)

где QP
– путевой расход при расчетной скорости
VP


;
(65)

км/ч;

QP=32,4
л/100 км;

э.р. = 1,1·32,4=35,64 л/100 км;

3) контрольный расход
топлива Qк –
минимальный расход по топливной
характеристике

Qк=28
л/100 км

Таблица 20 – Топливная
экономичность автомобиля на высшей
передаче

Va,
км/ч

NК,
кВт

N
+ NВ,

кВт

U

E

KИ

KЕ

QS
,

л/100кмч

30,59

60,14

26,6

0,442

0,333

1,036

1,018

25,32

39,32

84,11

36,67

0,436

0,427

1,04

0,987

26,43

48,06

109,07

48,25

0,442

0,522

1,036

0,966

27,74

56,8

133,44

62,14

0,466

0,617

1,022

0,956

29,5

65,54

155,84

78,46

0,504

0,712

1,001

0,955

31,59

74,28

174,51

97,31

0,558

0,807

0,972

0,963

33,85

83,02

188,46

119,75

0,635

0,902

0,937

0,978

36,48

92

196,52

146,97

0,748

1

0,909

1

40,08

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

I. Механика

Тестирование онлайн

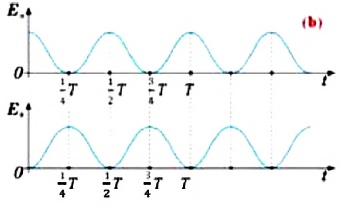
Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

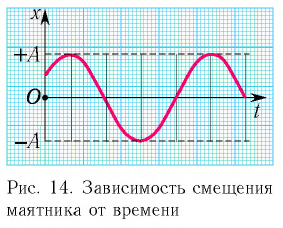
График гармонического колебания

График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

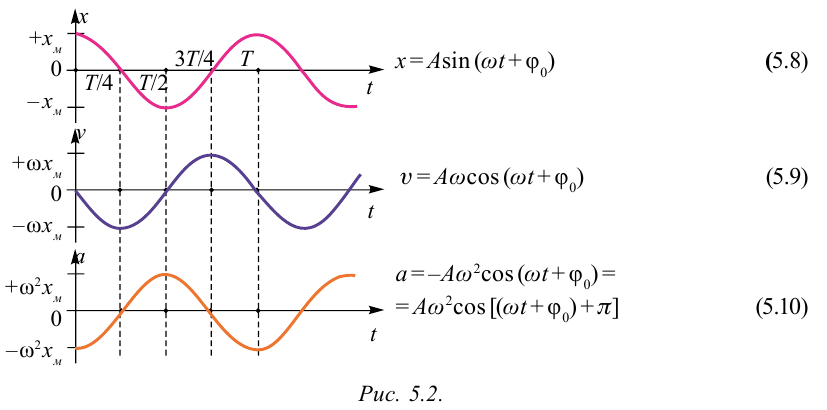
Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Гармонические колебания.

Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями.

Например, в случае механических гармонических колебаний:.

В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.

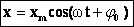
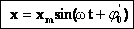
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.

Выражение, стоящее под знаком cos или sin, наз. фазой колебания: .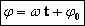

Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.

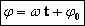
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).

Скорость и ускорение при гармонических колебаниях.

Согласно определению скорости, скорость – это производная от координаты по времени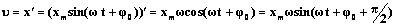

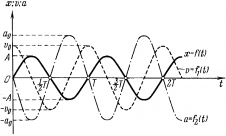
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.

Величина 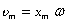— максимальная скорость колебательного движения (амплитуда колебаний скорости).

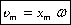
Следовательно, для скорости при гармоническом колебании имеем: 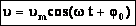, а для случая нулевой начальной фазы (см. график).

Согласно определению ускорения, ускорение – это производная от скорости по времени:

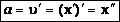— вторая производная от координаты по времени. Тогда: .

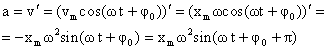Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).

Величина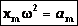

— максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: 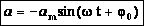, а для случая нулевой начальной фазы: 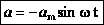(см. график).

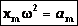
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).

Сравним выражения для смещения и ускорения при гармонических колебаниях:

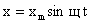и .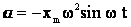

Можно записать: —

т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.

Часто бывает удобно записывать уравнения для колебаний в виде: ,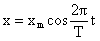

где T – период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: 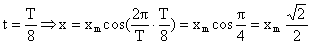. Аналогично для скорости и ускорения.

Гармонические колебания в физике — формулы и определение с примерами

Содержание:

Гармонические колебания:

Некоторые движения, встречающиеся в быту, за равные промежутки времени повторяются. Такое движение называется периодическим движением. Часто встречается движение, при котором тело перемещается то в одну, то в другую сторону относительно равновесного состояния. Такое движение тела называется колебательным движением или просто колебанием.

Колебания, совершаемые телом, которое выведено из равновесного состояния в результате действия внутренних сил, называются собственными (свободными) колебаниями. Величина удаления от равновесного состояния колеблющегося тела называется его смещением (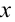

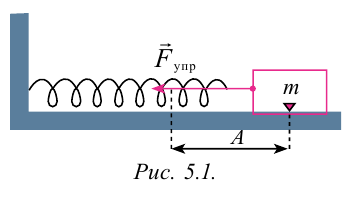
Для наблюдения механических колебаний ознакомимся с колебаниями груза, закрепленного на конце пружины (рис. 5.1). На этом рисунке груз, закрепленный на пружине, сможет двигаться без трения с горизонтальным стержнем, так как силу тяжести шарика приводит в равновесие реакционная сила стержня.
Коэффициент упругости пружины – 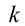, а ее масса ничтожна мала и можно ее не учитывать. Считаем, что масса системы сосредоточена в грузе, а упругость в пружине.

Если груз, который находится в равновесии, потянем вправо на расстояние 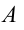и отпустим, то под действием силы упругость, которая появляется в пружине, груз смещается в
сторону равновесного состояния.

С течением времени смещение груза уменьшается относительно , но скорость груза при этом увеличивается. Когда груз доходит до равновесного состояния, его смещение (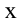) равняется нулю и соответственно сила упругости равняется нулю. Но груз по инерции начинает двигаться в левую сторону. Модуль силы упругости, которая появляется в пружине, тоже растет. Однако из-за того, что сила упругости постоянно направлена против смещения груза, она начинает тормозить груз. В результате движение груза замедляется, и, в результате, прекращается. Теперь груз под воздействием эластической силы сжатой пружины начинает двигаться в сторону равновесного состояния.
Для определения закономерности изменения в течение времени системы, которая периодически совершает колебания, заполним воронку песком, подвесим на веревке, подложим бумагу под систему и раскачаем воронку. В ходе колебания начинаем равномерно вытягивать бумагу из-под системы. В результате мы увидим, что следы песка на бумаге образуют синусоиду. Из этого можно сделать следующий вывод: смещение периодически колеблющегося тела по истечении времени изменяется по закону синусов и косинусов. При этом самое большое значение смещения равняется амплитуде ():

здесь: 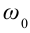– циклическая частота, зависящая от параметров колеблющихся систем, 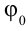– начальная фаза, (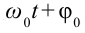) фаза колебания с течением времени .
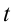Из математики известно, что 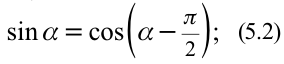поэтому формулу (5.2.) можно записать в виде

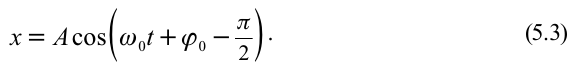
Колебания, в которых с течением времени параметры меняются по закону синуса или косинуса, называются гармоническими колебаниями.

Значит, пружинный маятник, вышедший из равновесного состояния, совершает гармоническое колебание. Для того чтобы система совершала гармоническое колебание: 1) при выходе тела из равновесного состояния, для возвращения его в равновесное состояние должна появиться внутренняя сила; 2) колеблющееся тело должно обладать инертностью и на него не должны оказывать воздействие силы трения и сопротивления. Эти условия называется условиями проявления колебательных движений.

Основные параметры гармонических колебаний

a) период колебания 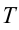– время одного полного колебания:

)

б) частота колебания 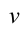– количество колебаний, совершаемых за 1 секунду:

Единица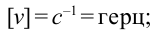
c) циклическая частота 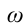– количество колебаний за 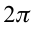секунд:

С учетом формул (5.5) и (5.6) уравнение гармонических колебаний (5.2) можно записать в следующей форме.

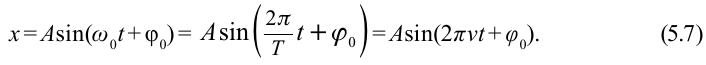
Большинство величин, количественно описывающих гармонические колебания, смещения которых с течением времени меняются по закону синусов или косинусов (скорость, ускорение, кинетическая и потенциальная энергия), тоже гармонически меняются.
Это подтверждается следующими графиками и уравнениями:

Пример решения задачи:

Точка совершает гармоническое колебательное движение. Максимальное смещение и скорость соответственно равны 0,05 м и 0,12 м/с. Найдите максимальное ускорение и скорость колебательного движения, а также ускорение точки в момент, когда смещение равно 0,03 м.

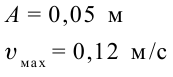
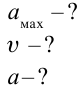
Формула и решение:

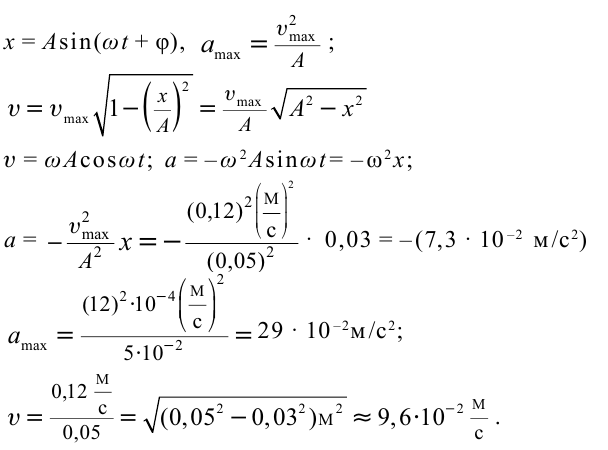
Гармонические колебания пружинного маятника

В 1985 году в городе Мехико произошла ужасная катастрофа, причина которой было землетрясение: 5526 человек погибли, 40 ООО человек ранены, 31000 человек остались без крова. Из проведенных затем исследований ученые выяснили, что главной причиной разрушений во время землетрясения является совпадение частоты свободных колебаний зданий с частотой вынужденных колебаний Земли. Поэтому при возведении новых зданий в сейсмически активной зоне необходимо, чтобы эти частоты не совпадали. Это даст возможность уменьшить последствия землетрясения. С этой целью важно знать, от чего зависят частота и период колебаний.

Одной из простейших колебательных систем, совершающих гармонические колебания, является пружинный маятник.

Пружинный маятник — это колебательная система, состоящая из пружины и закрепленного на ней тела. Колебания, возникающие в пружинном маятнике, являются гармоническими колебаниями:

Под гармоническими колебаниями подразумеваются колебания, возникающие под действием силы, прямо пропорциональной перемещению и направленной против направления перемещения.

Исследование колебаний пружинного маятника имеет большое практическое значение, например, при вычислении колебаний рессор автомобиля при езде; в исследовании воздействия колебаний на фундамент зданий и тяжелых станков, в определении эластичности ушных перепонок при диагностике лор-заболеваний. По этой причине изучение колебаний пружинного маятника является актуальной проблемой.

С целью уменьшения количества сил, действующих на колебательную систему, целесообразно использовать горизонтально расположенную колебательную систему пружина-шарик (d).

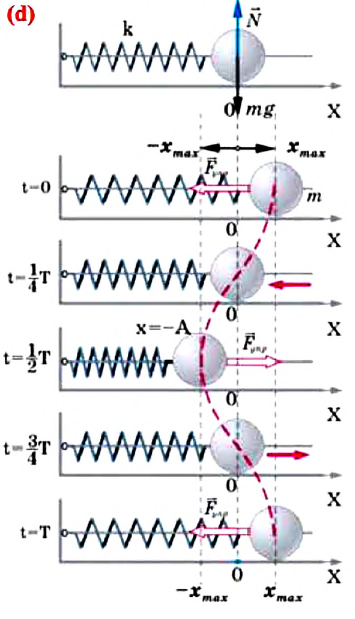
В этой системе действия силы тяжести и реакции опоры уравновешивают друг друга. При выведении шарика из состоянии равновесия, например, при растяжении пружины до положения сила упругости, возникающая в ней, сообщает шарику ускорение и приводит его в колебательное движение. По II закону Ньютона уравнение движения маятника можно записать так:

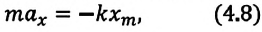
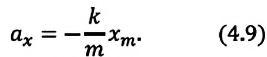
Формула (4.9) является уравнением свободных гармонических колебаний пружинного маятника.

Где 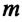— масса шарика, закрепленного на пружине, 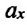— проекция ускорения шарика вдоль оси 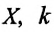— жесткость пружины, 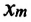-удлинение пружины, равное амплитуде колебания. Для данной колебательной системы отношение 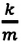— постоянная положительная величина (так как масса и жесткость не могут быть отрицательными). При сравнении уравнения колебаний (4.9) пружинного маятника с выражением для другого вида периодического движения — известным выражением центростремительного ускорения при равномерном движении по окружности получается, что отношение 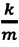соответствует квадрату циклической частоты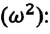

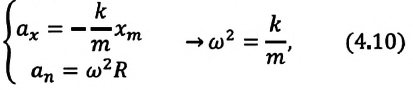
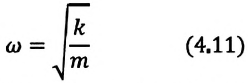
Таким образом, уравнение движения пружинного маятника можно записать и так:

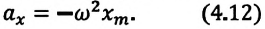
Уравнение (4.12) показывает, что колебания пружинного маятника с циклической частотой 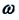являются свободными гармоническими колебаниями. Из математики известно, что решением этого уравнения является:

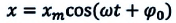
Так как тригонометрическая функция является гармонической функцией, то и колебания пружинного маятника являются гармоническими колебаниями.

Здесь 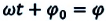фаза колебания, 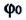— начальная фаза. Единица измерения фазы в СИ — радиан (1 рад). Фазу также можно измерять в градусах: 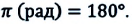Значение начальной фазы зависит от выбора начального момента времени. Начальный момент времени можно выбрить так, чтобы 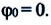В этом случае формулу гармонических колебаний пружинного маятника можно записать так:

или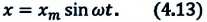

Из сравнения выражений (4.11) и (4.5) определяются величины, от которых зависят период и частота колебаний пружинного маятника:

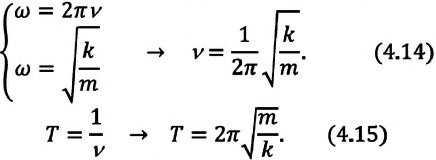
Из выражений (4.14) и (4.15) видно, что период и частота пружинного маятника зависят от жесткости пружины и массы груза, подвешенного к нему.

Гармонические колебания математического маятника

До наших дней дошла такая историческая информация: однажды в 1583 году итальянский ученый Г. Галилей, находясь в храме города Пиза, обратил внимание на колебательное движение люстры, подвешенной на длинном тросе. Он, сравнивая колебания люстры со своим пульсом, определил, что, несмотря на уменьшение амплитуды колебания, время, затрачиваемое на одно полное колебание (период колебания) люстры, не изменяется. Затем Галилей в результате многочисленных проведенных исследований, изменяя длину нитевого маятника, массу подвешенного к нему груза, высоту расположения маятника (по сравнению с уровнем моря), определил, от чего зависят период и частота колебаний маятника.

Гармонические колебания возникают также под действием силы тяжести. Это можно наблюдать с помощью математического маятника.

Математический маятник — это идеализированная колебательная система, состоящая из материальной точки, подвешенной на невесомой и нерастяжимой нити.

Для исследования колебаний математического маятника можно использовать систему, состоящую из тонкой длинной нити и шарика (b).

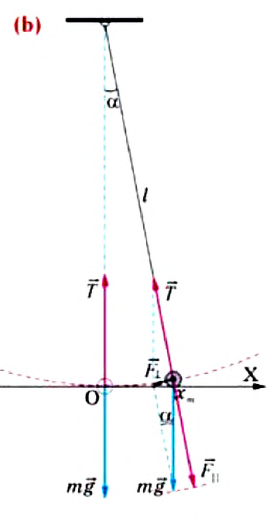
Сила тяжести 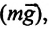действующая на шарик в положении равновесия маятника, уравновешивается силой натяжения нити 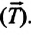Однако, если вывести маятник из состояния равновесия, сместив его на малый угол 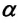в сторону, то возникают две составляющие вектора силы тяжести -направленная вдоль нити 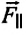и перпендикулярная нити 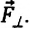Сила натяжения 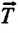и составляющая силы тяжести 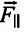уравновешивают друг друга. Поэтому равнодействующая сила будет равна составляющей 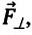«пытающейся» вернуть тело в положение равновесия (см.: рис. b). Учитывая вышеуказанное и ссылаясь на II закон Ньютона, можно написать уравнение колебательного движения тела массой 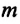в проекциях на ось ОХ:

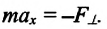
Приняв во внимание, что:

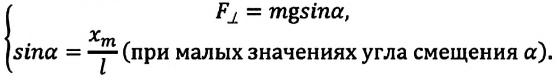
Для уравнения движения математического маятника получим:

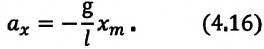
Где 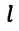— длина математического маятника (нити), 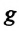— ускорение свободного падения, 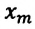— амплитуда колебания.

Для данной колебательной системы отношение — постоянная положительная величина, потому что ускорение свободного падения и длина нити не могут быть отрицательными. Если сравнить уравнения (4.16) и (4.10), с легкостью можно увидеть, что отношение также соответствует квадрату циклической частоты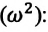

Таким образом, уравнение движения математического маятника можно записать и так:

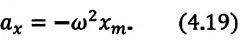
Уравнение (4.19) показывает, что колебания математического маятника являются гармоническими колебаниями с циклической частотой со. Из математики вы знаете, что решением этого уравнения является нижеприведенная функция:

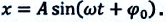
Так как эта функция является гармонической, то и колебания математического маятника являются гармоническими колебаниями.

Отсюда определяются величины, от которых зависят период и частота колебаний математического маятника:

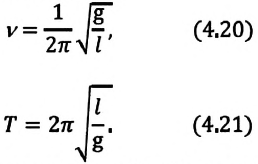
Таким образом, период и частота колебаний математического маятника зависят от длины маятника и напряженности гравитационного поля в данной точке.

Скорость и ускорение при гармонических колебаниях

Вы уже знакомы с основными тригонометрическими функциями и умеете строить графики тригонометрических уравнений, описывающих гармонические колебания.

При гармонических колебаниях маятника его смещение изменяется по гармоническому закону, поэтому не трудно доказать, что его скорость и ускорение также изменяются по гармоническому закону. Предположим, что смещение изменяется по закону косинуса и начальная фаза равна нулю

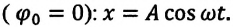
Так как скорость является первой производной смещения (координат) по времени, то:

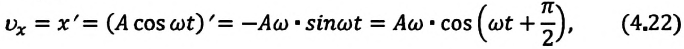
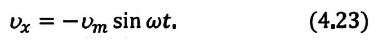
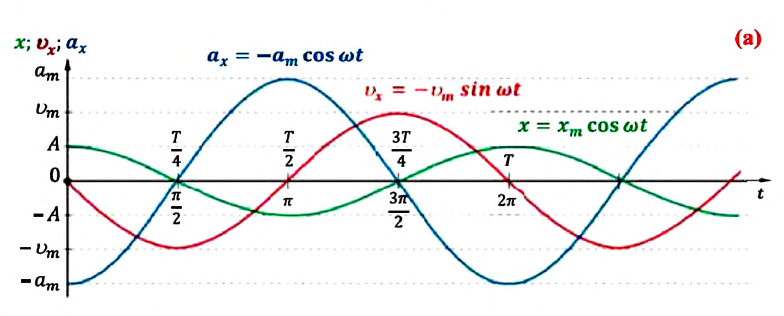
Как видно из выражения (4.23), скорость, изменяющаяся по гармоническому закону, опережает колебания смещения по фазе на (а).

Максимальное (амплитудное) значение скорости зависит от амплитуды, частоты и периода колебаний:

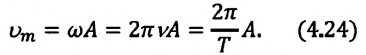
Так как ускорение является первой производной скорости по времени, то получим:

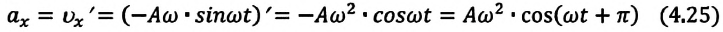
Как видим, колебания ускорения, изменяющегося по гармоническому закону, опережают колебания скорости по фазе на а колебания смещения на

(см.: рис. а). Максимальное (амплитудное) значение ускорения зависит от амплитуды, частоты и периода колебаний:

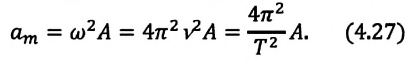
Превращения энергии при гармонических колебаниях

Теоретический материал

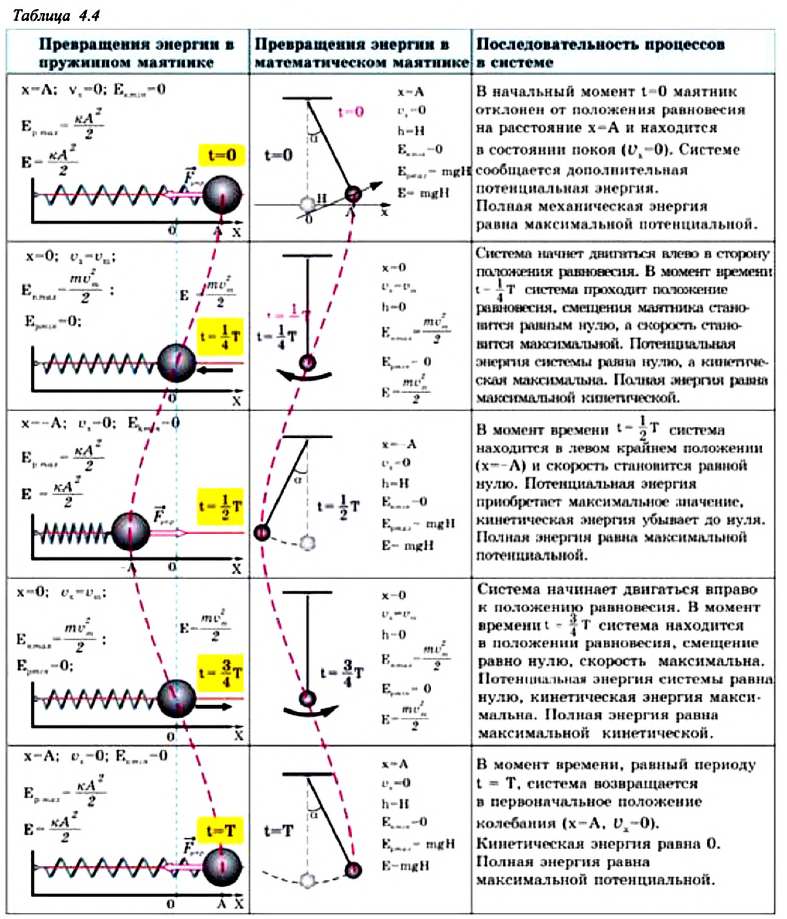
Потенциальная и кинетическая энергия свободных гармонических колебаний в замкнутой системе периодически превращаются друг в друга.

В таблице 4.4 дано сравнение превращений энергий в пружинном и математическом маятниках. Как видно из таблицы, потенциальная энергия колебательной системы в точке возвращения 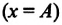имеет максимальное значение:

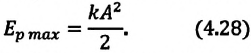
Если же маятник находится в точке равновесия, потенциальная энергия минимальна:

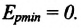
Кинетическая энергия системы, наоборот, в точке возвращения минимальна 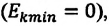а в точке равновесия максимальна:

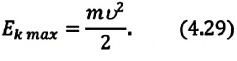
На рисунке (а) даны графики зависимости потенциальной и кинетической энергии при гармоническом колебательном движении от смещения.

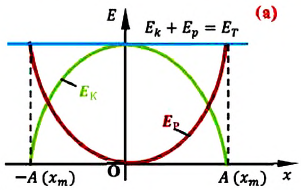
Полная механическая энергия замкнутой колебательной системы в произвольный момент времени 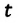остается постоянной (трение не учитывается):

a) для пружинного маятника:

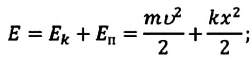
b) для математического маятника:

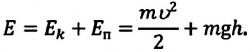
Если принять во внимание изменение смещения и скорости по гармоническому закону в формулах потенциальной и кинетической энергии колебательного движения, то станет очевидно, что при гармонических колебаниях эти энергии так же изменяются по гармоническому закону (b):

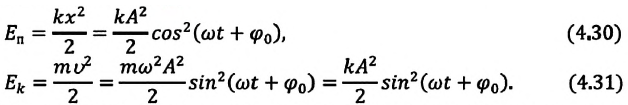
Как было отмечено выше, полная энергия системы не изменяется по гармоническому закону:

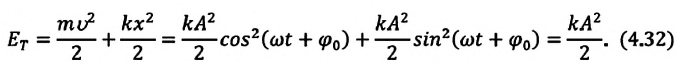
• Полная энергия гармонических колебаний прямо пропорциональна квадрату амплитуды колебаний.

Если же в системе существует сила трения, то его полная энергия не сохраняется — изменение полной механической энергии равно работе силы трения. В результате колебания затухают: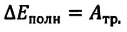

Превращения энергии при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий. Кинетической энергией тело обладает вследствие своего движения, а потенциальная энергия определяется взаимодействием тела с другими телами или полями. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силу трения не учитывают, то его механическая энергия сохраняется.

Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

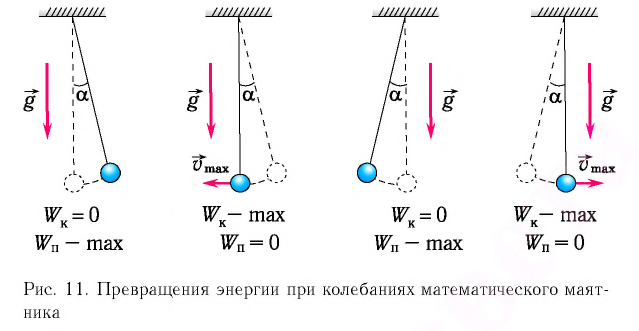
При отклонении маятника на угол а (рис. 7), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:


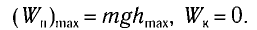
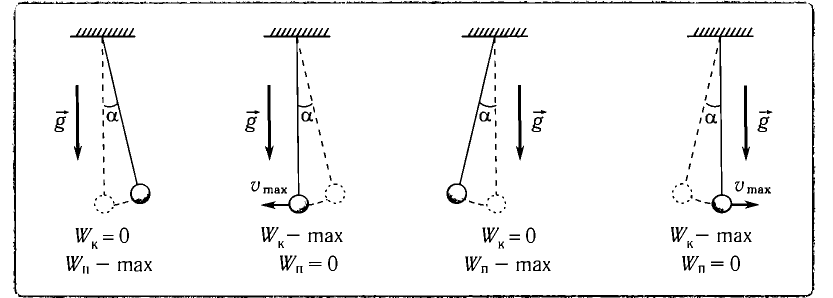
Рис. 7. Превращения энергии при колебаниях математического маятника

Поскольку при прохождении положения равновесия его потенциальная энергия равна нулю, то кинетическая энергия (а следовательно, и скорость) будет максимальна:

Из закона сохранения механической энергии следует (рис. 8), что

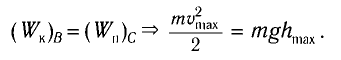(1)

Отсюда найдем модуль максимальной скорости маятника:

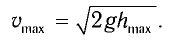(2)

Высоту можно выразить через длину маятника l и амплитуду колебаний А.

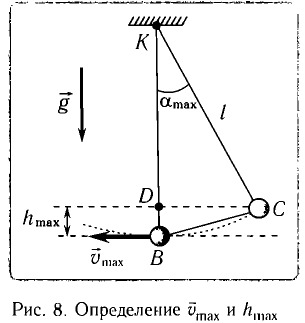
Если колебания малые, то 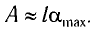Из треугольника KCD на рисунке 8 находим

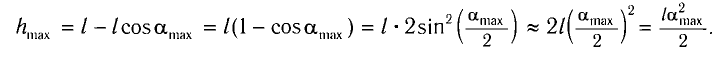
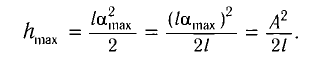
Подставив выражение для в формулу I (2), получим

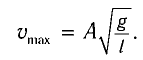
Подставляя выражения для и в соотношение (1), находим

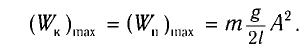
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную.

В любом промежуточном положении

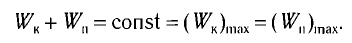
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 9). В крайних точках, когда координата груза принимает значение 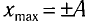, модуль его скорости равен нулю (v = 0) и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

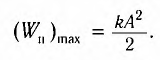
Таким образом, получаем, что механическая энергия гармонического осциллятора пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда x = 0, вся энергия осциллятора переходит в кинетическую энергию груза:

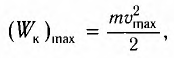
где 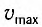— модуль максимальной скорости груза при колебаниях.

В промежуточных точках полная механическая энергия

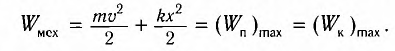
Отсюда можно вывести выражение для модуля скорости 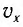груза в точке с

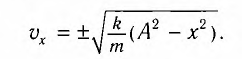
Так как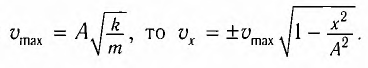

Энергия при гармонических колебаниях

Механическая энергия системы равна сумме ее кинетической и потенциальной энергии. Механическая энергия замкнутой системы, в которой не действуют силы трения (сопротивления), сохраняется.

Поскольку при колебаниях гармонического осциллятора силой трения пренебрегают, то его механическая энергия сохраняется. Рассмотрим превращения энергии при колебаниях математического маятника. Выберем систему отсчета таким образом, чтобы в положении равновесия его потенциальная энергия была равна нулю.

При отклонении маятника на угол 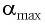(рис. 10), соответствующий максимальному смещению от положения равновесия, потенциальная энергия максимальна, а кинетическая энергия равна нулю:

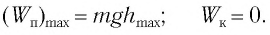
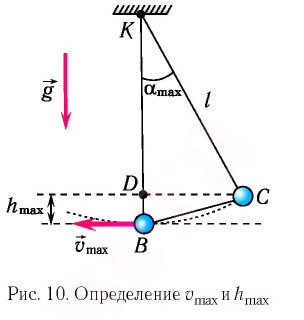
Поскольку при прохождении положения равновесия потенциальная энергия равна нулю 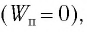то из закона сохранения механической энергии следует (см. рис. 10), что 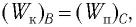т. е. кинетическая энергия маятника (а следовательно, и скорость) рис. ю. Определение^иhmax будет максимальна:

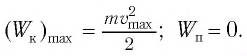
Запишем закон сохранения механической энергии, подставив в него выражения для потенциальной и кинетической энергии:

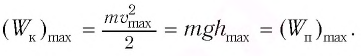
Отсюда найдем модуль максимальной скорости маятника:

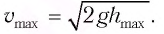
Высоту 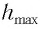можно выразить через длину 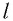маятника и амплитуду 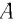колебаний. Если колебания малые, то 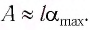Из 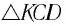(см. рис. 10) находим: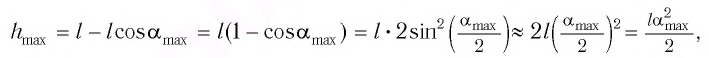

или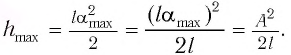

Подставив выражение (3) для 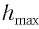в формулу (2), получим: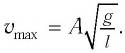

Подставляя выражения (3) для 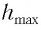и (4) для 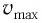в соотношение (1), находим:

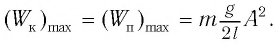
Таким образом, в положении равновесия потенциальная энергия полностью переходит в кинетическую, а в положениях максимального отклонения кинетическая энергия полностью переходит в потенциальную (рис. 11). В любом промежуточном положении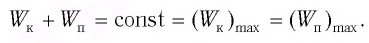

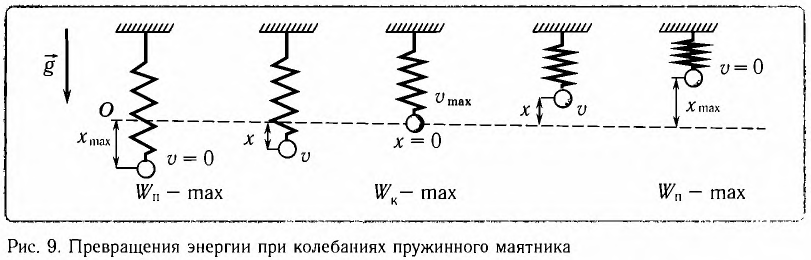
Покажем, что аналогичные превращения энергии имеют место и для пружинного маятника (рис. 12).

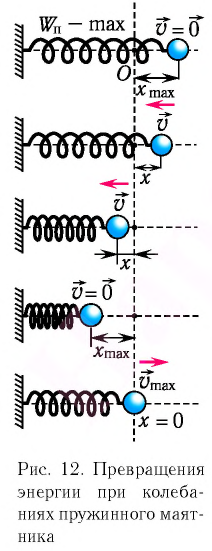
В крайних положениях, когда 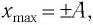модуль скорости маятника 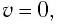и кинетическая энергия груза полностью переходит в потенциальную энергию деформированной пружины:

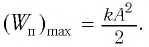
Таким образом, из соотношения (6) следует, что механическая энергия пружинного маятника пропорциональна квадрату амплитуды колебаний.

В положении равновесия, когда 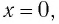вся энергия пружинного маятника переходит в кинетическую энергию груза:

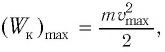
где 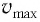— модуль максимальной скорости груза при колебаниях.

В положениях между крайними точками полная энергия

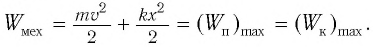
С учетом выражений для координаты 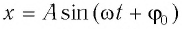и проекции скорости груза 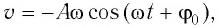а также для 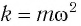находим его потенциальную энергию 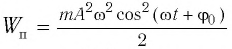и кинетическую энергию 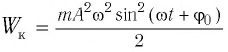в произвольный момент времени

Тогда полная механическая энергия пружинного маятника в этот же. момент времени есть величина постоянная и равная:

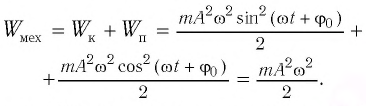
Таким образом, начальное смещение 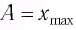определяет начальную потенциальную, а начальная скорость 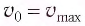определяет начальную кинетическую энергию колеблющегося тела. При отсутствии в системе потерь энергии процесс колебаний сопровождается только переходом энергии из потенциальной в кинетическую и обратно.

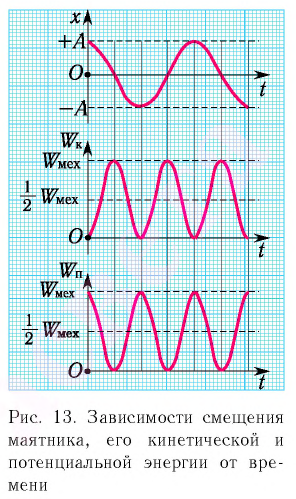
Заметим, что частота периодических изменений кинетической (потенциальной) энергии колеблющегося тела в два раза больше частоты колебаний маятника. Действительно, дважды за период механическая энергия тела будет полностью превращаться в потенциальную (в двух крайних положениях маятника) и дважды за период — в кинетическую (при его прохождении через положение равновесия) (рис. 13).

Пример №1

Математический маятник при колебаниях от одного крайнего положения до другого смещается на расстояние 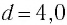см и при прохождении положения равновесия достигает скорости, модуль которой 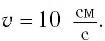Определите период 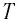колебании маятника.
Дано:


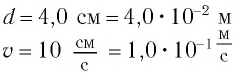
Решение

По закону сохранения механической энергии


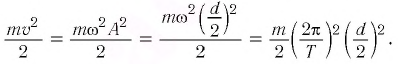
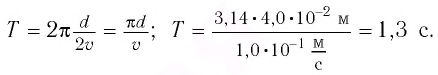
Ответ: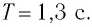

Пример №2

Груз массой 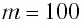г находится на гладкой горизонтальной поверхности и закреплен на легкой пружине жесткостью 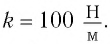Его смешают на расстояние 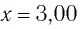см от положения равновесия и сообщают в направлении от положения равновесия скорость, модуль которой 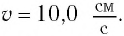Определите потенциальную 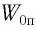и кинетическую 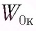энергию груза в начальный момент времени. Запишите кинематический закон движения груза.


Решение Потенциальная энергия груза: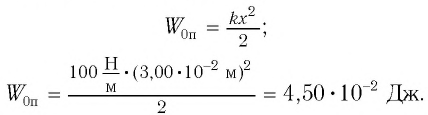

Кинетическая энергия груза: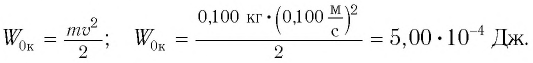

Начальное смещение груза не является амплитудой, так как вместе с начальным отклонением грузу сообщили и скорость. Однако полная энергия может быть выражена через амплитуду колебаний:

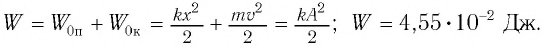
Отсюда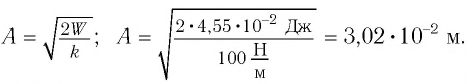

Циклическая частота: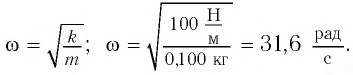

В начальный момент времени 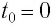координата груза 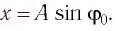Отсюда начальная фаза: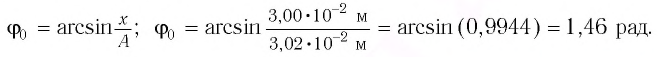

Тогда закон гармонических колебаний имеет вид (рис. 14):

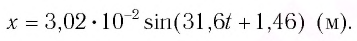
Ответ: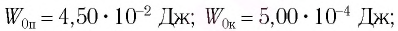

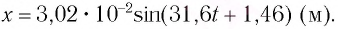
Рекомендую подробно изучить предметы:
  1. Физика
  2. Атомная физика
  3. Ядерная физика
  4. Квантовая физика
  5. Молекулярная физика
Ещё лекции с примерами решения и объяснением:
  • Вынужденные колебания в физике
  • Электромагнитные колебания
  • Свободные и вынужденные колебания в физике
  • Вынужденные электромагнитные колебания
  • Закон Архимеда
  • Движение жидкостей
  • Уравнение Бернулли
  • Механические колебания и волны в физике

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

источники:

http://www.eduspb.com/node/1780

http://www.evkova.org/garmonicheskie-kolebaniya-v-fizike

Источник

Добавить комментарий