Решение: : Рассмотрим уравнение координаты:
x = Xm∙соs(ω∙t + φ0),
где: х – координата тела, Хm – амплитуда, ω – угловая скорость, φ0 – начальная координата.
Для нахождения скорости возьмем первую производную по времени от х:
υ = – ω∙Хm∙sin(ω∙t+ φ0), υ = – 0,4∙π∙sin(4πt+π/4).
Для нахождения ускорения возьмем вторую производную по времени от х:
а = – ω2∙Хm∙соs(ω∙t+ φ0), а = -0,16∙π∙соs(4πt+π/4).
аmax = 0,5 м/с2, Fmax = m∙a, Fmax = 0,5 м/с2∙10∙10-3 кг, = 5∙10-3 Н.
[ {{E}_{Kmax }}=frac{mcdot upsilon _{max }^{2}}{2}, ]
υmax = 1,256 м/с, ЕКmax = 7,9∙10-3 Дж. Ответ: 5∙10-3 Н, 7,9∙10-3 Дж.
Условие задачи:
Материальная точка совершает гармонические колебания. Если при неизменной амплитуде увеличить частоту колебаний в два раза, во сколько раз изменится максимальное значение возвращающей силы, действующей на точку.
Задача №9.1.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(nu_2=2nu_1), (frac{F_{max2}}{F_{max1}}-?)
Решение задачи:
Если материальная точка совершает гармонические колебания, то уравнение этих колебаний можно представить в виде:
[x = Asin left( {omega t} right)]
В этой формуле (A) – амплитуда колебаний, (omega) – циклическая частота колебаний.
Чтобы найти уравнение ускорения точки при этих колебаниях, нужно дважды взять производную от уравнения колебаний. Сначала возьмем первую производную:
[x^{prime} = Aomega cos left( {omega t} right)]
Теперь берем вторую производную:
[x^{primeprime} = – A{omega ^2}sin left( {omega t} right)]
То есть мы имеем:
[a = – A{omega ^2}sin left( {omega t} right)]
Понятно, что максимальное по модулю значение ускорения в таком случае следует искать по формуле:
[{a_{max }} = A{omega ^2};;;;(1)]
Циклическая частота колебаний (omega) и частота колебаний (nu) связаны по известной формуле:
[omega = 2pi nu ]
Тогда формула (1) примет вид:
[{a_{max }} = 4{pi ^2}{nu ^2}A;;;;(2)]
Максимальную возвращающую силу (F_{max}) следует определять по формуле (это второй закон Ньютона):
[{F_{max }} = m{a_{max }}]
Тогда искомое отношение (frac{F_{max2}}{F_{max1}}) равно:
[frac{{{F_{max 2}}}}{{{F_{max 1}}}} = frac{{m{a_{max 2}}}}{{m{a_{max 1}}}}]
[frac{{{F_{max 2}}}}{{{F_{max 1}}}} = frac{{{a_{max 2}}}}{{{a_{max 1}}}}]
Учитывая формулу (2), имеем:
[frac{{{F_{max 2}}}}{{{F_{max 1}}}} = frac{{4{pi ^2}nu _2^2A}}{{4{pi ^2}nu _1^2A}}]
[frac{{{F_{max 2}}}}{{{F_{max 1}}}} = frac{{nu _2^2}}{{nu _1^2}}]
В условии говорится, что частоту колебаний увеличивают в два раза, то есть (nu_2=2nu_1), поэтому:
[frac{{{F_{max 2}}}}{{{F_{max 1}}}} = frac{{4nu _1^2}}{{nu _1^2}} = 4]
Ответ: увеличится в 4 раза.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.1.24 T=0,2 с – период гармонического колебания с амплитудой 10 см. Найти смещение тела
9.1.26 Материальная точка совершает гармонические колебания. Если при неизменной амплитуде
9.2.1 Во сколько раз изменится частота колебаний математического маятника
| 🎓 Заказ №: 21959 |
| ⟾ Тип работы: Задача |
| 📕 Предмет: Физика |
| ✅ Статус: Выполнен (Проверен преподавателем) |
| 🔥 Цена: 149 руб. |
👉 Как получить работу? Ответ: Напишите мне в whatsapp и я вышлю вам форму оплаты, после оплаты вышлю решение.
➕ Как снизить цену? Ответ: Соберите как можно больше задач, чем больше тем дешевле, например от 10 задач цена снижается до 50 руб.
➕ Вы можете помочь с разными работами? Ответ: Да! Если вы не нашли готовую работу, я смогу вам помочь в срок 1-3 дня, присылайте работы в whatsapp и я их изучу и помогу вам.
⚡ Условие + 37% решения:
Материальная точка массой 0,1 г колеблется согласно уравнению x = Asinɷt, где A = 5 см, 20 Гц . Определить максимальные значения возвращающей силы и кинетической энергии точки.
Решение Согласно условию задачи, материальная точка колеблется согласно уравнению x Аsint Где A – амплитуда колебаний; – циклическая частота. Взяв первую производную смещения по времени, найдем скорость колеблющейся точки: A t dt d A t dt dx cos sin (1) Для нахождения ускорения возьмем производную от скорости по времени: A t dt d A t dt d a sin cos 2 Возвращающую силу найдем исходя из второго закона Ньютона: F ma Где m – масса точки. Тогда из двух последних выражений можем записать: F m A sint 2 Отсюда видим, что максимальное значение силы Fmax будет равно: 2 Fmax mA
Готовые задачи по физике которые сегодня купили:
- Радиус-вектор частицы определяется выражением x y r t e t e 2 2 3 2 .
- Определить число полных колебаний маятника за промежуток времени, в течении которого амплитуда колебаний уменьшилась в три раза.
- Сколько метана(СН4) может вместить баллон емкостью 15 дм3 при давлении 106 Па и температуре 27 0С?
- Определить скорость поступательного движения сплошного цилиндра, скатившегося с наклонной плоскости высотой h 20 см.
- В сосуде вместимостью V 6 л находится при нормальных условиях двухатомный газ.
- Камень, привязанный к веревке длиной 1 м, свободно вращается в вертикальной плоскости с постоянной скоростью 1,4 м/с.
- При температуре t=50 °С давление насыщенного водяного пара p=12,3 кПа.
- Уравнение колебаний точки имеет вид x Acos t 0,2.
- Свободные пружины с пренебрежимо малой массой при подвешивании к ним грузов массами m 0,6 кг 1 и m 0,4 кг 2 , соответственно, одинаково удлинились на 0,1 м.
- Сосуд откачан до давления р = 1,33·10−9 Па; температура воздуха t = 15 °С.
6.33 Колебания материальной точки массой m=0,1 г происходят согласно уравнению x=A cos ωt, где A=5 см, ω=20 с-1. Определить максимальные значения возвращающей силы Fmax и кинетической энергии Tmax. |
| Задача из учебного пособия Чертов-Воробьев |
|
Данная задача находится в разделе Решебник Чертов-Воробьев на странице № 7 <<< Предыдущая задача из Чертов-Воробьев |
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146133.png)
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146127.png)
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146124.png)
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146122.png)
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146128.png)
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/146132.png)
Чтобы получить решение, напишите мне в WhatsApp, оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным, не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу, я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№5-2 7.1. Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.
Решение.
Уравнение гармонических колебаний точки имеет вид: , где м – амплитуда колебаний; рад/с – круговая частота колебаний. Найдём закон изменения скорости точки: . Определим зависимость от времени кинетической энергии точки:
- Частица массой m совершает колебания по закону x = A sinwt. Определить максимальное значение возвращающей силы и кинетической энергии. m = 60•10-3 кг, A = 9,0•10-2 м, w = 2,5 с-1.
- Материальная точка массой 5 г совершает гармонические колебания с частотой 0,5 с-1. Амплитуда колебаний 0,03 м. Определить скорость точки в момент, когда смещение её равно 1,5 см.
- Материальная точка массой 0,1 г колеблется согласно уравнению x = A sinwt, где A = 5 см, v = 20 Гц. Определить максимальные значения возвращающей силы и кинетической энергии точки.
- Колебания материальной точки массой m = 0,1 г происходит согласно уравнению x = A coswt, где A = 5 см, w = 20 с-1. Определить максимальное значение возвращающей силы и полную энергию колебаний.

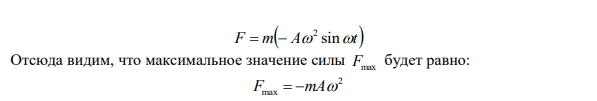

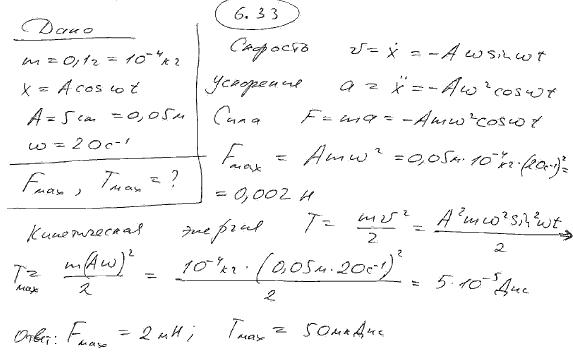
![Колебания материальной точки массой 0,1 г происходят по закону x = 0,05 cos(20t) [м]. Определить максимальные значения возвращающей силы и кинетической энергии.](https://natalibrilenova.ru/media/images/153204.png)
