Как найти максимальное значение выражения

Как найти наибольшее значение выражения

Чтобы найти множество значений функции, сначала необходимо узнать множество значений аргумента, а затем с использованием свойств неравенств отыскать соответственные наибольшее и наименьшее значения функции. К этому сводится решение многих практических задач.

Инструкция

Выполните нахождение наибольшего значения функции, которая на отрезке имеет конечное число критических точек. Для этого вычислите ее значение во всех точках, а также на концах отрезка. Из полученных чисел выберите наибольшее. Метод поиска наибольшего значения выражения используется для решения различных прикладных задач.

Выполните для этого следующие действия: переведите задачу на язык функции, выберите параметр x, через него выразите нужную величину как функцию f(x). Используя средства анализа, найдите наибольшее и наименьшее значения функции на определенном промежутке.

Воспользуйтесь следующими примерами для нахождения значения функции. Найти значения функции y=5-корень из (4 – x2). Следуя определению квадратного корня, получим 4 – x2 > 0. Решите квадратичное неравенство, в результате получите, что -2

Возведите в квадрат каждое из неравенств, затем умножьте все три части на –1, прибавьте к ним 4. Затем введите вспомогательную переменную и сделайте предположение, что t = 4 – x2, где 0 значение функции получится на окончаниях промежутка.

Произведите обратную замену переменных, в результате вы получите следующее неравенство: 0 значение, соответственно, 5.

Воспользуйтесь методом применения свойств непрерывной функции, чтобы определить наибольшее значение выражения. В данном случае используйте числовые значения, которые принимаются выражением на заданном отрезке. Среди них всегда присутствует наименьшее значение m и наибольшее значение M. Между этими числами заключается множество значений функции.

Возведите в квадрат каждое из неравенств, затем умножьте все три части на –1, прибавьте к ним 4. Затем введите вспомогательную переменную и сделайте предположение, что t = 4 – x2, где 0 значение функции получится на окончаниях промежутка.

Произведите обратную замену переменных, в результате вы получите следующее неравенство: 0 значение, соответственно, 5.

Воспользуйтесь методом применения свойств непрерывной функции, чтобы определить наибольшее значение выражения. В данном случае используйте числовые значения, которые принимаются выражением на заданном отрезке. Среди них всегда присутствует наименьшее значение m и наибольшее значение M. Между этими числами заключается множество значений функции.

Источники:

• найти наименьшее значение выражения

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Чтобы найти наибольшее значение тригонометрического выражения, во многих случаях достаточно знать область значений синуса, косинуса, тангенса, котангенса и свойства  неравенств.

Примеры.

Найти наибольшее значение выражения:

   

Решение:

Область допустимых значений данного выражения — вся числовая прямая:

ОДЗ: α∈(-∞; ∞).

Область значений косинуса — промежуток [-1;1]. Для оценки значений удобнее использовать двойное неравенство:

   

Умножаем неравенство почленно на 7. При умножении на положительное число знаки неравенства не изменяются:

   

   

Затем прибавляем почленно 5:

   

   

Таким образом, наибольшее значением выражения равно 12 (наименьшее — -2, область значений — [-2:12]).

   

Решение: ОДЗ: φ∈ (-∞; ∞).

Область значений синуса — промежуток [-1;1] или

   

При умножении на отрицательное число знаки неравенства меняются на противоположные:

   

   

Перепишем в порядке возрастания

   

Прибавляем почленно 4

   

   

Наибольшее значение выражения равно 7 (наименьшее — 1, область значений — [1;7]).

   

Решение:  ОДЗ:  х∈ (-∞; ∞).

   

   

   

   

   

Наибольшее значение выражения равно 10 (наименьшее — 8, область значений — [8;10]).

(Замечание. Если предварительно преобразовать данное выражение:

   

   

то можно упростить его оценку, поскольку в этом случае не нужно умножать неравенство на отрицательное число).

   

Решение: Дробь имеет смысл, если знаменатель отличен от нуля, поэтому ОДЗ: sinα≠0. Удобнее всего работать с ОДЗ на единичной окружности: точки α=0 и α=П, в которых sinα обращается в нуль, выкалываем:

 Теперь можно упростить выражение, сократив его

   

Осталось оценить полученное выражение.

   

Однако, с учетом ОДЗ, имеем:

   

(cosα=1 при α=0,  cosα=-1 при α=П).

   

   

   

Выражение не принимает ни наибольшего, ни наименьшего значений (область значений выражения — (8;10)).

В следующий раз продолжим рассматривать выражения с дробями, позже — выражения вида a∙sinα+b∙cosα.

We will learn how to find the maximum and minimum values of
the quadratic Expression ax^2 + bx + c (a ≠ 0).

When we find the maximum value and the minimum value of ax^2 + bx + c then let us assume y = ax^2 + bx + c.

Or, ax^2 + bx + c – y = 0

Suppose x is real then the discriminant of equation ax^2 + bx + c – y = 0 is ≥ 0

i.e., b^2 – 4a(c – y) ≥ 0

Or, b^2 – 4ac + 4ay ≥ 0

4ay ≥ 4ac – b^2

Case I: When a > 0 

When a > 0 then from 4ay ≥ 4ac – b^2 we get, y ≥
4ac – b^2/4a

Therefore, we clearly see that the expression y becomes
minimum when a > 0

Thus, the minimum value of the expression is 4ac – b^2/4a.

Now, substitute y = 4ac – b^2/4a in equation ax^2 + bx + c –
y = 0 we have,

ax^2 + bx + c – (4ac – b^2/4a) = 0

or, 4a^2x^2 + 4abx + b^2 = 0

or, (2ax + b)^2 = 0

or, x = -b/2a

Therefore, we clearly see that the expression y gives its
minimum value at x = -b/2a

Case II: When a < 0

When a < 0 then from 4ay ≥ 4ac – b^2 we get,

y ≤ 4ac – b^2/4a

Therefore, we clearly see that the expression y becomes
maximum when a < 0.

Thus, the maximum value of the expression is 4ac – b^2/4a.

Now substitute y = 4ac – b^2/4a in equation ax^2 + bx + c –
y = 0 we have,

ax^2 + bx + c -(4ac – b^2/4a) =0

or, 4a^2x^2 + 4abx + b^2 = 0

or, (2ax + b)^2 = 0

or, x = -b/2a.

Therefore, we clearly see that the expression y gives its
maximum value at x = -b/2a.

Solved examples to find the maximum and minimum values of
the quadratic Expression ax^2 + bx + c (a ≠ 0):

1. Find the values of x where the quadratic expression 2x^2 –
3x + 5 (x ϵ R) reaches a minimum value. Also find the minimum value.

Solution:

Let us assume y = 2x^2 – 3x + 5

Or, y = 2(x^2 – 3/2x) + 5

Or, y = 2(x^2 -2 * x * ¾ + 9/16 – 9/16) + 5

Or, y = 2(x – ¾)^2 – 9/8 + 5

Or, y = 2(x – ¾)^2 + 31/8

Hence, (x – ¾)^2 ≥ 0, [Since x ϵ R]

Again, from y = 2(x – ¾)^2 + 31/8 we can clearly see that y ≥
31/8 and y = 31/8 when (x – ¾)^2 = 0 or, x = ¾

Therefore, when x is ¾ then the expression 2x^2 – 3x + 5 reaches
the minimum value and the minimum value is 31/8.

2. Find the value of a when the value of 8a – a^2 – 15 is maximum.

Solution:

Let us assume y = 8a – a^2 -15

Or, y = – 15 – (a^2 – 8a)

Or, y = -15 – (a^2 – 2 * a * 4 + 4^2 – 4^2)

Or, y = -15 – (a – 4)^2 + 16

Or, y = 1 – (a – 4)^2

Hence, we can clearly see that (a – 4)^2 ≥ 0, [Since a is
real]

Therefore, from y = 1 – (a – 4)^2 we can clearly see that y ≤
1 and y = 1 when (a – 4)^2 = 0 or, a = 4.

Therefore, when a is 4 then the expression 8a – a^2 – 15 reaches
the maximum value and the maximum value is 1.

Математики и Data Science-специалисты должны хорошо разбираться в функциях. Предлагаем попрактиковаться в решении задач на обнаружение максимальных и минимальных значений у заданных функций.

Максимум

Задумываясь над тем, как найти максимальное значение функции, нужно четко понимать, с чем предстоит иметь дело. Для этого нужно запомнить такое определение:

Наибольшее значение функции y = f(x) на промежутке x – это max y = f(x₀). Оно будет при любом значении x€ X, x≠x₀ делает справедливым неравенство: f(x)≤f(x₀).

Максимальное значение (максимум) – это точка на функции, в которой значение функции больше, чем в соседних «отметках».

Минимум

Наименьшее значение функции находить так же легко, как и наибольшее. Но сначала нужно понимать, что это такое.

Значение функции на отрезке будет считаться минимумом, если оно меньше, чем в соседних «отметках». Здесь действует такое определение:

Наименьшее значение функции y=f(x) на промежутке x – это miny=f(x₀), которое при любом значении x€ X, x≠x₀ делает справедливым неравенство f(x)≥f(x₀).

Соответствующие определения являются достаточными и очевидными. Если говорить простыми словами, то максимум функции – это ее самое большое значение на заданном промежутке (участке) при абсциссе x₀, а минимум – самое маленькое.

Стационарные точки

При решении вопроса о том, как найти наибольшее или наименьшее значение функции, стоит обратить внимание на так называемые «стационарные точки». Это – значения аргумента функции, при которых ее производная будет равняться нулю.

Стационарная точка – это «отметка», в которой расположен экстремум дифференцируемой функции. А именно – локальный минимум или максимум. В одной из таких «отметок» записанное выражение будет достигать своих предельных параметров.

Здесь рекомендуется запомнить следующее:

1. Экстремум функции – это минимумы и максимумы.
2. Если определить производную в точках экстремумов, она будет равно 0.
3. Когда говорят «экстремумы», подразумевается значение функции. Если же речь идет об «отметках» экстремумов, рассматривать стоит x, в которых достигаются соответствующие пределы.

 Этого достаточно для того, чтобы разобраться, как найти наибольшее на заданном отрезке у выражения. Для реализации поставленной задачи вовсе не обязательно составлять график. Поэтому сначала воспользуемся записями формул и вычислений.

План действий

Пример – дана функция f(x) на отрезке [a, b]. Наибольшее и наименьшее значение такой непрерывной функции достигаются в определенных местах. Это – критические точки. Там, где производная записанного выражения будет равно нулю.

Для того, чтобы найти наибольшие значения уравнения, потребуется придерживаться следующего алгоритма:

1. Узнайте, какая перед вами функция. Для этого нужно проверить ее на непрерывность. В расчет обязательно берется заданный отрезок.
2. Если запись непрерывная – ищем производную.
3. После того, как найдем производную, приравниваем ее к нулю. Это поможет найти точки экстремумов. В результате получаются корни.
4. Образовавшиеся корни – это критические точки. Нужно выбрать те «параметры», что относятся к промежутку [a, b].
5. Вычислить значения функции на концах отрезка [a, b].
6. Определить значения имеющегося выражения в критических «отметках».

Теперь понятно, как найти наибольшие функции на заданном отрезке. После произведенных подсчетов остается выбрать из результатов M (максимум) и m (минимум).

На отрезке

Разобравшись в тем, как найти наибольшие «параметры» выражения «на бумаге», стоит рассмотреть соответствующий процесс на графиках. Определять максимумы/минимумы в данном случае будет проще.

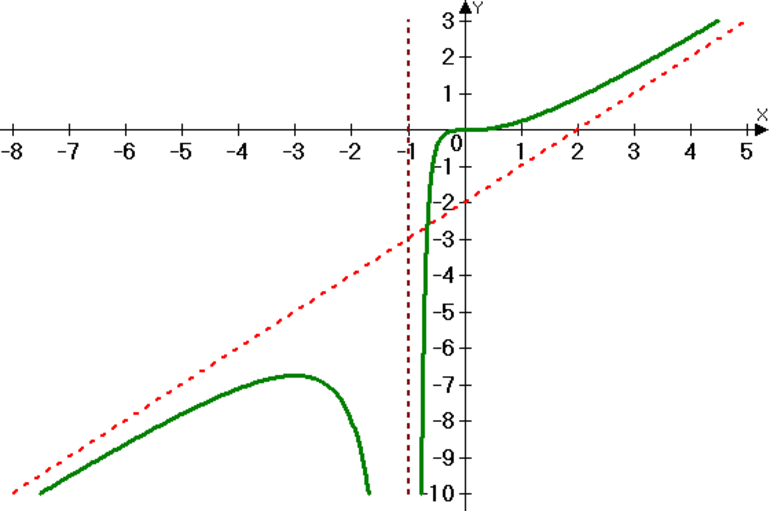
Первый график указывает на выражение, у которого точка минимума и максимума находятся в стационарных точках на промежутке [-6;6]. Соответствующие «пределы» обозначены жирным.

Второй график указывает на изменение отрезка. Теперь он будет [1;6]. Минимальное значение останется прежним. А вот максимальное – изменится. Оно образуется в правой части в точке с абсциссой. Поиск минимального «параметра» окажется в критической точке.

Задумываясь, как найти наименьшие или «самые крупные» параметры выражения на графике, можно также рассмотреть третий рисунок. Здесь функция принадлежала промежутку [-3;2]. Чтобы найти наибольшее и наименьшее в таком случае, предстоит учитывать абсциссы. В них достигаются соответствующие пределы.

Открытый интервал

Если промежуток задан конкретным числом, определить экстремумы будет не так сложно. Иначе происходит, если интервал открыт.

Здесь:

1. Функция будет принимать максимум/минимум по значению в стационарных точках на открытом интервале от -6 до 6. Ответ – на 4 рисунке.
2. Если взять отрезок [1;6), минимум будет достигнут в стационарной точке. А вот максимум – неизвестен. Связано это с тем, что 6 не принадлежит к заданному интервалу. Если бы «шестерка» относилась к соответствующему промежутку, ответ на вопрос относительно определения максимума оказался понятным. Максимальный параметр был бы в точке с абсциссой 6.
3. На рисунке 6, задумываясь, как найти наименьшие «параметры», нужно обратить внимание на заданный интервал. Он равен (-3;2]. Минимум будет достигнут в правой границе. А вот максимум – не определен.

Найти значения на графиках обычно проще, чем «в чистых формулах». Соответствующие задания можно отыскать тут.

Бесконечность

Иногда значения функций нужно найти на бесконечном промежутке. Графически возможны такие ситуации:

На 7 рисунке функция достигает максимума в стационарной точке с абсциссой 1. Минимум окажется на границе интервала справа. На минус бесконечности значения приближаются к y=3 асимптотически.

Если взять интервал от 2-х до «плюс бесконечности», заданная функция не будет иметь ни максимумов, ни минимумов. Значения здесь стремятся к бесконечности. Связано это с тем, что x=2 является вертикальной асимптотой. Если абсцисса стремится к плюс бесконечности, значения будут асимптотически подходить к y=3. Соответствующий пример показан на рисунке 8.

Чтобы не приходилось долго разбираться с тем, как найти наименьшее у заданной функции, не путаться с тем, какие знаки производной использовать, а также легко строить графики, можно воспользоваться специальными онлайн калькуляторами. А еще – закончить тематические дистанционные онлайн курсы.

Узнать ещё

Знание — сила. Познавательная информация

Найти наибольшее значение выражения

Чтобы найти наибольшее значение тригонометрического выражения, во многих случаях достаточно знать область значений синуса, косинуса, тангенса, котангенса и свойства неравенств.

Найти наибольшее значение выражения:

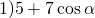
Область допустимых значений данного выражения — вся числовая прямая:

Область значений косинуса — промежуток [-1;1]. Для оценки значений удобнее использовать двойное неравенство:

Умножаем неравенство почленно на 7. При умножении на положительное число знаки неравенства не изменяются:

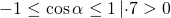0> right.]» title=»Rendered by QuickLaTeX.com»/>

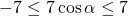
Затем прибавляем почленно 5:

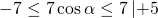
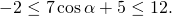
Таким образом, наибольшее значением выражения равно 12 (наименьшее — -2, область значений — [-2:12]).

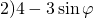
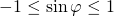
При умножении на отрицательное число знаки неравенства меняются на противоположные:

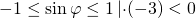
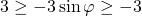
Перепишем в порядке возрастания

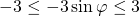
Прибавляем почленно 4

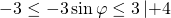
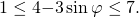
Наибольшее значение выражения равно 7 (наименьшее — 1, область значений — [1;7]).

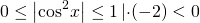
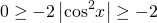
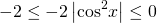
Наибольшее значение выражения равно 10 (наименьшее — 8, область значений — [8;10]).

(Замечание. Если предварительно преобразовать данное выражение:

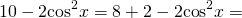
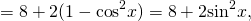
то можно упростить его оценку, поскольку в этом случае не нужно умножать неравенство на отрицательное число).

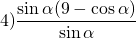
Решение: Дробь имеет смысл, если знаменатель отличен от нуля, поэтому ОДЗ: sinα≠0. Удобнее всего работать с ОДЗ на единичной окружности: точки α=0 и α=П, в которых sinα обращается в нуль, выкалываем:

Теперь можно упростить выражение, сократив его

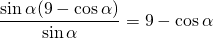
Осталось оценить полученное выражение.

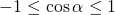
Однако, с учетом ОДЗ, имеем:

(cosα=1 при α=0, cosα=-1 при α=П).

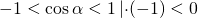
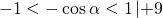
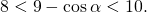
Выражение не принимает ни наибольшего, ни наименьшего значений (область значений выражения — (8;10)).

В следующий раз продолжим рассматривать выражения с дробями, позже — выражения вида a∙sinα+b∙cosα.

Источник

Как найти наибольшее и наименьшее значение функции

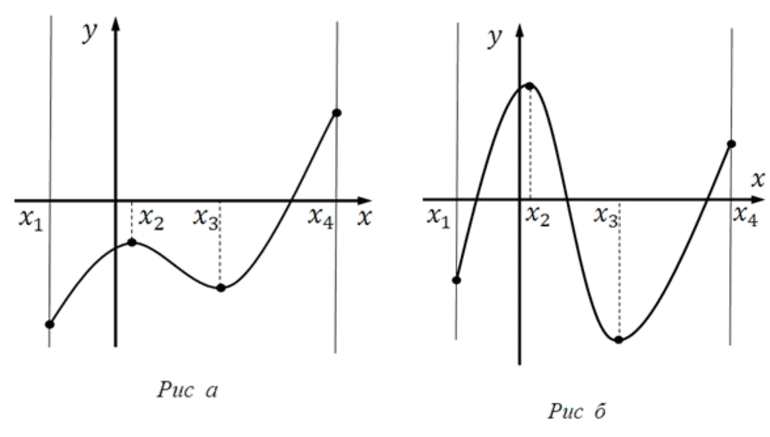
Общая информация

Исследование функции — распространенная задача, которая показывает ее поведение и свойства. Одним из элементов считается нахождение максимума и минимума функции. Существуют специальные программы для нахождения этих значений (онлайн-калькулятор). Однако каждому следует понимать принцип нахождения, поскольку это может пригодиться в жизни.

Для решения такого типа задач необходим определенный «багаж» знаний, поскольку без него вообще не обойтись. В его состав входят следующие элементы:

1. Нахождение области определения функции (ОДФ).
2. Понятие дифференциала и основные методы его нахождения.
3. Умение решать уравнения.
4. Знание графиков простых функций.
5. Основные типы функций, полуинтервал и интервал.

Все пять навыков приобрести несложно, кроме второго. В этом нужно подробно разобраться, поскольку очень важно уметь находить производные (дифференциалы) не только табличных элементарных функций, но и сложных. Важно знать основные свойства, которые применяются для нахождения производной.

Область определения

Область определения какой-либо функции вида y = f(x) — область значений аргумента, при которых она существует. У каждой функции существует два типа неизвестных: зависимые и независимые. К первым следует отнести переменную y, которая зависит от независимой переменной «х». Необходимо отметить, что бывают функции, в которых нет аргумента. Примером их считается функция вида y = const, где const — константа (любое число).

Область определения обозначается в теории литерой «D». Однако обозначение можно менять, когда исследуются несколько функций. Чтобы не путаться, специалисты рекомендуют следующую запись D(f(x)). Например, для y = x^2 — 27x и y = 12sinx ОДФ записывается таким образом: D(x^2 — 27x) и D(12sinx) соответственно.

Обозначение интервалов

Результатом решения задач на нахождение ОДЗ является определенный интервал. Важно правильно его обозначать, поскольку это существенно влияет на решение. Нужно руководствоваться следующими правилами:

1. Жесткая граница обозначается квадратной скобкой «[» или «]». Она обозначает, что число входит включительно в этот интервал. Можно использовать не только одну скобку, но и две одновременно.
2. Для обозначения числового значения, которое не входит в промежуток, пользуются круглыми скобками «(» и «)». Их можно применять одновременно.
3. Типы границ можно комбинировать.
4. Если нужно объединить интервалы, то следует использовать символ «U».

Очень важно правильно читать интервалы. Например, запись (1;4) читается следующим образом: переменная принимает значения, которые находятся в интервале от 1 не включительно до 4 не включительно. Это числа 2 и 3, поскольку 1 и 4 не входят в промежуток. Запись вида [5;10) читается таким образом: некоторое значение принадлежит интервалу от 5 включительно, до 10 не включительно.

Зависимость от типа

Функции различаются между собой. От этого и зависит нахождение их области определения. Они бывают простыми и сложными. Первые состоят из единичных элементов, а сложные включают в себя несколько типов. Их еще называют составными. Простые классифицируются на три вида:

1. Алгебраические: рациональные и иррациональные.
2. Тригонометрические: sin, cos, tg и ctg.
3. Трансцендентные: степенные, показательные и логарифмические.

Рациональные бывают целыми и дробными. Они не включают в себя выражения, содержащие такие элементы: корень, степень, логарифм и тригонометрические функции. D(f) этих функций — все действительные числа (Z). Если она является дробной, то это означает, что в ее числителе и (или) знаменателе находится аргумент, значение которого не должно обращать ее в пустое множество.

Когда под корнем находится выражение, содержащее независимую переменную, то она называется иррациональной. В этом случае D(f) — множество Z, кроме тех, которые превращают выражение под корнем четной степени в отрицательное значение. Функция, представленная степенными выражениями, имеет D(f) = Z, но только тогда, когда значение аргумента не превращает функцию в пустое множество.

Метод нахождения

Для решения любой задачи нужно применять определенные правила. Они называются алгоритмом. Для каждого типа функций существует конкретный вариант решения. Для дробной он является следующим:

1. Найти корни уравнения знаменателя, приравнивая его к 0.
2. Определить интервал, значения из которого может принимать аргумент.

В случае, когда выражение является иррациональной функцией, корень которой является четным, следует решать не уравнение, а неравенство. Его значение не должно быть меньше 0. Для логарифмического типа выражение натурального логарифма (ln) должно быть всегда больше 0.

Для sin(x) и cos(x) областью определения является множество значений Z. Однако для tg(x) и ctg(x) следует помнить, что аргумент не должен принимать значение x = (Pi / 2) + Pi * k и x = Pi * k соответственно. Следует отметить, что коэффициент k принадлежит множеству чисел Z.

Для примера нужно разобрать задачу, в которой следует найти D(3x / [(x — 1) * (x + 1) * (10 — x)^(1/2)]). Решать ее необходимо по такому алгоритму:

1. Знаменатель является сложным. Он состоит из двух выражений: (x — 1) * (x + 1) и (10 — x)^(1/2).
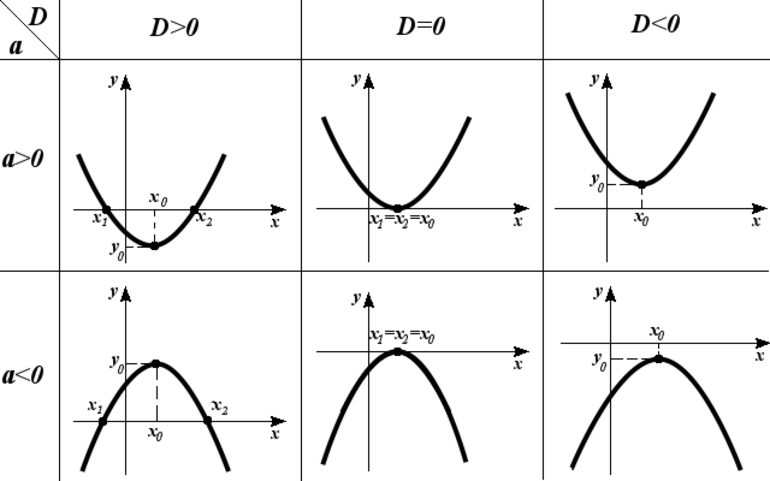
2. Первое выражение (решить уравнение): (x — 1) * (x + 1) = 0. Оно имеет два корня: x1 = -1 и x2 = 1. Числовой промежуток: (-бесконечность;-1) U (1;+бесконечность).
3. Второе (неравенство): (10 — x) a). Например, (a;+inf): х = lim [f(x)], где x->a и x->+inf.

Для нахождения минимального и максимального значения функции достаточно материала, изложенного выше. Специалисты рекомендуют разобраться с теорией, а затем переходить к практике.

Примеры решений

Дана квадратичная функция y = x^2 + 6x + 9. Необходимо найти наименьшее значение функции квадратного уравнения на отрезке [1;5]. Для этой цели нужно воспользоваться алгоритмом:

1. D(y): все множество Z.
2. Отрезок входит в D(y).
3. Производная: y’ = [x^2 + 6x + 9]’ = 2x + 6 (существует во всех точках).
4. Стационарные точки (y’ = 0): 2x + 6 = 0. Отсюда, x = -3.
5. Подставить в исходное выражение: y(-3) = (-3)^2 + 6 * (-3) + 9 = 9 — 18 + 9 = 0, y(1) = (1)^2 + 6 * (1) + 9 = 1 + 6 + 9 = 16 и y(5) = (5)^2 + 6 * (5) + 9 = 25 + 30 + 9 = 64.
6. Максимум и минимум (с учетом стационарной точки и интервала): MIN(y) = 0 и MAX(y) = 64.

Одним из простейших типов задач является следующая: найдите наибольшее значение линейной функции z = 5x + 10 на отрезке [-3;3]. Для ее решения можно также воспользоваться алгоритмом:

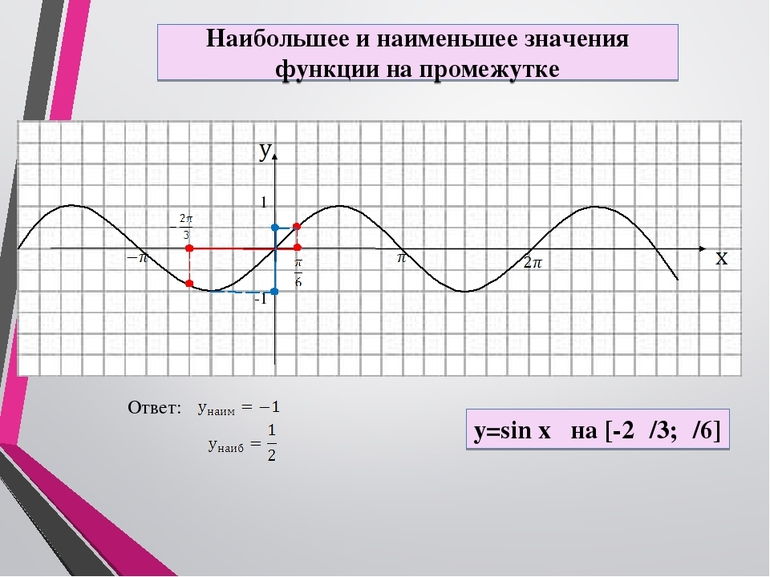
1. D(z) — все значения от бесконечно малого до бесконечно большого чисел.
2. Промежуток, на котором нужно найти максимум и минимум, полностью входит в D(f).
3. Дифференциал: z’ = 5 (существует во всех точках, а стационарных точек нет вообще).
4. Минимум и максимум: MIN(z(-3)) = 5 * (-3) + 10 = -5 и MAX(z(3)) = 5 * (3) + 10 = 25.

Последнюю задачу необязательно решать по алгоритму, поскольку она считается простейшей. Математики рекомендуют тренироваться в нахождении MIN и MAX функции, поскольку только практика позволяет быстро решать задачи.

Таким образом, для нахождения максимального и минимального значений заданной функции необходимо пользоваться специальным универсальным алгоритмом. Кроме того, нужно правильно находить дифференциалы, область определения, а также разбираться в интервалах.

Источник

Поиск наибольшего/наименьшего значения у сложных функций

(blacktriangleright) Для того, чтобы найти наибольшее/наименьшее значение функции на отрезке ([a,b]) , необходимо схематично изобразить график функции на этом отрезке.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ( (f’>0) ) и убывания ( (f’ ) функции, критические точки (где (f’=0) или (f’) не существует).

(blacktriangleright) Не стоит забывать, что наибольшее/наименьшее значение функция может принимать не только во внутренних точках отрезка ([a,b]) , а также на его концах.

(blacktriangleright) Наибольшее/наименьшее значение функции — это значение координаты (y=f(x)) .

(blacktriangleright) Производная сложной функции (f(t(x))) ищется по правилу: [<Large>]
[begin <|r|c|c|>hline & text <Функция >f(x) & text <Производная >f'(x)\ hline textbf <1>& c & 0\&&\ textbf <2>& x^a & acdot x^\&&\ textbf <3>& ln x & dfrac1x\&&\ textbf <4>& log_ax & dfrac1\&&\ textbf <5>& e^x & e^x\&&\ textbf <6>& a^x & a^xcdot ln a\&&\ textbf <7>& sin x & cos x\&&\ textbf <8>& cos x & -sin x\[1ex] hline end quad quad quad quad begin <|r|c|c|>hline & text <Функция >f(x) & text <Производная >f'(x)\ hline textbf <9>& mathrm, x & dfrac1<cos^2 x>\&&\ textbf <10>& mathrm, x & -,dfrac1<sin^2 x>\&&\ textbf <11>& arcsin x & dfrac1<sqrt<1-x^2>>\&&\ textbf <12>& arccos x & -,dfrac1<sqrt<1-x^2>>\&&\ textbf <13>& mathrm, x & dfrac1<1+x^2>\&&\ textbf <14>& mathrm, x & -,dfrac1<1+x^2>\[0.5ex] hline end]

Источник