Молекулярная физика, термодинамика, электродинамика. Расчётная задача
В. З. Шапиро
Задание № 25 открывает вторую часть экзаменационной работы по физике, которая посвящена решению задач. Оно представляет собой расчетную задачу с кратким ответом. Тематика этого задания – термодинамика и электродинамика. В этом номере не требуется подробного решения, в бланк ответа необходимо внести только численный результат. Но, в отличие от заданий части № 1, решение потребует более глубоких знаний по вышеуказанным темам.
1. Кусок льда опустили в термос с водой. Начальная температура льда 0 °С, начальная температура воды 30 °С. Теплоёмкостью термоса можно пренебречь. При переходе к тепловому равновесию часть льда массой 210г растаяла. Чему равна исходная масса воды в термосе?
Ответ: __________________________г.
Необходимая теория: Количество теплоты
Дано:
t1 = 0 °С;
t2 = 30 °С;
m1 =210 г = 0,21 кг.
Найти: m2 – ?
Решение:
Подобные задачи, в которых происходит теплообмен между телами, необходимо решать, составляя уравнение теплового баланса. Для этого рассмотрим, какие изменения происходят с каждым телом, вступающим в теплообмен.
Q1 – количество теплоты, необходимое для плавления льда массой m1.
Q1 = ?m1.
Q2 – количество теплоты, отданное водой при охлаждении от 30 °С до 0 °С.
Q2 = сm2(t1 – t2).
Составим уравнение теплового баланса:
Q1 + Q2 = 0.
?m1 + сm2(t1 – t2) = 0.
сm2(t1 – t2) = -?m1.
подставим численные значения и проведем расчет.
= 0,55 (кг) = 550 (г).
Ответ: 550 г.
Секрет решения. В задачах на теплообмен трудности возникают с момента прочтения и краткой записи условия. Особенно это касается расставления индексов для различных температур. Рационально поступить следующим образом: присваивать индексы 1, 2, 3 и т.д. согласно порядку перечисления температур в условии задачи. Затем необходимо расписать процессы, происходящие с каждым телом, вступающим в теплообмен. Если тело нагревается или охлаждается, то при использовании формулы Q = сm (tкон – tнач) на первом месте пишется конечная температура, на втором – начальная. Причем индексы для этих температур могут быть любые. Тогда при составлении уравнения теплового баланса, в котором сумма количеств теплоты равна нулю, с «+» получатся количества теплоты, которые поглощаются телами, а с «-» – количества теплоты, которые выделяются телами.
В некоторых случаях уравнение теплового баланса в общем виде может иметь громоздкий вид. Его решение с буквенными обозначениями представляется трудоемким. Поэтому на этом этапе рациональнее подставить численные значения и решить его относительно неизвестной величины.
2. Прямоугольный контур, образованный двумя рельсами и двумя перемычками, находится в однородном магнитном поле, перпендикулярном плоскости контура. Правая перемычка скользит по рельсам, сохраняя надежный контакт с ними. Известны величины: индукция магнитного поля В = 0,1 Tл, расстояние между рельсами l = 10 см, скорость движения перемычки u = 2 м/c, сопротивление контура R = 2 Ом. Какова сила индукционного тока в контуре?

Ответ: ___________________________ мА.
Необходимая теория: Электромагнитная индукция
Дано:
В = 0,1 Тл;
l = 10 cм = 0,1 м;
= 2 м/с;
R = 2 Ом.
Найти: I –?
Решение:
Согласно закону электромагнитной индукции, на концах проводника, движущегося в магнитном поле, возникает ЭДС индукции.
Формула для расчета ЭДС индукции для этого случая имеет вид:
Так как вектор магнитной индукции перпендикулярен вектору скорости
(см. рис), то
Формула для расчета ЭДС принимает вид:
Согласно закону Ома для участка цепи, сила тока в проводнике равна:
Проведем расчет для силы тока:
(мА).
Ответ: 10 мА.
Секрет решения. Данная задача является комбинированной, т.е. в ней совмещены темы из разных разделов физики. Безусловно, электромагнитная индукция и постоянный электрический ток, темы близкие, но изучаются в школьном курсе физики в разное время. Здесь надо добиться понимания единой картины процессов, происходящих в электродинамике.
3. В двух идеальных колебательных контурах происходят незатухающие электромагнитные колебания. Максимальное значение заряда конденсатора во втором контуре равно 6 мкКл. Амплитуда колебаний силы тока в первом контуре в 2 раза меньше, а период его колебаний в 3 раза меньше, чем во втором контуре. Определите максимальное значение заряда конденсатора
в первом контуре.
Ответ: _________________________мкКл.
Необходимая теория: Электромагнитные колебания
Дано:
Кл
Кл;
Найти:
Решение:
Колебания электрического заряда в контуре можно представить в виде формулы:
Колебания электрического заряда в контуре можно представить в виде формулы:
Силу тока необходимо выразить как производную от заряда.
Таким образом, колебания силы тока в контуре выражаются уравнением:
Сравнивая с уравнением для тока в общем виде,
получим, что амплитуда силы тока равна:
(1).
Запишем полученное уравнение для двух случаев:
(2).
(3).
Разделим (3) на (2).
Отсюда выразим максимальное значение заряда конденсатора в первом контуре:
Подставим численные значения и проведем расчет:
Кл=1 мкКл
Ответ: 1 мкКл.
Секрет решения. На первый взгляд, решение задачи выглядит очень сложным. Но здесь надо выделить ключевые моменты, которые не потребуют запоминания огромного числа формул.
- Сила тока – это первая производная от заряда
- Заряд может меняться c течением времени по законам:
или
В условии задачи об этом ничего не говорится, поэтому подойдет любая формула.
- Надо уметь находить производную сложной функции.
- Величина, стоящая перед функциями синус или косинус, является амплитудой физической величины.
- Общие формулы для любых колебательных процессов и равномерного движения тела по окружности имеют вид:
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 25 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
| Колебательные процессы возможны не только в механических системах. При определенных условиях и в электрических цепях возникают колебания силы тока и напряжения и других электромагнитных величин. Какие это условия? Как вычислить период электромагнитных колебаний? Какие аналогии существуют между колебаниями различной природы? |
![]()
Электрической емкостью C конденсатора называют физическую величину, характеризующую его способность накапливать электрические заряды и равную отношению заряда q конденсатора к напряжению U между его обкладками: Единицей электрической емкости в СИ является 1 фарад (1 Ф).
Энергия электростатического поля конденсатора: .
Энергія магнитного поля катушки с током: , L — индуктивность катушки, I — сила тока в цепи. Единицей индуктивности в СИ является 1 генри (1 Гн).
Возникновение электродвижущей силы (ЭДС) в замкнутом проводящем контуре при изменении магнитного потока, проходящего сквозь него, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью С и катушки индуктивностью L (рис. 52, а), называемую колебательным контуром или LC-контуром. Если электрическое сопротивление контура можно считать равным нулю (R = 0), то его называют идеальным. Идеальный колебательный контур является упрощенной моделью реального колебательного контура.
Подключив (при помощи ключа К) источник тока, зарядим конденсатор до напряжения U0, сообщив ему заряд q0 (рис. 52, б). Следовательно, в начальный момент времени (t = 0) конденсатор заряжен так, что на его обкладке 1 находится заряд +q0, а на обкладке 2 — заряд −q0, при этом . Электрическое поле, созданное зарядами обкладок конденсатора, обладает энергией
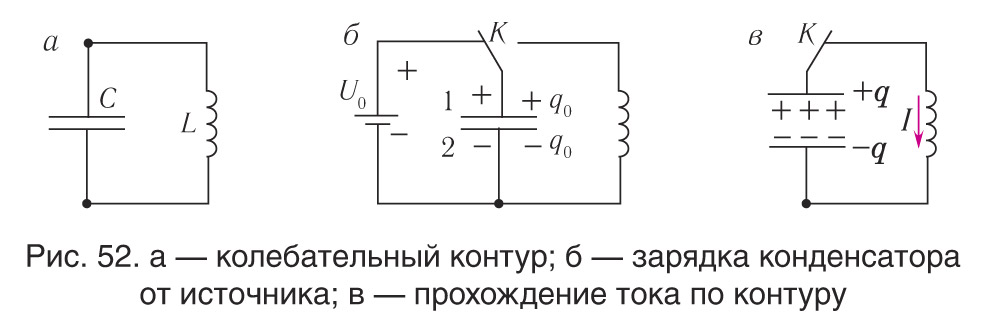
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа К) (рис. 52, в) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рис. 52, в стрелкой показано начальное направление тока в электрической цепи.
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила I(t) которого будет изменяться с течением времени (рис. 53, а). Но мгновенная разрядка конденсатора невозможна, вследствие явления самоиндукции. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению по модулю силы тока. Вследствие этого, модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения I0, определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 53, б).
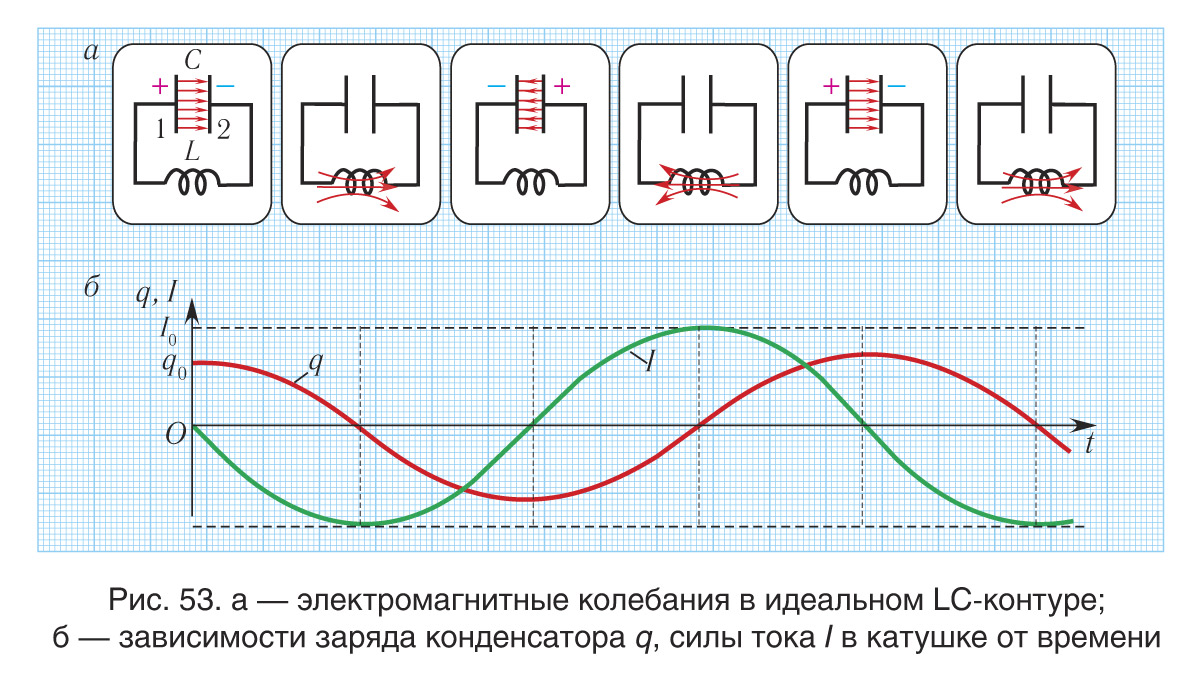
При разрядке конденсатора энергия его электрического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени. Следовательно, уменьшение энергии электрического поля конденсатора равно увеличению энергии магнитного поля катушки:
где q(t) — мгновенное значение заряда конденсатора и I(t) — сила тока в катушке в некоторый момент времени t после начала разрядки конденсатора.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального по модулю значения I0 (см. рис. 53, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электрического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его.
В результате, к моменту исчезновения тока заряд конденсатора достигнет максимального значения q0. При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится, отличаясь лишь тем, что электрический ток в контуре будет проходить в противоположном направлении (см. рис. 53, а).
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников и без потерь энергии на тепловыделение и излучение.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений q0 и I0 в различные моменты времени (см. рис. 53, а, б) (со сдвигом на ).
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии по аналогии с механическими колебаниями. Поскольку полная энергия идеального LC-контура, равная сумме энергий электрического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство:
| (1) |
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
| (2) |
где k — жесткость пружины, m — масса груза, x — проекция смещения тела от положения равновесия, vx — проекция его скорости на ось Ox.
Проанализируем соотношения (1) и (2). Видно, что энергия электрического поля конденсатора является аналогом потенциальной энергии упругой деформации пружины
. Соответственно, энергия магнитного поля катушки
, которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза
.
Следовательно, аналогом координаты x(t) пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора q(t). Тогда, соответственно, аналогом проекции скорости груза vx(t) будет сила тока I(t) в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора со временем.
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника жесткость k на
и массу m на индуктивность L. Тогда для периода свободных колебаний в LC-контуре получим формулу:
| (3) |
которая называется формулой Томсона.
Исходя из сказанного, сведем рассмотренные аналогии между физическими величинами при электромагнитных и механических колебаниях в таблицу 6.
Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого наблюдают осциллограмму колебаний U(t) (рис. 54).
|
Таблица 6. Сопоставление физических величин, характеризующих механические и электромагнитные колебания |
|
| Механические колебания пружинного маятника |
Электромагнитные колебания |
|
m (масса тела) |
L (индуктивность катушки) |
|
k (жесткость пружины) |
|
|
x(t) (координата тела) |
q(t) (заряд конденсатора) |
|
vx(t) (проекция скорости тела) |
I(t) (сила тока) |
| |
|
| |
|
| |
|
| |
Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты тела, совершающего гармонические колебания, от времени:
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Зависимость силы тока от времени в цепи колебательного контура имеет такой же вид, как и проекции скорости тела, совершающего гармонические колебания, от времени:
где, .
Зависимость напряжения на конденсаторе в колебательном контуре в соответствии с определением электроемкости
Для определения начальной фазы φ0 и максимального заряда q0 необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление R, которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они считаются происходящими сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Колебательный LC-контур широко используется в современных микросхемах для средств электроники и электротехнического оборудования.
Вопросы к параграфу
![]()
1. Из каких элементов состоит идеальный колебательный контур?
2. Какие электромагнитные колебания в контуре называются свободными?
3. От каких физических величин зависит период свободных колебаний в идеальном колебательном контуре?
4. По какому закону изменяются зависимости заряда конденсатора и силы тока в катушке идеального колебательного контура с течением времени?
5. Почему в контуре, состоящем из конденсатора и резистора, не могут возникнуть электромагнитные колебания?
6. В колебательном контуре изменили начальное значение заряда конденсатора. Какие величины, характеризующие электромагнитные колебания в контуре, изменятся, а какие останутся прежними?
7. Как распределена запасенная в идеальном колебательном контуре энергия между электрическим полем конденсатора и магнитным полем катушки в идеальном колебательном контуре в моменты времени после начала разрядки конденсатора?
8. Зависит ли период свободных электромагнитных колебаний в идеальном колебательном контуре от запасенной в нем энергии?
9. Чем отличаются процессы электромагнитных колебаний в реальном и идеальном колебательных контурах?
Примеры решения задач
1. Идеальный колебательный контур состоит из конденсатора емкостью C = 400 пФ и катушки индуктивностью L = 10 мГн. Определите максимальное значение силы тока I0 в контуре, если максимальное значение напряжения на конденсаторе U0= 500 B.
Решение:
Максимальная энергия электрического поля конденсатора
,
а максимальная энергия магнитного поля катушки:
Так как контур идеальный (R = 0), то его полная энергия сохраняется с течением времени. По закону сохранения энергии: WC = WL, т. е.
| Откуда: |
Ответ: I0 = 0,10 A.
2. При изменении емкости конденсатора идеального LC -контура на ΔC = 50 мФ частота свободных электромагнитных колебаний в нем увеличилась с ν1 = 100 кГц до ν2 = 120 кГц. Определите индуктивность катушки L контура.
Решение:
Частота колебаний в контуре
.
Поскольку
Из условия задачи получаем систему уравнений
Откуда:
Вычитая из первого уравнения второе, получаем:
Откуда находим:
Ответ: L = 0,15 Гн.
Упражнение 7
1. Определите период T свободных электромагнитных колебаний в идеальном колебательном контуре, состоящем из конденсатора емкостью, C = 15 мкФ и катушки индуктивностью L = 2,5 мГн.
2. Определите период колебаний колебательного контура, представленного на рисунке 55.
3. Конденсатор емкостью C = 1,2 мкФ соединен с катушкой индуктивностью L = 16 мкГн. Определите частоту ν свободных электромагнитных колебаний в контуре.
4. Как изменится период свободных электромагнитных колебаний в контуре, если индуктивность L катушки контура увеличить (уменьшить) в n = 16 раз при неизменной емкости конденсатора?
5. Определите напряжение U на конденсаторе емкостью C в момент времени: а) б)
если в начальный момент времени t0 = 0 напряжение на конденсаторе равно U0 = 48 B, а сила тока в катушке I0 = 0, Т — период колебаний в контуре.
6. Входной контур радиоприемника содержит катушку индуктивностью L = 0,32 мГн. В каких пределах должна изменяться емкость C конденсатора контура, чтобы радиоприемник мог принимать сигналы радиостанции, работающей в диапазоне частот от ν1=8,0 МГц до ν2=24,0 МГц?
7. Имеются два колебательных контура. Один содержит конденсатор емкостью C1 = 240 мФ и катушку индуктивностью L1 = 10,0 мГн, второй — C2 = 260 мФ и L2 = 6,00 мГн. Настроены ли эти контуры в резонанс? Во сколько раз k необходимо изменить емкость C2 или индуктивность L2, чтобы настроить эти контуры в резонанс?
8. В идеальном колебательном контуре, содержащем конденсатор емкостью С=52 мкФ, напряжение на конденсаторе изменяется по закону Определите период T электромагнитных колебаний, закон изменения силы тока I(t) , максимальную энергию электрического WCmax и магнитного WLmax поля.
9. Идеальный колебательный контур содержит катушку индуктивностью L=2,0 мГн и плоский конденсатор, площадь каждой обкладки которого S=1,2·103 см2, а расстояние между ними d=1,0 мм . Определите диэлектрическую проницаемость ε среды, заполняющей пространство между обкладками, если максимальное значение силы тока в контуре I0=12 мА, а максимальное значение напряжения U0=10 В.
10. Во сколько раз k уменьшится энергия заряженного конденсатора в идеальном колебательном контуре после подключения конденсатора к катушке индуктивности через промежуток времени ( T – период свободных колебаний)?
11. Период колебаний в идеальном колебательном контуре равен T=4,0 мс . Определите минимальный промежуток времени τmin, через который энергия электромагнитных колебаний в контуре распределится в отношении 1:4 между конденсатором и катушкой.
12. В колебательном контуре индуктивность катушки L=0,20 Гн, а максимальное значение силы тока I0=40 мА. Найдите энергию электрического поля WC конденсатора и магнитного поля WL катушки в тот момент, когда мгновенное значение силы тока в два раза меньше его максимального значения.
13. В колебательном контуре с конденсатором емкостью C=4,0 мкФ резонанс наступает при частоте ν1=400 Гц. Определите емкость С2 второго конденсатора, подключенного параллельно к исходному, если резонансная частота становится равной ν2=100 Гц.
14. Если в LC– контуре к конденсатору емкостью C параллельно присоединить конденсатор емкостью C1=4C, то частота колебаний в контуре уменьшится на Δν=400 Гц . Определите начальную частоту ν0 колебаний в контуре.
15. Идеальный колебательный контур содержит катушку индуктивности и два конденсатора одинаковой емкости. При параллельном соединении конденсаторов период колебаний в контуре равен T=16,0 мкс. Определите период T1 колебаний в контуре, если эти конденсаторы соединить последовательно.
Условие задачи:
Максимальная величина заряда на конденсаторе колебательного контура 1 мкКл, а максимальное значение силы тока через катушку этого же контура 10 А. Определите длину волны, испускаемой этим контуром.
Задача №9.13.7 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(q_m=1) мкКл, (I_m=10) А, (lambda-?)
Решение задачи:
Частоту электромагнитных волн, излучаемых колебательным контуром, можно определить по формуле:
[nu = frac{1}{{2pi sqrt {LC} }};;;;(1)]
В этой формуле (L) – индуктивность катушки, (C) – электроемкость конденсатора.
Известно, что электромагнитные волны распространяются со скоростью света (c) (в вакууме она равна 3·108 м/с). Между скоростью распространения электромагнитных волн (скоростью света (c)), частотой их колебаний (nu) и длиной волны (lambda) существует следующее соотношение:
[c = lambda nu ]
Откуда длина волны (lambda) равна:
[lambda = frac{c}{nu }]
В эту формулу поставим выражение (1):
[lambda = 2pi csqrt {LC};;;;(2)]
Также мы знаем, что максимальная энергия магнитного поля тока катушки колебательного контура равна максимальной энергии электрического поля конденсатора этого же контура, поэтому из закона сохранения энергии следует, что:
[frac{{LI_m^2}}{2} = frac{{q_m^2}}{{2C}}]
Откуда:
[LC = frac{{q_m^2}}{{I_m^2}}]
[sqrt {LC} = frac{{{q_m}}}{{{I_m}}}]
Учитывая последнее полученное равенство, формула (2) примет вид:
[lambda = frac{{2pi c{q_m}}}{{{I_m}}}]
Посчитаем численный ответ задачи:
[lambda = frac{{2 cdot 3,14 cdot 3 cdot {{10}^8} cdot {{10}^{ – 6}}}}{{10}} = 188,4;м]
Ответ: 188,4 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.13.6 Радиопередатчик искусственного спутника Земли работает на частоте 20 МГц
9.13.8 Колебательный контур создает в воздухе электромагнитные волны длиной 150 м
9.13.9 Если конденсатор с расстоянием между пластинами 1 см определенным образом
Колебательный контур:
Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре. Правило Ленца: возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится компенсировать изменение внешнего магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, содержащую конденсатор электроемкостью С и катушку (соленоид) индуктивностью L (рис. 15). Такая цепь называется идеальным колебательным контуром или LC-контуром.
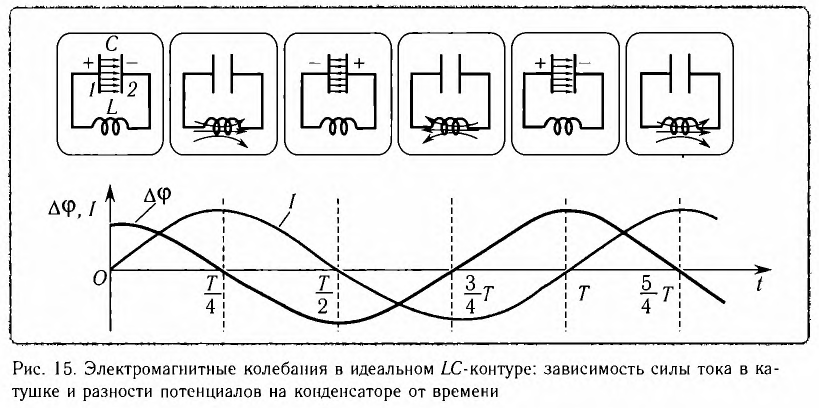
В отличие от реального колебательного контура, который всегда обладает некоторым электрическим сопротивлением (R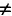
Пусть в начальный момент времени (t = 0) конденсатор С заряжен так, что на его первой обкладке находится заряд +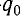 , а на второй —
, а на второй — . При этом конденсатор обладает энергией
. При этом конденсатор обладает энергией 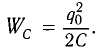
С течением времени конденсатор начнет разряжаться, и в цепи появится электрический ток, сила l(t) которого будет меняться с течением времени. Поскольку при прохождении такого электрического тока в катушке индуктивности возникнет изменяющийся во времени магнитный поток, то это вызовет появление ЭДС самоиндукции, препятствующей изменению силы тока.
Вследствие этого сила тока в колебательном контуре будет возрастать от нуля до максимального значения в течение некоторого промежутка времени, определяемого индуктивностью катушки.
В момент полной разрядки конденсатора (q = 0) сила тока в катушке I(t) достигнет своего максимального значения  . В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
. В соответствии с законом сохранения энергии первоначально запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
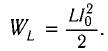
После разрядки конденсатора сила тока в катушке начнет убывать. Это также произойдет не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создаст индукционный ток. Он будет иметь такое же направление, как и уменьшающийся ток в цепи, и поэтому будет «поддерживать» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезарядит конденсатор до начального напряжения обратной полярности — знак заряда на каждой обкладке окажется противоположным начальному.
Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения  . При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.
. При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно (см. рис. 15). Далее процесс повторится с той лишь разницей, что электрический ток будет проходить в противоположном направлении.
Таким образом, в идеальном LC-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без потребления энергии от внешних источников.
Таким образом, возникновение свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора и возникновением в катушке ЭДС самоиндукции, которая «обеспечивает» эту перезарядку. Заметим, что заряд q(t) конденсатора и сила тока I(t) в катушке достигают своих максимальных значений  и
и  в различные моменты времени (см. рис. 15).
в различные моменты времени (см. рис. 15).
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальному значению заряда данной обкладки), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Период свободных электромагнитных колебаний в контуре определяется по формуле Томсона:
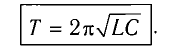
Получим эту формулу, используя закон сохранения энергии. Поскольку полная энергия идеального LC-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство
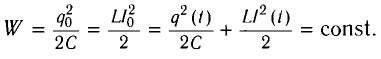 (1)
(1)
Поскольку закономерности гармонических колебаний носят универсальный характер, то можно сравнить колебания в LC-контуре с колебаниями пружинного маятника.
Для пружинного маятника полная механическая энергия в любой момент времени 2 ,
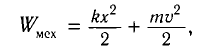 (2)
(2)
и период его колебаний
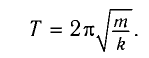
Проанализируем соотношения (1) и (2). Сравним выражения для энергии электростатического поля конденсатора 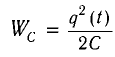 и потенциальной энергии упругой деформации пружины
и потенциальной энергии упругой деформации пружины 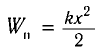 энергии магнитного поля катушки
энергии магнитного поля катушки 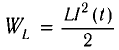 и кинетической энергии груза
и кинетической энергии груза 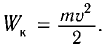 Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза
Аналогом координаты x(t) при колебаниях в электрическом контуре является заряд конденсатора q(t), а аналогом проекции скорости груза 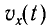 служит сила тока I(t) в колебательном контуре.
служит сила тока I(t) в колебательном контуре.
Следуя аналогии, заменим в формуле для периода колебаний пружинного маятника т на L и k на 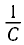 , тогда для периода свободных колебаний в LC-контуре получим формулу Томсона:
, тогда для периода свободных колебаний в LC-контуре получим формулу Томсона:
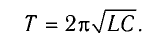
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
Таблица 4
Сопоставление физических величин, характеризующих электромагнитные и механические колебания
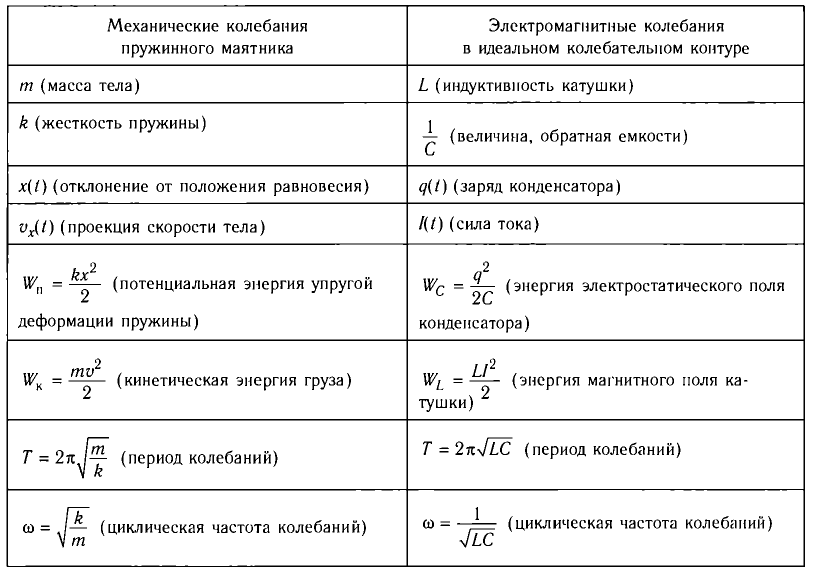
Соответственно, зависимость заряда конденсатора от времени будет иметь такой же характер, как и зависимость координаты (смещения) тела, совершающего гармонические колебания, от времени:
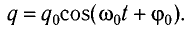
Также по гармоническому закону (но с другими начальными фазами) будут изменяться сила тока в цепи, напряжение на конденсаторе.
Для определения начальной фазы 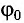 и амплитуды колебаний заряда
и амплитуды колебаний заряда 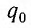 необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).
необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени (t = 0).
Полная энергия идеального колебательного контура (R = 0) с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется.
Как уже отмечалось, реальный колебательный контур всегда имеет некоторое сопротивление R, обусловленное сопротивлением катушки, соединительных проводов и т. д. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они «будут происходить» сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без трения, а механическим аналогом реального колебательного контура — пружинный маятник с трением.
Пример №1
При изменении емкости конденсатора идеального LC-контура на 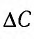 = 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с
= 50 пФ частота свободных электромагнитных колебаний в нем увеличилась с 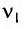 = 100 кГц до
= 100 кГц до 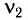 = 120 кГц. Определите индуктивность L контура.
= 120 кГц. Определите индуктивность L контура.
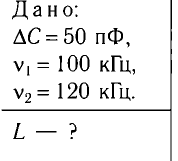
Решение
Частота колебаний в контуре
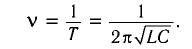
Поскольку частота колебаний в контуре увеличилась (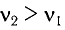 ), то электроемкость должна уменьшится, т. е.
), то электроемкость должна уменьшится, т. е. 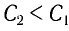 .
.
Из условия задачи получаем систему уравнений
Откуда 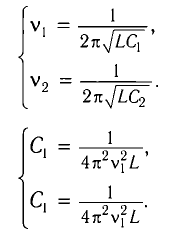
Вычитая из первого уравнения второе, получаем
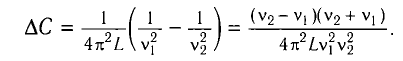
Откуда находим
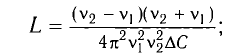
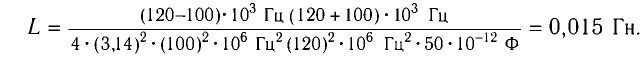
Ответ: L = 0,015 Гн.
Пример №2
Колебательный контур состоит из конденсатора емкостью С = 400пФ и катушки индуктивностью L=10 мГн. Определите амплитудное значение силы тока 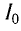 в контуре, если амплитудное значение напряжения на конденсаторе
в контуре, если амплитудное значение напряжения на конденсаторе 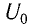 = 500 В.
= 500 В.
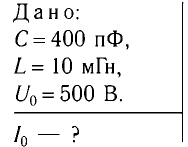
Решение
Максимальная энергия электростатического поля конденсатора
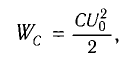
а максимальная энергия магнитного поля катушки
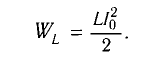
Так как контур идеальный (R = 0), то его полная энергия не меняется с течением времени. Кроме того, в момент, когда заряд конденсатора максимален, сила тока в катушке равна нулю, а в момент, когда заряд конденсатора равен нулю, сила тока в ней максимальна. Это позволяет утверждать, что максимальные энергии в конденсаторе и катушке равны: 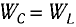 , т. е.
, т. е.
откуда 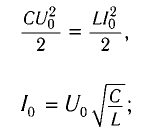
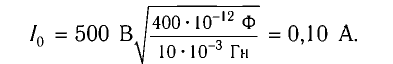
Ответ: 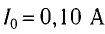 .
.
Колебательный контур и свободные электромагнитные колебания в контуре
Явление возникновения ЭДС в любом контуре при изменении магнитного потока через поверхность, ограниченную контуром, называется явлением электромагнитной индукции.
Под явлением самоиндукции понимают возникновение в замкнутом проводящем контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.
Правило Ленца: возникающий в замкнутом проводящем контуре индукционный ток имеет такое направление, при котором созданный им магнитный поток через поверхность, ограниченную контуром, стремится компенсировать изменение магнитного потока, вызвавшее данный ток.
Рассмотрим электрическую цепь, состоящую из последовательно соединенных конденсатора электроемкостью 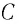 и катушки (соленоида) индуктивностью
и катушки (соленоида) индуктивностью 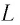 (рис. 29, а), называемую идеальным колебательным контуром или
(рис. 29, а), называемую идеальным колебательным контуром или 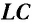 -контуром. Электрическое сопротивление идеального контура считают равным нулю
-контуром. Электрическое сопротивление идеального контура считают равным нулю 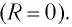 Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.
Следовательно, идеальный колебательный контур является упрощенной моделью реального колебательного контура.
Подключив (при помощи ключа 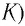 источник тока, зарядим конденсатор до напряжения
источник тока, зарядим конденсатор до напряжения 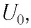 сообщив ему заряд
сообщив ему заряд 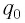 (рис. 29, б). Следовательно, в начальный момент времени
(рис. 29, б). Следовательно, в начальный момент времени 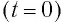 конденсатор заряжен так, что на его обкладке 1 находится заряд
конденсатор заряжен так, что на его обкладке 1 находится заряд 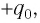 а на обкладке 2 — заряд
а на обкладке 2 — заряд 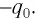 При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией
При этом электростатическое поле, создаваемое зарядами обкладок конденсатора, обладает энергией 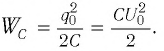
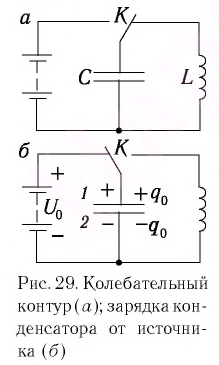
Рассмотрим процесс разрядки конденсатора в колебательном контуре. После соединения заряженного конденсатора с катушкой (при помощи ключа 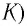 (рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.
(рис. 30) он начнет разряжаться, так как под действием электрического поля, создаваемого зарядами на обкладках конденсатора, свободные электроны будут перемещаться по цепи от отрицательно заряженной обкладки к положительно заряженной. На рисунке 30 стрелкой показано начальное направление тока в электрической цепи.
Таким образом, в контуре появится нарастающий по модулю электрический ток, сила 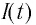 которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.
которого будет изменяться с течением времени (рис. 31, а). Но мгновенная разрядка конденсатора невозможна, так как изменение магнитного поля катушки, создаваемое нарастающим по модулю током, вызывает возникновение вихревого электрического поля. Действительно, в катушке индуктивности возникнет изменяющийся во времени магнитный поток, который вызовет появление ЭДС самоиндукции. Согласно правилу Ленца ЭДС самоиндукции стремится противодействовать вызвавшей ее причине, т. е. увеличению силы тока по модулю.
Вследствие этого модуль силы тока в колебательном контуре будет в течение некоторого промежутка времени плавно возрастать от нуля до максимального значения 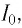 определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).
определяемого индуктивностью катушки и электроемкостью конденсатора (рис. 31, б).
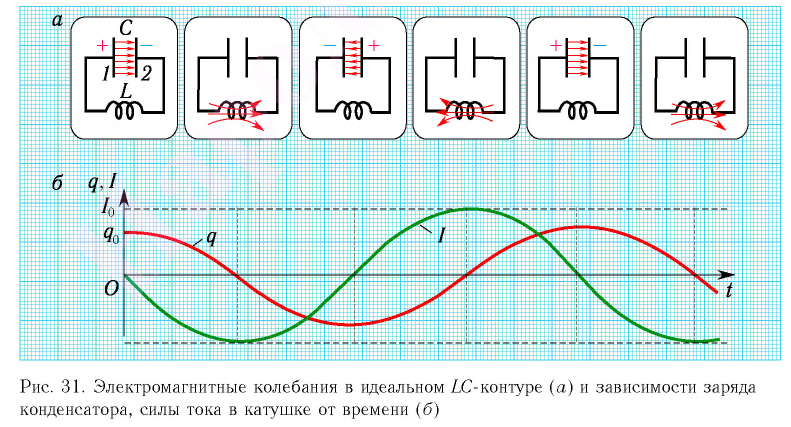
При разрядке конденсатора энергия его электростатического поля превращается в энергию магнитного поля катушки с током. Согласно закону сохранения энергии суммарная энергия идеального колебательного контура остается постоянной с течением времени (уменьшение энергии электростатического поля конденсатора равно увеличению энергии магнитного поля катушки):
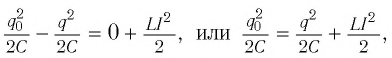
где 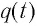 — мгновенное значение заряда конденсатора и
— мгновенное значение заряда конденсатора и 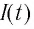 — сила тока в катушке в некоторый момент времени
— сила тока в катушке в некоторый момент времени 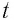 после начала разрядки конденсатора.
после начала разрядки конденсатора.
В момент полной разрядки конденсатора 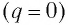 сила тока в катушке
сила тока в катушке 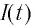 достигнет своего максимального по модулю значения
достигнет своего максимального по модулю значения 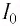 (см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
(см. рис. 31, б). В соответствии с законом сохранения энергии запасенная в конденсаторе энергия электростатического поля перейдет в энергию магнитного поля, запасенную в этот момент в катушке:
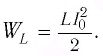
После разрядки конденсатора сила тока в катушке начинает убывать по модулю. Это также происходит не мгновенно, поскольку вновь возникающая ЭДС самоиндукции согласно правилу Ленца создает индукционный ток. Он имеет такое же направление, как и уменьшающийся по модулю ток в цепи, и поэтому «поддерживает» его. Индукционный ток, создаваемый ЭДС самоиндукции катушки, перезаряжает конденсатор до начального напряжения 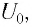 но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения
но знак заряда на каждой обкладке оказывается противоположным знаку начального заряда. Соответственно, к моменту исчезновения тока заряд конденсатора достигнет максимального значения 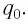 При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.
При этом его обкладка, первоначально заряженная положительно, будет заряжена отрицательно. Далее процесс повторится с той лишь разницей, что электрический ток в ко туре будет проходить в противоположном направлении, что отражено на рисунке 31, а.
Таким образом, в идеальном 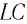 -контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
-контуре будут происходить периодические изменения значений силы тока и напряжения, причем полная энергия контура будет оставаться постоянной. В этом случае говорят, что в контуре возникли свободные электромагнитные колебания.
Свободные электромагнитные колебания в LC-контуре — это периодические изменения заряда на обкладках конденсатора, силы тока и напряжения в контуре, происходящие без пополнения энергии от внешних источников.
Таким образом, существование свободных электромагнитных колебаний в контуре обусловлено перезарядкой конденсатора, вызванной возникновением ЭДС самоиндукции в катушке. Заметим, что заряд 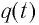 конденсатора и сила тока
конденсатора и сила тока 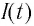 в катушке достигают своих максимальных значений
в катушке достигают своих максимальных значений 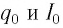 в различные момента времени (см. рис. 31 а, б).
в различные момента времени (см. рис. 31 а, б).
Наименьший промежуток времени, в течение которого LC-контур возвращается в исходное состояние (к начальным значениям заряда на каждой из обкладок), называется периодом свободных (собственных) электромагнитных колебаний в контуре.
Получим формулу для периода свободных электромагнитных колебаний в контуре, используя закон сохранения энергии. Поскольку полная энергия идеального 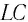 -контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство:
-контура, равная сумме энергий электростатического поля конденсатора и магнитного поля катушки, сохраняется, то в любой момент времени справедливо равенство:
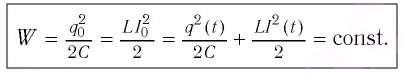
Процессы, происходящие в колебательном контуре, аналогичны колебаниям пружинного маятника. Для полной механической энергии пружинного маятника в любой момент времени:
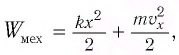
где 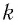 — жесткость пружины,
— жесткость пружины, 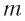 — масса груза,
— масса груза, 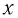 — проекция смещения тела от положения равновесия,
— проекция смещения тела от положения равновесия, 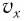 — проекция его скорости на ось
— проекция его скорости на ось 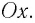
Период его колебаний:
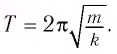
Проанализируем соотношения (1) и (2). Видно, что энергия электростатического поля конденсатора 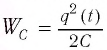 является аналогом потенциальной энергии упругой деформации пружины
является аналогом потенциальной энергии упругой деформации пружины 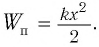 Соответственно, энергия магнитного поля катушки
Соответственно, энергия магнитного поля катушки 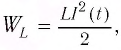 которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза
которая обусловлена упорядоченным движением зарядов, является аналогом кинетической энергии груза 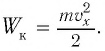 Следовательно, аналогом координаты
Следовательно, аналогом координаты 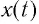 пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора
пружинного маятника при колебаниях в электрическом контуре является заряд конденсатора 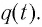 Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.
Тогда, соответственно, аналогом проекции скорости груза будет сила тока в колебательном контуре, поскольку сила тока характеризует скорость изменения заряда конденсатора с течением времени.
Следуя проведенной аналогии, заменим в формуле для периода колебаний пружинного маятника массу 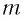 на индуктивность
на индуктивность 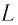 и жесткость
и жесткость 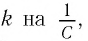 тогда для периода свободных колебаний в
тогда для периода свободных колебаний в 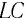 -контуре получим формулу:
-контуре получим формулу:
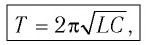
которая называется формулой Томсона.
Несложные дальнейшие рассуждения позволяют установить аналогии между физическими величинами при электромагнитных и механических колебаниях (табл. 4).
 Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).
Для наблюдения и исследования электромагнитных колебаний применяют электронный осциллограф, на экране которого получают временную развертку колебаний (рис. 32).
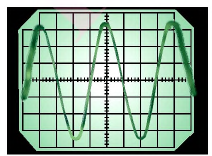
Зависимость заряда конденсатора от времени имеет такой же вид, как и зависимость координаты (проекции смещения) тела, совершающего гармонические колебания, от времени:
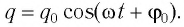
Также по гармоническому закону изменяются сила тока (но с другой начальной фазой) в цепи и напряжение на конденсаторе.
Для определения начальной фазы 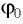 и максимального заряда
и максимального заряда 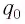 необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени
необходимо знать заряд конденсатора и силу тока в катушке в начальный момент времени 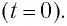
Отметим, что колебательный контур, в котором происходит только обмен энергией между конденсатором и катушкой, называется закрытым.
Полная энергия идеального колебательного контура 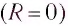 с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление
с течением времени сохраняется, поскольку в нем при прохождении тока теплота не выделяется. Реальный колебательный контур всегда имеет некоторое электрическое сопротивление 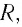 которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.
которое обусловлено сопротивлением катушки и соединительных проводов. Это приводит к тому, что электромагнитные колебания в реальном контуре с течением времени затухают, тогда как в идеальном контуре они будут происходить сколь угодно долго.
Таким образом, механическим аналогом идеального колебательного контура является пружинный маятник без учета трения, а механическим аналогом реального колебательного контура — пружинный маятник с учетом трения.
Пример решения задачи:
Идеальный колебательный контур состоит из конденсатора емкостью 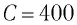 пФ и катушки индуктивностью
пФ и катушки индуктивностью 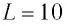 мГн. Определите максимальное значение силы тока
мГн. Определите максимальное значение силы тока 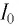 в контуре, если максимальное значение напряжения на конденсаторе
в контуре, если максимальное значение напряжения на конденсаторе 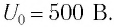
Дано:
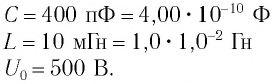

Решение
Максимальная энергия электростатического поля конденсатора:
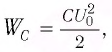
а максимальная энергия магнитного поля катушки:
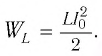
Так как контур идеальный 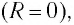 то его полная энергия сохраняется с течением времени. По закону сохранения энергии
то его полная энергия сохраняется с течением времени. По закону сохранения энергии 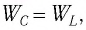 т. е.
т. е.
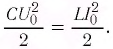
Отсюда
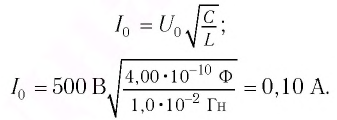
Ответ: 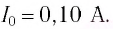
- Исследовательские методы в физике
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Распространение механических волн в средах
- Электромагнитное поле
- Опыты Фарадея в физике
- Электромагниты и их применение в физике
Тема: В идеальном колебательном контуре (Прочитано 12964 раз)
0 Пользователей и 1 Гость просматривают эту тему.
В идеальном колебательном контуре в начальный момент времени ток равен нулю, а заряд имеет максимальное значение, равное qm. Через какую долю периода, начиная от начального значения, энергия в контуре распределится поровну между катушкой и конденсатором? Сделать рисунок.

Записан
Решение
Зависимость заряда на обкладках конденсатора от времени описывается уравнениями:
[ q(t)={{q}_{max}}sin(omega t+{{varphi }_{0}}) или q(t)={{q}_{max}}cos(omega t+{{varphi }_{0}}), ]
где qmax — максимальное значение заряда (амплитуда заряда); φ — фаза колебаний, φ = ωt + φ0; φ0 — начальная фаза колебаний.
Если колебания начинаются при полностью заряженном конденсаторе (в начальный момент времени заряд конденсатора максимален), то для описания колебаний заряда выбирают формулу:
[ q={{q}_{max}}cosomega t.(1) ]
При электромагнитных гармонических колебаниях, возникающих в идеальном колебательном контуре, полная электромагнитная энергия контура сохраняется (остается постоянной).
Полная электромагнитная энергия идеального колебательного контура складывается из энергии электрического поля конденсатора и энергии магнитного поля катушки индуктивности:
E = WC + WL ,(2)
где WC — энергия электрического поля конденсатора, WC = q2/2C; WL — энергия магнитного поля катушки, WL = LI2/2; C — электрическая емкость конденсатора; U — напряжение (разность потенциалов) между обкладками конденсатора; q — заряд на обкладках конденсатора; L — индуктивность катушки; I — сила тока в катушке.
При гармонических электромагнитных колебаниях локализация электромагнитной энергии изменяется с течением времени, поэтому целесообразно рассмотреть энергию контура в трех состояниях:
1) при полностью заряженном конденсаторе заряд на обкладках конденсатора имеет максимальное значение q max, поэтому энергия электрического поля также максимальна:
[ W_{max}^{С}=frac{{{q}_{max }}^{2}}{2C}.(3) ]
энергия магнитного поля катушки равна нулю, так как ток в катушке отсутствует; полная энергия совпадает с максимальной энергией электрического поля конденсатора:
[ E=W_{max}^{С}. ]
2) в промежуточном состоянии электромагнитная энергия контура частично локализована в конденсаторе (в виде электрической энергии), а частично — в катушке (в виде магнитной энергии), т.е. обкладки конденсатора имеют некоторый заряд q, а в катушке течет ток силой I, поэтому полная энергия представляет собой сумму
[ E=frac{{{q}^{2}}}{2C}+frac{L{{I}^{2}}}{2}.(4) ]
По условию в нужный нам момент – энергия в контуре распределится поровну между катушкой и конденсатором: [ frac{{{q}^{2}}}{2C}=frac{L{{I}^{2}}}{2} ]
Закон сохранения полной механической энергии имеет вид:
[ begin{align}
& frac{{{q}_{max }}^{2}}{2C}=frac{{{q}^{2}}}{2C}+frac{L{{I}^{2}}}{2}; \
& frac{{{q}_{max }}^{2}}{2C}=2frac{{{q}^{2}}}{2C}Rightarrow {{q}_{max }}^{2}=2{{q}^{2}}Rightarrow {{q}_{max }}=sqrt{2}q.(5) \
end{align} ]
Для нахождения нужного нам момента времени подставляем (5) в (1)
[ begin{align}
& q={{q}_{max}}cosomega tRightarrow q=sqrt{2}qcosomega tRightarrow \
& frac{q}{sqrt{2}q}=cosomega tRightarrow frac{1}{sqrt{2}}=cosomega tRightarrow omega t=arccos (frac{1}{sqrt{2}})Rightarrow omega t=arccos (frac{1sqrt{2}}{sqrt{2}sqrt{2}})Rightarrow omega t=arccos (frac{sqrt{2}}{2})Rightarrow \
& omega t=frac{pi }{4}Rightarrow frac{2pi }{T}t=frac{pi }{4}Rightarrow t=frac{T}{8}. \
end{align}
]
Ответ: T/8.
« Последнее редактирование: 03 Августа 2016, 17:51 от alsak »

Записан

