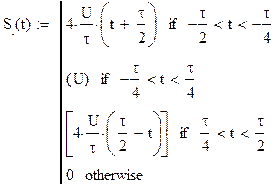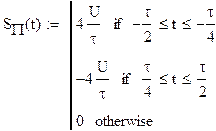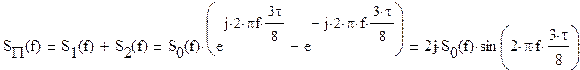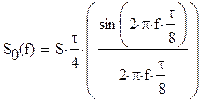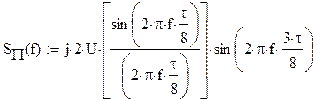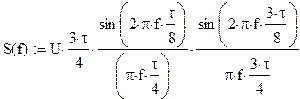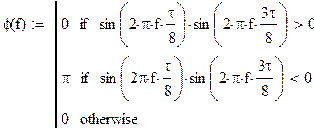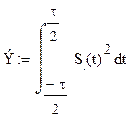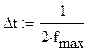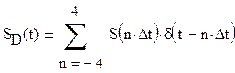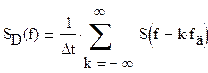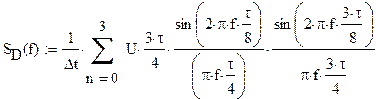Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
_____________________________________________________________________
Кафедра теоретических основ радиотехники (ТОР)
РАДИОТЕХНИЧЕСКИЕ
ЦЕПИ И СИГНАЛЫ
ЗАДАНИЕ
N 2
СПЕКТРАЛЬНЫЙ АНАЛИЗ СИГНАЛОВ
ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ
Вариант N 2
Подвариант N 4
Факультет РЭФ Преподаватель: проф.
Яковлев А.Н.
Группа РТ- 5 – 45
Студент: Дашеев Р.В.
Дата сдачи « 14 » апреля 2006 г.
Новосибирск, 2006
2.4.1. Спектральный
анализ сигналов
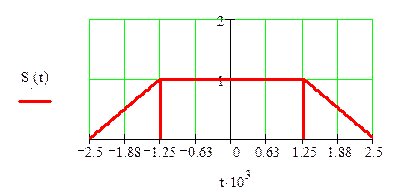
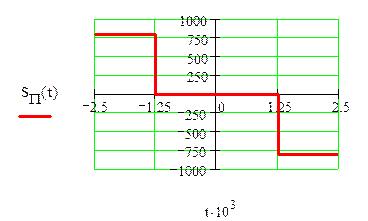
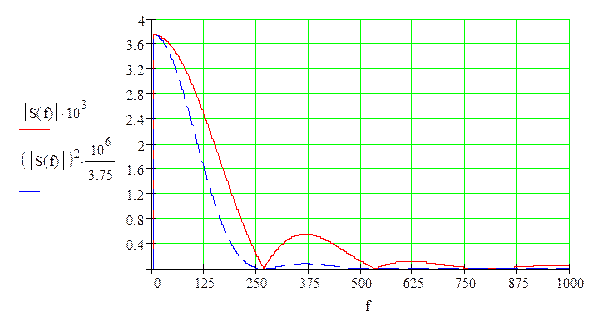
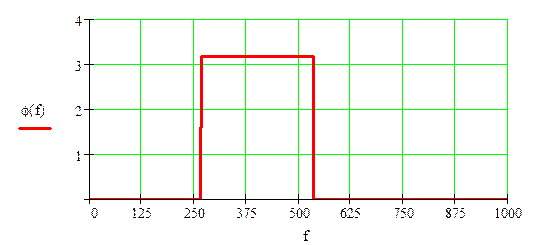
а) определить спектральную плостность S(f) сигнала S(t).
Построить спектральные диаграммы модуля |S(f)| и фазы f(f), диаграмму энергитического спектра |S(f)|2;
б) найти ширину “лепестка”
спектра одиночного импульса и сигнала;
в) вычислить энергию сигнала;
г) рассчитать коэффициенты Cn и Аn комплексного и тригонометрического ряда Фурье для
периодического сигнала ST(t),
полученного путем повторения заданного сигнала S(t) с периодом Tn . Построить соответствующие
спектральные диаграммы |Cn|,
Fn
è |An|,fn .
Вароиант №
2 Подвариант № 4
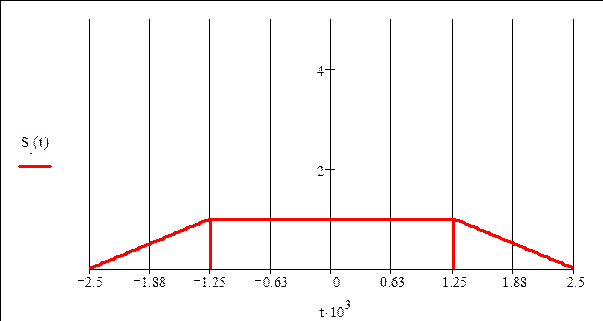
Запись исходного сигнала S(t) через временные интервалы:
а) Определим
спектральную плостность S(f) сигнала S(t)
Для того ,чтобы перейти от данного сигнала к
прямоугольному необходимо от данного сигнала взять производную
Имеем два прямоугольных импульса.Для определения
спектра S(t) воспользуемся теоремой о спектре суммы сигналов.
Для того , чтобы определить спектр S(t) сигнала S(t) необходимо воспользоваться
теоремой о интегрировании спектра сигнала.
б) Ширина
“лепестка” спектра одиночного импульса и сигнала
– ширина лепестка спектра одиночного импульса
– ширина лепестка спектра сигнала
в) Вычисление
энергии сигнала
г) Рассчет
коэффициентов Cn и Аn комплексного и
тригонометрического ряда Фурье для периодического сигнала ST(t)
Период повторения заданного импульса:
Частота периодического сигнала:
Число гармоник n возмем равным:
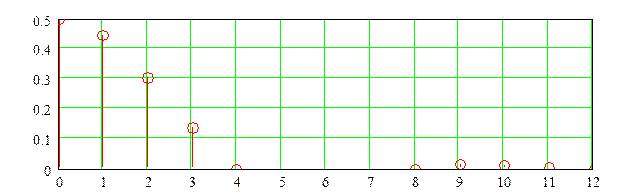
Определим коэффициенты комплексного ряда Фурье:
Коэффициенты комплексного ряда Фурье связанны с
коэффициентами тригононометрического ряда следующими соотношениями:
2.4.3.
Дискритизация непрерывных сигналов
а) вычислить максимальную частоту fmax в спектре сигнала;
б) определить интервал дискретизации;
в) построить графики дискретизированного сигнала, если за
дискретизирующую систему функций принять последовательность дельта-импульсов d(t);
г) определить спектр SD(f) дискетизированного в
соответствии с п.”3″ сигнала. Построить диаграмму спектральной
плотности |SD(f)|.
а) Максимальная
частотя fmax в спектре
сигнала;
За максимальную частоту fmax в спектре сигнала можно принять ширену первого
“лепестка”. Она будет равна:
б) Интервал
дискретизации;
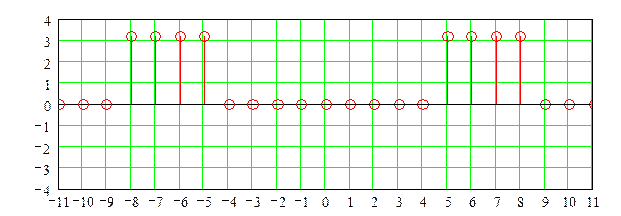
в) График
дискретизированного сигнала
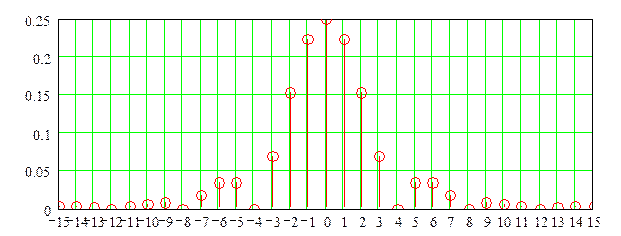
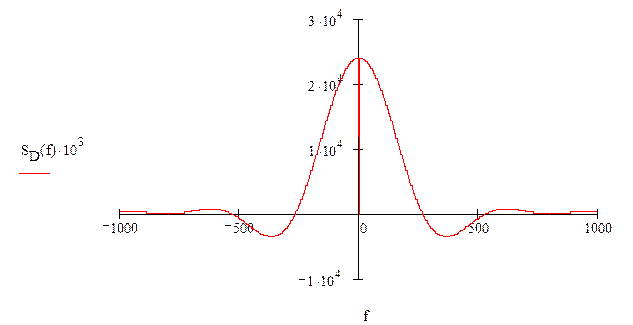
г) Спектр SD(f) дискетизированного в
соответствии с п.”3″ сигнала
Спектр SD(f)
дискетизированного сигнала связан со спектром исходного сигнала следующим
соотношением:
Добавил:
Upload
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Предмет:
Файл:
ТПИ Задания 14.doc
Скачиваний:
31
Добавлен:
31.03.2015
Размер:
171.01 Кб
Скачать
-
Сформировать
сигнал x(t),соответствующий
своему варианту. (
Здесь и в последующих заданиях номер
варианта равен номеру М в журнале
группы. М =п1п2. Символы п1 и п2 –это
первая и вторая цифры номера.)
Все сигналы рассматриваются только в
диапазоне изменения времени от -1 до
+1. За пределами этого диапазона значение
сигнала равно нулю. Частота ω0=π/2.
Варианты сигналов: 1) cos(ω0 *t); 2)cos2(ω0 *t); 3) 1 -t;
4) 1 –t2; 5)exp(- |t|); 6) 1 –t4;
7) 1 -t3; 8) 1-tg(t);
9)cos(2ω0*t);
10) 1/(1 +t2); 11)sin2(ω0
*t); 12) (sin2(ω0
*t))1/2 ; 13)cos2(ω0 *t); 14)cos(2*ω0 *t); 15)t;
16)t2 ; 17)t3
;18)sin(3*ω0*t);
19)sin(ω0*t);
20)t*sin(ω0*t); 21) 1; 22)
0.5 +cos(ω0 *t);
23) 1-cos2(ω0 *t);
24)cos2(2*ω0 *t).
-
Построить график
сигнала x(t)
в диапазоне от (-3 <t<3). -
Найти
прямое преобразование Фурье сигнала
x(t)
и его амплитудно-частотную
характеристику.
Пределы интегрирования ( -1 до +1)
F(f)
= ∫ x(t)*exp(-ј*2*π*f*t)dt
= ∫ x(t)*cos
(-ј*2*π*f*t)dt
+ ј∫ x(t)*sin
(-ј*2*π*f*t)dt.
Преобразование
Фурье имеет мнимую и действительную
части
F(f) = Re[F(f)] + ј*Im[F(f)].
Амплитудно-частотная характеристика
сигнала
A(f)
= {( Re[F(f)])2
+(
Im[F(f)])2
}1/2.
-
Построить
график A(f)
(частотный спектр сигнала). По графику
определить максимальную частоту fмакс.
в спектре
сигнала из условия А(fмакс
) < = 0.05 *
A(f)макс. -
Найти
обратное преобразование Фурье
x1(t) = ∫
F(f) *exp(-ј*2*π*f*t)df.
Интегрирование осуществляется в
диапазоне частот (-fмакс
до +fмакс
). Вычислить
и построить разность сигналов ε=x1(t)
– x(t).
Записать максимальное по модулю значение
εмакс.
Задание 2
Дискретизация сигналов во времени.
-
По
найденному в задании 1 п.4 fмакс
вычислитьT=1/(4*fмакс
). -
Построить периодическую функцию δT
(t) =∑ δ(t–n*T).
Суммирование ведётся поnв диапазоне его изменения от -20 до + 20
Функция δ (t) = 1,
если толькоt= 0, и равна
«0» приt≠ 0. -
Построить дискретный периодический
сигнал xД (t)=x1(t)* δT
(t). Функцияx1(t)
получена в задании 1 п.5. -
Вычислить максимальное значение второй
производной сигнала x(t)
(см. п.1 задания 1). -
При восстановлении сигнала по его
дискретным отсчётам путём линейной
интерполяции интервал квантования
выбирают из условия T1 =
(8*εмакс)/|x(2)(t)макс.Вычислить T1. Величина εмакс
берётся из п.5 задания 1,x(2)(t)
– вторая производная сигналаx(t). -
Выполнить п.2,3 задания, заменив TнаT1 иx1(t)
наx(t).
Контрольные вопросы к заданию
-
Суть дискретизации сигналов во времени
по Котельникову. -
Суть дискретизации сигналов во времени
по величине ошибки аппроксимации. -
Как соотносятся спектры сигналов x1(t)
наx(t)? -
Сигнал, квантованный по Котельников,
воспроизводиться с использованием
аппроксимации полиномом первой степени.
Какова при этом будет ошибка воспроизведения
сигнала x(t)? -
Целесообразно ли увеличивать степень
аппроксимирующего полинома при
квантовании сигнала по времени? -
При воспроизведении исходного сигнала
из квантованного по времени чаще всего
используют полиномы нулевой или первой
степени. Почему? -
Суть неравномерного квантования по
времени. -
Приведите несколько примеров, где
используются квантованные во времени
сигналы. -
С какой частотой дожжен квантоваться
речевой сигнал? -
Как непрерывный сигнал преобразуют в
цифровую форму? -
Имеются ли ограничения на число разрядов
при оцифровке речевых сигналов? -
Какова должна быть частота следования
в линии связи импульсов неизбыточного
кода при цифровой передачи речевого
сигнала? -
Возможно ли технически реализовать
сигнал x1(t)
наx(t)?
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
It’s not quite clear what you’re asking, but I think this does something like it.
Regarding how magnitude relates to dB: decibels are a relative scale, so you need to decide what it’s relative to. Since you agreed in the comments that it was dBFS, I took the largest value in the data (e.g. np.max(data)).
With that in mind, then the dB scale is:
fft_db = 20*np.log10(np.abs(fft)/np.max(np.abs(fft)))
Python code below
import numpy as np
import matplotlib.pyplot as plt
fft_db = np.random.random(100)*100 - 130
fft_db[80:100] = -130
fft_db_flip = np.flip(fft_db)
requested_value = len(fft_db) - np.argmax(fft_db_flip > -60) - 1
plt.plot(fft_db)
plt.plot(requested_value, fft_db[requested_value],'r.')
plt.plot([0,100],[-60,-60],'g:')
© [ Алгоритм безопасности №3, 2003, www.algoritm.org]
Потребителям нередко навязывается мнение, что совсем не обязательно передавать видеосигнал в полном спектре, а качество видеосистемы можно оценивать просто по экрану монитора, удовлетворяясь при этом «приемлемым изображением». Что же принять в качестве критерия «разумной достаточности» на этапе утверждения технического задания, при проектировании видеосистемы и сдаче ее заказчику?
Обычно на первое место ставится согласование параметров основных устройств системы – видеокамеры, устройств обработки видеосигнала и видеомонитора.
Какой способ передачи видеосигнала при этом использовать, иногда даже не обсуждается. Под системой в целом понимают перечень основных устройств, забывая про аппаратуру передачи, соединяющую эти устройства воедино. Какими бы хорошими параметрами не обладала видеокамера, для полной их реализации на мониторе, необходим соответствующий канал передачи видеосигнала.
Недооценка глубокой проработки этого элемента системы говорит о том, что о видеосигнале многие проектировщики и специалисты по монтажу судят, в худшем случае, по изображению на мониторе, а в лучшем случае по временному представлению сигнала, – осциллограмме.
Испытательные таблицы позволяют произвести итоговую оценку параметров системы. На уже построенной видеосистеме это позволит сделать вывод о степени реализации заявленных параметров.
Главное, на что хочется обратить внимание, что при передаче видеосигнала передаются «не просто импульсы», а по сути дела «спектр» со всем многообразием его составляющих, занимающих строго определенный диапазон частот. Задача выбора системы передачи сводится к тому, чтобы предотвратить искажение спектра видеосигнала в процессе передачи.
Начиная разговор о частотном представлении сигнала, рассмотрим, как зависит от характера передаваемого изображения, положение тех или иных его составляющих на оси частот.
Распределение сигналов по оси частот
Управление работой развертывающих устройств, как видеокамеры, так и кинескопа видеомонитора, осуществляется с помощью строчных и кадровых синхронизирующих импульсов. Именно видеокамера вырабатывает импульсы синхронизации для видеомонитора.
Но благодаря этому, комплексный сигнал изображения носит импульсный характер, что приводит к большой ширине спектра частот видеосигнала, во многие сотни раз превышающей полосу частот при передаче речи или музыки.
Необходимо знать основные параметры спектра частот телевизионного сигнала и использовать их для подбора аппаратуры. Для качественной передачи видеоизображения аппаратура должна иметь полосу пропускания, соответствующую спектру этого сигнала.
Низшая частота сигнала изображения
На рисунке 1 во фрагменте (1) показан самый низкочастотный сигнал, который получается при передаче неподвижного изображения, состоящего из двух горизонтальных полос – одной белой и одной черной.
Соответствующий этому изображению сигнал представляет собой импульсы, следующие с частотой кадровой развертки Fкадр = 50 Гц.
Изображению (2) соответствует сигнал с частотой основной гармоники в три раза более высокой (mг/2), чем у (1), так как каждой паре полос соответствует один период сигнала.
Частота основной гармоники изображения (3) будет равна частоте строк. Частота основной гармоники изображения (4) будет в четыре раза более высокой (mв/2), чем (3). С увеличением числа вертикальных полос и с уменьшением их ширины частота сигнала изображения будет соответственно расти. При равенстве ширины полос размерам элементов разложения частота сигнала изображения достигает своего максимального значения.
На рисунке 1 наглядно видно, какой характер изображения на экране монитора соответствует тому или иному положению сигнала на оси частот. Исходя из этого, выбирается требуемая полоса пропускания системы передачи. Под системой передачи будем подразумевать кабельную линию, имеющую точно определенную характеристику затухания видеосигнала на различных частотах, и соответствующие этой линии передающее и приемное устройство, в комплексе обеспечивающие коррекцию частотных искажений.
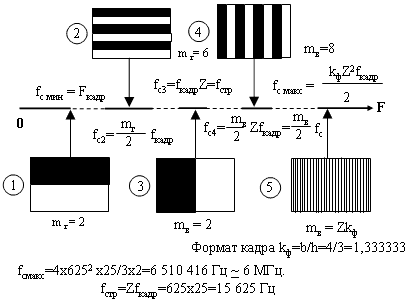
В.Д. Крыжановский, Ю.В. Костыков «Телевидение цветное и черно-белое». Изд-во «Связь», Москва, 1980, с. 33.
Какой же полосой пропускания должна обладать по-настоящему качественная система передачи аналогового видео сигнала?
Найдем максимальную частоту видеосигнала.
При том типе развертки, которая применяется в системах замкнутого телевидения (чересстрочной), частота следования кадров fкадр = 25 Гц. Максимальная частота видеосигнала при этом будет равна: fмакс = 4х6252х25/3х2 = 6 510 416 Гц, т.е. примерно 6 МГц.
Применение чересстрочной развертки позволяет:
- с одной стороны, взять частоту полукадров (частоту кадровой развертки Fкадр), определяющую мерцание экрана, равной частоте электросети 50 Гц и этим самым ликвидировать мерцание и ослабить помехи от сети переменного тока;
- с другой стороны, частота кадров fкадр при этом оказывается равной 25 Гц, что определяет высшую частоту сигнала изображения – 6 МГц.
При построчной развертке с fкадр = 50 Гц высшая частота сигнала изображения была бы 13 МГц.
Минимальная частота сигнала изображения fс.мин остается, равной частоте кадровой развертки, Fкадр = 50 Гц (т.е., частоте полукадров – полей), частота кадров fкадр = 25 Гц – в два раза ниже.
Очевидно, что полоса частот видеосигнала простирается от 50 Гц до 6 МГц и вся она занята сигналом.
Спектральное представление сигналов
При чересстрочной развертке существуют значительная взаимная зависимость между видеосигналами в соседних полях и кадрах. Это позволяет считать видеосигнал периодичным с частотой кадровой развертки при передаче изображений неподвижных объектов.
Видеосигналу присуща также определенная периодичность с частотой строк в результате высокой степени связи сигналов в соседних строках.
С учетом высокой взаимной связи между строками и кадрами можно представить напряжение сигнала как временную функцию с периодом повторения строчной Тс.р. и кадровой Тк.р. разверток.
Периодичность видеосигнала при передаче изображений неподвижных объектов является его главной особенностью.
Периодическое колебание состоит из суммы постоянной составляющей (частота которой равна нулю) и ряда гармонических (синусоидальных) колебаний. Амплитуда частотных составляющих телевизионного сигнала падает с ростом частоты (номера гармоники). Первая гармоническая составляющая с частотой fк1 = Fкадр = 50 Гц. Далее низкочастотный участок спектра занят гармониками частоты кадровой развертки. Вторая гармоника имеет частоту fк2 = 2Fкадр = 100 Гц.
Частота строк (625-я гармоника частоты кадров) и все ее гармоники являются гармониками частоты кадров.
fстр = Zfкадр.= 625х25 = 15625 Гц.
Как видно из рисунка 2, при передаче неподвижных изображений около составляющих спектра гармоник частоты строк fстр группируются боковые спектры, имеющие также вид дискретных линий, кратных частоте кадровой развертки Fкадр (± 50 Гц).
В случае однокадровой передачи, когда частота кадров стремится к нулю и спектральные линии сольются, спектр преобразуется в непрерывный.
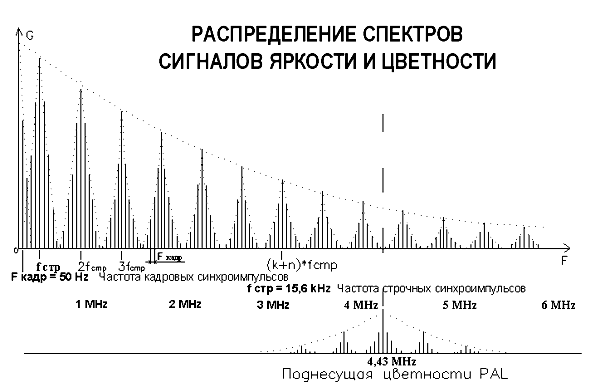
Наличие в полном (композитном) телевизионном сигнале строчных гасящих и синхронизирующих импульсов увеличивает интенсивность гармоник спектра сигнала, кратных строчной частоте, по их числу и амплитуде.
На рисунке 2 спектр видеосигнала представлен схематически. Главной задачей было показать, что амплитуды спектральных составляющих убывают с ростом частоты, причем скорость убывания амплитуд и ширина спектра определяются содержанием изображения. Спектр состоит из «сгустков энергии» (максимумов) на частотах, кратных частоте строк и, расположенных между ними, «нулей» – минимумов.
На самом деле максимумов и минимумов в спектре гораздо больше, чем изображено на рисунке 2.
Достаточно сказать, что частоте 1 МГц – соответствует 64-я гармоника частоты строк.
Сто двадцать восьмая гармоника частоты строк fс128 = 2 МГц, fс192 = 3 МГц, fс256 = 4 МГц, fс320 = 5 МГц, fс384 = 6 МГц, fс400 = 6,25 МГц.
В системах замкнутого телевидения в основном передаются движущиеся изображения, поэтому сигнал последующего кадра будет несколько отличаться от сигнала предыдущего. Считать его чисто периодическим его уже нельзя, следовательно, и его спектр дискретным уже не будет.
Дискретные линии спектра неподвижного изображения при движущемся изображении «расплывутся» в полосы, участки, заполненные сигналом. Это хорошо видно на рисунке 3.
Около каждой дискретной составляющей спектра появляются дополнительные верхняя и нижняя боковые полосы, в результате спектр видеосигнала становится более плотным.
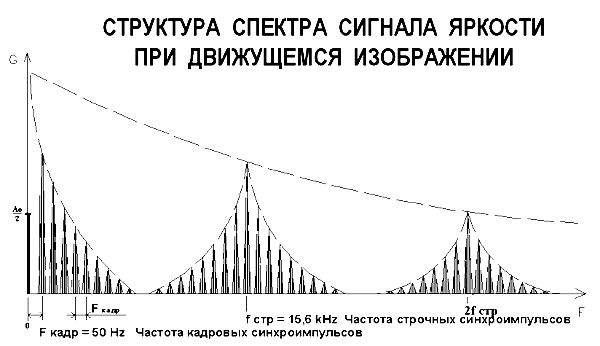
На практике отклонение частоты повторения сигнала от частоты строчной развертки fстр = 15625 Гц составляет всего лишь «единицы Гц». При изменении динамики изображения меняется и положение линий спектра. Спектр как бы «дышит» относительно гармоник частоты строк.
Участки полос сигнала будут тем больше, а пустые промежутки тем меньше, чем выше скорость движения деталей передаваемого объекта. Но даже при сравнительно высоких скоростях, пустые промежутки в спектре сигнала оказываются настолько значительными, что в них можно поместить дополнительную информацию о цветности передаваемых объектов.
Речь идет о поднесущей цветности, которая представляет собой радиоимпульс с длительностью 2,25 мкс и несущей частотой 4,4336 МГц. «Импульсный характер» цветового синхроимпульса определяет то, что его спектр имеет достаточно большую ширину и по форме также является дискретным. На рисунке 2 видно, как сгустки энергии спектра цветового синхроимпульса размещаются в промежутках спектра сигнала яркости. Происходит так называемое «переплетение спектров», когда спектры двух сигналов: яркостного сигнала и сигнала цветности занимают общие участки частотной оси, не нарушая при этом выполнения каждым из сигналов своих функций. На рисунке 2 спектр сигнала цветности вынесен, для наглядности, несколько вниз.
Главное состоит в том, что все это многообразие частотных составляющих надо при передаче сохранить. Чем больше гармонических составляющих принимает участие в формировании выходного сигнала, тем более точно он соответствует входному, исходному сигналу.
Не имеет значения, что более высокочастотные гармоники спектра видеосигнала имеют малые амплитуды. Они и должны быть такими и их значением нельзя пренебрегать. Нельзя запросто ограничить спектр полосой частот в 3 МГц и ждать от системы хорошего распознавания деталей. Скорее всего, такая система позволит очень хорошо отличать только день от ночи.
Большинство видеосистем наблюдения имеют ограниченное число видеокамер, необходимая зона видимости перекрывается за счет применения широкоугольных объективов, при этом линейные размеры человека (а именно он в охранном телевидении является интересующим нас объектом) на экране монитора измеряются миллиметрами. Для решения задачи опознавания людей, автомобилей и других специфических объектов, необходимо обеспечить высокую разрешающую способность видеосистемы.
На разрешающей способности мы остановимся ниже, а сейчас еще раз отметим, что только в системе с полосой пропускания не менее 6 МГц можно обеспечить потенциально высокое разрешение.
При наличии определенного опыта оценить качество видеосигнала можно и с помощью осциллографа. Для этого надо представлять, как влияют частотные искажения на форму строчных синхроимпульсов.
Временное представление видеосигнала
В составе полного телевизионного сигнала (см. Рис.4) строчные и кадровые синхроимпульсы располагаются ниже уровня черного, совпадающего с уровнем вводимых в сигнал гасящих импульсов. При этом гасящие импульсы служат пьедесталом для синхроимпульсов.
Во время обратного хода по строкам и кадрам сигнал принимает минимальное значение – уровень черного. Уровень «черного» всегда стабилизируют. Наибольшее значение сигнала называют уровнем белого. Уровень белого, а вместе с ним и средний уровень сигнала (постоянная составляющая), изменяется и зависит от яркости наиболее светлых участков передаваемого изображения.
Такие соотношения характерны для качественного видеосигнала, с которым будут хорошо работать любые цифровые устройства.
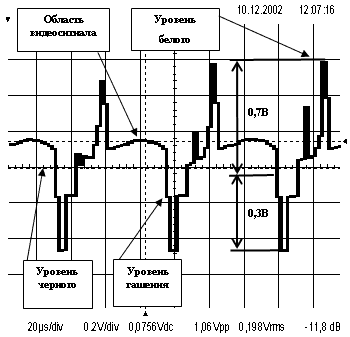
На рисунке 5 приведена осциллограмма видеосигнала, поступающего от цветной видеокамеры. Документирование видеосигнала было произведено при большом усилении канала вертикальной развертки (50 мВ/деление), чтобы можно было зафиксировать импульс цветовой синхронизации – «вспышку поднесущей».
Это двухполярный радиоимпульс с частотой 4,43 МГц и размахом около 0,3 В (точнее 0,286 В), расположенный, как на пьедестале, на удлиненной полочке строчного гасящего импульса за строчным синхроимпульсом.
На осциллограмме, размах синхроимпульса цветности не достиг даже величины 0,1 В. Это следствие того, что граничная частота используемого осциллографа составляет всего 5 МГц. Для измерения параметров радиоимпульсов (с частотным заполнением) этого не достаточно.
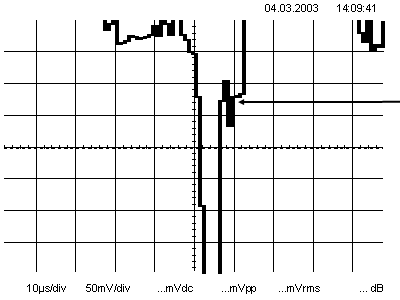
Трудность в фиксации на обычном осциллографе, не имеющем системы выбора строки, заключается еще и в том, что так называемая «вспышка поднесущей» в системе PAL действует в течение ограниченного времени, – в течение 8-ми полей, поочередно дважды по два периода в четных и нечетных строках.
Таким образом, в отличие от строчных синхроимпульсов, следующих с постоянной частотой 15625 Гц, «вспышка поднесущей» представляет собой «пачку» из 8-10 импульсов с частотой fстр с последующим перерывом более чем на 600 тактов строчной развертки. Все это накладывает свой отпечаток на спектр последовательности этих сигналов: в спектре появляются новые составляющие и они расширяются.
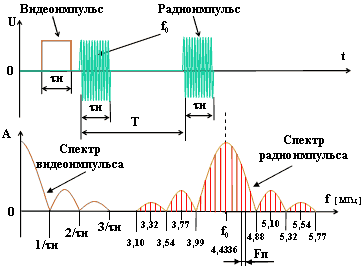
Возникает законный вопрос, почему с помощью осциллографа с граничной частотой 5 МГц нельзя без искажения формы и амплитуды наблюдать радиоимпульс с частотой 4,43 МГц?
На первый взгляд кажется, что если полосу пропускания устройства передачи ограничить частотой, несколько превышающей частоту цветовой поднесущей, то можно обеспечить передачу цветного изображения. На самом деле, спектр радиоимпульса, которым является «вспышка поднесущей» цветовой синхронизации, достаточно широкий. Он занимает полосу частот от 3,10 МГц до 5,77 МГц с центральной частотой 4,43 МГц. Поэтому, для качественной передачи цветного видеосигнала необходима полоса пропускания системы не ниже 5,77 МГц. Это практически те же 6 МГц, которые мы определили при нахождении максимальной граничной частоты видеосигнала.
На рисунке 1 при вычислениях получилось число fс макс = 6,5 МГц. Как будет показано при рассмотрении разрешающей способности системы, в системах замкнутого телевидения для обеспечения высокого разрешения по горизонтали, в некоторых случаях необходимо обеспечить полосу частот до 7 МГц.
Теперь должно стать понятным, почему на осциллограмме (Рис.5.) радиоимпульс отображается с небольшой амплитудой – усилитель осциллографа с полосой 5 МГц его просто «зарезал».
Чтобы при прохождении через усилительные цепи осциллографа не было ограничения спектра радиоимпульса, ширина полосы пропускания осциллографа должна быть не менее 6 МГц, а лучше – 10 МГц.
Те же самые ограничения спектра происходят и в усилителях устройств передачи видеосигналов.
Если полоса пропускания устройств передачи видеосигнала ограничивает его спектр, то на приемной стороне мы будем наблюдать искаженный сигнал, а на мониторе – искаженное изображение.
Разрешающая способность видеосистемы
Любое преобразование информации, а также передача ее по каналу связи всегда сопровождается определенными потерями. В видеосистеме существуют три вида потерь информации: пространственные, градационные и временные. Временные потери связаны со снижением частоты кадров.
Градационные потери определяются уменьшением числа уровней различимых перепадов яркости (полутонов), на которых основана распознаваемость деталей объектов.
Пространственные потери информации связаны с уменьшением амплитуд отдельных гармонических составляющих, из которых складывается исходное изображение, и зависят от формы переходной характеристики. С ними неразрывно связана разрешающая способность системы.
Разрешающая способность является важнейшим параметром видеосистемы, характеризующим ее способность раздельно воспроизводить мелкие детали. От разрешающей способности зависит четкость изображения, являющаяся показателем его качества. Разрешающая способность системы определяется максимальной пространственной частотой, которую обеспечивают все звенья видеосистемы: объектив, ПЗС-матрица, тракт передачи видеосигналов и кинескоп монитора. Максимальная пространственная частота определяет пороговый контраст воспроизводимого на экране кинескопа изображения предельно контрастной штриховой таблицы (миры), состоящей из чередующихся черных и белых полос, помещенной перед объективом видеокамеры.
В телевидении пространственную частоту выражают числом «полупериодов» гармонической составляющей изображения, укладывающейся не на единицу длины, а на высоту растра.
Эти величины принято измерять не в миллиметрах, а числом строк разложения. Причем числом активных строк Zа, приходящихся только на время прямого хода кадровой развертки (на высоту растра), строк разложения.
Единицей измерения пространственной частоты при этом является телевизионная линия (твл).
Вертикальная (поперечная) разрешающая способность ограничивается числом горизонтальных строк разложения. Для существующего стандарта при числе строк Z = 625, число активных строк Zа = 575, чему соответствует максимальное вертикальное разрешение, равное 430 твл.
Для исключения зависимости разрешающей способности от расстояния наблюдения, необходимо рассматривать изображение горизонтальных полос таблицы на сравнительно близком расстоянии.
При реальном практическом наблюдении следует ограничиться для вертикального разрешения 400 твл.
В реальных условиях, если известен характер объекта, можно при проектировании системы заранее определить условия обнаружения или опознавания мелких деталей изображения по числу линий.
Экспериментально установленное число различимых элементов, приходящихся на вертикальный размер обнаруживаемой детали, следующее:
- лицо человека может быть узнано при – 30 различимых элементов.
- автомобиль в движении – при 3.
- автомобиль в неподвижном состоянии – при 8.
Общие рекомендации:
- обнаружение объекта требует примерно 2-3 твл, приходящихся на его минимальный размер;
- различение – 8 твл;
- опознавание – 12,8 твл.
Таким образом, чем крупнее деталь, тем меньшая разрешающая способность системы требуется для ее обнаружения или опознавания.
Горизонтальная (продольная) разрешающая способность определяется количеством вертикальных линий, которое можно наблюдать на экране монитора. При известном разрешении видеокамеры и монитора, горизонтальное разрешение телевизионной системы зависит от АЧХ устройств передачи видеосигнала.
Если задаются определенным, достаточно высоким разрешением видеосистемы, то недостаточно установить видеокамеру и монитор соответствующего разрешения. Нужно подумать и о том, как сохранить высокое разрешение видеокамеры при передаче видеосигнала на расстояние нескольких километров.
Принимая во внимание формат телевизионного кадра 4:3 (отношение ширины к высоте), и то, что вертикальное разрешение на практике равно 400 твл, а максимальное – 430 твл, определим максимальное число вертикальных линий – горизонтальное разрешение в телевизионных линиях (твл).
430х4/3 = 573 твл.
Горизонтальное разрешение видеосистемы, имеющей в своем составе видеокамеру высокого разрешения 570 твл, может быть ухудшено за счет потерь высокочастотных составляющих спектра видеосигнала, внесенных несовершенной системой передачи.
Практически, чтобы увидеть 570 твл на испытательной таблице, необходима полоса пропускания устройства передачи не менее 7 МГц. Другое дело, что такое разрешение не всегда требуется.
Далее приведем практические данные для требуемой полосы частот в зависимости от заданного разрешения.
- При полосе пропускания системы передачи видеосигнала с максимальной граничной частотой 3 МГц будет обеспечено на выходе около 240 твл.
- Устройство передачи с максимальной граничной частотой 4 МГц обеспечит передачу – 320 твл.
- Устройство передачи с максимальной граничной частотой 5 МГц обеспечит передачу – 400 твл.
- Устройство передачи с максимальной граничной частотой 6 МГц обеспечит передачу – 480 твл.
- Устройство передачи с максимальной граничной частотой 7 МГц обеспечит передачу – 570 твл.
Известно, что в формировании фронтов и спадов импульсов особую роль играют гармоники высшего порядка, несмотря на то, что их амплитуда оказывается значительно ниже амплитуд первых гармоник.
Вот почему в аппаратуре передачи видеосигналов должна обеспечивается достаточно равномерная амплитудно-частотная характеристика по всему спектру частот от 50 Гц до 6 МГц для стандартного разрешения и до 7 МГц – для высокого. Неравномерность АЧХ не должна превышать ± 1 дБ, чтобы устройство передачи не оказывало заметного влияния на спектр видеосигнала и не снижало его качество.
Для оценки требуемой полосы частот можно использовать следующие практические соотношения:
- черно-белое изображение с разрешением 380 твл – допустима полоса пропускания до 5 МГц;
- цветное изображение с разрешением 380 твл – необходима полоса пропускания до 6 МГц;
- черно-белое изображение с разрешением 480 твл – необходима полоса пропускания до 6 МГц.
Бытует мнение, что не обязательно передавать видеосигнал, особенно черно-белый, с полосой 6 МГц, достаточно, мол, 3-4 МГц. При этом ссылаются на практику применения подобных устройств и экспериментальные исследования.
Приведем один абзац, который, будучи неправильно понятым, может привести к большим заблуждениям.
«В результате экспериментальных исследований установлено, что для черно-белых изображений почти вся мощность видеосигналов сосредоточена в области частот от 0 до 1,5 МГц, причем основная мощность сигнала сосредоточена в области от 200-300 к Гц. Наивысшая частота эффективной части спектра черно-белого видеосигнала составляет 6 МГц».
А.В. Петраков, В.С. Лагутин «Утечка и защита информации в телефонных каналах». Изд-во «Энергоатомиздат», Москва, 1998, с. 35-36.
Хочется предостеречь от ошибки тех, кто на основании этих справедливых утверждений делает вывод о том, что АЧХ можно сузить до 1,5 МГц. Уважаемые мною авторы указанной книги говорят о суммарной мощности основных частотных составляющих и в этом они абсолютно правы. Но для формирования деталей и мелких элементов видеоизображения необходимы все частотные составляющие вплоть до 6 МГц, несмотря на то, что их амплитуды малы по сравнению с амплитудами основных гармоник.
Работа с цифровыми устройствами регистрации видеосигнала
При работе аппаратуры передачи видеосигналов на оконечные устройства цифровой обработки видеосигнала, (квадраторы, мультиплексоры или системы наблюдения и регистрации на базе персонального компьютера), специалистам-монтажникам необходимо анализировать форму строчного синхронизирующего импульса с помощью осциллографа с граничной частотой не менее 5 МГц.
Все недостатки системы передачи неминуемо отразятся на форме строчного синхроимпульса, по которому можно судить о качестве системы передачи в целом.
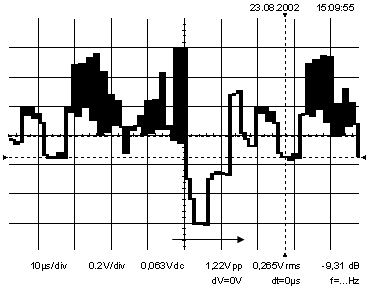
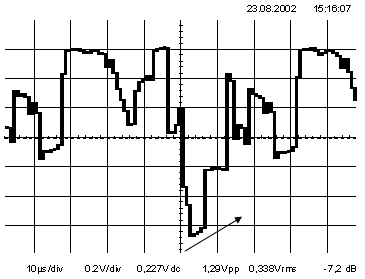
На рисунке 7, на первой осциллограмме строчный синхроимпульс не имеет искажений в виде скосов плоской вершины и существенных выбросов на фронтах. Система передачи работает правильно, видеосигнал – стандартный.
На второй осциллограмме видно, что плоская вершина синхроимпульса имеет скос «по типу дифференцирования». Это явление называется перекоррекцией.
При этом происходит завышение амплитуд высокочастотных гармоник, что вызывает дополнительный выброс, как на фронте строчного синхроимпульса, так и на переднем фронте гасящего импульса. Это неизбежно приводит к сбоям в работе цифровых устройств. Наблюдается «переконтраст» изображения.
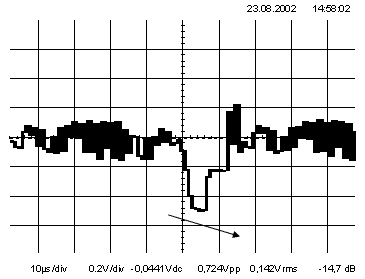
На третьей осциллограмме наблюдается скос строчного синхроимпульса «по типу интегрирования».
Это явление называется недокоррекцией.
Недокоррекция не вызывает срывов строчной синхронизации при работе на цифровые устройства, но делает изображение размытым, не позволяет различить мелкие детали, снижает контрастность изображения.
При недокоррекции снижается разрешающая способность и связанная с нею видимая четкость изображения.
Выводы:
- Независимо от выбора способа передачи аналогового видеосигнала необходимо использовать такие устройства передачи, которые обеспечивают необходимую коррекцию частотных искажений, вносимых кабельной линией, в полосе видеосигнала, по меньшей мере, от 50 Гц до 6 МГц.
- При использовании для передачи видеосигнала на расстояния 300 – 400 метров коаксиального кабеля надо учитывать его характеристику затухания. Кабель RG-59 B/U имеет на частотах видеосигнала затухание 3,6 дБ/100 м. На трассе в 200 метров видеосигнал на высоких частотах получит затухание 7,2 дБ, что приведет к снижению амплитуд наиболее высокочастотных гармоник видеосигнала, к потере информации о мелких деталях изображения и снижению разрешающей способности. Изображение на экране монитора будет казаться размытым и при просмотре обстановки создастся впечатление, что это следствие плохой фокусировки объектива видеокамеры.
- Максимальное расстояние передачи видеосигнала по коаксиальному кабелю зависит от целевой задачи видеоконтроля и определяется исходя из допустимого затухания видеосигнала в кабеле. Для обеспечения задач обнаружения допустимое затухание – 6 дБ. Для обеспечения возможности идентификации требуется более высокое качество, при этом допустимое затухание не должно превышать 3 дБ.
- Скомпенсировать в какой то мере частотные искажения в коаксиальном кабеле можно, используя на приемной стороне видео усилитель-корректор (ВУК).
- При длине кабельной трассы свыше 300-400 метров, более целесообразно использовать аппаратуру передачи видеосигнала по витой паре. Это позволит одновременно решить вопрос как повышения помехозащищенности канала передачи видеосигнала, так и улучшения качества передаваемого изображения. При этом под «витой парой» не обязательно понимается компьютерный кабель для локальных вычислительных сетей.
- Наилучшими характеристиками для передачи видеосигнала «по витой паре» на расстояния до 2000 метров обладает экранированный кабель телефонной городской связи ТППэп Nх2х0,5. По своим частотным характеристикам, при длине от 1000 метров и выше, он значительно превосходит кабели AWG 24 (5-й категории) и П-274М (полевой). Последние два кабеля допускаются к использованию для качественной передачи видеосигнала только до 1000 метров и требуют введения дополнительной частотной коррекции.
- Оценить качество будущей системы передачи видеосигнала на этапе проектирования можно по сквозной амплитудно-частотной характеристике устройства передачи. Сквозная АЧХ с «нулевыми» частотными искажениями (± 0 дБ) является идеальной. Поэтому та система совершенней, которая ближе к идеалу.
- «Нулевая» сквозная АЧХ свидетельствует о том, что «какой видеосигнал пришел на вход системы передачи, таким он и будет на выходе системы передачи». При этом имеет место точная передача всех частотных составляющих спектра видеосигнала. Идеальное изделие при передаче видеосигнала производит коррекцию искажений на всех частотах ровно настолько, насколько на каждой из этих частот вносит затухание кабель.
В зависимости от дальности допустимой является неравномерность АЧХ: ± 1,5…2,0 дБ. - Чем больший запас по затуханию имеет устройство передачи, тем большее число раз можно организовать ретрансляцию видеосигнала с целью увеличения общей дальности передачи. Это наиболее актуально при построении видеосистем для охраны периметров объектов. При ретрансляции следует принимать в расчет наихудшую ситуацию – когда происходит сложение неравномерностей с одинаковым знаком.
- В вещательном телевидении стандарт PAL ограничивает видеосигнал полосой 5 МГц. Это вынужденная мера частотной совместимости при многопрограммном вещании. В системах замкнутого телевидения для обеспечения высокой разрешающей способности по горизонтали, в пределах 570 твл, для передачи необходимо устройство с полосой пропускания до 7 МГц.
В. Майстренко
ООО «Тахион»
Макеты страниц
Итак, вычисление любых значений функции 


Пример 1. Вычислим среднее значение функции 

Имеем

Изменив порядок интегрирования и суммирования, получаем

Но

Поэтому

Отношение 



Пример 2. Вычислим корреляционную функцию

Имеем


Но

Отсюда

Положим 

где 

Из него следует, что дискретизация сигнала приводит к дискретизации корреляционной функции.
Пример 3. Вычислим фурье-образ функции 

Последний интеграл есть фурье-образ функции 
Имеем 
Следовательно,

где

Окончательно получаем

Из последнего выражения следует, что фурье-образ 




Итак, для вычисления фурье-образа сигнала на интервале 


Дискретизация с целью восстановления непрерывного сигнала.
Хотя интерполяционная формула Шеннона (7.7) теоретически и обоснована, ее практическое применение, особенно при приближенных вычислениях, затруднительно. На практике важно знать минимальное расстояние между двумя соседними точками дискретизации на временной оси, позволяющее применить достаточно простую интерполяционную формулу и тем самым восстановить непрерывный сигнал. Наиболее простой является линейная интерполяция с последующим применением низкочастотной фильтрации с целью сглаживания угловых точек интерполяционной линии (такой тип интерполяции соответствует распространенному на практике методу получения графиков, когда экспериментальные точки соединяются вручную). Следовательно, частота дискретизации зависит от допустимой ошибки при восстановлении функции по ее дискретным значениям и, конечно, от формы сигнала. Эта ошибка может быть
вычислена обычным способом, поскольку она не является статистической.
Обозначим через 






где 


Пусть спектр сигнала обрезан максимальной частотой 

Например, если ошибка