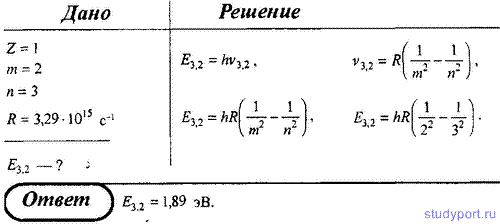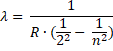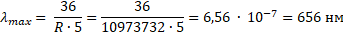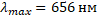Се́рия Ба́льмера — одна из спектральных серий атома водорода, наблюдающаяся для переходов между вторым энергетическим (первым возбуждённым) уровнем атома и вышележащими уровнями[1]. В отличие от ультрафиолетовой серии Лаймана, связанной с переходами на основной уровень, четыре первые линии серии Бальмера лежат в видимой области спектра.
Названа в честь швейцарского математика Иоганна Бальмера, описавшего в 1885 году эту серию формулой (см. ниже Формула Бальмера).
Образование серии Бальмера[править | править код]
Своим красным цветом эмиссионная Туманность Ориона обязана нейтральному атомарному водороду, излучающему в первой линии Бальмера Hα с длиной волны 656,3 нм.
Серия была обнаружена в спектре Солнца[2]. Благодаря распространённости водорода во Вселенной, серия Бальмера наблюдается в спектрах большинства космических объектов.
Данная серия образуется при переходах электронов с возбужденных энергетических уровней с главным квантовым числом n>2 на второй уровень (n=2) в спектре излучения и со второго уровня на все вышележащие уровни при поглощении.
Переход с третьего энергетического уровня на второй обозначается греческой буквой α, с 4-го на 2-й — β и т. д. Для обозначения самой серии используется латинская буква H. Таким образом, полное обозначение спектральной линии, возникающей при переходе электрона с третьего уровня на второй — Hα (произносится Бальмер-альфа).
Видимые линии излучения водорода в серии Бальмера.
Hα
— красная линия справа, имеющая длину волны 656,3 нм.
Две самые левые линии — H
ε и H
ζ, лежат уже в ультрафиолетовой области спектра и имеют длины волн 397,0 нм и 388,9 нм, соответственно.
Формула Бальмера[править | править код]
Схема энергетических уровней атома водорода и спектральные серии
Для описания длин волн λ четырёх видимых линий спектра водорода И. Бальмер предложил формулу:
- где n = 3, 4, 5, 6;
- b = 3645,6 Å.
В настоящее время для серии Бальмера используют частный случай формулы Ридберга:
- где λ — длина волны,
- R ≈ 109737,3157 см−1 — постоянная Ридберга,
- n — главное квантовое число исходного уровня — натуральное число, большее или равное 3.
Первые 4 линии серии находятся в видимом диапазоне, остальные — в ультрафиолетовом диапазоне:
| Обозначение | Hα | Hβ | Hγ | Hδ | Hε | Hζ | Hη | Граница серии |
|---|---|---|---|---|---|---|---|---|
| n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ∞ |
| Длина волны, нм | 656,3 | 486,1 | 434,1 | 410,2 | 397,0 | 388,9 | 383,5 | 364,6 |
Граница серии соответствует захвату протоном свободного электрона с нулевой начальной энергией на второй (то есть первый возбуждённый) уровень. За границей в сторону более коротких длин волн простирается бальмеровский континуум — непрерывная (не линейчатая) часть спектра, соответствующая захватам протоном свободного электрона с произвольной положительной начальной энергией на второй уровень атома водорода.
Кроме серии Бальмера, существуют серии линий излучения, лежащие целиком (за исключением континуума серии) в инфракрасной области спектра (серии Пашена, Брэкета, Пфунда и т. д., соответствующие переходам на 3-й, 4-й, 5-й… энергетические уровни), а также лежащая целиком в ультрафиолетовой области серия Лаймана, соответствующая переходам на основной уровень атома водорода.
История создания формулы Бальмера и её значение[править | править код]
Иоганн Бальмер не был спектрографистом. Его заслуга состоит в том, что он описал известный к тому времени спектр атомов водорода простой формулой:
где n = 3, 4, 5, 6; b = 3645,6 Å (известна как постоянная Бальмера).
Будучи убеждённым последователем пифагорейцев, Бальмер считал, что тайну единства всех наблюдаемых явлений следует искать в различных комбинациях целых чисел[3]. Существует версия, согласно которой Бальмер однажды похвастался, что может найти формулу для последовательности любых четырёх чисел, и его друг Эдуард Хагенбах-Бишофф на спор дал ему длины волн красной, зелёной, синей и фиолетовой линий водородного спектра[4][5]. Бальмер не только описал длины волн четырёх известных линий водорода, но и предсказал существование пятой линии (при n=7) с длиной волны 397 нм, в ближней ультрафиолетовой области, которую наблюдал Ангстрем, и более дальних линий ряда, которые были обнаружены Г.Фогелем и У. Хаггинсом в спектрах белых звёзд.
В 1886 году К. Рунге предложил использовать в формуле Бальмера вместо длины волны λ её частоту ν = c/λ:
где c — скорость света; k = 2; n = 3, 4, 5, 6; b = 3645,6 Å.
В 1890 году Й. Ридберг предложил записывать формулу в том виде, который она сохранила до сих пор:
В 1908 году В. Ритц выразил частоту волны в виде разницы двух термов:
предложив метод, впоследствии названный его именем.
Так предложенная Бальмером формула, описывающая четыре линии видимого спектра излучения водорода, получила развитие до принципов, позволяющих описать спектр любого химического элемента.
Безрезультатные попытки объяснить физический смысл формулы Бальмера продолжались почти 28 лет. В начале 1913 года Нильс Бор работал над тем, чтобы устранить противоречия между классическими законами физики и предложенной Резерфордом планетарной моделью атома. Спектроскопист Ханс Хансен (sv:Hans Marius Hansen) посоветовал Бору обратить внимание на спектральные формулы. Впоследствии Бор неоднократно говорил:
-
- Как только я увидел формулу Бальмера, все немедленно прояснилось передо мной[4][6].
Целые числа в формуле оказались разрешёнными орбитами, а спектральные линии — следствием квантовых переходов электронов с одной орбиты на другую[7].
Примечания[править | править код]
- ↑ «Физическая энциклопедия», т. 1, статья «Бальмера серия»
- ↑ См. статью Фраунгоферова линия.
- ↑ Л. Пономарев. По ту сторону кванта / Москва // Молодая гвардия, 1971, с. 304.
- ↑ 1 2 Данин Д. С. Вероятностный мир. — М.: Знание. — 1981. — С. 78, 79, 77
- ↑ W. F. Magie. A Source Book in Physics (неопр.). — Cambridge, Mass: Harvard University Press, 1969. — С. 360.
- ↑ Д. С. Данин. «Нильс Бор» (недоступная ссылка) // «Молодая гвардия», 1978 г
- ↑ См. статью «Боровская модель атома».
См. также[править | править код]
- Модель Бора
- Спектральные серии водорода
- Атом водорода
- Бальмеровский декремент
- Формула Бальмера — Ридберга
- Серия Пашена
- Серия Брэккета
- Серия Пфунда
- Атом водорода
- Закон Мозли
- Серия Хамфриса
Ссылки[править | править код]
- Спектр водорода (анимация)
- Eisberg and Resnick. Quantum Physics. — John Wiley and Sons. — 1985.
В сегодняшней статье нашей традиционной рубрики «Физика» займемся решением задач. Тема: постулаты Бора.
Ищите полезную информацию для учебы? Подпишитесь на наш телеграм-канал! А если хотите заказ со скидкой, загляните на второй канал для клиентов – там много всяческих бонусов.
Нужна помощь?
Доверь свою работу кандидату наук!
Задачи на тему постулаты Бора с решениями
Постулаты Бора – сложная тема. Но решение задач по ней довольно простое, достаточно знать и уметь применять лишь несколько формул. Кстати, для удобства мы собрали полезные формулы в одном месте. А если вообще не знаете, как подступиться к задачам по физике, прочтите общую памятку по решению.
Задача на постулаты Бора №1
Условие
Вычислить энергию ε фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.
Решение
Энергия фотона, испускаемого атомом водорода при переходе с одного энергетического уровня на другой, равна:
ε=Ei1n21-1n22Ei=13,6 эВ
Здесь Ei – энергия ионизации атома водорода.
Рассчитаем:
ε=13,6112-132=12,09 эВ
Ответ: 12,09 эВ.
Задача на постулаты Бора №2
Условие
Найдите максимальную длину волны, излучаемой в серии Бальмера.
Решение
Запишем формулу Бальмера-Ридберга:
1λ=R122-1n2
Максимальная длина волны соответствует минимальному значению разности:
122-1n2
То есть:
122-132=536
Отсюда найдем:
λmax=36R·5R=1,0973732 м-1λmax=361,0973732·5=656 нм
Ответ: 656 нм.
Задача на постулаты Бора №3
Условие
При переходе электрона в атоме из стационарного состояния с энергией – 4,8 эВ излучается фотон, энергия которого равна 3,1 эВ. Определите энергию конечного состояния электрона.
Решение
Атом испускает фотон, а значит, электрон переходит в стационарное состояние с меньшей энергией, которая будет равна разности энергии первоначального состояния и энергии испущенного фотона:
Е=-4,8-3,1=-7,9 эВ
Ответ: -7,9 эВ.
Задача на постулаты Бора №4
Условие
Определить изменение энергии ∆E электрона в атоме водорода при излучении атомом фотона с частотой ϑ=6,28·1014 Гц. Ответ дать в электрон-вольтах.
Решение
Изменение энергии электрона равно энергии испущенного фотона:
∆E=εф
Энергия фотона равна:
εф=hϑ
Рассчитаем:
εф=6,62·10-34·6,28·1014=4,16·10-19 Дж=4,16·10-191,6·10-19=2,6 эВ
Ответ: 2,6 эВ.
Задача на постулаты Бора №5
Условие
На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ=486 нм?
Решение
Согласно второму постулату Бора:
∆E=Ek-En=hϑhϑ=hcλ∆E=6,62·10-34·3·108486·10-9=4,086·10-19Дж=2,554 эВ
Ответ: 2,554 эВ.
Вопросы на тему постулаты Бора
Вопрос 1. Сформулируйте постулаты Бора.
Ответ. Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
- Первый постулат: атом может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует своя энергия; в стационарном состоянии атом не излучает. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Следовательно, электрон может находиться на нескольких вполне определенных орбитах. Каждой орбите электрона соответствует вполне определенная энергия.
- Второй постулат: при переходе из одного стационарного состояния в другое испускается или поглощается квант электромагнитного излучения.
Вопрос 2. В каком случае энергия поглощается атомом, а в каком испускается?
Ответ. При переходе электрона с ближней орбиты на более удаленную орбиту, атомная система поглощает квант энергии. При переходе с более удаленной орбиты электрона на ближнюю орбиту по отношению к ядру атомная система излучает квант энергии.
Вопрос 3. Какие противоречия есть в теории Бора?
Ответ. Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями. С одной стороны она применяет законы классической физики, а с другой – основывается на квантовых постулатах. Теория Бора рассматривает спектры атома водорода и водородоподобных систем и позволяет вычислить частоты спектральных линий, однако не может объяснить их интенсивности и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора также является невозможность описания с ее помощью спектра атома гелия – одного из простейших атомов, непосредственно следующего за атомом водорода.
Вопрос 4. Чему равна энергия фотона, испускаемого атомом при переходе в другое энергетическое состояние?
Ответ. Энергия фотона равна разности энергий атома в двух состояниях.
Вопрос 5. Может ли атом излучать и поглощать фотоны с любой частотой?
Ответ. Нет! Согласно постулатам Бора, атом может поглощать и излучать фотоны только с некоторыми определенными значениями частоты.
Посмотри примеры работ и убедись, что мы поможем на совесть!
Нужна помощь в решении задач? Профессиональный сервис для учащихся готов ее предоставить!
Как определить максимальную длину волны?
Постоянная Ридберга
равна 1,097•107 1/м. Найти максимальную длину волны линии в видимой
области спектра излучения атома водорода.
Решение.
Формула Бальмера для
длины волны в спектре излучения атома водорода в видимой области записывается в
следующем виде.
N =
3,4,5, … ; R –
постоянная Ридберга.
Для первой линии Hα в
видимой области n = 3.
Ответ: максимальная
длинна волны в спектре излучения атома водорода равна 655 нм.
Источник: Пособие-репетитор для подготовки к централизованному тестированию. С.Н.Капельян, Л.А.Аксенович.
Страница 1 из 2
6. Элементы квантовой физики атомов, молекул и твердых тел
1. Определите энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
2. Определите максимальную и минимальную энергии фотона в видимой серии спектра водорода (серии Бальмера).
3. Определите длину волны λ, соответствующую второй спектральной линии в серии Пашена.
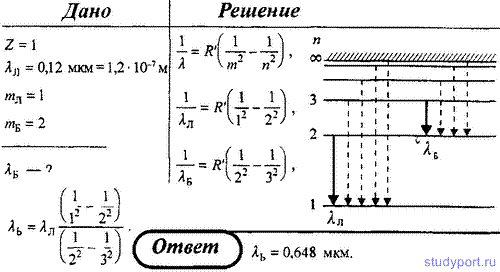
4. Максимальная длина волны спектральной водородной линии серии Лаймана равна 0,12 мкм. Предполагая, что постоянная Ридберга неизвестна, определите максимальную длину волны линии серии Бальмера.
5. Определите длину волны спектральной линии, соответствующей переходу электрона в атоме водорода с шестой боровской орбиты на вторую. К какой серии относится эта линия и какая она по счету?
6. Определите длины волн, соответствующие: 1) границе серии Лаймана; 2) границе серии Бальмера; 3) границе серии Пашена. Проанализируйте результаты.
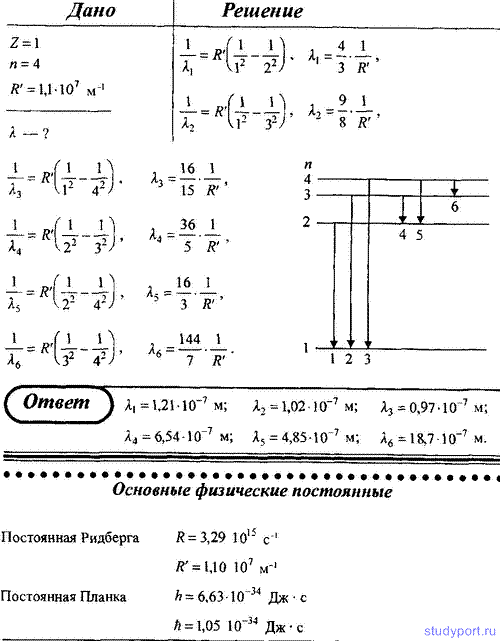
7. Атом водорода находится в возбужденном состоянии, характеризуемом главным квантовым числом n = 4. Определите возможные спектральные линии в спектре водорода, появляющиеся при переходе атома из возбужденного состояния в основное.
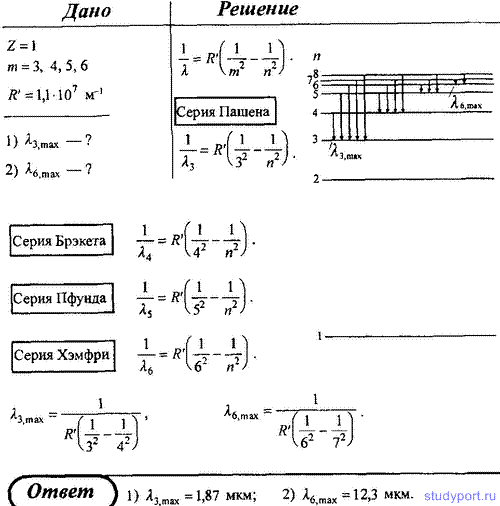
8. В инфракрасной области спектра излучения водорода обнаружено четыре серии—Пашена, Брэкета, Пфунда и Хэмфри. Запишите спектральные формулы для них и определите самую длинноволновую линию: 1) в серии Пашена; 2) в серии Хэмфри.
9. Определите число спектральных линий, испускаемых атомарным водородом, возбужденным на n-й энергетический уровень.
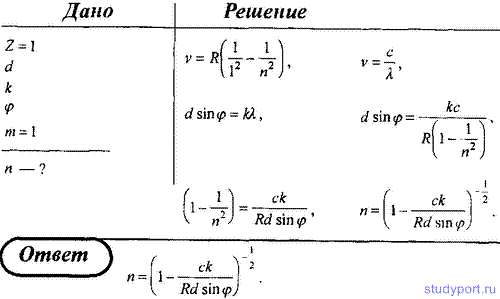
10. На дифракционную решетку с периодом d нормально падает пучок света от разрядной трубки, наполненной атомарным водородом. Оказалось, что в спектре дифракционный максимум k-го порядка, наблюдаемый под углом φ, соответствовал одной из линий серии Лаймана. Определите главное квантовое число, соответствующее энергетическому уровню, с которого произошел переход.
11. Используя теорию Бора для атома водорода, определите: 1) радиус ближайшей к ядру орбиты (первый боровский радиус); 2) скорость движения электрона по этой орбите.
12. Определите, на сколько изменилась энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ = 4,86*10-7 м.
13. Определите длину волны λ спектральной линии, излучаемой при переходе электрона с более высокого уровня энергии на более низкий уровень, если при этом энергия атома уменьшилась на ΔE = 10 эВ.
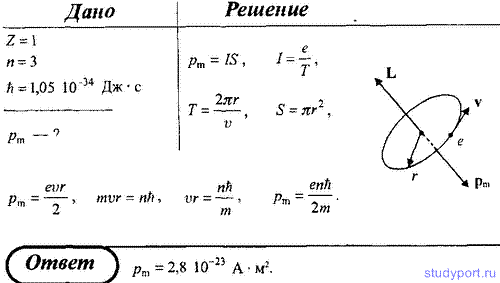
14. Используя теорию Бора, определите орбитальный магнитный момент электрона, движущегося по третьей орбите атома водорода.
15. Определите изменение орбитального механического момента электрона при переходе его из возбужденного состояния в основное с испусканием фотона с длиной волны λ = 1,02*10-7 м.
16. Позитроний — атомоподобная система, состоящая из позитрона и электрона, вращающегося относительно общего центра масс. Применяя теорию Бора, определите минимальные размеры подобной системы.
17. Предполагая, что в опыте Франка и Герца вакуумная трубка наполнена не парами ртути, а разреженным атомарным водородом, определите, через какие интервалы ускоряющего потенциала φ возникнут максимумы на графике зависимости силы анодного тока от ускоряющего потенциала.
19. Докажите, что энергетические уровни атома водорода могут быть описаны выражением En = -2πh/n2, где R — постоянная Ридберга.
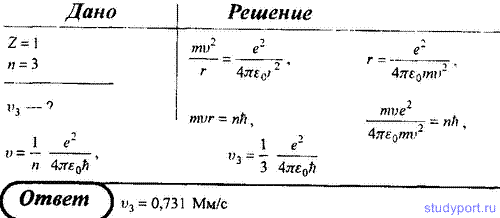
20. Определите скорость v электрона на третьей орбите атома водорода.


Максимальная длина волны, излучаемой в серии Бальмера равна ___ нм.
Решение:
Из формулы Бальмера-Ридберга:
Максимальная длина волны соответствует минимальному значению разности:
R = 10973732 м-1.
Ответ:
5. Задание:
В чем достижения и недостатки теории Бора?
Решение: Теория Бора истолковала существования линейчатых спектров водородоподобных систем. Она дала объяснение физической природы характеристических рентгеновских лучей. Теория Бора сыграла существенную роль в развитии атомной спектроскопии. При использовании теории Бора был собран экспериментальный материал о спектрах атомов и молекул.
К недостаткам теории Бора относят ее внутреннюю противоречивость. Она соединяет классическую физику с квантовыми постулатами. Эта теория неприменима к атомам, которые имеют более одного электрона. Развитие физики показало, что теория, созданная Бором, верно истолковывает одни факты и не способна объяснить другие. Эта теория является переходной при создании последовательной квантовой теории. Недостатки теории Бора проявились уже в применении к атому водорода. Так, правильно определяя частоты линий спектра, эта теория не дает возможности найти их интенсивность. Теория не рассматривает вопросы поляризации и когерентности. С помощью разработок Бора не было возможности пояснить дублетный характер спектров щелочных металлов Дифракция частиц, также осталась вне рамок теории.