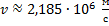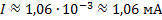Как найти максимальную длину волны фотона - Сайт, где вы сможете решить свои вопросы

Решение задач по теме «Модель атома Н. Бора»

Задача 1

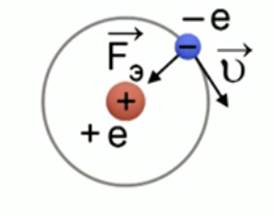
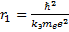
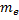
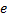
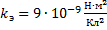
Определите скорость v и ускорение a электрона на первой боровской орбите, радиус которой определяется формулой , где и – масса и заряд электрона; .

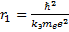
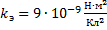
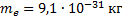
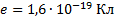
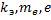
Дано: – формула радиуса первой боровской орбиты; – коэффициент пропорциональности закона Кулона; – масса электрона; – заряд электрона ( – постоянные величины)

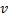
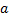
Найти: – скорость электрона, – ускорение электрона

Решение

В формуле радиуса первой боровской орбиты:

– квантовая постоянная Планка

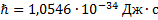
Радиус окружности, по которому происходит движение, равен:

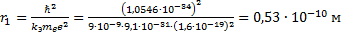
Рис. 1. Иллюстрация к задаче №1

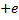
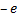
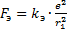
Согласно модели Бора, вокруг ядра атома водорода, заряд которого , вращается электрон, заряд которого (см. Рис. 1). Вращение происходит за счёт силы электрического притяжения электрона к ядру. Эта сила, по закону Кулона, равна:

Также эта сила является центростремительной, то есть:

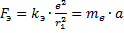
Следовательно, ускорение равно:

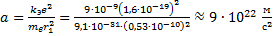
Центростремительное ускорение равно:

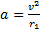
Отсюда скорость равна:

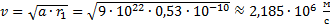
Ответ: ;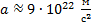

Задача 2

Найти силу электрического тока, который вызывает электрон, двигаясь по первой боровской орбите.

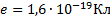
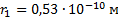
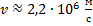
Дано: – заряд электрона; – радиус орбиты; – скорость электрона (найдена в задаче 1)

Найти: 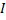– силу тока

Решение

Известно, что сила тока равна:

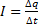
Для данной задачи:

– период обращения электрона

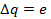
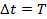
Период обращения электрона равен:

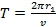
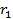
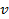
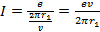
Следовательно, сила тока, возникающего при движении электрона по орбите радиусом со скоростью , равна:

Подставим в данное выражение известные данные:

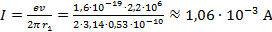
Ответ:

Задача 3

Найти максимальную частоту, максимальную длину волны и максимальный импульс фотона в видимой части спектра, излучённого при переходе электрона на второй энергетический уровень в атоме водорода.

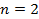
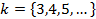
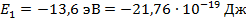
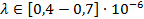
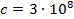
Дано: – второй энергетический уровень; – энергетические уровни, с которых может осуществляться переход электрона; – энергия на первом уровне; м – видимая область спектра; – скорость света

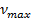
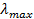
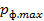
Найти: – максимальную частоту фотона; – максимальную длину волны фотона; – максимальный импульс фотона

Решение

Согласно второму постулату Бора:

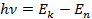
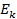
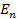
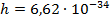
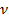
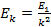
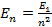
где и – энергии стационарных состояний атома соответственно до и после излучения фотона; – постоянная Планка; – частота излучения фотона.

Следовательно, частота излучения фотона равна:

Частота и длина волны связаны следующим соотношением:

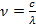
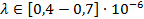
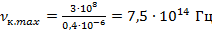
Зная световой диапазон в длинах волн (), можно вычислить максимальное значение частоты кванта, который принадлежит световому диапазону:

Более высокие частоты относятся к ультрафиолетовой части спектра и человеческим глазом не фиксируются.

Минимальное значение частоты при излучении будет при :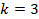

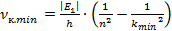
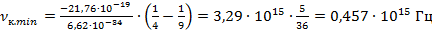
Подставим данное значение в формулу связи между длиной волны и частотой. Если частота минимальная, то значение длины волны будет максимальное:

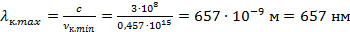
Данное значение входит в световой диапазон – это красная линия в излучении атома водорода.

Для того чтобы вычислить максимальное значение частоты фотона в видимой части спектра, необходимо подставлять значения k от 4-х и выше.

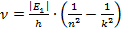
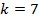
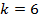
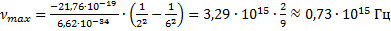
Если подставить значение , то мы выходим за диапазон видимой части спектра, поэтому максимальное значение . Именно для этого значения k находим максимальное значение частоты фотона:

Мы попали в световой диапазон, так как он ограничивается значением .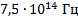

Полученная максимальная частота соответствует минимальной длине волны, равной:

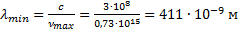
Минимальная длина волны была найдена для определения максимального импульса фотона.

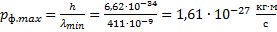
Ответ: ; ; .

Источник

Длина волны фотонов говорит нам об их энергии. Итак, в этой статье мы рассмотрим, что такое длина волны фотонов и как ее найти. Начнем.

Фотоны путешествуют через электромагнитные волны. Поскольку фотон в конечном счете является частью электромагнитной волны, его длина волны будет такой же, как у электромагнитной волны. Если известны энергия и частота фотона, то по ним можно легко найти длину волны фотона.

Прежде чем мы перейдем к длине волны фотона, давайте посмотрим, что такое фотон.

Фотон:

Поскольку энергия, содержащаяся в фотонах, неделима, их часто называют энергетическими пакетами. Максвелл описал фотоны как электрические поля, перемещающиеся в пространстве. Или, другими словами, энергия фотона хранится в виде колеблющегося электрического поля, которое может колебаться на любой частоте. Таким образом квант электромагнитного излучения или энергии называется фотоном.

Фотоны — это частицы, не имеющие ни заряда, ни массы. В результате они могут путешествовать со скоростью света. Скорость электрического поля может определять скорость фотонов в свободном пространстве. Испускание фотонов возможно с помощью действия заряженных частиц и некоторых других способов, таких как радиоактивный распад.

Какова длина волны фотона?

Свойства фотонов такие же, как у электромагнитных волн. В результате каждый фотон связан со своим уникальным частота и длина волны.

Фотоны движутся волнами, как будто каждый из них едет на американских горках, которые многократно повторяют одну и ту же дорожку. Длина волны фотонной волны — это длина волны, точнее, расстояние между двумя последовательными точками одной и той же фазы волны.

На диаграмме ниже показаны три различных длины волны. Хотя фотоны не имеют цвета, они будут соответствовать свету этого конкретного цвета.

Как найти длину волны фотона?

Длина волны электрического поля или фотонной волны равна длине волны фотона.

Для определения длины волны фотона используется либо его энергия, либо частота. В результате, если какой-либо из них известен, можно легко найти длину волны фотона.

Давайте посмотрим, как найти длину волны фотона, используя частоту и энергию.

Как найти длину волны фотона с частотой?

Частота и длина волны фотона связаны друг с другом.

Длина фотонной волны дает длину волны фотонной волны. В то время как количество длин волн фотонов, которые распространяются каждую секунду, дает нам частоту фотонных волн. В результате, если длина волны фотона короткая, его частота будет высокой, и его частота будет низкой, если длина волны большая.

Поскольку одно увеличивается, а другое уменьшается, мы можем сказать, что они имеют обратную зависимость. Выведем математическое уравнение, отражающее связь между частотой фотона и длиной волны.

Для описания волны можно использовать несколько величин, таких как длина волны, период, частота и т. д. Как мы знаем, частота фотонной волны определяет количество фотонных волн, которые распространяются каждую секунду. В результате частоту фотонной волны можно рассчитать следующим образом:

………. (1)

Где f — частота фотонной волны, а T — период фотонной волны, т. е. время, за которое фотонная волна совершает один цикл.

После одного периода каждая точка волны возвращается к одному и тому же значению. Это происходит потому, что в волне за один период происходит одно колебание, и каждое колебание проходит за это время расстояние в одну длину волны.

Расстояние, пройденное любой волной в единицу времени, определяет ее скорость. Но так как волна распространяется со скоростью света, то мы обозначаем ее буквой с, и это можно определить как:

………. (2)

Из уравнений (1) и (2) можно написать:

с = 𝜆f ……….(3)

Таким образом, длина волны фотона определяется выражением:

………. (4)

Поскольку скорость света c постоянна и имеет значение 3 · 10⁸ м/с, из приведенного выше уравнения можно сделать вывод, что длина волны фотона обратно пропорциональна его частоте.

Как рассчитать длину волны фотона с заданной энергией?

Компания частота фотона связана как с его энергией, и длина волны. В результате длина волны фотона также связана с его энергией.

Длина волны фотонной волны содержит информацию о ее энергии. Фотонная волна с более короткой длиной волны будет иметь более высокую частоту и, следовательно, более высокую энергию. Точно так же фотонная волна с большей длиной волны будет иметь более низкую частоту и, следовательно, меньшую энергию.

Кроме того, в этом случае более длинная длина волны соответствует более низкой энергии волны, тогда как более короткая длина волны соответствует более высокой энергии волны. Как результат, можно утверждать, что длина волны фотонной волны и ее энергия обратно пропорциональны. С точки зрения уравнения, давайте посмотрим на связь между энергией и длиной волны фотонной волны.

По словам великого ученого Макса Планка, свет состоит из дискретных пакетов энергии, известных как кванты света, которые также известны как фотоны. Энергия света может иметь только дискретные значения. Далее Планк сказал, что энергия определяется произведением частоты фотонов на постоянную, известную как постоянная Планка. Мы можем выразить это математически следующим образом:

Е = hf ……….(5)

Где h = постоянная Планка (6.626 X 10^-34 Дж с)

Когда мы сравниваем уравнения (4) и (5), мы получаем следующее выражение для энергии:

………. (6)

Преобразовывая уравнение Планка, длина волны фотона с точки зрения энергии определяется выражением:

………. (7)

Таким образом, если энергия фотона или световой волны известна, длину волны фотона можно определить с помощью уравнения Планка.

Некоторые проблемы нахождения длины волны фотона по частоте и энергии:

Задача: Какова длина световой волны с частотой 7 х 10¹⁴ Гц?

Данные параметры:

Частота фотона f =7 X 10¹⁴ Hz

Скорость света с = 3 х 10⁸ м/с

Найти:

Длина волны фотона 𝜆 = ?

Решение:

𝜆 = с / ж

𝜆 = 3 х 10⁸ / 7 х 10¹⁴

∴ 𝜆 = 0.428 х 10^-6 m

∴ 𝜆 = 428 нм

В результате фотон с частотой 7 X 10¹⁴ Гц имеет длину волны 428 нм.

Задача: Какую длину волны будет иметь фотон, если его энергия равна 4 х 10^-15 J?

Данные параметры:

Энергия фотона E = 4 X 10^-15 J

Постоянная Планка h = 6.626 x 10^-34 Js

Скорость света с = 3 х 10⁸ м/с

Найти:

Длина волны фотона 𝜆 = ?

Решение:

𝜆 = hc / E

𝜆 = 6.626 х 10^-34 Х 3 Х 10⁸ / 4 х 10^-15

∴ 𝜆 = 5 х 10^-11 m

∴ 𝜆 = 500 нм

AВ результате фотон с энергией 4×10^-15 J имеет длину волны 500 нм.

Задача: если энергия фотона равна 2.19 × 10¹¹ ev, определите длину волны этого фотона.

Данные параметры:

Энергия фотона E = 2.19 × 10¹¹ ev

∴ Е = 2.19 × 10¹¹ Х 1.6 Х 10-19

∴ Е = 3.05 × 10^-8 Дж = 350 х 10^-10 J

Постоянная Планка h = 6.626 x 10^-34 Js

Скорость света с = 3 х 10⁸ м/с

Найти:

Длина волны фотона 𝜆 = ?

Решение:

𝜆 = hc / E

𝜆 = 6.626 х 10^-34 Х 3 Х 10⁸ / 350 х 10^-10

∴ 𝜆 = 0.056 х 10^-16 m

В результате фотон с энергией 2.19×10¹¹ ev имеет длину волны 0.056 X 10^-16 m.

Источник

Атом Бора.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев.

Темы кодификатора ЕГЭ: постулаты Бора.

Планетарная модель атома, успешно истолковав результаты опытов по рассеянию alpha -частиц, в свою очередь столкнулась с очень серьёзными трудностями.

Как мы знаем, любой заряд, движущийся с ускорением, излучает электромагнитные волны. Это — неоспоримый факт классической электродинамики Максвелла, подтверждаемый многочисленными наблюдениями.

Нам также хорошо известно, что электромагнитные волны несут энергию. Стало быть, ускоренно движущийся заряд, излучая, теряет энергию, которая этим излучением уносится.

А теперь давайте возьмём произвольный электрон в планетарной модели. Он двигается вокруг ядра по замкнутой орбите, так что направление его скорости постоянно меняется. Следовательно, электрон всё время имеет некоторое ускорение (например, при равномерном движении по окружности это будет центростремительное ускорение), и поэтому должен непрерывно излучать электромагнитные волны. Расходуя свою энергию на излучение, электрон будет постепенно приближаться к ядру; в конце концов, исчерпав запас своей энергии полностью, электрон упадёт на ядро.

Если исходить из того, что механика Ньютона и электродинамика Максвелла работают внутри атома, и провести соответствующие вычисления, то получается весьма озадачивающий результат: расход энергии электрона на излучение (с последующим падением электрона на ядро) потребует совсем малого времени — порядка $10^{-8}$ секунды. За это время атом должен полностью “коллапсировать” и прекратить своё существование.

Таким образом, классическая физика предрекает неустойчивость атомов, устроенных согласно планетарной модели. Этот вывод находится в глубоком противоречии с опытом: ведь на самом деле ничего такого не наблюдается. Предметы нашего мира вполне устойчивы и не коллапсируют на глазах! Атом может сколь угодно долго пребывать в невозбуждённом состоянии, не излучая при этом электромагнитные волны.

Постулаты Бора.

Оставалось признать, что внутри атомов перестают действовать известные законы классической физики. Микромир подчиняется совсем другим законам.

Первый прорыв в познании законов микромира принадлежит великому датскому физику Нильсу Бору. Он предложил три постулата, резко расходящиеся с механикой и электродинамикой, но тем не менее позволяющих правильно описать простейший из атомов — атом водорода.

Классическая физика хорошо описывает непрерывные процессы — движение материальной точки, изменение состояния идеального газа, распространение электромагнитных волн… Энергия объекта, подчиняющегося механике или электродинамике, в принципе может принимать любые значения. Однако линейчатые спектры указывают на дискретность процессов, происходящих внутри атомов. Эта дискретность должна фигурировать в законах новой теории.

Первый постулат Бора. Всякий атом (и вообще, всякая атомная система) может находиться не во всех состояниях с любым, наперёд заданным значением энергии. Возможен лишь дискретный набор избранных состояний, называемых стационарными, в которых энергия атома принимает значения $E_{1}, E_{2},...E_{n},...$ Находясь в стационарном состоянии, атом не излучает электромагнитные волны.

Как видим, первый постулат Бора вопиющим образом противоречит классической физике: налагается запрет на любые значения энергии, кроме избранного прерывистого набора, и признаётся, что электроны, вроде бы движущиеся ускоренно, на самом деле не излучают.

Выглядит фантастически, не правда ли? Однако в том же 1913 году, когда Бор предложил свои постулаты, существование стационарных состояний было подтверждено экспериментально — в специально поставленном опыте немецких физиков Франка и Герца. Таким образом, стационарные состояния — это не выдумка, а объективная реальность.

Значения разрешённого набора $E_{1}, E_{2},...E_{n},...$ называются уровнями энергии атома. Что происходит при переходе с одного уровня энергии на другой?

Второй постулат Бора. Если атом переходит из стационарного состояния с большей энергией $E_{n}$ в стационарное состояние с меньшей энергией $E_{k}$ , то разность этих энергий может высвободиться в виде излучения. В таком случае излучается фотон с энергией

$hnu =E_{n}-E_{k}$ . (1)

Эта же формула работает и при поглощении света: в результате столкновения с фотоном атом переходит из состояния $E_{k}$ в состояние с большей энергией $E_{n}$ , а фотон при этом исчезает.

Для примера на рис. 1 показано излучение фотона при переходе атома с энергетического уровня $E_{3}$ на уровень $E_{1}$ . Переход заключается в том, что электрон “соскакивает” с одной орбиты на другую, расположенную ближе к ядру.

Рис. 1. Излучение фотона атомом

Формула (1) даёт качественное представление о том, почему атомные спектры испускания и поглощения являются линейчатыми.

В самом деле, атом может излучать волны лишь тех частот, которые соответствуют разностям значений энергии разрешённого дискретного набора $E_{1}, E_{2},...E_{n},...$ ; соответственно, набор этих частот также получается дискретным. Вот почему спектр излучения атомов состоит из отдельно расположенных резких ярких линий.

Вместе с тем, атом может поглотить не любой фотон, а только тот, энергия hnu которого в точности равна разности $E_{n}-E_{k}$ каких-то двух разрешённых значений энергии $E_{n}$ и $E_{k}$ . Переходя в состояние с более высокой энергией $E_{n}$ , атомы поглощают ровно те самые фотоны, которые способны излучить при обратном переходе в исходное состояние $E_{k}$ . Попросту говоря, атомы забирают из непрерывного спектра те линии, которые сами же и излучают; вот почему тёмные линии спектра поглощения холодного атомарного газа находятся как раз в тех местах, где расположены яркие линии спектра испускания этого же газа в нагретом состоянии.

Качественного объяснения характера атомных спектров, однако, недостаточно. Хотелось бы иметь теорию, позволяющую вычислить частоты наблюдаемых спектров. Бору удалось это сделать в самом простом случае — для атома водорода.

Атом водорода.

Атом водорода состоит из ядра с зарядом , которое называется протоном, и одного электрона с зарядом (через обозначена абсолютная величина заряда электрона). При построении своей теории атома водорода Бор сделал три дополнительных предположения.

1. Прежде всего, мы ограничиваемся рассмотрением только круговых орбит электрона. Таким образом, электрон движется вокруг протона по окружности радиуса с постоянной по модулю скоростью (рис. 2).

Рис. 2. Модель атома водорода

2. Величина mvr , равная произведению импульса электрона на радиус орбиты , называется моментом импульса электрона. В каких единицах измеряется момент импульса?

Смотрим:

[mvr] =кг*м/с*м=(кг*м/ $c^{2}$ )*м*с=Н*м*с=Дж*с.

Это в точности размерность постоянной Планка! Именно здесь Бор увидел появление дискретности, необходимой для квантового описания атома водорода.

Правило квантования (третий постулат Бора). Момент импульса электрона может принимать лишь дискретный набор значений, кратных “перечёркнутой” постоянной Планка:

$mvr=nh^{mkern -14mu-}, (n=1,2,3,...)$ , (2)

3. Выше мы говорили, что классическая физика перестаёт работать внутри атома. Так оно в действительности и есть, но вопреки этому мы предполагаем, что электрон притягивается к протону с силой, вычисляемой по закону Кулона, а движение электрона подчиняется второму закону Ньютона:

$dfrac{mv^{2}}{r}=dfrac{ke^{2}}{r^{2}}$ . (3)

Эти три предположения позволяют довольно просто получить формулы для уровней энергии атома водорода. Переписываем соотношение (3) в виде:

$mv^{2}=dfrac{ke^{2}}{r^{2}}$ . (4)

Из правила квантования (2) выражаем :

$v=dfrac{nh^{mkern -14mu-}}{mr}$ ,

и подставляем это в (4):

$dfrac{n^{2}(h^{mkern -14mu-})^{2}}{mr^{2}}=dfrac{ke^{2}}{r}$ .

Отсюда получаем формулу для допустимых радиусов орбит электрона:

$r_{n}=dfrac{(h^{mkern -14mu-})^{2}n^{2}}{kme^{2}}$ . (5)

Теперь перейдём к нахождению энергии электрона. Потенциальная энергия кулоновского взаимодействия электрона с ядром равна:

$W=dfrac{k(+e)(-e)}{r}=- dfrac{ke^{2}}{r}.$

(Она отрицательна, так как отсчитывается от бесконечно удалённой точки, в которой достигает максимального значения.)

Полная энергия электрона равна сумме его кинетической и потенциальной энергий:

$E=dfrac{mv^{2}}{2}-dfrac{ke^{2}}{r}$ .

Вместо $mv^{2}$ подставим правую часть выражения (4):

$E=dfrac{ke^{2}}{2r}-dfrac{ke^{2}}{r}=-dfrac{ke^{2}}{2r}$ . (6)

Полная энергия, как видим, отрицательна. Если на радиус орбиты никаких ограничений не накладывается, как это имеет место в классической физике, то энергия может принимать любые по модулю значения. Но согласно (5) существует лишь дискретный набор возможных значений радиуса; подставляя их в (6), получаем соответствующий набор допустимых значений энергии атома водорода:

$E=-dfrac{ke^{2}}{2r_{n}}=-dfrac{k^{2}me^{4}}{2(h^{mkern -14mu-})^{2}n^{2}}, (n=1,2,3,...)$ . (7)

Основное состояние атома водорода — это состояние с наименьшей энергией $E_{1}$ . В основном состоянии атом может находиться неограниченно долго. Вычисление даёт:

$E_{1}=-2,18 cdot 10^{-18}$ Дж =-13,6 эВ:

Мы видим, что если атом находится в основном состоянии, то для выбивания электрона нужно сообщить атому энергию, равную как минимум 13,6 эВ. Эта величина носит название энергии ионизации атома водорода.

По формуле (5) легко вычислить радиус орбиты основного состояния:

$r_{1}=dfrac{(h^{mkern -14mu-})^{2}}{kme^{2}}=5cdot 10^{-9}$ см.

То есть, диаметр атома оказывается равным как раз $10^{-8}$ см — величине, известной из опыта. Таким образом, теория Бора впервые смогла объяснить размер атома!

Кроме того, в рамках теории Бора удаётся получить формулы для вычисления частот (или длин волн) спектра атома водорода. Так, согласно второму постулату Бора и формуле (7) имеем:

$nu =dfrac{E_{n}-E_{k}}{h}=dfrac{k^{2}me^{4}}{4pi (h^{mkern -14mu-})^{3}}(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})$ . (8)

На практике чаще имеют дело с длинами волн. Учитывая, что , формулу (8) можно переписать так:

$dfrac{1}{lambda} =dfrac{k^{2}me^{4}}{4pi (h^{mkern -14mu-})^{3}}(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})=R(dfrac{1}{k^{2}}-dfrac{1}{n^{2}})$ . (9)

Константа $R=1,1 cdot 10^{-7}$ м $^{-1}$ называется постоянной Ридберга. Теория Бора даёт значение этой постоянной, очень хорошо согласующееся с экспериментом.

Длины волн спектра атома водорода образуют серии, характеризующиеся фиксированным значением в формуле (9). Все длины волн данной серии излучаются при переходах на уровень $E_{k}$ с вышележащих энергетических уровней $E_{n}, (n=k+1, k+2, k+3,...)$ .

Переходы в основное состояние:

$E_{2}rightarrow E_{1}, E_{3}rightarrow E_{1}, E_{4}rightarrow E_{1},...$

образуют серию Лаймана. Длины волн этой серии описываются формулой (9) при k=1 :

$dfrac{1}{lambda} =R(1-dfrac{1}{n^{2}})$ .

Линии серии Лаймана лежат в ультрафиолетовом диапазоне.

Переходы на второй уровень:

$E_{4}rightarrow E_{2}, E_{3}rightarrow E_{2}, E_{5}rightarrow E_{2},...$

образуют серию Бальмера. Длины волн этой серии подчиняются формуле (9) при k=2 :

$dfrac{1}{lambda} =R(dfrac{1}{4}-dfrac{1}{n^{2}})$ .

Первые четыре линии серии Бальмера лежат в видимом диапазоне (рис. 3), остальные — в ультрафиолетовом.

Рис. 3. Видимый спектр атома водорода (серия Бальмера)

Переходы на третий уровень:

$E_{4}rightarrow E_{3}, E_{5}rightarrow E_{3}, E_{6}rightarrow E_{3},...$

образуют серию Пашена. Длины волн этой серии описываются формулой (9) при k=3 :

$dfrac{1}{lambda} =R(dfrac{1}{9}-dfrac{1}{n^{2}})$ .

Все линии серии Пашена лежат в инфракрасном диапазоне.

Имеются ещё три “именованных” серии: это серия Брэккета (переходы на уровень k=4 ), серия Пфунда (переходы на уровень k=5 ) и серия Хэмпфри (переходы на уровень k=6 ). Все линии этих серий лежат в далёкой инфракрасной области.

Достоинства и недостатки теории Бора.

О достоинствах модели атома водорода, предложенной Бором, мы так или иначе уже сказали. Резюмируем их.

— Теория Бора продемонстрировала, что для описания атомных объектов принципиально недостаточно представлений классической физики. В микромире работают другие, совершенно новые законы.
Для микромира характерно квантование — дискретность изменения величин, описывающих состояние объекта. В качестве меры квантования, как показала теория Бора, может выступать постоянная Планка $h^{mkern -14mu-}$ , которая является универсальной константой и играет фундаментальную роль во всей физике микромира (а не только в явлениях излучения и поглощения света).

— Теория Бора впервые и совершенно точно указала на факт наличия стационарных энергетических состояний атома, образующих дискретный набор. Этот факт оказался общим свойством объектов микромира.

— В рамках модели Бора удалось получить формулы для вычисления частот спектра атома водорода и объяснить размер атома. Классическая физика была не в состоянии решить эти проблемы.

Однако теория Бора, разумеется, не могла претендовать на роль общей теории, описывающей микромир. Модель Бора обладала рядом существенных недостатков.

— Теория Бора непоследовательна. С одной стороны, она отвергает описание атома на основе классической физики, так как постулирует наличие стационарных состояний и правила квантования, непонятных с точки зрения механики и электродинамики. С другой стороны, классические законы — второй закон Ньютона и закон Кулона — используются для записи уравнения движения электрона по круговой орбите.

— Теория Бора не смогла дать адекватное описание самого простого после водорода атома гелия. Подавно не могло быть и речи о распространении теории Бора на более сложные атомы.

— Даже в самом атоме водорода теория Бора смогла описать не всё. Например, дав выражения для частот спектральных линий, модель Бора не объясняла различие в их интенсивностях. Кроме того, неясен оставался механизм образования молекулы водорода из двух атомов.

Несмотря на свои недостатки, теория Бора стала важнейшим этапом развития физики микромира. Полуклассическая-полуквантовая модель Бора послужила промежуточным звеном между классической физикой и последовательной квантовой механикой , построенной десятилетием позже — в 1920-х годах.

Разберем задачи ЕГЭ на темы: «Строение атома», «Модель Резерфорда-Бора», «Энергетические уровни», «Излучение фотона».

Задача 1.

На рисунке изображена схема низших энергетических уровней атома. В начальный момент времени атом находится в состоянии с энергией Е⁽²⁾. Согласно постулатам Бора, с какой энергией данный атом может излучать фотоны? (Ответ дать в 10⁻¹⁹ Дж.)

Решение:

Согласно постулатам Бора, атом, находящийся в стационарных состояниях, не излучает энергии. Излучение энергии возможно при переходе атома с уровня с большим значением энергии на уровень с меньшим значением энергии. Поглощение энергии, наоборот, возможно при переходе атома с меньшим уровнем энергии на больший.

С учетом представленной диаграммы, излучение атома возможно при переходе с уровня Е⁽²⁾ на уровень Е⁽¹⁾, так как Е⁽²⁾> Е⁽¹⁾. Поэтому, энергия излучаемых фотонов (hv) может быть определена, как разность энергий

$hnu=E^{(2)}-E^{(1)}.$

Подставив численные значения, рассчитаем энергию излучаемых фотонов.

$hnu=-5cdot 10^{-19}-(-8cdot 10^{-19})=-5cdot 10^{-19}+8cdot 10^{-19}=3cdot 10^{-19}$ (Дж).

Ответ: 3.

Задача 2.

Электрон в атоме водорода находится в основном (самом низком, с номером n = 1) энергетическом состоянии. Атом поглощает фотон с импульсом 6,8 · 10^–27 кг·м/с. Найдите номер энергетического уровня, на который в результате этого перейдёт электрон.

Дано:
n₁=1;
p = 6,8·10^–27 кг·м/с.

Найти:
n-?

Решение:

Уровни энергии в атоме водорода определяются формулой:

$E_{n}=dfrac{-13,6}{n^{2}}$ (эВ), где n=1, 2, 3… и т. д. (1)

Следовательно, атом на уровне n₁=1 обладает энергией, которую можно рассчитать по формуле (1).

$E_{1}=dfrac{-13,6}{1^{2}}=-13,6$ (эВ).

Найдем связь между импульсом фотона и его энергией:

p=mc;

$E=hnu =mc^{2};$

(2)

Таким образом, энергия фотона может быть определена по формуле (2).

$E=6,8cdot 10^{-27}cdot 3cdot 10^{8}=20,4cdot 10^{-19}$ (Дж).

С учетом, что 1 эВ $=1,6cdot 10^{-19}$ , получим $E=dfrac{20,4cdot 10^{-19}}{1,6cdot 10^{-19}}=12,75$ (эВ).

Атом, получив энергию от фотона, переходит в стационарное состояние с большим уровнем энергии.

$E_{n}=E_{1}+E;$

$E_{n}=-13,6+12,75=-0,85$ (эВ).

Из формулы (1) необходимо вывести номер энергетического уровня.

$n=sqrt{dfrac{-13,6}{E_{n}}};$

$n=sqrt{dfrac{-13,6}{-0,85}}=4.$

Ответ: 4.

Задача 3.

На рисунке изображена упрощенная диаграмма нижних энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какой из этих четырех переходов связан с поглощением света наибольшей энергии, а какой — с излучением света с наибольшей длиной волны?

Установите соответствие между процессами поглощения и испускания света и стрелками, указывающими энергетические переходы атома.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ПРОЦЕССЫ
А) поглощение света наибольшей энергии;
Б) излучение света с наибольшей длиной волны.

ЭНЕРГЕТИЧЕСКИЕ ПЕРЕХОДЫ
1) 1
2) 2
3) 3
4) 4

Ответ:

Решение:

По указанной диаграмме необходимо определить переходы, соответствующие поглощению и излучению света.

Переходы, указанные стрелками 1 и 2, соответствуют излучению энергии, так как атом переходит с большего уровня энергии на меньший.

Здесь надо учесть, что

$Delta E_{10} =E_{1}-E_{0}$ и $Delta E_{20}=E_{2}-E_{0}.$

Так как $Delta E_{20} textgreater Delta E_{10}$ , то, согласно формуле Планка $E=hnu =hdfrac{c}{lambda }$ , меньшая длина волны соответствует большему значению энергии излучения. Поэтому при переходе 2to 0 будет излучаться большее количество энергии. Вторая стрелка будет соответствовать излучению света с наименьшей длиной волны.

Стрелки 3 и 4 соответствуют поглощению энергии, так как в этих случаях атом переходит на уровни, соответствующие большему значению энергии. Рассуждения, аналогичные первому случаю, приводят к следующему выводу:

$Delta E_{30} =E_{3}-E_{0}$ и $Delta E_{40}=E_{4}-E_{0}.$

Так как $Delta E_{40} textgreater Delta E_{30}$ , то четвертая стрелка будет соответствовать поглощению света наибольшей энергии.

Ответ:

Задача 4.

Значения энергии электрона в атоме водорода задаются формулой: $E_{n}=dfrac{-13,6}{n^{2}}$ (эВ), где n=1, 2, 3… и т. д.

При переходах с верхних уровней энергии на нижние атом излучает фотон. Переходы с верхних уровней на уровень c n = 1 образуют серию Лаймана, на уровень c n = 2 – серию Бальмера и т. д. Найдите отношение γ максимальной длины волны фотона в серии Бальмера к максимальной длине волны фотона в серии Лаймана.

Решение:

Рис. 1. Серия Лаймана

Согласно формуле Планка $E=hnu =hdfrac{c}{lambda }$ , максимальная длина волны соответствует излучению света с наименьшим значением энергии. Поэтому для серии Лаймана это переход с уровня 2 на уровень 1 (см. рис. 1). Рассчитаем значение энергии, которая излучается в этом случае.

$E_{21}=E_{2}-E_{1};$

$E_{21}=dfrac{-13,6}{2^{2}}-left ( -dfrac{-13,6}{1^{2}} right )=dfrac{-13,6}{2^{2}}+dfrac{13,6}{1^{2}}=10,2$ (эВ).

$E_{21}=10,2$ (эВ).

Длина волны, соответствующая этому переходу, может быть определена из формулы:

$E_{21}=hnu _{21}=hdfrac{c}{lambda _{21}};$

$lambda _{21}=hdfrac{c}{E_{21}}.$ (1)

Аналогично для серии Бальмера, излучение с наибольшей длиной волны (наименьшей энергии излучения), соответствует переходу с уровня 3 на уровень 2 (см. рис. 2).

Рис. 2. Серия Бальмера

$E_{32}=E_{3}-E_{2};$

$E_{32}=dfrac{-13,6}{3^{2}}-left ( -dfrac{-13,6}{2^{2}} right )=dfrac{-13,6}{3^{2}}+dfrac{13,6}{2^{2}}approx 1,89$ (эВ).

$E_{32}approx 1,89$ (эВ).

Длина волны, соответствующая этому переходу, может быть определена из формулы:

$E_{32}=hnu _{32}=hdfrac{c}{lambda _{32}};$

$lambda _{32}=hdfrac{c}{E_{32}}.$ (2)

Тогда, для нахождения соотношения для длин волн $gamma=dfrac{lambda _{32}}{lambda _{21}}.$

Разделим уравнение (2) на уравнение (1):

$gamma=dfrac{lambda _{32}}{lambda _{21}}=hdfrac{c}{E_{32}}div hdfrac{c}{E_{21}}=hdfrac{c}{E_{32}}cdot dfrac{E_{21}}{hcdot c}=dfrac{E_{21}}{E_{32}}.$

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{E_{21}}{E_{32}}.$

В расчетах значения энергий можно оставить в эВ, так как перевод в систему «СИ» ответа не изменит.

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{10,2}{1,89}approx 5,4.$

С учетом системы «СИ»:

$gamma=dfrac{lambda _{32}}{lambda _{21}}=dfrac{10,2cdot 1,6cdot 10^{-19}}{1,89cdot 1,6cdot 10^{-19}}approx 5,4.$

(1 эВ $=1,6cdot 10^{-19}$ Дж).

Ответ: 5,4.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Атом Бора.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

В сегодняшней статье нашей традиционной рубрики «Физика» займемся решением задач. Тема: постулаты Бора.

Ищите полезную информацию для учебы? Подпишитесь на наш телеграм-канал! А если хотите заказ со скидкой, загляните на второй канал для клиентов – там много всяческих бонусов.

Нужна помощь?

Доверь свою работу кандидату наук!

Задачи на тему постулаты Бора с решениями

Постулаты Бора – сложная тема. Но решение задач по ней довольно простое, достаточно знать и уметь применять лишь несколько формул. Кстати, для удобства мы собрали полезные формулы в одном месте. А если вообще не знаете, как подступиться к задачам по физике, прочтите общую памятку по решению.

Задача на постулаты Бора №1

Условие

Вычислить энергию ε фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.

Решение

Энергия фотона, испускаемого атомом водорода при переходе с одного энергетического уровня на другой, равна:

ε=Ei1n21-1n22Ei=13,6 эВ

Здесь Ei – энергия ионизации атома водорода.

Рассчитаем:

ε=13,6112-132=12,09 эВ

Ответ: 12,09 эВ.

Задача на постулаты Бора №2

Условие

Найдите максимальную длину волны, излучаемой в серии Бальмера.

Решение

Запишем формулу Бальмера-Ридберга:

1λ=R122-1n2

Максимальная длина волны соответствует минимальному значению разности:

122-1n2

То есть:

122-132=536

Отсюда найдем:

λmax=36R·5R=1,0973732 м-1λmax=361,0973732·5=656 нм

Ответ: 656 нм.

Задача на постулаты Бора №3

Условие

При переходе электрона в атоме из стационарного состояния с энергией – 4,8 эВ излучается фотон, энергия которого равна 3,1 эВ. Определите энергию конечного состояния электрона.

Решение

Атом испускает фотон, а значит, электрон переходит в стационарное состояние с меньшей энергией, которая будет равна разности энергии первоначального состояния и энергии испущенного фотона:

Е=-4,8-3,1=-7,9 эВ

Ответ: -7,9 эВ.

Задача на постулаты Бора №4

Условие

Определить изменение энергии ∆E электрона в атоме водорода при излучении атомом фотона с частотой ϑ=6,28·1014 Гц. Ответ дать в электрон-вольтах.

Решение

Изменение энергии электрона равно энергии испущенного фотона:

∆E=εф

Энергия фотона равна:

εф=hϑ

Рассчитаем:

εф=6,62·10-34·6,28·1014=4,16·10-19 Дж=4,16·10-191,6·10-19=2,6 эВ

Ответ: 2,6 эВ.

Задача на постулаты Бора №5

Условие

На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ=486 нм?

Решение

Согласно второму постулату Бора:

∆E=Ek-En=hϑhϑ=hcλ∆E=6,62·10-34·3·108486·10-9=4,086·10-19Дж=2,554 эВ

Ответ: 2,554 эВ.

Вопросы на тему постулаты Бора

Вопрос 1. Сформулируйте постулаты Бора.

Ответ. Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).

Первый постулат: атом может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует своя энергия; в стационарном состоянии атом не излучает. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Следовательно, электрон может находиться на нескольких вполне определенных орбитах. Каждой орбите электрона соответствует вполне определенная энергия.
Второй постулат: при переходе из одного стационарного состояния в другое испускается или поглощается квант электромагнитного излучения.

Вопрос 2. В каком случае энергия поглощается атомом, а в каком испускается?

Ответ. При переходе электрона с ближней орбиты на более удаленную орбиту, атомная система поглощает квант энергии. При переходе с более удаленной орбиты электрона на ближнюю орбиту по отношению к ядру атомная система излучает квант энергии.

Вопрос 3. Какие противоречия есть в теории Бора?

Ответ. Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями. С одной стороны она применяет законы классической физики, а с другой – основывается на квантовых постулатах. Теория Бора рассматривает спектры атома водорода и водородоподобных систем и позволяет вычислить частоты спектральных линий, однако не может объяснить их интенсивности и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора также является невозможность описания с ее помощью спектра атома гелия – одного из простейших атомов, непосредственно следующего за атомом водорода.

Вопрос 4. Чему равна энергия фотона, испускаемого атомом при переходе в другое энергетическое состояние?

Ответ. Энергия фотона равна разности энергий атома в двух состояниях.

Вопрос 5. Может ли атом излучать и поглощать фотоны с любой частотой?

Ответ. Нет! Согласно постулатам Бора, атом может поглощать и излучать фотоны только с некоторыми определенными значениями частоты.

Посмотри примеры работ и убедись, что мы поможем на совесть!

Нужна помощь в решении задач? Профессиональный сервис для учащихся готов ее предоставить!

Источник

Задания Д32 C3 № 6913

Значения энергии электрона в атоме водорода задаются формулой: При переходах с верхних уровней энергии на нижние атом излучает фотон. Переходы с верхних уровней на уровень c n = 1 образуют серию Лаймана, на уровень c n = 2 – серию Бальмера т. д. Найдите отношение γ максимальной длины волны фотона в серии Бальмера к максимальной длине волны фотона в серии Лаймана.

Спрятать решение

Решение.

Энергия перехода – это разница между энергий конечного состояния и энергией начального Энергия выражается через длину волны фотона по формуле: где h – постоянная Планка, с – скорость света.

Переход с максимальной длиной волны соответствует переходу с минимальным изменением энергии. Для серии Лаймана – это переход со второго на первый уровень, для серии Бальмера – с третьего на второй.

Тогда

Ответ: 5,4.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания	Баллы
Приведено полное решение, включающее следующие элементы: I) записаны положения теории и физические законы, закономерности, применение которых необходимо для решения задачи выбранным способом (в данном случае — закон преломления света, понятие предельного угла полного внутреннего отражения и геометрические соотношения); II) описаны все вновь вводимые в решении буквенные обозначения физических величин (за исключением обозначений констант, указанных в варианте КИМ, обозначений величин, используемых в условии задачи и стандартных обозначений величин, используемых при написании физических законов); III) проведены необходимые математические преобразования, приводящие к правильному ответу; IV) представлен правильный ответ.	3
Правильно записаны все необходимые положения теории, физические законы, закономерности и проведены необходимые преобразования, но имеются следующие недостатки. Записи, соответствующие пункту II, представлены не в полном объёме или отсутствуют. ИЛИ Лишние записи, не входящие в решение (возможно, неверные), не отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.). ИЛИ В необходимых математических преобразованиях или вычислениях допущены ошибки, и (или) преобразования/вычисления не доведены до конца. ИЛИ Отсутствует пункт IV, или в нём допущена ошибка.	2
Представлены записи, соответствующие одному из следующих случаев. Представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа. ИЛИ В решении отсутствует одна из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ В одной из исходных формул, необходимых для решения задачи (или в утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи.	1
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла.	0
Максимальный балл	3

Раздел кодификатора ФИПИ/Решу ЕГЭ:

Источник

Решение задач по теме «Модель атома Н. Бора»

Задача 1

Задача 2

Задача 3

Фотон:

Какова длина волны фотона?

Как найти длину волны фотона?

Как найти длину волны фотона с частотой?

Как рассчитать длину волны фотона с заданной энергией?

Задача: Какова длина световой волны с частотой 7 х 1014 Гц?

Задача: Какую длину волны будет иметь фотон, если его энергия равна 4 х 10-15 J?

Задача: если энергия фотона равна 2.19 × 1011 ev, определите длину волны этого фотона.

Атом Бора.

Постулаты Бора.

Атом водорода.

Достоинства и недостатки теории Бора.

Задачи на тему постулаты Бора с решениями

Задача на постулаты Бора №1

Задача на постулаты Бора №2

Задача на постулаты Бора №3

Задача на постулаты Бора №4

Задача на постулаты Бора №5

Вопросы на тему постулаты Бора

Вам также может понравиться

Как правильно составить письмо для предложения сотрудничества

Всякая насильственная реформа достойна порицания так как не исправит зла

Как составить договор подряда с юристом

Добавить комментарий Отменить ответ

Задача: Какова длина световой волны с частотой 7 х 10¹⁴ Гц?

Задача: Какую длину волны будет иметь фотон, если его энергия равна 4 х 10^-15 J?

Задача: если энергия фотона равна 2.19 × 10¹¹ ev, определите длину волны этого фотона.