Как найти максимальную длину волны излучения

Как определить максимальную длину волны?

Примеры решения задач

Пример 18.
Определите максимальную длину волны
излуче­ния, способного вызвать
диссоциацию молекул кислорода. При­нять,
что вся энергия фотона расходуется на
процесс диссо­циации, а энергия связи
для одного моля кислорода, равная 498,3
кДж/моль, эквивалентна энергии диссоциации.

Решение.
Поглощение фотонного излучения может
привести к фо­тодиссоциации молекул
кислорода:

O₂
+ hv

O
+ O

По условию задачи
энергия диссоциации молекулы O₂
равна
энергии связи и равна энергии фотона:

Е_дис
= Е_св
= Е_ф,

где Е_св
– энергия
связи в одной молекуле кислорода

Е_св
мож­но
найти, разделив значение энергии связи
для одного моля на число молекул в одном
моле, т. е. на число Авогадро:

Е_св
= 498,3
(кДж/моль)/(6,02 ^.
10²³)(мол./моль)
=

= 8,28 ^.
10^–22(кДж/мол.)
= 8,28 ^.
10^–19(Дж/мол.)

Энергия фотона
связана с длиной волны излучения
уравне­нием Эйнштейна:

Е_ф
= hc/,

где h
– постоянная
Планка;

с – скорость света
в вакууме;

 – длина волны
излучения.

Отсюда можно
определить максимальную длину волны
из­лучения, способного вызвать
диссоциацию молекул кислорода:

 = hc/E_ф
= hc/E_св,

 = 6,626
^.
10^–34
(Дж ^.
с)
^.
2,997
^.
10⁸
(м/с)/[8,28 ^.
10^–19
(Дж/мол.)] =

= 2,40
^.
10^–7(м)
= 240 (нм)

Ответ:
максимальная длина волны излучения,
способного вызвать диссоциацию молекулы
кислорода, составляет 240 нм.

5. Химия стратосферы

Наиболее важные
физико-химические процессы, протекающие
в стратосфере, связаны с наличием в этой
зоне атмосферы области с повышенным
содержанием озона, часто называемой
озоновым сло­ем. Поэтому представляется
необходимым более подробно рассмо­треть
фотохимические превращения этого
соединения.

5.1. Озон в атмосфере

Озон – О₃
– аллотропная модификация кислорода.
Общая масса озона в атмосфере оценивается
примерно в 3,3 млрд т. Это высокотоксичный
газ, его токсичность примерно на порядок
превышает токсичность диоксида серы.
Озон – сильнейший окислитель, реа­гирующий
практически с любыми веществами – от
автомобильных покрышек до тканей легких
человека. Поэтому дышать озоном не­льзя,
и его присутствие в воздухе тропосферы
даже в сравнительно небольших количествах
представляет опасность для всего живого.

Важной особенностью
озона является его способность погло­щать
излучение:

О₃
+ hv

O₂
+ O
(34)

Озон разрушается,
поглощая излучение с длиной волны
мень­ше 1130 нм (инфракрасное излучение),
но максимум поглощения наблюдается при
длине волны короче 320 нм (ультрафиолетовое
излучение). Озон поглощает ультрафиолетовое
излучение в тыся­чи раз лучше, чем
кислород, и количества озона в стратосфере,
где концентрация его достигает
максимальных значений, в десятки и сотни
раз превышающих среднее его содержание
в тропосфере, достаточно для практически
полного поглощения жесткого
ультра­фиолетового излучения Солнца.
Поэтому озон стратосферы выпол­няет
защитную функцию, и уменьшение его
количества в этой обла­сти атмосферы
может представлять опасность для биоты
и, прежде всего для человека.

Зона с максимальными
значениями концентрации озона нахо­дится
на высотах от 15 до 35 км. На больших высотах
концентрация озона резко снижается, и
на высоте более 85 км озон практически
отсутствует. Поэтому озон мезосферы
хотя и поглощает ультрафио­летовое
излучение, однако вносит лишь небольшой
вклад в защиту биосферы от солнечного
излучения в этой области спектра. Озон
мезосферы играет важную роль в поддержании
теплового баланса планеты и формировании
нижнего слоя ионосферы.

Для характеристики
содержания озона в атмосфере часто
ис­пользуются два принципиально
разных подхода. В начальные пе­риоды
изучения озонового слоя планеты (в 20-х
годах прошлого столетия) основным
прибором для измерения содержания озона
в атмосфере был спектрометр Добсона.
Этот прибор позволял доста­точно
надежно определять общее количество
озона, находящегося в столбе воздуха
над наблюдателем. Полученные значения
суммарного объема озона в столбе
атмосферы единичной площади сечения
приводили к нормальным условиям и
определяли высоту, которая приходится
в этом столбе атмосферы на весь озон.
Слой озона вы­сотой 10^–5
м принимается
равным одной единице Добсона (е.Д.). Общее
количества озона в атмосфере меняется
от 120 до 760 е.Д. (наиболее часто –
200-400 е.Д.) при
среднем для всего земного ша­ра
значении 290 е.Д. Таким образом, весь озон,
собранный из атмосферы к поверхности
Земли, мог бы покрыть ее слоем, толщи­на
которого в среднем составила бы 2,9 мм.
Ошибочная трактовка данного способа
выражения общего содержания озона в
атмосфере привела к формированию в
массовом сознании понятия озонового
слоя, или тонкого озонового экрана,
якобы существующего в атмо­сфере. В
реальных условиях весь озон неравномерно
распределен в слое воздуха от поверхности
Земли практически до верхней грани­цы
мезосферы. Характер этого распределения
связан с процессами образования и гибели
озона. В общем виде высотный профиль
концентраций озона приведен на рисунке
3.

Рис. 3. Изменение
концентрации озона в атмосфере по высоте

Общее
содержание озона в атмосфере над
конкретной территорией изменяется в
достаточно широких пределах. Помимо
фотохимических процессов значительный
вклад в изменение содержания озона и
его концентрации на различных высотах
вносят процессы движения воздушных
масс. В настоящее время выявлены общие
закономерности ряда таких изменений,
связанные со временем года и географической
широтой местности. Так, в северном
полушарии на широтах более 30° с.ш. общее
содержание озона в атмосфере максимально
в конце зимы – начале весны, а минимально
осенью (сентябрь
–
октябрь).
Наибольшие изменения характерны для
высоких широт (70-80° с.ш.), где среднее
содержание озона может менять­ся от
450 е.Д. – в марте до 280 е.Д. в сентябре. На
широте 40-43° с.ш. изменения менее контрастны
(от 370 е.Д. весной до 280 е.Д. осенью). На
низких широтах (менее 30° с.ш.) сезонные
изменения практически отсутствуют (не
превышают 20 е.Д.). В южном полу­шарии
общая картина сезонных изменений такая
же, хотя и менее выраженная.

В целом в атмосфере
по характеру сезонных колебаний и
высот­ному профилю концентраций озона
принято выделять три зоны:

1. полярная зона –
   характеризуется наибольшими значениями
   среднегодового общего содержания
   (около 400 е.Д.) и концентра­ций озона,
   наибольшими сезонными колебаниями
   (около 50%); зона максимальной концентрации
   озона расположена наиболее близко к
   поверхности – на высотах 13-15км,
   концентрация озо­на в этой зоне
   (содержание молекул озона в 1 см³)
   составляет (4 
   5) ^.
   10¹²см
   ^–3;

2. тропическая зона
   – среднегодовые значения общего
   содержания озона невелики и составляют
   примерно 265 е.Д., сезонные колебания не
   превышают 10-15%; зона максимальной
   концентрации озона находится на высотах
   24-27км, концентрация озона в этой зоне
   составляет (1 
   2) ^.
   10¹²см
   ^–3;

3. средние широты –
   занимают промежуточное положение,
   сезон­ные изменения составляют 30-40%
   от средних значений, зона максимальной
   концентрации озона находится на высотах
   19-21км, концентрация озона в этой зоне
   достигает 3 ^.
   10¹²
   см ^–3.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

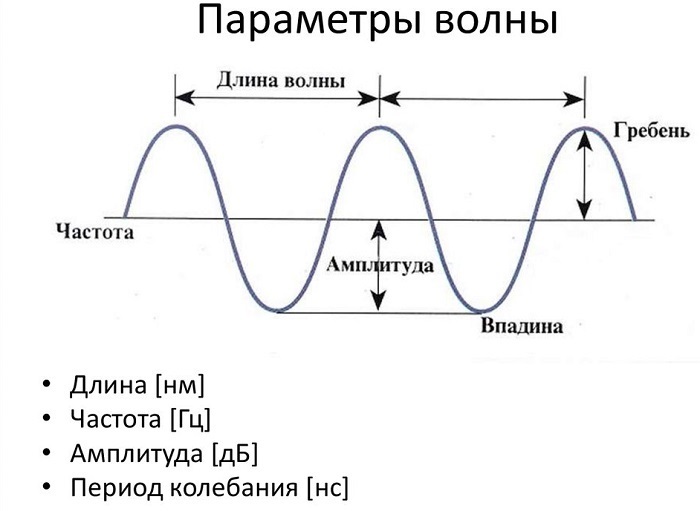
Длина волны – это расстояние между двумя последовательными пиками (гребнями) или впадинами. Самое высокое положение волны называется пиком. Самое нижнее положение волны называется впадиной. 

Цикл – это полное колебание, например, кривая между двумя гребнями или двумя впадинами. Максимальное расстояние волны от равновесного положения называется амплитудой.

На рисунке показаны основные параметры волны, используемые в физике:

Определение и формула длины волн

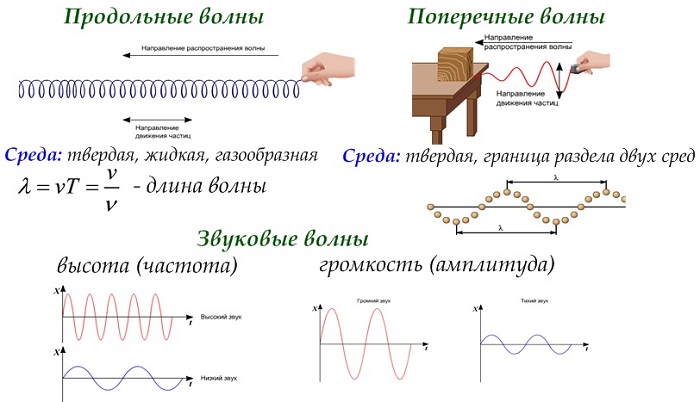
Волна – это возмущение, распространяющееся от точки, в которой она возникла, в окружающую среду. Такое возмущение переносит энергию без чистого переноса вещества. 

Длина представляет собой фактическое расстояние, пройденное волной, которое не всегда совпадает с расстоянием среды, или частиц, в которых распространяется волна. Ее также определяют как пространственный период волнового процесса.

Греческая буква “λ” (лямбда) в физике используется для обозначения длины в уравнениях. Она обратно пропорциональна частоте волны.

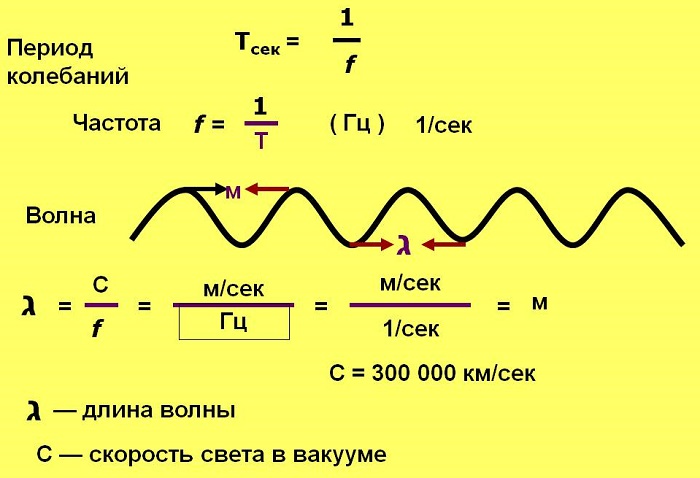
Период Т — время завершения полного колебания, единица измерения секунды (с).

Длинная волна соответствует низкой частоте, а короткая – высокой. Длина измеряется в метрах. Количество волн, излучаемых в каждую секунду, называется частотой и обратно пропорционально периоду.

У различных длин разная скорость распространения. Например, скорость света в воде равна 3/4 от скорости в вакууме.

Пространственный период волны – это расстояние, которое точка с постоянной фазой «пролетает» за интервал времени, соответствующий периоду колебаний.

Частота f — количество полных колебаний в единицу времени. Измеряется в Герцах (Гц).

При одном полном колебании в секунду f = 1 Гц; при 1000 колебаний в секунду f = 1 килогерц (кГц); 1 млн. колебаний в секунду f = 1 мегагерц (1 МГц).

Зная, что скорость света в вакууме с — 300 000 км/с, или 300 000 000 м/с, то для перевода длины волны в частоту нужно 3 х 10⁸ м/с поделить на длину в метрах.

Единицы измерения длины волны λ – нанометры и ангстремы, где нанометр является миллиардной частью метра (1 м = 109 нм) и ангстрем является десятимиллиардной частью метра (1 м = 1010 А), то есть нанометр эквивалентен 10 ангстрем (1 нм = 10 А).

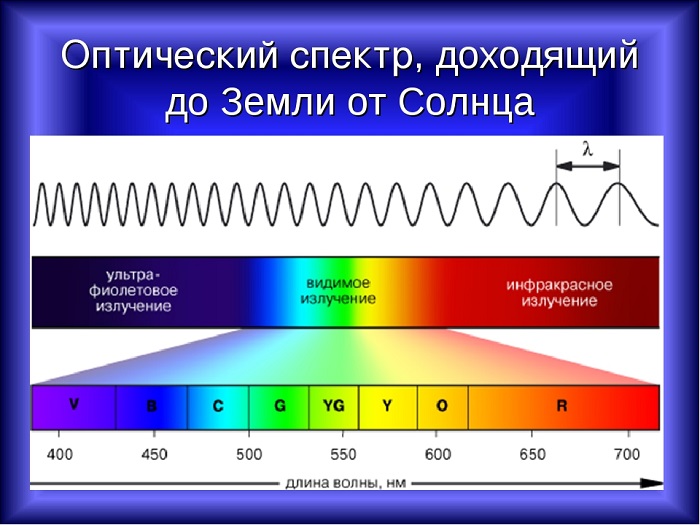
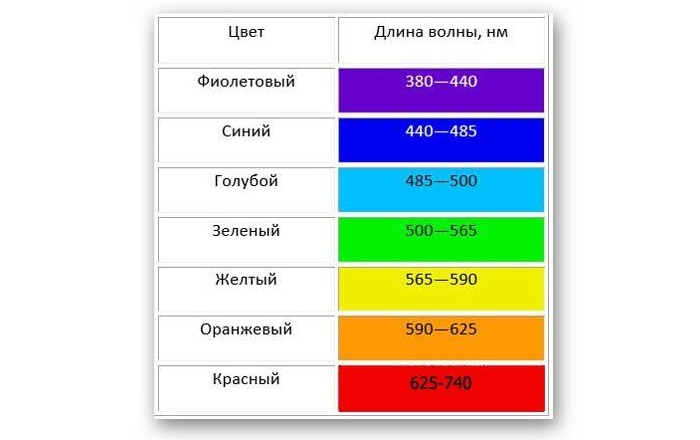
Свет, который исходит от Солнца, является электромагнитным излучением, которое движется со скоростью 300 000 км/с, но длина не одинакова для любого фотона, а колеблется между 400 нм и 700 нм. Длина световой волны влияет на цвет.

Белый свет разлагается на спектр различных цветных полос, каждая из которых определяется своей длиной волны. Таким образом, светом с наименьшей длиной является фиолетовый, который составляет около 400 нм, а светом с наибольшей длиной – красный, который составляет около 700 нм.

Таблица показывает длину волны в зависимости от цвета:

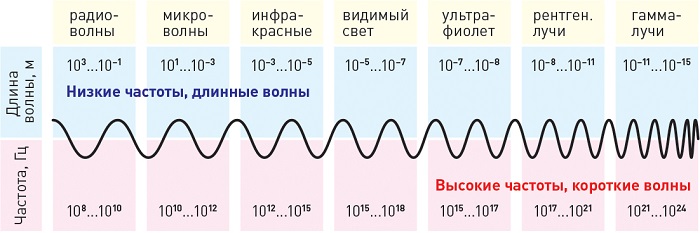
Излучения с длиной меньше фиолетового называются ультрафиолетовым излучением, рентгеновским и гамма-лучами в порядке уменьшения. Излучения больше красного называются инфракрасными, микроволнами и радиоволнами, в порядке возрастания. 

Предельная дальность связи зависит от длины. Размеры антенны часто превышают рабочую длину радиоэлектронного средства.

Рисунок показывает длину волн и частоту (нм), исходящих от различных источников:

Примеры расчета длины волны для звуковых, электромагнитных и радиоволн

Задача №1

Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача №2

Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с. прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача №3

Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

0 Пользователей и 1 Гость просматривают эту тему.