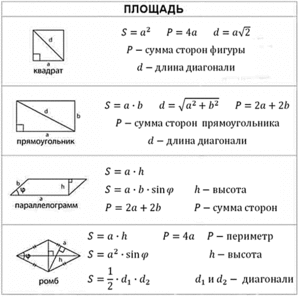
Алгоритм решения задач вида: найти “наибольшую площадь“, “наибольший объем“.
Данный вид задач подразумевает нахождение точек максимума площади (объема) в зависимости от длин сторон фигуры.
- шаг – записываем формулу площади (объема) (S=a*b).
- шаг – выражаем одну сторону фигуры через другую. Например в задаче “Проволока длинной 76 см согнута в прямоугольник , найдите длину сторон, при которых площадь прямоугольника наибольшая” была указана связь между сторонами прямоугольника – известный периметр, что позволило выразить одну сторону через другую и периметр (b = frac{P}{2}-a)), аналогично и в задаче Периметр основания прямоугольного параллелепипеда .
- шаг – подставляем подученную формулу в формулу порщади (объема)(например для прямоугольника (S=a*b = a*(frac{P}{2}-a) = a*frac{P}{2}-a^2).
- шаг – находим первую производную и приравниваем ее к нулю (S’= (a*frac{P}{2}-a^2)` = frac{P}{2}-2*a = 0)
- шаг – решаем полученное уравнение и находим корни уравнения (т.е. значения неизвестного при котором значение функции (производной) равно 0). Это и будет ответ, т.е. длина стороны при которой площадь будет наибольшей (аналогично и с объемом) (frac{P}{2}-2*a = 0 => a = frac{P}{4}).
- шаг – желательно проверить истинность полученного решения – подставить найденное значение в функцию (площади или объема) и рассчитать ее, а для сравнения взять соседнее значение стороны (больше или меньше) и так же подставить. Если площадь получится меньше, значит задача решена верно, если нет, то нужно искать ошибку.
P.S. вопросы и пожелания пишите в личку.
Изопериметри́ческое нера́венство — геометрическое неравенство, связывающее периметр замкнутой кривой на плоскости и площадь участка плоскости, ограниченной этой кривой.
Этот термин также используется для различных обобщений данного неравенства.
Изопериметрический буквально означает «имеющий тот же самый периметр».
В частности, изопериметрическое неравенство утверждает, что при длине L замкнутой кривой и площади A плоской области, ограниченной этой кривой,
и это неравенство превращается в равенство тогда и только тогда, когда кривая является окружностью.
Целью изопериметрической задачи является поиск фигуры наибольшей возможной площади, граница которой имеет заданную длину[1].
Изопериметрическая задача была обобщена многими путями для других неравенств между характеристиками фигур, множеств, многообразий. К изопериметрической задаче относятся также оценки величин физического происхождения (моменты инерции, жёсткость кручения упругой балки, основная частота мембраны, электростатическая ёмкость и др.) через геометрические характеристики. Например, есть обобщения для кривых на поверхностях и на области в пространствах большей размерности.
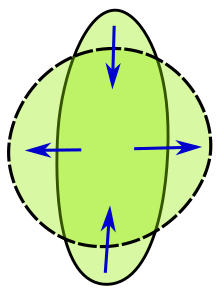
Возможно, наиболее известным физическим проявлением 3-мерного изопериметрического неравенства является форма капли воды. А именно, капля принимает обычно круглую форму. Поскольку количество воды в капле фиксировано, поверхностное натяжение заставляет каплю принять форму, минимизирующую поверхность капли, а минимальной поверхностью будет сфера.
История[править | править код]
В близкой по содержанию задаче Дидоны требуется найти область максимальной площади, ограниченную прямой линией и криволинейной дугой, концы которой лежат на этой прямой. Задача связана с древней легендой об основании Карфагена Дидоной, сестрой царя финикийского города Тира.
Решением изопериметрической задачи является окружность, и это было известно уже в Древней Греции. В своём трактате «Об изопериметрических фигурах» (др.-греч. Περὶ ἰσοπεριμέτρων σχημάτων) Зенодор (II век до н. э.) решает изопериметрическую задачу на плоскости и получает частные результаты в пространстве. Первое математически строгое доказательство изопериметрического неравенства в пространстве было получено в 1884 году Германом Шварцем. С тех пор появилось много других доказательств.
Изопериметрическая задача на плоскости[править | править код]
Если область не выпуклая, «выемку» можно «отразить», что приведёт к увеличению области при сохранении периметра
Вытянутую фигуру можно сделать более округлой, что не изменит периметр, зато увеличит площадь
Классическая изопериметрическая задача датируется античными временами. Задачу можно сформулировать следующим образом: Среди всех замкнутых кривых на плоскости с заданным периметром, какая кривая (если такая есть) максимизирует площадь ограниченной ею области? Можно показать, что этот вопрос эквивалентен следующей задаче: Среди всех замкнутых кривых на плоскости, ограничивающих область заданной площади, какая (если такая есть) минимизирует периметр?
Задача концептуально связана с принципом наименьшего действия в физике и может быть переформулирована согласно этому принципу: что за действия включают большую область с максимальной экономией поддержки? Философ и учёный XV века, кардинал Николай Кузанский, обсуждал вращение, процесс, в котором генерируются окружности, как наиболее прямое отражение процессов, в которых вселенная была создана. Немецкий астроном и астролог Иоганн Кеплер использовал изопериметрический принцип при обсуждении строения солнечной системы в книге Тайна мироздания (1596).
Хотя окружность является очевидным решением задачи, доказательство этого факта не является простой задачей. Первый прогресс по пути доказательства был сделан швейцарским геометром Якобом Штейнером в 1838 с использованием геометрического метода, получившего впоследствии название симметризация Штейнера[2]. Штейнер показал, что если решение существует, оно должно быть окружностью. Доказательство Штейнера было завершено позднее некоторыми другими математиками.
Штейнер начинает с некоторых геометрических построений, которые легко понять. Например, можно показать, что любая замкнутая кривая, ограничивающая область, не являющуюся полностью выпуклой, можно модифицировать для получения большей площади путём «отражения» вогнутых участков, чтобы они стали выпуклыми. Затем можно показать, что любая замкнутая кривая, не являющаяся полностью симметричной, может быть «наклонена» таким образом, что она будет заключать большую площадь. Единственная фигура, которая полностью выпукла и симметрична, — это окружность, хотя это рассуждение не представляет строгого доказательства (смотрите внешние ссылки).
Изопериметрическое неравенство[править | править код]
Решение изопериметрической задачи обычно выражается в виде неравенства, связывающего длину L замкнутой кривой и площадь A плоскости, ограниченной этой кривой. Изопериметрическое неравенство утверждает, что
и что это неравенство превращается в равенство тогда и только тогда, когда кривая является окружностью. В самом деле, площадь круга радиуса R равна πR2, а длина окружности равна 2πR, так что обе стороны неравенства становятся равными 4π2R2.
Можно найти десятки доказательств изопериметрического неравенства. В 1902 году Гурвиц опубликовал короткое доказательство[источник не указан 548 дней], использующее ряды Фурье, которое применимо к произвольным спрямляемым кривым (не обязательно гладким). Элегантное прямое доказательство, основанное на сравнении гладкой простой замкнутой кривой с подходящей окружностью, дал Е. Шмидт (E. Schmidt) в 1938 году[источник не указан 548 дней]. Доказательство использует только формулу длины кривой, формулу площади плоской области из теоремы Грина и неравенство Коши — Буняковского.
Для заданной замкнутой кривой изопериметрический коэффициент определяется как отношение площади фигуры к площади круга, имеющего тот же периметр. То есть
и изопериметрическое неравенство утверждает, что Q ⩽ 1.
Изопериметрический коэффициент правильного n-угольника равен
Изопериметрическое неравенство на сфере[править | править код]
Пусть C — простая замкнутая кривая на сфере радиуса 1. Обозначим через L длину кривой C и через A площадь области, ограниченной кривой C. Сферическое изопериметрическое неравенство утверждает, что
и это неравенство превращается в равенство тогда и только тогда, когда кривая является окружностью. Фактически имеется два способа измерить площадь сферической области, но неравенство симметрично для выбора дополнения.
Это неравенство было открыто Полем Леви (1919), который обобщил его на более высокие размерности и более общие поверхности[источник не указан 548 дней].
Для случая произвольного радиуса R известно[3], что
Изопериметрическое неравенство в пространствах более высоких размерностей[править | править код]
Изопериметрическая теорема обобщается для поверхностей трёхмерного евклидова пространства. Среди всех простых замкнутых поверхностей с заданной площадью поверхности сфера заключает область максимального объёма. Аналогичные утверждения выполняются в евклидовых пространствах любой размерности.
В общем виде [4] изопериметрическое неравенство утверждает, что для любого множества S ⊂ Rn, замыкание которого имеет конечную меру Лебега,
где M*n−1 является (n − 1)-мерной ёмкостью Минковского, Ln является n-мерной мерой Лебега, а ωn — объёмом единичного шара в Rn. Если граница S является спрямляемой, то ёмкость Минковского равна (n − 1)-мерной мере Хаусдорфа.
Изопериметрическое неравенство в размерности n можно быстро доказать с помощью неравенства Брунна — Минковского[3][4].
Изопериметрическое неравенство в n-мерном пространстве эквивалентно (для достаточно гладких доменов) неравенству Соболева[en] в Rn с оптимальной константой:
для всех u ∈ W1,1(Rn).
Изопериметрическое неравенство в пространствах с мерой[править | править код]
Большинство работ по изопериметрической задаче сделаны в контексте гладких областей евклидовых пространств, или для более общих римановых многообразий. Однако изопериметрическую задачу можно существенно обобщить, используя понятие ёмкости Минковского.
Пусть 
Мера границы, или ёмкость Минковского, измеримого подмножества A из X определяется как lim inf:
где
является ε-расширением множества A.
Изопериметрическая задача в X спрашивает, насколько мало может быть 
Функция
называется изопериметрическим профилем метрического измеримого пространства 
Изопериметрическое неравенство для графов[править | править код]
В теории графов изопериметрические неравенства находятся в центре изучения экспандеров, разреженных графов, имеющих сильную связность. Построение экспандеров породило исследования в чистой и прикладной математике с применением в теории вычислительной сложности, разработке устойчивых компьютерных сетей и теории корректирующих кодов[5].
Изопериметрические неравенства для графов соотносят размер подмножеств вершин к размеру границ этих подмножеств, что обычно понимается как число рёбер, покидающих подмножество или число соседних вершин. Для графа 

- Рёберный изопериметрический параметр:
- Вершинный изопериметрический параметр:
Здесь 





Пример: Изопериметрическое неравенство для гиперкубов[править | править код]





Ниже следуют два изопериметрических неравенства для булева гиперкуба[7].
Изопериметрическое неравенство для рёбер[править | править код]
Изопериметрическое неравенство для рёбер гиперкуба гласит: 
Изопериметрическое неравенство для вершин[править | править код]
Теорема Харпера[8] утверждает, что шары Хэмминга имеют наименьшую вершинную границу среди всех множеств заданного размера. Шары Хэмминга — это множества, которые содержат все точки с весом Хэмминга[en], не превосходящим 

Из теоремы следует, что любое множество 


В частном случае, когда размер множества 



Изопериметрическое неравенство для треугольников[править | править код]
Изопериметрическое неравенство для треугольников в терминах периметра p и площади T утверждает, что[10]
с равенством в случае правильного треугольника.
Примечания[править | править код]
- ↑ Blåsjö, 2005, p. 526—566.
- ↑ Steiner, 1838, p. 281—296.
- ↑ 1 2 Osserman, 1978.
- ↑ 1 2 Федерер, 1987.
- ↑ 1 2 Hoory, Linial, Widgerson, 2006.
- ↑ Определения 4.2 и 4.3 в Hoory, Linial, Widgerson, 2006.
- ↑ См. Bollobás, 1986 и секцию 4 в Hoory, Linial, Widgerson, 2006.
- ↑ См. Calabro, 2004 или Bollobás, 1986.
- ↑ Leader, 1991.
- ↑ Chakerian, 1979.
Литература[править | править код]
- Viktor Blåsjö. The Evolution of the Isoperimetric Problem (англ.) // Amer. Math. Monthly. — 2005. — Vol. 112.
- Blaschke, Leichtweiß. Elementare Differentialgeometrie (нем.). — 5th, completely revised by K. Leichtweiß. — New York Heidelberg Berlin: Springer-Verlag, 1973. — Bd. 1. — (Die Grundlehren der mathematischen Wissenschaften). — ISBN 0-387-05889-3.
- Бляшке. Круг и шар. — М.: Наука. — 1967.
- Béla Bollobás. Combinatorics: set systems, hypergraphs, families of vectors, and combinatorial probability (англ.). — Cambridge University Press, 1986. — ISBN 978-0-521-33703-8.
- Burago. Encyclopedia of Mathematics (англ.) / Michiel Hazewinkel. — Springer, 2001. — ISBN 978-1-55608-010-4.
- Chris Calabro. Harper’s Theorem (англ.). — 2004.
- Luca Capogna, Donatella Danielli, Scott Pauls, Jeremy Tyson. An Introduction to the Heisenberg Group and the Sub-Riemannian Isoperimetric Problem (англ.). — Birkhäuser Verlag, 2007. — ISBN 3-7643-8132-9.
- G. D. Chakerian. Mathematical Plums (англ.) / R. Honsberger. — Washington, DC: Mathematical Association of America, 1979.
- Т. Боннезен, В. Фенхель. Теория выпуклых тел. — 2002. — (Библиотека студента-математика).
- Протасов В. Ю. Максимумы и минимумы в геометрии. — М.: МЦНМО. — 56 с. — (Библиотека «Математическое просвещение», выпуск 31).
- Г. Федерер. Геометрическая теория меры. — М.: Наука, 1987.
- M. Gromov. Paul Levy’s isoperimetric inequality (англ.). — Boston, Massachusetts: Birkhäuser Boston, Inc.,, 1999. — Vol. 152. — (Progress in Mathematics).
- J. Steiner. Einfacher Beweis der isoperimetrischen Hauptsätze (нем.). — J. reine angew Math.. — 1838. Также сборник трудов, том 2, Reimer, Berlin, (1882).
- Г. Хадвигер. Лекции об объёме, площади поверхности и изопериметрии. — М.: Наука, 1966.
- Shlomo Hoory, Nathan Linial, Avi Widgerson. Expander graphs and their applications (англ.) // Bulletin (New series) of the American Mathematical Society. — 2006. — Vol. 43, iss. 4. — doi:10.1090/S0273-0979-06-01126-8.
- Imre Leader. Proceedings of Symposia in Applied Mathematics (англ.). — 1991. — Vol. 44. — P. 57—80.
- Robert Osserman. The isoperimetric inequality (англ.) // Bull. Amer. Math. Soc.. — 1978. — Vol. 84, iss. 6. — P. 1182—1238. — doi:10.1090/S0002-9904-1978-14553-4.
Ссылки[править | править код]
- History of the Isoperimetric Problem at Convergence
- Treiberg: Several proofs of the isoperimetric inequality
- Isoperimetric Theorem at cut-the-knot
Как найти максимально возможную площадь прямоугольника зная только периметр?
Николай Николаевич Кривой
Ученик
(206),
закрыт
5 лет назад
К примеру, с периметром в 4 клеточки макс. площадь: 1 кл.
Лучший ответ
НатУша
Искусственный Интеллект
(197725)
5 лет назад
максимально возможная площадь у квадрата. Значит этот прямоугольник – квадрат.
Значит периметр надо разделить на 4., узнать сторону квадрата, а потом и площадь
Сторона квадрата 1 клеточка. Площадь 1*1 = 1 клеточла в квадрате
Николай Николаевич КривойУченик (206)
5 лет назад
как узнать после деления на 4 сторону квадрата?
туплю сегодня
***fillskii@mail.ru
Просветленный
(28631)
Вот это вообще финиш…
Остальные ответы
kjsdgjkkjsgx kjsdgjkjksdg
Мастер
(2347)
5 лет назад
Площадь 1/2*a1*h, если есть клетки то вычислить вообще можно без проблем
***fillskii@mail.ru
Просветленный
(28631)
5 лет назад
P=2*a+2*b
a=(P/2)-b
S=a*b
S(b)=b*((P/2)-b)
Дальше ищешь максимум функции (тема производной).
Похожие вопросы
Как найти максимальную площадь четырехугольника
Яхуб нарисовал множество из n точек на декартовой плоскости. Он назвал их «особыми точками». Четырехугольник — это многоугольник без самопересечений, имеющий четыре стороны (или ребра) и четыре вершины (или угла). Пожалуйста, обратите внимание, что четырехугольник может не быть выпуклым. Особый четырехугольник — это такой четырехугольник, в котором все четыре вершины принадлежат множеству особых точек. Вам дано множество особых точек. Пожалуйста, вычислите максимальную площадь особого четырехугольника.
В первой строке записано целое число n ( 4 ≤ n ≤ 300 ). В каждой из следующих n строк записано по два целых числа: x i, y i ( – 1000 ≤ x i, y i ≤ 1000) — декартовы координаты i -той особой точки. Гарантируется, что никакие три точки не лежат на одной прямой. Гарантируется, что никакие две точки не совпадают.
Выведите единственное вещественное число — максимальную площадь особого четырехугольника. Ответ будет считаться правильным, если его относительная или абсолютная погрешность не превышает 10 – 9 .
Максимальная площадь четырехугольника
Для четырех сторон четырехугольника a, b, c, d найдите максимально возможную площадь четырехугольника от заданных сторон.
Согласно формуле Бретшнейдера , площадь общего четырехугольника определяется как
Здесь a, b, c, d — стороны четырехугольника, s — полупериметр четырехугольника, а углы — два противоположных угла.
Таким образом, эта формула максимизируется только тогда, когда противоположные углы суммируются с пи (180), тогда мы можем использовать упрощенную форму формулы Бретшнейдера, чтобы получить (максимальную) площадь K.
Эта формула называется формулой Брахмагупты .
Ниже приведена реализация данного подхода
// Программа CPP, чтобы найти максимум
// четырехугольник
#include
using namespace std;
double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt ((semiperimeter – a) *
double a = 1, b = 2, c= 1, d = 2;
printf ( “%.2fn” ,maxArea(a, b, c, d));
// Java-программа для поиска максимального значения
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2 ;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.sqrt((semiperimeter – a) *
public static void main (String[] args)
double a = 1 , b = 2 , c= 1 , d = 2 ;
System.out.println(maxArea(a, b, c, d));
// Этот код предоставлен sunnysingh
# Python3 программа для поиска максимума
# площадь четырехугольника
def maxArea (a , b , c , d ):
semiperimeter = (a + b + c + d) / 2
# Применение формулы Брахмагупты к
# получить максимальную площадь четырехугольника
return math.sqrt((semiperimeter – a) *
print ( “%.2f” % maxArea(a, b, c, d))
# Этот код предоставлен “Sharad_Bhardwaj”.
// C # программа для поиска максимума
// четырехугольник
static double maxArea( double a, double b,
double c, double d)
double semiperimeter = (a + b + c + d) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return Math.Sqrt((semiperimeter – a) *
public static void Main ()
double a = 1, b = 2, c= 1, d = 2;
Console.WriteLine(maxArea(a, b, c, d));
// Этот код предоставлен vt_m.
// PHP-программа, чтобы найти максимум
// четырехугольник
function maxArea( $a , $b , $c , $d )
$semiperimeter = ( $a + $b + $c + $d ) / 2;
// Применение формулы Брахмагупты к
// получаем максимальную площадь четырехугольника
return sqrt(( $semiperimeter – $a ) *
$a = 1; $b = 2; $c = 1; $d = 2;
echo (maxArea( $a , $b , $c , $d ));
// Этот код предоставлен vt_m.
?>
Формулы вычисления площади произвольного четырёхугольника
В школьных математических заданиях часто требуется определить площадь четырёхугольника. Все довольно просто, если задан частный случай фигуры — квадрат, ромб, прямоугольник, трапеция, параллелограмм, ромбоид. В случае же произвольного четырёхугольника все несколько сложнее, но также вполне доступно для среднего школьника. Ниже мы изучим различные методы расчётов площади произвольных четырёхугольников, запишем формулы и рассмотрим различные вспомогательные примеры.
Определения и соглашения
В приведённой ниже таблице будут указаны определения и договорённости, которые будут использоваться в дальнейшем во время наших рассуждений.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
- Диагональ — отрезок, соединяющий вершины многоугольника не лежащие на одной стороне (её обозначение – латинская буква d).
- Площадь фигуры — это численное значение территории, заключённой внутри многоугольника (её обозначение – латинская буква S).
- Синус угла — это число равное отношению противоположного катета к гипотенузе в прямоугольном треугольнике. (её обозначение – запись sin).
- Косинус угла — это число равное отношению прилежащего катета к гипотенузе в прямоугольном треугольнике. В дальнейшем в статье для его обозначения будем использовать латинскую запись cos.
- Описанная окружность — это окружность, которой принадлежат все вершины многоугольника ( её радиуса обозается буквой R).
- Вписанная окружность — это окружность, которая касается всех сторон многоугольника. В дальнейшем в статье для обозначения её радиуса будем использовать латинскую букву r.
- Угол между сторонами a и b будем обозначать следующей записью (a,b).
Нахождение площади четырёхугольника различными способами и методами
Узнаем как найти площадь четырёхугольника когда даны его диагонали и образуемый при их пересечении острый угол. Тогда площадь четырёхугольника будет вычисляться по формуле: S = 1/2*d1*d2*sin(d1,d2).
Рассмотрим пример. Пусть d1 = 15 сантиметров, d2 = 12 сантиметров, и угол между ними 30 градусов. Определим S. S = 1/2*15*12*sin30 = 1/2*15*12*1/2 = 45 сантиметров квадратных.
Теперь пусть даны стороны и противолежащие углы четырёхугольника.
Пусть a, b, c, d известные стороны многоугольника; p – его полупериметр. Корень квадратный выражения условимся обозначать как rad (от латинского radical). Формула площади четырёхугольника будет находиться по формуле: S = rad(( p − a ) ( p − b ) ( p − c ) ( p − d ) − a b c d ⋅ c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d).
На первый взгляд, формула кажется очень сложной и вычурной. Однако ничего сложного здесь нет, что мы и докажем, рассмотрев пример. Пусть данные нашего условия следующие: a = 18 миллиметров, b = 23 миллиметра, c = 22 миллиметра, d = 17 миллиметров. Противолежащие углы будут равны (a,b) = 0,5 градуса и (c,d) = 1,5 градуса. Для начала находим полупериметр: p = 1/2*(18 + 23 + 22 + 17) = 1/2*80 = 40 миллиметров.
Теперь найдём квадрат косинуса полусуммы противолежащих углов: c o s^2( (a,b) + (c,d))/2) = c o s^2(0,5 + 1,5)/2 = c o s1*c o s1 = (1/2)*(1/2) = 0,9996.
Подставим полученные данные в нашу формулу, получим: S = rad((40 – 18)*(40 – 23)*(40 – 22)*(40 – 17) – 18*23*22*17*0,97) = rad(22*17*18*23 – 18*23*22*17*1/4) = rad((22*17*18*23*(1 – 0,9996)) = rad(154836*0,0004) = rad62 = 7,875 миллиметра квадратного.
Разберёмся как находить площадь с помощью вписанной и описанной окружностей. При решении задач данной темы имеет смысл сопровождать свои действия вспомогательным рисунком, хотя это требование и не является обязательным.
Если есть вписанная окружность и нужно найти площадь четырёхугольника формула имеет вид:
Снова возьмём на рассмотрение пример: a = 16 метров, b = 30 метров, c = 28 метров, d = 14 метров, r = 6 метров. Подставим аши значения в формулу, получим:
S = ((16 +30 + 28 + 14)/2)*6 = 44*6 = 264 метров квадратных.
Теперь займёмся вариантом когда окружность описана вокруг четырёхугольника. Здесь мы сможем воспользоваться следующей формулой:
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине длины периметра. Пускай в нашем случае стороны имеют следующие значения a = 26 дециметров, b = 35 дециметров, c = 39 дециметров, d = 30 дециметров.
Первым делом определим полупериметр, p = (26 + 35 + 39 + 30)/2 = 65 дециметров. Подставим найденное значение в нашу формулу. Получим:
S = rad((65 – 26)*(65 – 35)*(65 – 39)*(65 – 30)) = rad(39*30*26*35) = 1032 (округлённо) дециметров квадратных.
Заключение
Внимательно изучив все вышеизложенное, можно сделать вывод — определение площади произвольного четырёхугольника с разными сторонами сложнее, чем у них же специальных видов – квадрата, прямоугольника, ромба, трапеции, параллелограмма. Однако внимательно изучив все приведённые методы, можно с лёгкостью решать задачи необходимые для школьников. Сведём все наши формулы в одну таблицу:
- S = 1/2*d1*d2*sin(d1,d2);
- S = rad(( p − a )*( p − b )*( p − c )*( p − d ) − a*b*c*d*c o s^2( (a,b) + (c,d))/2), где p = 1/2*(a + b + c + d);
- S = ((a + b+ c + d)/2)*r
S = rad((p − a )*( p − b )*( p − c )*( p − d ), где p равно половине периметра.
Таким образом, реально сложной является только формула номер 2, но и она вполне доступна, при условии хорошего понимания данных в статье определений и соглашений.
Видео
Разобраться в этой теме вам поможет видео.
[spoiler title=”источники:”]
http://espressocode.top/maximum-area-quadrilateral/
http://liveposts.ru/articles/education-articles/matematika/formuly-vychisleniya-ploshhadi-proizvolnogo-chetyryohugolnika
[/spoiler]
Let me first formulate the problem as I believe it was meant:
-
The rectangle to be found has horizontal (constant y) and vertical (constant x) borders, i.e. no “rotations”.
-
The rectangle has at least one point on the ‘internal’ (‘open’) part of each of its edges, i.e. not at a corner.
(it may have more than one point on any edge, and ALSO points at its corners.)
This rules out the ‘infinite’ solutions, because all points have finite x,y.
It also rules out the cases where we might intend to define the rectangle by only TopLeft and BottomRight points and similar constructs. -
we look for the rectangle with the maximum area among all that satisfy the above conditions.
Assuming the above to be a correct (re)formulation of the problem, I believe that it is a two-dimensional optimization problem with potentially many ‘local’ optima.
Any approach of the type “start at something and gradually improve” will only find the local optimum, but not necessarily the global one.
I have not been able to come up with something better than a O(N^2) approach, involving – roughly speaking – N times a local optimization, where each local optimization is O(N).
I’ll sketch the method with some code snippets (partially pseudo-code or remarks) for the essential part of the local optimization.
The remainder is “more of the same” and should not be difficult to fill in.
To cut down on wording without becoming inaccurate, henceforth I will mean by “a point on the edge (of a recctangle)” a point that is on the ‘inner’ part of the edge, not at a corner.
Likewise, by ‘rectangle’ I will mean an “eligible” reactangle, i.e. one that satisfies the basic conditions: no points inside, and at least one point on each of its edges.
Now, the LOCAL optimization is “defined” by a specific point from the points-set, in combination with a specific “border-type” from {Left, Top, Right, Bottom}.
Assume that we have chosen a point L and border-type “Left”; The locally optimal solution is defined as the ‘best” (largest area) rectangle that has L on its Left edge.
We’re going to construct all (L,Left)-rectangles and keep track of the largest one that we find on the way.
Observe: any (L,Left)-rectangle that has point R on its right border, must have a point T on its Top border and a point B on its bottomm border, where
L.x < T.x < R.x
L.x < B.X < R.X
B.y < L.y < T.y
B.y < R.y < T.Y
Image now, that we scan the points in x-ordered fashion, starting after L.
At the one hand: before we can find R, the above conditions show that we must first encounter T and B.
At the other hand, as soon as we’ve found R, from all the points with y > L.y that we’ve encountered in-between, we will by now be bounded by the one with the lowest y. and likewise for the bottom-border.
With N the number of points {P},
Let index_X[] be the array of indices for the x-sorted points, such that P[index_X[i]]x <= P[index_X[j]].x whenever i is less than j.
Furthermore, let iL be the index of L in the x-sorted array: P[index_X[iL]] = L.
In the following code-snippets (VB-syntax; it shouldn’t be too difficult to translate in whatever language you use), we first determine “some” T (a top-edge point) and “some” B (a bottom-edge point).
Then, we keep scanning, and whenever we find a point R that completes a rectangle, we:
(a) calculate the area to update the optimum if it is larger;
(b) replace T or B by the found R (depending on whether R is above L or below), and repeat the search for R.
Dim indx As Integer = iL + 1 'first point to consider on the right of L
Dim T As PointF = Nothing
Dim B As PointF = Nothing
' find T,B
While (indx < N AndAlso (T = Nothing OrElse B = Nothing))
Dim Q As PointF = Pts(indx_X(indx))
If (Q.Y > L.Y) Then
' a candidate for T
If (T = Nothing) OrElse (Q.Y < T.Y) Then
T = Q
End If
ElseIf (Q.Y < L.Y) Then
' a candidate for B
If (B = Nothing) OrElse (Q.Y > B.Y) Then
B = Q
End If
Else
Return -1 'Failure for L altogether: Q has exactly the same y-value as L and we didn't find yet both T and B.
End If
indx += 1
End While
If (T = Nothing OrElse B = Nothing) Then
Return -1 'Failure for L: we have exhausted all points on the right without finding both T and B.
End If
' we have "some" T and B, now proceed to find all (L,Left) rectangles
' intialize result (= max area from (L,Left)-rectangles).
Dim result As Double = -1
' the next point to consider
indx += 1
' find successive rectangles, by searching for R, given L (fixed) and T,B (occasionally updated).
While (indx < N)
Dim R As PointF = Pts(indx_X(indx)) 'candidate
If (R.Y = L.Y) Then
' rectangle found, process it.
Dim area As Double = (R.X - L.X) * (T.Y - B.Y)
If area > result Then
result = area
End If
' it all stops here: no further rectangles {L,Left) are possible as they would have this R inside.
Exit While
End If
If (R.Y > L.Y) Then
' a point with y > L.Y:
' if it is above T we can ignore it.
' if is below T, it is the R-bound for the rectangle bounded by L,T,B
If (R.Y < T.Y) Then
' process the rectangle
Dim area As Double = (R.X - L.X) * (T.Y - B.Y)
If area > result Then
result = area
End If
' move on, understanding that for any NEXT rectangle this R must be the upperbound.
T = R
End If
Else 'R.Y < L.Y
' a point with y < L.Y
' if it is below B we can ignore it.
' if it is above B, it is the R-bound for the rectangle bounded by L,T,B
If (R.Y > B.Y) Then
' process the rectangle
Dim area As Double = (R.X - L.X) * (T.Y - B.Y)
If area > result Then
result = area
End If
' move on, understanding that for any NEXT rectangle this R must be the lowerbound.
B = R
End If
End If
indx += 1
End While
Return result
The overall solution is, of course:
find for each point P, the optimum among opt(P,Left), opt(P,Right), opt(P,Top), opt(P,Bottom), and then find the maximum over all P.
The varieties for Right, Top, Bottom are of course very similar to the opt(Left) that I sketched out above.
The pre-sorting (to get indices for x-order and for y-order (for handling the (P,Top) and (P,Bottom)-cases) are O(nLogn), the local optimizations are each O(n) – view the code. So the overall complexity is O(n^2).
Note added – because the original formulation was not absolutely clear to me:
IF rectangles can also be bounded by CORNER-points, then the above needs a few minor adjustments (mostly adding equal signs to inequality conditions), but it won’t change the algorithm in essence.














 Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.
Четырёхугольник – это фигура из четырёх точек (вершин), из которых любые три не лежат на одной прямой, и четырёх отрезков (сторон) последовательно их соединяющих.