Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
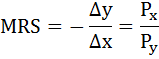
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
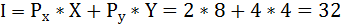
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.

Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:

Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
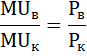
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
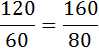
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
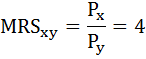
Запишем бюджетное ограничение:
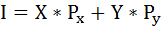
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
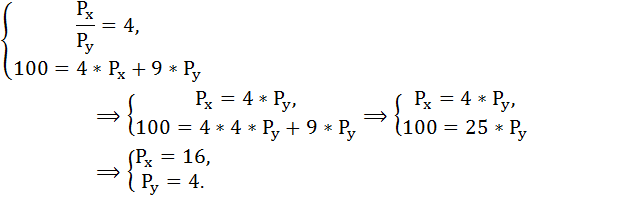
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
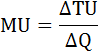
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.

Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
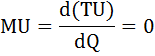
1) MU = –10 × Q = 0, следовательно, Q = 0;
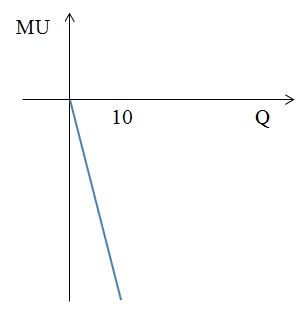
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
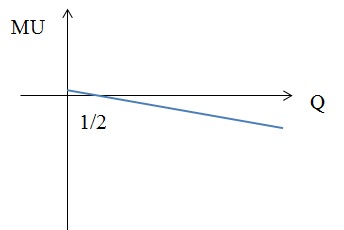
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
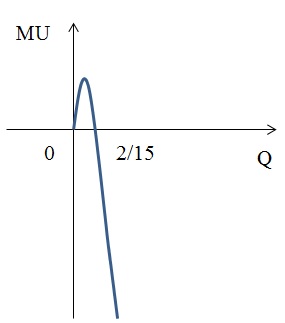
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
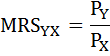
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
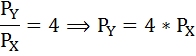
Далее воспользуемся формулой бюджетного ограничения:
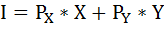
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
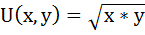
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
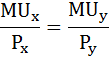
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
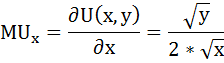
Аналогично находим предельную полезность товара y:
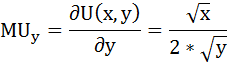
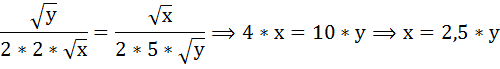
Далее воспользуемся бюджетным ограничением:
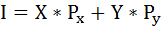
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
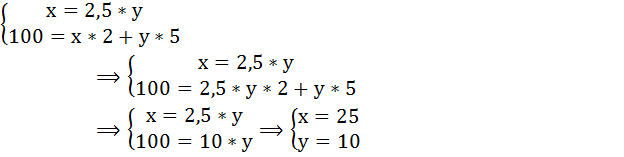
При х = 25 и у = 10 общая полезность достигнет максимума:
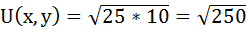
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
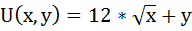
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
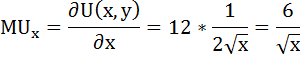
Оптимальный объём потребления будет достигнут при МU = P:
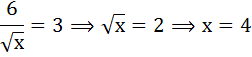
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Представители
количественной теории полезности (К.
Менгер, Е. Бем-Баверк, Г. Госсен и др.)
основывали свои рассуждения на
следующих предположениях (гипотезах):
–
при расходовании своего бюджета
потребитель стремится получить
максимум полезности (удовлетворения)
от приобретаемых благ;
–
потребитель способен произвести
количественную оценку полезности
благ;
–
последовательно потребляемые количества
какого-либо блага обладают убывающей
полезностью для потребителя.
Ученые
различали общую и предельную полезность
и измеряли ее в условных единицах —
утилях.
Общая
полезность TU
—
это удовлетворение, которое получает
потребитель от потребления определенного
количества благ. Эта зависимость
выражается функцией полезности
TU
= f(Qi).
Предельная
полезность MU—
это дополнительное удовлетворение,
получаемое от потребления еще одной
добавочной единицы потребленного
товара. Ее можно определить по двум
формулам:
1) MU(Qi)
= ![]()
2) как частную производную общей
полезности
MU(Qi)
= ![]() .
.
Графическое
изображение кривых общей и предельной
полезности дано на рис. 3.1. Геометрически
значение предельной полезности равно
тангенсу угла наклона касательной к
кривой TU.
Из рисунка видно, что когда функция
общей полезности достигает максимума,
то одновременно предельная полезность
товара становится нулевой.
Принцип
убывающей полезности (закон насыщения
потребности)
называют
первым законом Госсена — по имени
экономиста, впервые сформулировавшего
его. Он
содержит
два положения: первое констатирует
убывание последующих единиц блага в
одном непрерывном акте потребления,
так что в пределе достигается полное
насыщение этим благом; второе указывает
на убывание полезности первых единиц
блага при повторных актах потребления.
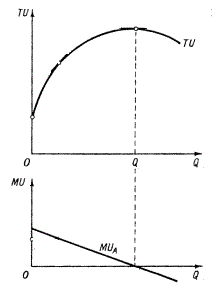
Рис.
3.1 — Зависимость между общей и предельной
полезностью
В
обычной жизни каждый потребитель
стремится повысить общую полезность
потребляемого блага. Принцип
максимизации
общей
полезности состоит
в следующем: каждый потребитель.
приобретая какой-то набор товаров,
должен распределить свой доход так,
чтобы полезность денежной единицы
(доллара, рубля и т. д.), израсходованной
на тот или иной товар, была одинаковой.
Второй закон Госсена — это закон
выравнивания предельных полезностей.
Условие
равновесия потребителя
выражается
формулой
![]() ,
,
где
λ — предельная полезность денег;
х,у,п
— виды приобретаемых товаров.
Последнюю
часть равенства можно записать как MUn
= Рпλ,
т.е.
предельная полезность блага равна
предельным затратам потребителя [10].
Пример
3.1
Потребитель
собирается приобрести на свой доход,
равный 10 денежным единицам, набор из
двух товаров: А
по цене 1 денежная единица за штуку
и В
по цене 2 денежных единицы за штуку.
Полезность товаров для потребителя в
утилях представлена в таблице.
Необходимо найти такую комбинацию
товаров, при которой предельная полезность
покупки окажется максимальной.
Расчет максимальной суммарной предельной полезности от покупки набора товаров
|
Единицы товара |
Предельная |
|||
|
Товар |
Товар |
|||
|
в |
в |
в |
в |
|
|
1-я |
20 |
20 |
48 |
24 |
|
2-я |
16 |
16 |
40 |
20 |
|
3-я |
14 |
14 |
36 |
18 |
|
4-я |
12 |
12 |
32 |
16 |
|
5-я |
10 |
10 |
24 |
12 |
|
6-я |
8 |
8 |
12 |
6 |
|
7-я |
6 |
6 |
8 |
4 |
Решение.
Прежде
всего следует купить 1 штуку товара В
за 2 денежных единицы, так как она
обеспечит наиболее возможную предельную
полезность первой покупки в расчете на
1 денежную единицу.
В
качестве второй покупки можно купить
товар А
либо товар В,
так как и тот и другой обеспечивают
одинаковую предельную полезность,
равную 20 утилям. Если мы купим товар А,
то третьей покупкой будет товар В.
Итак, на три единицы товара мы израсходовали
5 денежных единиц. Оставшиеся 5 денежных
единиц будут израсходованы в следующей
последовательности: 4-я штука — товар
В
дает 18 утилей; 5-я и 6-я штуки — товары А
и В,
так как у них одинаковая предельная
полезность. Итого
будет
приобретено
2 штуки товара А
и 4 штуки товара В.
Суммарная предельная полезность при
этом будет равна 192 утилям. Это
максимальная
величина полезности.
-
Порядковая
теория полезности
Авторы
порядкового направления (Ф. Эджуорт, Е.
Слуцкий, Дж.
Хикс)
предложили измерять субъективную
полезность с помощью
предпочтений.
При этом потребителю необходимо нишь
сделать
выбор между двумя наборами потребительских
благ.
Этот подход
базируется на следующих постулатах
[11]:
1)
предпочтения у потребителя уже сложились
и упорядочены;
2)
потребитель согласен отказаться от
небольшого количества блага у, если
ему предложат взамен большее количество
блага х;
3)
потребитель стремится иметь большее
количество любых товаров и услуг, если
он не пресыщен ни одним из них;
4)
удовлетворение потребителя зависит
только от количества потребляемых
им благ и не зависит от количества благ,
потребляемых другими.
Для
исследования равновесия потребителя
используются следующие понятия: кривая
безразличия, предельная норма замещения,
бюджетная линия.
Кривая
безразличия
U
—
это модель, представленная в виде кривой.
Каждая точка кривой представляет такой
набор из двух товаров, что потребителю
безразлично, какой из них выбрать.
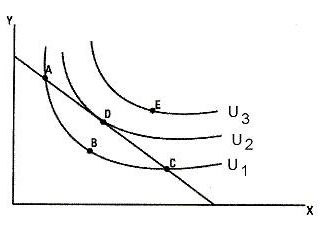
Чтобы построить кривую безразличия
(рис. 3.2), необходимо по оси абсцисс
отложить один вид товара, а по оси
ординат — другой. Точки А,
В,
С, лежащие на кривой, показывают наборы,
дающие одинаковую полезность (например,
10 утилей) для потребителя, и его выбор.
Все
множество кривых безразличия в
пространстве двух благ образует карту
безразличия. Кривые безразличия,
расположенные правее кривой U1,
показывают более высокий уровень
удовлетворенности потребителя.
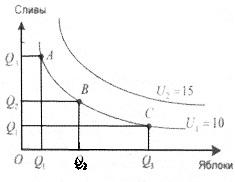
Рис.
3.2 — Кривые безразличия
Кривые
безразличия для отдельного потребителя
обладают следующими свойствами:
1)кривые
безразличия, лежащие выше и правее
первой кривой, имеют большую полезность;
2)кривые
безразличия имеют отрицательный наклон;
3)они
выпуклы к началу координат;
4)они
никогда не пересекаются.
Основным
рабочим понятием порядковой теории
полезности является предельная
норма замещения
MRSху.
Она показывает то количество блага х,
которое потребитель желает получить в
обмен на единицу блага у,
с тем чтобы уровень удовлетворения
остался неизменным, и определяется по
формуле
MRSху
=
![]() .
.
Предельная
норма замещения может принимать различные
значения: может быть равна нулю, быть
неизменной, меняться при движении вдоль
кривой безразличия. В случае выпуклости
к началу координат MRS
убывает,
т. е. потребитель соглашается отдавать
все меньшее количество замещаемого
блага за одно и то же количество
замещенного. Для двух взаимозаменяемых
товаров она является неизменной. В
случае двух взаимодополняемых товаров
кривая безразличия принимает вид двух
взаимно перпендикулярных отрезков.
Предельная
норма замещения, показывая возможности
замены
одного
блага другим, не позволяет в то же время
определить, какой именно набор товаров
потребитель считает наиболее выгодным.
Эту информацию дает бюджетная
линия
I.
Она представляет
собой
прямую линию с отрицательным наклоном,
графически
отображающую
множество наборов из двух товаров,
требующих одинаковых затрат на их
приобретение. Уравнение
бюджетной
линии имеет следующий вид:
I
= Рхх
+ Руу,
где
I
— доход потребителя;
Рх
— цена блага х;
Pу
—
цена блага у;
х,
у
—
соответственно количества приобретенных
благ.
Эту
формулу можно преобразовать в более
привычный вид
у
= а
– bх
или у
=![]() ,
,
где
![]()
угловой
коэффициент наклона прямой.
Точка
М
на оси ординат определяется делением
дохода на цену товара у
(рис. 3.3), если потребитель приобретает
только один товар — сливы. Точка N
определяется
делением дохода на цену товара х
при условии приобретения потребителем
тиара х
(яблок).
Следовательно,
бюджетная линия MN
характеризует
реальную покупательскую способность
и соотношение цен приобретаемых
товаров.
Точка
касания бюджетной линии с кривой
безразличия означает равновесие
потребителя
(см.
рис. 3.3). В точке равновесия Е
предельная норма замещения равна
соотношению цен товаров х
и у:
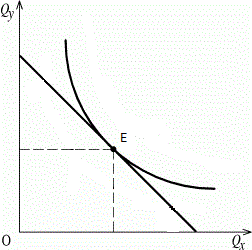
Рис.
3.3 — Равновесие потребителя
Изменение
соотношения цен на товары приводит к
изменению угла наклона бюджетной
линии.
Пример
3.2
Доход
потребителя, расходуемый на два товара
(молоко и
сметану),
равен 80 руб. Цена 1 л молока равна 8 руб.,
цена 1 кг
сметаны
— 20 руб. Предположим, что в состоянии
равновесия потребитель приобретает 2
л молока и 3,2 кг сметаны.
Необходимо:
а)построить
бюджетную линию и определить угол ее
наклона;
б)построить
новую бюджетную линию и определить yгoл
ее
наклона после повышения цены сметаны
до 25 руб. за 1 кг
при
сохранении неизменной цены молока.
Решение.
1.Для
построения бюджетной линии MN
на
нижеприведенном рисунке определим
значения крайних точек бюджетной линии,
находящиеся на осях абсцисс и ординат.
Значение точки М
на
оси ординат наймем, используя уравнение
бюджетной линии:
![]()
Значение
точки N
на
оси абсцисс определим по аналогичным
формулам:
I
= Pxx;
y
= ![]()
=
![]()
=
10.
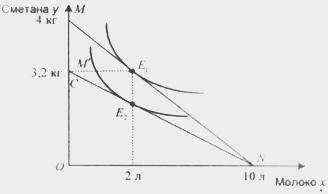
2.Выбираем
произвольно на бюджетной линии MN
точку
потребительского
равновесия и строим кривую безразличия.
Точка касания кривой безразличия и
бюджетной линии показывает
равновесный
набор, состоящий из двух товаров. Согласно
графику потребитель предпочитает набор
Е1,
в котором больше сметаны и меньше молока.
3.Определим
наклон бюджетной линии MN
двумя
способами. Первый способ позволяет
определить наклон бюджетной линии по
формуле
наклон
бюджетной линии = ![]()
= ![]()
= ![]()
= 0.4.
Второй
способ предполагает использование
соотношения цен товаров x
и у.
Наклон бюджетной линии определим по
формуле
наклон
бюджетной линии
= ![]()
= ![]()
=
0,4.
Крутизна
бюджетной линии в точке потребительского
равновесия показывает, от какого
количества единиц товара у
следует отказаться потребителю, чтобы
получить дополнительное количество
единиц товара х.
В нашем примере потребителю следует
отказаться от двух единиц товара у,
чтобы приобрести дополнительно пять
единиц товара х.
4.Повышение
цены сметаны с 20 руб. до 25 руб. приведет
к смещению точки М
вниз. Построим новую бюджетную линию
М’N
.
Значение точки М’
определим по формулам
![]()
Потребитель
после роста цены сможет купить только
3,2 кг сметаны. Новая бюджетная линия М‘N
станет
более пологой по сравнению с бюджетной
линией MN,
и
ее наклон будет равен
![]()
Новое
равновесие потребителя может находиться
на любой точке новой бюджетной линии
M‘N
в
зависимости от его предпочтений.
Предположим, что наш потребитель не
желает изменять количество потребляемого
молока. Тогда новая точка равновесия
установится в точке Е2.
Таким
образом, рост цены сметаны при неизменной
цене молока и неизменных предпочтениях
потребителя приводит его к выбору
набора, содержащего меньше сметаны и
столько же молока.
Используя
изменение соотношения цен, ученые
построили кривую «цена потребления».
Допустим, что цена яблок снижается
с Р]
до Р2,
а
доход является неизменным. Снижение
цены товара л- при неизменной цене товара
у
и неизменном доходе приводит к изменению
наклона бюджетной линии MN>
(рис.
3.4, а,
б).
Она становится длиннее и с меньшим углом
наклона MN’.
Для
каждой новой бюджетной линии можно
найти соответствующие кривые безразличия
U1,U2,
которые
будут соприкасаться с бюджетными линиями
в точках
Е1
и
Е2.
Соединив эти точки, получим кривую
цена-потребление
Gp.

Рис.
3.4 — Взаимосвязь кривой «цена-потребление»
(а)
и
кривой индивидуального спроса (б)
На
основе кривой «цена-потребление»
строится линия индивидуального
спроса на товар х.
Взаимодействие этих кривых показывает,
что наклон кривой спроса зависит от
предпочтений потребителя.
Изменение
цены какого-либо товара влияет на объем
спроса через эффект замены и эффект
дохода. Первым ученым, предложившим
разложить общий эффект от изменения
цен на эффект дохода и эффект замены,
является Е. Слуцкий, но более простым
для понимания является подход Дж. Хикса.
На
рис. 3.5 в точке Е2
показан набор товаров х,
у,
который выбрал потребитель в результате
снижения цены товара х.
Общий эффект выразился в увеличении
количества яблок с Qx1
до
Qx2,
(при абстрагировании от эффекта товара
у).
Этот эффект
раскладывается
на два эффекта: эффект замещения (Qx1
–
Qx3)
и
эффект
дохода (Qx3
–
Qx2).
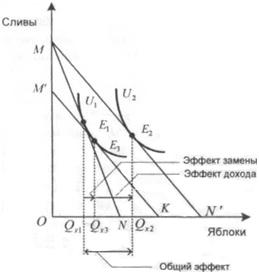
Рис.
3.5 — Разложение общего эффекта
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
11.05.2015110.59 Кб2pr.doc
- #
- #
- #
Правило максимизации полезности: формула
Почему люди готовы тратить свои деньги на покупку товаров и услуг? Ответ на этот вопрос довольно прост: потому что их потребление является источником удовольствия и удовлетворения. Потребности безграничны, деньги – нет. Поэтому для объяснения того, как у людей происходит принятие решения о покупке товара или услуги, необходимо изучить правило максимизации полезности.
Предпосылки
Что такое правило максимизации полезности? Кратко его можно объяснить так: потребитель распределяет свой доход таким образом, что каждая последняя денежная единица приносит ему одинаковое удовольствие и удовлетворение.
 Этот экономический закон базируется на трех предпосылках:
Этот экономический закон базируется на трех предпосылках:
- Покупатели стремятся распределить заработанные ими деньги так, чтобы полученная полезность купленных продуктов была наибольшей.
- Потребители являются рациональными экономическими субъектами. Это означает, что они способны самостоятельно использовать правило максимизации полезности, сравнивая различные наборы товаров.
- Цены на товары определяются рынком. Потребители не могут влиять на них.
Правило максимизации полезности: формула
- MU А / Цена А = MU Б / Цена Б.
Так выглядит формула на языке алгебры. Суть правила состоит в следующем: каждый последний доллар, потраченный на покупку товаров или услуг, должен приносить одинаковую предельную полезность (MU). Это означает, что потребитель израсходовал свои деньги правильно.
 Правило максимизации полезности требует, чтобы весь доход был растрачен полностью. Предположим, что у потребителя в кармане определенная сумма долларов. Цена и полезность каждого из продуктов также известна. Таким образом, вышеприведенное равенство выполняется. А правило максимизации полезности позволяет нам посчитать, сколько единиц товаров приобретет покупатель. За ним лежит важный психологический компонент: люди стремятся покупать только то, что им нравится. Если товар им безразличен, то он останется на прилавке магазина.
Правило максимизации полезности требует, чтобы весь доход был растрачен полностью. Предположим, что у потребителя в кармане определенная сумма долларов. Цена и полезность каждого из продуктов также известна. Таким образом, вышеприведенное равенство выполняется. А правило максимизации полезности позволяет нам посчитать, сколько единиц товаров приобретет покупатель. За ним лежит важный психологический компонент: люди стремятся покупать только то, что им нравится. Если товар им безразличен, то он останется на прилавке магазина.
Применение на практике
Предположим, покупатель делает выбор между кофе и чаем. Как будет работать правило максимизации общей полезности? Для этого нам нужно знать, как он оценивает удовлетворение от покупки первого и второго напитка. Предположим, он оценивает полезность кофе в 100 баллов, а чая – в 80. При этом цена первого напитка составляет 200 рублей, второго – 100. Очевидно, что при таком раскладе покупатель выберет чай на основании взвешенной полезности. Для кофе она равна 0,5 балла, для чая – 0,8.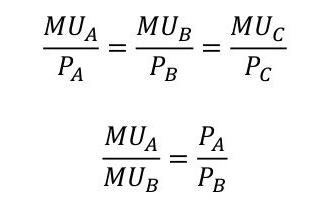 Но предположим, что этот же покупатель решил растратить все свои наличные на покупку этих двух напитков? Неужели он будет покупать только чай? Это нам позволяет понять правило максимизации полезности. На самом деле каждая следующая чашка любого из двух напитков приносит меньше удовольствия, чем предыдущая.
Но предположим, что этот же покупатель решил растратить все свои наличные на покупку этих двух напитков? Неужели он будет покупать только чай? Это нам позволяет понять правило максимизации полезности. На самом деле каждая следующая чашка любого из двух напитков приносит меньше удовольствия, чем предыдущая.
Полезность как объект изучения
Данный термин впервые был введен английским философом Бентамом. Он понимал под полезностью принцип, который помогает человеку определить, принесет ли следующее действие счастье. Бентам считал, что в своем выборе человек руководствуется своими вкусами и предпочтениями. Сегодня полезность блага определяют через его способность удовлетворять потребности определенного субъекта. Существует две основных теории изучения этого понятия: кардиналистская (количественная) и ординалистская (порядковая). Первая зародилась во второй половине 19 века. Ее апологетами являлись такие известные ученые, как Джевонс, Менгер и Вальрас. Они считали, что полезность можно измерить. Ординалисты, напротив, не видят возможности количественной оценки этого понятия. Представителями этого направления являются такие ученые, как Эджуорт, Парето и Фишер. Они считали, что достаточно качественной оценки полезности. Дальнейшее развитие их теория получила в работах Хикса и Аллена в 30-е годы прошлого века.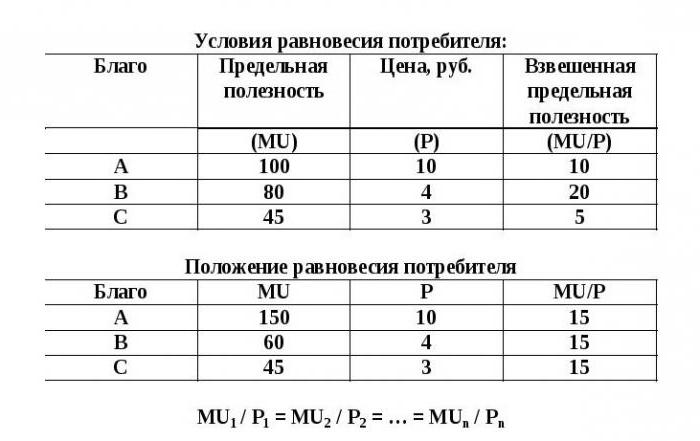
Различают два вида полезности. Субъективная (кардиналистская, количественная) представляет собой показатель, который можно измерить. Например, человек захотел съесть яблоко. Первый фрукт будет обладать для него наибольшей полезностью. А вот четвертое яблоко может вообще не приносить ему никакого удовлетворения. Такое сравнение характерно для количественной теории. Объективная полезность – это показатель, который нельзя измерить. Его исследованием занимается качественная (ординалистская) теория. В пример часто приводится полезность воды в море или песка в пустыне.
Закон убывания предельной полезности
Как мы уже убедились, удовлетворение от употребления каждой последующей единицы товара становится меньше. Закон убывания предельной полезности впервые сформулировали представители количественной теории – Джевонс, Менгер и Вальрас. Все трое писали свои исследования независимо друг от друга и опубликовали их практически в одно время. Сам термин «предельная полезность» был введен в научный оборот Фридрихом фон Визером. Она может меняться в зависимости от выбора субъекта, его состояния (например, сытый или голодный) и базовой потребности (зерно как семена для посева или продукт для изготовления хлеба). Суть закона состоит в том, что с ростом потребления общая полезность продукта растет все медленнее. Для того чтобы заставить человека покупать больше, нужно снижать цену. Однако есть некоторые ограничения в применении этого закона:
Однако есть некоторые ограничения в применении этого закона:
- Неоднородные единицы. Нельзя рассматривать сразу и яблоки, и бананы. Все исследуемые единицы товара должны быть однородными.
- Изменения во вкусах и предпочтениях. Закон убывающей полезности их не учитывает, но если это все-таки произошло, то он не будет правильно работать.
- Непрерывность потребления. Если в покупке товаров есть некоторая пауза, то каждая последующая единица может приносить такое же удовольствие, как и предыдущая.
- Изменения цен. Закон убывающей полезности не работает в условиях постоянного изменения рыночной конъюнктуры.
Выводы
Изучение поведения потребителей – это сложная наука. Она базируется на следующих гипотезах:
- Предпочтения потребителей определяют их выбор набора благ.
- Люди являются рациональными субъектами, которые знают, как максимально полно удовлетворить свои потребности.
- Человек стремится максимизировать получаемую им общую полезность.
- Цены на блага устанавливаются рынком.
- Выбор товаров ограничен доходом покупателя.
- Определение наиболее удачного набора благ происходит с учетом действия закона убывающей предельной полезности.
- 13.04.2016
- Сонера Рассказова
- Бизнес статьи
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | … | 20 | 19 | … | 22 | … |
| 2 | … | 15 | 30 | … | … | 10 |
| 3 | … | 12 | 38 | … | 39 | … |
| 4 | … | 8 | 43 | … | 44 | … |
| 5 | … | 6 | 45 | … | … | 3 |
Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара – Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) – TU(1)=30 – 19 = 11
MU(3)= TU(3) – TU(2)=38 – 30 = 8
MU(4)= TU(4) – TU(3)=43 – 38=5
MU(5)= TU(5) – TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) – TU(2)=39 – 32=7
MU(4)= TU(4) – TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:
| Количество товара | А | В | С | |||
|---|---|---|---|---|---|---|
| TU | MU | TU | MU | TU | MU | |
| 1 | 20 | 20 | 19 | 19 | 22 | 22 |
| 2 | 35 | 15 | 30 | 11 | 32 | 10 |
| 3 | 47 | 12 | 38 | 8 | 39 | 7 |
| 4 | 55 | 8 | 43 | 5 | 44 | 5 |
| 5 | 61 | 6 | 45 | 2 | 47 | 3 |
Download Article
Download Article
In economics, marginal utility (MU) is a way to measure how much value or satisfaction a consumer gets out of consuming something. As a general rule, MU is equal to the change in total utility divided by the change in the quantity of goods consumed.[1]
A common way of thinking of this is that MU is the utility someone gets from each additional unit of goods consumed.
-

1
Understand the economic concept of utility. Utility is the “value” or “satisfaction” that a consumer gets from consuming a certain number of goods. A good way of thinking of it is that utility is how much money a consumer would hypothetically pay for the satisfaction provided by a good.[2]
- For example, let’s say that you are hungry and are buying fish to eat for supper. Let’s also say that one fish costs $2. If you’re so hungry that you would pay $8 for the fish, the fish is said to provide $8 worth of utility. In other words, you’re willing to pay $8 to get the satisfaction from the fish no matter what it actually costs.
-

2
Find the total utility from consuming a certain number of goods. Total utility is just the concept of utility applied to more than one good. If consuming one good gives you a certain amount of utility, consuming more than one of the same good will give you an amount that is higher, lower, or the same.[3]
- For example, let’s say that you plan to eat two fish. However, after eating the first fish, you’re not quite as hungry as before. Now, you’d only pay $6 for the extra satisfaction of the second fish. It’s not worth as much to you now that you’re somewhat full. This means the two fish provide $6 + $8 (first fish) = $14 of “total utility” together.
- Note that it doesn’t matter whether or not you actually buy the second fish. MU is only concerned with what you would pay for it. In real life, economists use complex mathematical models to predict what consumers hypothetically would pay for something.
Advertisement
-

3
Find the total utility from consuming a different number of goods. To find MU, you need two different total utility measurements. You’ll use the difference between them to make your MU calculation.[4]
- Let’s say that, in the example situation in Step 2, you decide that you’re hungry enough to eat four whole fish. After the second fish, you’re feeling a little full, so you would only pay about $3 for the next fish. After the third fish, you’re almost completely full, so you would only pay $1 for the final fish.
- The satisfaction you would get from it is almost cancelled out by the feeling of being uncomfortably full. You can say that the four fish provide a total utility of $8 + $6 + $3 + $1 = $18.
-

4
Calculate MU. Divide the difference in total utility over the difference in units. The answer you get will be the marginal utility, or the utility given by each additional unit consumed.[5]
In the example situation, you would calculate your MU as follows:- $18 – $14 (example from Step 2) = $4
- 4 (fish) – 2 (fish) = 2
- $4/2 = $2
- This means that, between the second and the fourth fish, each extra fish is only worth $2 of utility to you. This is an average value; the third fish is actually worth $3 and the fourth is actually worth $1, of course.
Advertisement
-

1
Use the equation to find the MU for each additional unit. In the example above, we found the average MU for several goods being consumed. This is one valid way to use MU. However, it’s actually more often applied to individual units of goods consumed. This gives us the precise MU for each additional good (not an average value).[6]
- Finding this is easier than it sounds. Just use the normal equation to find the MU when the change in quantity of goods consumed is one.
- In the example situation, you already know the MUs for each individual unit. When you haven’t had any fish, the MU of the first fish is $8 ($8 of total utility – the $0 you had before/change of 1 unit), the MU of the second fish is $6 ($14 of total utility – the $8 you had before/change of 1 unit), and so on.
-

2
Use the equation to maximize your utility. In economic theory, consumers make decisions about how to spend their money in an effort to maximize their utility. In other words, consumers want to get as much satisfaction as possible for their money. This means that consumers will tend to buy products or goods until the marginal utility of buying one more good is smaller than the marginal cost (the price of one more unit).[7]
-

3
Determine lost utility. Let’s look at the example situation one more time. First we said that each fish costs $2. Then we determined that the first fish has an MU of $8, the second has an MU of $6, the third has an MU of $3, and the fourth has an MU of $1.[8]
- Given this information, you wouldn’t actually end up buying the fourth fish. Its marginal utility ($1) is less than its marginal cost ($2). Basically, you’re losing utility on this transaction, so it’s not in your favor.)
Advertisement
| Tickets Bought | Total utility | Marginal utility |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | -2 |
| 8 | 18 | -10 |
-

1
Assign columns for quantity, total utility, and marginal utility. Most MU charts have at least these three columns. There may sometimes be more, but these display the most crucial information. Typically, these are arranged from left to right.[9]
- Note that the column headers will not always match these exactly. For example, the “Quantity” column may be labeled “Items bought,” “Units purchased,” or something similar. The important thing is the information in the column.
-

2
Look for a trend of diminishing returns. A “classic” MU chart is often used to demonstrate that, as a consumer buys more of a certain good, the desire to purchase even more goods will drop. In other words, after a point, the marginal utility of each additional good purchased will start to decrease. Eventually, the consumer will start to be less satisfied overall than before buying the additional goods.[10]
- In the example chart above, this trend of diminishing returns starts almost immediately. The first ticket to the film festival provides lots of marginal utility, but each ticket after the first gives a little less. After six tickets, each extra ticket actually has a negative MU, which decreases the total satisfaction. An explanation for this might be that, after six visits, the consumer starts to get tired of seeing the same movies again and again.
-

3
Determine Maximum Utility. This is the point where marginal price exceeds MU. A marginal utility chart makes it easy to predict how many units of goods a consumer will buy. As a reminder, consumers tend to buy goods until the marginal price (the cost of one more unit of the goods) is greater than the MU. If you know how much the goods being analyzed in the chart cost, the point where utility is maximized is the last row where MU is higher than the marginal cost.[11]
- Let’s say that the tickets in the example chart cost $3 each. In this case, utility is maximized when the consumer buys 4 tickets. The next ticket after this has an MU of $2, which is less than the marginal cost of $3.
- Note that utility isn’t necessarily maximized when the MU starts to become negative. It’s possible for goods to give some benefit to the consumer without being “worth it.” For instance, the fifth ticket in the chart above still gives $2 worth of MU. This isn’t a negative MU but it still decreases the total utility because it’s not worth the cost.
-

4
Use the chart data to find additional information. Once you have the three “core” columns above, it becomes easy to get more numerical data about the model situation the chart is analyzing. This is especially true if you’re using a spreadsheet program such as Microsoft Excel that can do the math for you. Here are two types of data you may want to put in extra columns to the right of the three used above:[12]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
- Consumer Surplus: The marginal utility in each row minus the product’s marginal cost. It represents the “profit” in terms of utility the consumer gets from buying each product. It is also called “economic surplus.”[14]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
It’s important to understand that the situations in the examples are model situations. That is, they represent hypothetical consumers (rather than real ones). In real life, consumers aren’t perfectly rational; they may, for instance, not buy exactly as many goods as are needed to maximize utility. Good economic models are great tools for predicting consumer behavior on a broad scale, but they often don’t “match” real life exactly.[15]
-
If you add a consumer surplus column to your chart (as discussed above), the point at which utility is maximized will be the last row before consumer surplus becomes negative.
Advertisement
References
About This Article
Article SummaryX
Marginal utility is used to measure how satisfying or valuable something is to a consumer. To calculate the marginal utility of something, just divide the change in total utility by the change in the number of goods consumed. In other words, divide the difference in total utility by the difference in units to find marginal utility. To learn more from our Entrepreneur co-author, like how to use a marginal utility chart, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 659,353 times.
Reader Success Stories
-

Mujammil Islam
Apr 19, 2017
“Thank you for this article. At first I could not understand the total and marginal utility. Then I found this…” more
