Как найти максимальную последовательность одного элемента

В этой статье мы научимся находить максимальное значение в списке на Python. Для всестороннего понимания вопроса мы рассмотрим использование некоторых встроенных функций, простые подходы, а также небольшие реализации известных алгоритмов.

Сначала давайте вкратце рассмотрим, что такое список в Python и как найти в нем максимальное значение или просто наибольшее число.

В Python есть встроенный тип данных под названием список (list). По своей сути он сильно напоминает массив. Но в отличие от последнего данные внутри списка могут быть любого типа (необязательно одного): он может содержать целые числа, строки или значения с плавающей точкой, или даже другие списки.

Хранимые в списке данные определяются как разделенные запятыми значения, заключенные в квадратные скобки. Списки можно определять, используя любое имя переменной, а затем присваивая ей различные значения в квадратных скобках. Он является упорядоченным, изменяемым и допускает дублирование значений. Например:

list1 = ["Виктор", "Артем", "Роман"]
list2 = [16, 78, 32, 67]
list3 = ["яблоко", "манго", 16, "вишня", 3.4]

Далее мы рассмотрим возможные варианты кода на Python, реализующего поиск наибольшего элемента в списке, состоящем из сравниваемых элементов. В наших примерах будут использоваться следующие методы/функции:

1. Встроенная функция max()
2. Метод грубой силы (перебора)
3. Функция reduce()
4. Алгоритм Heap Queue (очередь с приоритетом)
5. Функция sort()
6. Функция sorted()
7. Метод хвостовой рекурсии

№1 Нахождение максимального значения с помощью функции max()

Это самый простой и понятный подход к поиску наибольшего элемента. Функция Python max() возвращает самый большой элемент итерабельного объекта. Ее также можно использовать для поиска максимального значения между двумя или более параметрами.

В приведенном ниже примере список передается функции max в качестве аргумента.

list1 = [3, 2, 8, 5, 10, 6]
max_number = max(list1)
print("Наибольшее число:", max_number)

Наибольшее число: 10

Если элементы списка являются строками, то сначала они упорядочиваются в алфавитном порядке, а затем возвращается наибольшая строка.

list1 = ["Виктор", "Артем", "Роман"]
max_string = max(list1, key=len)
print("Самая длинная строка:", max_string)

Самая длинная строка: Виктор

№2 Поиск максимального значения перебором

Это самая простая реализация, но она немного медленнее, чем функция max(), поскольку мы используем этот алгоритм в цикле.

В примере выше для поиска максимального значения нами была определена функция large(). Она принимает список в качестве единственного аргумента. Для сохранения найденного значения мы используем переменную max_, которой изначально присваивается первый элемент списка. В цикле for каждый элемент сравнивается с этой переменной. Если он больше max_, то мы сохраняем значение этого элемента в нашей переменной. После сравнения со всеми членами списка в max_ гарантировано находится наибольший элемент.

def large(arr): 
    max_ = arr[0]
    for ele in arr:
        if ele > max_:
           max_ = ele
    return max_ 


list1 = [1,4,5,2,6]
result = large(list1)
print(result)  # вернется 6

№3 Нахождение максимального значения с помощью функции reduce()

В функциональных языках reduce() является важной и очень полезной функцией. В Python 3 функция reduce() перенесена в отдельный модуль стандартной библиотеки под названием functools. Это решение было принято, чтобы поощрить разработчиков использовать циклы, так как они более читабельны. Рассмотрим приведенный ниже пример использования reduce() двумя разными способами.

В этом варианте reduce() принимает два параметра. Первый — ключевое слово max, которое означает поиск максимального числа, а второй аргумент — итерабельный объект.

from functools import reduce


list1 = [-1, 3, 7, 99, 0]
print(reduce(max, list1))  # вывод: 99

Другое решение показывает интересную конструкцию с использованием лямбда-функции. Функция reduce() принимает в качестве аргумента лямбда-функцию, а та в свою очередь получает на вход условие и список для проверки максимального значения.

from functools import reduce


list1 = [-1, 3, 7, 99, 0]
print(reduce(lambda x, y: x if x > y else y, list1))  # -> 99

№4 Поиск максимального значения с помощью приоритетной очереди

Heapq — очень полезный модуль для реализации минимальной очереди. Если быть более точным, он предоставляет реализацию алгоритма очереди с приоритетом на основе кучи, известного как heapq. Важным свойством такой кучи является то, что ее наименьший элемент всегда будет корневым элементом. В приведенном примере мы используем функцию heapq.nlargest() для нахождения максимального значения.

import heapq


list1 = [-1, 3, 7, 99, 0]
print(heapq.nlargest(1, list1))  # -> [99]

Приведенный выше пример импортирует модуль heapq и принимает на вход список. Функция принимает n=1 в качестве первого аргумента, так как нам нужно найти одно максимальное значение, а вторым аргументом является наш список.

№5 Нахождение максимального значения с помощью функции sort()

Этот метод использует функцию sort() для поиска наибольшего элемента. Он принимает на вход список значений, затем сортирует его в порядке возрастания и выводит последний элемент списка. Последним элементом в списке является list[-1].

list1 = [10, 20, 4, 45, 99]
list1.sort()
print("Наибольшее число:", list1[-1])

Наибольшее число: 99

№6 Нахождение максимального значения с помощью функции sorted()

Этот метод использует функцию sorted() для поиска наибольшего элемента. В качестве входных данных он принимает список значений. Затем функция sorted() сортирует список в порядке возрастания и выводит наибольшее число.

list1=[1,4,22,41,5,2]
sorted_list = sorted(list1)
result = sorted_list[-1]
print(result)  # -> 41

№7 Поиск максимального значения с помощью хвостовой рекурсии

Этот метод не очень удобен, и иногда программисты считают его бесполезным. Данное решение использует рекурсию, и поэтому его довольно сложно быстро понять. Кроме того, такая программа очень медленная и требует много памяти. Это происходит потому, что в отличие от чистых функциональных языков, Python не оптимизирован для хвостовой рекурсии, что приводит к созданию множества стековых фреймов: по одному для каждого вызова функции.

def find_max(arr, max_=None):
    if max_ is None:
        max_ = arr.pop()
    current = arr.pop()
    if current > max_:
        max_ = current
    if arr:
        return find_max(arr, max_)
    return max_


list1=[1,2,3,4,2]
result = find_max(list1)
print(result)  # -> 4

Заключение

В этой статье мы научились находить максимальное значение из заданного списка с помощью нескольких встроенных функций, таких как max(), sort(), reduce(), sorted() и других алгоритмов. Мы написали свои код, чтобы попробовать метод перебора, хвостовой рекурсии и алгоритма приоритетной очереди.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задачи по нахождению минимального и/или максимального элемента в массиве очень часто встречаются в различных учебных пособиях по программированию и, как правило, вызывают трудности у начинающих программистов или просто студентов, получивших такое задание.

В данной статье вы узнаете, как написать реализацию программы на языке C++, которая находит максимальный и минимальный элемент в массиве и выводит на экран. А узнать множество решений других задач можно в разделе с решениями задач по программированию на языке C++.

Что такое максимальный и минимальный элемент массива

Для начала поймем, что же такое максимальный или минимальный элемент в массиве? Всё просто, максимальный элемент массива — это элемент, который имеет самое большое числовое значение, а минимальный элемент массива — это элемент, имеющий самое маленькое значение.

Пример: в массиве, состоящем из таких элементов: 3, 1, 0, -4, 16, 2 — максимальный элемент равен 16, т.к. это число больше других, а минимальный элемент равен -4, т.к. оно меньше остальных.

Поняв это, можно приступить к решению задачи.

Алгоритм решения задачи

— Инициализация массива, переменных, хранящих минимальное и максимальное значение.

— Заполнение массива случайными числами при помощи цикла и функции, возвращающей случайные числа.

— Вывод массива.

— Сравнение каждого элемента массива: Если элемент больше переменной с максимальным значением, то значение записывается в переменную; Если элемент меньше переменной с минимальным значением, то значение записывается в переменную.

— Вывод переменных с максимальным и минимальным элементом.

Алгоритм решения на языке C++

Для начала нужно подключить заголовок ввода/вывода <iostream>, заголовок стандартных функций <cstdlib> в ней имеется функция rand(), которая позволит заполнить массив случайными числами. Заполнение каждого элемента массива вручную требует времени, его можно сэкономить автоматизировав процесс. Подключаем пространство имён std. Создаём константу N, она будет определять количество элементов в массиве.

#include <iostream> 
#include <cstdlib> 

using namespace std; //Пространство имён std

const int N = 10;//Количество элементов в массиве

int main() 
{

	return 0;
}

В теле функции main() инициализируем массив целых чисел из N лементов, целочисленные переменные max и min, они будут хранить значение максимального и минимального элементов массива соответственно.

	int mass[N], max, min;

Теперь заполним массив случайными числами. Для этого используем цикл от 0 до N (не включительно), который пройдется по каждому элементу массива и поместит случайное значение от 0 до 98. Это можно сделать, использовав функцию rand(), которая возвращает случайное число. Поделить возвращаемое значение на 99 и внести в ячейку остаток от деления, таким образом значение ячейки будет иметь значение в диапазоне от 0 до 99(не включая 99, т.к. остаток от деления не может быть кратным делителю).  При этом выведем значения элементов массива на экран.

	cout << "Элементы: |";
	for(int r = 0; r<N; r++) // Цикл от 0 до N
	{
		mass[r] = rand()%99; // Заполнение случайным числом
		cout << mass[r] << "|"; // Вывод значения
	}
	cout << endl;

В результате программа выведет на экран значения элементов массива, разделенное вертикальными чертами:

Элементы: |28|43|72|79|23|70|55|39|69|1|

Обратите внимание! Если вы программируете под Windows и у Вас не отображаются русские символы в консоли, то советую Вам почитать о решении этой проблемы в статье Русские символы(буквы) при вводе/выводе в консоль на C++.

Далее определим максимальный и минимальный элемент в массиве, для этого вновь пройдемся по массиву циклом. При помощи условия определим максимальный и минимальный элемент массива.

Перед циклом нужно будет занести первый элемент массива в переменные min и max, они будут хранить минимальное и максимальное значение изначально, а во время цикла поменяют его, если найдётся значение меньше для min или больше для max.

	max = mass[0];//Помещаем значения 1-го элемента
	min = mass[0];//массива в переменные
	for(int r = 1; r<N; r++)
	{
		if(max < mass[r]) max = mass[r]; //если значение элемента больше значения переменной max, то записываем это значение в переменную
		if(min > mass[r]) min = mass[r]; //аналогично и для min
	}

После цикла выведем значения min и max.

	cout << "Min: " << min << endl;
	cout << "Max: " << max << endl;

После компиляции и запуска прогамма выводит следующее

Элементы: |28|43|72|79|23|70|55|39|69|1|
Min: 1
Max: 79

Пробегаемся по элементам массива глазами и видим, что минимальное значение — 1, а максимальное — 79. Переменные min и max имеют эти же значения соответственно, следовательно алгоритм работает.

Весь листинг программы на C++

#include <iostream>
#include <cstdlib>

using namespace std;

const int N = 10;

int main() 
{
	int mass[N], max, min;

	cout << "Элементы: |";
	for(int r = 0; r<N; r++)
	{
		mass[r] = rand()%99;
		cout << mass[r] << "|";
	}
	cout << endl;
	
	max = mass[0];
	min = mass[0];
	for(int r = 1; r<N; r++)
	{
		if(max < mass[r]) max = mass[r];
		if(min > mass[r]) min = mass[r];
	}
	cout << "Min: " << min << endl;
	cout << "Max: " << max << endl;
	
	return 0;
}

Решаем задачу нахождения длины наибольшей возрастающей подпоследовательности

Задача

“Найти длину самой большой возрастающей подпоследовательности в массиве.”

Вообще, это частный случай задачи нахождения общих элементов 2-х последовательностей, где второй последовательностью является та же самая последовательность, только отсортированная.

На пальцах

Есть последовательность:

5, 10, 6, 12, 3, 24, 7, 8

Вот примеры подпоследовательностей:

10, 3, 8
5, 6, 3

А вот примеры возрастающих подпоследовательностей:

5, 6, 7, 8
3, 7, 8

А вот примеры возрастающих подпоследовательностей наибольшей длины:

5, 6, 12, 24
5, 6, 7, 8

Да, максимальных тоже может быть много, нас интересует лишь длина.
Здесь она равна 4.

Теперь когда задача определена, решать мы ее начинаем с (сюрприз!) вычисления чисел Фибоначчи, ибо вычисление их — это самый простой алгоритм, в котором используется “динамическое программирование”. ДП — термин, который лично у меня никаких правильных ассоциаций не вызывает, я бы назвал этот подход так — “Программирование с сохранением промежуточного результата этой же задачи, но меньшей размерности”. Если же посчитать числа Фибоначчи с помощью ДП для вас проще пареной репы — смело переходите к следующей части. Сами числа Фибоначчи не имеют отношения к исходной задаче о подпоследовательностях, я просто хочу показать принцип ДП.

Последовательность Фибоначчи O(n)

0, 1, 1, 2, 3, 5, 8, 13, 21, 34 …

Берем 0, прибавляем 1 — получаем 1.
Берем 1, прибавляем 1 — получаем 2.
Берем 1, прибавляем 2 — получаем, ну вы поняли, 3.

Собственно нахождение n-го элемента этой последовательности и будет нашей задачей. Решение кроется в самом определении этой последовательности. Мы заведем один мутабельный массив, в который будем сохранять промежуточные результаты вычисления чисел Фибоначчи, т.е. те самые n-1 и n-2.

Псевдокод:

int numberForIndex(int index) {

   int[] numbers = [0, 1]; // мутабельный массив, можем добавлять к нему элементы

    for (int i = 2; i < index + 1; i++) {
        numbers[index] = numbers[i - 1] + numbers[i - 2];
    }

    return numbers[index];
}

→ Пример решения на Objective-C

→ Тесты

Вот и всё, в этом массиве numbers вся соль ДП, это своего рода кэш (Caсhe), в который мы складываем предыдущие результаты вычисления этой же задачи, только на меньшей размерности (n-1 и n-2), что дает нам возможность за одно действие найти решение для размерности n.

Этот алгоритм работает за O(n), но использует немного дополнительной памяти — наш массив.

Вернемся к нахождению длины максимальной возрастающей подпоследовательности.

Решение за O( n ^ 2)

Рассмотрим следующую возрастающую подпоследовательность:

5, 6, 12

теперь взглянем на следующее число после последнего элемента в последовательности — это 3.

Может ли оно быть продолжением нашей последовательности? Нет. Оно меньше чем 12.

А 24 ?

Оно да, оно может.

Соответственно длина нашей последовательности равна теперь 3 + 1, а последовательность выглядит так:

5, 6, 12, 24

Вот где переиспользование предыдущих вычислений: мы знаем что у нас есть подпоследовательность 5, 6, 12, которая имеет длину 3 и теперь нам легко добавить к ней 24. Теперь у вас есть ощущение того, что мы можем это использовать, только как?

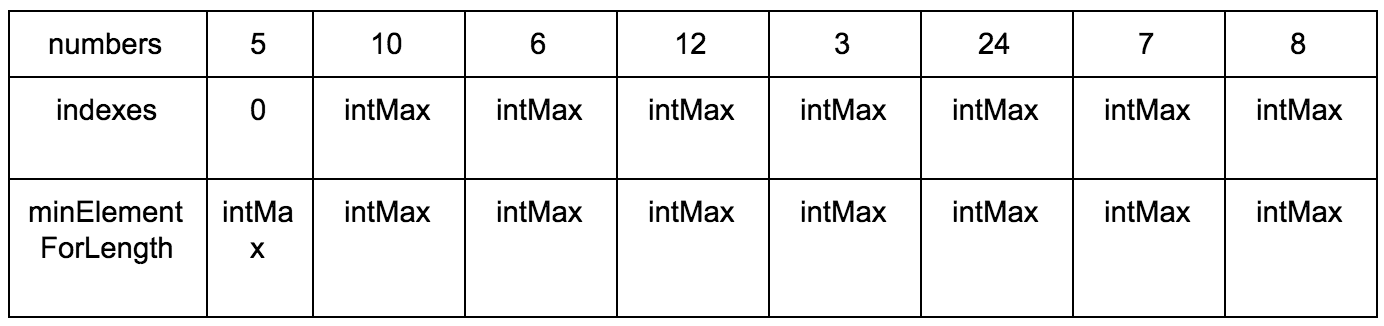
Давайте заведем еще один дополнительный массив (вот он наш cache, вот оно наше ДП), в котором будем хранить размер возрастающей подпоследовательности для n-го элемента.

Выглядеть это будет так:

Наша задача — заполнить массив counts правильными значениями. Изначально он заполнен единицами, так как каждый элемент сам по себе является минимальной возрастающей подпоследовательностью.

“Что за загадочные i и j?” — спросите вы. Это индексы итераторов по массиву, которые мы будем использовать. Изменяться они будут с помощью двух циклов, один в другом. i всегда будет меньше чем j.

Сейчас j смотрит на 10 — это наш кандидат в члены последовательностей, которые идут до него. Посмотрим туда, где i, там стоит 5.

10 больше 5 и 1 <= 1, counts[j] <= counts[i]? Да, значит counts[j] = counts[i] + 1, помните наши рассуждения в начале?

Теперь таблица выглядит так.

Смещаем j.

Результат:

Имея перед глазами эту таблицу и понимая какие шаги нужно делать, мы теперь легко можем реализовать это в коде.

int longestIncreasingSubsequenceLength( int numbers[]  ) {

    if (numbers.count == 1) {
        return 1;
    }

   int lengthOfSubsequence[] = Аrray.newArrayOfSize(numbers.count, 1);

    for (int j = 1; j < numbers.count; j++) {
        for (int k = 0; k < j; k++) {
            if (numbers[j] > numbers[k]) {
                if (lengthOfSubsequence[j] <= lengthOfSubsequence[k]) {
                 lengthOfSubsequence[j] = lengthOfSubsequence[k] + 1;
                }
            }
        }
    }

    int maximum = 0;

    for (int length in lengthOfSubsequence) {
        maximum = MAX(maximum, length);
    }

    return maximum;
}

→ Реализация на Objective-C
→ Тесты

Вы не могли не заметить два вложенных цикла в коде, а там где есть два вложенных цикла проходящих по одному массиву, есть и квадратичная сложность O(n^2), что обычно не есть хорошо.

Теперь, если вы билингвал, вы несомненно зададитесь вопросом “Can we do better?”, обычные же смертные спросят “Могу ли я придумать алгоритм, который сделает это за меньшее время?”

Ответ: “да, можете!”

Чтобы сделать это нам нужно вспомнить, что такое бинарный поиск.

Бинарный поиск O(log n)

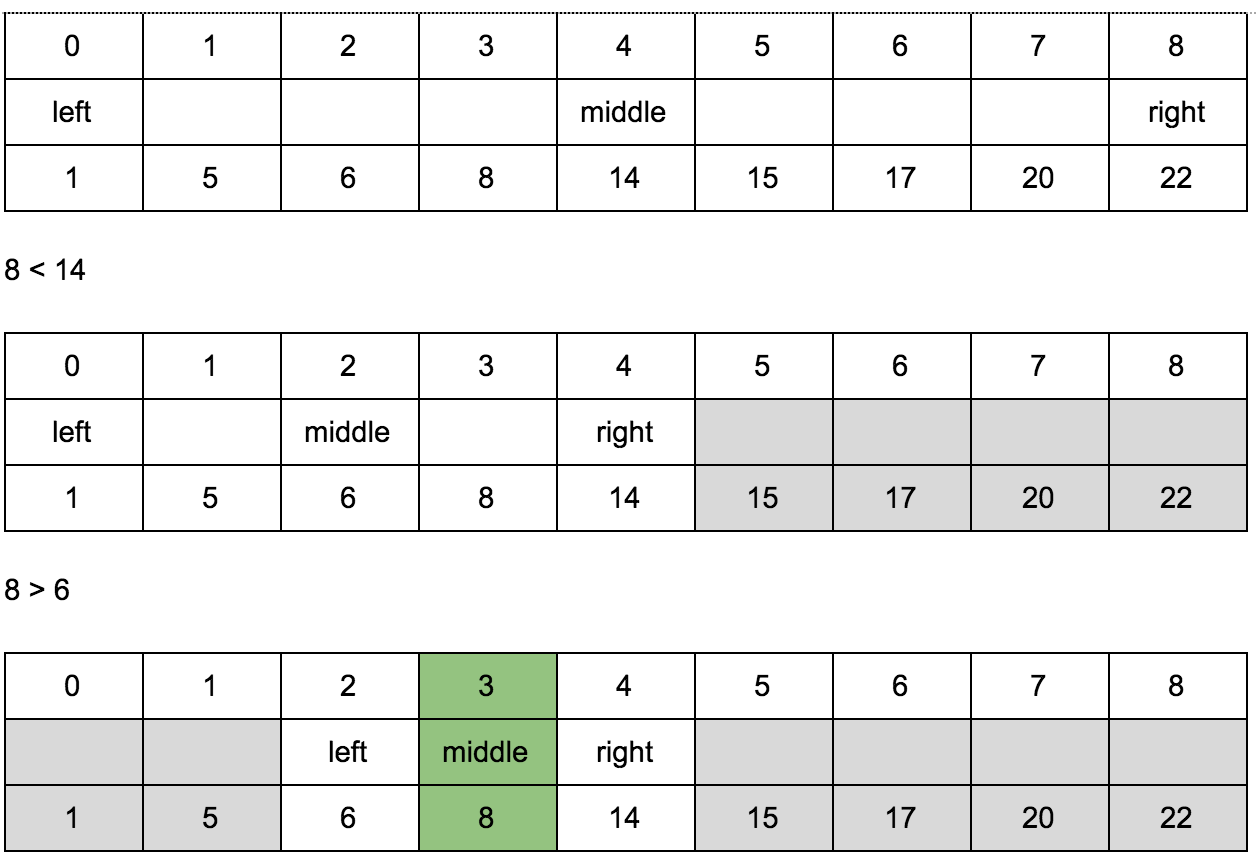
Бинарный поиск работает только на отсортированных массивах. Например, нам нужно найти позицию числа n в отсортированном массиве:
1, 5, 6, 8, 14, 15, 17, 20, 22

Зная что массив отсортирован, мы всегда можем сказать правее или левее определенного числа в массиве искомое число должно находиться.

Мы ищем позицию числа 8 в этом массиве. С какой стороны от середины массива оно будет находиться? 14 — это число в середине массива. 8 < 14 — следовательно 8 левее 14. Теперь нас больше не интересует правая часть массива, и мы можем ее отбросить и повторять ту же самую операцию вновь и вновь пока не наткнемся на 8. Как видите, нам даже не нужно проходить по всем элементам массива, сложность этого алгоритма < O( n ) и равна O (log n).

Для реализации алгоритма нам понадобятся 3 переменные для индексов: left, middle, right.

Ищем позицию числа 8.

Мы отгадали где находится 8 с трёх нот.

int binarySearch(int list [], int value) {

    if !list.isEmpty {
        int left = list.startIndex
        int right = list.endIndex-1

        while left <= right {

            let middle = left + (right - left)/2

            if list[middle] == value{
                return middle
            }

            if value < list[middle]{
                right = middle - 1
            }
            else{
                left = middle + 1
            }
        }
    }
    return nil
}

Решение за O (n * log n)

Теперь мы будем проходить по нашему исходному массиву при этом заполняя новый массив, в котором будет храниться возрастающая подпоследовательность. Еще один плюс этого алгоритма: он находит не только длину максимальной возрастающей подпоследовательности, но и саму подпоследовательность.

Как же двоичный поиск поможет нам в заполнении массива подпоследовательности?

С помощью этого алгоритма мы будем искать место для нового элемента в вспомогательном массиве, в котором мы храним для каждой длины подпоследовательности минимальный элемент, на котором она может заканчиваться.

Если элемент больше максимального элемента в массиве, добавляем элемент в конец. Это просто.

Если такой элемент уже существует в массиве, ничего особо не меняется. Это тоже просто.

Что нам нужно рассмотреть, так это случай когда следующий элемент меньше максимального в этом массиве. Понятно, что мы не можем его поставить в конец, и он не обязательно вообще должен являться членом именно максимальной последовательности, или наоборот, та подпоследовательность, которую мы имеем сейчас и в которую не входит этот новый элемент, может быть не максимальной.

Все это запутанно, сейчас будет проще, сведем к рассмотрению 2-х оставшихся случаев.

1. Рассматриваемый элемент последовательности (x) меньше чем наибольший элемент в массиве (Nmax), но больше чем предпоследний.
2. Рассматриваемый элемент меньше какого-то элемента в середине массива.

В случае 1 мы просто можем откинуть Nmax в массиве и поставим на его место x. Так как понятно, что если бы последующие элементы были бы больше чем Nmax, то они будут и больше чем x — соответственно мы не потеряем ни одного элемента.

Случай 2: для того чтобы этот случай был нам полезен, мы заведем еще один массив, в котором будем хранить размер подпоследовательности, в которой этот элемент является максимальным. Собственно этим размером и будет являться та позиция в первом вспомогательном массиве для этого элемента, которую мы найдем с помощью двоичного поиска. Когда мы найдем нужную позицию, мы проверим элемент справа от него и заменим на текущий, если текущий меньше (тут действует та же логика как и в первом случае)

Не расстраивайтесь, если не все стало понятно из этого текстового объяснения, сейчас я покажу все наглядно.

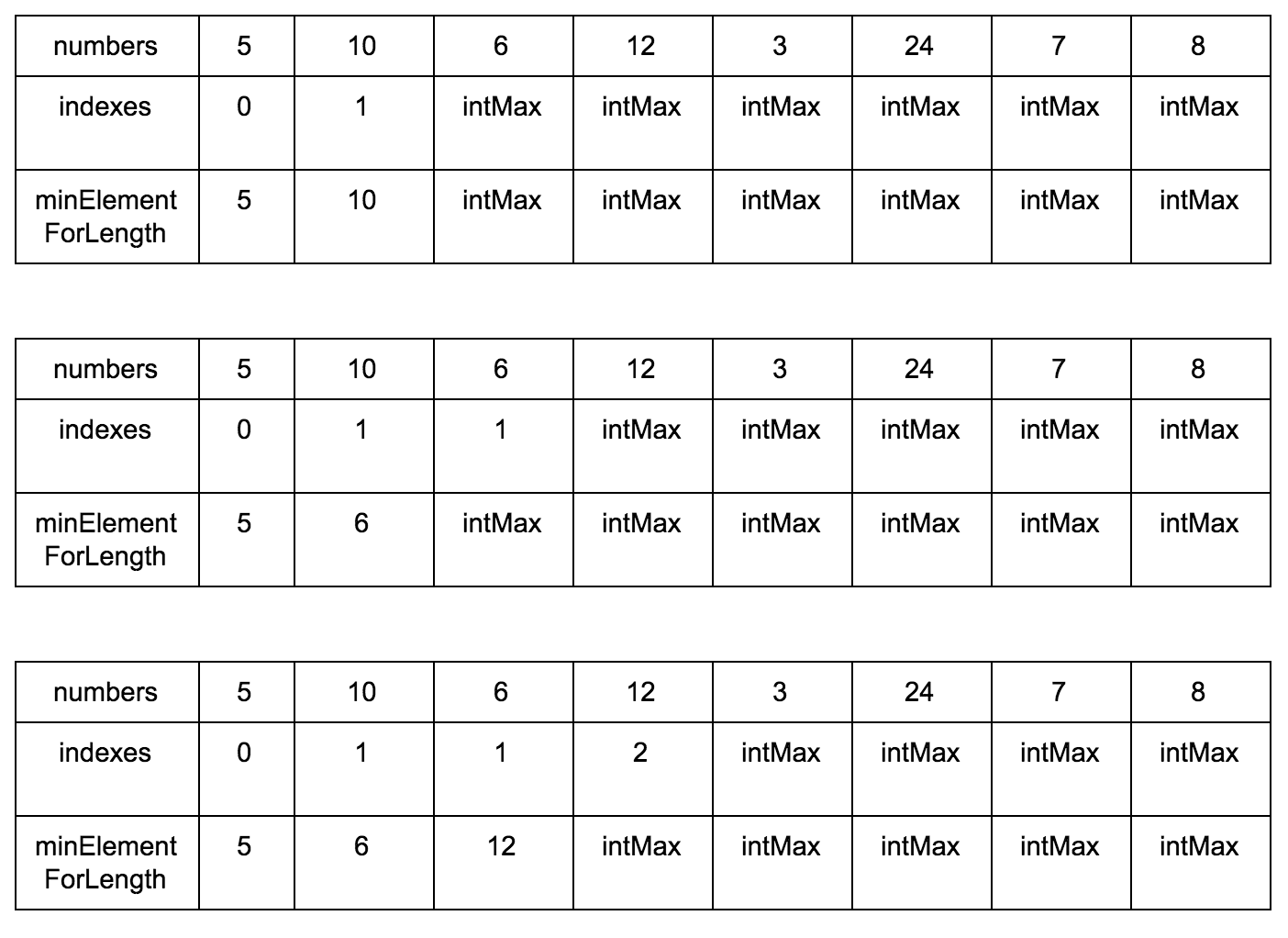
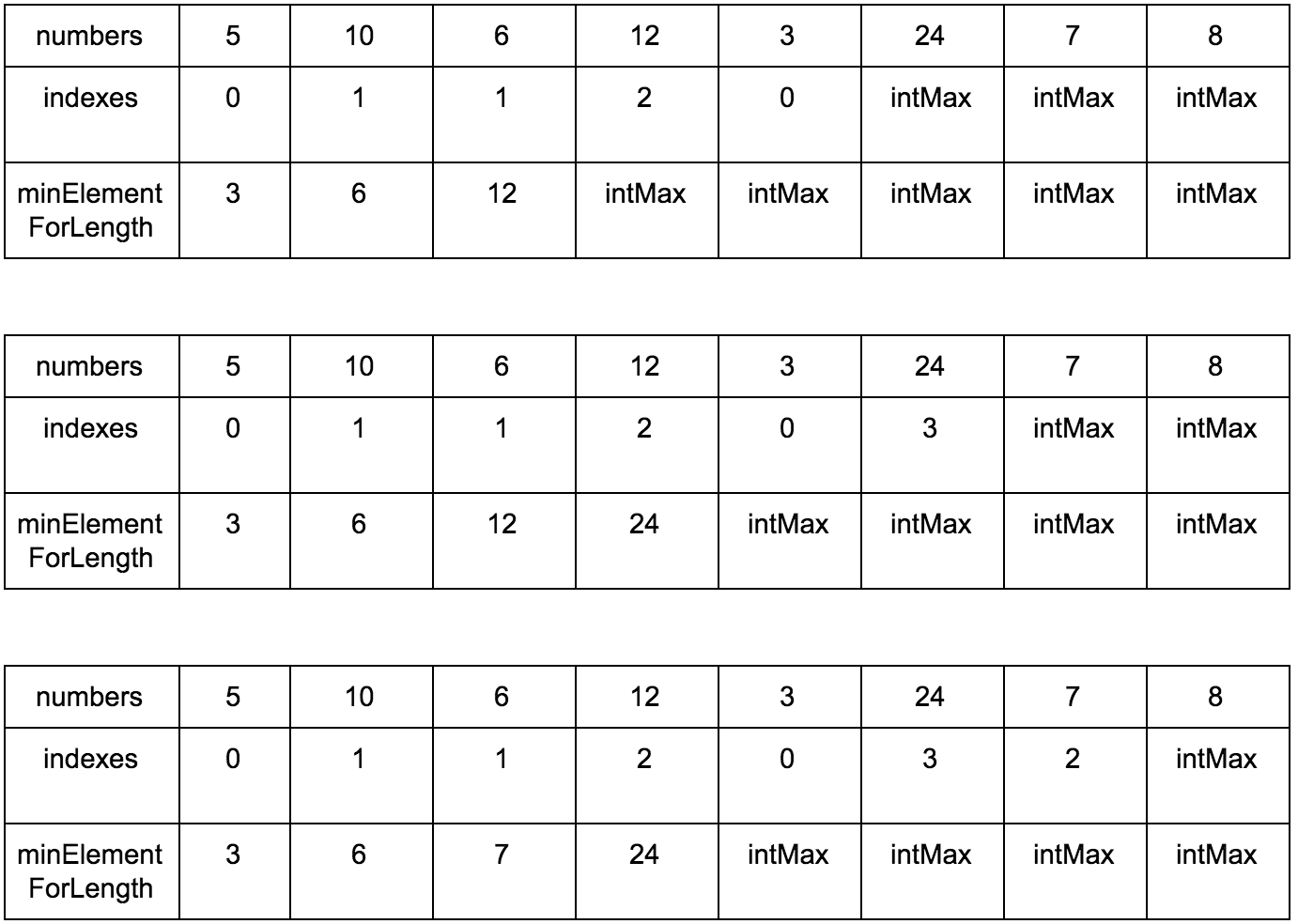
Нам нужны:

1. Исходная последовательность
2. Создаем мутабельный массив, где будем хранить возрастающие элементы для подпоследовательности
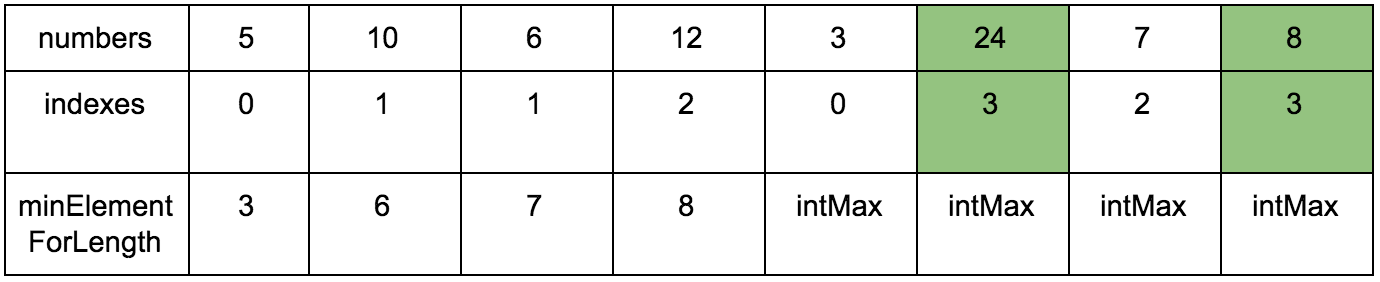
3. Создаем мутабельный массив размеров подпоследовательности, в которой рассматриваемый элемент является максимальным.

Результат:

int longestIncreasingSubsequenceLength(int numbers[]) {

    if (numbers.count <= 1) {
        return 1;
    }

    int lis_length = -1;

    int subsequence[];
    int indexes[];

    for (int i = 0; i < numbers.count; ++i) {
        subsequence[i] = INT_MAX;
        subsequence[i] = INT_MAX;
    }

    subsequence[0] = numbers[0];
    indexes[0] = 0;

    for (int i = 1; i < numbers.count; ++i) {
        indexes[i] = ceilIndex(subsequence, 0, i, numbers[i]);

        if (lis_length < indexes[i]) {
            lis_length = indexes[i];
        }
    }

    return lis_length + 1;
}

int ceilIndex(int subsequence[], 
              int startLeft, 
              int startRight,
              int key){

    int mid = 0;
    int left = startLeft;
    int right = startRight;
    int ceilIndex = 0;
    bool ceilIndexFound = false;

    for (mid = (left + right) / 2; left <= right && !ceilIndexFound; mid = (left + right) / 2) {
        if (subsequence[mid] > key) {
            right = mid - 1;
        }
        else if (subsequence[mid] == key) {
            ceilIndex = mid;
            ceilIndexFound = true;
        }
        else if (mid + 1 <= right && subsequence[mid + 1] >= key) {
            subsequence[mid + 1] = key;
            ceilIndex = mid + 1;
            ceilIndexFound = true;
        } else {
            left = mid + 1;
        }
    }

    if (!ceilIndexFound) {
        if (mid == left) {
            subsequence[mid] = key;
            ceilIndex = mid;
        }
        else {
            subsequence[mid + 1] = key;
            ceilIndex = mid + 1;
        }
    }

    return ceilIndex;
}

→ Реализация на Objective-C
→ Тесты

Итоги

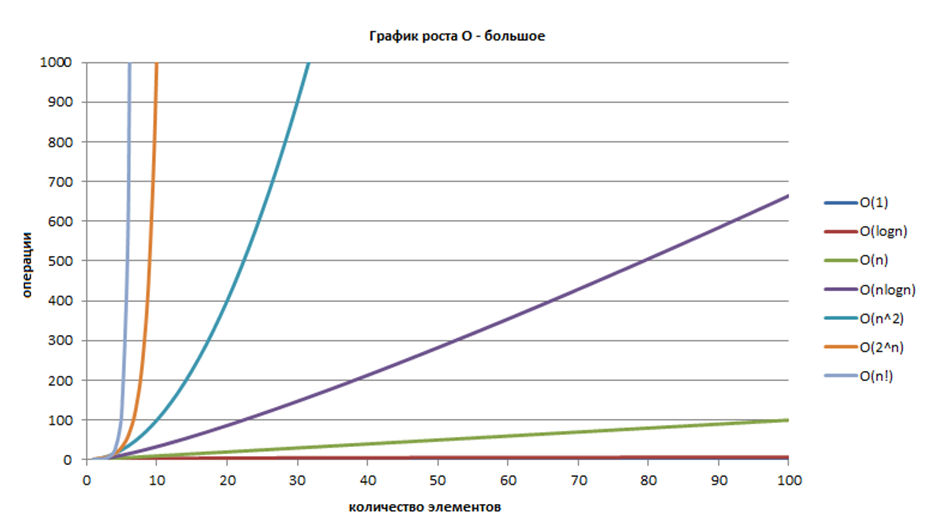
Мы с вами сейчас рассмотрели 4 алгоритма разной сложности. Это сложности, с которыми вам приходится встречаться постоянно при анализе алгоритмов:

О( log n ), О( n ), О( n * log n ), О( n ^ 2 )

Эта картинка из вот этой статьи

Еще мы рассмотрели примеры использования Динамического Программирования, тем самым расширив наш инструмент разработки и понимания алгоритмов. Эти принципы пригодятся вам при изучении других проблем.

Для лучшего понимания я рекомендую вам закодировать эти проблемы самим на привычном вам языке. А еще было бы здорово, если бы вы запостили ссылку на ваше решение в комментах.

Еще предлагаю подумать над тем как доработать последний алгоритм за O (n * log n ) так чтобы вывести еще и саму наибольшую подпоследовательность. Ответ напишите в комментах.

Всем спасибо за внимание, до новых встреч!

Ссылки:
Вопрос на Stackoverflow.com
Примеры реализации на C++ и Java
Видео с объяснением