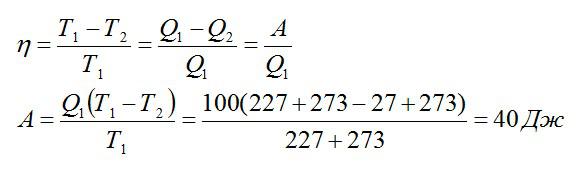В этой статье рубрики «физика для чайников» рассмотрим подробное решение нескольких задач на работу в термодинамике. Тем, кто хочет научиться решать задачи, рекомендуем систематически тренироваться, предварительно ознакомившись с теорией. А еще, полезно почитать памятку по решению физических задач и держать под рукой основные физические формулы.
Чтобы не заскучать, подписывайтесь на наш телеграм-канал. Там вас ждет ежедневная рассылка, которая будет полезна всем учащимся.
Примеры решения задач на работу в термодинамике
Задача №1. Работа расширения
Условие
При адиабатическом расширении 1 кг воздуха его объем увеличился в 10 раз. Найти работу расширения, если начальное давление 1 атм, а начальная температура 15 °С.
Решение
Зная молярную массу воздуха (29 г/моль), начальный объем можно найти из уравнения Клапейрона-Менделеева:
Не забываем переводить все физические величины из условия в систему СИ.
Из условия находим конечный объем:
Работа равна:
Ответ: 751 кДж.
Задача №2. Работа в цикле Карно
Условие
Температура нагревателя идеальной тепловой машины составляет 227 °С, а охладителя — 27 °С. За один рабочий цикл тепловая машина получает количество теплоты, равное 100Дж. Какую работу совершает рабочее тело идеальной тепловой машины за один цикл?
Решение
Из формулы для КПД можно выразить искомую работу:
Ответ: 40 Дж.
Задача №3. Работа при выдувании мыльного пузыря
Условие
Определить работу, которую необходимо совершить, чтобы выдуть мыльный пузырь диаметром 10 см.
Решение
Работа, которую нужно совершить, чтобы, выдувая мыльный пузырь, увеличить площадь поверхности мыльной пленки на дельта S, равна:
Здесь сигма – коэффициент поверхностного натяжения для мыльного раствора (берется из таблицы). S – общая площадь двух сферических поверхностей пленки мыльного пузыря (внешней и внутренней). S нулевое – площадь этих поверхностей до выдувания пузыря (этой величиной можно пренебречь).
Ответ: 2,5 мДж.
Задача №4. Графическое представление работы
Условие
Газ расширяется от объёма V1 до объёма V2 один раз изотермически, другой изобарно и третий адиабатно. При каком процессе газ совершает большую работу и при каком газу передаётся большее количество теплоты?

Решение
Работа численно равна площади криволинейной трапеции. Из рисунка очевидно, что работа при изобарном процессе будет максимальной, при адиабатном минимальной, т. е.
Ответ: см. выше.
Задача №5. Работа газа
Условие
Газ совершает круговой процесс, состоящий из нескольких этапов. Сначала газ изохорно охлаждается до температуры, при которой его давление равно P2 = 105 Па. Затем он изобарно охлаждается до состояния, из которого возвращается в начальное состояние таким образом, что его давление изменяется с изменением объема по закону Р = αV (α – постоянная величина). Начальные объем и давление газа известны: V1 = 2 м3, Р1 = 4·105 Па. Нарисовать график данного кругового процесса на РV-диаграмме и найти работу, совершенную газом.
Решение
Сначала выполним рисунок:
Точки состояния газа 1 и 3 лежат на прямой, проходящей через центр координат:
C учетом этого, получаем:
Работа газа в данном случае равна площади треугольника 123:
Подставим найденное ранее значение для V3, преобразуем и подставим значения из условия:
Ответ: 2,25*10^5 Дж.
Вопросы на тему «Работа в термодинамике»
Вопрос 1. Что такое работа в термодинамике?
Ответ. Работа – одна из форм обмена энергией термодинамической системы с окружающими телами. Работа, как и энергия, измеряется в Джоулях.
Вопрос 2. Сформулируйте первое начало термодинамики.
Ответ. Первое начало термодинамики гласит:
Изменение внутренней энергии системы равно сумме совершаемой над системой работы внешних сил и количества теплоты, переданной системе.
У первого начала термодинамики исторически есть несколько формулировок. Одна из них: невозможно построить вечный двигатель первого рода.
Вопрос 3. При каком из изопроцессов работа газа равна нулю?
Ответ. При изохорном процессе объем системы остается неизменным. Следовательно, газ в данном процессе не совершает работу.
Вопрос 4. Как, совершая работу, можно изменить внутреннюю энергию?
Ответ. Если работа совершается над телом (системой), то его внутренняя энергия увеличивается, если же тело само совершает работу, это ведет к уменьшению его внутренней энергии.
Вопрос 5. Как определить работу газа геометрически?
Ответ. Величина работы газа равна площади фигуры под графиком на диаграмме pV
Нужна помощь в решении задач или в выполнении других студенческих заданий? Обращайтесь в профессиональный студенческий сервис.
Примеры решения задач
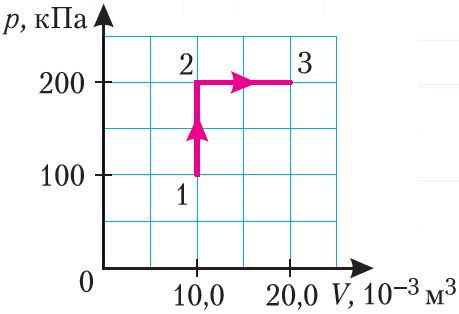
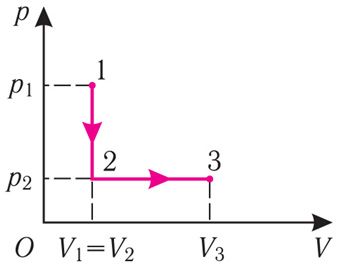
Пример 1. Определите работу, совершаемую силой давления идеального газа определённой массы при переходе из состояния 1 в состояние 3 (рис. 73).
Решение. I способ. Работа А газа в ходе всего процесса равна сумме работ на участках 12 и 2
3. Поскольку при переходе газа из состояния 1 в состояние 2 его объём не изменяется (изохорный процесс V2 = V1), то работа, совершаемая силой давления газа, А12 = 0. В процессе изобарного расширения (переход газа из состояния 2 в состояние 3) сила давления газа совершает работу
A23 = p2ΔV = p2(V3 – V1).
Тогда при переходе из состояния 1 в состояние 3 работа
А = А12 + А23 = p2(V3–V1).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
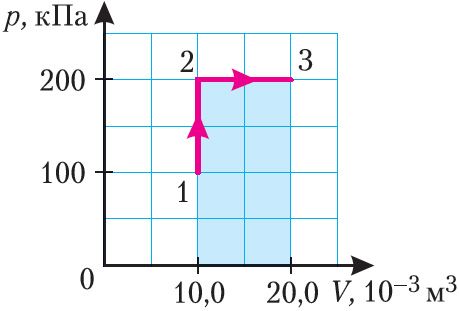
II способ. Работа газа численно равна площади заштрихованной фигуры, ограниченной графиком зависимости давления от объёма, осью ОV и прямыми, соответствующими значениям объёма V1 = 10,0 · 10–3 м3 и V2 = 20,0 · 10–3 м3 (закрашенная область на рисунке 74).
А = 2,00 · 105 Па · (2,00 · 10–2 м3 – 1,00 · 10–2 м3) = 2,00 · 103 Дж = 2,00 кДж.
Ответ: А = 2,00 кДж.
Пример 2. Определите работу, совершаемую силой давления идеального газа определённой массы при изобарном повышении его температуры от t1 = 12 °С до t2 = 87 °С, если давление газа p = 190 кПа, а его начальный объём V1 = 6,0 дм3.
Дано:
Т1 = 285 К
Т2 = 360 К
p = 190 кПа = 1,90 · 105 Па
V1 = 6,0 дм3 = 6,0 · 10–3 м3
А — ?
Решение: Сила давления газа совершает положительную работу, поскольку при изобарном нагревании увеличивается его объём. Поэтому
.
Согласно уравнению Клапейрона–Менделеева, и
. Следовательно,
.
.
Ответ: .
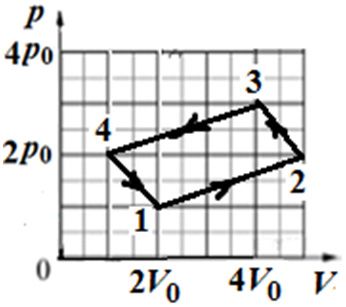
Пример 3. На рисунке 74.1 изображен процесс изменения состояния идеального газа определённой массы. На каком участке сила давления газа совершила наименьшую положительную работу? На каком участке внешняя сила совершила наибольшую положительную работу?
Решение. Работе силы давления газа соответствует площадь под графиком процесса. При расширении газа сила давления совершает положительную работу, а внешняя сила — отрицательную. При сжатии газа наоборот: сила давления совершает отрицательную работу, а внешняя сила — положительную. Анализ графика позволяет сделать вывод, что в процессе перехода из состояния 4 в состояние 1 сила давления газа совершила минимальную положительную работу (газ расширялся, а площадь под графиком минимальна). Максимальную же положительную работу внешняя сила совершает при сжатии, когда площадь под графиком максимальна (это процесс перехода из состояния 3 в состояние 4).
Пример 4. Состояние идеального газа, взятого в количестве ν = 1,0 моль при абсолютной температуре Т1 = 300 К, изменяется так, как изображено на рисунке 74.2. Определите работу газа в ходе всего процесса, если на изохоре 12 его давление уменьшается в три раза, а точки 1 и 3 лежат на одной изотерме.
Дано:
ν = 1,0 моль
Т1 = 300 К
p1 = 3p2
Т1 = Т3
A – ?
Решение: Работа А газа в ходе всего процесса равна сумме значений работы на участках 12 и 2
3 (рис. 74.2). Так как при переходе из состояния 1 в состояние 2 объём газа не меняется (процесс изохорный V2 = V1), то работа газа А12 = 0. Давление газа при переходе из состояния 2 в состояние 3 остаётся постоянным (р2 = р3), следовательно, работа газа А23 = p2(V3 − V1). Тогда А = А12 + А23 = p2(V3 − V1). Так как по условию Т1 = Т3, то воспользуемся уравнением Клапейрона:
, откуда
. Следовательно,
.
Согласно уравнению Клапейрона‒Менделеева, p1V1 = νRT1. Тогда .
Ответ: А = 1,7 кДж.
Речь в статье пойдет о КПД различных циклов, проводимых с газом. При этом давайте помнить, что внутренняя энергия изменяется тогда, когда изменяется температура, а в адиабатном процессе передачи тепла не происходит, то есть для совершения работы в таком процессе газ “изыскивает внутренние резервы”. Кроме того, работа численно равна площади под кривой процесса, а работа за цикл – площади внутри цикла.
Задача 1.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом. Участки и
– адиабаты. Вычислите КПД
данной тепловой машины и максимально возможный КПД
.
К задаче 1
КПД тепловой машины можно вычислить как
Машина получает тепло только на участке AB, и, так как работы здесь не совершается, то можно вычислить количество теплоты, полученное газом, как увеличение его внутренней энергии:
Работа численно равна площади, ограниченной циклом. Поэтому
Участк и
по условию – адиабаты, то есть передачи тепла газу на этих участках не происходит, следовательно, работа будет совершена за счет «внутренних резервов» – то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и
,
и
, это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать
. Но, так как
, а
,то изменение внутренней энергии будет равно
Определим максимальный КПД. Посчитаем его как КПД цикла Карно. Максимальная температура газа будет достигнута в точке , а минимальная – в точке
:
Ответ: ,
.
Задача 2.
Над идеальным одноатомным газом проводят цикл, включающий изобару, изохору, изотерму, при этом работа газа за цикл равна кДж. В процессе изотермического сжатия (3-1) внешние силы совершают над газом положительную работу
кДж. Найдите КПД данной тепловой машины.
К задаче 2
Работа газа в процессе 1-2– площадь под линией процесса 1-2. Работа внешних сил – площадь под циклом (под линией 3-1). Поэтому полная работа за цикл – это разность работы газа и работы внешних сил, площадь, ограниченная линиями цикла. Она будет равна 5 кДж.
Работа газа в процессе 1-2, таким образом, равна 8 кДж. А поскольку процесс изобарный, то кДж. Тогда КПД
Ответ: .
Задача 3.
КПД тепловой машины, работающей по циклу, включающему изотермический (1-2) и адиабатный (3-1) процессы, равен , причем работа, совершенная 2 моль одноатомного идеального газа в изотермическом процессе
кДж. Найдите разность
максимальной и минимальной температур газа в цикле.
К задаче 3
Полная площадь под кривой процесса 1-2 равна кДж. При этом, так как КПД машины 25%, то площадь внутри цикла равна
, а под кривой 3-1 –
. В процессе 1-2 изменения внутренней энергии не было, так как температура не менялась, а в процессе 3-1 газу не передавали тепло, следовательно, работа совершена за счет внутренней энергии. Т.е.
Ответ: 500 K.
Тема: Максимальная работа газа за цикл (Прочитано 20641 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Vlad1
Добрый вечер! У меня есть вопрос по задаче:
Тепловая машина работает с одним модем идеального газа по циклу из двух изохор и двух адиабат. Температура нагревателя t1, холодильника t2. Найти максимальную работу за цикл.
Нашел КПД,работу выразил но есть лишние переменные
« Последнее редактирование: 13 Февраля 2012, 06:32 от alsak »
Записан
И где ваш вопрос?
Вы никогда не решали задачи с лишними данными? Если хотите, что бы проверили ваше решение – выложите его. Например, сделайте фотоснимок (только уменьшите размер файла до 200-300 кб).
Записан
Vlad1
Кпд n=1-t2/t1 – получено через рассмотрение теплоты на каждом участке и уравнения адиабаты. Умножаю на всю полученную теплоту Q 3/2R(t4-t1) где t4 температура в “конце” адиабаты. Она лишняя,, но убрать ее мне кажется нельзя.
Записан
Цикл из двух изохор и двух адиабат на рис. 1. Так как это не цикл Карно (две адиабаты и две изотермы), то применять формулы Карно нельзя. Если рассмотреть все процессы и найти КПД двигателя, то он будет зависеть от четырех температур, а не от двух (и мне не понятно, как вы получили свою формулу для КПД).
Не совсем понятен вопрос о работе. О какой максимальной работе идет речь: о работе при адиабатном расширении или о полезной работе? И здесь для расчета работы нужно знать четыре температуры.
Посмотрите внимательно, полностью ли вы выложили условие на форум? Укажите книгу с которой вы взяли задачу.
Записан
Vlad1
Адиабата 1-2 Q=0
Изохора 2-3 Q=Cv(t3-t2)=3/2R(t3-t2) – т.к одноатомный газ
Адиабата 3-4 Q=0
Изохора 4-1 Q=Cv(t4-t1)=3/2R(t4-t1)
Уравнение адиабаты связывает температуры 1-2 и 3-4 с объемами
Тогда Кпд 3/2R(t3-t2)-3/2R(t4-t1)/3/2R(t3-t2)=1-(t4-t1)/(t3-t2) так как объемы v3=v2, v4=v1,то объемы в степенях адиабатических коэффициентов относятся как температуры или
t1V1#=t2V2#и t3V2#=t4V1#. где # – адиабатический коэффициент. Отнимаем от верхнего нижнее, получаем (t4-t1)/(t3-t2)=(V2/V1)#=t1/t2, подставляем в формулу кпд, умножаем на всю теплоту.Но там t4 стоит, вот в чем вопрос.)
Я думаю имеется в виду полезная работа.
Да,и ответ А=3/2RT1(1-(T2/T1)1/2)2 – где 1/2 – степень (T2/T1), а 2 – степень (1-(T2/T1)1/2)
« Последнее редактирование: 13 Февраля 2012, 18:06 от Vlad1 »
Записан
т.к одноатомный газ
Ваше решение посмотрю позже, но сразу возникает вопрос: покажите в условии, где вы это прочитали?
И еще
t1V1#=t2V2#и t3V2#=t4V1#. где # – адиабатический коэффициент
с трудом можно сообразить, что вы написали.
Почитайте Помощь и оформляйте задачи по правилам так, чтобы это было понятно всем.
« Последнее редактирование: 13 Февраля 2012, 18:41 от alsak »
Записан
(t4-t1)/(t3-t2)=(V2/V1)#=t1/t2
И здесь не понятно: в вашей формуле обозначения температур соответствуют графику, изображенному на рис. 1 (см. выше). А вы уверены, что температура T2 по условию (температура холодильника) – это температура точки 2 на графике?
Дальнейший разговор будет после того, как вы укажите первоисточник: книгу, из которой взяли задачу.
« Последнее редактирование: 13 Февраля 2012, 19:13 от alsak »
Записан
Vlad1
Извините,я случайно пропустил одноатомный,
Источник – задавальник МФТИ ФОПФ. нулевая группа – соответствует школьному уровню (ну может олимпиадно-школьному).Да температуры нагревателя и холодильника не те что на графике, честно говоря не знаю как тут выкрутиться)
Записан
Выложите фотографию условия задачи.
И укажите точнее данные книги: автор, название, год издания, номер задачи.
Записан
Vlad1
Задавальник – это книжка, в которой собраны все задачи (или их номера в соот-щих учебниках) которые студент должен решить за семестр.Эта задача приведена без сноски, то есть прямым текстом. Печатается каждый год заново и раздается навсегда в начале семестра.
Записан
Внутренняя энергия газа может изменяться в результате совершения газом работы и сообщения ему теплоты. Поэтому принято говорить о двух формах передачи энергии от одних тел к другим: о теплоте и работе.
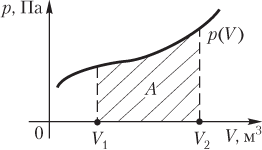
Работа газа при произвольном процессе рассчитывается как площадь криволинейной трапеции под графиком p(V). На рис. 6.1 показана произвольная зависимость давления газа p от его объема V (объем газа в начальном состоянии V 1; объем газа в конечном состоянии V 2). Площадь заштрихованной фигуры совпадает с работой, совершенной газом.
Если зависимость p(V) представляет собой прямую линию, то работа численно равна площади прямолинейной трапеции.
В Международной системе единиц работа, совершаемая газом, измеряется в джоулях (1 Дж).
Работа газа при изобарном процессе (p = const) может быть вычислена по одной из формул:
A = p∆V, или A = νR∆T,
где p — давление газа; ΔV — изменение объема газа при переходе из начального в конечное состояние, ΔV = V 2 − V 1; V 1 — объем газа в начальном состоянии; V 2 — объем газа в конечном состоянии; ν — количество вещества (газа); R — универсальная газовая постоянная, R ≈ 8,31 Дж/(моль ⋅ К); ΔT — соответствующее изменение температуры газа, ΔT = T 2 − T 1; T 1 — абсолютная температура начального состояния; T 2 — абсолютная температура конечного состояния.
Работа газа при изохорном процессе (V = const) не совершается:
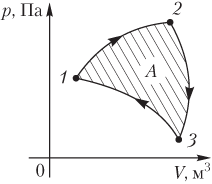
Работа газа при круговом (циклическом) процессе рассчитывается как площадь фигуры, ограниченной графиком функции p(V). На рис. 6.2 показан график произвольного кругового процесса; цифрами обозначены: 1 — исходное состояние идеального газа (оно совпадает с конечным); 2, 3 — промежуточные состояния газа.
Площадь заштрихованной фигуры совпадает с работой, совершенной газом при циклическом процессе.
Работа, совершаемая газом за цикл, может быть:
· положительной (прямой цикл);
· отрицательной (обратный цикл).
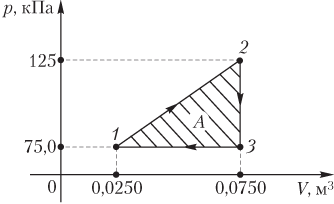
Пример 3. График циклического процесса, происходящего с некоторой массой идеального газа, в координатах p(V) имеет вид прямых, соединяющих точки (0,0250 м 3 ; 75,0 кПа), (0,0750 м 3 ; 125 кПа), (0,0750 м 3 ; 75,0 кПа). Определить абсолютную величину работы, совершаемой газом за цикл.
Решение. На рисунке изображен график циклического процесса в указанных термодинамических координатах p(V).
Величина искомой работы равна площади треугольника, ограниченного прямыми, соединяющими указанные точки:
A=12(125−75,0)⋅103⋅(0,0750−0,0250)=1,25⋅103 Дж=1,25 кДж.
Газ за цикл совершает работу 1,25 кДж.
Пример 4. Газ, состоящий из смеси 2,0 г водорода и 4,2 г гелия, при изобарном нагревании совершил работу 46 кДж. Во сколько раз увеличился объем газа, если его начальная температура была равна 300 К? Молярные массы водорода и гелия равны 2,0 и 4,0 г/моль соответственно.
Решение. Запишем формулу для расчета работы смеси газов при изобарном процессе:
где p — давление смеси газов (постоянная величина), p = const; V 1 — объем смеси газов в начальном состоянии; V 2 — объем смеси газов в конечном состоянии.
Давление смеси газов определяется законом Дальтона:
где p 1 — парциальное давление водорода; p 2 — парциальное давление гелия.
Давления указанных газов в смеси определяются следующими выражениями:
· парциальное давление водорода
где m 1 — масса водорода; M 1 — молярная масса водорода; T 1 — температура смеси газов в начальном состоянии; V 1 — объем смеси газов в начальном состоянии; R — универсальная газовая постоянная, R = 8,31 Дж/(моль ⋅ К);
· парциальное давление гелия
где m 2 — масса гелия; M 2 — молярная масса гелия.
Подстановка закона Дальтона и явного вида выражений для парциальных давлений водорода и гелия в формулу для работы, совершаемой смесью указанных газов, дает
Преобразование данного уравнения к виду
позволяет выразить искомое отношение объемов
Следовательно, при совершении указанной работы объем смеси увеличился в 10 раз.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9364 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Условие задачи:
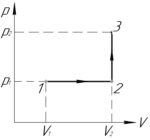
Задача №5.3.22 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
(V_1=2) л, (V_2=3) л, (p_1=400) кПа, (p_2=600) кПа, (A-?)
Решение задачи:
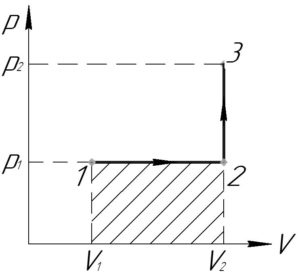
Процесс 1-2 — изобарный, поэтому работу газа (A_<1 — 2>) в этом процессе следует искать по такой формуле (численно работа равна площади фигуры под графиком процесса, на схеме к решению — заштриховано):
Процесс 2-3 — изохорный, работа газа (A_<2 — 3>) в этом процессе равна нулю, так как газ не изменяет своего объема (площадь фигуры под графиком этого процесса в координатах p-V также равна нулю).
В итоге формула (1) примет такой вид:
Переведём объемы газа (V_1) и (V_2) в систему СИ:
Ответ: 400 Дж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода.
Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
На диаграмме p—V работе, совершаемой газом при переходе из начального состояния в конечное, соответствует площадь под линией, изображающей процесс перехода. Для процесса 1—2—3 эта площадь показана на рисунке штриховкой. Таким образом, при переходе из состояния 1 в состояние 3 газ совершает работу
Поясните,почему умножение идет 2х10^5 ,когда газ совершает работу от 1 до 2, вроде должно быть 1х10^5,а по ответу получается от 0 до 2.
На участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется. Вся работа совершается на участке 2-3. Общее правило следующее, если процесс изображен на диаграмме , то работа равна площади под графиком со знаком плюс, если объем увеличивается, и со знаком минус, если уменьшается. Для тепловой машины, работающей по циклу, полезная работа равна площади ограниченной этим циклом, это укладывается в ранее озвученное правило. Когда мы идем по “верхней” части цикла, работа идет в +, потом возвращаемся по “нижней” в исходную точку, работа теперь идет в -, в результате остается только кусок внутри.
Алексей, вот Вы сказали, что “на участке 1-2 вообще не совершается работа, так как объем газа на этом этапе не изменяется.”
а на участке 2-3 ведь не меняется давление.Так почему работа там совершается? Разве не A=pV ?
Не, не так. Давайте разбираться.
Будем выводить формулу, по которой можно посчитать работу совершенную газом. Когда газ работает? Когда он что-то перемешает. Для этого должен как-то меняться его объем. Например, газ расширяется и толкает поршень вверх, а с ним и какой-то груз, вот Вам и работа. То есть без изменения объема нет работы.
Чтобы вывести формулу, рассмотрим модельную задачу. Рассмотрим цилиндрический сосуд с газом. Пусть сосуд закрыт подвижным поршнем площади . Давление газа равно
. Определим, какую работу совершит газ, когда поршень сдвинется на малое расстояние
. Так как это работа на малом перемещении, то назовем ее элементарной работой и обозначим через
. Работа газа равна произведению силы, с которой он давит на поршень, на перемещение поршня (газ давит нормально, поэтому косинуса не возникает):
. Но сила, с которой газ давит на поршень связана с давлением газа соотношением:
. Если перемещение поршня мало, то можно считать, что давление газа не изменяется сильно и что оно остается постоянным. Тогда:
. Но
— это как раз изменение объема газа
. Окончательно имеем:
.
Получив эту формулу, можно забыть о том, как она выводилась (про сосуд и поршень), она оказывается верной для любого малого изменения объема.
Теперь, чтобы найти работу на конечном изменении объема нужно просуммировать работы по малым изменения, в математике это делается при помощи интеграла: Если внимательно приглядеться, то тут можно как раз увидеть площадь под линией процесса на диаграмме
. Вот почему говорят, что для поиска работы надо искать площадь под графиком на этой диаграмме.
Для частных случаев формула приобретает вид:
1) при изобарном процессе давление выносится за знак интеграла и получаем:
2) при изохорном объем не изменяется, поэтому пределы интегрирования совпадают, интеграл равен нулю, работа равна нулю.
3) при изотермическом процессе, давление уже изменяется с объемом, поэтому надо добавить в рассмотрение уравнение Клапейрона-Менделеева: . Следовательно,
. А значит работа при изотермическом процессе равна: