Как найти максимальную силу действующую на точку

Содержание:

1. Динамика материальной точки
2. Прямая задача динамики точки
3. Основные законы динамики
4. Уравнения движения материальной точки в декартовых и естественных системах отсчета
5. Две основные задачи динамики материальной точки
6. Порядок решения прямой задачи динамики невольной материальной точки
7. Примеры решения задач на тему: Динамика материальной точки
8. Решение задач на тему: Движение материальной точки по криволинейной траектории

Динамика − раздел механики, в котором изучается движение тел под действием приложенных сил. Основной задачей динамики является определение кинематического уравнения движения материальной точки, если известны, приложенные силы к ней со стороны окружающих тел и начальные условия, положение и скорость тела в начальный момент времени.

На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.

Динамика материальной точки

Динамикой называется раздел теоретической механики, в котором изучается механическое движение материальных объектов в зависимости от физических факторов, то есть от причин, вызывающих это движение.

Напомним, что в классической механике движение материальных объектов рассматривается с помощью абстрактных моделей: материальной точки, механической системы и абсолютно твердого тела.

Материальная точка – это материальное тело, размерами и разницей в движении его частей которого можно пренебречь.

Механической системой (системой материальных точек) называется совокупность материальных точек, которые между собой взаимодействуют, то есть, положение и движение которых взаимосвязаны.

Абсолютно твердым телом называется совокупность материальных точек, расстояния между которыми во время движения не меняются.

Движение механической системы определяется движением всех его точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.

В динамике точки рассматриваются две основные задачи:

– движение точки задается, а необходимо найти силы, которые это движение реализуют (первая, или прямая задача);
– силы задаются, а необходимо определить закон движения, который является результатом действия этих сил.

Для решения этих задач используются базовые сведения из статики и кинематики, а также законы динамики, то есть, общие законы движения тел и механических систем под действием приложенных к ним сил. Эти законы впервые в наиболее полном виде сформулированы Исааком Ньютоном в конце XVII века.

Прямая задача динамики точки

Первая (прямая) задача динамики содержит условие: По заданному движению, совершаемому точкой данной массы, требуется найти неизвестную действующую силу.

Основные законы динамики

В динамике изучается движение материальных систем в связи с действующими на них силами. Самым простым объектом механики является материальная точка.

Материальная точка – тело, размерами которого при решении данной задачи можно пренебречь.

Если на положение материальной точки и на ее движение не наложены никакие ограничения, точка называется свободной, в противном случае имеем дело с движением несвободной точки.

Движение механической системы определяется движением всех ее материальных точек. Поэтому изучение динамики начинается с изучения движения одной материальной точки.

В основе динамики лежат три закона И. Ньютона, которые впервые в наиболее полном и законченном виде были сформулированы в книге “Математические начала натуральной философии” (1686 г.).

2. Второй закон (основной закон динамики):
cила, которая действует на материальную точку, равна произведению массы точки на ее ускорение, а направление силы совпадает с направлением ускорения:

Если на точку действует несколько сил, то их можно заменить равнодействующей:

Если точка движется по какой-то поверхности, то на нее, кроме активных сил действует и реакция связи .

Таким образом в общем случае в уравнении (1.1):

3. Третий закон (закон равенства действия и противодействия):
Силы взаимодействия двух материальных точек равны между собой по модулю и направлены вдоль одной прямой, которая соединяет эти точки, в противоположные стороны.

Уравнения движения материальной точки в декартовых и естественных системах отсчета

Вместо уравнения движения (1.1) в векторной форме можно получить уравнение в скалярной форме, если спроектировать (1.1) на оси декартовой или естественной систем координат.

Уравнение движения в декартовых координатах:

Здесь  – проекции силы на соответствующие декартовые оси координат;

 – проекции ускорения на те же оси.

Две основные задачи динамики материальной точки

Первая задача (прямая): зная массу точки и законы ее движения, например, в декартовых координатах:

определить равнодействующую приложенных к точке сил.

Сначала нужно определить проекции ускорения точки на оси координат:

Используя уравнение движения точки в декартовых координатах (1.3), определяем значения проекций равнодействующей приложенных к точке сил, а также ее модуль:

Направление вектора силы относительно осей координат определяется с помощью направляющих косинусов:

Вторая задача (обратная): зная силы, которые действуют на материальную точку, ее массу, а также первоначальные условия (положение точки и ее скорость в некоторые моменты времени, не обязательно в начальный), получить уравнение движения точки.

Порядок решения прямой задачи динамики невольной материальной точки

1. Изобразить на рисунке материальную точку в промежуточном положении.
2. Показать активные силы и реакции связей, которые на нее действуют.
3. Выбрать систему отсчета.
4. Записать векторное уравнение движения точки в форме второго закона динамики (1.1).
5. Спроектировать векторное уравнение движения точки на выделенные оси координат.
6. Из полученных уравнений определить необходимые величины.

Примеры решения задач на тему: Динамика материальной точки

Задача № 1

В шахту начинает опускаться равноускорено лифт, масса которого В первые 10 с он проходит 35 м.

Определить натяжение каната, на котором висит лифт.

Решение. Изобразим кабину лифта в произвольном положении (рис.1.1). На лифт действует сила тяжести , которая направлена вниз, и натяжение каната , который направлен вдоль троса вверх.

Движение происходит по вертикали, поэтому направим ось вертикально вниз в соответствии с направлением скорости и ускорения.

Запишем уравнение движения кабины лифта в форме второго закона Ньютона:

где  – ускорение кабины лифта.

С учетом сил, действующих на кабину лифта, уравнение будет иметь вид:

Спроектируем это уравнение на ось :

С учетом того, что , находим

Мы получили зависимость натяжения каната от ускорения, с которым движется кабина лифта.

Проанализируем эту зависимость. Может быть три случая:

В первом случае

То есть, если кабина лифта движется без ускорения в любом направлении, натяжение троса будет равняться силе тяжести кабины лифта.

Во втором случае натяжение троса меньше силы тяжести кабины лифта, потому что , а если , то 

В третьем случае натяжение троса всегда больше силы тяжести кабины лифта, потому что  и 

Например, когда  то есть натяжение троса вдвое превышает силу тяжести кабины лифта.

В нашей задаче ускорение определится с выражения для пути при равнопеременном движении с учетом того, что начальная скорость :

Тогда:

Ответ: натяжение троса 

Задача № 2

К телу весом которое лежит на столе, привязали нить, второй конец которой (рис.1.2) держат в руке.

Определить, с каким ускорением надо поднимать тело вверх вертикально, чтобы нить оборвалась, если она рвется когда натяжение достигает величины

Решение: Изобразим тело с привязанной к нему нитью (рис.1.2). Покажем силы, которые действуют на тело: сила тяжести и натяжение нити . Ось направляется по вертикали вверх в положительном направлении скорости и ускорения.

Запишем уравнение движения тела в векторной форме:

Спроектируем это уравнение на ось :

Откуда:

Если учесть числовые данные, то

Ответ: 

Задача № 3

Пуля весом падает вертикально вниз под действием силы тяжести и испытывает опору среды (рис.1.3). Закон движения шара соответствует уравнению , причем выражается в сантиметрах, – в секундах.

Определить силу сопротивления среды  в виде функции скорости, то есть

Решение. Изобразим шар в произвольном положении на траектории и покажем силы, которые на него действуют (рис.1.3):

 – сила тяжести;

– сила сопротивления среды.

Движение шара происходит вдоль вертикали, поэтому направим ось вертикально вниз по направлению скорости. Тогда положение шара будет определяться координатой .

Запишем уравнение движения шара в векторной форме:

и спроектируем его на ось :

откуда 

Таким образом, чтобы определить силу сопротивления , необходимо знать ускорение шара .

Поскольку закон изменения координаты известен, то

Находим первую и вторую производные от закона движения пули:

Таким образом,

Из выражения (с учетом того, что ) вытекает

то есть 

Ответ: 

Задача № 4

Движение тела массой выражается уравнениями:

где  и  – в метрах, а  – в секундах.

Определить силу , которая действует на тело, принимая его за материальную точку (рис.1.4).

Решение. Проекции на оси координат силы , которая приложена к телу, определяются по формулам:

где  и  – проекции ускорения тела на оси координат.

В данном случае

Итак

Модуль силы  равен:

Сила направлена вертикально вниз, поскольку Таким образом, искомая сила, модуль которой равен , является силой тяжести.

Ответ: 

Задача № 5

Прямолинейное движение ножа резального аппарата жатки зерноуборочного комбайна (рис.1.5) приближено выражается уравнением ( – в метрах; – в секундах).

Определить силу , которая приводит нож к движению, в зависимости от расстояния . Вес ножа

Объяснение: Для привода ножа резального аппарата жатки используются плоские и пространственные механизмы. Среди плоских механизмов нашли применение кривошипно-шатунные, которые состоят из кривошипа 1, шатуна 2 и ножа жатки 3. Механизм преобразует вращательное движение кривошипа 1 в обратно поступательное движение ножа 3.

В уборочных машинах ось кривошипного пальца находится выше линии движения ножа .

Решение. Изобразим нож резного аппарата в среднем положении на перемещении и покажем силы, которые действуют на него.

На нож действует сила веса , нормальная реакция опорной поверхности направляющих ножа и сила со стороны шатуна , которая вызывает движение ножа.

Запишем уравнение движения ножа в векторной форме:

Проектируем это уравнение на направление движения ножа (ось ):

 или 

Из последнего уравнения следует, что для определения силы необходимо знать ускорение .

Поскольку задан закон движения ножа : то ускорение определяется как вторая производная от закона движения по времени:

Итак, 

Учтем, что  и получим:

Ответ: 

Задача № 6

Нагруженная вагонетка массой опускается по канатной железной дороге с наклоном и имеет скорость (рис.1.6).

Определить натяжение каната при равномерном опускании и при торможении вагонетки, если время торможения , общий коэффициент сопротивления движению . При торможении вагонетка движется равнозамедленно.

Решение. Изобразим вагонетку в произвольном положении. Покажем силы, которые действуют на нее: силу тяжести , нормальную реакцию железной дороги , натяжение каната и силу сопротивления .

Выбираем декартовую систему координат: ось направим параллельно дороге в сторону движения; ось – вверх перпендикулярно дороге. Запишем векторное уравнение движения вагонетки в форме второго закона Ньютона:

Проектируем векторное уравнение движения на оси координат:

Поскольку все время движения вагонетки, то , и из уравнение (2) легко находим величину нормальной реакции:

Тогда общая сила сопротивления движению составляет:

Для определения натяжения  используем уравнение (1)

При равномерном опусканье и составит:

При равнозамедленном торможении 

где  – начальная скорость;

 – конечная скорость.

Таким образом 

Тогда

Ответ: 

Из полученных результатов следует, что при торможении нагрузка на канат увеличивается по сравнению с нагрузкой при равномерном движении.

Задача № 7

Вагон весом скатывается по колее, которая наклонена к горизонту под углом .

Определить силу торможения вагона , которая вызывается трением колес по рельсам, предполагая, что движение вагона происходит с постоянным ускорением, а также то значение угла , при котором вагон будет скатываться равномерно.

Решение. Изображаем вагон в виде материальной точки в произвольном положении на наклонной плоскости и показываем силы, которые на него действуют (рис.1.7): – сила тяжести вагона; – нормальная реакция рельсов; – сила трения.

Выбираем декартовую систему координат, причем ось направим параллельно рельсам в сторону движения вагона; а ось  – перпендикулярно рельсам.

Запишем уравнение движения вагона в векторной форме:

и спроектируем его на оси выбранной системы координат:

По уравнению (2) определим силу торможения вагона:

По условиям задачи вагон движется с ускорением  которое направлено вдоль оси , то есть .

Если подставим в уравнение (3) , то получим:

Определим значение угла , при котором вагон будет скатываться равномерно. Поскольку

то

где  – коэффициент трения.

Откуда получим

Из этого уравнения вытекает, что при изменении угла , можно найти значение угла, при котором . Если в уравнении (4) присвоить , то

Поскольку известно, что коэффициент трения равен тангенсу угла трения , то

Таким образом, при углу наклона рельсов к горизонту, что равен углу трения , вагон будет скатываться равномерно.

Ответ: 

Задачи, которые рекомендуются для самостоятельной работы: 26.2, 26.8, 26.10, 26.20, 26.24 [2].

Решение задач на тему: Движение материальной точки по криволинейной траектории

При решении задач, связанных с движением точки по криволинейной траектории, если траектория известна, удобно рассматривать движение точки в естественной системе координат  (рис.1.8):

где  – модуль скорости точки,

 – радиус кривизны траектории в заданном положении точки.

В уравнениях (1.6) и (1.8) суммы проекций сил, действующих на точку, на направления осей: касательной (), нормальной () и бинормальной () к  траектории в заданном положении точки.

Порядок решения прямой задачи динамики точки в случае использования уравнений (1.6) и (1.8) совпадает с рекомендациями пунктов 1 и 6 занятия № 1.

Если задано уравнение движения материальной точки по траектории в виде , то для нахождения равнодействующей приложенных к этой точке сил, необходимо сначала найти проекции и полного ускорения точки:

Далее, с уравнений (1.6), (1.7) находим значения касательной и нормальной проекции силы :

Модуль приложенной к материальной точке силы, при естественном способе обозначения движения, будет равен

Задача № 1

Материальная точка массой движется по окружности с радиусом согласно закону

Определить модуль равнодействующей сил, приложенных к материальной точке.

Решение. В задаче движение материальной точки задано естественным способом, поэтому для определения равнодействующей сил воспользуемся зависимостями (1.6) и (1.7):

Определим касательное и нормальное ускорение материальной точки:

Поскольку , то проекция равнодействующей на касательную ось равняется нулю.

Находим нормальную составляющую равнодействующей сил:

Модуль равнодействующей определим из выражения (1.11):

Таким образом, заданное движение материальной точки происходит под действием силы, постоянной по модулю и направленной вдоль радиуса к центру окружности.

Ответ: 

Задача № 2

Материальная точка массой движется по окружности с радиусом согласно закону

Определить проекцию равнодействующей сил, приложенных к материальной точке, на касательную к траектории в момент времени

Решение. Для определения проекции  воспользуемся уравнением (1.6):

Сначала найдем значение скорости материальной точки:

При 

Определяем величину касательного ускорения

при 

Подставив в уравнение (1) значения  и , получим:

Ответ: 

Задача № 3

Материальная точка массой движется по окружности с радиусом согласно закону

Определить модуль равнодействующей сил, действующих на точку, в момент времени

Решение. Поскольку движение материальной точки задано естественным способом, то модуль равнодействующей сил, приложенных к точке, определяется по зависимостям (1.10) и (1.11):

Величины касательного и нормального ускорения материальной точки определяются по уравнениям (1.9):

Учитывая, что скорость точки 

то касательное ускорение точки равно:

Поскольку в момент времени скорость точки:

то нормальное ускорение точки составит:

Определяем и по уравнениям (1.10):

Тогда модуль равнодействующей сил, действующих на материальную точку, равен:

Ответ: 

Задача № 4

На криволинейных участках железнодорожного пути наружный рельс поднимают выше над внутренним (рис.1.9). При движении поезда на этом участке его скорость поддерживают такой, чтобы давление вагона на рельсы было направлено перпендикулярно железнодорожному полотну.

Определить величину повышения внешнего рельса над внутренним при следующих данных: радиус закругления железнодорожного пути , скорость поезда , расстояние между рельсами

Решение. На вагон действуют: сила тяжести , которая направлена вертикально вниз, и реакции рельсов на колеса  и , которые направлены перпендикулярно железнодорожному полотну.

Запишем уравнение движения вагона в векторной форме:

где  – ускорение вагона.

Поскольку движение происходит по криволинейной траектории, то выбираем естественную систему координат: ось направим по нормали к центру кривизны траектории, а ось  – по касательной в сторону движения вагона. Бинормаль, ось , на рис. 1.9 не показано.

Проектируем уравнение движения (1) на ось :

 или 

Из рис. 1.8 видно, что 

Итак, 

Подставив числовые значения известных величин, получаем:

Ответ: 

Задача № 5

Груз весом который подвешен к нитке длиной в неподвижной точке , представляет собой конический маятник (рис.1.10), то есть движется по окружности в горизонтальной плоскости, при этом нитка с вертикалью образует угол ­ .

Определить величину скорости груза и модуль силы натяжения нити .

Решение. Изобразим груз в любом положении и покажем силы, которые на него действуют: силу тяжести , которая направлена вертикально вниз, и натяжение нити , которое направлено к точке подвеса .

Для решения задачи выбираем естественную систему координат: ось  направлена по касательной к окружности в сторону движения груза, ось – по нормали к центру кривизны и ось – вертикально вверх.

Запишем уравнение движения груза в векторной форме:

Проектируем это векторное уравнение на оси координат:

Модуль силы натяжения нити найдем из третьего из уравнений (1), учитывая, что :

Из второго из уравнений (1) найдем , если учесть, что 

Тогда

Откуда

Ответ: 

Задача № 6

Материальная точка весом движется по горизонтальной поверхности под действием силы . В период разгона точки путь, который она проходит, меняется по закону ( – в секундах, – в метрах). Траекторией движения точки на плоскости (рис.1.11) является окружность с радиусом

Определить модуль силы , которая действует, в момент, когда модуль скорости точки равен

Решение. Изобразим точку  в любом положении на окружности (рис.1.11). Покажем силы, действующие на материальную точку: силу тяжести ; реакцию поверхности , которая перпендикулярна поверхности, и заданную силу , которая лежит в плоскости движения точки и направлена в сторону центра кривизны траектории.

С точкой повяжем естественную систему координат. Ось направим по касательной к окружности в сторону движения, а ось – перпендикулярно ей в сторону центра кривизны окружности.

Запишем уравнение движения точки в виде второго закона Ньютона:

Спроектируем это векторное уравнение на оси выбранной системы координат:

Поскольку закон движения известен, то: 

По условиям Найдем момент времени, когда это условие выполняется:

Тогда:

Учитывая, что масса точки равна , находим:

Определяем модуль искомой силы:

Ответ: 

Задача № 7

Радиус закругления моста в точке равен  (рис.1.12).

Определить, с какой силой автомобиль давит на мост в точке , если его масса , а модуль скорости движения

Решение. Рассмотрим автомобиль как материальную точку, поскольку его размерами по сравнению с размерами моста можно пренебречь. Изобразим автомобиль в точке моста (рис.1.12) и покажем силы, которые действуют на него: – силу тяжести автомобиля и – реакцию моста.

Поскольку автомобиль движется по криволинейной траектории, то для решения задачи воспользуемся естественной системой координат .

Запишем уравнение движения автомобиля в векторной форме:

и спроектируем его на оси выбранной системы координат:

 (поскольку  то ),                           (1)

Из уравнения (2) определяем реакцию моста по модулю:

Сила давления  автомобиля на мост равна по модулю реакции моста, но направлена вниз.

Поскольку вес автомобиля равен

то, если мост выпуклый, сила давления автомобиля на него уменьшается по сравнению с тем случаем, когда автомобиль движется по горизонтальному мосту.

Зададим дополнительный вопрос: с какой скоростью должен двигаться автомобиль, чтобы сила давления автомобиля на мост равнялась нулю?

Поскольку , то 

 или

Отсюда

Ответ: 

Задача № 8

Камень весом  который привязан к нитке длиной , описывает окружность в вертикальной плоскости (рис.1.13).

Определить наименьшее значение угловой скорости вращения, при которой нить разорвется, если ее сопротивление разрыву составляет 

Решение. Представим камень в любом положении на дуге окружности. Положение точки определяется углом , который отсчитывается от вертикали в направлении угловой скорости.

На камень (точку ) действуют сила тяжести и сила натяжения нити .

С точкой свяжем естественную систему координат и запишем уравнение движения точки в векторной форме:

Спроектируем это уравнение на оси выбранной системы координат:

Заметим, что , а . То есть уравнение (2) преобразуется в вид:

Отсюда

Из уравнения (3) вытекает, что при угловая скорость  является только функцией угла . Наименьшее значение , когда нить разрывается, будет при , то есть, когда , что соответствует положению камня в точке . Таким образом:

Ответ: 

Задача № 9

Трек для испытания автомобилей на кривых отрезках пути имеет виражи, профиль которых (рис.1.14) в поперечном пересечении является прямой, которая наклонена к горизонту так, что внешний край трека выше внутреннего.

Определить, с какой наименьшей и самой большой скоростью можно ехать по виражу, имеющему радиус кривизны и угол наклона к горизонту ­? Коэффициент трения шин о поверхность трека считать известным.

Решение. На автомобиль, который движется по виражу, действуют: сила тяжести , сила нормального давления со стороны поверхности виража и сила трения , которая направлена вдоль поверхности виража в плоскости, которая перпендикулярна направлению скорости. Возникновение силы трения обуславливается трением колес автомобиля о поверхность виража.

Рассмотрим движение центра тяжести автомобиля (точка ), считая, что все силы приложены к этой точке. Первым рассмотрим случай движения автомобиля, когда сила трения (рис.1.14, а). С точки  повяжем естественную систему координат : нормаль направим в центр кривизны, – перпендикулярно .

Запишем уравнение движения автомобиля в векторной форме:

и спроектируем это уравнение на оси координат и :

Из уравнения (1) найдем величину нормальной реакции :

Подставим найденное значение в уравнение (2) и определим скорость автомобиля, когда сила трения о поверхность трека равна нулю:

При максимальной скорости автомобиля сила трения направлена к нижнему краю виража (рис.1.14, б) и равняется

Векторное уравнение движения автомобиля в этом случае будет иметь вид:

Проектируем уравнение (4) на оси :

Уравнение (5) перепишем в виде:

откуда

Подставим значение в уравнение (6) и определим максимальное значение скорости :

Отсюда:

Если скорость автомобиля минимальная  (рис.1.14, в), то трение направлено к верхнему краю трека и проекции уравнения (4) на оси будут иметь вид:

Из уравнений (8) и (9) получаем:

Ответ: 

Услуги по теоретической механике:

1. Заказать теоретическую механику
2. Помощь по теоретической механике
3. Заказать контрольную работу по теоретической механике

Учебные лекции:

1. Статика
2. Система сходящихся сил
3. Момент силы
4. Пара сил
5. Произвольная система сил
6. Плоская произвольная система сил
7. Трение
8. Расчет ферм
9. Расчет усилий в стержнях фермы
10. Пространственная система сил
11. Произвольная пространственная система сил
12. Плоская система сходящихся сил
13. Пространственная система сходящихся сил
14. Равновесие тела под действием пространственной системы сил
15. Естественный способ задания движения точки
16. Центр параллельных сил
17. Параллельные силы
18. Система произвольно расположенных сил
19. Сосредоточенные силы и распределенные нагрузки
20. Кинематика
21. Кинематика твердого тела
22. Движения твердого тела
23. Динамика механической системы
24. Динамика плоского движения твердого тела
25. Динамика относительного движения материальной точки
26. Динамика твердого тела
27. Кинематика простейших движений твердого тела
28. Общее уравнение динамики
29. Работа и мощность силы
30. Обратная задача динамики
31. Поступательное и вращательное движение твердого тела
32. Плоскопараллельное (плоское) движение твёрдого тела
33. Сферическое движение твёрдого тела
34. Движение свободного твердого тела
35. Сложное движение твердого тела
36. Сложное движение точки
37. Плоское движение тела
38. Статика твердого тела
39. Равновесие составной конструкции
40. Равновесие с учетом сил трения
41. Центр масс
42. Колебания материальной точки
43. Относительное движение материальной точки
44. Статические инварианты
45. Дифференциальные уравнения движения точки под действием центральной силы и их анализ
46. Динамика системы материальных точек
47. Общие теоремы динамики
48. Теорема об изменении кинетической энергии
49. Теорема о конечном перемещении плоской фигуры
50. Потенциальное силовое поле
51. Метод кинетостатики
52. Вращения твердого тела вокруг неподвижной точки

80

Механические
и электромагнитные колебания и волны

Основные формулы

Уравнение гармонических колебаний
Соотношение между периодом, частотой и круговой (циклической) частотой
Скорость точки при гармонических колебаниях
Ускорение точки при гармонических колебаниях
Сила, действующая на колеблющуюся материальную точку
Полная энергия колеблющейся материальной точки
Период колебаний математического маятника
Период колебаний пружинного маятника
Длина волны
Уравнение плоской волны
Скорость света в среде
Связь между разностью фаз и разностью хода
Период колебаний идеального колебательного контура

Примеры решения
задач

Пример 1.
Написать уравнение гармонического
колебания материальной точки с амплитудой
А
= 0,1 м, периодом Т
= 2 с и начальной
фазой φ₀
= 0. Найти амплитудные значения скорости
υ_max
и ускорения
а_max;
скорость υ
и ускорение
а
в момент времени t
= 1/6 c.
Построить графики зависимости смещения,
скорости и ускорения от времени.

Дано: А = 0,1 м; Т = 2 с; φo = 0; t = 1/6 c. Найти: υmax; аmax; υ; а.

Решение:
Запишем уравнение гармонического
колебания в виде:

.
(1)

Скорость материальной
точки равна производной от смещения по
времени:

.

(2)

Отсюда максимальная
скорость

.
(3)

Ускорение
определяется как производная от скорости
точки по времени:

.
(4)

Амплитудное
значение ускорения

.
(5)

Подставляя числовые
значения в (1), (3) и (5), получим:
,

,

.

Проведя
вычисления по формулам (2) и (4), найдём
значения скорости и ускорения в момент
времени t
= 1/6 с:

,
.

Рис. 1

На
рис.1 представлены графики зависимости
смещения, скорости и ускорения от времени
для материальной точки, совершающей
гармоническое колебание при начальной
фазе _
= 0.

Ответ:
x
= 0,1cоsπ∙t;
_max
= 0,3 м/с; а_max
=
1 м/с²;

= –0,16 м/с;
а
=
– 0,85 м/с².

Пример
2.
Материальная точка массой m
= 10 г колеблется по закону x
= 0,05sin6t.
Найти максимальную силу, действующую
на точку, и её полную энергию. Построить
графики зависимости потенциальной,
кинетической и полной энергий от времени.

Дано: m = 10 г = 10-2 кг; x = 0,05sin6t. Найти: Fmax; W.

Решение:
Модуль
силы, действующей на точку, совершающую
гармонические колебания, найдём по
второму закону Ньютона

F
= ma,
(1)

где
a
= ²x–
ускорение материальной точки.

Отсюда

F
= m²x
= mA²
sint.

(2)

Максимальная сила

.
(3)

По
условию задачи А
= 0,05 м, 

= 6 рад/c,
следовательно

.

Кинетическая
энергия гармонически колеблющейся
точки

.
(4)

В
процессе гармонических колебаний сила
изменяется пропорционально смещению,
поэтому в каждый момент времени
потенциальная энергия материальной
точки

,
(5)

где k
= m²
– постоянный коэффициент для данной
системы.

Полная
энергия колебаний определяется по
формуле

.
(6)

Отсюда
найдём
.

Для
построения графиков определим период
колебаний материальн
ой
точки
.

Рис.
2. Графики зависимости смещения,
потенциальной, кинетической и полной
энергий от времени при гармонических
ко-лебаниях (_
=
0)

Из
графиков (рис. 2) и формул (3) и (4) следует,
что W_п
и
W_к
изменяются в противофазе, с частотой в
2 раза большей, чем частота колебаний
материальной точки, а полная энергия W
= W_п
+ W_к

с течением времени не изменяется.

Ответ:
F_max
= 18 мН; W
= 0,45 мДж.

Пример
3. Как
изменится период колебаний математического
маятника при переносе его с Земли на
Луну?

Дано: Мз = 5,98· 1024 кг; Мл = 7,33·1022 кг; Rз= 6,37·103 км = 6,37 ·106 м; Rл= 1,74·103 км = 1,74·106 м. Найти: Тз / Тл.

Решение:
Периоды колебаний математического
маятника на Земле и на Луне соответственно
равны

и

,
(1)
где g_з,
g_л
– ускорения свободного падения на
поверхности Земли и Луны, l
– длина маятника.

Из
закона всемирного тяготения находим
ускорения g_з
и
g_л

;

,
(2)

где
G
–
гравитационная постоянная.

Найдём
отношение периодов колебаний маятника

.
(3)

Подставив
числовые данные в (3), получим:
.

Ответ:
Период
колебаний маятника на Луне больше, чем
на Земле,
в 2,5 раза.

Пример
4.
Цилиндр высотой h
= 10 см, плотность материала которого 
= 0,8·10³
кг/м³,
плавает в воде (рис. 3). Если его погрузить
в воду несколько глубже, а затем отпустить,
то цилиндр начнёт совершать колебания
около положения равновесия. Считая
колебания цилиндра гармоническими и
незатухающими, определить период Т
его колебаний.

Дано: h = 10 см = 0,1 м;  = 0,8·103 кг/м3; в = 103 кг/м3. Найти: Т.

Р ис. 3

Решение:
В задаче рассматриваются незатухающие
колебания, поэтому силами сопротивлений
можно пренебречь. На плавающий цилиндр
действуют сила тяжести
,
направленная вертикально вниз, и сила
Архимеда
,
направленная вертикально вверх. Сила
тяжести при колебаниях цилиндра
постоянна, а архимедова сила меняется,
так как зависит от объёма его погружённой
части.

Когда
цилиндр плавает, колебания не наблюдаются,
следовательно, векторная сумма сил
равна нулю:

.

Выбрав
вертикальную ось координат и проецируя
на неё эти силы, получим

или
,
(1)

где V
= S·x_
– объём погружённой части цилиндра в
положении равновесия; S
– площадь поперечного сечения; x_
– глубина погружения.

Масса
цилиндра

m
= ·S·h.
(2)

Небольшое
погружение цилиндра в воду на некоторую
глубину Δх
относительно положения равновесия
приводит к увеличению объёма погружённой
части

V
= S(x_
+ Δx).

Архимедова
сила увеличится

F_A=
_в·gS(·x
+ Δx).

В
результате равновесие нарушится,
следовательно, равнодействующая сила

F
= mg
– F‘_A.

С
учётом (1)

.
(3)

Цилиндр
совершает гармонические колебания
только в том случае, если сила в процессе
колебаний изменяется пропорционально
смещению Δх
и направлена к положению равновесия:

.
(4)

Сравнивая
выражения (3) и (4), находим

. (5)

Если
колебания совершаются под действием
силы, изменяющейся по закону (4), то
независимо от природы этой силы период
колебаний

.
(6)

Подставив
выражения (2) и (5) в формулу (6), получим:

. (7)

Период
колебаний цилиндра
.

Ответ:
Т
= 0,56 с.

Пример
5.
Звуковые колебания, имеющие частоту 
= 0,5
кГц и амплитуду А
=
0,25 мм, распространяются в воздухе со
скоростью

=
340 м/с. Определить длину волны ,
фазу 
колебаний,
смещение (х,t)
и
скорость

частиц среды, отстоящих на расстоянии

х₁
= 0,4 м от источника волн в момент времени
t
= 2 мс.

Дано:  = 0,5 кГц = 500 Гц; А = 0,25 мм = 0,25·10-3 м;  = 340 м/с; х1 = 0,4 м; t = 2 мс. Найти: ;  ; ; .

Р ис. 4

Решение:
Длина
волны 
равна расстоянию, на которое распространяется
колебание за один период (рис. 4):

.
(1)

Подставляя
значения величин 
и ,
получим:
.

Уравнение
плоской волны:

,
(2)

где 
–
смещение колеблющихся частиц, находящихся
на расстоянии х
от источника; 
– скорость распространения волны.

Фаза
колебаний частиц с координатой х₁
= 0,4 м в момент времени
t
=
2 мс определяется выражением

.
(3)

Взяв
производную от смещения по времени,
находим скорость
:

.
(4)

Подставив
значения величин в выражения (2), (3), (4),
в момент времени t
= 2 с для частиц среды с координатой х
= 0,4 м получим:

фазу
колебаний

или

= 148 º;

смещение

;

скорость
.

Ответ:

= 0,68 м; 
=
2,58 рад; 
= 0,21 мм;
.

Пример
6. Волны
частотой ν
= 0,5 кГц распространяются со скоростью

=
400 м/с. Чему равна разность фаз двух точек
волны, если они удалены друг от друга
на расстояние Δr
= 0,2 м и лежат на прямой, перпендикулярной
фронту волны?

Дано:  =400 м; ν = 0,5 кГц = 500 Гц; Δr = 0,2 м. Найти: Δ.

Решение:
Если две точки волны удалены друг от
друга на расстояние, равное длине волны
,
то разность фаз между ними равна 2.
Следовательно, если точки отстоят друг
от друга на
Δr,
то разность фаз этих точек найдём по
формуле

.
(1)

Длина
волны .
(2)

Из (1)
и (2) следует

Ответ:
Δ

=
0,5
рад.

Пример
7.
Длина волны красного света в вакууме
(воздухе)
₁
= 0,7 мкм. Какой будет длина волны
₂
и её скорость 
распространения
в воде? Какой цвет видит человек, открывший
глаза в воде?

Дано: 1 = 0,7 мкм = 0,7·10-6 м; с =3·108 м/с; п = 1,33. Найти: 2; .

Решение:
По определению абсолютный показатель
преломления среды показывает, во сколько
раз скорость света в вакууме больше
скорости света в данной среде:

,


(1)

где с
– скорость света в вакууме; 
– скорость света в среде.

Из
формулы (1) находим скорость распространения
света в воде:
.

Длина
волны света в вакууме
. (2)

Длина
волны в среде
(3)

Следовательно,
.

Воспринимаемый
глазом цвет излучения зависит от частоты
света, которая при переходе света из
одной среды в другую не меняется. В воде
человек увидит красный цвет.

Ответ:

= 2,25·10⁸
м/с; ₂
= 0,53 мкм.

Пример
8. На
какой диапазон длин
волн и
частот
можно настроить колебательный контур
радиоприёмника, если в контур включены
катушка переменной индуктивности от
L₁
= 0,5 мкГн до L₂
= 10 мкГн и конденсатор переменной ёмкости
от С₁
= 10 пФ до С₂
=
500 пФ. Активным сопротивлением контура
пренебречь.

Дано: L1 = 0,5 мкГн = 0,5·10-6 Гн; L2 = 10 мкГн = 10-5 Гн; С1 = 10 пФ = 10-11 Ф; С2 = 500 пФ = 5·10-10 Ф;  = 3·108 м/с. Найти: от 1 до 2; от 1 до2.

Решение:
Длина волны

связана с периодом колебаний Т
следующим соотношением:

 =
·Т,
(1)

где 
=
3·10⁸
м/с
–
скорость распространения электромагнитных
волн в вакууме.

Период
колебаний идеального колебательного
контура определяется по формуле

.
(2)

Минимальная
длина волны диапазона

,
(3)

Длине
волны ₁

соответствует
максимальная частота

.
(4)

Максимальная длина
волны диапазона

,
(5)

ей соответствует
минимальная частота

. (6)

Подставив
числовые значения величин в формулы
(3), (4), (5), (6), получим: ,
,

,
.

Ответ:
₁
= 0,2 м; ₂
= 2,1 м; ₁
= 15∙10⁸
Гц; ₂
= 1,43∙10⁸
Гц.

Пример
9. Маленький
шарик подвешен на нити длиной l
=
1 м к потолку вагона. При какой скорости
вагона шарик будет особенно сильно
раскачивается под действием ударов
колёс о стыки рельсов? Длина рельсов s
= 12,5 м.

Дано: l = 1 м; s = 12,5 м. Найти: .

Решение: Шарик
совершает вынужденные колебания, которые
вызваны ударами колёс вагона о стыки
рельсов. Частота 
вынуждающей
силы равна:

,
(1)

где 
– скорость движения вагона.

Размеры
шарика малы по сравнению с длиной нити,
поэтому период его колебаний определим
как для математического маятника:

.

Частота собственных
колебаний шарика

. (2)

Амплитуда
вынужденных незатухающих колебаний
максимальна в случае резонанса, когда

(3)

Подставляя
в условие (3) выражения (1) и (2), найдём

,

откуда

.

С
учётом числовых значений
.

Ответ:

= 6,2 м/с.

Пример
10.
На гладком горизонтальном столе лежит
шар массой
М
= 240 г, прикреплённый к невесомой пружине,
жёсткость которой
k
= 40 кН/м. Другой конец пружины закреплён.
В шар попадает пуля массой m
= 10 г, имеющая в момент удара скорость
₁
= 400 м/с, направленную вдоль оси пружины
(рис. 5). Пуля застревает в шаре. Определить
амплитуду колебаний шара.

Дано: М =240 г = 24·10-2 кг; k = 40 кН/м = 40·103 Н/м; m =10 г = 10-2 кг; 1 = 400 м/с. Найти: А.

Р ис. 5

Решение:
Скорость шара ₂
после
неупругого удара (рис. 5а ) определяется
из закона сохранения импульса:

, (1)

откуда

. (2)

В
момент соударения пуля сообщает шару
кинетическую энергию, вследствие чего
шар и пуля начинают сжимать пружину.
Сжатие пружины будет продолжаться до
тех пор, пока вся кинетическая энергия
движения шара и пули Е₁
не перейдёт в потенциальную энергию
деформации пружины Е₂.
Согласно закону сохранения энергии

Е₁
= Е₂. (3)

В
начальный момент движения энергия
колеблющейся системы

Е₁
=
Е_ш
+Е_пр
+Е_п,

где
Е_ш,
Е_пр,
Е_п
–
энергии шара, пружины, пули, соответственно.

Учитывая,
что в начале пружина не деформирована,
то есть Е_пр
=
0, а шар и пуля движутся со скоростью
₂,
находим

. (4)

Потенциальная
энергия пружины достигнет максимума,
когда кинетическая энергия шара и пули
станет равной нулю (рис. 5б). При этом
смещение шара и пули от положения
равновесия будет максимальным:

Е_ш
=
0, Е_п
=
0,

.

Следовательно,
энергия системы тел

.
(5)

Подставляя
(4) и (5) в (3), получим

(6)

С
учётом (2) имеем

.
(7)

Из
уравнения (7) амплитуда колебаний шара
А
равна:

.
(8)

Подставим
в (8) значения величин и вычислим:

.

Ответ:
А
= 4 см.

Соседние файлы в папке Физика_Шилова

• #
• #
• #
• #
• #
• #
• #
• #

Уравнение колебаний материальной точки имеет вид найти максимальную силу

Гармоническое колебательное движение и волны

Уравнение колебаний материальной точки массой m = 10 г имеет вид Найти максимальную силу F _max, действующую на точку, и полную энергию W колеблющейся точки.

Дано:

m = 10 г = 10·10 -3 кг

Решение:

По второму закону Ньютона

Уравнение колебаний запишем в виде

Скорость колеблющейся точки

Ускорение колеблющейся точки

Уравнение колебаний силы

Полная энергия W колеблющейся точки

Уравнение колебаний материальной точки массой 20 г имеет вид х = 5sin(πt/5+π/4) см.

Готовое решение: Заказ №10195

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Физика

Дата выполнения: 16.11.2020

Цена: 227 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Уравнение колебаний материальной точки массой 20 г имеет вид х = 5sin(πt/5+π/4) см. Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки

Смещение точки при гармонических колебаниях:

где А=5 см=0,05 м – амплитуда колебаний,

j0= π/4 рад- начальная фаза,

w= π/5 рад/с- циклическая частота.

Скорость при гармонических колебаниях: .

Изучите химию на странице ➔ решение заданий и задач по химии.

• Азот массой 200 г расширяется изотермически при температуре 280 К, причем объем газа увеличивается в два раза.
• Чему равно изменение энтропии при протекании следующих процессов: а) изобарическом нагревании 0,1 кг азота от 0 до 125оС.
• Две материальные точки движутся согласно уравнениям: х1 = 4t + 8t2 – 16t3 и х2 = 2t – 4t2 + t3.
• Обруч катится по горизонтальной дороге со скоростью 18 км/ч. На какое расстояние он может вкатиться по наклонной плоскости за счет кинетической энергии.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Матереальная точка массой m = 10 г колеблется по закону x = 0, 05sin(0, 6t + 0, 8)?

Физика | 10 – 11 классы

Матереальная точка массой m = 10 г колеблется по закону x = 0, 05sin(0, 6t + 0, 8).

Найти модуль максимальной силы действующей на точку и полную энергию или энергию колеблющейся точке.

Максимальная сила равна произведению максимального ускорения – а = w ^ 2A на массу, амплитуда равна 0.

05, циклическая частота 0.

k = mg / A = 2 H / m ;

Материальная точка массой 10 г колеблется согласно уравнению х = 5cos(pi / 5 * t + pi / 4) см?

Материальная точка массой 10 г колеблется согласно уравнению х = 5cos(pi / 5 * t + pi / 4) см.

Найти максимальную силу, действующую на точку и полную энергию колеблющейся точки.

Материальная точка массой 1, 25 совершает колебания по закону x = cos(2t + п / 4) (м) Найдите максимальную силу действующую на точку (Н)?

Материальная точка массой 1, 25 совершает колебания по закону x = cos(2t + п / 4) (м) Найдите максимальную силу действующую на точку (Н).

Уравнение колебаний материальной точки массой 10 г?

Уравнение колебаний материальной точки массой 10 г.

Имеет вид x = 5cos( / 5 * t).

Определить максимальную силу, действующую на материальную точку и полную энергию колебаний.

Полная энергия точки, совершающая гармоническое колебания, равна 3 * 10 – 5дж, максимальная сила, действующая на точку, равна 1, 5 * 10 – 3н?

Полная энергия точки, совершающая гармоническое колебания, равна 3 * 10 – 5дж, максимальная сила, действующая на точку, равна 1, 5 * 10 – 3н.

Написать уравнение колебательного движения точки, если период колебания 2с, а начальная фаза равна 600.

Маятник совершает колебания от точки 1 до точки 3?

Маятник совершает колебания от точки 1 до точки 3.

В точке 1 полная механическая энергия равна 5 Дж.

Чему равна полная энергия в точке2?

Чему равна полная энергия колеблющегося тела в любой точки траектории?

Чему равна полная энергия колеблющегося тела в любой точки траектории?

Материальная точка массой 10 грамм колеблется по закону x = 0?

Материальная точка массой 10 грамм колеблется по закону x = 0.

8) Найдите максимальную силу действующую на точку и полную энергию колеблющейся точки.

Груз массой 470 г колеблется на пружине жесткостью 56 Н / м с амплитудой 4, 2 см?

Груз массой 470 г колеблется на пружине жесткостью 56 Н / м с амплитудой 4, 2 см.

Найти : 1) полную механическую энергию ; 2)потенциальную энергию в точке с координатой 2, 1 см ; 3) кинетическую энергию в этой точке ; 4) скорость прохождения грузом этой точки.

На какую максимальную высоту от положения равновесия может подняться повышенная на нити колеблющаяся материальная точка массой 2 кг, если ее полная энергия равна 64 Дж?

На какую максимальную высоту от положения равновесия может подняться повышенная на нити колеблющаяся материальная точка массой 2 кг, если ее полная энергия равна 64 Дж.

Колебания точки массой 10г заданы уравнением х = 5 * 10 ^ ( – 2) sin0, 5t (м) Определить : силу , действующую на точку в момент времени t = 2 c ; полную энергию точки?

Колебания точки массой 10г заданы уравнением х = 5 * 10 ^ ( – 2) sin0, 5t (м) Определить : силу , действующую на точку в момент времени t = 2 c ; полную энергию точки.

На этой странице находится вопрос Матереальная точка массой m = 10 г колеблется по закону x = 0, 05sin(0, 6t + 0, 8)?. Здесь же – ответы на него, и похожие вопросы в категории Физика, которые можно найти с помощью простой в использовании поисковой системы. Уровень сложности вопроса соответствует уровню подготовки учащихся 10 – 11 классов. В комментариях, оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С ними можно обсудить тему вопроса в режиме on-line. Если ни один из предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой строке, расположенной вверху, и нажмите кнопку.

[spoiler title=”источники:”]

http://natalibrilenova.ru/uravnenie-kolebanij-materialnoj-tochki-massoj-20-g-imeet-vid-h–5sint54-sm-/

http://fizika.my-dict.ru/q/5274221_materealnaa-tocka-massoj-m-10-g/

[/spoiler]

Страница 1 из 4

12.1. Написать уравнение гармонического колебательного движения с амплитудой A = 5см, если за время t = 1мин совершается 150 колебаний и начальная фаза колебаний φ = P/4. Начертить график этого движения.

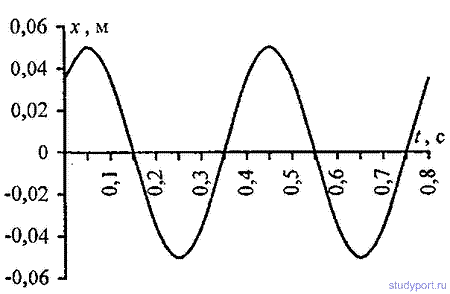
12.2. Написать уравнение гармонического колебательного движения с амплитудой A = 0,1M, периодом T = 4с и начальной фазой φ = 0.

12.3. Написать уравнение гармонического колебательного движения с амплитудой A = 50мм, периодом T = 4с и начальной фазой φ = P/4 . Найти смещение х колеблющейся точки от положения равновесия при t = 0 и t= 1,5 с. Начертить график этого движения.

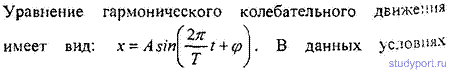
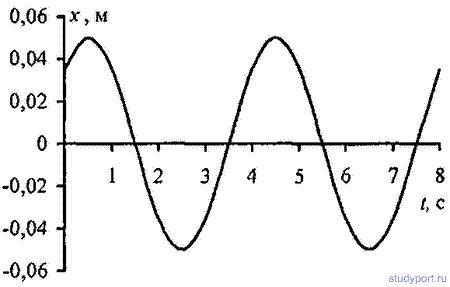
12.4. Написать уравнение гармонического колебательного движения с амплитудой А = 5 см и периодом Т = 8 с, если начальная фаза φколебаний равна: а) 0; б) P/2; ^в) P ^г) 3P/2 д) 2P. Начертить график этого движения во всех случаях.

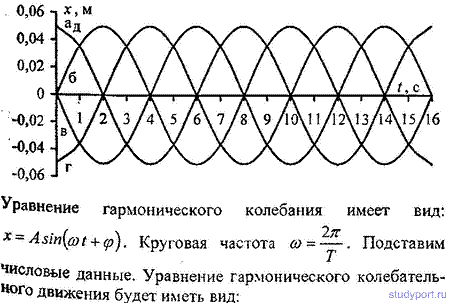
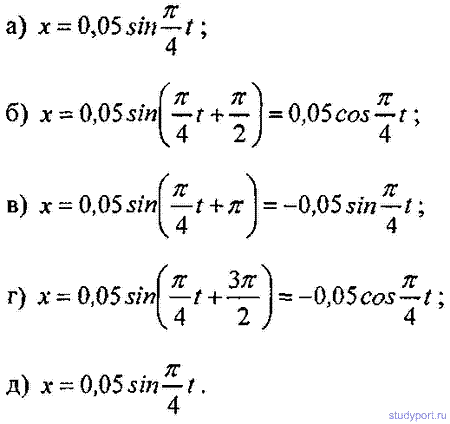
12.5. Начертить на одном графике два гармонических колебания с одинаковыми амплитудами A₁ = А₂ = 2 см и одинаковыми периодами T₁ = Т₂ = 8 с, но имеющие разность фаз φ₂–φ₁,

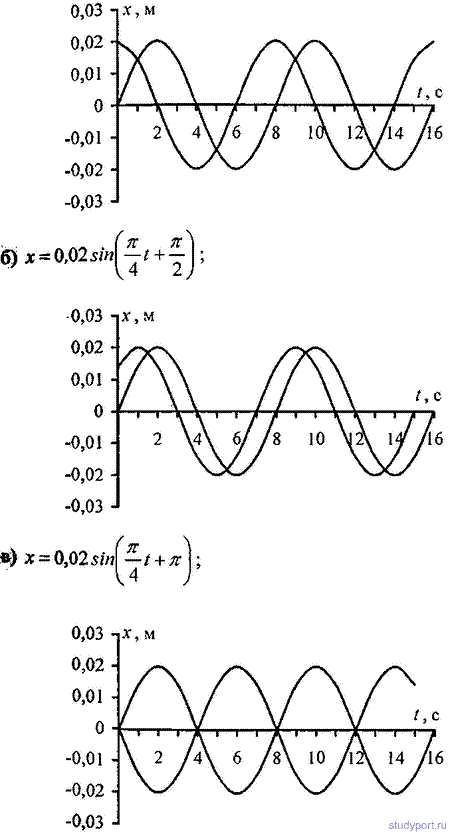
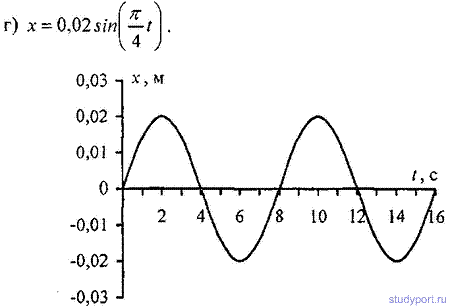
равную: а) P/4; о) P/2; в) P; г) 2P.

12.6. Через какое время от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ = 0.

12.7. Начальная фаза гармонического колебания φ= 0. Через какую долю периода скорость точки будет равна половине ее максимальной скорости?

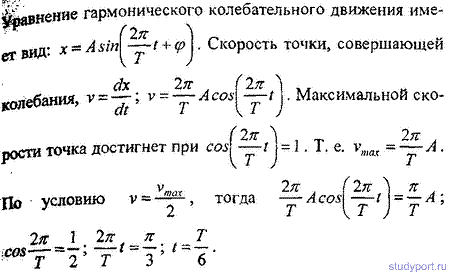
12.8. Через какое время от начала движения точка, совершающая колебательное движение по уравнению х = 7 sinP/2*t, проходит путь от положения равновесия до максимального смещения?

12.9. Амплитуда гармонического колебания /4 = 5 см, период Г = 4с. Найти максимальную скорость v_mat колеблющейся _Точ кн и ее максимальное ускорение a_тах.

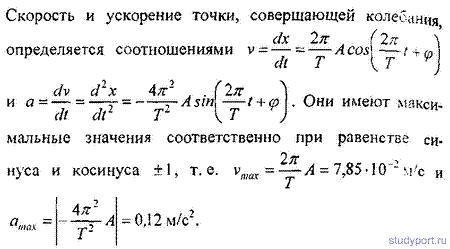
12.10. Уравнение движения точки дано в виде х = 2si>i^( ^{+ СМ}‘ ^^{аити пе}Р^П0‘^а колебаний Г, максимальную скорость >_тах и максимальное ускорение a_та точки.

t2.ll. Уравнение движения точки дано в виде x = sin—t. > 6

ahftm моменты времени /, в которые достигаются максималь-

^шГскорость и максимальное ускорение.

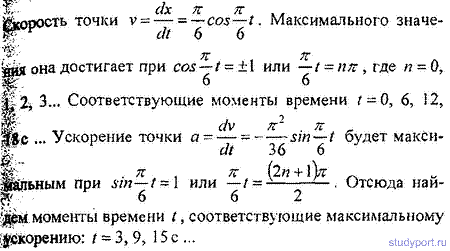
12.12. Точка совершает гармоническое колебание. Период колебаний Т = 2 с, амплитуда А = 50 мм, начальная фаза <р = 0. .$айти скорость v точки в момент времени, когда смешение точ-^;виот положения равновесия х = 25 мм.

12.13. Написать уравнение гармонического колебательного ^юкения, если максимальное ускорение точки a_тах =49,3 см/с²,

период колебаний T = 2с и смещение точки от положения равновесия в начальный момент времени х₀ = 25 мм.

12.14. Начальная фаза гармонического колебания φ= 0 . При смещении точки от положения равновесия х₁ = 2,4 см скорость точки v₁ = 3 см/с, а при смещении x₂ = 2,8 см ее скорость v₂ = 2 см/с. Найти амплитуду А и период Т этого колебания.

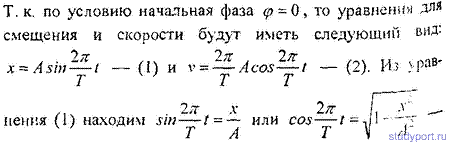
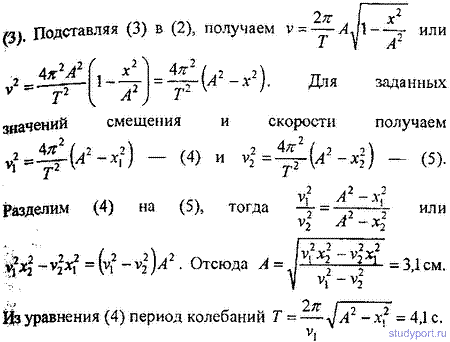
12.15. Уравнение колебания материальной точки массой

m=16г имеет вид х = 0,1 sin(P/8*t+P/4)- Построить график

зависимости от времени t ( в пределах одного периода) силы F, действующей на точку. Найти максимальную силу F_max.

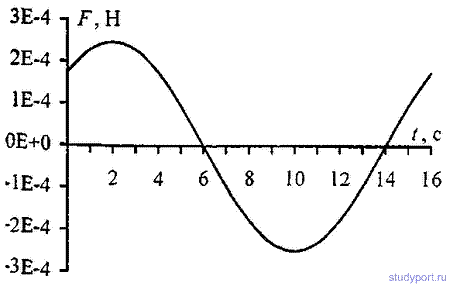
12.16. Уравнение колебаний материальной точки массой

m=10г имеет вид x=5sin(P/5*t+P/4) см. Найти максимальную силу F_mix, действующую на точку, и полную энергию Wколеблющейся точки.

12.17. Уравнение колебания материальной точки массой

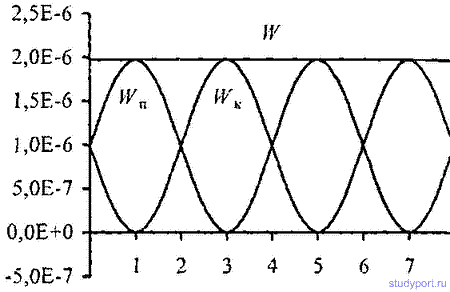
m=16г имеет вид х = 2sin(P/4*t+P/4) см. Построить график зависимости от времени t ( в пределах одного периода) кинетической W_K, потенциальной W„ и полной W энергии ТОЧКИ.

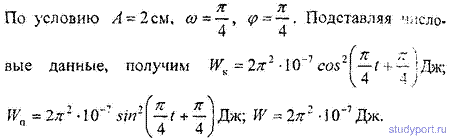
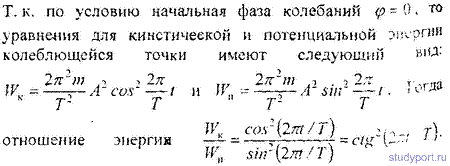
12.18. Найти отношение кинетической W_K энергии точки, совершающей гармоническое колебание, к ее потенциальной энергии W_n для моментов времени: a) t = T/12; б) t=T/8 в) t= T/6 . Начальная фаза колебаний φ= 0.

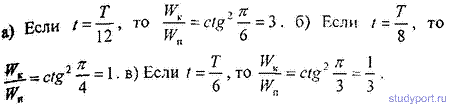
12.19. Найти отношение кинетической энергии W_K точки, совершающей гармоническое колебание, к ее потенциальной энергии W_a для моментов, когда смещение точки от положения равновесия составляет: а) х = A/4; б) х = A/2 ; в) х = А , где А — амплитуда колебаний.

12.20. Полная энергия тела, совершающего гармоническое колебательное движение, W=30 мкДж; максимальная сила, действующая на тело, F_mm. = 1,5 мН. Написать уравнение движения этого тела, если период колебаний Т = 2с и начальная фаза φ=P/3